Introduction

In recent years mechanical ventricular dyssynchrony has become an important clinical parameter, as it may indicate the effectiveness of cardiac resynchronization therapy (CRT) in heart failure patients [1–5]. Additionally, several studies have demonstrated that ventricular dyssynchrony can be used as an independent predictor for adverse cardiac events [6, 7].

Ventricular dyssynchrony can be quantified by a range of imaging modalities, such as echocardiography, magnetic resonance imaging (MRI) and nuclear imaging techniques [8–11]. Despite the large base of evidence and the widespread availability of echocardiography, it is also highly user dependent. Radionuclide ventriculography has been used to study inter- and intraventricular dyssynchrony and has proven to be a reproducible and precise technique [5]. Still, this nuclear technique only provides functional information on the contractility. MRI and nuclear perfusion imaging are not only reproducible but also incorporate pathophysiological information on left ventricular function and the location of myocardial scarring. These factors were found to be additive to the dyssynchrony analysis in the prediction of CRT response [12, 13]. Even so, MRI has some important disadvantages such as limited availability, complicated image analysis and incompatibility with cardiac devices [10, 11]. Nuclear imaging techniques, and gated single photon emission computed tomography (SPECT) myocardial perfusion imaging (MPS) in particular, are generally used in daily clinical practice and have the ability to quantify cardiac perfusion in relation to regional cardiac function.

With the introduction of automated algorithms by Emory Cardiac Toolbox (ECTb) [14] gated MPS has become a valid tool for dyssynchrony analysis. This count-based algorithm, which determines myocardial contraction based on the time-activity relation, is already applied in several MPS dyssynchrony studies [3, 15–21]. More recently, Corridor4DM also implemented an automated tool which uses geometrical algorithms, rather than count-based methods, to quantify ventricular dyssynchrony. This method of automated dyssynchrony detection has not previously been evaluated in clinical patients. Therefore, the aim of this study was to assess the feasibility of this geometrical dyssynchrony method in clinical patients with a normal MPS. Subsequently, the results of this normal population were compared to patient data with proven ventricular dyssynchrony to assess the discriminatory value of the geometrical method.

Materials and methods

Patient selection

For this retrolective study patients with a normal MPS were selected. The MPS acquisition was considered normal when no significant perfusion defects were present (summed stress score ≤2 and summed rest score ≤2, visually confirmed by an expert reviewer) and left ventricular ejection fraction (LVEF) was 55–80% [22, 30]. In all acquisitions image quality had to be optimal, which implies that there was no patient movement, triggering problems or subdiaphragmatic tracer uptake overlapping the myocardial wall. Patients with arrhythmias on electrocardiogram (ECG) or implantable cardiac devices were also excluded. Equally sized groups were created for the post-stress MPS (male physical stress, male adenosine stress, female physical stress, female adenosine stress), so it was also possible to assess the impact of stress induction on the dyssynchrony parameters. All MPS studies were part of standard clinical care and the retrolective nature of the study exempted the need for an Institutional Review Board waiver.

For comparison, patients with congestive heart failure and proven cardiac dyssynchrony on MRI (septal to lateral delay >30 ms, methods described in [22]) were included. All heart failure patients had a New York Heart Association scale II–IV under optimal cardiac medication. The MRI acquisition protocols, image processing techniques and the results have previously been reported by Marsan et al. [22].

Data acquisition

Patients underwent a 2-day stress/rest MPS protocol, with post-stress acquisition on the first day. Stress was induced by physical exercise limited by symptoms or when contraindications to exercise were present by intravenous infusion of adenosine (140 μg kg−1 min−1) for 6 min. At peak exercise, or in the third minute of adenosine infusion, an average dose of 500 MBq 99mTc-tetrofosmin was injected. Post-stress and rest images were made approximately 45 min after tracer administration. Projections were acquired using a dual-head gamma camera equipped with a low-energy high-resolution collimator over 180° (6° per step, 40 s per projection). ECG gating was applied at 16 frames per cardiac cycle, with a tolerance window of 50%. The data were pre-filtered with a low-pass Butterworth filter (8th order, cutoff frequency 0.26 cycles/pixel) and reconstructed using filtered backprojection to yield short-axis images. No attenuation or scatter correction was applied. Acquisitions were post-processed with the Corridor4DM software package (Version 6.1, INVIA Solutions, Ann Arbor, MI, USA) [23].

Contraction analysis

Initial localization of the endocardial and epicardial borders by Corridor4DM is performed based on gradient operators and predefined information on shape, location and continuity of the ventricular wall. Using a cylindrical-spherical sampling structure intensity profiles are created contained by the endocardial and epicardial boundaries [24, 25]. Refined surface estimates are determined by a set of one- and two-dimensional weighted splines. A Gaussian function is applied to the intensity profiles contained by these new surface estimates to locate peak myocardial activity. The full-width at half-maximum (FWHM) of the Gaussian is utilized to produce the myocardial thickness and is scaled to an average thickness of 10 mm in end diastole for gated studies [24, 25]. In the other frames myocardial thickness is scaled with preservation of the myocardial mass [24, 25]. The resulting endocardial and epicardial borders are used to calculate the time-volume curve.

Polar maps are constructed by radial sampling of 460 sectors within the myocardial volume (bounded by the cardiac borders) at each gating interval. The perfusion maps are based on the maximal count value within each sector. Wall thickening, which is based on these perfusion maps, is defined as the difference between the maximum count value occurring within a sector during the cardiac cycle and the count value at end diastole [25].

Wall motion is based on a adapted implementation of the centerline technique [26, 27]. A midline is positioned between the endocardial surface at end diastole and end systole (see Fig. 1). Perpendicular to this midline, normal vectors are placed connecting corresponding sectors in the end-diastolic and end-systolic frame. Maximal motion of a sector is defined as the absolute length of a vector between the end-systolic and end-diastolic positions of that segment and is depicted in millimetres. The time to peak motion is used to describe the timing of ventricular contraction patterns. The moment of peak motion in a sector is defined as the percentage of the cardiac cycle at which the motion vector is maximal (% RR cycle).

Fig. 1
figure 1

A diagram illustrating the generation of the endocardial model for the end-diastolic and end-systolic phases. The endocardial border of the myocardium in end diastole (red) and end systole (blue) is determined and used to position a centerline (black dashed line). Based on this, centerline perpendiculars (grey) are drawn between equivalent segments on the endocardial border in different frames during the cardiac cycle. The distance between two connectors is the maximal motion

Full size image

In this study LVEF, end-diastolic volume (EDV), end-systolic volume (ESV), mean wall motion and mean wall thickening are used to describe global cardiac function. The myocardial contraction is described by the time to peak motion, standard deviation (SD) of time to peak motion and the bandwidth. These parameters have been shown to identify ventricular dyssynchrony in other studies [14].

Statistical analysis

Continuous variables are expressed as mean ± SD, and categorical data are expressed as frequencies and/or percentages. In the normal population distinction was made between parameters acquired at rest, after physical stress or after adenosine stress. Possible differences in the dyssynchrony indices between rest and post-stress MPS in the normal population were evaluated with paired Student’s t tests. The distribution of the MPS parameters in the normal population and in the population with proven dyssynchrony was compared with independent Student’s t tests. Statistical significance was defined as <0.05; two-sided p values were used for all tests.

Results

Normal population

The normal population consisted of 80 patients (20 male physical stress, 20 male adenosine stress, 20 female physical stress, 20 female adenosine stress; mean age 56.4 ± 10.5 years). The main indications for MPS were preoperative screening (n = 22, 27.5%), chest pain (n = 24, 30%), increased risk profile for coronary artery disease (CAD) (n = 15, 18.8%), abnormal ECG on stress test (n = 11, 18.8%), evaluation of suspected ischaemia (n = 6, 7.5%) or evaluation of abnormality found on other imaging modality (n = 2, 2.5%).

The global rest MPS and dyssynchrony indices of the normal population are shown in Table 1. Significant gender-related differences were found for EDV and ESV, as could be expected. For all other parameters, including the dyssynchrony indices, no gender-related differences were found in the normal population.

Table 1 Parameters (rest) of the normal population
Full size table

Segmental wall motion was heterogeneous throughout the myocardium in the normal population. Maximal amplitudes were observed in the anterior (11.1 ± 1.7 mm) and lateral (10.0 ± 2.0 mm) segments, whereas the septal segment had the lowest amplitude (7.7 ± 1.6 mm) compared to the other segments. Such a heterogeneous distribution was not observed for the segmental quantification of the time to peak motion.

Rest versus post-stress MPS

As part of the 2-day stress/rest protocol patients underwent a post-stress MPS with either adenosine or exercise-induced stress. Comparison of the rest MPS indices of the exercise and adenosine subgroups showed no differences (p values ranged from 0.180 to 0.836) between these populations, suggesting that any difference that is to be found post-stress may be allocated to the stress induction. The evaluation of the post-stress and rest MPS parameters for the adenosine and exercise stressed subgroups is shown in Table 2. Significant differences were found for the volumetric parameters between rest and post-stress acquisitions in the exercise subgroup. The mean wall motion was also slightly higher (10.2 ± 1.3 mm, p value 0.002) compared to rest (wall motion 9.5 ± 1.3 mm). No profound differences were found between rest and post-stress for the dyssynchrony indices in this subgroup. In the adenosine MPS subgroup no significant differences were found between parameters obtained post-adenosine and at rest.

Table 2 Comparison of rest and post-stress parameters
Full size table

Differences between normal and dyssynchrony population

The included heart failure patients (n = 24, age 63.1 ± 9 years, 18 male, 92% ischaemic cardiomyopathy) had proven dyssynchrony on MRI (mean SL delay 73.7 ± 74.1 ms) [22]. In general, these patients had a depressed left ventricular function (rest LVEF 28.6 ± 9.5%) and abnormal perfusion patterns (summed rest score 25.2 ± 11.7) on MPS. Wall motion (2.7 ± 1.1 mm) and wall thickening (23.5 ± 7.7%) also indicated a depressed cardiac function.

The comparison of this abnormal population with the previous cohort of patients with normal MPS is shown in Fig. 2 and Table 3. For all dyssynchrony indices significant differences are found between the distributions of the two populations. These differences are most profound for the SD of time to peak motion (p value <0.001) and the bandwidth (p value <0.001). Figures 3 and 4 show examples of a normal and an abnormal patient, demonstrating the differences in these populations.

Fig. 2
figure 2

Comparison of the normal population with the dyssynchrony population (Dyssyn) for parameter values of wall motion, time to peak motion (TtPM), SD of time to peak motion (SD of PM) and the bandwidth. All differences between the groups are significant

Full size image
Table 3 MPS results of normal and heart failure populations
Full size table
Fig. 3
figure 3

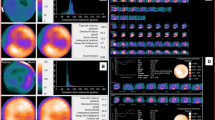
Patient referred for preoperative screening. a A normal MPS acquisition with no apparent regions of ischaemia (EDV 140; LVEF 64%; wall motion 9.3 mm). b Normal, narrow contractility histogram. The dark blue vertical lines indicate the bandwidth and colour coding demonstrates the deviation from the mean in standard deviations (time to peak motion 42.8 ± 2.1% RR cycle; bandwidth 9% RR cycle). c Normal contraction pattern in which all regions contract at the same time. The contraction is normalized to motion at end diastole

Full size image
Fig. 4
figure 4

Patient with dilated cardiomyopathy and left bundle branch block (LBBB). a Dilated myocardium with reduced tracer uptake in anterior, septal and apical regions (EDV 327; LVEF 30%; wall motion 1.7 mm). b The wide and highly distributed histogram is indicative of cardiac dyssynchrony (time to peak motion 48.5 ± 21.1% RR cycle; bandwidth 100% RR cycle). c Curves clearly demonstrate dyssynchrony of the septal region, as is typical in LBBB, and a reduced contraction of the inferior region

Full size image

Discussion

The results of the current study indicate that it is feasible to detect ventricular dyssynchrony using a geometrical method. In the population with normal MPS, there is low variance for time to peak motion (42.8 ± 5.1% RR cycle), SD of time to peak motion (3.5 ± 1.4% RR cycle) and bandwidth (18.2 ± 6.0% RR cycle). No gender-related differences were found for these indices. Additionally, the method of stress induction had no clinically relevant effect on the determination of dyssynchrony in the population with normal MPS. This independence of dyssynchrony to exercise is also described by Kühne et al. [28] for echocardiography and by Aljaroudi et al. [15] for MPS in normal populations. Comparison of the normal MPS with the heart failure patients showed profound differences especially for the SD of time to peak motion (p value <0.001) and the bandwidth (p value <0.001). All these observations suggest that the geometrical approach is a reliable method to diagnose dyssynchrony in either rest or post-stress MPS.

Automated assessment of dyssynchrony

The addition of a dyssynchrony toolbox to the arsenal of nuclear cardiology has potential clinical utility. A number of recent studies describe the long-term prognostic value of dyssynchrony analysis. In general dyssynchrony indices may provide better identification of CRT response or major cardiac events compared to other commonly used predictors such as LVEF and QRS duration [2, 3, 5, 6]. Although the present study primarily focuses on the geometrical approach, other feasible automated methods to determine ventricular dyssynchrony in MPS data have been proposed, most of which are count based.

Chen et al. performed count-based phase analysis on MPS data of 90 patients with a <5% likelihood of CAD (modification of the ECTb) [14]. In general, methods that apply Fourier analysis will provide information regarding the phase of contraction in degrees, which can be easily converted to percentage of RR cycle. The method provides a peak phase of 137.4 ± 14.6° (38.2 ± 4.1% RR cycle), a phase SD of 13.0 ± 5.2° (3.6 ± 1.4% RR cycle) and a bandwidth of 34.7 ± 10.7° (9.7 ± 3.0% RR cycle) for the normal population. Comparable with the results of our study, no gender-related differences were found. Subsequent studies show that this method produces repeatable dyssynchrony indices (coefficient of variation is 8.7% for bandwidth and 8.8% for SD of time to peak contraction) and can distinguish normal from dyssynchronous contraction in clinical populations [18, 21].

Kriekinge et al. evaluated their count-based phase analysis algorithm (modification of the Cedars-Sinai Quantitative Gated SPECT software) in 68 normal patients and 72 patients with left bundle branch block (LBBB), all with a normal MPS and low pre-test likelihood for CAD [29]. In the normal population significant gender-related differences were found for the global dyssynchrony indices (SD and bandwidth); these gender-related differences were not observed in the LBBB population. Comparison of the normal and LBBB populations showed significant differences in global dyssynchrony parameters, again indicating that this is also a feasible method to evaluate cardiac contraction in MPS.

It is well known that there are discrepancies between commercial software packages with respect to the algorithms for left ventricular segmentation and estimation of the myocardial count distribution [30, 31]. The main differences are found for the techniques to locate ventricular borders, the valve plane motion constraints and the methods applied to model wall thickening. All these factors will also play a role in the determination of dyssynchrony indices from MPS data. Consequently, the determination of dyssynchrony indices may also show algorithm-specific normal values.

Pros and cons of a geometrical approach

The ability to evaluate cardiac contraction depends on the capability of the software to detect endocardial and epicardial borders accurately [26]. Estimations of myocardial count distributions are not determined by perfusion alone, but also by factors such as extra-cardiac activity, attenuation, scatter, filtering and image reconstruction. Automated software packages can provide estimations of cardiac borders despite the presence of large perfusion defects due to predefined assumptions on continuity of the ventricular wall and the ability to detect very low count densities. Though border detection is very robust, it has an important drawback: the inability to recognize large left ventricular aneurysms. Generally, aneurysms do not convey with the assumption of ventricular continuity. Conflicts with this continuity assumption can also arise when extra-cardiac activity is projected over the ventricular wall. In these cases the geometrical approaches may be sensitive to errors and could provide incorrect parameter values. Still, the evaluation of regional cardiac perfusion is also considered to be unreliable in acquisitions with severe extra-cardiac activity. Accordingly, count-based methods to determine dyssynchrony indices may also prove erroneous in these cases.

A second factor that is known to affect perfusion and functional assessment of MPS is the quality of ECG gating. Studies of Nichols et al. indicated that inadequate ECG gating especially affected the wall thickening values. The volumetric indices on the other hand were not influenced by these gating errors [32, 33]. These results suggest that the border estimates are relatively insensitive to variations in count distributions throughout the cardiac cycle. Thus, it is plausible that geometrical methods to determine dyssynchrony are also less sensitive to gating errors compared to count-based methods. Nonetheless, the presence of inadequate ECG gating should always be recognized and subsequent errors in perfusion or functional estimates should be described.

Both geometrical and count-based techniques to calculate dyssynchrony from MPS data estimate the translational contraction patterns of the ventricle (i.e. the inward movement of the wall towards the heart axis). Systolic rotation and torque are also important aspects of a normal cardiac contraction pattern, but are difficult to determine using nuclear techniques. Still, these factors may play a role in characterizing the pathology of ventricular dyssynchrony [34]. Nichols et al. proposed a method to detect cardiac torsion in MPS data [35]. In short-axis images, the right ventricular attachment can be seen as a slight reduction of counts in the left ventricular wall generally at the 7 o’clock and 11 o’clock positions. These right ventricular insertion points were used as references during the cardiac cycle to detect torsion. They used theie data to improve the perfusion images by correcting for the rotational motion. Still, this method is not widely used, and implementation can be hampered by the limited resolution of MPS.

Limitations

The aim of this study was to evaluate the feasibility of a geometrical approach for the detection of ventricular dyssynchrony in MPS data. For this specific problem it is sufficient to differentiate between a normal and an abnormal population, as was done in this study. Still, one has to bear in mind that a technique does not need to be really sensitive to make a distinction between the two populations included in the present study. Although, the current study indicates that it is feasible to detect dyssynchrony using the geometrical approach, more extensive validation using this technique has to be done. Also, the additive value of the geometrical approach in specific patient cases, rather than a group comparison, needs to be determined. It will also be interesting to perform a direct comparison between the count-based and geometrical approaches, as these are the two main methods to assess dyssynchrony in MPS data that are currently used.

The normal population used in our study consisted of 80 patients with a normal perfusion pattern, no ventricular dysfunction and optimal image quality. Although this population was sufficient to evaluate the feasibility, the population is not optimal for determining normal ranges or cutoff values. First of all, these patients were selected from a single centre, so there was no variation in acquisition settings. Furthermore, the dependence of this geometrical approach on factors such as heart rate, scatter, extra-cardiac activity and image reconstruction needs to be established.

Conclusion

The results of the current study indicate that the geometrical approach is a feasible method for evaluating ventricular dyssynchrony in MPS data. Nonetheless, more research has to be performed to identify factors that influence the calculation of dyssynchrony indices, to evaluate the diagnostic or prognostic value of the dyssynchrony analysis and to establish normal ranges.