Abstract
Purpose
Parametric imaging of absolute myocardial blood flow (MBF) using [15O]H2O enables determination of MBF with high spatial resolution. The aim of this study was to develop a method for generating reproducible, high-quality and quantitative parametric MBF images with minimal user intervention.
Methods
Nineteen patients referred for evaluation of MBF underwent rest and adenosine stress [15O]H2O positron emission tomography (PET) scans. Ascending aorta and right ventricular (RV) cavity volumes of interest (VOIs) were used as input functions. Implementation of a basis function method (BFM) of the single-tissue model with an additional correction for RV spillover was used to generate parametric images. The average segmental MBF derived from parametric images was compared with MBF obtained using nonlinear least-squares regression (NLR) of VOI data. Four segmentation algorithms were evaluated for automatic extraction of input functions. Segmental MBF obtained using these input functions was compared with MBF obtained using manually defined input functions.
Results
The average parametric MBF showed a high agreement with NLR-derived MBF [intraclass correlation coefficient (ICC) = 0.984]. For each segmentation algorithm there was at least one implementation that yielded high agreement (ICC > 0.9) with manually obtained input functions, although MBF calculated using each algorithm was at least 10% higher. Cluster analysis with six clusters yielded the highest agreement (ICC = 0.977), together with good segmentation reproducibility (coefficient of variation of MBF <5%).
Conclusion
Parametric MBF images of diagnostic quality can be generated automatically using cluster analysis and a implementation of a BFM of the single-tissue model with additional RV spillover correction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Dynamic positron emission tomography (PET) can be used to measure regional myocardial blood flow (MBF) non-invasively using for example [13N]NH3, 82Rb or [15O]H2O [1–3]. The introduction of hybrid PET/CT scanners enables accurate diagnosis of coronary artery disease (CAD) by combining PET perfusion studies with CT coronary angiography (CTCA) [4–7]. Given the short half-life of 15O and 82Rb (122 and 76 s, respectively), repeat scans are feasible within a single scanning session, enabling stress-rest CTCA protocols with a total duration of less than 30 min. In contrast to 82Rb and [13N]NH3, [15O]H2O is freely diffusible and metabolically inert. Consequently, [15O]H2O is an ideal tracer for quantifying MBF, as changes in myocardial tracer activity are solely dependent on MBF and are not affected by variations in extraction fraction and/or metabolic interactions [6].
Kinetics of [15O]H2O can best be described using a single-tissue compartment model with parameters for MBF and, to correct for partial volume and spillover effects, perfusable tissue fraction (PTF) [8, 9], and left ventricular (LV) and right ventricular (RV) blood volume fractions [10]. Using least-squares fitting techniques on segmental [15O]H2O data, it has been shown that resulting MBF values correlated well with MBF based on microspheres using both 2-D [8, 11] and 3-D [12] PET data.
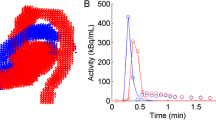
In order to solve the single-tissue compartment model, time-activity curves (TACs) of arterial blood and RV, CA(t) and CRV(t), respectively, have to be determined. It has been shown [10–13] that CA(t) can be obtained accurately from the dynamic data themselves, eliminating the need for online blood sampling. This can be achieved by drawing volumes of interest (VOIs) in ascending aorta (AA), LV or left atrium, and RV in a blood pool image obtained using [15O]CO and transferring these VOIs to the dynamic [15O]H2O data [13]. Although the LV is often used to define the arterial input function for [15O]H2O, previous studies have shown that the AA is preferable for [18F]fluorodeoxyglucose (FDG) [14]. In addition, perfusion values based on an AA image-derived input function (IDIF) were shown to correlate well with those based on online arterial sampling [15]. Performing an additional [15O]CO scan, however, is cumbersome and drawing VOIs is user dependent and time consuming. In addition, there is a chance of misalignment between blood pool and water scans due to patient movement. VOIs can also be drawn on the [15O]H2O data themselves using a frame during the first pass of the bolus, where the blood pool is best visible. Although this eliminates errors due to patient movement between scans, it remains user dependent and time consuming. Therefore, automatic methods for extracting CA(t) and CRV(t) directly from a dynamic scan are preferred.
Factor analysis [16, 17] has been used to extract blood and tissue TACs from dynamic PET images. Factor analysis separates a small number of underlying and unobservable factors that define the dynamic data. Its use in combination with dynamic [15O]H2O scans of the heart has been shown [18, 19], although it was found that frequent operator intervention was required. The low signal to noise ratio of [15O]H2O scans, however, may affect extraction of the various factors, thereby possibly affecting quantitative accuracy of MBF. Cluster analysis [20], k-means++ clustering [21, 22] and factor analysis of dynamic sequences [23] can be used as alternative segmentation algorithms. There are a number of prerequisites for a segmentation algorithm to be feasible for clinical use. Firstly, it should yield blood TACs that result in MBF values, which agree well with those obtained using manually defined blood TACs. Furthermore, segmentation reproducibility should be high, i.e. each segmentation of a single data set should yield the same flow value. Finally, it should be able to segment data reliably without or only with minimal operator intervention.
When arterial and RV TACs are available, segmental MBF can be calculated. Calculating MBF for heart segments has the obvious drawback of losing all information about the distribution of MBF within those segments. As an alternative, kinetic analyses can be performed for each voxel individually, thereby generating parametric MBF images. The gold standard for kinetic analysis, nonlinear least-squares regression (NLR), is slow and very sensitive to noise, making it unsuitable for generating parametric images. The basis function method (BFM) [24] is a much faster and less noise-sensitive method, as it linearizes the model equation and solves it for each voxel using standard linear regression applied to a limited number of predefined possible values of MBF. Its use for [15O]H2O scans has been reported [25], although the high noise level of [15O]H2O images on dedicated 2-D PET scanners with BGO detectors essentially ruled out calculation of MBF at the voxel level, as resulting parametric MBF images were very noisy [26]. Improved scanning statistics of current generation 3-D-only clinical PET/CT scanners [27] utilizing LSO or LYSO detectors and faster electronics, however, might result in parametric images of improved quality. Implementation of a correction for RV spillover [10], which has not been reported before in combination with parametric MBF images, may further improve quantitative accuracy of MBF images, especially in the septum.
The aim of this study was to develop a method for generating quantitative parametric MBF images of diagnostic quality with minimal user intervention. To this end the use of a BFM, incorporating RV spillover, was assessed after which quantitative accuracy and reproducibility of four different segmentation algorithms for definition of blood pool TACs were compared using data acquired on a clinical 3-D PET/CT scanner.
Materials and methods
Patients
Data were obtained from a cohort of patients, who were evaluated for CAD and therefore referred for CT angiography and MBF measurements. A total of 19 consecutive patients (9 men, age range 50–77 years, mean age 65 years; 10 women, age range 31–78 years, mean age 60 years) were included. None of the patients had a documented history of CAD. Electrocardiography did not show signs of a previous myocardial infarction, and echocardiography showed a normal LV function without wall motion abnormalities in all patients.
Image acquisition
Scans were performed on a Gemini TF 64 PET/CT (Philips Healthcare, Best, The Netherlands) [27]. A 5-ml bolus injection of 370 MBq [15O]H2O, followed by 35 ml saline (total duration 23 s), was administered simultaneously with the start of a list-mode emission scan of 6 min. The injected dose was chosen to remain within the linear range of the scanner, the upper limit of which is at a singles count rate of about 35 Mcps [28]. Singles count rates in the present study were approximately 32 Mcps during the first pass of the bolus. A slow low-dose CT scan (LDCT, 55 mAs, rotation time 1.5 s, pitch 0.825, collimation 16×0.625, acquiring 20 cm in 37 s compared to 5 s for a regular LDCT) was performed after each emission scan to correct for attenuation. The emission scan was reconstructed into 22 frames (1×10, 8×5, 4×10, 2×15, 3×20, 2×30 and 2×60 s) using the 3-D row action maximum likelihood algorithm (RAMLA), applying all appropriate corrections. Images consisted of 45 planes of 144×144 voxels with voxel dimensions of 4×4×4 mm. Two [15O]H2O scans were performed sequentially: one under adenosine-induced stress conditions, the other under rest conditions. Adenosine infusion was started 2 min prior to injection of [15O]H2O and continued during the LDCT following the stress scan. The time between both [15O]H2O injections was approximately 20 min to allow for decay of radioactivity.
Manually drawn blood VOIs
Using CAPP software (Siemens/CTI, Knoxville, TN, USA), 1-cm diameter regions of interest (ROIs) were placed over the centre of the AA in at least ten transaxial image planes in the frame showing the first pass of the injected bolus, as described previously [29]. These ROIs were combined into one VOI for the AA. A second set of ROIs was placed over the RV cavity in at least five transaxial planes, with ROI boundaries at least 1 cm from the RV wall to avoid spillover of myocardial activity. Again, these ROIs were combined into one RV VOI. Both VOIs were then transferred to the full dynamic images to obtain CA(t) and CRV(t).
Parametric images
Parametric MBF images were generated using a basis function implementation [24, 25] of the single-tissue compartment model with corrections for spillover and partial volume effects [9, 10]:
VA represents arterial blood volume and LV spillover fraction, VRV RV spillover fraction, and VT the partition coefficient of water in myocardial tissue, which was fixed to 0.91 ml×g−1 [8]. The last two terms of the model are used to correct for spillover effects, whilst PTF is used to correct for partial volume effects. A set of 30 basis functions was precomputed using logarithmically spaced values of MBFi between 0.1 and 1.8 ml×g−1×min−1 for rest scans and between 0.1 and 4.5 ml×g−1×min−1 for stress scans:
The linear combination of the three terms in Eq. 1, resulting in the minimal sum of squared differences, yielded PTF, MBF, VA and VRV. In voxels with PTF < 0.25 or VA+VRV > 0.75, MBF was set to zero in order to avoid spurious noise-induced high MBF values outside the heart or in blood vessels.
Segmentation algorithms
For segmentation of dynamic data, four different algorithms were used. Cluster analysis [20] iteratively computes, for each voxel, the probability that it belongs to one of the clusters, each of which is described by a multinomial distribution with a mean and variance TAC. Mean and variance of each cluster are calculated using probability weighted voxel TACs, after which new probabilities are calculated. The final probability maps are used for further analysis. Factor analysis of dynamic structures (FADS) [23] uses simple matrix calculations and positivity constraints to iteratively calculate factor images rather than probability densities. Factor analysis [16, 17] also uses matrix calculations and positivity constraints. However, calculations are performed on a new affine space defined using principal component analysis rather than the raw dynamic data. K-means++ [22] is a modified version of k-means clustering [21], which groups voxel TACs iteratively in clusters using the squared sum of differences (i.e. distances) between voxel and TACs. Each voxel is assigned to one cluster in order to minimize the distances within a cluster and maximize the distances between clusters. K-means++ uses different starting values, thereby increasing calculation speed and reliability. In the present study, a corner voxel, located outside the patient, was used as the first cluster centre.
Obtained factor or cluster images were normalized such that the sum of all factors and clusters was 1 for each pixel, after which they were thresholded, assigning voxels to only one factor or cluster. For k-means++ clustering, thresholding was not needed, as k-means++ already assigns voxels to only one cluster. Thresholded images were displayed in 3-D and, after visual inspection, arterial and RV factors or clusters were assigned manually. Next, to reduce partial volume and spillover effects, arterial and RV factors or clusters were morphologically eroded once, removing both the outer layer of voxels and possible isolated voxels. The average TACs of the remaining voxels were used as CA(t) and CRV(t). Each algorithm was tested for four to seven factors or clusters. Prior to analysis, to prevent memory issues, dynamic data were cropped to extract images of 28×28×18 cm located around the heart using fixed cropping parameters.
Data analysis
Validation of parametric images
Parametric PTF images were rotated in order to obtain short-axis images of the heart. Next, the same transformation was performed to the original dynamic [15O]H2O data. Myocardial segment VOIs according to the 17-segment model of the American Heart Association were drawn manually on the PTF short-axis image. This VOI template was transferred to the short-axis dynamic data to extract segmental [15O]H2O TACs. These TACs were used to derive MBF for each segment using NLR together with manually obtained CA(t) and CRV(t). Corresponding parametric MBF values were obtained by transferring the same VOI template to the parametric MBF images. Correlation and agreement between both sets of segmental MBF values and of coronary flow reserve (CFR, defined as stress MBF divided by rest MBF) was assessed using Deming regression, intraclass correlation coefficients (ICC) and Bland-Altman analysis [30].
Validation and reproducibility of segmentation methods
Segmental MBF was derived from corresponding TACs using NLR and the various CA(t) and CRV(t) obtained from all segmentation algorithms. Correlation and agreement of these MBF and corresponding CFR values with those obtained from manually defined CA(t) and CRV(t) were assessed using Deming regression, ICC and Bland-Altman analysis.
Segmentation reproducibility was only assessed for the number of factors that showed the highest correlation with manually derived blood curves. CA(t) and CRV(t) were determined 50 times for both rest and stress scans of three randomly selected patients using each of the algorithms. Using NLR, myocardial segment TACs were fitted for each CA(t) and CRV(t), after which the coefficient of variation (CoV) of MBF was calculated for each algorithm and used as a measure for segmentation reproducibility.
Results
Parametric images
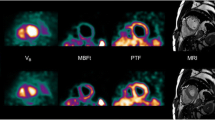
One patient showed MBF, as determined by NLR, outside the predefined range used for BFM. For this patient with very high stress MBF, the predefined range of MBF values was adjusted to 0.1–7.2 ml×g−1×min−1. In Fig. 1 parametric MBF images are shown of one patient with a normal flow distribution and another with a stress-inducible perfusion defect. Figure 2 shows regression and Bland-Altman plots of segmental MBF derived from parametric MBF images against those obtained from NLR analysis of corresponding VOIs. Agreement was high (ICC = 0.984 for MBF) and Bland-Altman plots showed no significant difference between both MBF values (mean difference 0.023, 95% confidence interval −0.355 to 0.401). Deming regression resulted in a slope of 0.977 and an intercept of 0.046. Both slope and intercept were significantly different from 1 and 0 (p < 0.05), respectively, indicating a very small but significant bias in parametric images relative to NLR.
Factor images
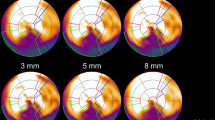
On average, all segmentation algorithms took about 20 s on a standard desktop PC with a maximum of 1 min. Factor images without threshold are shown in Fig. 3. Images obtained using cluster analysis contained many voxels with a value of 1, in contrast to FADS and factor analysis. A threshold of 1 for cluster analysis, 0.5 for FADS and 0.4 for factor analysis yielded 3-D images (Fig. 4, online resource 1), in which structures could clearly be identified. Note that arterial images include left atrium, LV and aorta and that venous images include vena cava superior, right atrium, RV and pulmonary artery (online resource 1). The chosen thresholds yielded arterial clusters of similar size for each segmentation algorithm. The low threshold for FADS and factor analysis resulted in noisy 3-D images. FADS and factor analysis generated relatively small RV factors or assigned more than one factor to the RV, making it difficult to extract CRV(t). For factor analysis, occasionally myocardium and RV were combined in one factor, leading to a more difficult extraction of CRV(t).
Factor images of arterial (a–c) and RV (d–f) factors obtained using cluster analysis with six clusters (a, d), FADS with seven factors (b, e) and factor analysis with five factors (c, f). The colour scale is the same for all images. RV is clearly visible in the factor images obtained using cluster analysis, but less so in images obtained using FADS and factor analysis
Typical 2-D thresholded factor images showing arterial (blue) and venous (red) factors, cropped around the heart. Factor images were obtained using cluster analysis with six factors (a), FADS with seven factors (b), factor analysis with five factors (c) and k-means++ using seven factors (d). Full 3-D images can be seen in the online supplement
Correlation with manually defined blood TACs
ICC, slope of Deming regression line, mean difference and limits of agreement for MBF and CFR calculated using each segmentation algorithm and those using manually defined CA(t) and CRV(t) are listed in Table 1, showing high ICC for most methods (ICC > 0.9). Figures 5 and 6 show corresponding regression and Bland-Altman plots of MBF calculated with each of the segmentation algorithms against MBF based on manually defined CA(t) and CRV(t). In general, all algorithms yielded high correlation with MBF and CFR based on manually defined blood TACs for at least one chosen implementation. For MBF, all regression lines had slopes significantly higher than 1 indicating positive bias. For CFR, slopes were closer to 1 indicating a smaller bias.
Regression plots of segmental MBF calculated using cluster analysis with six clusters (a), FADS with seven factors (b), factor analysis with five factors (c) and k-means++ with seven clusters (d) with MBF calculated using manually obtained CA(t) and CRV(t). Lines indicate a linear fit with zero intercept
Bland-Altman plots of segmental MBF calculated using cluster analysis with six clusters (a), FADS with seven factors (b), factor analysis with five factors (c) and k-means++ with seven clusters (d) with MBF calculated using manually obtained CA(t) and CRV(t). Continuous lines indicate mean difference; dashed lines mean ± 2 SD
Cluster analysis yielded the highest agreement with ICC of 0.977 for MBF when using six clusters. In addition, it provided high agreement for all implementations tested, indicating low sensitivity to the chosen number of clusters. FADS showed high agreement with MBF based on manually defined blood TACs when using five to seven factors (ICC of 0.971 for MBF when using seven factors). For factor analysis, it was not possible to segment all patients correctly using a fixed number of factors. In addition, quantitative results were very sensitive to the number of factors used. Five factors yielded the highest agreement (ICC of 0.940 for MBF). In addition, this number of factors appeared to be the most generally applicable for the patients included. For stress scans, k-means++ persistently included myocardial voxels in the arterial factor, resulting in large overestimations of both stress MBF and CFR. Nevertheless, agreement with MBF based on manually defined blood TACs was high (ICC of 0.886 for MBF, when using seven clusters).
Segmentation reproducibility
Segmentation reproducibility was assessed for cluster analysis with six clusters, FADS with seven factors, factor analysis with five factors and k-means++ with seven clusters. CoVs are shown in Table 2. As can be seen, both k-means++ and factor analysis yielded identical results for repetitive analyses, which is inherent to these methods. Cluster analysis and FADS, which both require random initial values, showed a small variation between repetitive analyses (CoV in MBF <5 and <8% for cluster analysis and FADS, respectively). In a limited number of cases (<5% of the total), cluster analysis was found to fail in separating aorta and LV from myocardial tissue. This segmentation error was obvious in the 3-D cluster images, and these cases were therefore removed after visual inspection of the cluster images. Repeating the segmentation reproducibility test after excluding these cases resulted in a reduction in CoV.
Discussion
In the present study four different algorithms for automatically segmenting blood pool TACs were compared. In addition, a BFM for generating absolute MBF parametric images, incorporating both LV and RV spillover corrections, was validated.
Agreement of average segmental MBF and CFR, derived directly from parametric images, with segmental MBF and CFR derived using NLR, was high. This indicates that it is possible to generate quantitatively accurate parametric MBF images using the BFM implementation proposed, together with manually obtained CA(t) and CRV(t). The slope of the Deming regression was 0.977 and was significantly different from 1, indicating a small but significant underestimation of MBF in parametric images. However, an underestimation as small as 2.3% in the parametric images can be considered irrelevant for clinical practice and therefore this was considered not an issue for quantification of MBF.
Generated images (Fig. 1) were of diagnostic quality. For one patient, the predefined range of possible MBF values had to be increased due to a high stress MBF. However, stress MBF > 4.5 ml×g−1×min−1 can be considered to be outside the clinically relevant range of MBF, as stress MBF below 1.5–2.5 ml×g−1×min−1 (the actual level being dependent on age) is generally considered to be ischaemic [7], and therefore this issue should have no influence on clinical diagnosis.
Agreement between all segmentation algorithms and manually obtained blood curves was high (ICC > 0.9 for at least one number of clusters or factors), with the highest agreement obtained for cluster analysis with six clusters (Table 1). The segmentation reproducibility of each algorithm was very good to excellent with CoVs of MBF <5% for cluster analysis, <8% for FADS and, inherently, 0% for both factor analysis and k-means++. Each algorithm overestimated MBF compared to MBF based on manually defined blood pool TACs. A possible explanation is the fact that manually obtained TACs were derived from a small volume in the AA. In contrast, the segmentation algorithms included the entire LV, AA and descending aorta (Fig. 4, online resource 1). This larger volume introduces dispersion and partial volume effects in CA(t), resulting in higher apparent MBF compared to MBF based on a manually defined AA TAC. To verify this, CA(t) was also obtained from manually drawn ROIs over both AA and LV, which showed a similar effect on MBF (data not shown). This effect was much smaller for CFR (Table 1), indicating that relative overestimations in stress and rest MBF were similar and cancelled out when calculating CFR.
Each algorithm had its own shortcomings. Occasionally (< 5% of cases), cluster analysis failed to separate aorta from myocardium. When looking at the 3-D images, however, it was easy to determine whether the analysis succeeded or failed (online resource 2). Consequently, due to the random starting values, a failed analysis could easily be resolved by restarting the analysis using the same number of clusters. Although this meant that the method sporadically required user intervention, this was not considered a major drawback of cluster analysis due to the ease of determining the success or failure of an analysis.
An important drawback of k-means++ is that it persistently included myocardial voxels in the arterial factor when segmenting stress scans, resulting in large overestimations of both stress MBF and CFR. This problem was independent of the number of clusters used.
FADS and factor analysis were unable to segment the RV correctly, resulting in incorrect spillover corrections. Furthermore, in contrast to cluster analysis, a low threshold had to be applied to the factor images obtained with both FADS and factor analysis, resulting in noisy images and inclusion of voxels that belonged for up to 60% to other factors. The effects of this on absolute MBF values, however, were small as seen in Table 1.
As described previously, it is essential to use the correct number of factors when using factor analysis for segmentation [18, 19]. Similar results were found in the present study. In particular, it was not possible to find a single number of factors that could be used for segmenting all patients. As frequent user intervention, i.e. manually changing the number of factors, is required to prevent erroneous results, factor analysis was not considered feasible for clinical use. El Fakhri et al. [31] presented a method that modifies factors and factor images after analysis by penalizing overlap in factor images. This method has not been tested in the present study, as cluster analysis did not suffer from overlap in factor images and provided good results. Furthermore, post-processing was not expected to improve feasibility of factor analysis, as incorrect segmentations were not expected to be corrected by penalizing overlap.
A limitation of the present study was that, in order to prevent memory issues during analysis, data were cropped around the heart using fixed parameters. The choice of these parameters and additional pre-processing may affect the optimal number of clusters. When different pre-processing steps are incorporated, the optimal number of clusters should be reassessed. Nevertheless, as cluster analysis was insensitive to the number of clusters chosen, this effect may be small.
Conclusion
This study demonstrates that it is possible to generate good quality parametric images of absolute MBF using [15O]H2O and a clinical PET/CT scanner. This can be achieved with minimal user intervention by using an automatic definition of blood pool TACs and on a BFM including RV spillover correction for calculation of parametric MBF images. Cluster analysis with six clusters proved to be the best segmentation algorithm for automatic definition of blood pool TACs, resulting in high correlation and agreement of MBF values with those based on manually defined blood pool VOIs. Consequently, absolute MBF images, generated from a [15O]H2O scan, are now available for clinical use.
References
Schelbert HR, Phelps ME, Huang SC, MacDonald NS, Hansen H, Selin C, et al. N-13 ammonia as an indicator of myocardial blood flow. Circulation 1981;63:1259–72.
Selwyn AP, Allan RM, L’Abbate A, Horlock P, Camici P, Clark J, et al. Relation between regional myocardial uptake of rubidium-82 and perfusion: absolute reduction of cation uptake in ischemia. Am J Cardiol 1982;50:112–21.
Bergmann SR, Fox KA, Rand AL, McElvany KD, Welch MJ, Markham J, et al. Quantification of regional myocardial blood flow in vivo with H215O. Circulation 1984;70:724–33.
Di Carli MF, Hachamovitch R. New technology for noninvasive evaluation of coronary artery disease. Circulation 2007;115:1464–80.
Kajander S, Ukkonen H, Sipilä H, Teräs M, Knuuti J. Low radiation dose imaging of myocardial perfusion and coronary angiography with a hybrid PET/CT scanner. Clin Physiol Funct Imaging 2009;29:81–8.
Knaapen P, de Haan S, Hoekstra OS, Halbmeijer R, Appelman YE, Groothuis JG, et al. Cardiac PET-CT: advanced hybrid imaging for the detection of coronary artery disease. Neth Heart J 2010;18:90–8.
Kajander S, Joutsiniemi E, Saraste M, Pietilä M, Ukkonen H, Saraste A, et al. Cardiac positron emission tomography/computed tomography imaging accurately detects anatomically and functionally significant coronary artery disease. Circulation 2010;122:603–13.
Iida H, Kanno I, Takahashi A, Miura S, Murakami M, Takahashi K, et al. Measurement of absolute myocardial blood flow with H215O and dynamic positron-emission tomography. Strategy for quantification in relation to the partial-volume effect. Circulation 1988;78:104–15.
Iida H, Rhodes CG, de Silva R, Yamamoto Y, Araujo LI, Maseri A, et al. Myocardial tissue fraction–correction for partial volume effects and measure of tissue viability. J Nucl Med 1991;32:2169–75.
Hermansen F, Rosen SD, Fath-Ordoubadi F, Kooner JS, Clark JC, Camici PG, et al. Measurement of myocardial blood flow with oxygen-15 labelled water: comparison of different administration protocols. Eur J Nucl Med 1998;25:751–9.
Araujo LI, Lammertsma AA, Rhodes CG, McFalls EO, Iida H, Rechavia E, et al. Noninvasive quantification of regional myocardial blood flow in coronary artery disease with oxygen-15-labeled carbon dioxide inhalation and positron emission tomography. Circulation 1991;83:875–85.
Schäfers KP, Spinks TJ, Camici PG, Bloomfield PM, Rhodes CG, Law MP, et al. Absolute quantification of myocardial blood flow with H(2)(15)O and 3-dimensional PET: an experimental validation. J Nucl Med 2002;43:1031–40.
Iida H, Rhodes CG, de Silva R, Araujo LI, Bloomfield PM, Lammertsma AA, et al. Use of the left ventricular time-activity curve as a noninvasive input function in dynamic oxygen-15-water positron emission tomography. J Nucl Med 1992;33:1669–77.
van der Weerdt AP, Klein LJ, Boellaard R, Visser CA, Visser FC, Lammertsma AA. Image-derived input functions for determination of MRGlu in cardiac (18)F-FDG PET scans. J Nucl Med 2001;42:1622–9.
van der Veldt AA, Hendrikse NH, Harms HJ, Comans EF, Postmus PE, Smit EF, et al. Quantitative parametric perfusion images using 15O-labeled water water and a clinical PET/CT scanner: test-retest variability in lung cancer. J Nucl Med 2010;51:1684–90.
Barber DC. The use of principal components in the quantitative analysis of gamma camera dynamic studies. Phys Med Biol 1980;25:283–92.
di Paola R, Bazin JP, Aubry F, Aurengo A, Cavailloles F, Herry JY, et al. Handling of dynamic sequences in nuclear medicine. IEEE Trans Nucl Sci 1982;29:1310–21.
Hermansen F, Ashburner J, Spinks TJ, Kooner JS, Camici PG, Lammertsma AA. Generation of myocardial factor images directly from the dynamic oxygen-15-water scan without use of an oxygen-15-carbon monoxide blood-pool scan. J Nucl Med 1998;39:1696–702.
Ahn JY, Lee DS, Lee JS, Kim SK, Cheon GJ, Yeo JS, et al. Quantification of regional myocardial blood flow using dynamic H2(15)O PET and factor analysis. J Nucl Med 2001;42:782–7.
Ashburner J, Haslam J, Taylor C, Cunningham VJ, Jones T. A cluster analysis approach for the characterization of dynamic PET data. Quantification of brain function using PET. San Diego: Academic; 1996. p. 301–6.
Lloyd S. Least squares quantization in PCM. IEEE Trans Inf Theory 1982;28:129–37.
Arthur D, Vassilvitskii S. k-means++: the advantages of careful seeding. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms 2007, 1027–35.
Bruyant PP, Sau J, Mallet JJ. Noise removal using factor analysis of dynamic structures: application to cardiac gated studies. J Nucl Med 1999;40:1676–82.
Gunn RN, Lammertsma AA, Hume SP, Cunningham VJ. Parametric imaging of ligand-receptor binding in PET using a simplified reference region model. Neuroimage 1997;6:279–87.
Watabe H, Jino H, Kawachi N, Teramoto N, Hayashi T, Ohta Y, et al. Parametric imaging of myocardial blood flow with 15O-water and PET using the basis function method. J Nucl Med 2005;46:1219–24.
Boellaard R, Knaapen P, Rijbroek A, Luurtsema GJ, Lammertsma AA. Evaluation of basis function and linear least squares methods for generating parametric blood flow images using 15O-water and positron emission tomography. Mol Imaging Biol 2005;7:273–85.
Surti S, Kuhn A, Werner ME, Perkins AE, Kolthammer J, Karp JS. Performance of Philips Gemini TF PET/CT scanner with special consideration for its time-of-flight imaging capabilities. J Nucl Med 2007;48:471–80.
Lubberink M, van der Veldt A, Knaapen P, Harms H, Smit E, Hendrikse H, et al. Measurement of tumor and myocardial perfusion using 15O-water and a clinical PET-CT scanner. J Nucl Med 2009;50(Suppl 2):238.
Lubberink M, Harms HJ, Halbmeijer R, de Haan S, Knaapen P, Lammertsma AA. Low-dose quantitative myocardial blood flow imaging using 15O-water and PET without attenuation correction. J Nucl Med 2010;51:575–80.
Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307–10.
El Fakhri G, Sitek A, Guérin B, Kijewski MF, Di Carli MF, Moore SC. Quantitative dynamic cardiac 82Rb PET using generalized factor and compartment analyses. J Nucl Med 2005;46:1264–71.
Acknowledgements
The authors would like to thank Suzette van Balen, Judith van Es, Amina Elouahmani, Femke Jongsma, Nazerah Sais en Annemiek Stiekema for scanning patients, and Dr. Gert Luurtsema, Robert Schuit, Kevin Takkenkamp and Henri Greuter for production of [15O]H2O. This work was supported financially by Philips Healthcare.
Conflicts of interest
None.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Three-dimensional cluster or factor images for cluster analysis (A), FADS (B), factor analysis (C) and k-means++ (D). Arterial clusters or factors are represented in black, whilst venous clusters or factors are represented in grey (AVI 378 kb)
(AVI 378 kb)
(AVI 378 kb)
(AVI 378 kb)
Three-dimensional cluster images of a successful (A) and failed cluster analysis (B). It can clearly be seen that in the failed analysis myocardial voxels are included in the arterial cluster (black), whilst the LV cavity is not included (AVI 98 kb)
(AVI 98 kb)
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Harms, H.J., Knaapen, P., de Haan, S. et al. Automatic generation of absolute myocardial blood flow images using [15O]H2O and a clinical PET/CT scanner. Eur J Nucl Med Mol Imaging 38, 930–939 (2011). https://doi.org/10.1007/s00259-011-1730-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00259-011-1730-3