Abstract
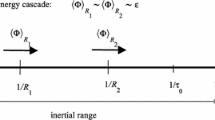
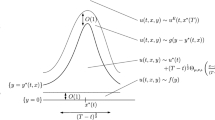
The formation of singularities in the three-dimensional Euler equation is investigated. This is done by restricting the number of Fourier modes to a set which allows only for local interactions in wave number space. Starting from an initial large-scale energy distribution, the energy rushes towards smaller scales, forming a universal front independent of initial conditions. The front results in a singularity of the vorticity in finite time, and has scaling form as function of the time difference from the singularity. Using a simplified model, we compute the values of the exponents and the shape of the front analytically. The results are in good agreement with numerical simulations.
Similar content being viewed by others
References
L. Onsager, “Statistical hydrodynamics”, Nuovo Cimento 6, 279 (1949)
R. H. Morf, S. A. Orszag, and U. Frisch, “Spontaneous Singularity in Three-Dimensional, Inviscid, Incompressible Flow”, Phys. Rev. Lett. 44, 572 (1980)
M.E. Brachet et al., “Small-scale structure of the Taylor-Green vortex”, J. Fluid Mech. 130, 411 (1983)
E. D. Siggia, “Collapse and amplification of a vortex filament”, Phys. Fluids 28, 794 (1985)
A. Pumir and E. D. Siggia, “Collapsing solutions of the 3-D Euler equations”, Phys. Fluids A 2, 220 (1990)
R. Grauer and T. C. Sideris, “Numerical Computation of 3D Incompressible Ideal Fluids with Swirl”, Phys. Rev. Lett. 67, 3511 (1991)
A. Pumir and E. D. Siggia, “Development of singular solutions of the axisymmetric Euler equation”, Phys. Fluids A 4, 1472 (1992)
M. J. Shelley, D. I. Meiron, and S. A. Orszag, “Dynamical aspects of vortex reconnection of perturbed anti-parallel vortex tubes”, J. Fluid Mech. 246, 613 (1993)
R. M. Kerr, “Evidence for a singularity of the three-dimensional, incompressible Euler equations”, Phys. Fluids A 5, 1725 (1993)
M.E. Brachet et al., “Numerical evidence of smooth self-similar dynamics and possibility of subsequent collapse for three-dimensional ideal flows”, Phys. Fluids A 4, 2845 (1992)
J. Eggers, “Universal pinching of 3D Axisymmetric Free-Surface Flow”, Phys. Rev. Lett. 71, 3458 (1993)
A. N. Kolmogorov, “The local structure of turbulence in incompressible viscous liquids”, Dokl. Akad. Nauk SSSR 30, 9 (1941)
J. Eggers and S. Grossmann, “Does deterministic chaos imply intermittency in fully developed turbulence?”, Phys. Fluids A 3, 1985 (1991)
S. Grossmann and D. Lohse, “Intermittency in the Navier-Stokes Dynamics”, Z. Phys. B 89, 11 (1992)
S. Grossmann and D. Lohse, “Intermittency exponents”, Europhys. Lett. 21, 201 (1993)
S. Grossmann and D. Lohse, “Scale resolved intermittency in turbulence”, Phys. Fluids 6, 611 (1994)
C. Uhlig and J. Eggers, “Local coupling of shell models leads to anomalous scaling”, Z. Phys. B in press (1997)
M. Nelkin, “What do we know about self-similarity in fluid turbulence?”, J. Stat. Phys. 54, 1 (1989)
J. Eggers, “Multifractal scaling from nonlinear turbulence dynamics: analytical methods”, Phys. Rev. E 50, 285 (1994)
A. M. Obukhov, “Some general properties of equations describing the dynamics of the atmosphere”, Atmos. Ocean. Phys. 7, 471 (1971)
E. B. Gledzer, “Systems of hydrodynamic type admitting two quadratic integrals of motion”, Sov. Phys. Dokl. 18, 216 (1973)
M. Yamada and K. Ohkitami, “Lyapunov spectrum of a chaotic model of three-dimensional turbulence”, J. Phys. Soc. Jpn 56, 4210 (1987)
M. H. Jensen, G. Paladin, and A. Vulpiani, “Intermittency in a cascade model for three-dimensional turbulence”, Phys. Rev. A 43, 798 (1991).
L. P. Kadanoff, D. Lohse, J. Wang, and R. Benzi, “Scaling and Dissipation in the GOY shell model”, Phys. Fluids 7, 617 (1995)
N. Schörghofer, L. P. Kadanoff, and D. Lohse, “How the viscous subrange determines inertial range properties in turbulence shell models”, Physica D 88, 40 (1995)
U. Frisch, “Turbulence”, (Cambridge University Press, 1st ed., 1995)
J.T. Beale, T. Kato, and A. Majda, “Remarks on the breakdown of smooth solutions for the 3D Euler equations”, Comm. Math. Phys. 94, 61 (1984)
S. Grossmann, D. Lohse, and A. Reeh, “Developed Turbulence: From Full Simulations to Full Mode Reductions”, Phys. Rev. Lett. 77, 5369 (1996)
G. L. Eyink, “Energy dissipation without viscosity in ideal hydrodynamics, I”, Physica D 78, 222 (1994)
G. L. Eyink, “Local energy flux and the refined similarity hypothesis”, J. Stat. Phys. 78, 335 (1995)
Barenblatt, G. I., Scaling, self-similarity, and intermediate asymptotics, (Cambridge University Press, 1996)
A. Guderley, “Starke kugelige und zylindrische Verdichtungsstösse in der Nähe des Kugelmittelpunktes bzw. der Zylinderachse”, Luftfahrtforschung 19, 302 (1942)
D. T. Papageorgiou, “On the breakup of viscous liquid threads”, Phys. Fluids 7, 1529 (1995)
W. van Saarloos, “Front propagation into unstable states: Marginal stability as a dynamical mechanism for velocity selection”, Phys. Rev. A 37, 211 (1988)
D. G. Aronson, “The porous medium equation”, in: Nonlinear Diffusion Problems, edited by A. Fasano and M.Primicario, Lecture Notes in Mathematics, (Springer, 1986)
T. Dombre and J.-L. Gilson, “Intermittency, chaos and singular fluctuations in the mixed Obukhov-Novikov shell model of turbulence”, submitted to Physica D (1997)