Viscoelasticity of multicellular systems caused by collective cell migration: dynamics at the biointerface

Abstract

Viscoelasticity of multicellular systems caused by collective cell migration depends on (1) viscoelasticity of migrating clusters, (2) viscoelasticity of surrounding resting cells and (3) the size, slip effects and thickness of the biointerface. A previously developed model for a sharp biointerface is expanded for the case of a finite biointerface based on thermodynamic and rheological considerations to estimate the influence of the biointerface properties on viscoelasticity. These properties of the interface layer are one of the key factors which influence the overall properties of the mixture, such as its viscoelasticity. Sliding of cell clusters through dense surroundings induces generation of significant shear stress, within the biointerface, which influences (1) the active (contractile) or passive state of single cells and (2) the state of cell–cell adhesion contacts. Cells retain collectivity in migration patterns even upon a reduction of cell–cell adhesion caused by stress generation. A greater size to the biointerface leads to the weakening of multicellular systems for the same volume fraction of migrating cells due to energy dissipation. Various factors such as (1) increase of the interface size, (2) reduction in slip effects under the constant thickness of the biointerface and (3) decrease in the biointerface thickness under constant slip effects induce an increase of the shear rate as well as the overall energy dissipation and can lead to circular cell movement within the biointerface layer. Additional experiments at subcellular and cellular levels are needed to determine the influence of mechanical factors on collective cell migration.

Appendices

Appendix 1

Model development for the sharp biointerface: formulation of the corresponding modulus ratio $\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}$

Complex modulus for the sharp biointerface ${G}_{T}^{*}\left(r,\omega \right)$ for steady condition (i.e. ${\upphi }_{m}\left(r\right)$ is time-independent) and parallel mode coupling is obtained based on the following steps:

Fourier transform of Eq. 5 can be expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)={\upphi }_{m}{\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)+\left(1-{\upphi }_{m}\right){\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right).$$

(20)

$${\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{m}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right).$$

(21)

Total stress and stresses of migrating and resting pseudo-phases from eq. 20 are obtained after Fourier transform of the corresponding constitutive model equations and expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)={G}_{T}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right),$$

(22)

$${\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)={G}_{m}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{m}\left(r,\omega \right),$$

$${\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right)={G}_{r}^{\mathrm{*}}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right).$$

Eqs 22 are introduced into eq. 20. Based on the strain equality described by eq. 21, the complex modulus ${G}_{T}^{*}\left(r,\omega \right)$ for the parallel mode coupling can be expressed as:

$$\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}={\upphi }_{m}\left(r\right)\frac{{G}_{m}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}+\left(1-{\upphi }_{m}\left(r\right)\right).$$

(23)

Complex modulus for the sharp biointerface ${G}_{T}^{*}\left(r,\omega \right)$ for steady condition ($i.e. {\upphi }_{m}\left(r\right)$ is time-independent) and series mode coupling is obtained based on following steps:

Fourier transform of Eq. 6 can be expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)={\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)={\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right).$$

(24)

$${\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right)={\upphi }_{m}{\left(r\right)\stackrel{\sim }{\varepsilon }}_{m}\left(r,\omega \right)+\left(1-{\upphi }_{m}\left(r\right)\right){\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right).$$

(25)

Eqs 22 were introduced into eq. 25. Based on the stress equality described by eq. 24, the complex modulus ${G}_{T}^{*}\left(r,\omega \right)$ for the series mode coupling can be expressed as:

$$\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}=\frac{1}{\left(1-{\upphi }_{m}\left(r\right)\right)+\frac{{\upphi }_{m}\left(r\right)}{\frac{{G}_{m}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}}}.$$

(26)

Appendix 2

Model development for the finite biointerface: formulation of the modulus ratio $\frac{{G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}$

Complex modulus for the finite biointerface ${G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)$ for steady conditions (i.e. ${\upphi }_{m}\left(r\right)$ and ${\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)$ are time-independent) and parallel mode coupling is obtained based on the following steps:

Fourier transform of Eq. 11 can be expressed as:

$${\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={\upphi }_{m}^{*}\left(r\right){\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r\right){\stackrel{\sim }{\sigma }}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right).$$

(27)

$${\stackrel{\sim }{\varepsilon }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{m}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{int}\left(r,\omega \right).$$

(28)

where the volume fractions are ${\upphi }_{m}^{*}\left(r\right)=\frac{{\upphi }_{m}\left(r\right)}{1-{\upphi }_{r}\left(r\right)}$ and ${\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}^{*}=\frac{{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)}{1-{\upphi }_{r}\left(r\right)}$.

The stress ${\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)$, stress of migrating pseudo phase ${\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)$ and stress of the interface ${\stackrel{\sim }{\sigma }}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)$ from eq. 27 are obtained after Fourier transform of the corresponding constitutive model equations and expressed as:

$${\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right),$$

(29)

$${\stackrel{\sim }{\sigma }}_{m}\left(r,\omega \right)={G}_{m}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{m}\left(r,\omega \right),$$

$${\stackrel{\sim }{\sigma }}_{int}\left(r,\omega \right)={G}_{\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right).$$

Eqs 29 are introduced into eq. 27. Based on the strain equality described by eq. 28, the complex modulus ${G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)$ for the parallel mode coupling can be expressed by Eq. 15:

$$\frac{{G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}={\upphi }_{m}^{*}\left(r\right)\frac{{G}_{m}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r\right)\frac{{G}_{\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}.$$

(30)

Appendix 3

Model development for the finite biointerface: formulation of the corresponding modulus ratio $\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}$

Complex modulus for the finite biointerface ${G}_{T}^{*}\left(r,\omega \right)$ for steady conditions (i.e. ${\upphi }_{m}\left(r\right)$ and ${\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)$ are time-independent) and parallel mode coupling is obtained based on the following steps:

Fourier transform of Eq. 12 can be expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)=\left({\upphi }_{m}\left(r\right)+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)\right){\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)+{{\upphi }_{r}\left(r\right)\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right).$$

(31)

$${\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right).$$

(32)

Total stress and stresses of the pseudo-phases from eq. 31 are obtained after Fourier transform of the corresponding constitutive model equations and expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)={G}_{T}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right),$$

(33)

$${\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right),$$

$${\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right)={G}_{r}^{*}\left(r,\omega \right){\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right),$$

where the complex modulus ${G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)$ is expressed by eq. 30 (Appendix 2).

Eqs 33 are introduced into eq. 31. Based on the strain equality described by eq. 32, the complex modulus ${G}_{T}^{*}\left(r,\omega \right)$ for the parallel mode coupling can be expressed as:

$$\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}=\left({\upphi }_{m}\left(r\right)+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)\right)\frac{{G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}+\left(1-{\upphi }_{m}\left(r\right)-{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)\right),$$

(34)

Complex modulus for the finite biointerface ${G}_{T}^{*}\left(r,\omega \right)$ for steady conditions and series mode coupling is obtained based on the following steps:

Fourier transform of Eq. 13 can be expressed as:

$${\stackrel{\sim }{\sigma }}_{T}\left(r,\omega \right)={\stackrel{\sim }{\sigma }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)={\stackrel{\sim }{\sigma }}_{r}\left(r,\omega \right),$$

(35)

$${\stackrel{\sim }{\varepsilon }}_{T}\left(r,\omega \right)=\left({\upphi }_{m}\left(r\right)+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)\right){\stackrel{\sim }{\varepsilon }}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}\left(r,\omega \right)+{{\upphi }_{r}\left(r\right)\stackrel{\sim }{\varepsilon }}_{r}\left(r,\omega \right),$$

(36)

Eqs 33 were introduced into eq. 36. Based on the stress equality described by eq. 35, the complex modulus ${G}_{T}^{*}\left(r,\omega \right)$ for the series mode coupling can be expressed as:

$$\frac{{G}_{T}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}=\frac{1}{\left(1-{\upphi }_{m}\left(r\right)-{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)\right)+\frac{{\upphi }_{m}\left(r\right)+{\upphi }_{\mathrm{i}\mathrm{n}\mathrm{t}}\left(r\right)}{\frac{{G}_{m-\mathrm{i}\mathrm{n}\mathrm{t}}^{*}\left(r,\omega \right)}{{G}_{r}^{*}\left(r,\omega \right)}}}.$$

(37)

Glossary of key terminology

Collective and coordinated cell migration

Morphogenesis, wound healing, regeneration, and cancer invasion involve rearrangements of tissues which depend on the migration of large cell clusters. These clusters are closely connected and move in the same direction and at similar speeds to minimize energy dissipation and reach their target positions

Stress accumulation caused by collective cell migration

Movement of cell clusters within dense surroundings made by (passive) “resting” cells induces generation of residual stress which has a feedback impact on configuration and volume fraction of migrating cells. Residual stress accumulation represents the consequence of cell–cell interactions at the biointerface between (active) migrating cells and (passive) resting cells

Cell–cell adhesion contacts

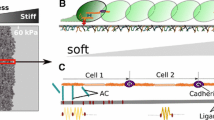
Adherens junctions (AJs) and tight junctions (TJs) significantly influence cell polarization, signalling and migration. AJs are cadherin-catenin complexes linked to actin filaments. Cadherins are transmembrane glycoproteins containing an extracellular domain that mediates cell–cell adhesion via homophilic or heterophilic interactions and an intracellular domain that controls signalling cascades involved in a variety of cellular processes, including polarity, gene expression, etc. Mechanosensitivity of E-cadherin turnover depends on p120-catenin, a protein that binds to the E-cadherin tail and blocks access to the endocytic machinery. TJs are high-affinity complexes formed by transmembrane proteins, including claudins, occludins and tricellulins associate with numerous peripheral proteins. These complexes are also linked to actin filaments. AJs form relatively weak adhesion contacts compared with TJs

Stiffness of migrating clusters

Transversal stiffness is a prerequisite of migrating clusters to keep their integrity during movement through dense surroundings. The stiffness is influenced by the state and types of adhesion contacts, the distribution of cell–cell adhesion contacts, as well as the establishment of some level of supracellular cytoskeletal organization