1 Introduction

With roots in the classical Faustmann problem of forest rotation (for modern references, see [1, 2, 23]), the research on resource extraction problems in random environments is vast. In this literature, a trade-off between profitable resource extraction and sustainability is an underlying theme: a business wants to extract resources at a reasonable rate to gain profit, while a too aggressive extraction strategy may lead to extinction. Many articles focus on the single-player problem, where a single agent extracts resources from a stochastically fluctuating population (see [10, 12, 16, 17]). The problem is closely connected with the dividend problem in finance, also known as the De Finetti problem (see [5, 24]), where the objective is to maximize the expected value of dividend payments up to default. However, there are also application specific differences in the model set-ups, such as different dynamics used for the underlying process, different boundary conditions at extinction/default, differences regarding whether exerting control is costly or not, and whether the extraction rate is controlled directly or indirectly via an effort control.

In many applications, however, several agents are present and thus strategic considerations need to be taken into account. In [13, 22], the specific case of competitive resource extraction from a common pool of fish is considered in particular diffusion models, and with specific choices of market prices and extraction costs. In such a framework, [13] obtains an explicit feedback Nash equilibrium in which extraction rates are proportional to the current stock of biomass. In an extended model allowing for a two-species fish population with interaction, [22] shows that the corresponding results also hold in higher dimensions. Related literature includes [11, 14] where cooperative equilibria are discussed, and [20] in which a myopic setting is used. On the financial side, dividend payments from a common source is not so natural, and the literature on strategic considerations for the dividend problem is more sparse; the reference that is closest in spirit that we have found is [25], in which a non-zero-sum game between insurance companies is studied where the control of each company is a dividend flow as in the De Finetti problem.

The objective of the present paper is to study the effect of strategic considerations for resource extraction in a random environment. In particular, we introduce a stylized dynamic model for markets with competition and study the qualitative behavior of agents in this market. Our model is intended as a theoretical starting point for more realistic, and complicated, models suitable for the study of more specific situations; this could for example include modeling of regulated international fishing waters. To isolate the effects of the introduction of strategic elements, we work in a diffusion model with absorption stripped from most application specific features (such as costly controls and effort controls), and with the objective functions being simply the value of discounted accumulated resource extraction until extinction. In this setting, we show that if the derivative of the drift function is bounded by the discount rate and the agents have identical maximal extraction rates, then a symmetric feedback Nash equilibrium in threshold strategies (i.e. strategies where maximal extraction is employed above a certain threshold and no extraction is employed below it) is obtained. Moreover, we demonstrate the natural result that increased competition lowers the equilibrium threshold and the individual equilibrium value. Furthermore, the total equilibrium value decreases in the number of agents if the individual extraction rates are decreased so that the total extraction rate is kept constant, and extinction is accelerated. Added competition is thus inhibiting both for total profitability and for sustainability. Finally, an asymmetric version is studied, in which each agent is equipped with an individual maximal extraction rate. Again, an equilibrium in threshold strategies is obtained, and the corresponding thresholds are shown to be ordered in the same way as the extraction rates.

2 Mathematical Setup

On a family of complete filtered probability spaces \(\{(\Omega ,{\mathcal {F}},({\mathcal {F}}_t)_{t\ge 0},{\mathbb {P}}_x), x\ge 0\}\) satisfying the usual conditions we consider a one-dimensional process \(X=(X_t)_{t\ge 0}\)—corresponding to the total value of a scarce resource—given under \({\mathbb {P}}_x\) by

$$\begin{aligned} dX_t = \left( \mu (X_t)-\sum _{i=1}^n{\lambda _{it}}\right) dt + \sigma (X_t)\, dB_t, X_0=x, \end{aligned}$$
(2.1)

where \(\mu \) and \(\sigma \) are given functions (satisfying certain conditions, see Assumption 2.2 below), \(B=(B_t)_{t\ge 0}\) is a one-dimensional Wiener process, and \(\lambda _i =(\lambda _{it})_{t\ge 0},i=1,\ldots ,n\) are non-negative controls that satisfy \(\lambda _{it}\le K\) at all times, where \(K>0\) is a given maximal extraction rate. In view of the given Markovian structure, we focus on Markovian controls of the type \(\lambda _{it}=\lambda _i(X_t)\), where \(\lambda _i:[0,\infty )\rightarrow [0,K]\) is measurable. We refer to such a Markovian control as an admissible (resource extraction) strategy, and an n-tuple \(\varvec{\lambda }=(\lambda _1,\ldots ,\lambda _n)\) of admissible strategies is said to be an admissible strategy profile. We note that the conditions on the coefficients \(\mu \) and \(\sigma \) specified in Assumption 2.2 below guarantee that (2.1) has a unique strong solution for any given admissible strategy profile, cf. [15, Proposition 5.5.17]. For a given admissible strategy profile \(\varvec{\lambda }\), the reward of each agent i is given by

$$\begin{aligned} J_i(x;\varvec{\lambda }) := {\mathbb {E}}_x\left( \int _0^{\tau } e^{-rt}{\lambda _{it}}\,dt\right) , \end{aligned}$$
(2.2)

where \(r>0\) is a constant discount rate, \({\tau } :=\inf \{t\ge 0: X_t\le 0\}\) is the extinction time and \(\lambda _{it}:=\lambda _i(X_t)\).

In this setting we allow each agent i to select the strategy \(\lambda _i\). Naturally, each agent i seeks to make this choice in order to maximize the reward (2.2), and we define a Nash equilibrium accordingly. Note that while our main emphasis is on the strictly competitive case \(n\ge 2\), our results also hold for the one-player game with \(n=1\). In that case, the strategic element is eliminated, and the set-up reduces to a classical problem of stochastic control.

Definition 2.1

(Nash equilibrium) For a fixed initial value \(x \ge 0\), an admissible strategy profile \(\varvec{{{\hat{\lambda }}}}=(\hat{\lambda }_1,\ldots ,{\hat{\lambda _n}})\) is a Nash equilibrium if, for each \(i=1,\ldots ,n\),

$$\begin{aligned} J_i(x; \varvec{{{\hat{\lambda }}}}) \ge J_i(x;({\lambda _{i}},\varvec{{{\hat{\lambda }}}}_{-i})) \end{aligned}$$

for any admissible strategy profile \(({\lambda _{i}},\varvec{\hat{\lambda }}_{-i})\), which is the strategy profile obtained when replacing \({{\hat{\lambda }}}_i\) with \(\lambda _i\) in \(\varvec{\hat{\lambda }}\). The corresponding equilibrium values are \(J_i(x; \varvec{{{\hat{\lambda }}}}),i=1,\ldots ,n\).

Assumptions and Preliminaries: Throughout the paper we rely on the following standing assumption.

Assumption 2.2

   

  1. (A.1)

    The functions \(\sigma ,\mu \in {{{\mathcal {C}}}}^1([0,\infty ))\).

  2. (A.2)

    \(\sigma ^2(x)>0\) and \(\vert \sigma (x)\vert +\vert \mu (x)\vert \le C(1+x)\) for some \(C>0\), for all \(x\ge 0\).

  3. (A.3)

    The function \(\mu \) satisfies \(\mu '(x) < r\) for all \(x\ge 0\). Moreover, there exists a constant \(c>0\) such that \(\mu (x)\le rx-c^{-1}\) for \(x\ge c\).

Remark 2.3

The aim of the present paper is to investigate Nash equilibria corresponding to threshold strategies. A main finding is that the conditions in Assumption 2.2, which are parallel to the conditions in, e.g., [18] and [21] for non-competitive cases, are sufficient for the existence of such equilibria; cf. Theorem 3.4. In view of the proof of Theorem 3.4 it can however be seen that it would be enough, in order to guarantee the existence of such equilibria, to instead impose appropriate conditions on the functions \(\psi \) and \(\varphi _{nK}\) below. In line with much of the literature on the optimal dividend problem for diffusions (cf. e.g. the discussion and the references in Appendix A, Remark 3.9 and Remark 3.10 in [9]) we choose however to present our main results under assumptions placed directly on the model primitives (as in Assumption 2.2). The most interesting assumption to relax is perhaps (A.3), without which threshold strategies are no longer necessarily optimal; see e.g [3] and [7] for results in the non-competitive setting. We also remark that there are studies, again in the non-competitive setting, showing that if \(\mu '(x)-r\) is positive on an interval \((0,x_0)\) and negative on \((x_0,\infty )\), then threshold strategies are optimal provided the condition \(\mu (0)\ge 0\) is also imposed, cf. [4] and [7].

For any fixed constant \(A\ge 0\) we define the downwards shifted drift function

$$\begin{aligned} \mu _A(x)= \mu (x)- A, \end{aligned}$$

and we denote by \(\psi _A\) (\(\varphi _A\)) a positive and increasing (decreasing) solution to

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)f''(x)+\mu _A(x)f'(x) -rf(x)=0 \end{aligned}$$

with \(\psi _A(0)=\varphi _A(\infty )=0\). Then, \(\psi _A\) and \(\varphi _A\) are unique up to multiplication with positive constants, cf. [8, p. 18-19], and \(\mathcal C^3([0,\infty ))\). Moreover,

$$ \begin{aligned} \frac{\varphi _A(y)}{\varphi _A(x)} = {{\,\mathrm{{\mathbb {E}}}\,}}_y \left[ e^{-r\tau _x}\right] \quad \quad \& \quad \quad \frac{\psi _A(x)}{\psi _A(y)} = {{\,\mathrm{{\mathbb {E}}}\,}}_x \left[ e^{-r\tau _y}\right] \end{aligned}$$
(2.3)

for \(x<y\), where \(\tau _z:=\inf \{t\ge 0;Y_t=z\}\) and Y is defined up to absorption at 0 by

$$\begin{aligned} \left\{ \begin{array}{ll} dY_t=\mu _A(Y_t)\,dt + \sigma (Y_t)\,dW_t\\ Y_0=y.\end{array}\right. \end{aligned}$$
(2.4)

We use the normalization given by \(\psi _A'(0)=1\) and \(\varphi _A(0)=1\). If \(A=0\) so that \(\mu _A = \mu \), then we for notational convenience write \(\psi \) and \(\varphi \) instead of \(\psi _0\) and \(\varphi _0\).

Most parts of the following lemma are well-known, compare [19, Lemma 2.2], [6, Proposition 2.5] and [21, Lemma 4.1]. For the convenience of the reader, however, we provide a full proof.

Lemma 2.4

Under (A.1)–(A.3):

  1. (i)

    \(\psi '(x)>0\) for \(x\ge 0\) and \(\psi \) is (strictly) concave-convex on \([0,\infty )\) with a unique inflection point \(b^* \in [0,\infty )\). In fact, if \(\mu (0)>0\) then \(b^*>0\), and \(\psi ''(b^*)=0\), \(\psi ''(x)<0\) for \(x<b^*\) and \(\psi ''(x)>0\) for \(x>b^*\); and otherwise \(b^*=0\) and \(\psi ''(x)>0\) for \(x> 0\).

  2. (ii)

    \(\varphi _A'(x)<0\) and \(\varphi _A''(x)>0\) for \(x\ge 0\), for all \(A \ge 0\).

Proof

First we show that \(\psi '>0\) everywhere. To see this, note that \(\psi '(0)=1\), and if \(\psi '(x)=0\) at some \(x>0\), then \(\psi '\) has a local minimum at x so that \(\psi ''(x)=0\). Consequently,

$$\begin{aligned}0=\frac{\sigma ^2}{2}\psi ''=-\mu \psi '+r\psi =r\psi >0\end{aligned}$$

at x, which is a contradiction, so \(\psi '>0\) everywhere.

Next assume that \(\psi ''(x)\le 0\) at some point \(x>0\), and assume that y is a point in (0, x) such that \(\psi ''(y)=0\) and \(\psi ''\le 0 \) on (y, x). Then \(\psi '''(y)\le 0\), but we also have

$$\begin{aligned}\frac{\sigma ^2}{2}\psi '''=-(\mu + \sigma \sigma ')\psi ''+(r-\mu ')\psi '=(r-\mu ')\psi '>0\end{aligned}$$

at y by (A.3). The existence of a unique inflection point \(b^*\) (possibly taking degenerate values 0 or \(\infty \)) thus follows.

To rule out \(b^*=\infty \), note that in that case \(\psi \) is concave on \([0,\infty )\), so

$$\begin{aligned}0\ge \frac{\sigma ^2}{2}\psi '' =-\mu \psi '+r\psi \ge -\mu ^+\psi '+r\psi \ge (rx-\mu ^+)\frac{\psi }{x}>0\end{aligned}$$

for x large, where \(\mu ^+=\max \{\mu ,0\}\). Consequently, \(b^*<\infty \). Moreover, \(\frac{\sigma ^2}{2}\psi ''(0)=-\mu (0)\), so \(b^*>0\) if \(\mu (0)>0\) and \(b^*=0\) if \(\mu (0)<0\). If \(\mu (0)=0\), then \(\psi ''(0)=0\), but then \(\psi '''(0)=\frac{2(r-\mu '(0))}{\sigma ^2(0)}>0\) so that \(b^*=0\) also in this case.

For (ii), first note that if \(\varphi '_A(x)=0\) at some \(x\ge 0\), then \(\varphi ''_A(x)=\frac{2r}{\sigma ^2(x)}\varphi _A(x)> 0\) so that \(\varphi '_A>0\) in a right neighborhood of x, which contradicts the monotonicity of \(\varphi _A\). Thus \(\varphi '_A<0\) everywhere.

Now, assume that there exists a point \(x\ge 0\) with \(\varphi _ A''(x)=0\). Then

$$\begin{aligned} \frac{\sigma ^2}{2}\varphi _A'''=-(\mu + \sigma \sigma ')\varphi _A''+(r-\mu ')\varphi _A'=(r-\mu ')\varphi _A'<0\end{aligned}$$

at x, so then \(\varphi _A\) is concave on \([x,\infty )\). This is, however, impossible, since \(\varphi _A\) is strictly decreasing and bounded. It follows that \(\varphi _A''>0\) everywhere. \(\square \)

Remark 2.5

It is well-known that the inflection point \(b^*\) is the level at which X should be reflected in the single-agent version (\(n=1\)) of the game described above when allowing for unbounded extraction rates (i.e. singular control). Specifically, consider the problem an agent would face if she were alone (\(n=1\)) and could instead of \(\int _0^t\lambda _{1t}ds\), cf. (2.1), select any non-decreasing adapted RCLL process \(\Lambda \) (satisfying admissibility in the sense that \(\Lambda _{0-}=0\) and \(X_{\tau }\ge 0\)) in order to maximize the reward

$$\begin{aligned}{\mathbb {E}}_x\left( \int _0^{\tau } e^{-rt} d\Lambda _{t}\right) , \end{aligned}$$

(cf. (2.2)); see [21] for the original formulation. In the present setting and in case \(\mu (0)>0\) this problem has the value function

$$\begin{aligned} U(x)= {\left\{ \begin{array}{ll} C^*\psi (x), &{} 0\le x\le b^*,\\ x- b^* + C^*\psi (b^*), &{} x \ge b^*, \end{array}\right. } \end{aligned}$$

where \(C^*= (\psi '(b^*))^{-1}\) so that \(U'(b^*)=1\) and \(U''(b^*)=0\), with \(b^*>0\), and the optimal policy is to reflect the state process X at a barrier consisting of the inflection point \(b^*\), with an immediate dividend of \(x-b^*\) in case \(x > b^*\), and in case \(\mu (0)\le 0\) the optimal policy is immediate payout of all surplus x; see [21, Theorem 4.3] and [9, Proposition 2.6].

3 A Threshold Nash Equilibrium

The main objective of the present paper is to find and study Nash equilibria (Definition 2.1) of threshold type, i.e. Nash equilibria where each extraction rate \(\lambda _i\) has the form

$$\begin{aligned} \lambda _{it}=KI_{\{ X_t\ge b_i\}} \text{ for } \text{ some } \text{ constant } b_i\ge 0 \text{ and } \text{ all } t\ge 0. \end{aligned}$$

With a slight abuse of notation we write a strategy profile comprising only threshold strategies as \(\varvec{\lambda }=(b_1,\ldots ,b_n)\).

3.1 Deriving a Candidate Nash Equilibrium

In this section we derive a candidate Nash equilibrium of threshold type. We remark that this section is mainly of motivational value and that a verification result is reported in Sect. 3.2.

Since the agents are identical it is natural to search for a symmetric Nash equilibrium, i.e. an equilibrium of the kind \(\varvec{{{\hat{\lambda }}}} = ({{\hat{\lambda }}},\ldots ,{{\hat{\lambda }}})\) for some admissible strategy \({{\hat{\lambda }}} =({\hat{\lambda _t}})_{t\ge 0}\). Clearly, if \(\varvec{{{\hat{\lambda }}}}\) is such a symmetric equilibrium, then the corresponding equilibrium values are all identical, and we will denote this shared equilibrium value function by \(V= \{V(x),x\ge 0\}\).

Now, if agent n (who is singled out without loss of generality) deviates from such an equilibrium by using an alternative strategy \(\lambda \), then the corresponding state process is given by

$$\begin{aligned} dX_t = \left( \mu (X_t)- (n-1){{\hat{\lambda }}}(X_t)-\lambda (X_t) \right) dt + \sigma (X_t) dB_t. \end{aligned}$$
(3.1)

For \(\varvec{{{\hat{\lambda }}}}\) to be a Nash equilibrium it should be the case that setting \(\lambda ={{\hat{\lambda }}}\) in (3.1) maximizes the corresponding reward for agent n and that this strategy gives the equilibrium value V. Hence, from standard martingale arguments it follows that V should satisfy

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)V''(x)+\left( \mu (x)-(n-1){{\hat{\lambda }}}(x)-\lambda \right) V'(x) -rV(x) + \lambda&\le 0 \end{aligned}$$
(3.2)

for all \(\lambda \in [0,K]\) and \(x>0\), and that equality in (3.2) should be obtained when \(\lambda = {{\hat{\lambda }}}\), i.e.

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)V''(x)+\left( \mu (x)-n{{\hat{\lambda }}}(x)\right) V'(x) -rV(x) + {{\hat{\lambda }}}(x)= 0. \end{aligned}$$
(3.3)

Subtracting Equation (3.3) from Equation (3.2) yields

$$\begin{aligned} \left( V'(x)-1\right) ({{\hat{\lambda }}}(x) - \lambda )\le 0 \end{aligned}$$

for all \(\lambda \in [0,K]\). Hence one finds that

$$\begin{aligned} {{\hat{\lambda }}}(x)= {\left\{ \begin{array}{ll} 0, &{}x \in \{x: V'(x)>1\}\\ K, &{}x \in \{x: V'(x)<1\}, \end{array}\right. } \end{aligned}$$
(3.4)

i.e.

  1. (i)

    each agent extracts resources according to the maximal extraction rate K when \(V'(x)<1\),

  2. (ii)

    no resources are extracted when \(V'(x)>1\).

Since we seek a Nash equilibrium of threshold type we now make the Ansatz \({{\hat{\lambda }}}(x)= KI_{\{ x\ge {{\hat{b}}}\}}\) for some threshold \({{\hat{b}}} \ge 0\). In this case it should hold, cf. (3.3), that

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)V''(x)+\mu (x) V'(x)-rV(x) = 0, \text{ for } 0<x <{{\hat{b}}} \end{aligned}$$
(3.5)

and

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)V''(x)+\left( \mu (x)-nK\right) V'(x)-rV(x) + K = 0, \text{ for } x > {{\hat{b}}} \end{aligned}$$
(3.6)

as well as \(V'({{\hat{b}}})=1\) in case \({{\hat{b}}}>0\). We treat the cases \({{\hat{b}}}=0\) and \({{\hat{b}}}>0\) separately.

Suppose first that \({{\hat{b}}}=0\). Solving (3.6) then yields \(V(x)=C_1\psi _{nK}(x)+C_2\varphi _{nK}(x)+\frac{K}{r}\) for constants \(C_1\) and \(C_2\). Imposing \(V(\infty )=K/r\) (corresponding to maximal extraction for an infinite time) and \(V(0)=0\) yields \(C_1=0\) and \(C_2=-K/r\) so that

$$\begin{aligned} V(x)=\frac{K}{r}(1-\varphi _{nK}(x)). \end{aligned}$$
(3.7)

Moreover, in view of (3.4), we find that \(V'(x)\le 1\) must hold for all \(x\ge 0\). In view of the convexity of \(\varphi _{nK}\), we conclude that the case \({{\hat{b}}} = 0\) requires that

$$\begin{aligned} \varphi _{nK}'(0)\ge -r/K. \end{aligned}$$
(3.8)

Next, if instead

$$\begin{aligned} \varphi _{nK}'(0)< -r/K, \end{aligned}$$
(3.9)

then we expect that \({{\hat{b}}}>0\) and a corresponding equilibrium value function of the form

$$\begin{aligned} V(x)= {\left\{ \begin{array}{ll} D_1\psi (x)+D_2\varphi (x), &{} 0<x <{{\hat{b}}},\\ D_3\psi _{nK}(x) + D_4\varphi _{nK}(x)+ \frac{K}{r}, &{} x > {{\hat{b}}},\\ \end{array}\right. } \end{aligned}$$

for some constants \(D_i\), \(i=1,\ldots ,4\) and \({{\hat{b}}}\) to be determined. Imposing the boundary conditions \(V(0)=0\) and \(V(\infty )=K/r\) gives \(D_2=0\) and \(D_3=0\). We also make the Ansatz that V(x) is differentiable at \({{\hat{b}}}\), which determines \(D_1\) and \(D_4\). We thus obtain

$$\begin{aligned} V(x)= {\left\{ \begin{array}{ll} D_1\psi (x), &{} 0<x\le {{\hat{b}}},\\ D_4\varphi _{nK}(x) + \frac{K}{r}, &{} x \ge {{\hat{b}}}, \end{array}\right. } \end{aligned}$$
(3.10)

where

$$\begin{aligned} D_1=\frac{-\frac{K}{r}\varphi _{nK}'({{\hat{b}}})}{\varphi _{nK}({{\hat{b}}})\psi '({{\hat{b}}})-\varphi _{nK}'({{\hat{b}}})\psi ({{\hat{b}}}) } \end{aligned}$$
(3.11)

and

$$\begin{aligned} D_4= \frac{-\frac{K}{r}\psi '({{\hat{b}}})}{\varphi _{nK}({{\hat{b}}})\psi '({{\hat{b}}}) -\varphi _{nK}'({{\hat{b}}})\psi ({{\hat{b}}})}. \end{aligned}$$
(3.12)

Finally, in line with the arguments above, we determine \({{\hat{b}}}\) by imposing the condition

$$\begin{aligned} V'({{\hat{b}}})=1. \end{aligned}$$
(3.13)

Differentiating (3.10) thus gives the equation

$$\begin{aligned} \frac{K}{r}\frac{\psi '({{\hat{b}}})\varphi _{nK}'({{\hat{b}}})}{\varphi _{nK}'({{\hat{b}}})\psi ({{\hat{b}}})-\varphi _{nK}({{\hat{b}}})\psi '({{\hat{b}}}) }=1, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \frac{\psi ({{\hat{b}}})}{\psi '({{\hat{b}}})}-\frac{\varphi _{nK}({{\hat{b}}})}{\varphi _{nK}'({{\hat{b}}})}=\frac{K}{r}. \end{aligned}$$
(3.14)

Remark 3.1

Using

$$\begin{aligned}(\mu (0)-nK)\varphi '_{nK}(0) -r\varphi _{nK}(0)=-\frac{\sigma ^2(0)}{2}\varphi ''_{nK}(0)\le 0,\end{aligned}$$

it can be shown that if (3.9) holds then \(\mu (0)>0\) (equivalently, if \(\mu (0)\le 0\) then (3.8) holds). Hence, if (3.9) holds then \(b^*>0\) and if \(b^*=0\) then (3.8) holds (see Lemma 2.4). In view of Remark 2.5 and Theorem 3.4 (below) we thus find that the Nash equilibrium is for each agent to always extract maximally (\({{\hat{b}}}=0\)) whenever the optimal policy in the singular extraction (\(K=\infty \)) single-agent (\(n=1\)) version of the game is immediate payout of all surplus (\(b^*=0\)). The dependence of \({{\hat{b}}}\) on n and K is further analyzed in Sect. 3.3.

Lemma 3.2

Suppose (3.9) holds. Then Eq. (3.14) has a unique positive solution \({{\hat{b}}}\). Moreover, \(0<{{\hat{b}}} \le b^*\), where \(b^*\) is the unique inflection point of \(\psi \) (see also Remark 2.5).

Proof

Define the function \(f:[0,\infty )\rightarrow {\mathbb {R}}\) by

$$\begin{aligned} f(b)=\frac{\psi (b)}{\psi '(b)}-\frac{\varphi _{nK}(b)}{\varphi _{nK}'(b)}, \end{aligned}$$
(3.15)

and note that \(f(0)=-1/\varphi _{nK}'(0)<K/r\) by (3.9). Thus any solution to the equation \(f({{\hat{b}}})=K/r\) satisfies \({{\hat{b}}}>0\). Differentiation shows that

$$\begin{aligned} \frac{\sigma ^2(b)}{2}f'(b)&= \frac{\sigma ^2(b)}{2}\left( \frac{\varphi _{nK}(b)\varphi _{nK}''(b)}{(\varphi _{nK}'(b))^2}-\frac{\psi (b)\psi ''(b)}{(\psi '(b)) ^2}\right) \nonumber \\&= \frac{f(b)}{\varphi _{nK}'(b)}(\mu _{nK}(b)\varphi _{nK}'(b)-r\varphi _{nK}(b))+\frac{\psi (b)}{\psi '(b)}(nK-rf(b))\nonumber \\&\ge \frac{\psi (b)}{\psi '(b)}(nK-rf(b)), \end{aligned}$$
(3.16)

where we have used the ODEs that \(\varphi _{nK}\) and \(\psi \) satisfy and, in the last inequality, that \(\varphi _{nK}\) is convex so that

$$\begin{aligned}\mu _{nK}(b)\varphi _{nK}'(b)-r\varphi _{nK}(b)=-\frac{\sigma ^2(b)}{2}\varphi _{nK}''(b)\le 0.\end{aligned}$$

It follows that f is increasing as long as \(f\le nK/r\). Consequently, the equation \(f({{\hat{b}}})=K/r\) has at most one positive solution. Moreover, by similar calculations as in (3.16),

$$\begin{aligned} \frac{\sigma ^2(b)}{2}f'(b)&=\frac{f(b)}{\psi '(b)}(\mu \psi '(b)-r\psi (b))+\frac{\varphi _{nK}(b)}{\varphi _{nK}'(b)}(nK-rf(b)), \end{aligned}$$

so at the inflection point \(b^*\) of \(\psi \) we have

$$\begin{aligned}\frac{\sigma ^2(b^*)}{2}f'(b^*)=\frac{\varphi _{nK}(b^*)}{\varphi _{nK}'(b^*)}(nK-rf(b^*)).\end{aligned}$$

Comparing with (3.16) we find that

$$\begin{aligned}\frac{\psi (b^*)}{\psi '(b^*)}(nK-rf(b^*))\le \frac{\varphi _{nK}(b^*)}{\varphi _{nK}'(b^*)}(nK-rf(b^*)),\end{aligned}$$

which implies that \(f(b^*)\ge nK/r\). Thus, by continuity there exists a point \({{\hat{b}}}\in (0,b^*]\) such that \(f({{\hat{b}}})=K/r\), which completes the proof. \(\square \)

Note that if \({{\hat{b}}}=0\), then \(D_4=-K/r\) and the representation of V in (3.10) yields (3.7). Let us summarize the above discussion by specifying the candidate equilibrium threshold \({{\hat{b}}}\) and the corresponding equilibrium value function V. If (3.8) holds, then we define \({{\hat{b}}}=0\). If instead (3.9) holds, then we define \({{\hat{b}}}\) as the unique positive solution of (3.14). In both cases

$$\begin{aligned} V(x) = {\left\{ \begin{array}{ll} D_1\psi (x), &{} 0<x\le {{\hat{b}}},\\ D_4\varphi _{nK}(x) + \frac{K}{r}, &{} x \ge {{\hat{b}}}, \end{array}\right. } \end{aligned}$$
(3.17)

with \(D_1\) and \(D_4\) specified in (3.11)–(3.12). Note that \(V \in {\mathcal {C}}^1([0,\infty )) \cap \mathcal C^2([0,\infty )\setminus \{{{\hat{b}}}\})\) and that it satisfies (3.5)–(3.6). Moreover, if \({{\hat{b}}}>0\) then also (3.13) holds.

Lemma 3.3

The function V is concave.

Proof

If (3.8) holds, then \(D_4=-K/r\) and so \(V(x)=\frac{K}{r}(1-\varphi _{nK}(x))\). The concavity of V thus follows from convexity of \(\varphi _{nK}\). If instead (3.9) holds, then the claim is verified using (3.17), Lemma 3.2 and Lemma 2.4. \(\square \)

3.2 A Verification Theorem for the Threshold Nash Equilibrium

Theorem 3.4

A Nash equilibrium of threshold type exists. In particular, define \({{\hat{b}}}=0\) if (3.8) holds, and let \({{\hat{b}}}\) be the unique solution to (3.14) if instead (3.9) holds. Then, \(\varvec{{{\hat{\lambda }}}}=({{\hat{b}}},\ldots ,{{\hat{b}}})\) is a Nash equilibrium and the corresponding equilibrium value functions are identical and given by V defined in (3.17).

Proof

Suppose an arbitrary agent i deviates from \(\varvec{\hat{\lambda }}=({{\hat{b}}},\ldots ,{{\hat{b}}})\). More precisely, consider the strategy profile \((\lambda ,\varvec{{{\hat{\lambda }}}}_{-i})\) (cf. Definition 2.1), where \(\lambda \) is an arbitrary admissible strategy. Then X is given by

$$\begin{aligned} dX_t = \left( \mu (X_t)-\lambda (X_t)-(n-1)KI_{\{X_t\ge {{\hat{b}}}\}}\right) dt + \sigma (X_t)\,dB_t. \end{aligned}$$

Using Itô’s formula we obtain

$$\begin{aligned} e^{-r(\tau \wedge \theta _t)}V(X_{\tau \wedge \theta _t })&= V(x) + \int _0^{\tau \wedge \theta _t } e^{-rs} \left( \mu (X_s)-\lambda (X_s)-(n-1)KI_{\{X_s\ge {{\hat{b}}}\}} \right) V'(X_s)\,ds\\&\quad +\int _0^{\tau \wedge \theta _t }e^{-rs} \left( \frac{1}{2}\sigma ^2(X_s)V''(X_s)I_{\{X_s\ne {{\hat{b}}}\}}-rV(X_s)\right) ds\\&\quad + \int _0^{\tau \wedge \theta _t } e^{-rs} \sigma (X_s)V'(X_s)\,dB_s, \end{aligned}$$

where \(\theta _t:= \inf \{s\ge 0: X_s \ge t\}\wedge t\) (with the standard convention that the infimum of the empty set is infinite). It is directly verified, cf. (3.5)–(3.6), that

$$\begin{aligned} \frac{1}{2}\sigma ^2(x)V''(x)+\left( \mu (x)-nKI_{\{x\ge {{\hat{b}}}\}}\right) V'(x)-rV(x)+KI_{\{x\ge {{\hat{b}}}\}} = 0 \end{aligned}$$

for all \(x\ne {{\hat{b}}}\), which implies that

$$\begin{aligned} e^{-r({\tau \wedge \theta _t})}V(X_{\tau \wedge \theta _t })&= V(x) + \int _0^{\tau \wedge \theta _t } e^{-rs} \left( \left( V'(X_s)-1\right) \left( KI_{\{X_s\ge {{\hat{b}}}\}}-\lambda (X_s) \right) -\lambda (X_s) \right) ds\nonumber \\&\quad + \int _0^{\tau \wedge \theta _t } e^{-rs} \sigma (X_s)V'(X_s)\,dB_s. \end{aligned}$$
(3.18)

In case (3.8) holds, we have \(V(x)=\frac{K}{r}(1-\varphi _{nK}(x))\). By concavity of V (cf. Lemma 3.3) we thus obtain \(V'(x)\le V'(0)\le 1\), so

$$\begin{aligned} \left( V'(x)-1\right) \left( KI_{\{x\ge {{\hat{b}}}\}}-\lambda \right) \le 0, \text{ for } \text{ all } \lambda \in [0,K]\text{. } \end{aligned}$$
(3.19)

Similarly, if (3.9) holds, then it follows by concavity of V and \(V'({{\hat{b}}})=1\) that (3.19) holds. Hence

$$\begin{aligned} V(x)&\ge - \int _0^{\tau \wedge \theta _t} e^{-rs} \sigma (X_s)V'(X_s)\,dB_s + e^{-r({\tau \wedge \theta _t})}V(X_{\tau \wedge \theta _t }) + \int _0^{\tau \wedge \theta _t} e^{-rs}\lambda (X_s)\,ds. \end{aligned}$$

Taking expectation yields

$$\begin{aligned} V(x) \ge {\mathbb {E}}_x\left( e^{-r({\tau \wedge \theta _t })}V(X_{\tau \wedge \theta _t })\right) + {\mathbb {E}}_x\left( \int _0^{\tau \wedge \theta _t } e^{-rs}\lambda (X_s)\,ds\right) , \end{aligned}$$

where we used that \(V'(\cdot )\) and \(\sigma (\cdot )\) are bounded on the stochastic interval \([0,\theta _t]\) so that the expectation of the stochastic integral vanishes. Since \(V\ge 0\), using monotone convergence we find that

$$\begin{aligned} V(x) \ge {\mathbb {E}}_x\left( \int _0^{\tau } e^{-rs}\lambda (X_s)\,ds\right) = J_i(x;({\lambda _{i}},\varvec{{{\hat{\lambda }}}}_{-i})). \end{aligned}$$

Furthermore, using the threshold strategy \(KI_{\{X_s\ge {{\hat{b}}}\}}\) instead of the arbitrary strategy \(\lambda (X_s)\) from the beginning of the proof yields, from (3.18),

$$\begin{aligned} V(x) = {\mathbb {E}}_x\left( e^{-r({\tau \wedge \theta _t })}V(X_{\tau \wedge \theta _t })\right) + {\mathbb {E}}_x\left( \int _0^{\tau \wedge \theta _t } e^{-rs}KI_{\{X_s\ge {{\hat{b}}}\}}\,ds\right) . \end{aligned}$$
(3.20)

Let us now consider what happens if we send \(t\rightarrow \infty \), so that \(\tau \wedge \theta _t \rightarrow \tau \). In this case, the first term in the right hand side of (3.20) converges to zero; to see this we use that the limit is \(\lim _{t\rightarrow \infty }e^{-r(\tau \wedge \theta _t)}V(X_{\tau \wedge \theta _t})=0\) (note that the function V is bounded and that \(V(0)=0\)), so we obtain that the limit of the first term is zero using dominated convergence. Moreover, using monotone convergence we find that the second term in the right hand side of (3.20) converges to \({\mathbb {E}}_x\left( \int _0^{\tau } e^{-rt}KI_{\{X_t\ge {{\hat{b}}}\}}\,dt\right) \). Hence,

$$\begin{aligned} V(x) = {\mathbb {E}}_x\left( \int _0^{\tau } e^{-rt}KI_{\{X_t\ge {{\hat{b}}}\}}\,dt\right) =J_i(x;\varvec{{{\hat{\lambda }}}}). \end{aligned}$$

Consequently, \(\varvec{{{\hat{\lambda }}}}=({{\hat{b}}},\ldots ,{{\hat{b}}})\) is a Nash equilibrium. \(\square \)

3.3 Properties of the Threshold Nash Equilibrium

To understand the effect of competition, we also provide a study of the dependence on the number n of agents for the equilibrium threshold and for the corresponding equilibrium value. Our first result in this direction shows that increased competition lowers the equilibrium threshold and decreases each agent’s equilibrium value.

Theorem 3.5

(The effect of increased competition.) With all other parameters being held fixed, the threshold \({{\hat{b}}}={{\hat{b}}}(n)\) in the symmetric threshold strategy \(\varvec{{{\hat{\lambda }}}}=({{\hat{b}}},\ldots ,{{\hat{b}}})\) is decreasing in n. In fact, there exists a number \({{\bar{n}}}\) such that \({{\hat{b}}}\) is decreasing for \(n < {{\bar{n}}}\) and \({{\hat{b}}}=0\) for \(n \ge {\bar{n}}\). Moreover, the equilibrium value \(V(x)=V(x;n)\) is decreasing in n.

Proof

First note that the stochastic representation (2.3) gives that

$$\begin{aligned}\varphi _{nK}(y)={{\,\mathrm{{\mathbb {E}}}\,}}_y[e^{-r\tau _0}],\end{aligned}$$

where \(\tau _0\) is the first hitting time of 0 by a process Y, cf. (2.4), with drift \(\mu _{nK}\). Since the drift of Y decreases in n, this implies that \(\varphi _{nK}(y)\) is increasing in n, and therefore \(\varphi _{nK}(0)=1\) yields that \(\varphi _{nK}'(0)\) is increasing in n. Thus there exists \({{\bar{n}}}\) such that condition (3.8) holds if \(n\ge {{\bar{n}}}\) (so that \({{\hat{b}}}=0\) for such n), and (3.9) holds if \(n<{{\bar{n}}}\). Moreover, (2.3) also yields that the expression

$$\begin{aligned}\frac{\varphi _{nK}(y)}{\varphi _{nK}(x)}\end{aligned}$$

is increasing in n for \(x<y\). Therefore, \(\frac{\varphi _{nK}'(x)}{\varphi _{nK}(x)}\) is increasing in n, so \(-\frac{\varphi _{mK}}{\varphi _{mK}'}\le -\frac{\varphi _{nK}}{\varphi _{nK}'}\) if \(m\le n\). Consequently, the function \(f=f_n\) in (3.15) is increasing in n, so it follows that \({{\hat{b}}}={{\hat{b}}}(n)\) is decreasing in n for \(n<{{\bar{n}}}\) (cf. the proof of Lemma 3.2).

To show that V is decreasing in n, let \(m\le n\) and denote by \({{\hat{b}}}_m,{{\hat{b}}}_n\) and \(V_m,V_n\) the corresponding thresholds and equilibrium values, respectively. By the above, \({{\hat{b}}}_m\ge {{\hat{b}}}_n\).

If \({{\hat{b}}}_m\ge {{\hat{b}}}_n>0\), then \(V_m=A_m\psi \) and \(V_n=A_n\psi \) on \([0,{{\hat{b}}}_m]\) and \([0,{{\hat{b}}}_n]\), respectively, so \(V_n'({{\hat{b}}}_n)=1\le V_m'(b_n)\) by the concavity of \(V_m\). Thus \(A_m\ge A_n\), and

$$\begin{aligned} V_m\ge V_n \text{ on } [0,{{\hat{b}}}_n]. \end{aligned}$$
(3.21)

Clearly, (3.21) holds also (trivially) in the case \({{\hat{b}}}_n=0\).

As a consequence of (3.21), we also have \(V_m\ge V_n\) on \([0,{{\hat{b}}}_m]\) since \(V'_n\le 1\le V'_m\) on \([{{\hat{b}}}_n,{{\hat{b}}}_m]\). On the interval \([{{\hat{b}}}_m,\infty )\), the function \(u:=V_m-V_n\) satisfies

$$\begin{aligned}\frac{\sigma ^2}{2}u''+(\mu -nK)u'-ru=-(n-m)KV_m'\le 0\end{aligned}$$

with boundary conditions \(u({{\hat{b}}}_m)\ge 0\) and \(u(\infty )=0\). The maximum principle then yields \(u\ge 0\) on \([{{\hat{b}}}_m,\infty )\). Consequently, \(V_m\ge V_n\) everywhere, which completes the proof. \(\square \)

Intuitively, the effect in Theorem 3.5 of adding more agents of the same type is negative as it both adds competition and also increases the maximal total push rate nK (while the individual push rate K is constant). In the following result we isolate the effect of increased competition by studying the case with a fixed maximal total push rate \({{\overline{K}}}\).

Theorem 3.6

(The effect of increased competition with constant total extraction rate.) Let the maximal individual extraction rate be \(K={{\overline{K}}}/n\) (so that the total maximal extraction rate \({{\overline{K}}}\) is independent of n). Then the equilibrium threshold \({{\hat{b}}}={{\hat{b}}}(n)\) and the total equilibrium value nV(x) are both decreasing in n.

Proof

The function f in (3.15) is in this case given by \(f(b)=\frac{\psi (b)}{\psi '(b)}-\frac{\varphi _{\overline{K}}(b)}{\varphi _{{{\overline{K}}}}'(b)}\), which is independent of n, and the threshold \({{\hat{b}}}={{\hat{b}}}(n)\) is given as the unique solution of \(f({{\hat{b}}})=K/r={{\overline{K}}}/(rn)\) provided \(\varphi _{\overline{K}}'(0)<-rn/{{\overline{K}}}\), and \({{\hat{b}}}(n)=0\) otherwise. Since f is increasing as long as \(f<{{\overline{K}}}/r\) (cf. the proof of Lemma 3.2), the solution of \(f({{\hat{b}}}(n))=\overline{K}/(nr)\) is decreasing in n.

It remains to show that nV(x) decreasing. Recall that

$$\begin{aligned} V(x)= {\left\{ \begin{array}{ll} D_1(n)\psi (x), &{} 0<x\le {{\hat{b}}}(n),\\ D_4(n)\varphi _{{{{\overline{K}}}}}(x) + \frac{{{{\overline{K}}}}}{nr}, &{} x \ge {{\hat{b}}}(n), \end{array}\right. } \end{aligned}$$

where \({{\hat{b}}}(n)\) solves

$$\begin{aligned}f({{\hat{b}}}(n)):=\frac{\psi ({{\hat{b}}}(n))}{\psi '({{\hat{b}}}(n))} - \frac{\varphi _{{{\overline{K}}}}({{\hat{b}}}(n))}{\varphi _{{{\overline{K}}}}'({{\hat{b}}}(n))}=\frac{{{\overline{K}}}}{nr}\end{aligned}$$

if (3.9) holds, and \({{\hat{b}}}(n)=0\) otherwise. Moreover,

$$\begin{aligned} D_1(n)=\frac{-\frac{{{\overline{K}}}}{nr}\varphi _{{{{\overline{K}}}}}'({{\hat{b}}}(n))}{\varphi _{{{{\overline{K}}}}}({{\hat{b}}}(n))\psi '({{\hat{b}}}(n))-\varphi _{{{{\overline{K}}}}}'({{\hat{b}}}(n))\psi ({{\hat{b}}}(n))} \end{aligned}$$

and

$$\begin{aligned} D_4(n)= \frac{-\frac{{{\overline{K}}}}{nr}\psi '({{\hat{b}}}(n))}{\varphi _{{{{\overline{K}}}}}({{\hat{b}}}(n))\psi '({{\hat{b}}}(n)) -\varphi _{{{{\overline{K}}}}}'({{\hat{b}}}(n))\psi ({{\hat{b}}}(n))}. \end{aligned}$$

In order to show that nV(x; n) is decreasing in n we now show that \(nD_1(n)\) and \(nD_4(n)\) are decreasing in n. We begin with \(nD_1(n)\). Since \({{\hat{b}}}(n)\) is decreasing in n (Theorem 3.5), it suffices to show that \(\frac{\varphi _{{{{\overline{K}}}}}'(x)}{\varphi _{{\overline{K}}}(x)\psi '(x)-\varphi _{{{{\overline{K}}}}}'(x)}\) is decreasing for \(x\in (0,{{\hat{b}}}(1))\), which is equivalent to

$$\begin{aligned} \psi ''(x)/\psi '(x)-\varphi ''_{{{{\overline{K}}}}}(x)/\varphi '_{{\overline{K}}}(x) \le 0. \end{aligned}$$

However,

$$\begin{aligned} \frac{\sigma ^2(x)}{2}(\psi ''(x)/\psi '(x)- \varphi ''_{{\overline{K}}}(x)/\varphi '_{{{{\overline{K}}}}}(x))=rf(x)-{{\overline{K}}}\le 0 \end{aligned}$$
(3.22)

for \(x\in (0,{{\hat{b}}}(1))\) (cf. the proof of Lemma 3.2), so \(nD_1(n)\) is decreasing in n. For \(nD_4(n)\) we want to show for \(x\in (0,{{\hat{b}}}(1))\), that \(\frac{\psi '(x)}{\varphi _{{{{\overline{K}}}}}(x)\psi '(x) -\varphi _{{{{\overline{K}}}}}'(x)\psi (x)}\) is decreasing, which is equivalent to

$$\begin{aligned} \psi '(x)\varphi _{{{{\overline{K}}}}}''(x) -\varphi _{{{{\overline{K}}}}}'(x)\psi ''(x)\le 0. \end{aligned}$$

Hence, also in this case (3.22) gives us what is needed.

Now, since \(nD_1(n)\) and \(nD_4(n)\) are decreasing in n, it follows that \(mV(x;m)\ge nV(x;n)\) for \(x\in [0,{{\hat{b}}}(n)]\cup [{{\hat{b}}}(m),\infty )\) if \(m<n\). Moreover, on \([{{\hat{b}}}(n),{{\hat{b}}}(m)]\) we have that the function \(H(x):=mV(x;m)-nV(x;n)\) satisfies

$$\begin{aligned}\frac{\sigma ^2}{2}H''+(\mu -{{\overline{K}}}) H'-rH= -{{\overline{K}}}(mV'(x;m)-1)\le 0\end{aligned}$$

since \(V'(x;m)\ge 1\) on \([{{\hat{b}}}(n),{{\hat{b}}}(m)]\). Since \(H>0\) at the boundary points \(\{{{\hat{b}}}(n),{{\hat{b}}}(m)\}\), a maximum principle gives \(H\ge 0\), so \(mV(x;m)\ge nV(x;n)\) everywhere. \(\square \)

Remark 3.7

In the single-agent game, the optimal threshold (given by \({{\hat{b}}}={{\hat{b}}}(K)\) determined with \(n=1\)) can be shown to be increasing as a function of the maximal extraction rate K. Indeed, implicit differentiation of the relation \(f({{\hat{b}}}(K))=K/r\) yields

$$\begin{aligned}{{\hat{b}}}'(K)=\frac{\sigma ^2({{\hat{b}}})\psi '({{\hat{b}}})}{2K(\mu ({{\hat{b}}})\psi '({{\hat{b}}})-r\psi ({{\hat{b}}}))}\ge 0,\end{aligned}$$

where the inequality is a consequence of \(\psi ''({{\hat{b}}})\le 0\). In the competitive setting of the current paper (where we may have \(n\ge 2\)), however, the effect of an increase in the extraction rate is ambiguous as it facilitates fast extraction not only for you but also for your competitors. We therefore do not expect any monotone relationship between \({{\hat{b}}}\) and K; see Fig. 3 for an illustration of this relationship in the case of constant coefficients.

3.4 The Case of Constant Coefficients

Consider the case of constant drift and diffusion coefficients \(\mu >0\) and \(\sigma >0\). In this case

$$\begin{aligned} \psi (x) = \frac{e^{\alpha x}- e^{ \beta x}}{\alpha -\beta } \text{ and } \varphi _{nK}(x)=e^{\gamma x} \end{aligned}$$

where

$$\begin{aligned} \alpha :&= -\frac{\mu }{\sigma ^2} + \sqrt{\frac{\mu ^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}>0, \\ \beta :&= -\frac{\mu }{\sigma ^2} - \sqrt{\frac{\mu ^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}<0, \text{ and } \\ \gamma :&=-\frac{\mu -nK}{\sigma ^2} - \sqrt{\frac{(\mu -nK)^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}<0. \end{aligned}$$

Let us use Theorem 3.4 to find the Nash equilibrium for this model. First note that condition (3.9) is equivalent to

$$\begin{aligned} \frac{K}{r}\left( \frac{\mu -nK}{\sigma ^2} +\sqrt{\frac{(\mu -nK)^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}\right) >1. \end{aligned}$$
(3.23)

Hence, if (3.23) does not hold, then \({{\hat{b}}}=0\) is the equilibrium threshold, and if (3.23) holds, then the equilibrium threshold is strictly positive and determined by the equation

$$\begin{aligned} \frac{e^{\alpha {{\hat{b}}} }- e^{\beta {{\hat{b}}} }}{\alpha e^{\alpha {{\hat{b}}} }- \beta e^{\beta {{\hat{b}}} }} - \frac{1}{\gamma } =\frac{K}{r}, \end{aligned}$$

cf. (3.14). In the latter case, we find

$$\begin{aligned} {{\hat{b}}} = \frac{\ln {\left( \frac{1-(K/r+1/\gamma )\beta }{1-(K/r+1/\gamma )\alpha }\right) }}{\alpha -\beta }. \end{aligned}$$

Moreover, (3.17) yields a closed formula for the equilibrium value function V. Figures 1, 2 and 3, illustrate the monotonicities in K and n obtained in Theorem 3.5 and Theorem 3.6, as well as the non-monotonicity of \({{\hat{b}}}\) in K, cf. Remark 3.7. The remaining parameters are held fixed, with \(\mu =4\), \(\sigma ^2=2\) and \(r=0.05\).

Fig. 1
figure 1

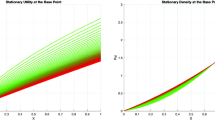
Left: The individual equilibrium value function V(x) (same for each agent) when the number of competitors n is varied and the individual maximal extraction rate K is fixed.Right: The total equilibrium value function nV(x) when n is varied and the total maximal extraction rate \({{\bar{K}}}\) is fixed. (Larger n correspond to lower equilibrium values)

Full size image
Fig. 2
figure 2

The equilibrium threshold \({{\hat{b}}}\) as a function of the number of competitors n when the individual maximal extraction rate K is fixed (left), and when the total maximal extraction rate \({{\bar{K}}}\) is fixed (right), respectively

Full size image
Fig. 3
figure 3

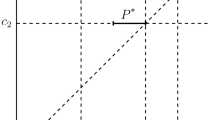
The equilibrium threshold \({{\hat{b}}}\) as a function of the individual extraction rate K, with the number of competitors fixed at \(n=30\). The non-monotone dependence is a consequence of competing effects, where a larger individual maximal extraction rate gives more freedom both to you and to your competitors

Full size image

Let us further interpret the relationship between the maximal individual push rate K and the equilibrium threshold \({{\hat{b}}}\) indicated by Fig. 3. The non-monotone behavior is a consequence of the double role of the maximal push rate K: firstly, a large K gives larger freedom for each agent, thereby pushing up the threshold level, and secondly, it gives more freedom for the competitors, which is likely to reduce the threshold. The overall effect is therefore a non-monotone relationship as depicted in Fig. 3. These two effects are separated in Sect. 4 below, where agents are equipped with individual extraction rates, cf. Fig. 5. Note that one may explain the general hump form a follows. First, a very small maximal rate K implies that (3.8) holds, so then \({{\hat{b}}}=0\) by Theorem 3.4. Second, the strictly competitive game (\(n\ge 2\)) with unbounded extraction rates would degenerate into immediate depletion of resources; this indicates that \({{\hat{b}}}(K)\) is small for large values of K.

4 Individual Extraction Rates

In this section we consider the asymmetric case when maximal extraction rates are not necessarily identical. In particular, a Markovian control \(\lambda _{it}=\lambda _i(X_t)\) is in this section an admissible strategy for agent i if it takes values in \([0,K_i]\), where \(K_1,\ldots ,K_n\) are given positive constants. Again we will search for Nash equilibria of threshold type, which in this section means that for all \(i=1,\ldots ,n\) we have

$$\begin{aligned} \lambda _{it}=K_iI_{\{ X_t\ge b_i\}} \text{ for } \text{ some } \text{ constant } b_i\ge 0 \text{ and } \text{ all } t\ge 0\text{. } \end{aligned}$$

In Sect. 4.1 we report a verification type result for the asymmetric game. In Section 4.2 we establish the existence of a Nash equilibrium of threshold type using a fixed-point argument. The corresponding thresholds are shown to be ordered in the same way as the maximal extraction rates.

4.1 A Single-Agent Problem and a Verification Result

By definition a threshold strategy \(({{\hat{b}}}_1,\ldots ,{{\hat{b}}}_n)\) is a Nash equilibrium if the threshold strategy corresponding to \({{\hat{b}}}_i\) is optimal (in the usual sense) for any agent i in case the other agents use the fixed threshold strategy \(({{\hat{b}}}_1,\ldots ,{{\hat{b}}}_{i-1},{{\hat{b}}}_{i+1},\ldots ,{{\hat{b}}}_n)\) (we use this notation to mean the threshold strategy obtained when removing the threshold of agent i also in case \(i=1\) or \(i=n\)). Thus, all we need in order to verify that a proposed threshold equilibrium is indeed an equilibrium is to solve a single-agent version of the problem investigated in the previous section, but with the complication of a drift function with negative jumps; in particular, the problem of selecting an admissible strategy \(\lambda _{i}=(\lambda _{it})_{t\ge 0}\) for agent i in

$$\begin{aligned} dX_t = \left( \mu (X_t)- \sum _{j\ne i}K_jI_{\{ X_t\ge b_j\}}- \lambda _{it}\right) dt + \sigma (X_t) dB_t, \end{aligned}$$
(4.1)

in order to maximize the reward

$$\begin{aligned} {\mathbb {E}}_x\left( \int _0^{\tau } e^{-rt}{\lambda _{it}}\,dt\right) , \end{aligned}$$
(4.2)

for fixed constants \(b_1,\ldots ,b_{i-1},b_{i+1},\ldots ,b_n\in [0,\infty ), K_1,\ldots ,K_n \in (0,\infty )\).

In line with Sect. 3.1, we thus denote by \(\psi ^{(i)}(x)=\psi ^{(i)}(x;b_1,\ldots ,b_{i-1},b_{i+1},\ldots ,b_n)\) the increasing positive solution of

$$\begin{aligned}&\frac{1}{2}\sigma ^2(x)h''(x)+\left( \mu (x)-\sum _{j \ne i}K_jI_{\{x\ge b_j\}}\right) h'(x) -rh(x)=0, \end{aligned}$$
(4.3)

and by \(\varphi ^{(i)}(x)=\varphi ^{(i)}(x;b_1,\ldots ,b_{i-1},b_{i+1},\ldots ,b_n)\) the decreasing positive solution of

$$\begin{aligned}&\frac{1}{2}\sigma ^2(x)h''(x)+\left( \mu (x)-K_i-\sum _{j\ne i}K_jI_{\{x\ge b_j\}}\right) h'(x) -rh(x)=0, \end{aligned}$$
(4.4)

with the boundary specifications \(\psi ^{(i)}(0)=\varphi ^{(i)}(\infty )=0\), \({\psi ^{(i)}}'(0)=1\) and \(\varphi ^{(i)}(\infty )(0)=1\). Note that these functions are analogous to \(\psi \) and \(\varphi _{nK}\) of the previous section, but due to the discontinuities of the drift function we now merely have that \(\psi ^{(i)},\varphi ^{(i)}\in {\mathcal {C}}^1(0,\infty ) \cap \mathcal C^2\left( [0,\infty )\backslash \{b_1,\ldots ,b_{i-1},b_{i+1},\ldots ,b_n\}\right) \). However, since the jumps of the drift are negative, we may use approximation by drift coefficients for which (A.1) and (A.3) are valid. More specifically, consider drift coefficients \(\{\mu _k\}_{k=1}^\infty \) satisfying (A.1) and (A.3), and with \(\mu _k\uparrow \mu -\sum _{j \ne i}K_jI_{\{\cdot \ge b_j\}}\) pointwise. We then see that the conclusions of Lemma 2.4 still hold. In fact, the corresponding fundamental solutions converge pointwise from above to \(\psi ^{(i)}\) and \(\varphi ^{(i)}\), as \(k\rightarrow \infty \). Using that the pointwise limit of concave/convex functions is again concave/convex, Lemma 2.4 extends as follows.

Lemma 4.1

  1. (i)

    Each function \(\psi ^{(i)}\) is (strictly) concave-convex on \([0,\infty )\) with a unique inflection point \(b^{**}_i\in [0,\infty )\). In particular, if \(\mu (0)-\sum _{j\ne i}K_jI_{\{ b_j=0\}}>0\) then \(b_i^{**}>0\), and otherwise \(b_i^{**}=0\) and \(\psi ^{(i)}\) is convex everywhere.

  2. (ii)

    Each function \(\varphi ^{(i)}\) is convex.

Remark 4.2

In practice, each \(\psi ^{(i)}\) can be found by (i) identifying the fundamental increasing and decreasing solutions to (4.3) separately on the intervals on which the drift function does not jump, (ii) on each interval forming linear combinations of the increasing and decreasing fundamental solutions, (iii) pasting the linear combinations together to form a function \({\mathbb {R}}_+\rightarrow {\mathbb {R}}\), (iv) choosing the constants of the linear combinations so that the resulting \({\mathbb {R}}_+\rightarrow {\mathbb {R}}\) function is continuously differentiable and the boundary conditions are satisfied; this function is then \(\psi ^{(i)}\). We can similarly obtain \(\varphi ^{(i)}\).

Remark 4.3

As in Remark 2.5, the inflection point \(b^{**}_i\) corresponds to the optimal barrier policy in case the maximal push rate of agent i is \(K_i=\infty \).

Relying on Lemma 4.1, the reasoning in Sect. 3.1 extends to the present case. In particular, by relying on a single-agent version of Theorem 3.2 for the present setting, we can verify if it is optimal for any agent i to comply with a proposed threshold equilibrium. We thus obtain the following verification type result.

Theorem 4.4

Suppose a threshold strategy \(({{\hat{b}}}_1,\ldots , {{\hat{b}}}_n)\) satisfies \(V_i'({{\hat{b}}}_i) = 1\) if \({{\hat{b}}}_i >0\) and \(V_i'({{\hat{b}}}_i) \le 1\) if \({{\hat{b}}}_i =0\), for \(i=1,\ldots ,n\), where

$$\begin{aligned} V_i(x) := {\left\{ \begin{array}{ll} E_{1,i} \psi ^{(i)}(x) &{} 0\le x \le {{\hat{b}}}_i \\ E_{4,i} \varphi ^{(i)}(x) + \frac{K_i}{r} &{} x\ge {{\hat{b}}}_i ,\\ \end{array}\right. } \end{aligned}$$
(4.5)

and

$$\begin{aligned} E_{1,i}&:= \frac{-\frac{K_i}{r}{\varphi ^{(i)}}'({{\hat{b}}}_i)}{\varphi ^{(i)}({{\hat{b}}}_i){\psi ^{(i)}}'({{\hat{b}}}_i)-{\varphi ^{(i)}}'({{\hat{b}}}_i){\psi ^{(i)}}({{\hat{b}}}_i)},\nonumber \\ E_{4,i}&:= \frac{-\frac{K_i}{r}{\psi ^{(i)}}'({{\hat{b}}}_i)}{\varphi ^{(i)}({{\hat{b}}}_i){\psi ^{(i)}}'({{\hat{b}}}_i)-{\varphi ^{(i)}}'({{\hat{b}}}_i){\psi ^{(i)}}({{\hat{b}}}_i)}. \end{aligned}$$
(4.6)

Then, \(({{\hat{b}}}_1,\ldots , {{\hat{b}}}_n)\) is a threshold Nash equilibrium and \(V_i(x),i=1,\ldots ,n\) are the corresponding equilibrium value functions.

We will now report a boundedness and continuity result that is essential for the fixed-point argument in Sect. 4.2. Consider the problem stated in the beginning of this section, see (4.1)–(4.2). Relying again on Lemma 4.1 and reasoning similar to that of Sect. 3.1 we find, as noted above, that the solution is a threshold strategy. In particular, if agents \(1,\ldots ,i-1,i+1,\ldots ,n\) use a fixed strategy \((b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n)\), then the optimal strategy of agent i is a threshold strategy, which we denote by \(b^Z=b^Z(b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n)\). This induces mappings

$$\begin{aligned} (b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n) \in {\mathbb {R}}^{n-1}_+ \mapsto b_i^Z=b^Z_i(b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n), \end{aligned}$$
(4.7)

for \(i=1,\ldots ,n\). The interpretation is that \(b_i^Z\) is the optimal threshold strategy for agent i under the assumption that the other agents use a fixed threshold strategy \((b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n)\).

Proposition 4.5

For each \(i=1,\ldots ,n\), the mapping (4.7) is bounded by c and continuous.

Proof

Suppose without loss of generality that \(i=n\). Let us first show that the function \((b_1,\ldots ,b_{n-1}) \mapsto b^{**}_n\) is bounded. Consider any \(x>0\) with \(x \ne b_i\) for all \(i<n\) and suppose \({\psi ^{(n)}}''(x)<0\). The function \({\psi ^{(n)}}(y) - y{\psi ^{(n)}}'(y)\) is zero for \(y=0\) and increasing on [0, x], so \({\psi ^{(n)}}(x) \ge x{\psi ^{(n)}}'(x)\) for such x. This implies that

$$\begin{aligned} \frac{1}{2}\sigma ^2(x){\psi ^{(n)}}''(x)&= r{\psi ^{(n)}}(x) - \left( \mu (x)-\sum _{i\le n-1}K_iI_{\{x\ge b_i\}}\right) {\psi ^{(n)}}'(x)\\&\ge \left( rx- \mu (x) + \sum _{i\le n-1}K_iI_{\{x\ge b_i\}}\right) {\psi ^{(n)}}'(x). \end{aligned}$$

By Assumption 2.2(A.3), the last expression above is positive whenever \(x\ge c\); thus, in order for \({\psi ^{(n)}}''(x)<0\) to hold we must have \(x<c\). Consequently, \(b_n^{**}\le c\), and since c does not depend on \(b_1,\ldots ,b_{n-1}\), it follows that \((b_1,\ldots ,b_{n-1}) \mapsto b^{**}_n\) is bounded.

It can now be seen (cf. the single-agent, \(n=1\), version of Theorem 3.2), that the optimal value function corresponding to \(b_n^Z=b^Z_n(b_1,\ldots ,b_{n-1})\) is

$$\begin{aligned} Z(x):= {\left\{ \begin{array}{ll} E_1 {\psi ^{(n)}}(x) &{} 0\le x \le b_n^Z \\ E_4 {\varphi ^{(n)}}(x) + \frac{K_n}{r} &{} x\ge b_n^Z ,\\ \end{array}\right. } \end{aligned}$$
(4.8)

(where \(E_1\) and \(E_4\) are defined so that Z is \({{{\mathcal {C}}}}^1\) at \(b_n^Z\), i.e. analogously to the constants in Theorem 4.4) and \(b_n^Z \in (0,b_n^{**}]\) is the unique threshold satisfying \(Z'(b^Z_n)=1\) in case

$$\begin{aligned} {\varphi ^{(n)}}'(0) < -\frac{r}{K_n} \end{aligned}$$

and \(b^{**}_n>0\) hold, and \(b^Z_n=0\) otherwise. We thus find (i) since \(b_n^Z\le b^{**}_n\), it holds that \(b_n^Z\) is bounded, and (ii) since the solutions \({\psi ^{(n)}}\) and \({\varphi ^{(n)}}\) to the ODEs (4.3) and (4.4) (with \(i=n\)) depend continuously on the parameters \(b_1,\ldots ,b_{n-1}\), it holds that the continuity of \(b^Z_n\) can be obtained from the explicit defining relations above, see e.g. (4.8). \(\square \)

4.2 Existence of Asymmetric Threshold Nash Equilibrium

Theorem 4.6

Suppose, without loss of generality, that \(K_n \ge ... \ge K_1\ge 0\). Then, there exists a threshold type Nash equilibrium \(\varvec{{{\hat{\lambda }}}}= ({{\hat{b}}}_1,\ldots ,{{\hat{b}}}_n)\) that satisfies \({{\hat{b}}}_n\ge ...\ge {{\hat{b}}}_1\ge 0\). Moreover, the corresponding equilibrium value functions are given by (4.5) and satisfy \(V_n(x)\ge ... \ge V_1(x)\) for all \(x\ge 0\).

Proof

For any fixed i, the mapping \(b_i^Z\) defined in (4.7) produces the optimal threshold strategy for agent i under the assumption that the other agents use a fixed threshold strategy \((b_1,\ldots ,b_{i-1},b_{i+1},\ldots , b_n)\). Recall that each \(b_i^Z\) is a bounded and continuous mapping by Proposition 4.5; in fact, \(b^Z_i\le c\) for all i and \((b_1,\ldots ,b_n)\). Define the hyper-cube \(\mathcal K=\left[ 0,c\right] ^n\) and the composite mapping

$$\begin{aligned} {\mathcal {K}}\ni (b_1,\ldots ,b_n) \mapsto (b^Z_1,\ldots ,b^Z_n). \end{aligned}$$

Note that this is a continuous mapping from \({\mathcal {K}}\) to \({\mathcal {K}}\) and with Brouwer’s fixed-point theorem we conclude that it has a fixed-point \(({{\hat{b}}}_1,\ldots ,{{\hat{b}}}_n)\). Clearly, the threshold strategy profile \(({{\hat{b}}}_1,\ldots ,{{\hat{b}}}_n)\) is then a Nash equilibrium and the corresponding equilibrium value functions are given by (4.5).

For the ordering result, it suffices to consider the case \(n=2\) since the strategies of the remaining agents can be considered already locked in. Assume that \(K_1\le K_2\) and consider a threshold type equilibrium \(({{\hat{b}}}_1, {{\hat{b}}}_2)\) as obtained above. Now assume (to reach a contradiction) that \({{\hat{b}}}_1> {{\hat{b}}}_2\). If \({{\hat{b}}}_2>0\), then

$$\begin{aligned} V_i(x) = A_i\psi (x), x \le {{\hat{b}}}_2. \end{aligned}$$

Using strict concavity of \(\psi \) (on the interval \((0,{{\hat{b}}}_2)\)) and \(V_i'({{\hat{b}}}_i)=1\) we obtain \(A_1>A_2>0\), so \(V_1({{\hat{b}}}_2)> V_2({{\hat{b}}}_2)\). Moreover, \(V_i'(x)\ge 1\) for \(x\le {{\hat{b}}}_i\) and \(V_i'(x)\le 1\) for \(x\ge {{\hat{b}}}_i\), so

$$\begin{aligned} V'_1({{\hat{b}}}_1)> V'_2({{\hat{b}}}_1) \text{ and } V_1({{\hat{b}}}_1) > V_2({{\hat{b}}}_1). \end{aligned}$$
(4.9)

A similar reasoning shows that (4.9) also holds in the case \(0={{\hat{b}}}_2<{{\hat{b}}}_1\). Define

$$\begin{aligned}x_0=\inf \{x\ge {{\hat{b}}}_1:V'_1({{\hat{b}}}_1) - V'_2({{\hat{b}}}_1)\le 0\}.\end{aligned}$$

If \(x_0<\infty \), then \(V_1-V_2\ge 0\), \(V_1'-V_2'=0\) and \(V''_1-V''_2\le 0\) at \(x_0\). Consequently,

$$\begin{aligned} 0= & {} \frac{\sigma ^2}{2}(V_1''-V_2'')+(\mu -K_1-K_2)(V'_1-V_2')-r(V_1-V_2)+(K_1-K_2)\\\le & {} -r(V_1-V_2)+(K_1-K_2)<0. \end{aligned}$$

Thus \(x_0=\infty \), so \(V_1(x)-V_2(x)\ge V_1({{\hat{b}}}_1)-V_2({{\hat{b}}}_1)>0\) for all \(x\ge {{\hat{b}}}_1\), which contradicts \(V_1(\infty )=\frac{K_1}{r}\le \frac{K_2}{r}= V_2(\infty )\). It follows that \({{\hat{b}}}_1\le {{\hat{b}}}_2\).

Now that \({{\hat{b}}}_1\le {{\hat{b}}}_2\), a similar reasoning as above shows that \(V_1\le V_2\) on \((0,{{\hat{b}}}_2)\). Since \(u:=V_2-V_1\) on \(({{\hat{b}}}_2,\infty )\) satisfies

$$\begin{aligned}\frac{\sigma ^2}{2}u''+(\mu -K_1-K_2)u'-ru = K_1-K_2\le 0,\end{aligned}$$

and \(u\ge 0\) for \(x\in \{{{\hat{b}}}_2,\infty \}\), the maximum principle (see, e.g., [19, Chapter 1.1]) shows that \(u=V_2- V_1\ge 0\) everywhere. \(\square \)

4.3 The Case of Constant Coefficients

We consider two agents \(i=1,2\) with maximal extraction rates \(K_2 \ge K_1 >0\) and constant drift and diffusion coefficients \(\mu >0\) and \(\sigma >0\). Then existence of a threshold equilibrium \(({{\hat{b}}}_1,{{\hat{b}}}_2)\) satisfying \({{\hat{b}}}_2 \ge {{\hat{b}}}_1 \ge 0\) follows from Theorem 4.6. Hence, an equilibrium of either of the following kinds can be found (i) \(({{\hat{b}}}_1,{{\hat{b}}}_2)=(0,0)\), (ii) \((0,{{\hat{b}}}_2)\) with \({{\hat{b}}}_2>0\), and (iii) \(({{\hat{b}}}_1,{{\hat{b}}}_2)\) with \({{\hat{b}}}_2\ge {{\hat{b}}}_1>0\). We will now describe how to determine if an equilibrium of the last kind exists and how it can be found. Equilibria of the other kinds can be investigated similarly.

Using the program in Remark 4.2 we find that

$$\begin{aligned} {\psi ^{(1)}}(x)&= \frac{e^{\alpha x}- e^{ \beta x}}{\alpha -\beta }, 0\le x \le b_1\\ {\psi ^{(2)}}(x)&= \left\{ \begin{array}{l} \frac{e^{\alpha x}- e^{ \beta x}}{\alpha -\beta }, 0\le x \le b_1 \\ F_1 e^{\alpha _1 x}- F_2 e^{ \beta _1 x}, b_1 \le x \le b_2, \end{array} \right. \\ {\varphi ^{(1)}}(x)&= \left\{ \begin{array}{l} F_3 e^{\alpha _1 x}- (F_3-1)e^{ \beta _1x}, 0\le x \le b_2 \\ F_4e^{ \beta _2 x} , x \ge b_2 \end{array} \right. \\ {\varphi ^{(2)}}(x)&= C {\varphi ^{(1)}}(x), x\ge b_2 \end{aligned}$$

for some constant \(C>0\) implying that the boundary condition \({\varphi ^{(2)}}(0)=1\) is satisfied (there is no need to determine these functions outside the specified intervals and the constant C will cancel in the relevant calculations); here \(\alpha \) and \(\beta \) are as in Sect. 3.4, and

$$\begin{aligned} \alpha _1:&= -\frac{\mu -K_1}{\sigma ^2} + \sqrt{\frac{(\mu -K_1)^2}{\sigma ^4}+\frac{2r}{\sigma ^2}},\\ \beta _1:&= -\frac{\mu -K_1}{\sigma ^2} - \sqrt{\frac{(\mu -K_1)^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}, \text{ and } \\ \beta _2:&= -\frac{\mu -K_1-K_2}{\sigma ^2} - \sqrt{\frac{(\mu -K_1-K_2)^2}{\sigma ^4}+\frac{2r}{\sigma ^2}}, \end{aligned}$$

and the constants \(F_i\) (which depend on \(b_1\) and \(b_2\)) are determined so that the functions are continuously differentiable, i.e. according to the linear equation systems

$$\begin{aligned} \left\{ \begin{array}{l} e^{\alpha _1 b_1}F_1- e^{ \beta _1 b_1}F_2 = \frac{e^{\alpha b_1}- e^{ \beta b_1}}{\alpha -\beta } \\ \alpha _1 e^{\alpha _1 b_1}F_1 - \beta _1e^{ \beta _1 b_1}F_2 = \frac{\alpha e^{\alpha b_1}- \beta e^{ \beta b_1}}{\alpha -\beta } \end{array}\right. \end{aligned}$$
(4.10)

and

$$\begin{aligned} \left\{ \begin{array}{l} (e^{\alpha _1b_2}- e^{ \beta _1b_2})F_3 - e^{\beta _2 b_2}F_4 = - e^{ \beta _1b_2} \\ (\alpha _1 e^{\alpha _1b_2}- \beta _1e^{\beta _1b_2})F_3 - \beta _2 e^{\beta _2 b_2}F_4 = - \beta _1e^{\beta _1b_2}.\end{array}\right. \end{aligned}$$
(4.11)

From Theorem 4.4 we know that if the system \(V_i'({{\hat{b}}}_1)=E_{1,i}{\psi ^{(i)}}'({{\hat{b}}}_i)=1,i=1,2\), (with \(E_{1,i}\) as in (4.6)) has a solution \(({{\hat{b}}}_1, {{\hat{b}}}_2)\) then it is an equilibrium. Using the definition of \(E_{1,i}\) in (4.6), we rewrite the equation system as

$$\begin{aligned} \frac{K_i}{r}=\frac{{\psi ^{(i)}}({{\hat{b}}}_i)}{{\psi ^{(i)}}'({{\hat{b}}}_i)}-\frac{{\varphi ^{(i)}}({{\hat{b}}}_i)}{{\varphi ^{(i)}}'({{\hat{b}}}_i)}, i=1,2, \end{aligned}$$

which, in the present case with constant coefficients, is equivalent to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{K_1}{r} = \frac{e^{\alpha {{\hat{b}}}_1}- e^{\beta {{\hat{b}}}_1}}{\alpha e^{\alpha {{\hat{b}}}_1} - \beta e^{ \beta {{\hat{b}}}_1}} -\frac{F_3 e^{\alpha _1 {{\hat{b}}}_1}- (F_3-1)e^{ \beta _1{{\hat{b}}}_1}}{\alpha _1 F_3 e^{\alpha _1 {{\hat{b}}}_1}- \beta _1(F_3-1)e^{ \beta _1{{\hat{b}}}_1}}\\ \frac{K_2}{r} =\frac{e^{\alpha _1{{\hat{b}}}_2}F_1- e^{\beta _1 {{\hat{b}}}_2}F_2}{\alpha _1e^{\alpha _1{{\hat{b}}}_2}F_1- \beta _1e^{\beta _1 {{\hat{b}}}_2}F_2}- \frac{1}{\beta _2}. \end{array}\right. \end{aligned}$$
(4.12)

Determining expressions for \(F_1({{\hat{b}}}_1)\) and \(F_2({{\hat{b}}}_1)\) (using (4.10)), using these in the second equation of (4.12), and solving for \({{\hat{b}}}_2\) yields

$$\begin{aligned} {{\hat{b}}}_2 ({{\hat{b}}}_1)= \frac{\ln \left( \frac{ e^{-\beta _1 {{\hat{b}}}_1}\left( \alpha e^{\alpha {{\hat{b}}}_1}-\beta e^{\beta {{\hat{b}}}_1} -\alpha _1\left( e^{\alpha {{\hat{b}}}_1}-e^{\beta {{\hat{b}}}_1} \right) \right) }{ e^{-\alpha _1 {{\hat{b}}}_1}\left( \alpha e^{\alpha {{\hat{b}}}_1}-\beta e^{\beta {{\hat{b}}}_1} -\beta _1\left( e^{\alpha {{\hat{b}}}_1}-e^{\beta {{\hat{b}}}_1} \right) \right) }\frac{1-(K_2/r+1/\beta _2)\beta _1}{1-(K_2/r+1/\beta _2)\alpha _1}\right) }{\alpha _1-\beta _1}. \end{aligned}$$
(4.13)

The problem of finding a Nash equilibrium \(({{\hat{b}}}_1,{{\hat{b}}}_2)\) is thus effectively transformed to a one-dimensional problem. Indeed, relying on (4.11) we find

$$\begin{aligned} F_3= \frac{-(\beta _1-\beta _2)e^{\beta _1{{\hat{b}}}_2}}{ e^{\alpha _1{{\hat{b}}}_2}(\alpha _1-\beta _2) - e^{\beta _1{{\hat{b}}}_2}(\beta _1-\beta _2)}. \end{aligned}$$
(4.14)

This expression together with (4.13) induces an explicit mapping \({{\hat{b}}}_1 \mapsto F_3\). In particular, using (4.13) and (4.14) we find

Fig. 4
figure 4

The individual equilibrium value functions with \(K_1=0.1\) and \(K_2=0.2\)

Full size image
$$\begin{aligned} F_3=F_3( {{\hat{b}}}_1) := \frac{-(\beta _1-\beta _2) }{\frac{ e^{-\beta _1 {{\hat{b}}}_1}\left( \alpha e^{\alpha {{\hat{b}}}_1}-\beta e^{\beta {{\hat{b}}}_1} -\alpha _1\left( e^{\alpha {{\hat{b}}}_1}-e^{\beta {{\hat{b}}}_1} \right) \right) }{ e^{-\alpha _1 {{\hat{b}}}_1}\left( \alpha e^{\alpha {{\hat{b}}}_1}-\beta e^{\beta {{\hat{b}}}_1} -\beta _1\left( e^{\alpha {{\hat{b}}}_1}-e^{\beta {{\hat{b}}}_1} \right) \right) }\frac{1-(K_2/r+1/\beta _2)\beta _1}{1-(K_2/r+1/\beta _2)\alpha _1}(\alpha _1-\beta _2) - (\beta _1-\beta _2)}. \end{aligned}$$
(4.15)

On the other hand, solving for \(F_3\) in the first part of (4.12) yields another explicit mapping \({{\hat{b}}}_1 \mapsto F_3\)

$$\begin{aligned} F_3= {{\tilde{F}}}_3({{\hat{b}}}_1) := \frac{\left( \frac{e^{\alpha {{\hat{b}}}_1}- e^{\beta {{\hat{b}}}_1}}{\alpha e^{\alpha {{\hat{b}}}_1} - \beta e^{ \beta {{\hat{b}}}_1}} - \frac{K_1}{r}\right) \beta _1 e^{ \beta _1{{\hat{b}}}_1}-e^{ \beta _1{{\hat{b}}}_1}}{e^{\alpha _1 {{\hat{b}}}_1}-e^{ \beta _1{{\hat{b}}}_1}- \left( \frac{e^{\alpha {{\hat{b}}}_1}- e^{\beta {{\hat{b}}}_1}}{\alpha e^{\alpha {{\hat{b}}}_1} - \beta e^{ \beta {{\hat{b}}}_1}} - \frac{K_1}{r}\right) (\alpha _1 e^{\alpha _1 {{\hat{b}}}_1}-\beta _1 e^{ \beta _1{{\hat{b}}}_1})}. \end{aligned}$$
(4.16)

Now \({{\hat{b}}}_1\) can be determined by considering the equation

$$\begin{aligned} F_3({{\hat{b}}}_1) = {{\tilde{F}}}_3({{\hat{b}}}_1) \end{aligned}$$
(4.17)
Fig. 5
figure 5

Left: The equilibrium thresholds when \(K_2\) is varied and \(K_1=0.1\).Right: The equilibrium threshold \({{\hat{b}}}_2(K_2)\) when \(K_2\) is varied and \(K_1=0.1\) (solid). For comparison we have also included the optimal thresholds in the corresponding one-player game (dashed), which are determined according to Sect. 3.4. The straight line is the optimal barrier in the corresponding one-player singular stochastic control problem, cf. Remark 2.5

Full size image

(where the left and right hand side are given in (4.15) and (4.16)) which can be easily studied numerically. In particular, if the Eq. (4.17) has a solution \({{\hat{b}}}_1\), then \(({{\hat{b}}}_1,{{\hat{b}}}_2)\), with \({{\hat{b}}}_2={{\hat{b}}}_2({{\hat{b}}}_1)\) determined according to (4.13), is an equilibrium; if no solution exists then an equilibrium of either of the other kinds mentioned above can be found using methods similar to that described above.

Let \(\mu =4\), \(\sigma ^2=2\), and \(r=0.05\), and consider the individual maximal extraction rates \(K_1=0.1\) and \(K_2=0.2\). Using the program above we determine a Nash equilibrium \(({{\hat{b}}}_1,{{\hat{b}}}_2)=(0.521229,0.704502)\). The corresponding equilibrium value functions are illustrated in Fig. 4. In Fig. 5, the equilibrium thresholds are illustrated when varying one of the maximal extraction rates. At least for the chosen parameter values, the effect of a change in \(K_2\) on \({{\hat{b}}}_1\) is relatively small.