Abstract
In recent work (Lohmann et al. in J Math Pures Appl, 2022, https://doi.org/10.1016/j.matpur.2022.05.021, Theorem 1.3.4) we have shown the equivalence of the widely used nonconvex (generalized) branched transport problem with a shape optimization problem of a street or railroad network, known as (generalized) urban planning problem. The argument was solely based on an explicit construction and characterization of competitors. In the current article we instead analyse the dual perspective associated with both problems. In more detail, the shape optimization problem involves the Wasserstein distance between two measures with respect to a metric depending on the street network. We show a Kantorovich–Rubinstein formula for Wasserstein distances on such street networks under mild assumptions. Further, we provide a Beckmann formulation for such Wasserstein distances under assumptions which generalize our previous result in [16]. As an application we then give an alternative, duality-based proof of the equivalence of both problems under a growth condition on the transportation cost, which reveals that urban planning and branched transport can both be viewed as two bilinearly coupled convex optimization problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classical optimal transport takes two probability measures \(\mu _+,\mu _-\in {\mathcal {P}}({\mathcal {C}})\) on some compact domain \({\mathcal {C}}\subset {\mathbb {R}}^n\) and computes the optimal assignment \(\pi \) between them, where \(\pi \) is a probability measure on \({\mathcal {C}}\times {\mathcal {C}}\) with the interpretation that \(\pi \) at (x, y) represents the mass transported from x to y. Optimality is here assessed with respect to the cost \(\int _{{\mathcal {C}}\times {\mathcal {C}}}c(x,y)\,\mathrm {d}\pi (x,y)\) for some given transportation cost c. The special case \(c(x,y)=|x-y|\) yields the so-called Wasserstein transport, inducing the Wasserstein-1 distance \(W_1(\mu _+,\mu _-)\) between both measures.
An important reformulation of the Wasserstein transport is the so-called Beckmann formulation, obtained by dualizing the problem twice as we quickly recapitulate (rather formally) below: Introducing Lagrange multipliers \(\phi ,\psi \) for the constraint of \(\pi \) being an assignment between \(\mu _{+}\) and \(\mu _{-}\), one obtains
By classical Lagrange or Fenchel–Rockafellar duality one can swap \(\inf \) and \(\sup \) and then minimize for \(\pi \) to arrive at
Now it is not difficult to show that in the optimum \(\psi \) has to equal \(-\phi \) so that the above turns into the so-called Kantorovich–Rubinstein formula
where we exploited that the constraint turns into 1-Lipschitz continuity of \(\phi \), which can equivalently be expressed by constraining \(\nabla \phi \). Introducing a vector-valued Radon measure \({\mathcal {F}}\in {\mathcal {M}}^n({\mathcal {C}})\) on \(\mathcal C\) as Lagrange multiplier for the new constraint we get
where \(|{\mathcal {F}}|({\mathcal {C}})\) denotes the total variation of \({\mathcal {F}}\). An integration by parts now moves the derivative from \(\phi \) onto \({\mathcal {F}}\). Furthermore, again by Lagrange or Fenchel–Rockafellar duality we can swap \(\inf \) and \(\sup \) and then minimize explicitly over \(\phi \), which finally yields the Beckmann formulation of the Wasserstein-1 distance,
In this article we aim to derive the Kantorovich–Rubinstein and the Beckmann formula for the setting where c(x, y) is replaced by a (pseudo-)metric which stems from a street network or more generally a countably 1-rectifiable set \(S\subset \mathcal C\) on which the transport is cheaper than on its complement. These formulations are needed to understand the relation between the so-called urban planning and branched transport problem.
The urban planning problem was proposed by Brancolini and Buttazzo [3] as well as Buttazzo et al. [6]. It is a shape optimization problem in which one seeks an optimal street geometry for public transportation. The cost for a commuter to travel from one position to another (e. g. from home to work) is descibed using the urban metric, the minimum travel distance based on the street network. The corresponding objective functional can be decomposed into the total cost for commuting (a Wasserstein-1 distance with respect to the urban metric) and for maintenance (proportional to the total length of the street network). The urban planning problem and urban metric were generalized in [16]: As an additional parameter, a friction coefficient was introduced which assigns a different street quality to different parts of the network. Both the urban metric and the maintenance cost in the generalized model depend on this friction coefficient.
The branched transport problem on the other hand is a non-convex and non-smooth variational problem on Radon measures in which one optimizes over mass fluxes from a given initial to a final mass distribution. A good introduction to classical branched transport is given in [4].
In [16] it was shown that the generalized urban planning problem is equivalent to the branched transport problem with concave transportation cost, extending a result from [8] (equivalence between the classical urban planning problem and the branched transport problem with a specific transportation cost). The main step was to prove a Beckmann-type flux formulation of the Wasserstein-1 distance with respect to the generalized urban metric. To this end it was assumed that the generalized urban planning problem has finite cost, which allowed to derive a particular property of the network (namely, for any \(C>0\) smaller than the friction outside the network, streets with friction smaller than C have finite total length). This property was used to construct a minimizer for the Beckmann problem from a minimizer of the Wasserstein distance and vice versa. Without this assumption an explicit construction of minimizers is not possible since the Beckmann problem may not admit a minimizer. The main aim of the current work is to prove the Beckmann formulation using duality arguments (as recapitulated above for the Euclidean setting) without making use of the assumption. We prove it for the case of finite friction outside the network, but also show that this reformulation will stay true under mild assumptions (related to the network property from above) if the friction outside the network is infinite. We will first prove a Kantorovich–Rubinstein formula for the Wasserstein distance (under these mild assumptions) in which the gradients of the Kantorovich potentials are bounded in terms of the friction coefficient and then apply Fenchel duality to obtain the Beckmann formulation.
Apart from this result, we will provide a dual representation of the total network transportation cost induced by a mass flux from the branched transport problem (it is known that such a flux can be decomposed into a part concentrated on a network-like set and a diffuse part) under the assumption that the right derivative of the transportation cost is finite in zero. We will use this expression and the previously mentioned duality results to give a short alternative proof of the urban planning formulation of branched transport under the same assumption on the transportation cost.
In the remainder of this section, we introduce the terminology used in urban planning and branched transport. Further, we summarize our main results and list the used notation and definitions. In Sect. 2 we will derive the Kantorovich–Rubinstein formula for the Wasserstein distance with respect to the generalized urban metric under mild assumptions on the street network. We will afterwards use this result to prove the Beckmann formulation under these mild assumptions or for the case of finite friction outside the network. Finally, in Sect. 3 we will introduce the friction coefficients as dual variables in a formula for the total network transportation cost of a mass flux from branched transport and give an alternative proof of the urban planning formulation of branched transport under the above-mentioned growth condition on the transportation cost.
1.1 Generalized Urban Planning
The original urban planning problem was introduced in [3, 6]. We will directly introduce the generalized setting and refer the reader to [16, Sect. 1.2] for a brief description of the relation between classical and generalized urban planning. We first introduce the set of admissible street networks.
Definition 1.1.1
(Street network, friction coefficient, city) A street network is a pair (S, b) with
-
\(S\subset {\mathbb {R}}^n\) countably 1-rectifiable and Borel measurable,
-
\(b:S\rightarrow [0,\infty )\) lower semicontinuous.
The function b is called friction coefficient. A city is a triple (S, a, b), where (S, b) is a street network and \(a\in [0,\infty ]\) satisfies \(b\le a\) on S.
The (friction) coefficients b and a describe the cost for travelling on and outside the network S (b may vary on S since the street quality may vary). Note that, in general, offroad movement may be limited through buildings or the like. However, the results in this article will still hold true if we exclude finitely many sufficiently regular connected sets in \({\mathbb {R}}^n\backslash S\). The cost for travelling from x to y is desribed by the following (pseudo-)metric (in which \({\mathcal {H}}^1\) denotes the one-dimensional Hausdorff measure).
Definition 1.1.2
(Generalized urban metric) Let (S, a, b) be a city. The associated generalized urban metric is defined as
where the infimum is taken over Lipschitz paths \(\gamma :[0,1]\rightarrow {\mathbb {R}}^n\) with \(\gamma (0)=x\) and \(\gamma (1)=y\).
Let \(\mu _+\) and \(\mu _-\) be probability measures on \({\mathbb {R}}^n\), which may for example describe the distribution of homes and workplaces. The total cost for the commuting population is then given by the Wasserstein distance with respect to \(d_{S,a,b}\).
Definition 1.1.3
(Wasserstein distance, transport plans) Let (S, a, b) be a city. The Wasserstein distance between \(\mu _+\) and \(\mu _-\) with respect to \(d_{S,a,b}\) is defined as
where the infimum is taken over all probability measures \(\pi \) on \({\mathbb {R}}^n\times {\mathbb {R}}^n\) with \(\pi (B\times {\mathbb {R}}^n)=\mu _+(B)\) and \(\pi ({\mathbb {R}}^n\times B)=\mu _-(B)\) for all Borel sets \(B\in {\mathcal {B}}({\mathbb {R}}^n)\). Any such measure is called a transport plan. The set of transport plans is denoted by \(\Pi (\mu _+,\mu _-)\).
The Wasserstein distance is the first term which appears in the cost functional of the generalized urban planning problem. The second term corresponds to the total maintenance cost of the street network.
Definition 1.1.4
(Maintenance cost) A maintenance cost is a non-increasing function \(c:[0,\infty )\rightarrow [0,\infty ]\).
The maintenance cost \(c\circ b\) has the interpretation of a cost per length for maintaining a street with friction coefficient b.
Definition 1.1.5
(Generalized urban planning cost) Given a maintenance cost c, set
The generalized urban planning cost of a city (S, a, b) is given by
and the generalized urban planning problem is the optimization problem
Note that \(c\circ b\) is upper semi-continuous due to the assumptions on b and c.
1.2 Generalized Branched Transport
To describe branched transport we use the Eulerian formulation due to Xia [24], which uses vector-valued Radon measures. Let \(\mu _+\) and \(\mu _-\) be probability measures on \({\mathbb {R}}^n\) that describe the initial an final distribution of mass (or of commuters in the context of urban planning). The cost to move an amount of mass per unit distance is given by the following function.
Definition 1.2.1
(Transportation cost) A transportation cost is a non-decreasing concave function \(\tau :[0,\infty )\rightarrow [0,\infty )\) with \(\tau (0)=0\).
A classical example for a transportation cost is \(\tau (m)=m^\alpha \) for some \(\alpha \in (0,1)\). The concavity of \(\tau \) encodes that the transport gets cheaper per mass particle if more mass is transported together.
To describe transport along a finite graph we define polyhedral mass fluxes (or equivalently, finite oriented weighted graphs) between distributions \(\mu _+\) and \(\mu _-\) which are concentrated in finitely many points.
Definition 1.2.2
(Polyhedral mass flux and branched transport cost) Assume that \(\mu _+\) and \(\mu _-\) are finite sums of weighted Dirac measures, i. e.,
where \(f_i,g_j\in [0,1]\) satisfy \(\sum _if_i=\sum _jg_j=1\) and \(x_i,y_j\in {\mathbb {R}}^n\). A polyhedral mass flux between \(\mu _+\) and \(\mu _-\) is a vector-valued Radon measure \({\mathcal {F}}\in {\mathcal {M}}^n({\mathbb {R}}^n)\) which satisfies \(div ({\mathcal {F}})=\mu _+-\mu _-\) in the distributional sense and can be written as

where the sum is over finitely many edges \(e=x_e+[0,1](y_e-x_e)\subset {\mathbb {R}}^n\) with orientation \(\vec {e}=(y_e-x_e)/|y_e-x_e|\), the coefficients \(m_e\) are positive real weights, and  is the restriction of the one-dimensional Hausdorff measure to e. The branched transport cost of \({\mathcal {F}}\) with respect to a transportation cost \(\tau \) is defined as
is the restriction of the one-dimensional Hausdorff measure to e. The branched transport cost of \({\mathcal {F}}\) with respect to a transportation cost \(\tau \) is defined as
We use the lower semi-continuous envelope of \({\mathcal {J}}^{\tau ,\mu _+,\mu _-}\) to get the branched transport cost of a general vector-valued Radon measure with distributional divergence equal to \(\mu _+-\mu _-\).
Definition 1.2.3
(Mass flux and branched transport cost) A vector-valued Radon measure \({\mathcal {F}}\in {\mathcal {M}}^n({\mathbb {R}}^n)\) is called mass flux between the probability measures \(\mu _+\) and \(\mu _-\) if there exist two sequences of probability measures \(\mu _+^k,\mu _-^k\) and a sequence of polyhedral mass fluxes \({\mathcal {F}}_{k}\) with \(div ({\mathcal {F}}_k)=\mu _{+}^k-\mu _{-}^k\) such that  and
and  , where
, where  indicates the weak-\(*\) convergence in duality with continuous functions. We write
indicates the weak-\(*\) convergence in duality with continuous functions. We write  . If \({\mathcal {F}}\) is a mass flux, then the branched transport cost of \({\mathcal {F}}\) is defined as
. If \({\mathcal {F}}\) is a mass flux, then the branched transport cost of \({\mathcal {F}}\) is defined as

The corresponding branched transport problem is the optimization problem
1.3 Summary of Results
Our main results are
-
A Kantorovich–Rubinstein formula for the Wasserstein distance \(W_{d_{S,a,b}}\) under mild assumptions on the city (S, a, b) (Theorem 1.3.2),
-
A Beckmann formula for \(W_{d_{S,a,b}}\) under the same assumptions on the city or \(a<\infty \) (Theorem 1.3.4),
-
A dual formula for a total network transportation cost under the growth condition \(\tau '(0)<\infty \) (Theorem 1.3.7), and
-
A new proof of the equivalence between urban planning and branched transport for the case \(\tau '(0)<\infty \) using our duality results (Theorem 1.3.8).
Let \(\mu _+,\mu _-\) be probability measures on \({\mathbb {R}}^n\) with bounded supports, contained in \({\mathcal {C}}=[-1,1]^n\) without loss of generality. We will prove our first main result under the following assumption.
Assumption 1.3.1
(Regularity of the city (S, a, b)) The friction coefficient b is bounded away from 0, and the function which maps \(x\in {\mathbb {R}}^n\) to the friction coefficient at x, i.e. b(x) if \(x\in S\), a else, is lower semi-continuous.
The last condition in Assumption 1.3.1 is for instance automatically satisfied if the set S of streets is closed. Note, though, that it is strictly weaker than requiring closedness of S (which typically is not satisfied for branched transport networks, see Example 1.3.9).
Theorem 1.3.2
(Version of the Kantorovich–Rubinstein formula) Let (S, a, b) be a city such that Assumption 1.3.1 is satisfied. Then the Wasserstein-1 distance between \(\mu _+\) and \(\mu _-\) is given by
where the supremum is taken over functions \(\varphi \in C^1({\mathcal {C}})\) with \(|\nabla \varphi |\le b\) on S and \(|\nabla \varphi |\le a\) in \({\mathcal {C}}\backslash S\).
The work here is to show that one may restrict the supremum to differentiable functions with the given gradient constraint; for lower regularity requirements on \(\varphi \) it is a standard result.
Assumption 1.3.3
(Finite friction outside network) The cost a for travelling outside the network is finite.
The Beckmann formulation of the Wasserstein distance will actually be true under Assumptions 1.3.1or 1.3.3.
Theorem 1.3.4
(Beckmann-type formulation of \(W_{d_{S,a,b}}(\mu _+,\mu _-)\)) Let (S, a, b) be a city and suppose that Assumptions 1.3.1 or 1.3.3 is satisfied. Then we have
where the infimum is taken over  and \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with
and \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with  and
and  .
.
It is unclear whether the result even stays true if one drops all assumptions—we expect this to be the case, but the method of proof via duality does not allow to draw such conclusions. A brief summary of the Beckmann formulation of the Wasserstein distance with respect to \(d_{S,a,b}\) is given in Fig. 1.
Summary of the cases for which the Beckmann formulation of the Wasserstein distance with respect to \(d_{S,a,b}\) has been proven. The requirement in [16, Asm. 1.3.1] is that for every \(C\in [0,a)\) we have \({\mathcal {H}}^1(\{ b\le C\})<\infty \). In all four cases a minimizer for \(W_{d_{S,a,b}}(\mu _+,\mu _-)\) exists (if the Wasserstein distance is finite). The same holds true for the Beckmann formulation except for \(a\in (0,\infty ]\) with no additional condition (see [16, Exm. 1.3.1])
The analogue of Assumption 1.3.3 in the context of branched transport turns out to be the following.
Assumption 1.3.5
(Growth condition) The average transportation cost per unit mass \(m\mapsto \tau (m)/m\) is bounded, i. e., \(\tau '(0)=\lim _{m\searrow 0}\tau (m)/m<\infty \).
The maintenance cost corresponding to a transportation cost for the branched transport problem is defined via convex conjugation.
Definition 1.3.6
(Maintenance cost associated with \(\tau \)) Let \(\tau :[0,\infty )\rightarrow [0,\infty )\) be a transportation cost. We extend \(\tau \) to a function on \({\mathbb {R}}\) via \(\tau (m)=-\infty \) for all \(m<0\). The associated maintenance cost is defined by \(\varepsilon (b)=(-\tau )^*(-b)=\sup _{m\ge 0}\tau (m)-bm\) for any \(b\in [0,\infty )\).
It can be shown that the branched transport cost of a mass flux  with divergence equal to \(\mu _+-\mu _-\) can be decomposed into the total cost for transportation on the network S and a cost term for the diffuse part \({\mathcal {F}}^\perp \) (see [9, Prop. 2.32] or [16, Lemma 3.1.8]). The next formula shows that the network cost term can be seen as an optimization problem over friction coefficients.
with divergence equal to \(\mu _+-\mu _-\) can be decomposed into the total cost for transportation on the network S and a cost term for the diffuse part \({\mathcal {F}}^\perp \) (see [9, Prop. 2.32] or [16, Lemma 3.1.8]). The next formula shows that the network cost term can be seen as an optimization problem over friction coefficients.
Theorem 1.3.7
(Dual formula for total network transportation cost) Assume that \(S\subset {\mathcal {C}}\) is countably 1-rectifiable and Borel measurable. Furthermore, let  represent a mass flux on S and suppose that \(\tau \) is a transportation cost which satisfies Assumption 1.3.5. Then we have
represent a mass flux on S and suppose that \(\tau \) is a transportation cost which satisfies Assumption 1.3.5. Then we have
where the infimum is taken over lower semi-continuous functions \(b:S\rightarrow [0,\tau '(0)]\).
At the end of this article, we will use the previous duality results to provide an alternative proof of the urban planning formulation of branched transport under Assumption 1.3.5.
Theorem 1.3.8
(Bilevel formulation of the branched transport problem [16, Theorem 1.3.4]) Let \(\tau \) be a transportation cost with associated maintenance cost \(\varepsilon \). Then the branched transport problem can equivalently be written as urban planning problem,
where the infima are taken over \({\mathcal {F}}\in {\mathcal {M}}^n({\mathcal {C}})\) with \(div ({\mathcal {F}})=\mu _+-\mu _-\) and street networks (S, b) with \(S\subset {\mathcal {C}}\) and \(b\le a=\tau '(0)\) on S.
Theorems 1.3.4, 1.3.8 and 1.3.7 reveal the convex duality structure that connects branched transport with urban planning: Essentially, both problems can be (formally) written as

with \(a=\sup _S b\), which is separately convex in \((\xi ,\mathcal F^\perp )\) and in b. Eliminating \((\xi ,{\mathcal {F}}^\perp )\) (by minimizing in those variables) leads to urban planning, eliminating (b, a) to branched transport. The nonconvexity of the problem arises from the bilinearity in which \((|\xi |,|{\mathcal {F}}^\perp |)\) and (b, a) are coupled.
To the end of this section, we briefly discuss Assumptions 1.3.1 and 1.3.3 with regard to Theorem 1.3.2. The conditions in Theorem 1.3.2 are sharp (cf. Examples 2.1.13 and 2.1.14). We believe that the condition that b is bounded away from zero in Theorem 1.3.2 can be dropped under Assumption 1.3.3. We use this condition in the proof of Proposition 2.1.1 to get uniformly bounded lenghts of certain almost optimal paths with respect to \(d_{S,a,b}\). It is possible to relax this condition to the requirement that there exists some constant \(C>0\) such that \({\mathcal {H}}^1(\{ b\le C\})<\infty \) (an implication of [16, Asm. 1.3.1]), but this would make the arguments more technical. Moreover, we will use the boundedness away from zero in the proof of Theorem 1.3.4 under Assumption 1.3.1. For the sake of completeness, we finally give an example which shows that it is reasonable not to restrict to closed networks S in the context of branched transport. The requirement that b, extended with value a, is lower semi-continuous in \({\mathbb {R}}^n\) from Assumption 1.3.1 turns out to be a natural weakening of the requirement that S is closed.
Sketches for Example 1.3.9
Example 1.3.9
(Examples of branched transport networks)
-
(a)
Clearly, any polyhedral mass flux induces a closed network S of finite length (Fig. 2a). If b is lower semi-continuous on S with \(b\le a\in [0,\infty ]\), then the extension of b with value a to \({\mathbb {R}}^n\) is automatically lower semi-continuous so that Assumption 1.3.1 is fulfilled as soon as b is bounded away from zero.
-
(b)
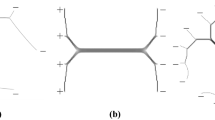
Recall from Theorem 1.3.8 that, in the context of branched transport, the friction coefficient a equals \(\tau '(0)\), where \(\tau \) is some transportation cost of the branched transport problem. For finite a, e. g. for \(\tau (m)=m\) (Wasserstein transport), the network S induced by an optimal mass flux is not necessarily closed: Let \(\mu _+=\sum _im_i\delta _{x_i}\) with \(m_i\in (0,1]\) be a probability measure concentrated on pairwise disjoint points \(x_i\in {\mathbb {R}}^n\) such that \(\bigcup _i\{ x_i\}\) is not closed (e. g. the point cloud \(({\mathbb {Q}}\cap (0,1))^2\) in Fig. 2b). Define \(\mu _-(B)=\mu _+(B-v)\) for some fixed \(v\in {\mathbb {R}}^n\backslash \{ 0 \}\). Then an optimal Wasserstein mass flux is concentrated on the set \(S=\bigcup _i[x_i,x_i+v]\), which is not closed. Nevertheless, the induced city satisfies Assumption 1.3.1: From Theorem 1.3.7 we see directly that \(b\equiv 1\) on S is the right choice so that the extension to \({\mathbb {R}}^n\) with value \(a=\tau '(0)=1\) is lower semi-continuous.
-
(c)
For an example with \(a=\infty \) we can choose \(\mu _+=\delta _0\) and
 the Lebesgue measure on some open and bounded set \(U\subset {\mathbb {R}}^n\) with \({\mathcal {L}}^n(U)=1\) (in Fig. 2c given by a ring). It can then be shown that the branched transport problem with classical transportation cost \(\tau (m)=m^\alpha \) admits a minimizer with finite energy if \(\alpha \in (1-1/n,1)\) [24, Thm. 3.1], where any optimal mass flux is of the form
the Lebesgue measure on some open and bounded set \(U\subset {\mathbb {R}}^n\) with \({\mathcal {L}}^n(U)=1\) (in Fig. 2c given by a ring). It can then be shown that the branched transport problem with classical transportation cost \(\tau (m)=m^\alpha \) admits a minimizer with finite energy if \(\alpha \in (1-1/n,1)\) [24, Thm. 3.1], where any optimal mass flux is of the form 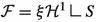 with S countably 1-rectifiable (which we will later see from the formula in Lemma 3.0.7, in which the diffuse part \({\mathcal {F}}^\perp \) must vanish). If S was closed, then we would get \(U\subset S\) which cannot be true for \(n>1\) by \({\mathcal {L}}^n(S)=0\)—rather S will be an infinitely refining, fractal network whose first iterations are illustrated in Fig. 2c and whose mass flux becomes the smaller the finer the branches are. From Theorem 1.3.7 one can already guess that the corresponding b will tend to infinity the smaller the flux and branches are (its values along one path are indicated in Fig. 2c; compare with the formula in Remark 3.1.6. Since \(a=\tau '(0)=\infty \), Assumption 1.3.1 is fulfilled.
with S countably 1-rectifiable (which we will later see from the formula in Lemma 3.0.7, in which the diffuse part \({\mathcal {F}}^\perp \) must vanish). If S was closed, then we would get \(U\subset S\) which cannot be true for \(n>1\) by \({\mathcal {L}}^n(S)=0\)—rather S will be an infinitely refining, fractal network whose first iterations are illustrated in Fig. 2c and whose mass flux becomes the smaller the finer the branches are. From Theorem 1.3.7 one can already guess that the corresponding b will tend to infinity the smaller the flux and branches are (its values along one path are indicated in Fig. 2c; compare with the formula in Remark 3.1.6. Since \(a=\tau '(0)=\infty \), Assumption 1.3.1 is fulfilled.
1.4 Notation and Definitions
Throughout the article we will use the following notation and definitions.
-
\(I= [0,1]\) denotes the unit interval. We will use this notation if I represents the domain of a path.
-
\({\mathcal {S}}^{n-1}\) denotes the unit sphere.
-
\({\mathcal {C}}\) denotes the hypercube \([-1,1]^n\).
-
We write \(B_r(x)\) for the open Euclidean ball with radius \(r>0\) and centre \(x\in {\mathbb {R}}^n\) and \({\overline{B}}_r(x)\) for its closure.
-
\({\mathcal {L}}^k\) denotes the k-dimensional Lebesgue measure. We write \({\mathcal {L}}={\mathcal {L}}^1\).
-
\({\mathcal {H}}^k\) indicates the k-dimensional Hausdorff measure.
-
Let V be a normed vector space. We write \(V^*\) for the topological dual space. For \(v\in V\) and \(v^*\in V^*\) we denote the pairing between v and \(v^*\) by \(\langle v,v^*\rangle \).
-
Let A be a topological space. We write \({\mathcal {B}}(A)\) for the \(\sigma \)-algebra of Borel subsets of A.
-
\(C({\mathcal {C}})\) denotes the space of real-valued continuous functions on \({\mathcal {C}}\). The subspace of Lipschitz functions is denoted \(C^{0,1}({\mathcal {C}})\). Further, we write \(C^1({\mathcal {C}})\) for the space of functions \(f\in C({\mathcal {C}})\) which are continuously differentiable on \((-1,1)^n\) such that \(f'\) can be continued to an element of \(C({\mathcal {C}})\).
-
Assume that \((\Omega ,{\mathcal {A}},\mu )\) is a measure space. We write \(L^1(\mu ;{\mathbb {R}}^n)\) for the Lebesgue space of equivalence classes of \({\mathcal {A}}\)-\({\mathcal {B}}({\mathbb {R}}^n)\)-measurable functions \(f:\Omega \rightarrow {\mathbb {R}}^n\) with \(\int _\Omega |f|\,\mathrm {d}\mu <\infty \), where two such functions belong to the same class if they coincide \(\mu \)-almost everywhere. For \(\sigma \)-finite \(\mu \) this definition corresponds to the quotient of the Lebesgue space \(L_1(\mu ,{\mathbb {R}}^n)\) defined in [14, § 2.4.12] by the subspace \(\{ f\,|\, f=0\, \mu \text {-almost everywhere} \}\).
-
Let \(\mu :{\mathcal {A}}\rightarrow X\) be a map from a \(\sigma \)-algebra \({\mathcal {A}}\) to some set X (e. g., a scalar- or vector-valued measure). For any \(A\in {\mathcal {A}}\) we define the restriction
 of \(\mu \) to A by
of \(\mu \) to A by 
-
A set \(S\subset {\mathbb {R}}^n\) is said to be countably k-rectifiable (following [14, p. 251]) if it is the countable union of k-rectifiable sets. More precisely,
$$\begin{aligned} S=\bigcup _{i=1}^\infty f_i(A_i), \end{aligned}$$where \(A_i\subset {\mathbb {R}}^k\) is bounded and \(f_i:A_i\rightarrow {\mathbb {R}}^n\) Lipschitz continuous. If S is countably k-rectifiable and \({\mathcal {H}}^k\)-measurable, then we can apply [14, Lem. 3.2.18] which yields the existence of bi-Lipschitz functions \(g_i:C_i\rightarrow S\) with \(C_i\subset {\mathbb {R}}^k\) compact, \(T_i=g_i(C_i)\) pairwise disjoint and
$$\begin{aligned} S=T_0\cup \bigcup _{i=1}^\infty T_i \end{aligned}$$with \({\mathcal {H}}^k(T_0)=0\). The sequence
$$\begin{aligned} S^N=\bigcup _{i=1}^NT_i \end{aligned}$$will be called an approximating sequence for S.
-
\({\mathcal {M}}^k(A)=\{{\mathcal {F}}:{\mathcal {B}}(A)\rightarrow {\mathbb {R}}^k\,\sigma \text {-additive}\}\) denotes the set of \({\mathbb {R}}^k\)-valued Radon measures on a Polish space A. Note that every \({\mathcal {F}}\in {\mathcal {M}}^k(A)\) is automatically regular and of bounded variation (cf. [12, p. 343] and [15, XI, 4.5., Thm. 8]). More specifically, the total variation measure \(|{\mathcal {F}}|\) is regular and satisfies \(|{\mathcal {F}}|(A)<\infty \). We indicate the weak-\(*\) convergence of Radon measures by \({\mathop {\rightharpoonup }\limits ^{*}}\). The measure \({\mathcal {F}}\in {\mathcal {M}}^k(A)\) is called \({\mathcal {H}}^l\)-diffuse if \({\mathcal {F}}(B)=0\) for all \(B\in {\mathcal {B}}(A)\) with \({\mathcal {H}}^l(B)<\infty \) [20, p. 2].
-
For any closed subset \(A\subset {\mathbb {R}}^n\) we write \({{\mathcal {D}}}{{\mathcal {M}}}^n(A)=\{{\mathcal {F}}\in {\mathcal {M}}^n(A)\,|\,div ({\mathcal {F}})\in {\mathcal {M}}^1(A) \}\), where \(div \) denotes the distributional divergence. These vector-valued Radon measures were termed divergence measure vector fields in [20, p. 2].
-
We write the arc length of a Lipschitz path \(\gamma :I\rightarrow {\mathcal {C}}\) as \(\text {len}(\gamma )=\int _{I}|{\dot{\gamma }}|\,\mathrm {d}{\mathcal {L}}\).
-
We write \(\Gamma ^{xy}=\{f:I\rightarrow {\mathcal {C}} Lipschitz \,|\,f(0)=x,f(1)=y\}\) for \(x,y\in {\mathcal {C}}\).
-
We will identify the image of a Lipschitz path \(\gamma :I\rightarrow {\mathcal {C}}\) with its parameterization, i. e., we simply write \(\gamma \) instead of \(\gamma (I)\) when no confusion is possible (for instance when we integrate over \(\gamma (I)\)).
-
For any Lipschitz continuous function \(f:(X,d_X)\rightarrow (Y,d_Y)\) from one metric space to another we denote the Lipschitz constant by \(\text {Lip}(f)=\sup _{x_1\ne x_2}d_Y(f(x_1),f(x_2))/d_X(x_1,x_2)\).
-
For any set A we write \(\iota _A\) for the indicator function and \(1_A\) for the characteristic function,
$$\begin{aligned} \iota _A(x)={\left\{ \begin{array}{ll} 0&{} \text { if }x \in A,\\ \infty &{}\text { else}, \end{array}\right. } \qquad 1_A(x)={\left\{ \begin{array}{ll} 1&{}\text { if }x \in A,\\ 0&{}\text { else}. \end{array}\right. } \end{aligned}$$ -
For \(x,y\in {\mathcal {C}}\) we define [x, y] as the line segment \(\{ x+t(y-x)\,|\, t\in [0,1] \}\). The sets (x, y], [x, y) and (x, y) are defined similarly, e. g., \((x,y]=[x,y]\setminus \{ x \}\).
-
For any function \(f:X\rightarrow V\) with values in some normed vector space \((V,\Vert .\Vert )\) and \(A\subset X\) we write
$$\begin{aligned} |f|_{\infty ,A}=\sup _{x\in A}\Vert f(x)\Vert . \end{aligned}$$ -
The effective domain of a convex function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\cup \{ \infty \}\) is denoted \(\text {dom}(f)=\{ x\in {\mathbb {R}}\,|\, f(x)<\infty \}\).
-
We write the convex conjugate of a function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\cup \{ \infty \}\) as
$$\begin{aligned} f^*(x)=\sup _{m\in {\mathbb {R}}}mx-f(m). \end{aligned}$$ -
A sequence \(x:{\mathbb {N}}\rightarrow M\) of elements in some set M will be indicated by the notation \((x_i)\subset M\) with \(x_i=x(i)\).
-
If a sequence of Lipschitz paths \(\gamma _j:I\rightarrow {\mathbb {R}}^n\) converges uniformly to some \(\gamma \), then we write \(\gamma _j\rightrightarrows \gamma \).
-
For two functions \(f,g:M\rightarrow {\mathbb {R}}\) on some set M we write \(f\wedge g=\min \{ f,g\}\) and \(f\vee g=\max \{ f,g\}\) for the pointwise minimum/maximum.
2 Beckmann Formulation of \(\varvec{W_{d_{S,a,b}}}\) Using Duality
Let \(\mu _+,\mu _-:{\mathcal {B}}({\mathcal {C}})\rightarrow [0,1]\) be probability measures. Further, assume that (S, a, b) is a city. Throughout this section, we abbreviate the generalized urban metric \(d=d_{S,a,b}\). Recall that d(x, y) is the cost to travel from x to y in terms of the (friction) coefficients a and \(b:S\rightarrow [0,\infty )\). We extend b to \({\mathcal {C}}\setminus S\) with value a so that we may write
In Sect. 2.1 we prove Theorem 1.3.2, i.e., under Assumption 1.3.1 we have
where the set \(C_d^1\) is defined by
To this end, we show that \(C_d^1\) is dense (with respect to \(|.|_{\infty ,{\mathcal {C}}}\)) in
and then essentially apply the classical Kantorovich–Rubinstein formula [11, Thm. 4.1]. Note that the Lipschitz condition \(|\varphi (x)-\varphi (y)|\le d(x,y)\) does not directly imply continuity if \(a=\infty \). Further, observe that we have \(C_d^1\subset C_d\). Indeed, for \(\varphi \in C_d^1\) we get
for all \(x,y\in {\mathcal {C}}\) and \(\gamma \in \Gamma ^{xy}\). By taking the infimum over all such \(\gamma \) we conclude
which implies \(\varphi \in C_d\). In Sect. 2.2 we will then prove Theorem 1.3.4, the Beckmann formulation of the Wasserstein distance \(W_d(\mu _+,\mu _-)\), under Assumptions 1.3.1 or 1.3.3. We will occasionally write
for the length of a Lipschitz path \(\gamma :I\rightarrow {\mathcal {C}}\) associated with d.
Remark 2.0.1
(Formula for d) It is easy to see that (cf. [16, Lemma 2.2.1])
2.1 Kantorovich–Rubinstein Duality in Urban Planning
In this section we prove Theorem 1.3.2. To this end, we elaborate a version of the Stone–Weierstraß theorem to work out that \(C_d^1\) is a dense subset of \(C_d\). The first step is to provide a point separation statement for \(C_d^1\) ((Proposition 2.1.6). We will need to approximate the urban metric d. For this purpose, we define \(b_k:{\mathcal {C}}\rightarrow [0,\infty )\) by
and abbreviate \(d_k=d_{S,a,b_k}\) (which is well-defined if \(b_k\) is lower semi-continuous, see Proposition 2.1.1 below). Moreover, we write \(L_k\) for the path length associated with \(d_k\).
Proposition 2.1.1
(Pointwise approximation of urban metric) Let Assumption 1.3.1 be satisfied. Then the \(b_k\) are lower semi-continuous, and we have \(d_k\rightarrow d\) pointwise.
Proof
Fix k and let \((z_j)\subset {\mathcal {C}}\) be a sequence such that \(z_j\rightarrow z\in {\mathcal {C}}\). We can assume that \(\liminf _jb_k(z_j)=\lim _jb_k(z_j)<\infty \) so that every subsequence of \(j\mapsto b_k(z_j)\) has the same limit. For every \(z_j\) there exists some \({\tilde{z}}_j\in {\mathcal {C}}\cap {\overline{B}}_{1/k}(z_j)\) such that \(b_k(z_j)=k\wedge b({\tilde{z}}_j)\). By the compactness of \( {\mathcal {C}}\) we have \({\tilde{z}}_j\rightarrow {\tilde{z}}\in {\mathcal {C}}\) up to a subsequence. Note that \(|{\tilde{z}}_j-z|\le 1/k+|z_j-z|\) and thus \({\tilde{z}}\in {\mathcal {C}}\cap {\overline{B}}_{1/k}(z)\) by letting \(j\rightarrow \infty \). This yields
where we used the lower semi-continuity of b. It remains to prove that \(d_k\rightarrow d\) pointwise. Let \((x,y)\in {\mathcal {C}}\times {\mathcal {C}}\) be arbitrary with \(x\ne y\). Since \(d_k\le d\) it sufficies to show \(d(x,y)\le \liminf _kd_k(x,y)\) under the assumption that the right hand side is finite. Let \((\gamma _k)\subset \Gamma ^{xy}\) be a sequence of Lipschitz paths such that \(L_k(\gamma _k)\le d_k(x,y)+1/k\). Using that b is bounded away from zero we obtain
for all \(k>\inf b\). Thus, the lengths of the \(\gamma _k\) are uniformly bounded. We can thus reparameterize each \(\gamma _k\) by arc length and get \(\gamma _k\rightrightarrows \gamma :I\rightarrow {\mathcal {C}}\) up to a subsequence by the Arzelà–Ascoli theorem. This also yields \(|{\dot{\gamma }}|\le \liminf _k|{\dot{\gamma }}_k|\) almost everywhere in I. Now fix any \(t\in I\). Once more we get \(b_k(\gamma _k(t))=k\wedge b(z_k)\) for some \(z_k\in {\mathcal {C}}\cap {\overline{B}}_{1/k}(\gamma _k(t))\). Clearly, we must have \(z_k\rightarrow \gamma (t)\). Using again the lower semi-continuity of b we estimate
Finally, using Fatou’s lemma
which shows the pointwise convergence \(d_k\rightarrow d\). \(\square \)
The following two examples illustrate that the conditions on b in Proposition 2.1.1 cannot be dropped.
Example 2.1.2
(Counterexample for b not lower semi-continuous in \({\mathcal {C}}\)) Take \(S={\mathbb {Q}}\cap [0,1]\) and \(a,b\in (0,\infty ]\) with \(b<a\), which implies that the extension of b with value a to \({\mathcal {C}}\) is not lower semi-continuous (see Fig. 3a). Then, we obtain \(d(0,1)=a>b=d_k(0,1)\) since \(b_k=b\) in [0, 1] for all k.
Example 2.1.3
(Counterexample for b not bounded away from zero) Let \(x=(0,1),y=(1,2)\), and \(S=S_1\cup S_2\) with \(S_1=(x,y)\) and \( S_2=[-x,x]\cup \{ (t,\sin (1/t))\,|\, t\in (0,1]\}\cup [(1,\sin (1)),y]\), see Fig. 3b. Set \(a=\infty \), \(b=1\) on \(S_1\), and \(b=0\) on \(S_2\). Note that b (continued with value a outside S) is lower semi-continuous. Moreover, we have \(d(x,y)=\sqrt{2}\), because it is impossible to reach y from x using \(S_2\) without travelling on the complement of S, which produces an infinite cost. However, we have \(d_k(x,y)=0\): Choose \(t_k\in (0,1]\) such that \(z_k=(t_k,\sin (1/t_k))\in B_{1/k}(x)\). Then any injective Lipschitz path \(\gamma \) on \([x,z_k]\cup \{ (t,\sin (t))\,|\, t\in (t_k,1] \}\cup [(1,\sin (1)),y]\) from x to y satisfies \(L_k(\gamma )=0\).
An immediate consequence is the lower semi-continuity of the urban metric.
Corollary 2.1.4
(Lower semi-continuity of urban metric) Under Assumption 1.3.1d is lower semi-continuous.
Proof
The (pseudo-)metric d is the pointwise supremum of the Lipschitz-continuous metrics \(d_k\). \(\square \)
Example 2.1.5
(Counterexample if b is not bounded away from zero) For \(a<\infty \) it is not difficult to see that the urban metric d is continuous even without Assumption 1.3.1 [16, Prop. 2.2.3]. In the situation of Example 2.1.3, where b was not bounded away from zero and \(a=\infty \), we get that d is not lower semi-continuous. Indeed, letting \((x_j)\subset S_2\backslash [-x,x]\) with \(x_j\rightarrow x\) we obtain
Proposition 2.1.6
(Point separation with tolerance) Let Assumption 1.3.1 be satisfied. Then for arbitrary \(x,y\in {\mathcal {C}}\) and \(t_1,t_2\in {\mathbb {R}}\) with \(|t_2-t_1|<d(x,y)\) there is a function \(f\in C_d^1\) such that \(f(x)\le t_1\) and \(f(y)\ge t_2\).
Proof
If \(t_1>t_2\), then one can take \(f\equiv (t_1+t_2)/2\), so we may assume \(t_2\ge t_1\). Further, it is enough to prove the claim for \((t_1,t_2)\) replaced by (0, t) with \(0<t<d(x,y)\). Indeed, given some \({{\tilde{f}}}\in C_d^1\) with \({{\tilde{f}}}(x)\le 0\) and \(\tilde{f}(y)\ge t\) for the choice \(t=t_2-t_1\), the desired f is obtained as \(t_1+{{\tilde{f}}}\).
We will now mollify the functions \(g_k(z)=d_k(x,z)\). For this purpose, we assume that \(g_k\) is defined on \({\mathbb {R}}^n\), or equivalently, for the rest of the proof we assume that
where the infimum is over Lipschitz paths \(\gamma :I\rightarrow {\mathbb {R}}^n\) with \(\gamma (0)=z_1\) and \(\gamma (1)=z_2\). Clearly, the functions \(g_k\) are Lipschitz with \(Lip (g_k)\le k\). Now let \(\eta \) be a smooth mollifier on \({\mathbb {R}}^n\) with unit integral and support on \(B_1(0)\). We define \(g_k^\varepsilon =\eta _\varepsilon *g_k\) for the scalings \(\eta _\varepsilon (z)=\varepsilon ^{-n}\eta (\varepsilon ^{-1}z)\). Then the functions \(f_k^\varepsilon =g_k^\varepsilon -g_k^\varepsilon (x)\) satisfiy \(f_k^\varepsilon (x)=0\) and \(f_k^\varepsilon (y)\rightarrow g_k(y)\) as \(\varepsilon \rightarrow 0\) due to the pointwise convergence \(g_k^\varepsilon \rightarrow g_k\) and \(g_k(x)=0\). Now fix k sufficiently large so that \(t<g_k(y)=d_k(x,y)<d(x,y)\) (possible by Proposition 2.1.1) and then \(\varepsilon \) small enough such that \(t\le f_k^\varepsilon (y)\). It remains to prove that the restriction of \(f=f_k^\varepsilon \) to \({\mathcal {C}}\) is an element of \(C_d^1\). By definition f is smooth and we have \(\nabla f=\nabla g_k^\varepsilon \). Let \(z\in {\mathcal {C}}\) be arbitrary and choose \(\varepsilon <1/k\) (if not a priori satisfied). We then have \(b_k\le k\wedge b(z)\le b(z)\) in \(B_\varepsilon (z)\). Now let \(y\in B_\varepsilon (z)\) be any point of total differentiability of \(g_k\). Then for all \(\nu \in {\mathcal {S}}^{n-1}\) and \(h>0\) sufficiently small such that \([y,y+h\nu ]\subset B_\varepsilon (z)\) we have
by the triangle inequality and the choice of \(\varepsilon ,h\). It follows that the directional derivative \(\partial _\nu g_k(y)\) is bounded by b(z). By the arbitrariness of y and \(\nu \) we thus obtain \(|\nabla g_k(y)|\le b(z)\) for \({\mathcal {L}}^n\)-almost every \(y\in B_\varepsilon (z)\). Using this we obtain the final estimate
which shows that f is an element of \(C_d^1\). \(\square \)
Remark 2.1.7
(Regularity of f) Following the proof of Proposition 2.1.6 we actually have \(f\in C_{d_k}^1\subset C_d^1\). It can be shown that Proposition 2.1.1 and Corollary 2.1.4 are also true for \(b_k\) replaced by \(z\mapsto \min _{{\mathcal {C}}\cap {\overline{B}}_{1/k}(z)}b\). However, using these functions, the mollfications of \(z\mapsto d_k(x,z)\), which we employ in the following, would not be real-valued.
We can now show a version of the Stone–Weierstraß theorem which states that \(C_d^1\) is a dense subset of \(C_d\). We follow the proofs in [22, Appendix A]. For \(f,g\in C^1({\mathcal {C}})\) we will need to approximate \(f\wedge g\) and \(f\vee g\) by smooth functions, for which we require the following property of mollified Heaviside step functions.
Lemma 2.1.8
( [22, Lem. A.3]) For all \(\delta >0\) there is a monotone (smoothed Heaviside step) function \(H_\delta \in C^\infty ({\mathbb {R}})\) such that \(H_\delta =0\) on \((-\infty ,-\delta ]\), \(H_\delta =1\) on \([\delta ,\infty )\) and \(|tH_\delta '(t)|\le \delta \) for all \(t\in {\mathbb {R}}\).
Let \(H_\delta \) be as in Lemma 2.1.8. We define
for all \(\delta >0\) and \(f,g\in C^1({\mathcal {C}})\). Then \(f\wedge _\delta g,f\vee _\delta g\in C^1({\mathcal {C}})\) are approximations of \(f\wedge g\) and \(f\vee g\) with respect to \(|.|_{\infty ,{\mathcal {C}}}\).
Lemma 2.1.9
(Smooth min and max operation, cf. [22, Lem. A.4]) Let \(\delta >0\) and \(f,g\in C_d^1\). Then we have \(f\wedge _\delta g,f\vee _\delta g\in (1+2\delta ) C_d^1\) as well as \(|f\wedge _\delta g-f\wedge g|,|f\vee _\delta g-f\vee g|\le \delta \) in \({\mathcal {C}}\).
Proof
We have \(f\wedge _\delta g\in C^1({\mathcal {C}} )\) by definition. Furthermore, we can estimate
thus \(f\wedge _\delta g\in (1+2\delta ) C_d^1\). Additionally, we have \(f\wedge _\delta g=f\wedge g\) if \(|f-g|\ge \delta \). The function \(f\wedge _\delta g\) is a convex combination of f and g , therefore, we conclude \(|f\wedge _\delta g-f\wedge g|\le \delta \). The proof for \(f\vee _\delta g\) is analogous. \(\square \)
We can now use the operations \(\wedge _\delta \) and \(\vee _\delta \) to obtain “\(C^1\)-gluings” of functions on certain open covers of \({\mathcal {C}}\).
Proposition 2.1.10
(Version of the Stone–Weierstraß theorem, cf. [22, Prop. A.5]) Let Assumption 1.3.1 be satisfied. Then \(C_d^1\) is a dense subset of \(C_d\) with respect to the uniform norm \(|.|_{\infty ,{\mathcal {C}} }\).
Proof
We have already seen that \(C_d^1\) is a subset of \(C_d\) in the introduction of Sect. 2. For the denseness, let \(\varepsilon >0\) and \(g\in C_d\). By \(\lambda {\tilde{g}}\rightrightarrows {\tilde{g}}\) as \(\lambda \nearrow 1\) for all \({\tilde{g}}\in C_d\) we can assume \(g\in \lambda C_d\) for some \(\lambda \in (0,1)\). Now let \(x\in {\mathcal {C}}\) be arbitrary. For each \(y\in {\mathcal {C}}\setminus \{ x\}\) we have \(d(x,y)=\infty \) or \(|g(x)-g(y)|\le \lambda d(x,y)<d(x,y)\) so that by Proposition 2.1.6 (point separation) there exists a function \(f_y\in C_d^1\) with \(f_y(x)\ge g(x)\) and \(f_y(y)\le g(y)\). Define the (relatively) open sets \(V_y=\{ f_y<g+\varepsilon /4\}\) (\(f_y\) and g are continuous). There exists a finite cover \(V_{y_1},\ldots ,V_{y_k}\) of \({\mathcal {C}}\) by the compactness of \({\mathcal {C}}\) (Heine-Borel theorem). For \(\delta >0\) define \({\tilde{F}}_x=(\ldots ((f_{y_1}\wedge _\delta f_{y_2})\wedge _\delta f_{y_3})\ldots \wedge _\delta f_{y_k})\). Then \({\tilde{F}}_x\in (1+2\delta )^k C_d^1\) and \(|{\tilde{F}}_x-\min \{ f_{y_1},\ldots ,f_{y_k}\} |\le k\delta \) by Lemma 2.1.9 and induction. Now assume without loss of generality that \(g,f_{y_1},\ldots ,f_{y_k},{{\tilde{F}}}_x\) are all nonnegative (otherwise we can just add the same, sufficiently large constant to all of them). The function \(F_x=(1+2\delta )^{-k}{\tilde{F}}_x\in C_d^1\) satisfies
for \(\delta \) sufficiently small. Now let \(W_x=\{ F_x>g-\varepsilon /4\}\). Then we obtain
for \(\delta \) sufficiently small. Thus, we have \(x\in W_x\). Again, there exists a finite (relatively) open cover \(W_{x_1},\ldots ,W_{x_l}\) of \({\mathcal {C}}\). For \({\tilde{\delta }}>0\) and \({\tilde{f}}=(\ldots ((F_{x_1}\vee _{{\tilde{\delta }}} F_{x_2})\vee _{{\tilde{\delta }}} F_{x_3})\ldots \vee _{{\tilde{\delta }}} F_{x_l})\) we have \(f=(1+2{\tilde{\delta }})^{-l}{\tilde{f}}\in C_d^1\),
and
for \({\tilde{\delta }}\) sufficiently small using also that g is bounded. In conclusion, we get \(f\in C_d^1\) and \(|f-g|_{\infty ,{\mathcal {C}} }\le \varepsilon \). \(\square \)
Example 2.1.11
(Counterexample for b not lower semi-continuous) Proposition 2.1.10 is in general not true without the condition that b is lower semi-continuous in \({\mathcal {C}}\). Assume that (S, a, b) are as in Example 2.1.2 and \(a<\infty \). Then we have \(d(x,y)=a|x-y|\). The function \(g(z)=az\) satisfies \(|g(x)-g(y)|=d(x,y)\) for all \(x,y\in [0,1]\), thus \(g\in C_d\). However, for \(\varepsilon >0\) sufficiently small, no \(f\in C_d^1\) can satisfy the inequality \(|f-g|_{\infty ,{\mathcal {C}} }<\varepsilon \). To see this, choose some \(\varepsilon <(a-b)/2\). Assume that there exists some \(f\in C_d^1\) with \(|f-g|_{\infty ,{\mathcal {C}} }<\varepsilon \), then \(|f'|\le b\) on [0, 1] by continuity and thus \(f(1)\le f(0)+b\le \varepsilon +b<a-\varepsilon =g(1)-\varepsilon \), which is a contradiction.
Remark 2.1.12
We believe that it is possible to remove the assumption that b is bounded away from zero in Proposition 2.1.10. A strategy to prove this might be as follows. Let \(D(x,y)=\lim _kd_k(x,y)\) (which would be equal to d(x, y) under Assumption 1.3.1). By Propositions 2.1.6 and 2.1.10 it would then be sufficient to prove that \(C_d=\{ \varphi \in C({\mathcal {C}})\,|\, |\varphi (x)-\varphi (y)|\le D(x,y)\}\) which would follow if we had \(D(x,y)=\sup _{\phi \in C_d}|\phi (x)-\phi (y)|\).
Our main result of this subsection now follows from the previous density result and the classical Kantorovich–Rubinstein duality argument.
Proof of Theorem 1.3.2
Since d is bounded below and lower semi-continuous by Corollary 2.1.4, the dual formulation of the Wasserstein distance is known to be (see for instance [19, Thm. 1.42] or [23, Thm. 5.10(i)])
Moreover, it is a classical argument (compare with the condition in the above supremum) that given \(\phi \) the optimal \(\psi \) is equal to (functions of this form are called d-convex)
so that we may restrict the \(\psi \)’s in the supremum to d-convex functions [23, Thm. 5.10(i)]. Again it is not difficult to show that a function \(\zeta \) is d-convex if and only if \(|\zeta (x)-\zeta (y)|\le d(x,y)\) for all \(x,y\in {\mathcal {C}}\) [23, Case 5.4]. Thus, we obtain
The condition \(\phi (x)-\psi (y)\le d(x,y)\) now implies \(\psi \ge \phi \) so that we may directly assume \(\psi =\phi \) without changing the supremum. We therefore end up with \(W_d(\mu _+,\mu _-)=\sup _{\psi \in C_d}\int _{\mathcal C}\psi \,\mathrm {d}(\mu _+-\mu _-)\).
Furthermore, we have
for all \(f\in C({\mathcal {C}} )\) so that the claim now follows from Proposition 2.1.10. \(\square \)
Example 2.1.13
(Counterexample if b is not lower semi-continuous in \({\mathcal {C}}\)) Assume that (S, a, b) are as in Example 2.1.2. Then for \(\mu _+=\delta _0\) and \(\mu _-=\delta _1\) we get
Example 2.1.14
(Counterexample if b is not bounded away from zero) We do not have a Kantorovich–Rubinstein formula without the assumption that b is bounded away from 0. Indeed, take \(\mu _+=\delta _x\) and \(\mu _-=\delta _y\) in Example 2.1.3. Then we directly get
since every element in \(\phi \in C_d\) is constant on \(S_2\) and thus \(\phi (x)=\phi (y)\).
2.2 Wasserstein Distance as Min-Cost Flow Using Fenchel-Duality
In this section we prove Theorem 1.3.4 by applying Fenchel’s duality Theorem [7, Thm. 4.4.18]. We will interpret the Beckmann problem as the dual problem to the Kantorovich–Rubinstein formula from Theorem 1.3.2. Consequently, the primal variables lie in \(C^1({\mathcal {C}})\), whereas the dual variables correspond to Radon measures as in the following lemma. We abbreviate \(B(\mu _+,\mu _-)=B_{S,a,b}(\mu _+,\mu _-)\) (see Theorem 1.3.4).
Lemma 2.2.1
(Version of the Beckmann problem) The Beckmann problem from Theorem 1.3.4 is equivalent to a problem on Radon measures,

where the infimum is taken over \({\mathcal {F}}\in {{\mathcal {D}}}{{\mathcal {M}}}^n({\mathcal {C}})\).
Proof
Clearly, the infimum on the right-hand side is no larger than \(B(\mu _+,\mu _-)\). For the reverse inequality we assume that there exists \({\mathcal {F}}\in {{\mathcal {D}}}{{\mathcal {M}}}^n({\mathcal {C}})\) such that \(div \,{\mathcal {F}}=\mu _+-\mu _-\). By [20, Thm. 3.1] we have  for some \(M\subset {\mathcal {C}}\) countably 1-rectifiable and \({\mathcal {H}}^1\)-measurable,
for some \(M\subset {\mathcal {C}}\) countably 1-rectifiable and \({\mathcal {H}}^1\)-measurable,  , and an \({\mathcal {H}}^1\)-diffuse vector measure \({\mathcal {G}}\in {\mathcal {M}}^n({\mathcal {C}})\). Let
, and an \({\mathcal {H}}^1\)-diffuse vector measure \({\mathcal {G}}\in {\mathcal {M}}^n({\mathcal {C}})\). Let
and  . Then
. Then  , \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with
, \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with  , and
, and

because  . Therefore, the measure
. Therefore, the measure  satisfies the divergence constraint. Finally, we estimate
satisfies the divergence constraint. Finally, we estimate

\(\square \)
Remark 2.2.2
(Monotonicity of Beckmann problem) An immediate consequence is \(B_{{{\tilde{S}}},{{\tilde{a}}},{{\tilde{b}}}}\ge B_{S,a,b}\) for any \({{\tilde{S}}}\subset S\), \({{\tilde{a}}}\ge a\), \(\tilde{b}\ge b\).
We can now prove strong duality for the Fenchel problems \(W_d(\mu _+,\mu _-)\) (primal) and \(B(\mu _+,\mu _-)\) (dual) using [7, Thm. 4.4.18, second constraint qualification] under Assumption 1.3.1, from which we will afterwards deduce the result under Assumption 1.3.3.
Proposition 2.2.3
(Dual formulation of Beckmann problem \(\widehat{=}\) Theorem 1.3.4 under Assumption 1.3.1) Under Assumption 1.3.1 we have
Proof
We want to apply Fenchel’s duality theorem [7, Thm. 4.4.18]. As usual we extend b to \({\mathcal {C}}\setminus S\) by a. Consider the Banach spaces \(X=C^1({\mathcal {C}} )\) and \(Y=C({\mathcal {C}} ;{\mathbb {R}}^n)\) equipped with \(|\varphi |_X=|\varphi |_{\infty ,{\mathcal {C}}}+|\nabla \varphi |_{\infty ,{\mathcal {C}} }\) for \(\varphi \in X\) and \(|s|_Y=|s|_{\infty ,{\mathcal {C}}}\) for \(s\in Y\). Define the mappings
Clearly, f and g are convex and lower semi-continuous. Furthermore, A is linear and bounded by \(|A\varphi |_Y\le |\varphi |_X\) for all \(\varphi \in X\). Hence, by Fenchel’s duality theorem [7, Thm. 4.4.18]
where \(Y^*={\mathcal {M}}^n(S)\times {\mathcal {M}}^n({\mathcal {C}})\). In addition, we get
for all \(\mu \in X^*\supset {\mathcal {M}}^n({\mathcal {C}})\). For \(\varphi \in X\) and \({\mathcal {F}}\in Y^*\) we obtain
We now calculate \(g^*\).
Let \({\mathcal {F}}\in {\mathcal {M}}^n({\mathcal {C}})\). Invoking [19, p. 130] there is some Borel measurable function \(\xi :{\mathcal {C}}\rightarrow {\mathbb {R}}^n\) with \({\mathcal {F}}=\xi |{\mathcal {F}}|\) and \(|\xi |=1\) \(|{\mathcal {F}}|\)-almost everywhere on \(\mathcal C\). Thus,
For the reverse inequality let \(b_k:{\mathcal {C}}\rightarrow [0,\infty )\) be a sequence of Lipschitz functions with \(b_k\nearrow b\) pointwise monotonically in \({\mathcal {C}}\) (such a sequence exists by [19, Box 1.5] due to the lower semi-continuity of b). Also note that by definition of the total variation there exists a sequence \(({\tilde{s}}_i)\subset C({\mathcal {C}};{\mathbb {R}}^n)\) with \(|{\tilde{s}}_i|_{\infty ,{\mathcal {C}}}\le 1\) and \(\langle {\tilde{s}}_i,{\mathcal {F}}\rangle \rightarrow |{\mathcal {F}}|({\mathcal {C}})\) for \(i\rightarrow \infty \). For fixed k we now define another sequence \((s_i)\subset C({\mathcal {C}};{\mathbb {R}}^n)\) by \(s_i=b_k{\tilde{s}}_i\) and estimate
using that \(|{\mathcal {F}}|\)-almost everywhere \(1-{\tilde{s}}_i\cdot \xi \in [0,2]\) and thus \(|1-{\tilde{s}}_i\cdot \xi |=1-{\tilde{s}}_i\cdot \xi \). Thus we have \(\langle s_i,{\mathcal {F}}\rangle \rightarrow \langle b_k,|{\mathcal {F}}|\rangle \) for \(i\rightarrow \infty \). Furthermore, \(\langle b_k,|{\mathcal {F}}|\rangle \nearrow \int _{\mathcal {C}} b\mathrm {d}|{\mathcal {F}}|\) by the monotone convergence theorem so that we end up with
The function g is continous in 0 by the assumption that \(b\ge \inf b>0\). Additionally, we have \(0\in \text {dom}(f)\) and thus \(0\in A\,\text {dom}(f)\). By [7, Thm. 4.4.18, second constraint qualification] strong duality holds, i. e.,
\(\square \)
The subsequent statements will be used in the proof of Theorem 1.3.4 under Assumption 1.3.3 at the end of this section. The first lemma is standard and uses the lower semi-continuity of d (which under Assumption 1.3.1 is Corollary 2.1.4 and under Assumption 1.3.3 follows from the continuity of d [16, Prop. 2.2.3]).
Lemma 2.2.4
(Existence of minimizer for \(W_d(\mu _+,\mu _-)\) (e.g. [19, Thm. 1.5])) Under Assumptions 1.3.1 or 1.3.3 there exists an optimal transport plan \(\pi \in \Pi (\mu _+,\mu _-)\) such that
We show \(W_d(\mu _+,\mu _-)=B(\mu _+,\mu _-)\) using standard approximation techniques to change Assumption 1.3.1 to Assumption 1.3.3. Henceforth, let \(S^N\) be an approximating sequence for S (see definition in Sect. 1.4). We write \(d^N=d_{S^N,a,b}\). Additionally, we use \(b_\lambda =\max \{\lambda ,b \}\) and \(d_\lambda =d_{S,a,b_\lambda }\) for \(\lambda \in (0,a)\).
Lemma 2.2.5
(Pointwise convergence of the \(d^N\) and \(d_\lambda \))) We have \(d_{\lambda }\searrow d\) pointwise as \(\lambda \rightarrow 0\). If Assumption 1.3.3 is satisfied, then additionally \(d^N\searrow d\) pointwise as \(N\rightarrow \infty \).
Proof
Let \(x,y\in {\mathcal {C}}\) with \(d(x,y) <\infty \) (else there is nothing to show since \(d_\lambda ,d^N\ge d\)). Let \(\varepsilon >0\) and \(\eta \in \Gamma ^{xy}\) with \(L(\eta )\le d(x,y)+\varepsilon /2\). This yields
for \(\lambda \) small enough by choosing \(\gamma =\eta \) in the second inequality. Note that all terms in the estimate are finite. Moreover, the last inequality followed from \({\mathcal {H}}^1(\eta \cap S\cap \{ \lambda >b \})\rightarrow 0\) for \(\lambda \rightarrow 0\). This proves that \(d_\lambda \searrow d\) pointwise. Assume now that Assumption 1.3.3 is satisfied. Then we obtain
for N sufficiently large (again by choosing \(\gamma =\eta \)). The last inequality is true, because \(\eta \cap S^N\) is an approximating sequence for \(\eta \cap S\). \(\square \)
Example 2.2.6
(\(d^N\searrow d\) in general not true without Assumption 1.3.3) Let \(a=\infty ,b\in [0,\infty )\), and \(S=[0,1]\). Assume that \((I_j)\) is a sequence of non-empty pairwise disjoint intervals with \(\bigcup _jI_j=S\). Set \(S^N=\bigcup _{j=1}^NI_j\) (see Fig. 4). Then we have \(d^N(0,1)=\infty >b=d(x,y)\) for all N.
Sketch for Example 2.2.6
Proof of Theorem 1.3.4 under Assumption 1.3.3
\(W_d(\mu _+,\mu _-)\le B(\mu _+,\mu _-)\): Initially, we show the inequality for the case \(\inf b>0\). Let \(\delta >0\) and fix \(\xi \) and \({\mathcal {F}}^\perp \) as in the Beckmann problem. We define measures by  . The function \(|\xi |\) is integrable with respect to
. The function \(|\xi |\) is integrable with respect to  . Consequently, we have
. Consequently, we have
for \(N\rightarrow \infty \). Thus, we can choose N sufficiently large such that \(|{\mathcal {G}}_N-{\mathcal {F}}^\perp |({\mathcal {C}})<\delta /a\).
Using in this order  , Proposition 2.2.3, Theorem 1.3.2, and \(d^N\ge d\), we can estimate
, Proposition 2.2.3, Theorem 1.3.2, and \(d^N\ge d\), we can estimate
where \(C_{d^N}^1=\{ \varphi \in C^1({\mathcal {C}})\,|\,|\nabla \varphi |\le b\text { on }S^N,|\nabla \varphi |\le a\text { in }{\mathcal {C}} \}\). Letting \(\delta \rightarrow 0\) yields the desired inequality. Now we concentrate on the case \(\inf b=0\). Using the functions \(b_\lambda \) we obtain
Moreover, we have
and therefore (monotone convergence)
by letting \(\lambda \rightarrow 0\).
\(W_d(\mu _+,\mu _-)\ge B(\mu _+,\mu _-)\): First assume that \(\inf b>0\). By Lemma 2.2.4 there exists an optimal transport plan \(\pi \in \Pi (\mu _+,\mu _-)\) such that \(W_d(\mu _+,\mu _-)=\langle d,\pi \rangle \). Let \(\delta >0\) be arbitrary. Using \(\langle d^N,\pi \rangle <\infty \) and \(d^N\searrow d\) pointwise by Lemma 2.2.5 the monotone convergence theorem implies the existence of some \(N=N(\delta )\) such that \(|\langle d^N-d,\pi \rangle |\le \delta \). Application of Proposition 2.2.3 and Remark 2.2.2 yields
Letting \(\delta \rightarrow 0\) yields the desired inequality. Now assume that \(\inf b=0\). Once more let \(\delta >0\). Again, by \(\langle d_{\lambda },\pi \rangle <\infty \) and \(d_{\lambda }\searrow d\) pointwise by Lemma 2.2.5 we can apply the monotone convergence theorem and choose \(\lambda \) sufficiently small such that
Letting \(\delta \rightarrow 0\) we obtain the desired inequality. \(\square \)
3 Urban Planning Formulation of Branched Transport Using Duality
In this section we prove Theorem 1.3.8 under Assumption 1.3.5. We will use the following formula for the branched transport problem [16, Lemma 3.1.8], which can be derived from [4, Lem. 5.15], [9, Prop. 2.32], and [20, Thm. 3.1].
Lemma 3.0.7
(Version of the branched transport problem) The branched transport problem can be written as

with \(S\subset {\mathcal {C}}\) countably 1-rectifiable and Borel measurable,  and \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with
and \({\mathcal {F}}^\perp \in {\mathcal {M}}^n({\mathcal {C}})\) with  .
.
In Sect. 3.1 we will prove a dual formula for the first network cost term, which will be used to introduce the friction coefficients b. Based on this formula and Theorem 1.3.4, we will provide a short proof of Theorem 1.3.8 under Assumption 1.3.5.
3.1 Duality for the Total Network Transportation Cost
We apply a generalization of Rockafellar’s duality theorem between a pair of decomposable spaces of vector-valued functions [10, Thm. VII-7]. Let \(S\subset {\mathcal {C}}\) be countably k-rectifiable and \({\mathcal {H}}^k\)-measurable (\(k=1\) and S even Borel in our setting). We denote the \(\sigma \)-algebra of \({\mathcal {H}}^k\)-measurable subsets of S (or more precisely subsets that are Carathéodory-measurable relative to \({\mathcal {H}}^k\)) by \({\mathscr {H}}^k(S)\). Using that the restriction of an outer measure like \({\mathcal {H}}^k\) on \({\mathbb {R}}^n\) to the Carathéodory-measurable sets yields a complete measure space, this property also holds for  . Furthermore, the measure space
. Furthermore, the measure space  is \(\sigma \)-finite (every member of an approximating sequence for S has finite measure).
is \(\sigma \)-finite (every member of an approximating sequence for S has finite measure).
Convention 3.1.1
In this section “measurability” and “integrability” will refer to the measure space  .
.
We remind the reader that a subset \(A\subset S\) is in \({\mathscr {H}}^k(S)\) if and only if \({\mathcal {H}}^k(B)={\mathcal {H}}^k(B\cap A)+{\mathcal {H}}^k(B\backslash A)\) for all \(B\subset S\). By Carathéodory’s criterion [21, Thm. 1.13] we have \({\mathcal {B}}(S)\subset {\mathscr {H}}^k(S)\). In our case, the “vector-valued functions” from [10, Chap. VII-7] are given through integrable and real-valued functions on S. We consider the following vector spaces:
Note that the elements of \({\mathscr {L}},{\mathscr {L}}_{\text {b}}\), and \({\mathscr {M}}_{\text {b}}\) are not equivalence classes. We follow here the setting in [10, Def. VII-3].
Definition 3.1.2
(Decomposable [10, Def. VII-3]) Let \(V\subset {\mathscr {L}}\) be a subspace. The space V is said to be decomposable if \(1_Af+1_{S\setminus A}g\in V\) for all \(A\in {\mathscr {H}}^k(S)\) with \({\mathcal {H}}^k(A)<\infty \), \(f\in {\mathscr {M}}_{\text {b}}\) and \(g\in V\).
The vector spaces \({\mathscr {L}}\) and \({\mathscr {L}}_{\text {b}}\) are decomposable: Let either \(V={\mathscr {L}}\) or \(V={\mathscr {L}}_{\text {b}}\) and A, f, g as in Definition 3.1.2. Then we have
and thus \(1_Af+1_{S\setminus A}g\in {\mathscr {L}}\). Further, if \(V={\mathscr {L}}_{\text {b}}\), then we obtain \(|1_Af+1_{S\setminus A}g|\le |f|_{\infty ,A}+|g|_{\infty ,A}<\infty \). Moreover, we get \(x\mapsto f(x)g(x)\in {\mathscr {L}}\) for all \(f\in {\mathscr {L}},g\in {\mathscr {L}}_{\text {b}}\) (cf. [10, Def. VII-3]), which needs to be satisfied to apply [10, Thm. VII-7].
For \(g\in {\mathscr {L}}\) and lower semi-continuous functions \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\cup \{ \infty \}\) we write
where \(f(g)^+\) denotes the positive part of \(f(g):S\rightarrow {\mathbb {R}}\cup \{ \infty \}\). By our construction we can apply the following statement to generate the friction coefficients \(b:S\rightarrow [0,\infty )\) of the urban planning problem. Essentially it characterizes the convex conjugate of integral functionals using \(L^1\)-\(L^\infty \)-type duality pairings: One may pull the convex conjugation inside the integral.
Proposition 3.1.3
(First part of [10, Thm. VII-7]) Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\cup \{ \infty \}\) be lower semi-continuous. Assume that \(I_f(g_0)\) is finite for at least one \(g_0\in {\mathscr {L}}_{\text {b}}\). Then we obtain
for all \(h\in {\mathscr {L}}\).
Fix a maintenance cost \(\varepsilon \) induced by a transportation cost \(\tau \), i. e., \(\varepsilon (b)=(-\tau )^*(-b)\), where \(\tau (m)=-\infty \) for \(m<0\). Then we get the following formula for the network cost term from Lemma 3.0.7.
Corollary 3.1.4
(Substitution of maintenance cost) Assume that \({\mathcal {H}}^k(S)<\infty \). Furthermore, let \(\xi :S\rightarrow {\mathbb {R}}^n\) be integrable. Let the transportation cost \(\tau \) be right-continuous in 0. Then we have
where the infimum is taken over \(b\in {\mathscr {L}}_{\text {b}}\).
Proof
The biconjugate equals the convex and lower semi-continuous envelope [17, Prop. 2.28]. The function \(-\tau \) is already convex and lower semi-continuous by assumption. Thus, we conclude
Furthermore, we have \(I_{\varepsilon }(v)<\infty \) for all \(v\in {\mathbb {R}}\) with \(\varepsilon (v)<\infty \) using \({\mathcal {H}}^k(S)<\infty \). We presumed \(|\xi |\in {\mathscr {L}}\) and can therefore apply Proposition 3.1.3:
\(\square \)
We now prove Theorem 1.3.7 in a slightly generalized setting (for arbitrary k and S not necessarily Borel measurable).
Theorem 3.1.5
(Generalization of Theorem 1.3.7) Let \(\xi :S\rightarrow {\mathbb {R}}^n\) be integrable. Assume that \(\tau \) satisfies Assumption 1.3.5. Then we have
where the infimum is taken over lower semi-continuous functions \(b: S\rightarrow [0,\tau '(0)]\).
Proof
\(\text {Formula true for functions } b\in {\mathscr {M}}_b\): Using the procedure in Sect. 1.4 (compare with the sets \(T_i\)), we can assume that S is a disjoint countable union of finitely k-rectifiable sets \(S_i\), i. e., the \(S_i\subset S\) are measurable with \({\mathcal {H}}^k(S_i)<\infty \) (we neglect nullsets due to the integration). Let \(\delta >0\) and \(\delta _i>0\) such that \(\sum _i\delta _i=\delta \). By Sect. 3.1.4 we can find functions \(b_i\in {\mathscr {L}}_b\) with
Define \({\tilde{b}}\in {\mathscr {M}}_\text {b}\) by \({\tilde{b}}=b_i\) on \(S_i\). Note that we can assume that each \(b_i\) is bounded by \(\tau '(0)\) because of \(\varepsilon ([\tau '(0),\infty ))=\{ 0\}\). Application of the monotone convergence theorem yields
where the infima are taken over functions \(b\in {\mathscr {M}}_\text {b}\). Notice that \(\varepsilon ,b\ge 0\) was used in the last equation. The reverse inequality is a direct consequence of the definition of the convex conjugate. More precisely, let \(b:S\rightarrow [0,\infty )\) be any measurable and bounded function. Then we obtain
by choosing \(v=v(x)=b(x)\) in the inequality. Taking the infimum over b shows the stated formula for \(b\in {\mathscr {M}}_\text {b}\).
\(\text {The functions }b \text { can be assumed to be lower semi-continuous}:\) As a first step, we simplify the statement to be shown. Write \(c=\inf \text {dom}(\varepsilon )\). Note that every function in the infimum of the stated formula of the theorem can be assumed to have values in \([c,\tau '(0)]\) by the properties of \(\varepsilon \). For \(f\in {\mathscr {M}}_{\text {b}}\) with \(f\ge 0\) define
Let \(b\in {\mathscr {M}}_{\text {b}}\) be arbitrary with \(F(b)<\infty \) (note that \(F(\tau '(0))<\infty \) by the integrability of \(|\xi |\) and \(\varepsilon (\tau '(0))=0\)). Let \(S^N\) be an approximating sequence for S. Define functions by
We have \(\varepsilon (b_N)\nearrow \varepsilon (b)\) and \(b_N|\xi |\searrow b|\xi |\) for \(N\rightarrow \infty \) pointwise  -almost everywhere. Furthermore, the \(b_N|\xi |\) satisfy
-almost everywhere. Furthermore, the \(b_N|\xi |\) satisfy
Hence, we get \(F(b_N)\rightarrow F(b)\) for \(N\rightarrow \infty \) by the monotone convergence theorem. Thus, for fixed N it is enough to find a lower semi-continuous funcion \(\ell _N:S\rightarrow [c,\tau '(0)]\) such that \(F(\ell _N)\) is arbitrarily close to \(F(b_N)\). This reduces to the problem of finding a lower semi-continuous function \(\ell _N:S^N\rightarrow [c,\tau '(0)]\) with \(F_N(\ell _N)\) being arbitrarily close to \(F_N(b_N)\), where
for \(f\in {\mathscr {M}}_{\text {b}}\) with \(f\ge 0\), because we can then replace \(\ell _N\) by the lower semi-continuous function (\(S^N\) is closed)
Note that \(F_N(b_N)\) is finite by \(F(b)<\infty \). For simplicity, we write S, F, b instead of \(S^N,F_N,b_N\) and assume that S is closed with \({\mathcal {H}}^k(S)<\infty \) (like the \(S^N\)) and \(F(b)<\infty \) (which implies \(\varepsilon (b)\in {\mathscr {L}}\)) for the rest of the proof. By [1, Rem. 2.50] (which refers to [1, Ex. 1.3]) the function \(b\in {\mathscr {M}}_\text {b}\) can be assumed to be Borel measurable. We will below use the functions \(b_\delta =b+\delta \) for \(\delta >0\). Without loss of generality the \(b_\delta \) have values in \([c+\delta ,\tau '(0)+\delta ]\). Since the restriction of  to \({\mathcal {B}}(S)\) now is a finite Radon measure on a compact set, we can apply the Vitali- Carathéodory theorem [18, 2.25] to the functions \(b_\delta \in {\mathscr {L}}\): for all \(\delta >0\) there exists a sequence of lower semi-continuous functions \(\ell _\delta ^i\) with \(b_\delta \le \ell _\delta ^i\le \tau '(0)+\delta \) on S and
to \({\mathcal {B}}(S)\) now is a finite Radon measure on a compact set, we can apply the Vitali- Carathéodory theorem [18, 2.25] to the functions \(b_\delta \in {\mathscr {L}}\): for all \(\delta >0\) there exists a sequence of lower semi-continuous functions \(\ell _\delta ^i\) with \(b_\delta \le \ell _\delta ^i\le \tau '(0)+\delta \) on S and
This yields \(\ell _\delta ^i\rightarrow b_\delta \) pointwise  -almost everywhere for \(i\rightarrow \infty \) up to a subsequence. Now let \(f_\delta ^i=\ell _\delta ^{i}|\xi |+\varepsilon (\ell _\delta ^{i})\). We obtain \(|f_\delta ^{i}|\le (\tau '(0)+\delta )|\xi |+\varepsilon (c+\delta )\in {\mathscr {L}}\) and \(f_\delta ^{i}\rightarrow b_\delta |\xi |+\varepsilon (b_\delta )\) pointwise
-almost everywhere for \(i\rightarrow \infty \) up to a subsequence. Now let \(f_\delta ^i=\ell _\delta ^{i}|\xi |+\varepsilon (\ell _\delta ^{i})\). We obtain \(|f_\delta ^{i}|\le (\tau '(0)+\delta )|\xi |+\varepsilon (c+\delta )\in {\mathscr {L}}\) and \(f_\delta ^{i}\rightarrow b_\delta |\xi |+\varepsilon (b_\delta )\) pointwise  -almost everywhere for \(i\rightarrow \infty \) (\(\varepsilon \) is continuous on \((c,\infty )\)). Thus, we have \(F(\ell _\delta ^{i})\rightarrow F(b_\delta )\) for \(i\rightarrow \infty \) by Lebesgue’s dominated convergence theorem. In addition, we have \(h_\delta =b_\delta |\xi |+\varepsilon (b_\delta )\rightarrow b|\xi |+\varepsilon (b)\) pointwise for \(\delta \rightarrow 0\) (\(\varepsilon \) is right-continuous in c) and \(|h_\delta |\le (\tau '(0)+\delta )|\xi |+\varepsilon (b)\in {\mathscr {L}}\), which yields \(F(b_\delta )\rightarrow F(b)\) for \(\delta \rightarrow 0\). This shows that b can be assumed to be lower semi-continuous (choose \(\delta \) sufficiently small and then i sufficiently large for the corresponding subsequence of the \(\ell _\delta ^{i}\)). \(\square \)
-almost everywhere for \(i\rightarrow \infty \) (\(\varepsilon \) is continuous on \((c,\infty )\)). Thus, we have \(F(\ell _\delta ^{i})\rightarrow F(b_\delta )\) for \(i\rightarrow \infty \) by Lebesgue’s dominated convergence theorem. In addition, we have \(h_\delta =b_\delta |\xi |+\varepsilon (b_\delta )\rightarrow b|\xi |+\varepsilon (b)\) pointwise for \(\delta \rightarrow 0\) (\(\varepsilon \) is right-continuous in c) and \(|h_\delta |\le (\tau '(0)+\delta )|\xi |+\varepsilon (b)\in {\mathscr {L}}\), which yields \(F(b_\delta )\rightarrow F(b)\) for \(\delta \rightarrow 0\). This shows that b can be assumed to be lower semi-continuous (choose \(\delta \) sufficiently small and then i sufficiently large for the corresponding subsequence of the \(\ell _\delta ^{i}\)). \(\square \)
Remark 3.1.6
(Construction of minimizer) If \(|\xi |\) is upper semi-continuous, then a minimizer b is given by (cf. proof of [16, Theorem 1.3.4])
3.2 Branched Transport as Street Network Optimization
Proof of Theorem 1.3.8 under Assumption 1.3.5
We apply Lemma 3.0.7, Theorems 1.3.7, 1.3.4 (the variables are as in the problems and statements):

\(\square \)
Remark 3.2.1
(Branched transport problem has minimizer under Assumption 1.3.5) The growth condition \(\tau '(0)<\infty \) implies
which by [9, Corollaries 2.19 & 2.20] guarantees that the branched transport problem is finite and has a solution \({\mathcal {F}}\).
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. Oxford University Press, New York (2000)
Ambrosio, L., Gigli, N., Savare, G.: Gradient flows. In: Metric Spaces and in the Space of Probability Measures. Lectures in Mathematics. ETH Zürich. Birkhäuser Basel (2008)
Brancolini, A., Buttazzo, G.: Optimal networks for mass transportation problems. ESAIM: Control Optim. Calc. Var. 11(1), 88–101 (2005)
Bernot, M., Caselles, V., Morel, J.-M.: Optimal Transportation Networks. Lecture notes in Mathematics, 1955th edn. Springer-Verlag, Berlin (2009)
Brieskorn, E.: Felix Hausdorff zum Gedächtnis—Band I, 1st edn. Vieweg\(+\)Teubner Verlag, Wiesbaden (1996)
Buttazzo, G., Pratelli, A., Stepanov, E., Solimini, S.: Optimal Urban Networks via Mass Transportation, 1st edn. Springer-Verlag, Berlin, Heidelberg (2009)
Borwein, J.M., Vanderwerff, J.: Convex Functions Constructions. Characterizations and Counterexamples, 109th edn. Cambridge University Press, New York (2010)
Brancolini, A., Wirth, B.: Equivalent formulations for the branched transport and urban planning problems. J. Math. Pures Appl. 106(4), 695–724 (2016)
Brancolini, A., Wirth, B.: General transport problems with branched minimizers as functionals of 1-currents with prescribed boundary. Calc. Var. Part. Differ. Equ. 57(3), 82 (2018)
Castaing, C., Valadier, M.: Convex Analysis and Measurable Multifunctions. Lecture Notes in Mathematics, 580th edn. Springer-Verlag, Berlin (1977)
Edwards, D.A.: On the Kantorovich–Rubinstein theorem. Expos. Math. 29(4), 387–398 (2011)
Elstrodt, J.: Maß-und Integrationstheorie, 8th edn. Springer Spektrum, Berlin, Heidelberg (2018)
Kenneth, J.F.: The Geometry of Fractal Sets, 1st edn. Cambridge University Press, Cambridge (1986)
Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, 153rd edn. Springer-Verlag, New York (1969)
Lang, S.: Real Analysis. Addison-Wesley Series in Mathematics. Addison-Wesley, Reading (1969)
Lohmann, J., Schmitzer, B., Wirth, B.: Formulation of branched transport as geometry optimization. J. Math. Pures Appl. (2022). https://doi.org/10.1016/j.matpur.2022.05.021
Rindler, Filip: Calculus of Variations, 1st edn. Springer International Publishing, Basel (2018)
Rudin, Walter: Real and Complex Analysis, 3rd edn. McGraw-Hill Education Ltd, New York (1986)
Santambrogio, F.: Optimal Transport for Applied Mathematicians. Calculus of Variations, PDEs, and Modeling, 1st edn. Birkhäuser Verlag, Basel (2015)
Šilhavý, M.: Divergence measure vectorfields: their structure and the divergence theorem. In: Mathematical Modelling of Bodies with Complicated Bulk and Boundary Behavior, 20th edn, pp. 217–237. Aracne, Napoli (2008)
Simon, L.M.: Introduction to Geometric Measure Theory. Lecture Notes. Beijing. https://web.stanford.edu/class/math285/ts-gmt.pdf (2014)
Schmitzer, B., Wirth, B.: Dynamic models of Wasserstein-1-type unbalanced transport. ESAIM: Control Optim. Calc. Var. 25, Paper No. 23, 54 (2019)
Villani, C.: Optimal Transport: Old and New. Grundlehren der mathematischen Wissenschaften, vol. 338. Springer, Berlin (2009)
Xia, Q.: Optimal paths related to transport problems. Commun. Contemp. Math. 5(2), 251–279 (2003)
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the priority program SPP 1962, Grant WI 4654/1-1, and under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics-Geometry-Structure. B.W.’s and J.L.’s research was supported by the Alfried Krupp Prize for Young University Teachers awarded by the Alfried Krupp von Bohlen und Halbach-Stiftung. B.S.’s research was supported by the Emmy Noether Programme of the DFG, Grant SCHM 3462/1-1.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was supported by the Deutsche Forschungsgemeinschaft under the priority program SPP 1962 (grant no. WI 4654/1-1), under Germany’s Excellence Strategy EXC 2044 (grant no. 390685587), the Alfried Krupp von Bohlen und Halbach-Stiftung (Alfried Krupp Prize for Young University Teachers), and the Emmy Noether Programme (grant SCHM 3462/1-1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lohmann, J., Schmitzer, B. & Wirth, B. Duality in Branched Transport and Urban Planning. Appl Math Optim 86, 45 (2022). https://doi.org/10.1007/s00245-022-09927-3
Accepted:
Published:
DOI: https://doi.org/10.1007/s00245-022-09927-3





 the Lebesgue measure on some open and bounded set
the Lebesgue measure on some open and bounded set 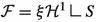 with S countably 1-rectifiable (which we will later see from the formula in Lemma
with S countably 1-rectifiable (which we will later see from the formula in Lemma  of
of 

