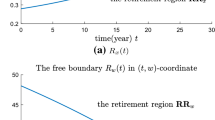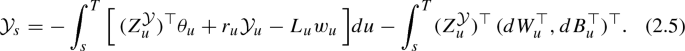Abstract
We study an optimal retirement, consumption/portfolio selection problem of an economic agent in a non-Markovian environment. We show that under a suitable condition the optimal retirement decision is to retire when the individual’s wealth reaches a threshold level. We express the value and the optimal strategy by using the strong solution of the backward stochastic partial differential variational inequality (BSPDVI) associated with the dual problem. We derive properties of the value function and the optimal strategy by analyzing the strong solution and the free boundary of the BSPDVI. We also make a methodological contribution by proposing an approach to investigate properties of the strong solution and the stochastic free boundary of BSPDVI by combining a probabilistic method and the theory of backward stochastic partial differential equations (BSPDEs).
Similar content being viewed by others
Notes
In order to save notation we will use the same notation C (and K) to denote different large enough positive constants. Their meanings, however, will be clear from the context in which they appear.
In this model, we suppose that the risky assets are driven by two independent Brownian motions W and B, and the coefficient \(r,\mu ,\varSigma \) are only \(\mathcal{P}^B-\)measurable (\(\mathcal{P}^B\) is the \(\sigma \)-algebra of predictable sets generated by B). We make this assumption to ensure that the differential operator in the associated BSPDE and BSPDVI is non-degenerate, and the BSPDE and BSPDVI have strong solutions. In fact, our model includes such commonly used models as some stochastic interest rate models and stochastic volatility models.
The negative of the present value \(-\mathcal{Y}_t\) is the initial level of wealth such that \(Y_T^{t,-\mathcal{Y}_t;T,0,0,\pi ^\mathcal{Y}}=0\) with an appropriate investment strategy \(\pi ^\mathcal{Y}\). So, if we let \(\mathcal{Y}=-Y^{t,-\mathcal{Y}_t;T,0,0,\pi ^\mathcal{Y}},\,Z^\mathcal{Y}=-\varSigma ^{\top }\pi ^\mathcal{Y}\), then \((\mathcal{Y}, Z^\mathcal{Y})\) is the unique solution of the following backward stochastic differential equation (BSDE)
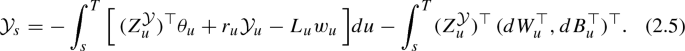
Note that \(L,\theta , r ,w\) are \(\mathcal{P}^B-\)measurable. Hence, \(\mathcal{Y}, Z^\mathcal{Y}\) are \(\mathcal{P}^B-\)measurable, and \(Z^\mathcal{Y}_i=0\) for \(i=1,\cdots ,N_1\).
See Yang and Koo [30] for similar transformations in a simpler context in a Markovian model with constant coefficients.
In fact, we will show that \({\underline{V}}\) and \(\widetilde{{\underline{V}}}\) are continuous with respect to y and x a.e. in \(\varOmega \times [\,0,T\,]\) in Theorem 1, respectively. So, we use \(\sup ,\inf \) rather than \(\mathrm{ess.sup},\mathrm{ess.inf}\) here.
By [27] \(\widetilde{{\underline{V}}}\) and \({\widehat{V}}\) defined in (3.15) are the viscosity solutions of BSPDE (3.10) and BSPDVI (3.16), respectively. In this paper, however, we do not need this result. We only focus on the verification theorem, i.e., we will construct the value V and the optimal strategies by means of the strong solutions of BSPDE (3.10) and BSPDVI (3.16) via Theorem 1 in Sect. 3.5.
Note that \(Z^\mathcal{Y}_{i}=0,i=1,\cdots ,N_1\).
Though \(\beta =0\) in Theorem 3.1 in [31], it is clear that the corresponding result still holds in the case of \(\beta \ne 0\). Moreover, \(v\in {\mathbb {H}}^{2,\,2},\,w\in {\mathbb {H}}^{1,\,2},\) and \(f\in {\mathbb {H}}^{0,\,2}\) are assumed in Theorem 3.1 in [31]. We relax the assumption, as we can construct a sequence of intervals \(\{[\,1/n,n\,]:n\in {\mathbb {Z}}^+\}\) which converges to \({\mathbb {R}}^+\).
In the Lemmas 2.2 and Lemma 5.1 in [31], the parameter \(\lambda \) in the random field space \({\mathbb {H}}^{i,\,2}_\lambda ,i=0,1,2\) is supposed to be zero. But we can utilize the transformation in the proof of Theorem 4.9 in [21] to relax the condition. Moreover, we can obtain the results in Lemmas 6 and 7 by another method as follows. Applying the method in [21], we can construct a \({\underline{v}}\) such that \({\underline{v}}<v\) under the conditions in Lemma 4. So BSPDVI (A.1) is equivalent to BSPDE (A.2), and Lemmas 6 and 7 follow from Lemmas 4 and 5, respectively.
In [21], \({\widehat{R}}_{1}(x)\) is supposed to be of polynomial growth with respect to x, which guarantees that \({\widehat{R}}_{1}({\widetilde{X}}^{t,{\widetilde{x}}})\in \mathcal{L}^2\). Now, we relax this condition to \({\widehat{R}}_{1}({\widetilde{X}}^{t,{\widetilde{x}}})\in \mathcal{L}^2\).
References
Ball, C.A., Torous, W.N.: Stochastic correlation across international stock markets. J. Empir. Financ. 7(3–4), 373–388 (2000)
Bensoussan, A., Friedman, A.: Nonlinear variational inequalities and differential games with stopping times. J. Funct. Anal. 16(3), 305–352 (1974)
Bodie, Z., Merton, R.C., Samuelson, W.F.: Labor supply flexibility and portfolio choice in a life cycle model. J. Econ. Dyn. Control 16(3–4), 427–449 (1992)
Choi, K.J., Shim, G.: Disutility, optimal retirement, and portfolio selection. Math. Financ. 16(2), 443–467 (2006)
Choi, K.J., Shim, G., Shin, Y.H.: Optimal portfolio, consumption-leisure and retirement choice problem with CES utility. Math. Financ. 18(3), 445–472 (2008)
Cox, J.C., Huang, C.: Optimal consumption and portfolio policies when asset prices follow a diffusion process. J. Econ. Theory 49(1), 33–83 (1989)
Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Cambridge University Press, Cambridge (1992)
Du, K., Tang, S.: Strong solution of backward stochastic partial differential equations in \(C^2\) domains. Prob. Theory Relat. Fields 154(1–2), 255–285 (2012)
Dybvig, P.H., Liu, H.: Lifetime consumption and investment: retirement and constrained borrowing. J. Econ. Theory 145(3), 885–907 (2010)
El Karoui, N., Kapoudjian, C., Pardoux, E., Peng, S., Quenez, M.C.: Reflected solutions of backward SDE’s, and related obstacle problems for PDE’s. Ann. Probab. 25(2), 702–C737 (1997)
Farhi, E., Panageas, S.: Saving and investing for early retirement: a theoretical analysis. J. Financ. Econ. 83(1), 87–121 (2007)
Friedman, A.: Stochastic games and variational inequalities. Arch. Ration. Mech. Anal. 51(5), 321–346 (1973)
Heath, D., Jarrow, R., Morton, A.: Bond pricing and the term structure of interest rates: a new methodology for contingent claims valuation. Econometrica 60(1), 77–105 (1992)
Hu, Y., Peng, S.: Adapted solution of a backward semilinear stochastic evolution equation. Stoch. Anal. Appl. 9, 445–459 (1991)
Hu, Y., Ma, J., Yong, J.: On semi-linear degenerate backward stochastic partial differential equations. Probab. Theory Relat. Fields 123, 381–411 (2002)
Inada, K.: On a two-sector model of economic growth: comments and a generalization. Rev. Econ. Stud. 30(2), 119–127 (1963)
Karatzas, I., Lehoczky, J.P., Sethi, S.P., Shreve, S.E.: Explicit solution of a general consumption/investment problem. Math. Oper. Res. 11(2), 261–294 (1986)
Karatzas, I., Lehoczky, J.P., Shreve, S.E.: Optimal portfolio and consumption decisions for a “small investor” on a finite horizon. SIAM J. Control Optim. 25(6), 1557–1586 (1987)
Karatzas, I., Shreve, S.E.: Methods of Mathematical Finance. Springer, New York (1998)
Karatzas, I., Wang, H.: Utility maximization with discretionary stopping. SIAM J. Control Optim. 39(1), 306–329 (2000)
Koo, H.K., Tang, S., Yang, Z.: A Dynkin game under Knightian uncertainty. Discret. Contin. Dyn. Syst. 35(11), 5467–5498 (2015)
Li, K., Liu, J.: Optimal dynamic momentum strategies. Working paper
Mao, X.: Stochastic Differential Equations and Applications. Woodhead Publishing, Cambridge (2011)
Nutz, M., Zhang, J.: Optimal stopping under adverse nonlinear expectation and related games. Ann. Appl. Prob. 25(5), 2503–2534 (2015)
Peskir, G., Shiryaev, A.: Optimal Stopping and Free-Boundary Problems. Birkhäuser Verlag, Basel (2006)
Qiu, J., Wei, W.: On the quasi-linear reflected backward stochastic partial differential equations. J. Funct. Anal. 267(10), 3598–3656 (2014)
Qiu, J.: Viscosity solutions of stochastic Hamilton-Jacobi-Bellman equations. SIAM J. Control Optim. 56(5), 3708–3730 (2018)
Tang, S., Koo, H.K.: Real options: a framework of optimal switching. In: Koo, H.K. (ed.) New Frontiers of Financial Engineering. IOS Press, Amsterdam (2012)
Uzawa, H.: On a two-sector model of economic growth II. Rev. Econ. Stud. 30(2), 105–118 (1963)
Yang, Z., Koo, H.K.: Optimal consumption and portfolio selection with early retirement option. Math. Oper. Res. 43(4), 1378–1404 (2018)
Yang, Z., Tang, S.: Dynkin game of stochastic differential equations with random coefficients and associated backward stochastic partial differential variational inequality. SIAM J. Control Optim. 51(1), 64–95 (2013)
Yong, J., Zhou, X.Y.: Stochastic control: Hamiltonian systems and HJB equations. Springer, New York (1999)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Yang is partially supported by NNSF of China [Grant No. 11771158, 11801091] and Guangdong Basic and Applied Basic Research Foundation [Grant No. 2019A1515011338]. Koo gratefully acknowledges support by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea [Grant No. NRF-2019S1A5A2A03054249]. Shin is supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) [Grant No. NRF-2019R1H1A2079177].
Appendices
A Few Existing Results About BSPDVI
For convenience of the reader we state the generalized Itô-Kunita-Wentzell’s formula, and results about BSPDE (refer to [8, 31]) and BSPDVI (refer to [21]) which were used in the paper.
We provide the generalized Itô–Kunita–Wentzell’s formula (refer to Theorem 3.1 in [31]) in the followingFootnote 9,
Lemma 3
Suppose that the random function \(v:\varOmega \times [\,0,T\,]\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) satisfies the following properties: v(x) is a continuous semimartingale and takes the following form
And \(v\in {\mathbb {H}}^{2,\,2}(D),\,w\in {\mathbb {H}}^{1,\,2}(D),\,f\in {\mathbb {H}}^{0,\,2}(D)\) for any compact subset D of \({\mathbb {R}}^+\). Let X be governed by (3.9), and Assumptions 2 and 3 be satisfied. Then we have
where the differential operator \(\mathcal{L}\) and \({{\mathcal {M}}}\) are defined in (3.11).
Remark 6
From the above integral representation of \(e^{-\beta (\cdot -t)}v_\cdot (X_\cdot )\), we know that the stochastic process \(v_\cdot (X_\cdot )\) has a continuous version.
We will now state results about a BSPDVI, which takes the following form
where the differential operator \(\widetilde{{{\mathcal {L}}}}\) and \(\widetilde{{{\mathcal {M}}}}\) are defined in (4.3).
First, we state a result about the existence and uniqueness of the strong solution to the BSPDVI (see Theorem 5.4 in [21]).
Lemma 4
Let Assumptions 2 and 3 be satisfied, \(\,f\in {\mathbb {H}}^{0,\,2}_\lambda ,\, \varphi \in {\mathbb {L}}^{1,\,2}_\lambda ,\,{\underline{v}}\,\in {\mathbb {H}}_\lambda ^{2,\,2}\) with some nonnegative number \(\lambda \). Moreover, the lower obstacle \({\underline{v}}\,\) is a continuous semimartingale of the following form
with some \(({\underline{w}}\,,\,{\underline{g}}\,)\in {\mathbb {H}}_\lambda ^{1,\,2}\times {\mathbb {H}}_\lambda ^{0,\,2}\), and \({\underline{v}}\,_T\le \varphi \). Then BSPDVI (A.1) has a unique strong solution \((v,w,k^+)\in {\mathbb {H}}_\lambda ^{2,\,2}\times {\mathbb {H}}_\lambda ^{1,\,2} \times {\mathbb {H}}_\lambda ^{0,\,2}\). Moreover, \(v\in {\mathbb {S}}_\lambda ^{1,\,2}\).
Next, we provide a comparison theorem for BSPDVI (refer to Theorem 5.2 in [21]).
Lemma 5
Let the assumptions in Lemma 4 be satisfied. Let \((v_i,w^i,k_i^+)\) be the strong solution to BSPDVI (A.1) associated with \((f_i,\,\varphi _i,\,{\underline{v}}\,_i)\) for \(i=1,2\). If \(f_1\ge f_2,\,\varphi _1\ge \varphi _2,\) and \({\underline{v}}\,_1\ge {\underline{v}}\,_2\), then \(v_1\ge v_2\) a.e. in \(\varOmega \times [\,0,T\,]\times {\mathbb {R}}\).
Consider the following BSPDE,
In view of the results for BSPDE (refer to Lemmas 2.2 and 5.1 in [31], or Theorem 5.3 and Corollary 3.4 in [8]), we can conclude the following results for BSPDEFootnote 10.
Lemma 6
Let Assumptions 2 and 3 be satisfied, \(\,f\in {\mathbb {H}}^{0,\,2}_\lambda ,\, \varphi \in {\mathbb {L}}^{1,\,2}_\lambda \) with some nonnegative number \(\lambda \). Then BSPDE (A.2) has a unique strong solution \((v,w)\in {\mathbb {H}}_\lambda ^{2,\,2}\times {\mathbb {H}}_\lambda ^{1,\,2}\). Moreover, \(v\in {\mathbb {S}}_\lambda ^{1,\,2}\).
Lemma 7
Let the assumptions in Lemma 6 be satisfied. Assume that \((v_i,w^i)\) be the strong solution to BSPDE (A.2) associated with \((f_i,\,\varphi _i)\) for \(i=1,2\). If \(f_1\ge f_2\) and \(\varphi _1\ge \varphi _2\), then \(v_1\ge v_2\) a.e. in \(\varOmega \times [\,0,T\,]\times {\mathbb {R}}\).
Finally, we give the result about the relationship between the strong solution \({\widehat{P}}\) of BSPDVI (4.4) and the value of the corresponding optimal stopping problem (refer to Theorem 5.4 in [21])Footnote 11.
Lemma 8
Let Assumptions 2 and 3 be satisfied. Suppose that \(\widetilde{{\underline{P}}}\) and \({\widehat{P}}\) are the strong solutions to BSPDE (4.2) and BSPDVI (4.4), respectively. The terminal value and lower obstacle in BSPDVI (4.4), \(\widehat{{\underline{P}}}_t({\widetilde{x}})=\widetilde{{\underline{P}}}_t({\widetilde{x}})-e^{{\widetilde{x}}}\mathcal{Y}_t\). Let \(\,{\widetilde{R}}_1,{\widehat{R}}_1\in {\mathbb {H}}^{0,\,2}_\lambda ,\,{\widetilde{R}}\,_2\in {\mathbb {L}}^{1,\,2}_\lambda \) be satisfied with some nonnegative number \(\lambda \). Moreover, suppose that \(\widehat{{\underline{P}}}\,({\widetilde{X}}^{t,{\widetilde{x}}}),\, {\widehat{P}}\,({\widetilde{X}}^{t,{\widetilde{x}}})\in {{\mathcal {S}}}^2,\,{\widehat{R}}_{1}({\widetilde{X}}^{t,{\widetilde{x}}})\in \mathcal{L}^2\), where \({\widetilde{X}}^{t,{\widetilde{x}}}=\log X^{t,x}\)Footnote 12. Then
and \({\widehat{P}}_t({\widetilde{x}})\) is the value of the following optimal stopping problem,
and its optimal stopping time \(\tau ^*\) can be described as
Properties of \(\varDelta R\)
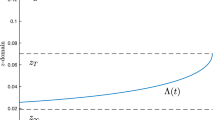
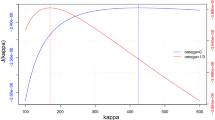
In this section, we deduce properties about \(\varDelta R\) defined in (5.3), which is important to derive the properties of the optimal retirement boundary.
Lemma 9
\(\mathrm{ess.sup}\{\varDelta R_t({\widetilde{x}}):(\omega ,t)\in \varOmega \times [\,0,T\,]\}<-e^{{\widetilde{x}}}\) provided \({\widetilde{x}}\) is small enough.
Proof
We prove the conclusion by considering the property of \(\varDelta R_t({\widetilde{x}})\) as \({\widetilde{x}}\rightarrow -\infty \) in six different cases.
1. Consider the case of \(0<\rho <1\) and \(0<\gamma \ne 1\). As \({\widetilde{x}}\rightarrow -\infty \), i.e., \(x\rightarrow 0^+\), then \(c^*=\mathcal{J}_{U_1}(x;l)\rightarrow +\infty \), and
So, we deduce that as \(x\rightarrow 0^+\),
And by computation we can show that as \(x\rightarrow 0^+\),
Note that \({\overline{x}}_t\) has a positive lower bound. Hence, we have that as \(x\rightarrow 0^+\),
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough, where we have used Assumption 2.
2. In the case of \(0<\rho <1\) and \(\gamma =1\), (B.1) still holds. And by computation we can show that as \(x\rightarrow 0^+\),
and
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough.
3. In the case of \(\rho =0\) and \(0<\gamma \ne 1\), the proof proceeds similarly to the above. Since
we have that
And by computation we can show that
Note that if \(\gamma >1\), then
and if \(0<\gamma <1\), then
We can conclude that \(U_1(c^*,l)-c^*x\) is strictly increasing with respect to l, and
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough.
4. In the case of \(\rho =0\) and \(\gamma =1\), (B.2) still holds and similarly to the above we have
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough.
5. In the case of \(\rho <0\) and \(0<\gamma \ne 1\), similarly to the above, as \({\widetilde{x}}\rightarrow -\infty \), i.e., \(x\rightarrow 0^+\), \(c^*=\mathcal{J}_{U_1}(x;l)\rightarrow +\infty \), and
So we deduce that as \(x\rightarrow 0^+\),
And by computation we can show that as \(x\rightarrow 0^+\),
Hence, we know that as \(x\rightarrow 0^+\),
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough.
6. In the case of \(\rho <0\) and \(\gamma =1\), (B.3) still holds. Similarly to the above, as \(x\rightarrow 0^+\),
and
provided x is enough near zero, i.e., \({\widetilde{x}}\) is small enough. Then we have finished the proof. \(\square \)
Lemma 10
\(\varDelta R_t({\widetilde{x}})>0\) for any \({\widetilde{x}}>\log {\overline{x}}_t\). Moreover, \(\mathrm{ess.inf}\{\varDelta R_t({\widetilde{x}}):(\omega ,t)\in \varOmega \times [\,0,T\,]\}>\epsilon e^{{\widetilde{x}}}\) provided \({\widetilde{x}}\) is large enough, where \(\epsilon \) is a positive constant independent of \({\widetilde{x}}\).
Proof
For any \({\widetilde{x}}>\log {\overline{x}}_t\), we have that
Moreover, if \({\widetilde{x}}\) is large enough, we know that
where \({c^*_t}=\mathcal{J}_{U_1}(x;{L_t})\), and we have used the fact \(U_1\) is concave with respect to l. Applying the same method as in the proof of Lemma 9, we can show that as \(x\rightarrow +\infty \),
So we derive that as \(x\rightarrow +\infty \),
Hence, by (B.4), we conclude that \(\varDelta R_t({\widetilde{x}})>\epsilon e^{{\widetilde{x}}}\) provided \({\widetilde{x}}\) is large enough, where \(\epsilon \) is a positive constant. \(\square \)
Lemma 11
If \(\gamma +\rho \le 1\), then \(\partial _{{\widetilde{x}}}\varDelta R\ge 0\).
Proof
From the definition of \(\varDelta R\), we can show that
Moreover, it is easy to check that
Since \(1-\gamma -\rho \ge 0\), we have that \(\partial _c U_1(c,l)\) is increasing with respect to l, and \(\mathcal{J}_{U_1}(x;l)\) is increasing with respect to l by \(\partial _{cc} U_1(c,l)<0\). Hence, \(\partial _{{\widetilde{x}}} \varDelta R\ge 0\). \(\square \)
Rights and permissions
About this article
Cite this article
Yang, Z., Koo, H.K. & Shin, Y.H. Optimal Retirement in a General Market Environment. Appl Math Optim 84, 1083–1130 (2021). https://doi.org/10.1007/s00245-020-09671-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-020-09671-6
Keywords
- Backward stochastic partial differential variational inequality
- Stochastic free boundary problem
- Early retirement
- Portfolio selection
- Consumption
- Leisure
- Non-Markovian market environment