Second Order Linear Evolution Equations with General Dissipation

Abstract

The contraction semigroup $S(t)=\mathrm{e}^{t\mathbb {A}}$ generated by the abstract linear dissipative evolution equation

$$\begin{aligned} \ddot{u} + A u + f(A) \dot{u}=0 \end{aligned}$$

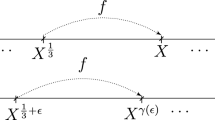
is analyzed, where A is a strictly positive selfadjoint operator and f is an arbitrary nonnegative continuous function on the spectrum of A. A full description of the spectrum of the infinitesimal generator $\mathbb {A}$ of S(t) is provided. Necessary and sufficient conditions for the stability, the semiuniform stability and the exponential stability of the semigroup are found, depending on the behavior of f and the spectral properties of its zero-set. Applications to wave, beam and plate equations with fractional damping are also discussed.

Appendix: Portraits of the Spectra

We illustrate some particular instances of the spectra of the operators $\mathbb {A}_\vartheta$, $\mathbb {A}_\vartheta ^0$ and $\mathbb {A}_\vartheta ^\omega$ discussed in Sect. 15.

Portraits of $\varvec{\sigma (\mathbb {A}_\vartheta )}$. Choosing $H=V=L^2(0,\pi )$ and $A=L$, the eigenvalues $\lambda _n$ are equal to

$$\begin{aligned} \lambda _n= n^2,\quad \,\, n=1,2,3,\ldots \end{aligned}$$

Accordingly, the eigenvalues $\xi _{\lambda _n}^{\pm }$ of $\mathbb {A}_\vartheta$ take the form

$$\begin{aligned} \xi _{\lambda _n}^{\pm }= {\left\{ \begin{array}{ll} \displaystyle -\frac{n^{2\vartheta }}{2} \pm \frac{\sqrt{n^{4\vartheta }-4n^2}}{2} &{}\quad \text {if }\, n^{2\vartheta -1}\ge 2,\\ \displaystyle -\frac{n^{2\vartheta }}{2} \pm \mathrm{i}\frac{\sqrt{4n^2-n^{4\vartheta }}}{2} &{}\quad \text {if }\, n^{2\vartheta -1}< 2. \end{array}\right. } \end{aligned}$$

Making use of Corollary 15.2 and the software Mathematica®, we have the following pictures of $\sigma (\mathbb {A}_\vartheta )$, corresponding to the cases $\vartheta =-1,0,1$ (Figs. 1, 2, 3).

Fig. 1

The case $\vartheta =-1$ (“subdamped” wave equation)

Fig. 2

The case $\vartheta =0$ (weakly damped wave equation)

Fig. 3

The case $\vartheta =1$ (strongly damped wave equation). Behavior around zero (left) and global behavior (right)

Fig. 4

The case $\vartheta =-1$ (“subdamped” beam equation)

Fig. 5

The case $\vartheta =0$ (beam equation with frictional damping)

Fig. 6

The case $\vartheta =1$ (beam equation with Kelvin–Voigt damping). Behavior around zero (left) and global behavior (right)

Fig. 7

The case $\vartheta =0$ and $\omega =1$ (beam equation with rotational inertia and frictional damping)

Portraits of $\varvec{\sigma (\mathbb {A}_\vartheta ^0)}$. Choosing $H=V=L^2(0,\pi )$, the eigenvalues $\lambda _n^2$ of the operator $A=L^2$ are equal to

$$\begin{aligned} \lambda _n^2= n^4,\quad \,\, n=1,2,3,\ldots \end{aligned}$$

Therefore, the eigenvalues $\xi _{\lambda _n^2}^{\pm }$ of $\mathbb {A}_\vartheta ^0$ are given by

$$\begin{aligned} \xi _{\lambda _n^2}^{\pm }= {\left\{ \begin{array}{ll} \displaystyle -\frac{n^{2\vartheta }}{2} \pm \frac{\sqrt{n^{4\vartheta }-4n^4}}{2} &{}\quad \text {if }\, n^{2(\vartheta -1)}\ge 2,\\ \displaystyle -\frac{n^{2\vartheta }}{2} \pm \mathrm{i}\frac{\sqrt{4n^4-n^{4\vartheta }}}{2} &{}\quad \text {if }\, n^{2(\vartheta -1)}< 2. \end{array}\right. } \end{aligned}$$

Making use of Theorem 15.4 and the software Mathematica®, we get the following pictures of $\sigma (\mathbb {A}_\vartheta ^0)$, corresponding to the choices $\vartheta =-1,0,1$ (Figs. 4, 5, 6).

Portraits of $\varvec{\sigma (\mathbb {A}_\vartheta ^\omega )}$. Choosing $H=V^1=H_0^1(0,\pi )$, the eigenvalues $\nu _n$ of the operator $A = (1+ \omega L)^{-1} L^2$ are equal to

$$\begin{aligned} \nu _n = \frac{n^4}{1+\omega n^2}. \end{aligned}$$

Hence, the eigenvalues $\xi _{\nu _n}^{\pm }$ of $\mathbb {A}_\vartheta ^\omega$ read

$$\begin{aligned} \xi _{\nu _n}^{\pm }= {\left\{ \begin{array}{ll} \displaystyle -\frac{1}{2}\Big [f\big (\tfrac{n^4}{1+\omega n^2}\big ) \mp \sqrt{\big [f\big (\tfrac{n^4}{1+\omega n^2}\big )\big ]^2-\tfrac{4n^4}{1+\omega n^2}}\Big ] &{}\quad \text {if } f\big (\tfrac{n^4}{1+\omega n^2}\big )\ge \frac{2n^2}{\sqrt{1+\omega n^2}},\\ \displaystyle -\frac{1}{2}\Big [f\big (\tfrac{n^4}{1+\omega n^2}\big ) \mp \mathrm{i}\sqrt{\tfrac{4n^4}{1+ \omega n^2}-\big [f\big (\tfrac{n^4}{1+\omega n^2}\big )\big ]^2}\Big ] &{}\quad \text {if } f\big (\tfrac{n^4}{1+\omega n^2}\big )< \frac{2n^2}{\sqrt{1+\omega n^2}}, \end{array}\right. } \end{aligned}$$

where f is given by (2.8). Making use of Theorem 15.6 and the software Mathematica®, we obtain the following pictures of $\sigma (\mathbb {A}_\vartheta ^\omega )$, corresponding to the choices $\vartheta =0,1$ (Figs. 7, 8).

Fig. 8

The case $\vartheta =1$ with $\omega =1$ (left) and $\omega =1/200$ (right) (beam equation with rotational inertia and Kelvin–Voigt damping). Note that the spectrum becomes close to two straight lines as $\omega \rightarrow 0$. Compare with Fig. 6