Small-Time Asymptotics for Gaussian Self-Similar Stochastic Volatility Models

Abstract

We consider the class of Gaussian self-similar stochastic volatility models, and characterize the small-time (near-maturity) asymptotic behavior of the corresponding asset price density, the call and put pricing functions, and the implied volatility. Away from the money, we express the asymptotics explicitly using the volatility process’ self-similarity parameter H, and its Karhunen–Loève characteristics. Several model-free estimators for H result. At the money, a separate study is required: the asymptotics for small time depend instead on the integrated variance’s moments of orders $\frac{1}{2}$ and $\frac{3}{2}$, and the estimator for H sees an affine adjustment, while remaining model-free.

Appendix: Proofs of the Main Theorems

Proof of Theorem 3

Fix $x> 0$, and denote

$$\begin{aligned} J_x(T)=\int _0^{\infty } u^{-1}\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{ 2T^{2H+1}u^2}+\frac{T^{2H+1}u^2}{8}\right] \right\} {\widetilde{p}}_1(u)du . \end{aligned}$$

(47)

It is clear from (13) that the small-time asymptotic behavior of the density $D_T(x)$ is determined by that of the integral $J_x(T)$.

The next lemma will allow us to use Theorem 2 to estimate the integral in (47). $\square$

Lemma 2

Fix $\alpha \in {\mathbb {R}}$, $b> 0$, and $\varepsilon > 0$. Let $x> s_0+\varepsilon$, and suppose f is an integrable function on [0, b]. Then

$$\begin{aligned}&\int _0^b u^{\alpha }\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2 }+\frac{T^{2H+1}u^2}{8}\right] \right\} |f(u)|du =O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^2\frac{x}{s_0}}{2b^2T^{2H+1}} \right\} \right) \end{aligned}$$

as $T\rightarrow 0$.

Proof

The lemma is trivial if $\alpha \ge 0$. For $\alpha < 0$, we have

$$\begin{aligned}&\int _0^b u^{\alpha }\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2 }+\frac{T^{2H+1}u^2}{8}\right] \right\} |f(u)|du \nonumber \\&\quad \le \int _0^b u^{\alpha }\exp \left\{ -\frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2} \right\} |f(u)|du. \end{aligned}$$

(48)

The following equality holds for every $A> 0$:

$$\begin{aligned} \left( u^{\alpha }\exp \left\{ -\frac{A}{u^2}\right\} \right) ^{\prime }=\left[ 2Au^{\alpha -3}+\alpha u^{\alpha -1} \right] \exp \left\{ -\frac{A}{u^2}\right\} . \end{aligned}$$

It follows that for $2A>-\alpha b^2$, the function $u\mapsto \frac{1}{u^{\alpha }}\exp \left\{ -\frac{A}{u^2}\right\}$ is increasing on the interval (0, b]. Set $A=\frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}}$. Next, using (48), we obtain

$$\begin{aligned}&\int _0^b u^{\alpha }\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2 }+\frac{T^{2H+1}u^2}{8}\right] \right\} |f(u)|du \nonumber \\&\quad \le b^{\alpha }\exp \left\{ -\frac{\log ^2\frac{x}{s_0}}{2b^2T^{2H+1}} \right\} \int _0^b|f(u)|du, \end{aligned}$$

(49)

provided that $\log ^2\frac{x}{s_0}> b^2T^{2H+1}$. It is clear that the previous inequality holds for small enough values of T provided that $x> s_0+\varepsilon$.

Finally, Lemma 2 follows from (49).

Using (10) with $t=1$ and formula (8) for centered processes, we obtain

$$\begin{aligned} {\widetilde{p}}_1(y)={\widetilde{A}}y^{n_1(1)-1}\exp \left\{ -\frac{y^2}{ 2\lambda _1(1)}\right\} \left( 1+O\left( y^{-1}\right) \right) \end{aligned}$$

(50)

as $y\rightarrow \infty$, where

$$\begin{aligned} {\widetilde{A}}=\frac{2^{1-\frac{n_1(1)}{2}}}{\Gamma \left( \frac{n_1(1)}{2} \right) } \lambda _1^{-\frac{n_1(1)}{2}}\prod _{k> n_1(1)}^{\infty }\left( \frac{ \lambda _1(1)}{\lambda _1(1)-\lambda _k(1)}\right) ^{\frac{1}{2}}. \end{aligned}$$

(51)

Let $y_0> 0$ be a constant such that the big-O estimate in (50) is valid. Our next goal is to replace the function ${\widetilde{p}}_1$ in (47) by its approximation from (50), using Lemma 2. The resulting formula is

$$\begin{aligned} J_x(T)&={\widetilde{A}}\int _0^{\infty }u^{n_1(1)-2}\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2}\right. \right. \nonumber \\&\quad \left. \left. +\left( \frac{T^{2H+1}}{8}+\frac{1}{2\lambda _1(1)} \right) u^2\right] \right\} \left( 1+O\left( u^{-1}\right) \right) du \nonumber \\&\quad +O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^2\frac{x}{s_0}}{2y_0^2T^{2H+1}} \right\} \right) \end{aligned}$$

(52)

as $T\rightarrow 0$. Formula (52) can be obtained as follows. Applying Lemma 2 with $\alpha =-1$, $b=y_0$, and $f={\widetilde{p}}_1$, to the integral with same integrand as in (47), we can include this integral in the error term in (52). Next, we can replace the function ${\widetilde{p}}_1$ in the integral over $[y_0,\infty )$ by the expression on the right-hand side of (50). Finally, we observe that

$$\begin{aligned}&\int _0^{y_0}u^{n_1(1)-2}\exp \left\{ -\left[ \frac{\log ^2\frac{x}{s_0}}{2T^{2H+1}u^2} +\left( \frac{T^{2H+1}}{8}+\frac{1}{2\lambda _1(1)} \right) u^2\right] \right\} \left( 1+O\left( u^{-1}\right) \right) du \nonumber \\&\quad =O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^2\frac{x}{s_0}}{2y_0^2T^{2H+1}} \right\} \right) \end{aligned}$$

(53)

as $T\rightarrow 0$. Indeed, formula (53) can be established by applying Lemma 2 to the expression on the left-hand side of (53) twice, first with $\alpha =n_1(1)-2$, $b=y_0$, and $f(u)=\exp \{-\frac{u^2}{2\lambda _1(1)}\}$, and then with $\alpha =n_1(1)-3$, $b=y_0$, and $f(u)=\exp \{-\frac{u^2}{2\lambda _1(1)}\}$. This proves formula (52). $\square$

To study the asymptotics of the function $T\mapsto J_{x}(T)$ defined by (52), we consider the following two integrals:

$$\begin{aligned}&{\widetilde{J}}_{x}(T)={\widetilde{A}}\int _{0}^{\infty }u^{n_{1}(1)-2} \exp \left\{ -\left[ \frac{\log ^{2}\frac{x}{s_{0}}}{2T^{2H+1}u^{2}} +\left( \frac{T^{2H+1}}{8}+\frac{1}{2\lambda _{1}(1)}\right) u^{2}\right] \right\} du \end{aligned}$$

and

$$\begin{aligned}&{\widehat{J}}_{x}(T)={\widetilde{A}}\int _{0}^{\infty }u^{n_{1}(1)-3} \exp \left\{ -\left[ \frac{\log ^{2}\frac{x}{s_{0}}}{2T^{2H+1}u^{2}} +\left( \frac{T^{2H+1}}{8}+\frac{1}{2\lambda _{1}(1)}\right) u^{2}\right] \right\} du. \end{aligned}$$

Set

$$\begin{aligned} \beta _{T}=\frac{\log ^{2}\frac{x}{s_{0}}}{2T^{2H+1}},\quad \gamma _{T}= \frac{T^{2H+1}}{8}+\frac{1}{2\lambda _{1}(1)}. \end{aligned}$$

Note that $\beta _{T}$ depends on x, while $\gamma _{T}$ does not. Then we have

$$\begin{aligned} {\widetilde{J}}_{x}(T)={\widetilde{A}}\int _{0}^{\infty }u^{n_{1}(1)-2}\exp \left\{ -\left[ \frac{\beta _{T}}{u^{2}}+\gamma _{T}u^{2}\right] \right\} du \end{aligned}$$

and

$$\begin{aligned} {\widehat{J}}_{x}(T)={\widetilde{A}}\int _{0}^{\infty }u^{n_{1}(1)-3}\exp \left\{ -\left[ \frac{\beta _{T}}{u^{2}}+\gamma _{T}u^{2}\right] \right\} du. \end{aligned}$$

Next, making a substitution

$$\begin{aligned} u=\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{1}{4}}v, \end{aligned}$$

we transform the previous integrals as follows:

$$\begin{aligned} {\widetilde{J}}_{x}(T)={\widetilde{A}}\left( \frac{\beta _{T}}{\gamma _{T}} \right) ^{\frac{n_{1}(1)-1}{4}}\int _{0}^{\infty }v^{n_{1}(1)-2}\exp \left\{ - \sqrt{\beta _{T}\gamma _{T}}\left[ \frac{1}{v^{2}}+v^{2}\right] \right\} dv \end{aligned}$$

and

$$\begin{aligned} {\widehat{J}}_{x}(T)={\widetilde{A}}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-2}{4}}\int _{0}^{\infty }v^{n_{1}(1)-3}\exp \left\{ -\sqrt{ \beta _{T}\gamma _{T}}\left[ \frac{1}{v^{2}}+v^{2}\right] \right\} dv. \end{aligned}$$

Let us denote

$$\begin{aligned} z(T)=\frac{1}{4}\sqrt{\frac{\lambda _{1}(1)T^{2H+1}+4}{\lambda _{1}(1)T^{2H+1}}}. \end{aligned}$$

(54)

Then we have $\sqrt{\beta _{T}\gamma _{T}}=z(T)\log \frac{x}{s_{0}}.$ Therefore,

$$\begin{aligned}&{\widetilde{J}}_{x}(T)={\widetilde{A}}\left( \frac{\beta _{T}}{\gamma _{T}} \right) ^{\frac{n_{1}(1)-1}{4}} \int _{0}^{\infty }v^{n_{1}(1)-2}\exp \left\{ -z(T) \log \frac{x}{s_{0}}\left[ \frac{1}{v^{2}}+v^{2}\right] \right\} dv \end{aligned}$$

(55)

and

$$\begin{aligned}&{\widehat{J}}_{x}(T) ={\widetilde{A}}\left( \frac{\beta _{T}}{\gamma _{T}} \right) ^{\frac{n_{1}(1)-2}{4}} \int _{0}^{\infty }v^{n_{1}(1)-3}\exp \left\{ -z(T) \log \frac{x}{s_{0}}\left[ \frac{1}{v^{2}}+v^{2}\right] \right\} dv. \end{aligned}$$

(56)

It follows from (54) that $z(T)\rightarrow \infty$ as $T\rightarrow 0$. Our next goal is to apply Laplace’s method to study the asymptotic behavior of the functions $T\mapsto {\widetilde{J}}_x(T)$ and $T\mapsto \widehat{ J}_x(T)$ as $T\rightarrow 0$. Note that the unique critical point of the function $\psi (v)=v^{-2}+v^2$ is at $v=1$. Moreover, we have $\psi ^{\prime \prime }(1)=8> 0$.

We will first reduce the integrals in (55) and (56) to the integrals over the interval [0, 2] and give an error estimate. The next assertion will be helpful.

Lemma 3

Suppose $a\in {\mathbb {R}}$ and $0<\varepsilon < s_0$. Then

$$\begin{aligned}&\int _2^{\infty }v^a \exp \left\{ -\sqrt{\beta _T\gamma _T}\left[ \frac{1}{v^2}+v^2 \right] \right\} dv =O_{\varepsilon }\left( \exp \left\{ -4\sqrt{\beta _T\gamma _T} \right\} \right) \end{aligned}$$

as $t\rightarrow 0$.

Proof

Fix a small number $r> 0$. Then for $0< T< T_0$, we have

$$\begin{aligned}&\int _2^{\infty }v^a \exp \left\{ -\sqrt{\beta _T\gamma _T}\left[ \frac{1}{v^2}+v^2 \right] \right\} dv \le \int _2^{\infty }v^a \exp \left\{ -\sqrt{\beta _T\gamma _T} v^2\right\} dv \\&\quad \le c_r\int _2^{\infty } \exp \left\{ -\left( \sqrt{\beta _T\gamma _T} -r\right) v^2\right\} dv \\&\quad =c_r\left( \sqrt{\beta _T\gamma _T}-r\right) ^{-\frac{1}{2}} \int _{2\sqrt{\sqrt{ \beta _T\gamma _T}-r}}^{\infty }e^{-u^2}du \le {\widetilde{c}}_r\exp \left\{ -4\left( \sqrt{\beta _T\gamma _T}-r\right) \right\} . \end{aligned}$$

The proof of Lemma 3 is thus completed. $\square$

Now, we are ready to apply Laplace’s method to the integrals in (55) and (56). The dependence of the parameter x in (55) and (56) is very simple. This allows us to obtain uniform error estimates. By taking into account Lemma 3, we see that for every $\varepsilon >0$ and all $x>s_{0}+\varepsilon$,

$$\begin{aligned} {\widetilde{J}}_{x}(T)&=\frac{{\widetilde{A}}\sqrt{\pi }}{2}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-1}{4}}\left( z(T)\log \frac{x}{s_{0}}\right) ^{-\frac{1}{2}}\exp \left\{ -2z(T)\log \frac{x}{s_{0}} \right\} \nonumber \\&\quad \times \, \left( 1+O_{\varepsilon }\left( \frac{1}{z(T)\log \frac{x }{s_{0}}}\right) \right) +O_{\varepsilon }\left( \exp \left\{ -4z(T) \log \frac{x}{s_{0}}\right\} \right) \end{aligned}$$

(57)

and

$$\begin{aligned} {\widehat{J}}_{x}(T)&=\frac{{\widetilde{A}}\sqrt{\pi }}{2}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-2}{4}}\left( z(T) \log \frac{x}{s_{0}} \right) ^{-\frac{1}{2}}\exp \left\{ -2z(T)\log \frac{x}{s_{0}}\right\} \nonumber \\&\quad \times \,\left( 1+O_{\varepsilon }\left( \frac{1}{z(T) \log \frac{x }{s_{0}} }\right) \right) +O_{\varepsilon }\left( \exp \left\{ -4z(T)\log \frac{x}{s_{0}}\right\} \right) \end{aligned}$$

(58)

as $T\rightarrow 0$. Recall that the $O_{\varepsilon }$ estimates in (57) and (58) are uniform with respect to $x>s_{0}+\varepsilon$. Since

$$\begin{aligned} J_{x}(T)={\widetilde{J}}_{x}(T)+O_{\varepsilon }\left( {\widehat{J}} _{x}(T)\right) +O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^{2}\frac{x}{ s_{0}}}{2y_0^2T^{2H+1}}\right\} \right) , \end{aligned}$$

as $T\rightarrow 0$, formulas (57) and (58) imply that

$$\begin{aligned} J_{x}(T)&= \frac{{\widetilde{A}}\sqrt{\pi }}{2}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-1}{4}}\left( z(T)\log \frac{x}{s_{0} } \right) ^{-\frac{1}{2}}\exp \left\{ -2z(T)\log \frac{ x}{s_{0}} \right\} \\&\quad \times \,\left( 1+O_{\varepsilon }\left( \left[ \frac{\beta _{T}}{\gamma _{T}}\right] ^{-\frac{1}{4} }\right) \right) \left( 1+O_{\varepsilon }\left( \frac{1}{z(T) \log \frac{x }{s_{0}}}\right) \right) \\&\quad +\, O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^{2}\frac{x}{s_{0}} }{2y_0^2T^{2H+1}}\right\} \right) +O_{\varepsilon }\left( \exp \left\{ -4z(T) \log \frac{x}{s_{0}}\right\} \right) \end{aligned}$$

as $T\rightarrow 0$. Since for $T<1$,

$$\begin{aligned} \frac{1}{4}\sqrt{\frac{\lambda _{1}(1)+4}{\lambda _{1}(1)}}T^{-H-\frac{1}{2} }>z(T)>\frac{1}{2}\lambda _{1}(1)^{-\frac{1}{2}}T^{-H-\frac{1}{2}}, \end{aligned}$$

(59)

we have

$$\begin{aligned}&O_{\varepsilon }\left( \exp \left\{ -\frac{\log ^{2}\frac{x}{s_{0}}}{ 2y_0^2T^{2H+1}}\right\} \right) +O_{\varepsilon }\left( \exp \left\{ -4z(T)\log \frac{x}{s_{0}}\right\} \right) \\&\quad =O_{\varepsilon }\left( \exp \left\{ -4z(T) \log \frac{x}{s_{0}} \right\} \right) \\&\quad =O_{\varepsilon }\left( \exp \left\{ -2\lambda _{1}(1)^{-\frac{1 }{2}}T^{-H-\frac{1}{2}}\log \frac{x}{s_{0}} \right\} \right) \end{aligned}$$

as $T\rightarrow 0$, and therefore,

$$\begin{aligned} J_{x}(T)&= \frac{{\widetilde{A}}\sqrt{\pi }}{2}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-1}{4}}\left( z(T) \log \frac{x}{s_{0} } \right) ^{-\frac{1}{2}}\exp \left\{ -2z(T)\log \frac{ x}{s_{0}} \right\} \\&\quad \times \, \left( 1+O_{\varepsilon }\left( \left[ \frac{\beta _{T}}{\gamma _{T}}\right] ^{-\frac{1}{4} }\right) \right) \left( 1+O_{\varepsilon }\left( \frac{1}{z(T) \log \frac{x }{s_{0}} }\right) \right) \\&\quad +\, O_{\varepsilon }\left( \exp \left\{ -2\lambda _{1}(1)^{-\frac{1 }{2}}T^{-H-\frac{1}{2}}\log \frac{x}{s_{0}} \right\} \right) \end{aligned}$$

as $T\rightarrow 0$. Moreover, for all $T<1$ and $x>s_{0}+\varepsilon$,

$$\begin{aligned} \left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{-\frac{1}{4}}\ge c_{1}\frac{ T^{\frac{2H+1}{4}}}{\sqrt{ \log \frac{x}{s_{0}} }}\ge c_{2}\frac{T^{\frac{2H+1}{2}}}{\log \frac{x}{s_{0}}} \ge c_{3}\frac{1}{z(T) \log \frac{x}{s_{0}} }, \end{aligned}$$

and hence

$$\begin{aligned}&\left( 1+O_{\varepsilon }\left( \left[ \frac{\beta _{T}}{\gamma _{T}}\right] ^{-\frac{1}{4} }\right) \right) \left( 1+O_{\varepsilon }\left( \frac{1}{z(T)\log \frac{x }{s_{0}}}\right) \right) \\&\quad =1+O_{\varepsilon }\left( \left[ \frac{\beta _{T}}{\gamma _{T}} \right] ^{-\frac{1}{4}}\right) =1+O_{\varepsilon }\left( T^{ \frac{2H+1}{4}}\left( \log \frac{x}{s_{0}}\right) ^{-\frac{1}{2} }\right) \end{aligned}$$

as $T\rightarrow 0$. Finally,

$$\begin{aligned} J_{x}(T)&=\frac{{\widetilde{A}}\sqrt{\pi }}{2}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-1}{4}}\left( z(T) \log \frac{x}{s_{0} }\right) ^{-\frac{1}{2}}\exp \left\{ -2z(T) \log \frac{ x}{s_{0}} \right\} \\&\quad \times \, \left( 1+O_{\varepsilon }\left( T^{\frac{2H+1}{4}}\left( \log \frac{x}{s_{0}}\right) ^{-\frac{1}{2}}\right) \right) \\&\quad +\, O_{\varepsilon }\left( \exp \left\{ -2\lambda _{1}(1)^{- \frac{1}{2}}T^{-H-\frac{1}{2}}\log \frac{x}{s_{0}} \right\} \right) \end{aligned}$$

as $T\rightarrow 0$.

Recall that we assumed $r=0$. It follows from (13) and (47) that

$$\begin{aligned} D_T(x)&=\frac{\sqrt{s_0}{\widetilde{A}}}{2\sqrt{2}}T^{-H-\frac{1}{2}}x^{-\frac{ 3}{2}}\left( \frac{\beta _T}{\gamma _T}\right) ^{\frac{n_1(1)-1}{4} }\left( z(T)\log \frac{x}{s_0}\right) ^{-\frac{1}{2}} \nonumber \\&\quad \times \, \exp \left\{ -2z(T)\log \frac{x}{s_0}\right\} \left( 1+O_{\varepsilon }\left( T^{\frac{2H+1}{4}} \left( \log \frac{x}{s_0} \right) ^{-\frac{1}{2}}\right) \right) \nonumber \\&\quad +\, O_{\varepsilon }\left( \exp \left\{ -2\lambda _1(1)^{-\frac{1}{2} } T^{-H-\frac{1}{2}}\log \frac{x}{s_0}\right\} \right) \end{aligned}$$

(60)

as $T\rightarrow 0$.

Our next goal is to remove the last $O_{\varepsilon }$-term from formula (60). Analyzing the expressions in (60), we see that in order to prove the statement formulated above, it suffices to show that there exists a constant $c>0$ independent of $T<T_{0}$ and $x>s_{0}+\varepsilon$ and such that

$$\begin{aligned} \left( \frac{x}{s_{0}}\right) ^{-2\lambda _{1}(1)^{-\frac{1}{2} }T^{-H-\frac{1}{2}}}&\le cT^{-H-\frac{1}{2}}x^{-\frac{3}{2}}\left( \log \frac{x}{s_{0}}\right) ^{\frac{n_{1}(1)-1}{4}}T^{-\frac{(2H+1)(n_{1}(1)-1)}{8 }}T^{\frac{2H+1}{4}} \nonumber \\&\quad \times \left( \log \frac{x}{s_{0}}\right) ^{-\frac{1}{2}}\left( \frac{x}{ s_{0}}\right) ^{-2z(T)}T^{\frac{2H+1}{4}}\left( \log \frac{x}{s_{0}}\right) ^{-\frac{1}{2}}. \end{aligned}$$

(61)

The previous inequality is equivalent to the following:

$$\begin{aligned} \left( \frac{x}{s_{0}}\right) ^{-2\lambda _{1}(1)^{-\frac{1}{2} }T^{-H-\frac{1}{2}}}&\le cT^{-\frac{(2H+1)(n_{1}(1)-1)}{8}}x^{-\frac{3}{2} }\left( \frac{x}{s_{0}}\right) ^{-2z(T)} \left( \log \frac{x}{s_{0}}\right) ^{\frac{n_{1}(1)-1}{4}-1} \end{aligned}$$

(62)

Using (54), we see that the inequality in (62) follows from the inequality

$$\begin{aligned} \left( \frac{x}{s_{0}}\right) ^{-2\lambda _{1}(1)^{-\frac{1}{2}}T^{-H-\frac{1}{2}}}&\le cT^{-\frac{(2H+1)(n_{1}(1)-1)}{8}} \left( \frac{x}{s_{0}}\right) ^{-\frac{3}{2}-\frac{1}{2} \lambda _{1}(1)^{-\frac{1}{2}}T^{-H-\frac{1}{2}}\sqrt{\lambda _{1}(1)T^{2H+1}+4}}\nonumber \\&\quad \times \, \left( \log \frac{x}{s_{0}}\right) ^{\frac{n_{1}(1)-1}{4} -1}. \end{aligned}$$

(63)

To prove the inequality in (63), we observe that for every small enough number $\tau >0$ there exists a constant $c_{\tau ,\varepsilon }$ such that

$$\begin{aligned} c_{\tau ,\varepsilon }\left( \frac{x}{s_{0}}\right) ^{-\tau }\le \left( \log \frac{x}{s_{0}}\right) ^{\frac{n_{1}(1)-1}{4}-1} \end{aligned}$$

for all $x>s_{0}+\varepsilon$. Moreover, there exists $T_{\tau ,\varepsilon }>0$ such that

$$\begin{aligned} \left( \frac{x_{0}}{s_{0}}\right) ^{-\tau T^{-H-\frac{1}{2}}}\le \left( \frac{s_{0}+\varepsilon }{s_{0}}\right) ^{-\tau T^{-H-\frac{1}{2}}}\le T^{- \frac{(2H+1)(n_{1}(1)-1)}{8}} \end{aligned}$$

for all $T<T_{\tau ,\varepsilon }$. Now, it is clear that (63) follows from the estimate

$$\begin{aligned}&\left( 2\lambda _{1}(1)^{-\frac{1}{2}}-\tau \right) T^{-H-\frac{1 }{2}} \ge \frac{3}{2}+\frac{1}{2}\lambda _{1}(1)^{-\frac{1}{2}}T^{-H-\frac{1}{2} }\sqrt{\lambda _{1}(1)T^{2H+1}+4}+\tau , \end{aligned}$$

(64)

for all $T<T_{\tau }$. It is not hard to see that there exist numbers $\tau$ and $T_{\tau }$, for which the inequality in (64) holds. This establishes (61), and it follows that

$$\begin{aligned} D_{T}(x)&=\frac{\sqrt{s_{0}}{\widetilde{A}}}{2\sqrt{2}}T^{-H-\frac{1}{2}}x^{- \frac{3}{2}}\left( \frac{\beta _{T}}{\gamma _{T}}\right) ^{\frac{n_{1}(1)-1}{ 4}}\left( z(T)\log \frac{x}{s_{0}}\right) ^{-\frac{1}{2}} \nonumber \\&\quad \times \exp \left\{ -2z(T)\log \frac{x}{s_{0}}\right\} \left( 1+O_{\varepsilon }\left( T^{\frac{2H+1}{4}}\left( \log \frac{x}{s_{0}} \right) ^{-\frac{1}{2}}\right) \right) \end{aligned}$$

(65)

as $T\rightarrow 0$, where ${\widetilde{A}}$ is given by (51). Formula (65) will help us to characterize the asymptotic behavior of the function $T\mapsto D_{T}(x)$.

Let us assume that $x> s_0+\varepsilon$. Then we have

$$\begin{aligned} \left( \frac{\beta _T}{\gamma _T}\right) ^{\frac{n_1(1)-1}{4}}= \lambda _1(1)^{ \frac{n_1(1)-1}{4}}\left( \log \frac{x}{s_0}\right) ^{\frac{n_1(1)-1}{2}} T^{- \frac{(2H+1)(n_1(1)-1)}{4}}(1+h)^{-\frac{n_1(1)-1}{4}} \end{aligned}$$

where $h=\frac{\lambda _1(1)T^{2H+1}}{4}$. Therefore,

$$\begin{aligned} \left( \frac{\beta _T}{\gamma _T}\right) ^{\frac{n_1(1)-1}{4}}&= \lambda _1(1)^{ \frac{n_1(1)-1}{4}}\left( \log \frac{x}{s_0}\right) ^{\frac{n_1(1)-1}{2}} T^{- \frac{(2H+1)(n_1(1)-1)}{4}} \nonumber \\&\quad \times \,\left( 1+O\left( T^{2H+1}\right) \right) \end{aligned}$$

(66)

as $T\rightarrow 0$. Moreover,

$$\begin{aligned} z(T)^{-\frac{1}{2}}&=2\left[ \frac{\lambda _1(1)T^{2H+1}+4}{ \lambda _1(1)T^{2H+1}}\right] ^{-\frac{1}{4}} =\sqrt{2}\lambda _1(1)^{\frac{1}{4}}T^{\frac{2H+1}{4}}\left( 1+O \left( T^{2H+1}\right) \right) \end{aligned}$$

(67)

and

$$\begin{aligned}&\exp \left\{ -2z(T)\log \frac{x}{s_0}\right\} =\left( \frac{x}{s_0}\right) ^{- \frac{\sqrt{4+\lambda _1(1)T^{2H+1}}}{2\sqrt{\lambda _1(1)} T^{H+\frac{1}{2}}} } \end{aligned}$$

(68)

as $T\rightarrow 0$. Next, combining (51), (65), (66), (67), and (68), and simplifying the resulting expressions, we obtain formula (14).

This completes the proof of Theorem 3.

Proof of Theorem 4

Let us consider the call pricing function $T\mapsto C(T)$ with $K> s_0$. It is known that

$$\begin{aligned} C(T)=\int _K^{\infty }(x-K)D_T(x)dx. \end{aligned}$$

(69)

Therefore, we can use the uniform estimate in formula (14) to characterize the small-time behavior of the call pricing function. Let us consider the following integrals:

$$\begin{aligned} I_1(T)&= \int _K^{\infty }(x-K)x^{-\frac{3}{2}}\left( \log \frac{x}{s_0}\right) ^{ \frac{n_1(1)-2}{2}} \exp \left\{ -2z(T)\log \frac{x}{s_0}\right\} dx \nonumber \\&= s_0^{-\frac{1}{2}}\int _K^{\infty }\left( \log \frac{x}{s_0}\right) ^{\frac{ n_1(1)-2}{2}} \exp \left\{ -\left( \frac{1}{2}+2z(T)\right) \log \frac{x}{s_0} \right\} dx \nonumber \\&\quad -s_0^{-\frac{3}{2}}K\int _K^{\infty }\left( \log \frac{x}{s_0}\right) ^{ \frac{n_1(1)-2}{2}} \exp \left\{ -\left( \frac{3}{2}+2z(T)\right) \log \frac{x}{ s_0}\right\} dx \end{aligned}$$

(70)

and

$$\begin{aligned} I_2(T)&=\int _K^{\infty }(x-K)x^{-\frac{3}{2}}\left( \log \frac{x}{s_0}\right) ^{ \frac{n_1(1)-3}{2}} \exp \left\{ -2z(T)\log \frac{x}{s_0}\right\} dx \nonumber \\&=s_0^{-\frac{1}{2}}\int _K^{\infty }\left( \log \frac{x}{s_0}\right) ^{\frac{ n_1(1)-3}{2}} \exp \left\{ -\left( \frac{1}{2}+2z(T)\right) \log \frac{x}{s_0} \right\} dx \nonumber \\&\quad -s_0^{-\frac{3}{2}}K\int _K^{\infty }\left( \log \frac{x}{s_0}\right) ^{ \frac{n_1(1)-3}{2}} \exp \left\{ -\left( \frac{3}{2}+2z(T)\right) \log \frac{x}{ s_0}\right\} dx, \end{aligned}$$

(71)

where we use the notation in (54) for the sake of shortness.

We will next make a substitution $u=(2z(T)-\frac{1}{2})\log \frac{x}{s_0}$ in the integral on the second line in (70). The resulting expression is as follows:

$$\begin{aligned} s_0^{\frac{1}{2}}\left( 2z(T)-\frac{1}{2}\right) ^{-\frac{n_1(1)}{2} }\int _{\left( 2z(T)-\frac{1}{2}\right) \log \frac{K}{s_0}} ^{\infty }u^{\frac{ n_1(1)-2}{2}}e^{-u}du, \end{aligned}$$

which is equal to

$$\begin{aligned} s_0^{\frac{1}{2}}\left( 2z(T)-\frac{1}{2}\right) ^{-\frac{n_1(1)}{2} }\Gamma \left( \frac{n_1(1)}{2}, \left( 2z(T)-\frac{1}{2}\right) \log \frac{K}{s_0 }\right) , \end{aligned}$$

where the symbol $\Gamma$ stands for the upper incomplete gamma function defined by

$$\begin{aligned} \Gamma (s,x)=\int _x^{\infty }v^{s-1}e^{-v}dv. \end{aligned}$$

Making similar transformations in the other integrals in (70) and (71), we finally obtain

$$\begin{aligned} I_1(T)&=s_0^{\frac{1}{2}}\left( 2z(T)-\frac{1}{2}\right) ^{-\frac{n_1(1)}{2} }\Gamma \left( \frac{n_1(1)}{2}, \left( 2z(T)-\frac{1}{2}\right) \log \frac{K}{s_0 }\right) \\&\quad -s_0^{-\frac{1}{2}}K\left( 2z(T)+\frac{1}{2}\right) ^{-\frac{n_1(1)}{2} }\Gamma \left( \frac{n_1(1)}{2}, \left( 2z(T)+\frac{1}{2}\right) \log \frac{K}{s_0 }\right) \end{aligned}$$

and

$$\begin{aligned} I_2(T)&=s_0^{\frac{1}{2}}\left( 2z(T)-\frac{1}{2}\right) ^{-\frac{n_1(1)-1}{2} }\Gamma \left( \frac{n_1(1)-1}{2}, \left( 2z(T)-\frac{1}{2}\right) \log \frac{K}{ s_0}\right) \\&\quad -s_0^{-\frac{1}{2}}K\left( 2z(T)+\frac{1}{2}\right) ^{-\frac{n_1(1)-1}{2} }\Gamma \left( \frac{n_1(1)-1}{2}, \left( 2z(T)+\frac{1}{2}\right) \log \frac{K}{ s_0}\right) . \end{aligned}$$

It is known that

$$\begin{aligned} \Gamma (s,x)=x^{s-1}e^{-x}\left( 1+(s-1)x^{-1}+O\left( x^{-2}\right) \right) \end{aligned}$$

(72)

as $x\rightarrow \infty$. Formula (72) can be easily derived from the recurrence relation

$$\begin{aligned} \Gamma (s,x)=(s-1)\Gamma (s-1,x)+x^{s-1}e^{-x} \end{aligned}$$

for the upper incomplete gamma function. It follows that

$$\begin{aligned} I_{1}(T)&=s_{0}^{2z(T)}K^{-2z(T)+\frac{1}{2}}\left( \log \frac{K}{s_{0}} \right) ^{\frac{n_{1}(1)-2}{2}} \\&\quad \times \, \left[ \frac{1}{2z(T)-\frac{1}{2}}\left( 1+\frac{n_{1}(1)-2}{ 2(2z(T)-\frac{1}{2})\log \frac{K}{s_{0}}}+O(T^{2H+1})\right) \right. \\&\quad \left. -\,\frac{1}{2z(T)+\frac{1}{2}}\left( 1+\frac{n_{1}(1)-2}{2(2z(T)+\frac{ 1}{2})\log \frac{K}{s_{0}}}+O(T^{2H+1})\right) \right] \\&=s_{0}^{2z(T)}K^{-2z(T)+\frac{1}{2}}\left( \log \frac{K}{s_{0}}\right) ^{ \frac{n_{1}(1)-2}{2}}\left( \frac{1}{4z(T)^{2}-\frac{1}{4}}+O\left( T^{3H+ \frac{3}{2}}\right) \right) \end{aligned}$$

as $T\rightarrow 0$. Therefore,

$$\begin{aligned}&I_{1}(T)=s_{0}^{2z(T)}K^{-2z(T)+\frac{1}{2}}\left( \log \frac{K}{s_{0}} \right) ^{\frac{n_{1}(1)-2}{2}}\left( 4z(T)^{2}-\frac{1}{4}\right) ^{-1} \nonumber \\&\quad \times \left( 1+O\left( T^{H+\frac{1}{2}}\right) \right) \end{aligned}$$

(73)

as $T\rightarrow 0$. Similarly,

$$\begin{aligned}&I_{2}(T)=s_{0}^{2z(T)}K^{-2z(T)+\frac{1}{2}}\left( \log \frac{K}{s_{0}} \right) ^{\frac{n_{1}(1)-3}{2}}\left( 4z(T)^{2}-\frac{1}{4}\right) ^{-1} \nonumber \\&\quad \times \left( 1+O\left( T^{H+\frac{1}{2}}\right) \right) \end{aligned}$$

(74)

as $T\rightarrow 0$. It is not hard to see that

$$\begin{aligned} \left( 4z(T)^{2}-\frac{1}{4}\right) ^{-1}=\lambda _{1}(1)T^{2H+1}. \end{aligned}$$

It follows from (73) and (74) that

$$\begin{aligned} I_{1}(T)&=\lambda _{1}(1)K^{\frac{1}{2}}\left( \log \frac{K}{s_{0}}\right) ^{\frac{n_{1}(1)-2}{2}}\left( \frac{s_{0}}{K}\right) ^{2z(T)}T^{2H+1} \left( 1+O\left( T^{H+\frac{1}{2}}\right) \right) \end{aligned}$$

(75)

as $T\rightarrow 0$. Similarly,

$$\begin{aligned} I_{2}(T)&=\lambda _{1}(1)K^{\frac{1}{2}}\left( \log \frac{K}{s_{0}}\right) ^{\frac{n_{1}(1)-3}{2}}\left( \frac{s_{0}}{K}\right) ^{2z(T)}T^{2H+1} \left( 1+O\left( T^{H+\frac{1}{2}}\right) \right) \end{aligned}$$

(76)

as $T\rightarrow 0$. Using (14), (69), (70) and (71), we see that

$$\begin{aligned} C(T)= & {} \frac{\sqrt{s_0}}{2^{\frac{n_1(1)}{2}}\Gamma \left( \frac{n_1(1)}{2} \right) }\lambda _1(1)^{-\frac{n_1(1)}{4}} \prod _{k> n_1(1)}^{\infty }\left( \frac{ \lambda _1(1)}{\lambda _1(1)-\lambda _k(1)}\right) ^{\frac{1}{2}} \\&\times \, T^{-\frac{(2H+1)n_1(1)}{4}} \left( 1+O\left( T^{2H+1}\right) \right) \left[ I_1(T)+O\left( T^{\frac{2H+1}{4}}I_2(T)\right) \right] \end{aligned}$$

as $T\rightarrow 0$. Next, (75) and (76), imply

$$\begin{aligned} C(T)&=\frac{(s_0K)^{\frac{1}{2}}}{2^{\frac{n_1(1)}{2}}\Gamma \left( \frac{ n_1(1)}{2}\right) } \lambda _1(1)^{-\frac{n_1(1)-4}{4}}\prod _{k> n_1(1)}^{\infty } \left( \frac{\lambda _1(1)}{\lambda _1(1)-\lambda _k(1)}\right) ^{\frac{1}{2}} \nonumber \\&\quad \times \, \left( \log \frac{K}{s_0}\right) ^{\frac{n_1(1)-2}{2}}T^{\frac{ (2H+1)(4-n_1(1))}{4}}\left( \frac{s_0}{K}\right) ^{2z(T)} \left( 1+O\left( T^{ \frac{2H+1}{4}}\right) \right) \end{aligned}$$

(77)

as $T\rightarrow 0$. We also have

$$\begin{aligned} \sqrt{\frac{\lambda _1(1)T^{2H+1}+4}{\lambda _1(1)T^{2H+1}}}-\sqrt{\frac{4}{ \lambda _1(1)T^{2H+1}}} =O\left( T^{H+\frac{1}{2}}\right) \end{aligned}$$

(78)

as $T\rightarrow 0$. Therefore,

$$\begin{aligned} \left( \frac{s_0}{K}\right) ^{2z(T)}&=\exp \left\{ -2z(T)\log \frac{K}{s_0} \right\} \\&=\exp \left\{ -\frac{1}{2}\sqrt{\frac{\lambda _1(1)T^{2H+1}+4}{ \lambda _1(1)T^{2H+1}}}\log \frac{K}{s_0}\right\} \\&=\exp \left\{ -\frac{1}{2} \sqrt{\frac{4}{\lambda _1(1)T^{2H+1}}}\log \frac{K}{s_0}\right\} \\&\quad \times \,\exp \left\{ -\frac{1}{2}\left[ \sqrt{\frac{\lambda _1(1)T^{2H+1}+4}{ \lambda _1(1)T^{2H+1}}}-\sqrt{\frac{4}{\lambda _1(1)T^{2H+1}}}\right] \log \frac{ K}{s_0}\right\} \end{aligned}$$

as $T\rightarrow 0$. Using (78), we obtain

$$\begin{aligned}&\left( \frac{s_0}{K}\right) ^{2z(T)}=\left( \frac{s_0}{K}\right) ^{ \lambda _1(1)^{-\frac{1}{2}}T^{-H-\frac{1}{2}}} \left( 1+O\left( T^{H+\frac{1}{2 }}\right) \right) \end{aligned}$$

(79)

as $T\rightarrow 0$.

Now, it is clear that Theorem 4 follows from (77) and (79). $\square$

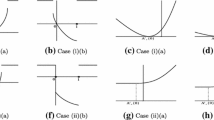
From top to bottom and left to right: IV with $\sigma =2$, $t\in [$1 day, 2 weeks], $H=0.25,$ 0.35,  0.40,  0.45,  0.49,  0.51,  0.55,  0.60,  0.75,  0.85.