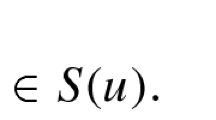Existence Results and Optimal Control for a Class of Quasi Mixed Equilibrium Problems Involving the (f, g, h)-Quasimonotonicity

Abstract

In this paper, by introducing a new concept of the (f, g, h)-quasimonotonicity and applying the maximal monotonicity of bifunctions and KKM technique, we show the existence results of solutions for quasi mixed equilibrium problems when the constraint set is compact, bounded and unbounded, respectively, which extends and improves several well-known results in many respects. Next, we also obtain a result of optimal control to a minimization problem. Our main results can be applied to the problems of evolution equations, differential inclusions and hemivariational inequalities.

1 Introduction

The study developed in this paper is based on the theory of equilibrium problems and multi-valued mapping. As an important and useful generalization of variational inequalities, the theory of equilibrium problems provides us with a unified and general framework to study a wide class of mathematical problems involving equilibria such as optimization, optimal control, convex analysis, transportation, economics, network and noncooperative games among others (see, for instance, [5, 8, 9, 15, 17, 21, 23, 26, 27, 30, 32]). Therefore, since the equilibrium problem unifies at least all the above mentioned problems in a common formulation and many techniques and methods established in order to solve one of them may be extended, it is worth to find out suitable ways to solve them efficiently. For more details, we refer to [2,3,4, 7, 10, 19].

In [10], Chadli, Ansari and Yao studied the existence of solutions for mixed equilibrium problems described by a bifunction as the sum of a monotone and maximal monotone bifunction and a bifunction which is, respectively, pseudomonotone and quasimonotone in topological sense. The concept of maximal monotonicity for bifunctions is in fact an extension to equilibrium problems of the corresponding one of nonlinear operators which can be seen in [1, 8].

Very recently, many authors studied the existence results for some types of hemivariational inequalities by introducing some general monotonicity (see [24, 31, 33, 34]). By introducing and applying some concepts of quasimonotonicity and KKM technique, the authors obtained some existence theorems when the constrained set is nonempty, bounded (or unbounded), closed and convex in a reflexive Banach space. For more about the hemivariational inequalities, we refer to [25, 28, 29].

The aim of this paper is to study the existence of solutions for a generalized problems of quasi mixed equilibrium in a reflexive Banach space. To establish our results, we introduce a new concept of stable (f, g, h)-quasimonotonicity, and use the properties of the maximal monotonicity of bifunctions and KKM technique. Our results extend and improve some results in [10, 24, 31, 33, 34] in many respects. The (f, g, h)-quasimonotonicity depends on f, g, h which is more general than usual monotonicity. Furthermore, our problem (2.1) is more general than that considered in [10], which involves a multi-valued mapping, and the conditions of g, h are different from the conditions in [10]. Moreover, the problems of hemivariational inequalities in [24, 31, 33, 34] are also our special cases. From the above, our problem in this paper is valuable and this fact is the motivation of the present work. It is worth to do further research on this subject.

The rest of this paper is organized as follows. In the next section, we will introduce some useful preliminaries and necessary materials. We introduce some kinds of generalized monotonicity of a mapping. In Sect. 3, we are devoted to proving our main results. We show the existence of solutions in the case when the constraint set is compact, bounded and unbounded in Theorems 3.1, 3.3 and 3.4, respectively. Theorem 3.5 provides a sufficient condition to the boundedness of the solution set. In Sect. 4, a result of optimal control to a minimization problem is given. Finally, we give an example of hemivariational inequalities to illustrate our main results.

2 Preliminaries

Let E be a real Banach space with the norm denoted by $\Vert \cdot \Vert _{E}$. Denote by $E^*$ its dual space and $\langle \cdot ,\cdot \rangle _{E}$ the duality pairing between $E^*$ and E. Let K be a nonempty, closed and convex subset of E. Let $F:K \rightrightarrows E^*$ be a multi-valued mapping, $f:K\times K\rightarrow E$ be a mapping. Let $g,h:K\times K\rightarrow \overline{\mathbb {R}}:=\mathbb {R}\cup \{\pm \infty \}$ be two bifunctions and $\mathcal {D}(g)=\{x\in K:g(x,y)\ne -\infty , \forall y\in K\}$ with $\mathcal {D}(g)\cap \mathcal {D}(h)\ne \emptyset$. In this paper, we first discuss the following quasi mixed equilibrium problems involving a multi-valued mapping:

$$\begin{aligned} \left\{ \begin{array}{llll} \text {Find}~x\in \mathcal {D}(g)\cap \mathcal {D}(h) ~\text {and}~ x^{*}\in F(x) ~\text {such~that} \\ \langle x^{*},f(x,y)\rangle _{E}+g(x,y)+h(x,y)\ge 0,\\ \forall y\in K. \end{array}\right. \end{aligned}$$

(2.1)

Then, we focus on the optimal control of (2.1). Let the control space V be a reflexive Banach space, and $U\subset V$ be the set of admissible controls. Through out this paper, we assume that U is nonempty, closed and convex. Given a control $u\in U$, we consider the following control system:

$$\begin{aligned} \left\{ \begin{array}{llll} \text {Find}~x\in \mathcal {D}(g)\cap \mathcal {D}(h) ~\text {and}~ x^{*}\in F(x) ~\text {such~that} \\ \langle x^{*}-B(u),f(x,y)\rangle _{E}+g(x,y)+h(x,y)\ge 0,\\ \forall y\in K, \end{array}\right. \end{aligned}$$

(2.2)

where $B:V\rightarrow E^*$ is a compact mapping.

Now, we introduce some basic preliminaries.

For $r>0$, let

$$\begin{aligned} B_{r}(x_{0}):=\{x\in K: \Vert x-x_{0}\Vert _{E}\le r\}. \end{aligned}$$

We denote by “$\rightarrow$” the strong convergence and “$\rightharpoonup$” the weak convergence.

Definition 2.1

A function $f:K\rightarrow \mathbb {R}$ is said to be

• (i) convex on K if for every finite subset $\{x_{1},\ldots ,x_{n}\}\subset K$ and $\{\lambda _{1},\ldots ,\lambda _{n}\}\subset \mathbb {R}_{+}$ such that $\sum _{i=1}^{n}\lambda _{i}=1$ and $\sum _{i=1}^{n}\lambda _{i}x_{i}\in K$, then

  $$\begin{aligned} f\left( \sum _{i=1}^{n}\lambda _{i}x_{i}\right) \le \sum _{i=1}^{n}\lambda _{i}f(x_{i}); \end{aligned}$$

• (ii) concave on K if $-f$ is convex on K.

Definition 2.2

[6] A function $f:K\rightarrow \mathbb {R}$ is said to be

• (i) (weakly) upper semicontinuous (u.s.c.) at $x_{0}$, if for any sequence $\{x_{n}\}_{n\ge 1}\subset K$ with ($x_{n}\rightharpoonup x_{0}$) $x_{n}\rightarrow x_{0}$, we have

  $$\begin{aligned} \limsup _{n\rightarrow \infty }f(x_{n})\le f(x_{0}); \end{aligned}$$

• (ii) (weakly) lower semicontinuous (l.s.c.) at $x_{0}$, if for any sequence $\{x_{n}\}_{n\ge 1}\subset K$ with ($x_{n}\rightharpoonup x_{0}$) $x_{n}\rightarrow x_{0}$, we have

  $$\begin{aligned} \liminf _{n\rightarrow \infty }f(x_{n})\ge f(x_{0}). \end{aligned}$$

  f is said to be (weakly) u.s.c. (l.s.c.) on K, if for all $x\in K$f is (weakly) u.s.c. (l.s.c.) at x.

Definition 2.3

[20] A multi-valued mapping $F:K\rightrightarrows E^{*}$ is said to be

• (i) strongly-weakly$^*$ closed, if for any sequence $\{x_{n}\}_{n\ge 1}\subset K,x_{n}^*\in F(x_{n})$ with $x_{n}\rightarrow x_{0}$ and $x_{n}^*\rightharpoonup x_{0}^*$, we have $x_{0}^*\in F(x_{0})$;

• (iii) quasi$^*$-compact, if for any relative compact subset $A\subset K$, F(A) is relative compact with respect to the weak$^*$ topology in $E^{*}$;

• (iii) lower semicontinuous (l.s.c.) at $x_{0}$, if for any $x_{0}^{*}\in F(x_{0})$ and sequence $\{x_{n}\}_{n\ge 1}\subset K$ with $x_{n}\rightarrow x_{0}$, there exists a sequence $x_{n}^{*}\in F(x_{n})$ such that $x_{n}^{*}\rightarrow x_{0}^{*}$;

• (iv) lower hemicontinuous (l.h.c.), if the restriction of F to every line segment of K is l.s.c. with respect to the weak$^*$ topology in $E^{*}$.

In order to obtain the main result of this paper, we need the following lemma.

Lemma 2.4

[18, Theorem 2.7.5] Let K be a nonempty subset of a Hausdorff topological vector space E and let $G:K\rightrightarrows E$ be a multi-valued mapping satisfying the following properties:

• (i) G is a KKM mapping, i.e.,

  $$\begin{aligned} conv\{x_{1},x_{2},\ldots ,x_{n}\}\subset \bigcup _{i=1}^{n}G(x_{i}),\qquad \text {for}~x_{i}\in K,~i=1,2,\ldots ,n; \end{aligned}$$

• (ii) G(x) is closed in E for every $x\in K$;

• (iii) $G(x_{0})$ is compact in E for some $x_{0}\in K$.

Then $\bigcap _{x\in K}G(x)\ne \emptyset$.

Definition 2.5

A bifunction $h:K\times K\rightarrow \mathbb {R}$ with $h(x,x)=0$ for all $x\in K$ is said to be maximal monotone if for every $x\in K$ and for every convex function $\psi :K\rightarrow \mathbb {R}$ with $\psi (x)=0$, we have

$$\begin{aligned} \psi (y)\ge h(y,x)\Rightarrow \psi (y)\ge -h(x,y),\qquad \forall y\in K. \end{aligned}$$

Clearly, if $h(x,y)+h(y,x)\ge 0$ then h is maximal monotone.

Lemma 2.6

[10, Lemma 2.4] Let $h:K\times K\rightarrow \mathbb {R}$ be a bifunction with $h(x,x)= 0$ for all $x\in K$. Suppose that h is upper hemicontinuous and convex with the second argument, then it is maximal monotone.

For more details about the maximal monotonicity, we refer [1, 8, 10].

Next, we introduce the concept of (f, g, h)-quasimonotonicity which is useful for establishing the existence theorems for the main results.

Definition 2.7

Let $F:K\rightrightarrows E^{*}$, $f:K\times K\rightarrow E$ and $g,h:K\times K\rightarrow \overline{\mathbb {R}}$. F is said to be

• (i) (f, g, h)-pseudomonotone, if for each $x,y\in K$,

  $$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)\ge h(y,x)\Rightarrow \langle y^{*},f(x,y)\rangle +g(x,y)\ge h(y,x), \end{aligned}$$

  $\forall x^{*}\in F(x)$ and $\forall y^{*}\in F(y)$;

• (ii) (f, g, h)-quasimonotone, if for each $x,y\in K$,

  $$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)> h(y,x)\Rightarrow \langle y^{*},f(x,y)\rangle +g(x,y)\ge h(y,x),\qquad \end{aligned}$$

  (2.3)

  $\forall x^{*}\in F(x)$ and $\forall y^{*}\in F(y)$;

• (iii) stably (f, g, h)-pseudomonotone with respect to the set $Z\subset E^*$, if F and $F(\cdot )-\zeta$ are (f, g, h)-pseudomonotone for every $\zeta \in Z$;

• (iv) stably (f, g, h)-quasimonotone with respect to the set $Z\subset E^*$, if F and $F(\cdot )-\zeta$ are (f, g, h)-quasimonotone for every $\zeta \in Z$.

Remark 2.8

• (i) It is easy to verify that the (f, g, h)-quasimonotonicity is weaker than the (f, g, h)-pseudomonotonicity;

• (ii) If $f(x,y)=y-x,~h\equiv 0$, then (2.3) becomes

  $$\begin{aligned} \langle x^{*},y-x\rangle +g(x,y)> 0\Rightarrow \langle y^{*},y-x\rangle +g(x,y)\ge 0, \end{aligned}$$

  $\forall x^{*}\in F(x)$ and $\forall y^{*}\in F(y)$, i.e., F is g-quasimonotone.

• (iii) If $f(x,y)=y-x,~h(y,x)=-J^{\circ }(Tx;Ty-Tx)$ (see Sect. 5), then (2.3) becomes

  $$\begin{aligned}&\langle x^{*},y-x\rangle +g(x,y)+J^{\circ }(Tx;Ty-Tx)> 0\Rightarrow \langle y^{*},y-x\rangle +g(x,y)\\&\quad +\,J^{\circ }(Tx;Ty-Tx)\ge 0, \end{aligned}$$

  $\forall x^{*}\in F(x)$ and $\forall y^{*}\in F(y)$. From [33] we know that F is stably g-quasimonotone with respect to some subset $Z\subset E^*$.

For more details about the general monotonicity, we refer to [31, 33, 34].

3 Existence Theorems

Now, we give some existence results for our problem.

At first, we give the following existence result when K is a compact and convex subset of E.

Theorem 3.1

Let K be a nonempty, compact and convex subset of a real Banach space E. Assume that:

$f:K\times K\rightarrow E$ is a mapping satisfying the following conditions:

• (i) $f(x,x)=0$ for all $x\in K$,

• (ii) for all $y\in K$, $f(\cdot ,y)$ is continuous,

• (iii) for all $x\in K,~n\in \mathbb {N}, y_{j}\in K,~\lambda _{j}\in [0,1],~j=1,2,\ldots ,n$ with $\sum _{j=1}^{n}\lambda _{j}=1$, one has

  $$\begin{aligned} f\left( x,\sum _{j=1}^{n}\lambda _{j}y_{j}\right) =\sum _{j=1}^{n}\lambda _{j}f(x,y_{j}); \end{aligned}$$

$g:K\times K\rightarrow \overline{\mathbb {R}}$ is a mapping satisfying the following conditions:

• (iv) $g(x,x)=0$ for all $x\in K$,

• (v) for all $y\in K$, $g(\cdot ,y)$ is u.s.c.,

• (vi) for all $x\in K$, $g(x,\cdot )$ is convex;

$h:K\times K\rightarrow \overline{\mathbb {R}}$ is a mapping satisfying the following conditions:

• (vii) $h(x,x)=0$ for all $x\in K$,

• (viii) for all $y\in K$, $h(\cdot ,y)$ is concave,

• (ix) for all $x\in K$, we have $\limsup _{n\rightarrow \infty } h(x,y_{n})\ge h(x,y)$ as $y_{n}\rightarrow y$;

$F:K\rightrightarrows E^{*}$ is strongly-weakly$^*$ closed and quasi$^*$-compact.

Then, there exist $x\in K$ and $x^{*}\in F(x)$ such that

$$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)\ge h(y,x),\qquad \forall y\in K. \end{aligned}$$

(3.1)

Furthermore, if h is maximal monotone then problem (2.1) has at least one solution.

Proof

The idea of the proof comes from Costea and Radulescu [14]. Arguing by contradiction, let us assume that problem (3.1) has no solution. Then, for each $x\in K$, there exists $y\in K$ such that

$$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y)\rangle +g(x,y)<h(y,x). \end{aligned}$$

(3.2)

For each $y\in K$, define a multi-valued mapping $\Gamma :K\rightrightarrows E$ as follows:

$$\begin{aligned} \Gamma (y):=\{x\in K: \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y)\rangle +g(x,y)\ge h(y,x)\}. \end{aligned}$$

We claim that the set $\Gamma (y)$ is nonempty and closed for each $y\in K$.

The fact that $\Gamma (y)$ is nonempty is obvious since $y\in \Gamma (y)$ for each $y\in K$.

In order to show the closedness of $\Gamma (y)$ for each $y\in K$, let us fix $y\in K$ and consider a sequence $\{x_{n}\}_{n\ge 1}\subset \Gamma (y)$ which converges to some $x_{0}\in K$. We shall prove that $x_{0} \in \Gamma (y)$. Since $x_{n}\in \Gamma (y)$, for each $n\ge 1$ we have that

$$\begin{aligned} \sup _{x_{n}^{*}\in F(x_{n})}\langle x_{n}^{*},f(x_{n},y)\rangle +g(x_{n},y)\ge h(y,x_{n}). \end{aligned}$$

Since F is strongly-weakly$^*$ closed and quasi$^*$-compact, for any $x_{n}^{*}\in F(x_{n})$ there exists $x_{0}^*\in E^*$, without loss of generality, such that $x_{n}^{*} \rightharpoonup x_{0}^{*}$ in $E^*$ and $x_{0}^{*}\in F(x_{0})$. Therefore, from (ii),(v) and (ix) we have that

$$\begin{aligned} h(y,x_{0})\le \limsup _{n\rightarrow \infty }h(y,x_{n})\le & {} \limsup _{n\rightarrow \infty }\left[ \sup _{x_{n}^{*}\in F(x_{n})}\langle x_{n}^{*},f(x_{n},y)\rangle +g(x_{n},y)\right] \\\le & {} \limsup _{n\rightarrow \infty }\sup _{x_{n}^{*}\in F(x_{n})}\langle x_{n}^{*},f(x_{n},y)\rangle +\limsup _{n\rightarrow \infty }g(x_{n},y)\\\le & {} \sup _{x_{0}^{*}\in F(x_{0})}\langle x_{0}^{*},f(x_{0},y)\rangle +g(x_{0},y). \end{aligned}$$

This shows that $x_{0}\in \Gamma (y)$. Hence $\Gamma (y)$ is closed.

According to (3.2) for each $x\in K$ there exists $y\in K$ such that $x\in [\Gamma (y)]^{c}=E-\Gamma (y)$ which is an open subset of E. This means that the family $\{[\Gamma (y)]^{c}\}_{y\in K}$ is an open covering of the compact set K. Therefore there exists a finite subset $\{ y_{1},\ldots ,y_{N}\}$ of K such that $\{[\Gamma (y_{j})]^{c}\}_{1\le j\le N}$ is a finite subcover of K. For each $j\in \{1,\ldots ,N\}$ let $d_{j}(x)$ be the distance between x and the set $\Gamma (y_{j})$ and define $\beta _{j}:K\rightarrow \mathbb {R}$ as follows:

$$\begin{aligned} \beta _{j}(x)=\frac{d_{j}(x)}{\sum _{i=1}^{N}d_{i}(x)}.\nonumber \end{aligned}$$

Clearly, for each $j\in \{1,\ldots ,N\}$, $\beta _{j}$ is a Lipschitz continuous function that vanishes on $\Gamma (y_{j})$ and $0\le \beta _{j}(x)\le 1$, for all $x\in K$. Moreover, $\sum _{j=1}^{N}\beta _{j}(x)=1$. Let us consider the operator $S:K\rightarrow K$ defined by

$$\begin{aligned} S(x)=\sum _{j=1}^{N}\beta _{j}(x)y_{j}. \end{aligned}$$

We will show that S is a completely continuous operator. It is easy to see that S is Lipschitz continuous hence continuous. Therefore, S is completely continuous by the compactnee of K. Thus, by Schauder’s fixed point theorem (see [6], p. 90), there exists $\overline{x}\in K$ such that $S(\overline{x})=\overline{x}$.

Let us define $\alpha :K\rightarrow \mathbb {R}$ by

$$\begin{aligned} \alpha (x)=\sup _{x^{*}\in F(x)}\langle x^{*},f(x,S(x))\rangle +g(x,S(x))-h(S(x),x). \end{aligned}$$

By the assumptions (iii), (vi), (viii) and the definition of S, for each $x\in K$, we have

$$\begin{aligned} \alpha (x)= & {} \sup _{x^{*}\in F(x)}\left\langle x^{*},f\left( x,\sum _{j=1}^{N}\beta _{j}(x)y_{j}\right) \right\rangle \\&+g\left( x,\sum _{j=1}^{N}\beta _{j}(x)y_{j}\right) -h\left( \sum _{j=1}^{N}\beta _{j}(x)y_{j},x\right) \\\le & {} \sum _{j=1}^{N}\beta _{j}(x)\left[ \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y_{j})\rangle +g(x,y_{j})-h(y_{j},x)\right] . \end{aligned}$$

Let $x\in K$. If $x\in [\Gamma (y_{j})]^{c}$, then we have that $\beta _{j}(x)>0$ and

$$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y_{j})\rangle +g(x,y_{j})-h(y_{j},x)<0. \end{aligned}$$

If $x\in \Gamma (y_{j})$, then we have that $\beta _{j}(x)=0$ and

$$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y_{j})\rangle +g(x,y_{j})-h(y_{j},x)\ge 0. \end{aligned}$$

Taking into account that $K\subseteq \bigcup _{j=1}^{N}[\Gamma (y_{j})]^{c}$, we deduce that there exists at least one index $j_{0}\in \{1,\ldots ,N\}$ such that $x\in [\Gamma (y_{j_{0}})]^{c}$. This shows that $\alpha (x)<0$ for all $x\in K$. However, $\alpha (\overline{x})=0$ and thus we have obtained a contradiction. Therefore, there exist $x\in K$ and $x^{*}\in F(x)$ such that

$$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)\ge h(y,x),\qquad \forall y\in K. \end{aligned}$$

Furthermore, if h is maximal monotone, by considering in Definition 2.5 the function $\psi$ defined by

$$\begin{aligned} \psi (y)=\langle x^{*},f(x,y)\rangle +g(x,y) \end{aligned}$$

which is convex, then

$$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)+h(x,y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

Obviously, we have $x\in \mathcal {D}(g)\cap \mathcal {D}(h)$. Hence, problem (2.1) has at least one solution, which completes the proof. $\square$

Remark 3.2

Costea and Radulescu in [14] studied the following quasi-hemivariational inequality problem: find $x\in K$ and $x^*\in F(x)$ such that

$$\begin{aligned} \langle x^*,y-x\rangle +P(x)J^{0}(ix;iy-ix)\ge \langle Qx,y-x\rangle ,\qquad \forall y\in K, \end{aligned}$$

where $Q: E\rightarrow E^*$ is a nonlinear operator. If $f(x,y)=y-x,g(x,y)=P(x)J^{0}(ix;iy-ix)$ and $h(y,x)=\langle Qx,y-x\rangle$, then Theorem 3.1 reduces to the Theorem 3.1 of [14].

We point out the fact that in the above case when K is a compact convex subset of E we do not impose any monotonicity conditions on F, nor we assume E to be a reflexive space. Next, we will consider the existence of solutions of problem (2.1) when K is a bounded, closed and convex subset of E. We shall use the maximal monotonicity in Definition 2.5 and the generalized monotonicity in Definition 2.7.

Theorem 3.3

Let K be a nonempty, bounded, closed and convex subset of a real reflexive Banach space E. Assume that:

$f:K\times K\rightarrow E$ is a mapping satisfying the following conditions:

• (i) $f(x,y)+f(y,x)=0$ for all $x,y\in K$,

• (ii) for all $y\in K$, $f(\cdot ,y)$ is continuous,

• (iii) for all $x\in K,~n\in \mathbb {N}, y_{j}\in K,~\lambda _{j}\in [0,1],~j=1,2,\ldots ,n$ with $\sum _{j=1}^{n}\lambda _{j}=1$, one has

  $$\begin{aligned} f\left( x,\sum _{j=1}^{n}\lambda _{j}y_{j}\right) =\sum _{j=1}^{n}\lambda _{j}f(x,y_{j}); \end{aligned}$$

$g:K\times K\rightarrow \overline{\mathbb {R}}$ is a mapping satisfying the following conditions:

• (iv) $g(x,x)=0$ for all $x\in K$,

• (v) $g(x,y)+g(y,x)\ge 0$ for all $x,y\in K$,

• (vi) for all $y\in K$, $g(\cdot ,y)$ is weakly u.s.c.,

• (vii) for all $x\in K$, $g(x,\cdot )$ is convex;

$h:K\times K\rightarrow \overline{\mathbb {R}}$ is a mapping satisfying the following conditions:

• (viii) $h(x,x)=0$ for all $x\in K$,

• (ix) for all $y\in K$, $h(\cdot ,y)$ is concave;

• (x) for all $x\in K$, $h(x,\cdot )$ is convex and l.s.c.;

$F:K\rightrightarrows E^{*}$ is a l.h.c. multi-valued mapping and (f, g, h)-quasimonotone.

Then, there exist $x\in K$ and $x^{*}\in F(x)$ such that

$$\begin{aligned} \langle x^{*},f(x,y)\rangle +g(x,y)\ge h(y,x),\qquad \forall y\in K. \end{aligned}$$

Furthermore, if h is maximal monotone then problem (2.1) has at least one solution.

Proof

For any $y\in K$ define a multi-valued mapping $G:K\rightrightarrows E$ as follows:

$$\begin{aligned} G(y):=\{x\in K: \inf _{y^{*}\in F(y)}\langle y^{*},f(x,y)\rangle +g(x,y)\ge h(y,x)\}. \end{aligned}$$

It is easy to verify that G(y) is nonempty and closed for each $y\in K$.

Consider two cased of G: (a) G is not a KKM mapping, and (b) G is a KKM mapping.

Case (a) If G is not a KKM mapping, then there exist $x_{i}\in K$ and $\lambda _{i}\in [0,1],~i=1,2,\ldots ,N$, with $\sum _{i=1}^{N}\lambda _{i}=1$ such that $x_{0}=\sum _{i=1}^{N}\lambda _{i}x_{i}\not \in \bigcup _{i=1}^{N}G(x_{i})$, that is

$$\begin{aligned} \inf _{x_{i}^{*}\in F(x_{i})}\langle x_{i}^{*},f(x_{0},x_{i})\rangle +g(x_{0},x_{i})<h(x_{i},x_{0}),\qquad \forall i\in \{1,2,\ldots ,N\}. \end{aligned}$$

(3.3)

We claim that there exists a neighborhood $B_{\delta }(x_{0})(\delta >0)$ of $x_{0}$ such that for all $y\in B_{\delta }(x_{0})\cap K$,

$$\begin{aligned} \inf _{x_{i}^{*}\in F(x_{i})}\langle x_{i}^{*},f(y,x_{i})\rangle +g(y,x_{i})<h(x_{i},y),\qquad \forall i\in \{1,2,\ldots ,N\}. \end{aligned}$$

(3.4)

If not, for any n, there exists $y_{n}\in B_{\frac{1}{n}}(x_{0})\cap K$ and $i_{n}\in \{1,2,\ldots ,N\}$ such that

$$\begin{aligned} \inf _{x_{i_{n}}^{*}\in F(x_{i_{n}})}\langle x_{i_{n}}^{*},f(y_{n},x_{i_{n}})\rangle +g(y_{n},x_{i_{n}})\ge h(x_{i_{n}},y_{n}). \end{aligned}$$

By $i_{n}\in \{1,2,\ldots ,N\}$, there exists a subsequence of $\{i_n\}$, still denoted by $\{i_n\}$, such that $i_n=i_0\in \{1,2,\ldots ,N\}$ for all n and

$$\begin{aligned} \inf _{x_{i_{0}}^{*}\in F(x_{i_{0}})}\langle x_{i_{0}}^{*},f(y_{n},x_{i_{0}})\rangle +g(y_{n},x_{i_{0}})\ge h(x_{i_{0}},y_{n}). \end{aligned}$$

By $y_{n}\rightarrow x_{0}$ and (ii), (vi), (x) of the assumptions, passing to the superior limit, we obtain that

$$\begin{aligned} \inf _{x_{i_{0}}^{*}\in F(x_{i_{0}})}\langle x_{i_{0}}^{*},f(x_{0},x_{i_{0}})\rangle +g(x_{0},x_{i_{0}})\ge h(x_{i_{0}},x_{0}), \end{aligned}$$

which is a contradiction with (3.3), hence we have the claim.

By the (f, g, h)-quasimonotonicity of F and (3.4), we get that for all $y\in B_{\delta }(x_{0})\cap K$,

$$\begin{aligned} \sup _{y^{*}\in F(y)}\langle y^{*},f(y,x_{i})\rangle +g(y,x_{i})\le h(x_{i},y),\qquad \forall i\in \{1,2,\ldots ,N\}, \end{aligned}$$

and hence

$$\begin{aligned} \sup _{y^{*}\in F(y)}\langle y^{*},f(y,x_{i})\rangle +g(y,x_{i})-h(x_{i},y)\le 0,\qquad \forall i\in \{1,2,\ldots ,N\}. \end{aligned}$$

From (iii), (vii), (ix) of the assumptions, we have that

$$\begin{aligned}&\sup _{y^{*}\in F(y)}\left\langle y^{*},f(y,x_{0})\right\rangle +g(y,x_{0})-h(x_{0},y)\\&\quad =\sup _{y^{*}\in F(y)}\left\langle y^{*},f\left( y,\sum _{i=1}^{N}\lambda _{i}x_{i}\right) \right\rangle +g\left( y,\sum _{i=1}^{N}\lambda _{i}x_{i}\right) -h\left( \sum _{i=1}^{N}\lambda _{i}x_{i},y\right) \\&\quad \le \sum _{i=1}^{N}\lambda _{i}\left[ \sup _{y^{*}\in F(y)}\langle y^{*},f(y,x_{i})\rangle +g(y,x_{i})-h(x_{i},y)\right] \le 0. \end{aligned}$$

From (i), (v) of the assumptions, we obtain that

$$\begin{aligned} \inf _{y^{*}\in F(y)}\langle y^{*},f(x_{0},y)\rangle +g(x_{0},y)+h(x_{0},y)\ge 0,\qquad \forall y\in B_{\delta }(x_{0})\cap K. \end{aligned}$$

(3.5)

Let $y'\in K$ be any element and define

$$\begin{aligned} x_{m}=\frac{1}{m}y'+\left( 1-\frac{1}{m}\right) x_{0},\qquad m\ge 1. \end{aligned}$$

Thus, $x_{m}\rightarrow x_{0}$ as $m\rightarrow \infty$ and hence there exists $N\in \mathbb {N}$ such that

$$\begin{aligned} x_{m}\in B_{\delta }(x_{0})\cap K,\qquad \forall m>N. \end{aligned}$$

For any given $x_{0}^{*}\in F(x_{0})$, since F is l.h.c., there exists a sequence $\{x_{m}^{*}\}$ in $F(x_{m})$ such that $x_{m}^{*}\rightharpoonup x_{0}^{*}$. It follows from (3.5) that for any $m>N$,

$$\begin{aligned} \langle x_{m}^{*},f(x_{0},x_{m})\rangle +g(x_{0},x_{m})+h(x_{0},x_{m})\ge 0, \end{aligned}$$

From (i), (iii), (iv), (vii), (viii), (ix) of the assumptions, we have that

$$\begin{aligned} 0\le & {} \left\langle x_{m}^{*},f\left( x_{0},\frac{1}{m}y'+\left( 1-\frac{1}{m}\right) x_{0}\right) \right\rangle +g\left( x_{0},\frac{1}{m}y'+\left( 1-\frac{1}{m}\right) x_{0}\right) \\&+h\left( x_{0},\frac{1}{m}y'+\left( 1-\frac{1}{m}\right) x_{0}\right) \\\le & {} \frac{1}{m}\left[ \langle x_{m}^{*},f(x_{0},y')\rangle +g(x_{0},y')+h(x_{0},y')\right] . \end{aligned}$$

Multiplying the last inequality by m and letting $m\rightarrow \infty$, we obtain that

$$\begin{aligned} \langle x_{0}^{*},f(x_{0},y')\rangle +g(x_{0},y')+h(x_{0},y')\ge 0,\qquad \forall y'\in K. \end{aligned}$$

(3.6)

Obviously, we have $x_{0}\in \mathcal {D}(g)\cap \mathcal {D}(h)$. Hence problem (2.1) has at least one solution.

Case (b)G is a KKM mapping. For any $y\in K$, we consider the following mapping:

$$\begin{aligned} x\mapsto \inf _{y^{*}\in F(y)}\langle y^{*},f(x,y)\rangle +g(x,y)-h(y,x). \end{aligned}$$

We claim that the above mapping is weakly u.s.c. Let $\{\mu _{n}\}\subset K$ such that $\mu _{n}\rightharpoonup \mu _{0}$. Since $f(\cdot ,y)$ is continuous, $g(\cdot ,y)$ is weakly u.s.c. and $h(x,\cdot )$ is weakly l.s.c. for all $x,y\in K$, we have

$$\begin{aligned}&\limsup _{n\rightarrow \infty }\left[ \inf _{y^{*}\in F(y)}\langle y^{*},f(\mu _{n},y)\rangle +g(\mu _{n},y)-h(y,\mu _{n})\right] \\&\quad \le \limsup _{n\rightarrow \infty }\left( \inf _{y^{*}\in F(y)}\langle y^{*},f(\mu _{n},y)\rangle \right) +\limsup _{n\rightarrow \infty }g(\mu _{n},y)+\limsup _{n\rightarrow \infty }-h(y,\mu _{n})\\&\quad \le \limsup _{n\rightarrow \infty }\left( \inf _{y^{*}\in F(y)}\langle y^{*},f(\mu _{n},y)\rangle \right) +\limsup _{n\rightarrow \infty }g(\mu _{n},y)-\liminf _{n\rightarrow \infty }h(y,\mu _{n})\\&\quad \le \inf _{y^{*}\in F(y)}\langle y^{*},f(\mu _{0},y)\rangle +g(\mu _{0},y)-h(y,\mu _{0}). \end{aligned}$$

Thus we have the claim. Then G(y) is weakly closed. It follows that K is weakly compact from the boundedness, convexity and closedness of a subset K in a reflexive Banach space E. Since $G(y)\subset K$, we get that G(y) is weakly compact for each $y\in K$. Thus, all the conditions of Lemma 2.4 are satisfied in the weak topology and hence we obtain that $\bigcap _{y\in K}G(y)\ne \emptyset$. Taking $x_{0}\in \bigcap _{y\in K}G(y)$, we have

$$\begin{aligned} \inf _{y^{*}\in F(y)}\langle y^{*},f(x_{0},y)\rangle +g(x_{0},y)-h(y,x_{0})\ge 0,\qquad \forall y\in K. \end{aligned}$$

(3.7)

Let $y_{0}\in K$ and $x_{n}=\frac{1}{n}y_{0}+(1-\frac{1}{n})x_{0},~ n\ge 1$. Then $x_{n}\in K$ for all $n\ge 1$. Since F is l.h.c., for any $x_{0}^{*}\in F(x_{0})$, there exists a sequence $\{x_{n}^{*}\}$ in $F(x_{n})$ such that $x_{n}^{*}\rightharpoonup x_{0}^{*}$. For any $n\ge 1$, we have from (3.7)

$$\begin{aligned} \langle x_{n}^{*},f(x_{0},x_{n})\rangle +g(x_{0},x_{n})-h(x_{n},x_{0})\ge 0. \end{aligned}$$

By (i), (iii), (iv), (vii), (viii),(ix) of the assumptions, we have

$$\begin{aligned} 0\le & {} \left\langle x_{n}^{*},f\left( x_{0},\frac{1}{n}y_{0}+\left( 1-\frac{1}{n}\right) x_{0}\right) \right\rangle +g\left( x_{0},\frac{1}{n}y_{0}+\left( 1-\frac{1}{n}\right) x_{0}\right) \\&-h\left( \frac{1}{n}y_{0}+\left( 1-\frac{1}{n}\right) x_{0},x_{0},\right) \\\le & {} \frac{1}{n}\left[ \langle x_{n}^{*},f(x_{0},y_{0})\rangle +g(x_{0},y_{0})-h(y_{0},x_{0})\right] . \end{aligned}$$

Multiplying the last inequality by n and letting $n\rightarrow \infty$, we obtain

$$\begin{aligned} \langle x_{0}^{*},f(x_{0},y_{0})\rangle +g(x_{0},y_{0})-h(y_{0},x_{0})\ge 0,\qquad \forall y_{0}\in K. \end{aligned}$$

Furthermore, if h is maximal monotone, choose a convex function $\psi$ by

$$\begin{aligned} \psi (y)=\langle x_{0}^{*},f(x_{0},y)\rangle +g(x_{0},y), \end{aligned}$$

then

$$\begin{aligned} \langle x_{0}^{*},f(x_{0},y)\rangle +g(x_{0},y)+h(x_{0},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(3.8)

Obviously, we have $x_{0}\in \mathcal {D}(g)\cap \mathcal {D}(h)$. Hence problem (2.1) has at least one solution. This completes the proof. $\square$

To omit the boundedness of K in Theorem 3.3, we need to introduce the following (f, g, h)-coercivity conditions:

• $(\mathrm{A})$ There exists $n_{0}\in \mathbb {N}$ such that for every $x\in K\setminus B_{n_{0}}(0)$, there exists some $y\in K$ with $\Vert y\Vert <\Vert x\Vert$ such that

  $$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y)\rangle +g(x,y)+h(x,y)\le 0. \end{aligned}$$

• $(\mathrm{B})$ There exists $n_{0}\in \mathbb {N}$ such that for every $x\in K\setminus B_{n_{0}}(0)$, there exists some $y\in K$ with $\Vert y\Vert <\Vert x\Vert$ such that

  $$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*},f(x,y)\rangle +g(x,y)+h(x,y)< 0. \end{aligned}$$

Theorem 3.4

Let K be a nonempty, unbounded, closed and convex subset of a real reflexive Banach space E. Assume that f, g, h, F are the mappings satisfying the conditions as in Theorem 3.3. In addition, If the condition (A) holds, then problem (2.1) has at least one solution.

Proof

Take $m> n_{0}$. Since $B_{m}(0)$ is bounded and convex, from (3.6) or (3.8) in Theorem 3.3, we can conclude that there exist $x_{m}\in B_{m}(0)\cap \mathcal {D}(g)\cap \mathcal {D}(h)$ and $x_{m}^{*}\in F(x_{m})$ such that

$$\begin{aligned} \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\ge 0,\qquad \forall y\in B_{m}(0)\cap K. \end{aligned}$$

(3.9)

Now, we consider two cases.

• (i) If $\Vert x_{m}\Vert =m$, then $\Vert x_{m}\Vert >n_{0}$. Since the condition (A) holds, there is some $y_{0}\in K$ with $\Vert y_{0}\Vert <\Vert x_{m}\Vert =m$ such that

  $$\begin{aligned} \langle x_{m}^{*},f(x_{m},y_{0})\rangle +g(x_{m},y_{0})+h(x_{m},y_{0})\le 0. \end{aligned}$$

  (3.10)

  Let $y\in K$. Since $\Vert y_{0}\Vert <\Vert x_{m}\Vert =m$, there exists $t\in (0,1)$ such that $y_{t}:=y_{0}+t(y-y_{0})\in B_{m}(0)\cap K$. From (3.9) and (3.10) it follows that for any $y\in K$,

  $$\begin{aligned} 0\le & {} \langle x_{m}^{*},f(x_{m},y_{t})\rangle +g(x_{m},y_{t})+h(x_{m},y_{t})\\= & {} \langle x_{m}^{*},f(x_{m},(1-t)y_{0}+ty)\rangle +g(x_{m},(1-t)y_{0}+ty)+h(x_{m},(1-t)y_{0}+ty)\\\le & {} (1-t)\left[ \langle x_{m}^{*},f(x_{m},y_{0})\rangle +g(x_{m},y_{0})+h(x_{m},y_{0})\right] \\&+\,t\left[ \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\right] \\\le & {} t\left[ \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\right] . \end{aligned}$$

  Dividing by t, we have that

  $$\begin{aligned} \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

  (3.11)

• (ii) If $\Vert x_{m}\Vert <m$, then for any $y\in K$, there exists $t\in (0,1)$ such that $y'_{t}:=x_{m}+t(y-x_{m})\in B_{m}(0)\cap K$. It follows from (3.9) that for any $y\in K$,

  $$\begin{aligned} 0\le & {} \langle x_{m}^{*},f(x_{m},y'_{t})\rangle +g(x_{m},y'_{t})+h(x_{m},y'_{t})\\\le & {} t\left[ \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\right] . \end{aligned}$$

  Dividing by t, we have that (3.11) holds. Hence

  $$\begin{aligned} \langle x_{m}^{*},f(x_{m},y)\rangle +g(x_{m},y)+h(x_{m},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

  This shows that problem (2.1) has at least one solution.

$\square$

If the constrained set K is bounded, then the solution set of problem (2.1) is obviously bounded. In the case of constrained set K is unbounded, the solution set of problem (2.1) may be unbounded. In the sequel, we provide a sufficient condition to guarantee the boundedness of the solution set of problem (2.1), when K is unbounded. The following result also generalized Theorem 4.5 of [31].

Theorem 3.5

Let K be a nonempty, unbounded closed and convex subset of a real reflexive Banach space E. Assume that f, g, h,  F are the mappings satisfying the conditions as in Theorem 3.3. If the condition (B) holds, then the solution set of problem (2.1) is nonempty and bounded.

Proof

Obviously, we have (B) $\Rightarrow$ (A). By Theorem 3.4, we know that the solution set of problem (2.1) is nonempty. If the solution set is unbounded, then there exist $x_{0}\in \mathcal {D}(g)\cap \mathcal {D}(h)$ and $x_{0}^{*}\in F(x_{0})$ such that $\Vert x_{0}\Vert >n_{0}$ and

$$\begin{aligned} \langle x_{0}^{*},f(x_{0},y)\rangle +g(x_{0},y)+h(x_{0},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(3.12)

Since $\Vert x_{0}\Vert >n_{0}$, it follows from condition (B) that, there exists $y_{0}\in K$ with $\Vert y_{0}\Vert <\Vert x_{0}\Vert$ such that

$$\begin{aligned} \sup _{x_{0}^{**}\in F(x_{0})}\langle x_{0}^{**},f(x_{0},y_{0})\rangle +g(x_{0},y_{0})+h(x_{0},y_{0})<0, \end{aligned}$$

which is a contradiction with (3.12). This completes the proof. $\square$

4 Existence Result for Optimal Control

In this section, we consider the existence of optimal control to problem (2.2) with $h\equiv 0$, i.e., for a control $u\in U$,

$$\begin{aligned} \left\{ \begin{array}{llll} \text {Find}~x\in \mathcal {D}(g)\cap \mathcal {D}(h) ~\text {and}~ x^{*}\in F(x) ~\text {such~that} \\ \langle x^{*}-B(u),f(x,y)\rangle +g(x,y)\ge 0,\\ \forall y\in K. \end{array}\right. \end{aligned}$$

(4.1)

Denote by Sol(u) the set of all solutions of (4.1) corresponding to the control u.

Given another Banach space (the so-called observation space) W, a compact mapping $\Sigma : E\rightarrow W$, and a target $\Upsilon \in W$, we consider the following cost function:

$$\begin{aligned} H(u,x):=\Vert \Sigma (x)-\Upsilon \Vert ^{2}+\epsilon \Vert u\Vert ^{2}, \end{aligned}$$

where $\epsilon >0$. The optimal control problem studied in this work is to seek an optimal pair $(u,x)\in U\times K$ that solves the following minimization problem:

$$\begin{aligned} \min _{u\in U,x\in Sol(u)}H(u,x). \end{aligned}$$

(4.2)

We first consider the topological property to the solution set of problem (4.1).

Theorem 4.1

Let K and U be nonempty closed and convex subsets of real reflexive Banach spaces E and V, respectively. Assume that:

• (i) f, g, h are the mappings satisfying the conditions as in Theorem 3.3;

• (ii) $F:K\rightrightarrows E^{*}$ is l.h.c. and stably (f, g, 0)-quasimonotone with respect to the set $\mathcal {R}(B)$ (the domain of B);

• (iii) the following condition holds: $(B')$ For any $u\in U$, there exists $n_{0}\in \mathbb {N}$ such that for every $x\in K\setminus B_{n_{0}}$, there exists some $y\in K$ with $\Vert y\Vert <\Vert x\Vert$ such that

  $$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*}-B(u),f(x,y)\rangle +g(x,y)< 0. \end{aligned}$$

Then, for any $u\in U$ the solution set Sol(u) of problem (4.1) is nonempty, bounded and closed.

Proof

From Theorem 3.5, for any $u\in U$, Sol(u) is nonempty and bounded. Now we show the closedness. For any $u\in U$, let $x_{n}\in Sol(u)$ such that $x_{n}\rightarrow x_{0}$ for some $x_{0}\in K$. Then for each $n\ge 1$ and some $x_{n}^{*}\in F(x_{n})$ we have

$$\begin{aligned} \langle x_{n}^*-B(u),f(x_{n},y)\rangle +g(x_{n},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

For any given $x_{0}^{*}\in F(x_{0})$, since F is l.s.c. with respect to the weak$^*$ topology of $E^*$, there exists a sequence $x_{n}^{*}\in F(x_{n})$, without loss of generality, such that $x_{n}^{*} \rightharpoonup x_{0}^{*}$ in $E^*$. Therefore, since $f(\cdot ,y)$ is continuous and $g(\cdot ,y)$ is u.s.c. for all $y\in K$, we have that

$$\begin{aligned} \langle x_{0}^*-B(u),f(x_{0},y)\rangle +g(x_{0},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

This shows that $x_{0}\in Sol(u)$ and hence Sol(u) is closed. $\square$

Next, we give the existence result for optimal pairs to problem (4.2).

Theorem 4.2

Let K and U be nonempty closed and convex subsets of real reflexive Banach spaces E and V, respectively. Let W be a Banach space, $\Upsilon \in W$ and $f\in E^*$. Assume that:

• (i) f, g are the mappings satisfying the conditions as in Theorem 3.3;

• (ii) $F:K\rightrightarrows E^{*}$ is bounded, l.h.c. and stably (f, g, 0)-pseudomonotone with respect to the set $\mathcal {R}(B)$;

• (iii) the following condition holds: $(B'')$ There exists $n_{0}\in \mathbb {N}$ such that for any $u\in U$ and for every $x\in K\setminus B_{n_{0}}$, there exists some $y\in K$ with $\Vert y\Vert <\Vert x\Vert$ such that

  $$\begin{aligned} \sup _{x^{*}\in F(x)}\langle x^{*}-B(u),f(x,y)\rangle +g(x,y)< 0. \end{aligned}$$

• (iv) $\Gamma : E\rightarrow W,~B:V\rightarrow E^*$ are compact.

Then the optimal control problem (4.2) has a solution (u, x(u)).

Proof

It is clear that F is stably (f, g, 0)-quasimonotone with respect to the set $\mathcal {R}(B)$ if F is stably (f, g, 0)-pseudomonotone with respect to the set $\mathcal {R}(B)$. By applying Theorem 3.3 and 3.4, for every control $u\in U$ (4.1) has a solution. Let $\{(u_{n},x_{n})\}\subset U\times K$ be a minimizing sequence. That is,

$$\begin{aligned} \lim _{n\rightarrow \infty }H(u_{n},x_{n})=\inf \{H(u,x):u\in U,x\in Sol(u)\}, \end{aligned}$$

where $u_{n}\in U$ and $x_{n}\in Sol(u_{n})$. Consequently, for some $x_{n}^{*}\in F(x_{n})$ we have

$$\begin{aligned} \langle x_{n}^*-B(u_{n}),f(x_{n},y)\rangle +g(x_{n},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(4.3)

As n is large enough, we have

$$\begin{aligned} \epsilon \Vert u_{n}\Vert ^{2}\le \Vert \Sigma (x_{n})-\Upsilon \Vert ^{2}+\epsilon \Vert u_{n}\Vert ^{2}\le \lim _{n\rightarrow \infty }H(u_{n},x_{n})+1, \end{aligned}$$

hence the sequence $\{u_{n}\}$ is bounded in the Banach space V. Since the space V is reflexive, there is a subsequence of $\{u_{n}\}$, denoted by $\{u_{n}\}$ again, such that $u_{n}\rightharpoonup \overline{u}$ for some $\overline{u}\in V$. Since U is closed and convex, from Theorem 1.33 of [25], we deduce that U is weakly closed, and hence $\overline{u}\in U$.

Next, we choose $\{x_{n}\}$ to be a subsequence of solutions of (4.1) that corresponds to the subsequence of controls $\{u_{n}\}$. We can show that $\{x_{n}\}$ remains bounded. In fact, if $\{x_{n}\}$ is unbounded, then there exist subsequence of $\{x_{n}\}$, denoted by $\{x_{n}\}$ again, and $x_{n}^{*}\in F(x_{0})$ such that $\Vert x_{n}\Vert >n_{0}$ and for any $u\in U$ we have

$$\begin{aligned} \langle x_{n}^{*}-B(u_{n}),f(x_{n},y)\rangle +g(x_{n},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(4.4)

Since $\Vert x_{0}\Vert >n_{0}$, it follows from condition $(B'')$ that, there exists $y_{0}\in K$ with $\Vert y_{n}\Vert <\Vert x_{n}\Vert$ such that

$$\begin{aligned} \sup _{x_{n}^{**}\in F(x_{n})}\langle x_{n}^{**}-B(u_{n}),f(x_{n},y_{n})\rangle +g(x_{n},y_{n})<0, \end{aligned}$$

which is a contradiction with (4.4).

Let $\{x_{n}\}$ be a subsequence converging weakly to $\overline{x}$ for some $\overline{x}\in K$. We will show that $\overline{x}\in Sol(\overline{u})$.

It follows from (4.3) that

$$\begin{aligned} \langle x_{n}^*-B(u_{n}),f(x_{n},y)\rangle +g(x_{n},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(4.5)

Since F is stably (f, g, 0)-pseudomonotone with respect to the set $\mathcal {R}(B)$ and combining (4.5), we have

$$\begin{aligned} \inf _{y^{*}\in F(y)}\langle y^{*}-B(u_{n}),f(x_{n},y)\rangle +g(x_{n},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

Letting $n\rightarrow \infty$ we obtain

$$\begin{aligned} \inf _{y^{*}\in F(y)}\langle y^{*}-B(\overline{u}),f(\overline{x},y)\rangle +g(\overline{x},y)\ge 0,\qquad \forall y\in K. \end{aligned}$$

(4.6)

Let $\overline{y}\in K$ and define

$$\begin{aligned} z_{n}=\frac{1}{n}\overline{y}+\left( 1-\frac{1}{n}\right) \overline{x},\qquad n\ge 1. \end{aligned}$$

Then $z_{n}\in K$ for all $n\ge 1$ and $z_{n}\rightarrow \overline{x}$ as $n\rightarrow \infty$. For any given $\overline{x}^{*}\in F(\overline{x})$, since F is l.h.c., there exists a sequence $\{z_{n}^{*}\}$ in $F(z_{n})$ such that $z_{n}^{*}\rightharpoonup \overline{x}^{*}$. From the assumptions and (4.6), we have that

$$\begin{aligned} 0\le & {} \langle z_{n}^{*}-B(\overline{u}),f(\overline{x},z_{n})\rangle +g(\overline{x},z_{n})\\= & {} \left\langle z_{n}^{*}-B(\overline{u}),f\left( \overline{x},\frac{1}{n}\overline{y}+\left( 1-\frac{1}{n}\right) \overline{x}\right) \right\rangle +g\left( \overline{x},\frac{1}{n}\overline{y}+\left( 1-\frac{1}{n}\right) \overline{x}\right) \\\le & {} \frac{1}{n}\left[ \langle z_{n}^{*}-B(\overline{u}),f(\overline{x},\overline{y})\rangle +g(\overline{x},\overline{y})\right] . \end{aligned}$$

Multiplying the last inequality by n and letting $n\rightarrow \infty$, we obtain that

$$\begin{aligned} \langle \overline{x}^{*}-B(\overline{u}),f(\overline{x},\overline{y})\rangle +g(\overline{x},\overline{y})\ge 0,\qquad \forall \overline{y}\in K. \end{aligned}$$

Therefore, $\overline{x}\in Sol(\overline{u})$.

Finally, we have

$$\begin{aligned} H(\overline{u},\overline{x})= & {} \Vert \Sigma (\overline{x})-\Upsilon \Vert ^{2}+\epsilon \Vert \overline{u}\Vert ^{2}\\\le & {} \liminf _{n\rightarrow \infty }\Vert \Sigma (x_{n})-\Upsilon \Vert ^{2}+\liminf _{n\rightarrow \infty }\epsilon \Vert u_{n}\Vert ^{2}\\\le & {} \liminf _{n\rightarrow \infty }H(u_{n},x_{n})\\= & {} \lim _{n\rightarrow \infty }H(u_{n},x_{n})\\= & {} \inf \{H(u,x):u\in U,x\in Sol(u)\}, \end{aligned}$$

which shows that $(\overline{u},\overline{x})$ is an optimal pair to problem (4.2). This completes the proof. $\square$

5 Example of Hemivairational Inequalities

At first, we consider two special cases of problem (2.1).

Case (a) Let $K=X, ~f(x,y)=y-x,~g(x,y)=\langle Ax,y-x\rangle ,~h(x,y)=\langle f,y-x\rangle ,~Lx=x'$. From [22] it is easy to verify that L satisfies the conditions of F. Then in this situation problem (2.1) turns to be the following problem:

$$\begin{aligned} x'+Ax+f=0, \end{aligned}$$

(5.1)

which is an evolution equation. As seen in Sect. 3 of [10], the results in [11, 12, 22] are a special case of our results under some suitable conditions.

Case (b) Let $K=X, ~f(x,y)=y-x,~g(x,y)=\langle Ax,y-x\rangle ,~h(x,y)=\langle Lx,y-x\rangle$, where $Lx=x'$. From [22] it is easy to verify that L satisfies the conditions of h. Then in this situation problem (2.1) turns to be the following problem:

$$\begin{aligned} x'+Ax+Fx\ni 0, \end{aligned}$$

(5.2)

which is a differential inclusion. Therefore, our main results can be applied to solve the inclusion problem (5.2).

Next, we consider the special case of hemivairational inequalities.

Let K be a nonempty subset of E. Let us recall the notations about the Clarke’s generalized directional derivative and generalized gradient for a locally Lipschitz function $\varphi :K\rightarrow \mathbb {R}$ (one can see [13, 16]). We denote by $\varphi ^{0}(x;y)$ the Clarke’s generalized directional derivative of $\varphi$ at the point $x\in K$ in the direction $y\in E$, that is

$$\begin{aligned} \varphi ^{0}(x;y):=\limsup _{\lambda \rightarrow 0^{+},\zeta \rightarrow x}\frac{\varphi (\zeta +\lambda y)-\varphi (\zeta )}{\lambda }. \end{aligned}$$

Recall also that the Clarke’s subdifferential or generalized gradient of $\varphi$ at $x\in K$, denoted by $\partial \varphi (x)$, is a subset of $E^{*}$ given by

$$\begin{aligned} \partial \varphi (x):=\{x^{*}\in E^{*}: \varphi ^{0}(x;y)\ge \langle x^{*},y\rangle _{E},~\forall y\in E\}.\nonumber \end{aligned}$$

Let $\Omega$ be a bounded open set in $\mathbb {R}^{N}~(N\ge 1)$ and $\partial \Omega$ be its boundary. Let $\Delta$ be $\Omega$ or $\partial \Omega$, $T:E\rightarrow L^{p}(\Delta ;\mathbb {R}^k)$ a linear compact operator, where $k\ge 1,~1<p<\infty$. Let $\widehat{x}:=Tx$. Let $j^{\circ }(\zeta ,\eta ;\theta )$ be the Clarke’s generalized directional derivative of a locally Lipschitz mapping $j(\zeta ,\cdot ): \mathbb {R}^{k}\rightarrow \mathbb {R}$ at the point $\eta \in \mathbb {R}^{k}$ with respect to direction $\theta \in \mathbb {R}^{k}$, where $\zeta \in \Delta$.

Let $j:\Delta \times \mathbb {R}^k\rightarrow \mathbb {R}$ be a function and the mapping

$$\begin{aligned} j(\cdot ,\eta ):\Delta \rightarrow \mathbb {R}~\text {is measurable, for every}\,\,\eta \in \mathbb {R}^k. \end{aligned}$$

(5.3)

We assume that at least one of the following conditions holds: either there exists $l\in L^{q}(\Delta ;\mathbb {R})~(q>1)$ such that

$$\begin{aligned} |j(\zeta ,\eta _{1})-j(\zeta ,\eta _{2})|\le l(\zeta )|\eta _{1}-\eta _{2}|,\qquad \forall \zeta \in \Delta ,~\forall \eta _{1}, \eta _{2}\in \mathbb {R}^k, \end{aligned}$$

(5.4)

or

$$\begin{aligned} \mathrm{the} \,\, \mathrm{mapping} \, j(\zeta ,\cdot )\,\,\mathrm{is}\,\, \mathrm{locally}\,\, \mathrm{Lipschitz },\qquad \forall \zeta \in \Delta , \end{aligned}$$

(5.5)

and there exist $C>0,~p>1(\frac{1}{p}+\frac{1}{q}=1)$ such that

$$\begin{aligned} |\omega |\le C(1+|\eta |^{p-1}),~\forall \zeta \in \Delta ,~\forall \omega \in \partial j(\zeta ,\eta ). \end{aligned}$$

(5.6)

Lemma 5.1

[13, Theorem 2.7.5] If

$$\begin{aligned} J(\phi )=\int _{\Delta }j(\theta ,\phi (\theta ))d\theta , \end{aligned}$$

(5.7)

and j satisfies the conditions (5.3) and (5.4) or (5.3) and (5.5)–(5.6), then J is Lipschitz on bounded subsets of $L^{p}(\Delta ;\mathbb {R}^k)$, and one has

$$\begin{aligned} \partial J(\phi ) \subset \int _{\Delta }\partial j(\theta ,\phi (\theta ))d\theta . \end{aligned}$$

Furthermore, if j is regular at $(x,\phi (x))$ then J is regular at $\phi$ and equality holds.

Let $J:L^{p}(\Delta ;\mathbb {R}^k)\rightarrow \mathbb {R}$ be an arbitrary locally Lipschitz functional. For each $x,y\in E$ there exists $z_{x,y}\in \partial J(\widehat{x})$ such that

$$\begin{aligned} J^{0}(\widehat{x};\widehat{y})=\langle z_{x,y},\widehat{y}\rangle _{L^{p}}=\max \{\langle \omega ,\widehat{y}\rangle _{L^{p}}:\omega \in \partial J(\widehat{x})\}. \end{aligned}$$

Denoting by $T^* :L^{q}(\Delta ;\mathbb {R}^k)\rightarrow E^*$ the adjoint operator of T, we define the subset Z(J, T) of $E^*$ as follows:

$$\begin{aligned} Z(J,T)=\{-z_{x,y}^{*}:x,y\in K, z_{x,y}^{*}=T^{*}z_{x,y}\}. \end{aligned}$$

From Remark 2.2 of [34] we have

$$\begin{aligned} J^{0}(\widehat{x};\widehat{y}-\widehat{x})=\langle z_{x,y}^{*},y-x\rangle _{E}. \end{aligned}$$

Consider the following hemivariational inequalities involving a multi-valued mapping:

$$\begin{aligned} \left\{ \begin{array}{llll} \text {Find}~x\in \mathcal {D}(g) ~\text {and}~ x^{*}\in F(x) ~\text {such~that} \\ \langle x^{*},y-x\rangle +g(x,y)+\int _{\Delta }j^{\circ }(\tau ,\widehat{x}(\tau );\widehat{y}(\tau )-\widehat{x}(\tau ))d\tau \ge 0,\\ \forall y\in K. \end{array}\right. \end{aligned}$$

(5.8)

For more details, we refer to [31, 33, 34].

Take $f(x,y)=y-x,h(y,x)=-J^{\circ }(\widehat{x};\widehat{y}-\widehat{x})$. From [33], we can assume that F is stably $g(\cdot ,\cdot )$-quasimonotone with respect to Z(J, T). By applying our main result in this paper, we can show that the following problem:

$$\begin{aligned} \left\{ \begin{array}{llll} \text {Find}~x\in \mathcal {D}(g) ~\text {and}~ x^{*}\in F(x) ~\text {such~that} \\ \langle x^{*},y-x\rangle +g(x,y)+J^{0}(\widehat{x};\widehat{y}-\widehat{x})\ge 0,\\ \forall y\in K, \end{array}\right. \end{aligned}$$

has at least one solution. Furthermore, if J is given by (5.7), then by Lemma 5.1, problem (5.8) has at least one solution.