Distension of the renal pelvis in kidney stone patients: sensory and biomechanical responses

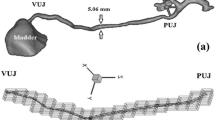
Abstract

The pathogenesis of symptoms in urolithiasis is poorly understood. Traditionally increased endoluminal pressure is considered the main mechanism causing pain in the upper urinary tract but clinical data are sparse. The aim of the present study was to develop a new model related to mechanosensation in order to describe the geometric and mechanical properties of the renal pelvis in patients with kidney stone disease. Pressure measurement in the renal pelvis was done during CT-pyelography in 15 patients who underwent percutaneus nephrolithotomy. The sensory intensity was recorded at the thresholds for first sensation and for pain. 3D deformation and strain were calculated in five patients. The deformation of pelvis during distension was not uniform due to the complex geometry. The pelvis deformed to 113 ± 6% and 115 ± 11% in the longitudinal and circumferential directions, respectively. Endoluminal pressure in the renal pelvis corresponded positively to the sensory ratings but the referred pain area was diffuse located and varied in size. The present study provides a method for describing the mechanosensory properties and 3D deformation of the complex renal pelvis geometry. Although there was a relation between pressure and pain score, the non-homogenous spatial strain distribution suggests that the 3D biomechanical properties of the renal pelvis are not reflected by simple estimates of tension based on pressure and volume.

Appendix

Strain calculation

The membrane strain in every triangle plane can be defined with the displacement of every point on the surface and the coordinates of each three points that define a triangle determine a plane. The coordinates of these points in that plane at VAS = 1 are denoted as x _i and y _i (i = 1, 2, 3, are three points of the plane). The displacement in the local system of the points at VAS = 1 to their position at VAS = 5 are denoted as u _i , v _i and w _i (u, v and w are, respectively, the displacement in x, y, and z directions, Fig. 6).

Fig. 6

Schematic diagram of the global coordinate system XYZ and the local coordinate system xyz on one triangle face with nodes 1, 2, and 3 at VAS = 1. The displacement at the local coordinate system on the node 3 (u3, v3 and w3) is illustrated as an example. All strains were calculated based on the local coordinate system. For details about the transformation between the global coordinate system and the local coordinate system, see [21]

The displacements are assumed to be in a displacement field that is a linear function of position in the plane of the triangle. For example

$$ u_{i} = a_{1} + a_{2} x_{i} + a_{3} y_{i} \,\left( {i = 1,2,3} \right) $$

(A1)

This equation with known displacement and the position of three markers substituted for u _i , x _i and y _i provides a set of three equations for the three coefficients, a ₁, a ₂ and a ₃.

Similarly, the data provide the information required to determine the coefficients in the following equations

$$ \begin{aligned} v_{i} & = a_{4} + a_{5} x_{i} + a_{6} y_{i} \\ w_{i} & = a_{7} + a_{8} x_{i} + a_{9} y_{i} \\ \end{aligned} $$

(A2)

where $a_{4} \cdots a_{9}$ are coefficients that could be defined with known displacement (v _i and w _i ) between surface of VAS = 1 and VAS = 5 and coordinates (x _i and y _i ) on surface of VAS = 1

The components of the Green strain in the plane are defined by the following equations

$$ \begin{aligned} E_{xx} & = \frac{\partial u}{\partial x} + 0.5\left[ {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial x}} \right)^{2} + \left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] \\ E_{yy} & = \frac{\partial v}{\partial y} + 0.5\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial w}{\partial y}} \right)^{2} } \right] \\ E_{xy} & = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + 0.5\left( {\frac{\partial u}{\partial x}\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\frac{\partial v}{\partial y} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right) \\ \end{aligned} $$

(A3)

with the known coefficients $a_{1} \cdots a_{9}$ and substituting Eqs. A1 and A2 into A3, the strain on the triangle plane can thus be obtained.

The principal strain and the corresponding principal orientation are calculated from:

$$ \left[ {\begin{array}{*{20}c} {E_{11} } & 0 \\ 0 & {E_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {l_{1} } & {l_{2} } \\ {m_{1} } & {m_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {E_{xx} } & {E_{xy} } \\ {E_{xy} } & {E_{yy} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {l_{1} } & {l_{2} } \\ {m_{1} } & {m_{2} } \\ \end{array} } \right]^{T} $$

(A4)

where E ₁₁, E ₂₂ are principal strains and {l ₁, m ₁}^T and {l ₂, m ₂}^T are corresponding principal directions in the local coordinate system. There is no shear strain in the principal directions. T means transpose of the matrix or vectors.

The equivalent strain is defined as:

$$ e = \sqrt {\frac{2}{9}\left( {\left( {E_{xx} - E_{yy} } \right)^{2} + E_{xx}^{2} + E_{yy}^{2} + 6E_{xy}^{2} } \right)} $$

(A5)