Biochemical Property Based Positional Matrix: A New Approach Towards Genome Sequence Comparison

Abstract

The growth of the genome sequence has become one of the emerging areas in the study of bioinformatics. It has led to an excessive demand for researchers to develop advanced methodologies for evolutionary relationships among species. The alignment-free methods have been proved to be more efficient and appropriate related to time and space than existing alignment-based methods for sequence analysis. In this study, a new alignment-free genome sequence comparison technique is proposed based on the biochemical properties of nucleotides. Each genome sequence can be distributed in four parameters to represent a 21-dimensional numerical descriptor using the Positional Matrix. To substantiate the proposed method, phylogenetic trees are constructed on the viral and mammalian datasets by applying the UPGMA/NJ clustering method. Further, the results of this method are compared with the results of the Feature Frequency Profiles method, the Positional Correlation Natural Vector method, the Graph-theoretic method, the Multiple Encoding Vector method, and the Fuzzy Integral Similarity method. In most cases, it is found that the present method produces more accurate results than the prior methods. Also, in the present method, the execution time for computation is comparatively small.

Introduction

The analysis of genome sequence comparison has become one of the key aspects of bioinformatics, where the size of the genomic databases is rapidly expanding due to species evolution. Consequently, the objective of the researchers is to create new techniques that require less computation time for comparative study of these genome sequences. Traditionally, alignment-based methods (Altschul et al. 1997; Thompson et al. 1994; Just 2001; Phillips et al. 2000; Bawono et al. 2017) are used to compute evolutionary relationships among various species. However, the limitations (Zielezinski et al. 2017; Katoh and Standley 2013) of these methods make them unreliable for datasets with varied lengths in less computational time (Just 2001). Therefore, to overcome the drawbacks (Bernard et al. 2019; Bhattacharya 2020; Zielezinski et al. 2019) of the alignment-based methods, it is felt better to choose the alignment-free techniques. These techniques aid in identifying appropriate sequence clustering, obtaining the phylogeny of diverse species, finding homologous sequences, and predicting the evolutionary relationships among various sequences. The main motivation to choose alignment-free method is to compute large-scale datasets of varied length with less time complexity and compare the proposed method with the existing similar phylogenetic methodologies.

The alignment-free techniques can be broadly classified into two categories: word-based methods (Vinga and Almeida 2003) and information-theory-based methods (Vinga 2014). However, there are several other alignment-free methods, which cannot be classified into either of the above categories. These methods include matching words [minimal absent word method (Pinho et al. 2009; Yang et al. 2013), common substring approach (Haubold et al. 2005; Ulitsky et al. 2006)] as well as iterated maps (Almeida 2014). Various alignment-free approaches are also achieved based on numerous mathematical concepts (Nandy et al. 2006). One of the alignment-free methods is the graphical approach where the two-dimensional (Wu et al. 2003, 2010; Randić et al. 2004; Liao et al. 2006; Wen and Zhang 2009; Das et al. 2015), three-dimensional (Liao and Wang 2004; Wang and Zhang 2006; Qi et al. 2007; Zhang et al. 2007; Randić et al. 2000; Aram and Iranmanesh 2012; Wąż and Bielińska-Wąż 2014) and four-dimensional (Randić and Balaban 2003; Chi and Ding 2005; Tan et al. 2015) representation methods have been proved relevant for sequence comparison. Moreover, the di-nucleotide and tri-nucleotide representations were more convenient than mono-nucleotide representations. In (Qi et al. 2012), a non-graphical method identifies adjacent and non-adjacent XY pairs using the frequency of the di-nucleotide. Here, X and Y are separated by a random number of nucleotides. Furthermore, the graphical descriptors can be obtained in two ways for sequential analysis: one from data points (Liao et al. 2013) and the other in the form of a matrix (Randić 2000). Next, based on the coordinates of the graph, a two-dimensional tri-nucleotide is represented as a three-dimensional graph coordinate (Das et al. 2018a). The third dimension coordinate is achieved as the product of ‘x’ and ‘y’ coordinates. In this case, the species are compared using four descriptors: mean, standard deviation, highest Eigen value in M/M matrix, and highest Eigen value in J/J matrix. It is found that the result produced by the J/J matrix provides better results among all other descriptors. All these methods using the graphical descriptors are more or less the same, varying only in the choice of usage. Now, various attempts have been made by the authors on Graph-theoretic approaches (Qi et al. 2011; Mathur and Adlakha 2016). The method described in (Das et al. 2020a) is quite prominent where only a complete bipartite graph defines a codons based genome sequence. Accordingly, a vector descriptor is formed using the weights of the edges of the graph. Another, new form of DNA sequence comparison is mentioned in (Mo et al. 2018). Here, a graphical representation of the DNA sequence is acquired using the Fermat spiral curve for global information. Then, to achieve the local information, each point in the curve is attached with the associated mass based on the relationship of the adjacent nucleotides. Then, a numerical descriptor is obtained by uniting the global and local information. Next, is the probabilistic approach, where a vector is formed using the concept of probability. In (Das et al. 2018b), by computing the frequency of substring k, where k = 3, the probability vector and the composition vector are produced. Subsequently, the distance matrix for genome sequence analysis is computed using the information-based similarity index. The Feature Frequency Profile (FFP) (Sims et al. 2009) method is also an example of the k-mer method. Moreover, the Markov Chain idea is used in the Fuzzy Integral Similarity (FIS) approach (Saw et al. 2019) to determine the degree of similarity among DNA sequences. Another, method is the Improved Complete Composition Vector (ICCV) method (Lu et al. 2008) which states that the existing string composition-based methods contain two problems, one is related to the Markov model assumption and the other one is associated with the denominator of the frequency normalization equation. Therefore, to overcome the aforesaid problem, ICCV method is proposed. It assumes a uniform and independent model to estimate sequence information contributing to the selection for sequence comparison. Also, the phylogenetic analysis using both simulated and experimental datasets demonstrate that this method is more robust as compared to existing alignment-based methods. Further, it optimizes the Composition Vector (CV) method (Wu et al. 2006) and the Complete Composition Vector (CCV) method (Gao and Qi 2007). Plenty of research work (Yang and Wang 2013; Li et al. 2014; Wen et al. 2014) has already been done based on this k-mer or word frequency method. Furthermore, many numerical vector descriptors are formed for the genome sequence comparison. (In Deng et al. 2011), a new vector representation is created based on three parameters; viz. frequency, mean values, and normalized central moments for all the DNA nucleotides to perform the phylogenetic analysis. Again, a Positional Correlation Natural Vector (PCNV) method (He et al. 2020) represents each DNA sequence by its positional distribution, correlation vector, co-variances, and variances among the nucleotide bases for comparative study. The Multiple Encoding Vector (MEV) method (Li et al. 2017) uses the three categories of biochemical properties of DNA (Purine [A, G] → R, Pyrimidine [C, T] → Y); (Amino [A, C] → M, Keto [G, T] → K); and (Strong hydrogen bond [C, G] → S, Weak hydrogen bond [A, T] → W) for sequence comparison. Here, the frequency, average, and variation of the position for each character representation are calculated. Another work is also performed in (Das et al. 2020b) based on the biochemical properties of DNA. An Accumulated Natural Vector (ANV) method (Dong et al. 2019) consists of the frequency, the positional mean, the variances, and the co-variances of each nucleotide, as its vector descriptor for phylogenetic comparison.

In our work, a numerical vector descriptor is proposed based on the biochemical properties of DNA and the Positional Matrix. It consists of the frequency and the positional average of each character with the mathematical concept of co-variances and variances as the four parameters. These parameters constitute a 21-dimensional numerical descriptor to represent a single genome sequence. The UPGMA/NJ method is used for the phylogenetic tree construction in MEGA11 (Tamura et al. 2021). Further, the proposed methodology is verified with the complete coding sequences of the beta-globin gene for 11 species, the complete coding sequence datasets of 38 species of Influenza A viruses, the whole-genome sequences of 41 mammalian mitochondrial genes, the complete genome sequences of 81 species of Hepatitis C viruses, the whole-genome sequences of 59 Ebola viruses, whole genome sequences of 21 Influenza A viruses and the complete genome sequences of 942 species of the SARS-CoV-2 based on different geographical location. Accordingly, our results are compared with the results of different former methods used in sequence comparison. It is found that, our approach efficiently generates the suitable phylogeny of evolutionary descent to distinguish various species from their common ancestors and is well suited for the whole genome sequence comparison.

Methodology

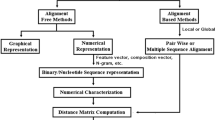
In this study, various genome sequence datasets are used to create a new 21-dimensional numerical descriptor based on the biochemical properties of DNA and the Positional Matrix. This vector descriptor is formed using the four parameters that include frequency, positional average, co-variances, and variances. Finally, a distance matrix is obtained from these parameters to construct a phylogenetic tree using the UPGMA/NJ clustering method. The steps to demonstrate the proposed method are as follows.

Group-Wise Representation Based on Biochemical Properties of Nucleotide

In DNA, the four nucleotides can be classified into three paired categories which constitutes two groups of nucleotides having specific denotations. Category I and II fall under chemical structures of DNA, and Category III falls under the physical properties of DNA. This whole concept is summarized in Table 1. Based on the Category I in Table 1, a genome sequence (S) of length ‘N’ can be converted into 2-character sequence, namely RY. Now, to construct the RY sequence, all 'A' and 'G' nucleotides in ‘S’ are replaced by 'R' and all 'C' and 'T' nucleotides in ‘S’ are replaced by 'Y'. Similarly, based on the Category II and the Category III, the MK and the SW sequences are formed as 2-character sequences respectively. Table 2 shows the following representation with an example, where S = “ACTGGCAAT”.

Table 1 Three paired categories of nucleotides

Table 2 Group-wise representation of sequences

Positional Matrix

A numerical matrix is created using ${\rho }_{{\lambda }_{t}}$ from newly obtained RY, MK, and SW sequences. The total number of each characters in these sequences is symbolized by ${\eta }_{\lambda }$ where λ $\in$ {R, Y, M, K, S, W}. Here, ${\rho }_{{\lambda }_{t}}$ is the position of the nucleotides λ at the $t$th occurrence where $t$ = 1, 2, 3…${\eta }_{\lambda }$. Now, clearly ${\rho }_{{\lambda }_{t-1}}< {\rho }_{{\lambda }_{t}}$ and ‘$t$’ lies between $2\le t < {\upeta }_{\lambda }$. The values ${{V}}_{\lambda }(i)$ ($i$ = 1, 2, 3 … N) in the matrix for each row is generated from the following formula (1).

$${{V}}_{\lambda }\left(i\right)=\left\{\begin{array}{c} 0\,; i< {\rho }_{{\lambda }_{t}}\, ; t=1\\ \frac{{\rho }_{{\lambda }_{t-1}}}{{\rho }_{{\lambda }_{t}} - {\rho }_{{\lambda }_{t-1}}}\, ; {\rho }_{{\lambda }_{t-1}} \le i < {\rho }_{{\lambda }_{t}}/, ;t=2, 3, 4\dots {\eta }_{\lambda }\\ \frac{{\rho }_{{\lambda }_{{\eta }_{\lambda }}}}{\left(N+1\right) - {\rho }_{{\lambda }_{{\eta }_{\lambda }}}} \,; {\rho }_{{\lambda }_{{\eta }_{\lambda }}} \le i \le N\, ;t={\eta }_{\lambda } . . . \left(N-2\right), \left(N-1\right), N\end{array}\right.$$

(1)

Therefore, the row-wise arrangement of the positions for λ is:

$$\underbrace {0,0,0, \ldots ,0}_{i{\text{ < }}{\rho _{{\lambda _1}}}}\underbrace {\frac{{{\rho _{{\lambda _1}}}}}{{{\rho _{{\lambda _2}}} - {\rho _{{\lambda _1}}}}},\frac{{{\rho _{{\lambda _1}}}}}{{{\rho _{{\lambda _2}}} - {\rho _{{\lambda _1}}}}},\frac{{{\rho _{{\lambda _1}}}}}{{{\rho _{{\lambda _2}}} - {\rho _{{\lambda _1}}}}},...,\frac{{{\rho _{{\lambda _1}}}}}{{{\rho _{{\lambda _2}}} - {\rho _{{\lambda _1}}}}}}_{{\rho _{{\lambda _2}}} - {\rho _{{\lambda _1}}}}\underbrace {\frac{{{\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}}{{{\rho _{{\lambda _{{\eta _\lambda }}}}} - {\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}},\frac{{{\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}}{{{\rho _{{\lambda _{{\eta _\lambda }}}}} - {\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}},\frac{{{\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}}{{{\rho _{{\lambda _{{\eta _\lambda }}}}} - {\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}},...,\frac{{{\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}}{{{\rho _{{\lambda _{{\eta _\lambda }}}}} - {\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}}}_{{\rho _{{\lambda _{{\eta _\lambda }}}}} - {\rho _{{\lambda _{{\eta _\lambda } - 1}}}}}\underbrace {\frac{{{\rho _{{\lambda _{{\eta _\lambda }}}}}}}{{\left( {N + 1} \right) - {\rho _{{\lambda _{{\eta _\lambda }}}}}}},\frac{{{\rho _{{\lambda _{{\eta _\lambda }}}}}}}{{\left( {N + 1} \right) - {\rho _{{\lambda _{{\eta _\lambda }}}}}}},\frac{{{\rho _{{\lambda _{{\eta _\lambda }}}}}}}{{\left( {N + 1} \right) - {\rho _{{\lambda _{{\eta _\lambda }}}}}}},...,\frac{{{\rho _{{\lambda _{{\eta _\lambda }}}}}}}{{\left( {N + 1} \right) - {\rho _{{\lambda _{{\eta _\lambda }}}}}}}}_{\left( {N + 1} \right) - {\rho _{{\lambda _{{\eta _\lambda }}}}}}$$

The above definition of Positional Matrix is illustrated with an example of the RY sequence which is “RYYRRYRRY” where N = 9; λ = Y; ${\rho }_{{Y}_{t}}$ $\in$ {2, 3, 6, 9}; ${\upeta }_{Y}$ = 4; ${\rho }_{{Y}_{1}}$= 2, ${\rho }_{{Y}_{2}}$= 3, ${\rho }_{{Y}_{3}}$= 6, and ${\rho }_{{Y}_{4}}$= 9.

If; $i< {\rho }_{{Y}_{1}}$; in other words $i$ = 1; then ${{V}}_{Y}(1)$ = 0.

If; ${\rho }_{{Y}_{1}} \le i < {\rho }_{{Y}_{2}}$; in other words $i$ = 2; then ${{V}}_{Y}(2)$ = $\frac{{\rho }_{{Y}_{1}}}{{\rho }_{{Y}_{2}}- {\rho }_{{Y}_{1}}}$ = $\frac{2}{3-2}$  = $\frac{2}{1}$.

If; ${\rho }_{{Y}_{2}} \le i < {\rho }_{{Y}_{3}}$; in other words $i$ = 3, 4, 5; then ${{V}}_{Y}(3)$ = ${{V}}_{Y}(4)$ = ${{V}}_{Y}(5)$ = $\frac{{\rho }_{{Y}_{2}}}{{\rho }_{{Y}_{3}}- {\rho }_{{Y}_{2}}}$ = $\frac{3}{6-3}$  = $\frac{3}{3}$.

If; ${\rho }_{{Y}_{3}} \le i < {\rho }_{{Y}_{4}}$; in other words $i$ = 6, 7, 8; then ${{V}}_{Y}(6)$ = ${{V}}_{Y}(7)$ = ${{V}}_{Y}(8)$ = $\frac{{\rho }_{{Y}_{3}}}{{\rho }_{{Y}_{4}}- {\rho }_{{Y}_{3}}}$ = $\frac{6}{9-3}$  = $\frac{6}{3}$.

If; ${\rho }_{{Y}_{4}} \le i \le N$; in other words $i$ = 9; then ${{V}}_{Y}(9)$ = $\frac{{\rho }_{{Y}_{4}}}{\left(N+1\right) - {\rho }_{{Y}_{4}}}$ = $\frac{9}{(9+1)-9}$  = 9.

Likewise, all the values of λ in the Positional Matrix can be obtained by using the formula explained in (1) for ${{V}}_{R}(i)$, ${{V}}_{K}(i)$, ${{V}}_{M}(i)$, ${{V}}_{S}(i)$, ${{V}}_{W}(i)$ as demonstrated in Table 3.

Representation of 21-Dimensional Numerical Descriptor

The newly obtained sequences and the Positional Matrix are used to compute the four parameters for descriptor representation. The first two parameters include the Frequency and the Positional Average of each element of λ. These two parameters represent six components individually summing up to 12 vectors. The third parameter is the co-variances of sequences, which adds up to three more components to the vector. Finally, the fourth parameter is the variances of each element of λ constituting the last six components of the numerical vector. Therefore, after accumulating all the components of the four parameters, 21 numerical values for the descriptor representation is obtained for a single genome sequence. All the parameters are illustrated one by one as follows:

• I. Frequency

  Let’s consider the previous example which is referred in Table 2 for the purpose of illustration. The frequency of R(${\eta }_{R}$) = 5, Y(${\eta }_{Y}$) = 4, M(${\eta }_{M}$) = 5, K(${\eta }_{K}$) = 4, S(${\eta }_{S}$) = 4, and W(${\eta }_{W}$) = 5. These are the first six components for the 21-dimensional numerical vector.

• II. Positional Average

  In Table 2, each new sequence is divided into two groups by indexing their positions. The Positional Average (${\tau }_{\lambda }$) is defined in formula (2), where ${\rho }_{{\lambda }_{t}}$ denotes the position of the elements of λ at the $t$th occurrence and ${\eta }_{\lambda }$ refers to the total number of elements present in λ.

  $${\tau }_{\lambda }= \frac{\sum_{t=1}^{{\upeta }_{\lambda }}{\rho }_{{\lambda }_{t}}}{{\upeta }_{\lambda }}$$

  (2)

  According to the earlier example: ${\tau }_{R}$ = $\frac{\sum_{t=1}^{{\upeta }_{R}}{\rho }_{{R}_{t}}}{{\upeta }_{R}}$ = $\frac{1+4+5+7+8}{5}$ = $\frac{25}{5}$  = 5.

  Similarly, ${\tau }_{Y}$ = $\frac{\sum_{t=1}^{{\upeta }_{Y}}{\rho }_{{Y}_{t}}}{{\upeta }_{Y}}$ = $\frac{2+3+6+9}{4}$ = $\frac{20}{4}$  = 5.

  Other values of λ computed for M, K, S, and W are as follows:

  ${\tau }_{M}$ = $\frac{\sum_{t=1}^{{\upeta }_{M}}{\rho }_{{M}_{t}}}{{\upeta }_{M}}$ = $\frac{1+2+6+7+8}{5}$ = $\frac{24}{5}$  = 4.8; ${\tau }_{K}$ = $\frac{\sum_{t=1}^{{\upeta }_{K}}{\rho }_{{K}_{t}}}{{\upeta }_{K}}$ = $\frac{3+4+5+9}{4}$ = $\frac{21}{4}$  = 5.25.

  ${\tau }_{S}$ = $\frac{\sum_{t=1}^{{\upeta }_{S}}{\rho }_{{S}_{t}}}{{\upeta }_{S}}$ = $\frac{2+4+5+6}{4}$ = $\frac{17}{4}$  = 4.25; ${\tau }_{W}$ = $\frac{\sum_{t=1}^{{\upeta }_{W}}{\rho }_{{W}_{t}}}{{\upeta }_{W}}$ = $\frac{1+3+7+8+9}{5}$ = $\frac{28}{5}$  = 5.6

  Thus, the next six components for the 21-dimensional numerical vector are obtained.

• III. Co-variances

  Let’s assume there are two sets of elements, α $\in$ {${x}_{1}, {x}_{2}, {x}_{3}, . . . , {x}_{N}$} and β $\in$ {${y}_{1}, {y}_{2}, {y}_{3}, . . . , {y}_{N}$} where ‘${x}_{N}$’ and ‘${y}_{N}$’ denotes the last element of their individual sets. As both the sets are having equal number of elements therefore ‘$N$’ can be referred to the length of the sets. The total number of elements present in set ‘α’ and in set ‘β’ are represented as ‘${\eta }_{\alpha }$’ and ‘${\eta }_{\beta }$’ respectively. Then, the co-variance between α and β is determined by (3):

  $$cov\left( {\alpha ,\beta } \right) = \sum\limits_{i = 1}^N {\frac{{\left( {{V_\alpha }\left( i \right) - {{\bar V}_\alpha }} \right) \times \left( {{V_\beta }\left( i \right) - {{\bar V}_\beta }} \right)}}{{{\eta _\alpha } \times {\eta _\beta }}}}$$

  (3)

  where, $\bar{V_{\alpha}}$ = $\frac{1}{N}{\sum }_{i=1}^{N}{V}_{\alpha }(i)$ = $\frac{1}{N}\sum_{t=1}^{{\upeta }_{\alpha }}{\rho }_{{\alpha }_{t}}$ and $\bar{V_\beta}$ = $\frac{1}{N}{\sum }_{i=1}^{N}{V}_{\beta }(i)$  = $\frac{1}{N}\sum_{t=1}^{{\upeta }_{\beta }}{\rho }_{{\beta }_{t}}$

  With the help of the formula (3) and the Positional Matrix in Table 3, the co-variances between the two characters in three sequences can be evaluated. For the purpose of demonstration, let us consider the sequence RY mentioned in Table 2.

  The Frequency, the mean values and the row-wise arrangement of the positions for ‘R’ and ‘Y’ characters are:

  ${\eta }_{R}$ = 5; ${\eta }_{Y}$ = 4; R = $( \frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{4}{1}, \frac{5}{2}, \frac{5}{2}, \frac{7}{1}, \frac{8}{2}, \frac{8}{2} )$ and Y = $( 0, \frac{2}{1}, \frac{3}{3}, \frac{3}{3}, \frac{3}{3}, \frac{6}{3}, \frac{6}{3}, \frac{6}{3}, \frac{9}{1} )$

  $\bar{V_R}$ = $\frac{1}{N}{\sum }_{i=1}^{N}{V}_{R}(i)$ = $\frac{( \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{4}{1} + \frac{5}{2} + \frac{5}{2} + \frac{7}{1} + \frac{8}{2} + \frac{8}{2} )}{9}$ = $\frac{1+4+5+7+8}{9}$  = $\frac{25}{9}$

  $\bar{V_Y}$ = $\frac{1}{N}{\sum }_{i=1}^{N}{V}_{Y}(i)$ = $\frac{( 0 + \frac{2}{1} + \frac{3}{3} + \frac{3}{3} + \frac{3}{3} + \frac{6}{3} + \frac{6}{3} + \frac{6}{3} + \frac{9}{1} )}{9}$ = $\frac{2+3+6+9}{9}$  = $\frac{20}{9}$

  According to the definition (3), the co-variance between ‘R’ and ‘Y’ is:

  $$cov \left( R, Y \right)={\sum }_{i=1}^{N}\frac{\left( {V}_{R}(i)- \bar{V_R} \right)\times \left( {V}_{Y}(i)- \bar{V_Y} \right)}{{\eta }_{R}\times {\eta }_{Y}}=\frac{1}{{\eta }_{R}\times {\eta }_{Y}}{\sum }_{i=1}^{N}\left( {V}_{R}(i)- \bar{V_R} \right)\times \left( {V}_{Y}(i)- \bar{V_Y}\right)$$
  $$= \frac{1}{5 \times 4} [ \left( \frac{1}{3}- \frac{25}{9} \right)\left( 0- \frac{20}{9} \right)+\left( \frac{1}{3}- \frac{25}{9} \right)\left( \frac{2}{1}- \frac{20}{9} \right)+\left( \frac{1}{3}- \frac{25}{9} \right)\left( \frac{3}{3}- \frac{20}{9} \right)+ \left( \frac{4}{1}- \frac{25}{9} \right)\left( \frac{3}{3}- \frac{20}{9} \right)+\left( \frac{5}{2}- \frac{25}{9} \right)\left( \frac{3}{3}- \frac{20}{9} \right)+\left( \frac{5}{2}- \frac{25}{9} \right)\left( \frac{6}{3}- \frac{20}{9} \right)+ \left( \frac{7}{1}- \frac{25}{9} \right)\left( \frac{6}{3}- \frac{20}{9} \right)+\left( \frac{8}{2}- \frac{25}{9} \right)\left( \frac{6}{3}- \frac{20}{9} \right)+\left( \frac{8}{2}- \frac{25}{9} \right)\left( \frac{9}{1}- \frac{20}{9} \right) ]$$

  $= \frac{1}{5 \times 4}$ [ (− $\frac{22}{9}$)(− $\frac{20}{9}$) + (− $\frac{22}{9}$)(− $\frac{2}{9}$) + (− $\frac{22}{9}$)(− $\frac{11}{9}$) + ($\frac{11}{9}$)(− $\frac{11}{9}$) + (− $\frac{5}{18}$)(− $\frac{11}{9}$) + (− $\frac{5}{18}$)(− $\frac{2}{9}$) + ($\frac{38}{9}$)(− $\frac{2}{9}$) + ($\frac{11}{9}$)(− $\frac{2}{9}$) + ($\frac{11}{9}$)($\frac{61}{9}$)]

  $= \frac{1}{20}$ [ ($\frac{440}{81}$) + ($\frac{44}{81}$) + ($\frac{242}{81}$) + ($-\frac{121}{81}$) + ($\frac{55}{162}$) + ($\frac{10}{162}$) + ($-\frac{76}{81}$) + ($-\frac{22}{81}$) + ($\frac{671}{81}$)]

  $= \frac{1}{20}$ [ ($\frac{1178}{81}$) + ($\frac{65}{162}$)] = $\frac{1}{20} \times \frac{2421}{162}$ = $\frac{2421}{3240}$  = 0.75

  Therefore, in this way, $cov \left( M, K\right)$ and $cov \left( S, W\right)$, the co-variances of the MK and SW sequences can be computed respectively. In a similar manner, the other three elements of the 21-dimensional numerical vector are also achieved.

• IV. Variances

  The co-variance is calculated between two sets (α and β) having equal length of elements. But if there is only one set (α) or both the sets are same (α $=$ β), then the variance is calculated for that set. The variance is defined by the formula (4).

  $$v \left( \alpha , \alpha \right)=\sum\limits_{i=1}^{N}\frac{{\left( {V}_{\alpha }(i)- \bar{V_{\alpha}} \right)}^{2}}{{\eta }_{\alpha }^{2}}$$

  (4)

  $\mathrm{where}, \bar{V_{\alpha}}= \frac{1}{N}\sum\limits_{i=1}^{N}{V}_{\alpha }(i)= \frac{1}{N}\sum_{t=1}^{{\upeta }_{\alpha }}{\rho }_{{\alpha }_{t}}$

  Let’s take an example to explain the formula (4) for λ = ‘Y’. Then, the row-wise arrangement of the position for ‘Y’ is mentioned in Table 3 as $( 0, \frac{2}{1}, \frac{3}{3}, \frac{3}{3}, \frac{3}{3}, \frac{6}{3}, \frac{6}{3}, \frac{6}{3}, \frac{9}{1} )$; the mean value is $\bar{V_{Y}}$ = $\frac{1}{N}{\sum }_{i=1}^{N}{V}_{Y}(i)$ = $\frac{( 0 + \frac{2}{1} + \frac{3}{3} + \frac{3}{3} + \frac{3}{3} + \frac{6}{3} + \frac{6}{3} + \frac{6}{3} + \frac{9}{1} )}{9}$ = $\frac{2+3+6+9}{9}$ = $\frac{20}{9}$ and ${\eta }_{Y}$ = 4.

  Table 3 Positional matrix for ${{V}}_{\uplambda }$

  According to the definition (4), the variance of ‘Y’ is:

  $$v \left( Y, Y \right)=\sum\limits_{i=1}^{N}\frac{{\left( {V}_{Y}(i)- \bar{V_{Y}} \right)}^{2}}{{\eta }_{Y}^{2}}=\frac{1}{{\eta }_{Y}^{2}}\sum\limits_{i=1}^{N}{\left( {V}_{Y}(i)- \bar{V_{Y}} \right)}^{2}$$
  $$= \frac{1}{{4}^{2}} [ {\left( 0- \frac{20}{9} \right)}^{2}+{\left( \frac{2}{1}- \frac{20}{9} \right)}^{2}+{\left( \frac{3}{3}- \frac{20}{9} \right)}^{2}+ {\left( \frac{3}{3}- \frac{20}{9} \right)}^{2}+{\left( \frac{3}{3}- \frac{20}{9} \right)}^{2}+{\left( \frac{6}{3}- \frac{20}{9} \right)}^{2}+ {\left( \frac{6}{3}- \frac{20}{9} \right)}^{2}+{\left( \frac{6}{3}- \frac{20}{9} \right)}^{2}+{\left( \frac{9}{1}- \frac{20}{9} \right)}^{2} ]$$

  $= \frac{1}{{4}^{2}}$ [$({\frac{-20}{9})}^{2}$ + $({\frac{-2}{9})}^{2}$+ $\{3 \times ({\frac{-11}{9})}^{2}\}$ + $\{3 \times ({\frac{-2}{9})}^{2}\}$  + $({\frac{61}{9})}^{2}$]

  $= \frac{1}{16}$ [ $\frac{400}{81}$ + $\frac{4}{81}$ + $\frac{363}{81}$ + $\frac{12}{81}$  + $\frac{3721}{81}$] = $\frac{1}{16}$ $\times$ $\frac{4500}{81}$ = $\frac{4500}{1296}$  = 3.47

  Therefore, in this way the variances of all other elements of λ such as $v \left( R, R\right)$, $v \left( M, M\right)$, $v \left( K, K\right)$, $v \left( S, S\right)$ and $v \left( W, W\right)$ can be computed to obtain the last six components for the 21-dimensional numerical vector.

Calculation of Distance Matrix

Based on the descriptor representation, each genome sequences are depicted as 21 numerical values. Therefore, to find the evolutionary relationship among the species, a distance matrix is created using the Euclidean distance formula. To exemplify, let’s take two sequences from two different species namely; S₁ and S₂ having vector values as x_j and y_j respectively where j = 1, 2, 3 …, 21. Consequently, the distance between them is calculated as (5):

$$\mathrm{Distance }(\mathrm{S}1,\mathrm{ S}2) =\sqrt{\sum_{j=1}^{21}{\left( {x}_{j}- {y}_{j} \right)}^{2}}$$

(5)

Now, if there are a set of genome sequences as S₁, S₂, S₃,..., S_M where ‘M’ is the total number of sequences, then a desired M × M distance matrix is formed based on the 21-dimensional numerical descriptor. One such distance matrix is illustrated in Table 4.

Table 4 Distance matrix of beta-globin gene for 11 species

Construction of Phylogenetic Tree

A phylogenetic tree, commonly known as an ultra-metric tree, is a tree like structure which depicts the evolutionary descent of biological species from its common ancestors based on the genetic similarity/dissimilarity features. In this study, the phylogenetic tree is constructed from the distance matrix by applying a standard UPGMA/NJ clustering method through MEGA11 (Tamura et al. 2021). A flowchart illustration of our proposed method is shown in, Fig. 1.

Fig. 1

Flowchart of our proposed approach (Colour figure online)

ALGORITHM

The proposed methodology is divided into two segments; SEGMENT A is used to calculate the 21-dimensional numerical descriptor, and SEGMENT B used to obtain the distance matrix from an input folder containing all sequence files. Subsequently, this matrix is applied in MEGA11 using the UPGMA/NJ clustering method to construct the phylogenetic tree. The detailed steps of different segments are given as follows:

SEGMENT A

Variable initialized.

N ← length of S // length of the genome sequence

RY ← MK ← SW ← “” // 3 two-character sequences

SIZE_RY ← SIZE_MK ← SIZE_SW ← 0 // length of 3 two-character sequences

NR ← NY ← NM ← NK ← NS ← NW ← 0 // frequency of each character

PR[0…N-1] ← PY[0…N-1] ← PM[0…N-1] ← PK[0…N-1] ← PS[0…N-1] ← PW[0…N-1] ← [empty] // stores all the positions of each character from their respective string

UR ← UY ← UM ← UK ← US ← UW ← 0 // mean positions for each character

M[6][N] = [empty] // positional matrix

KR ← KY ← KM ← KK ← KS ← KW ← 0 // counter for the positional matrix

TR ← TY ← TM ← TK ← TS ← TW ← 0 // positional average of each character

VR ← VY ← VM ← VK ← VS ← VW ← 0 // variance of each character

COV_RY ← COV_MK ← COV_SW ← 0 // co-variance of 3 two-character sequences

FMAT[21] ← [empty] // stores 21-dimensional numerical vector for a string

User-defined Method

• I. Convert the string ‘S’ based on Table 1 into the following

  • a. ‘R’ and ‘Y’ characters and store it in the string “RY”;

  • b. ‘M’ and ‘K’ characters and store it in the string “MK”;

  • c. ‘S’ and ‘W’ characters and store it in the string “SW”.

• II. Compute and store the following for the string “RY”

  for i ← 0 to (SIZE_RY – 1) do

  • if (RY(i) = ‘R’) then

    • PR[NR] ← i + 1

      NR ← NR + 1

      UR ← UR + (i + 1)

    end if

    if (RY(i) = ‘Y’) then

    • PY[NY] ← i + 1

      NY ← NY + 1

      UY ← UY + (i + 1)

    end if

  end for

• III. Repeat STEP 2 for sequences “MK” and “SW” having length SIZE_MK and SIZE_SW to store the required values in the respective variables.

• IV. Calculate the positional matrix for the character ‘R’ in M[0][N]

  • // First Part

    for i ← 1 to (PR[0] – 1) do

    • M[0][KR + 1] ← 0

  end for

  • // Middle Part

    for i ← 1 to NR do

    • for j ← PR[i-1] to (PR[i] – 1) do

      • M[0][KR + 1] ← PR[i-1]/(PR[i] − PR[i-1])

      end for

    end for

  // Last Part

  for i ← KR to (N – 1) do

  M[0][i] ← PR[NR-1]/(N − (PR[NR-1] − 1))

  end for

• V. Repeat STEP 4 to calculate the positional matrix for rest of the characters that is ‘Y’, ‘M’, ‘K’, ‘S’ and ‘W’ in M[1][0…N − 1], M[2] [0…N − 1], M[3][0…N − 1], M[4][0…N − 1] and M[5][0…N − 1]

• VI. Calculate the positional average for ‘R’: TR = UR/NR and the mean of the positions for ‘R’: UR = UR/N

• VII. Repeat STEP 6 for rest of the characters ‘Y’, ‘M’, ‘K’, ‘S’ and ‘W’ and store in respective variables.

• VIII. Calculate the variances and co-variances for the string “RY”

  for i ← 0 to (N – 1) do

  COV_RY ← COV_RY + (M[0][i]-UR)*(M[1][i]-UY)

  VR ← VR + (M[0][i]-UR)*(M[0][i]-UR)

  VY ← VY + (M[1][i]-UY)*(M[1][i]-UY)

  end for

  COV_RY ← COV_RY/(NR*NY)

  VR ← VR/(NR*NR)

  VY ← VY/(NY*NY)

• IX. Repeat STEP 8 to calculate the co-variances and variances for the string “MK” and “SW” and store the values in respective variables.

• X. Store all the 21 vectors (NR, NY, NM, NK, NS, NW, TR, TY, TM, TK, TS, TW, COV_RY, COV_MK, COV_SW, VR, VY, VM, VK, VS, VW) in FMAT[0…20] positions

• XI. Return FMAT[]

SEGMENT B

Variable initialized

SEQUENCES[]← stores all the sequences at individual index

FILES[]← name of all input files in a folder

TOTAL_FILES ← size of FILES[]

VECTOR[][]← stores all the 21-dimensional numerical vector for all sequences

DIST_MAT[][]← stores the distance matrix

User-defined Method

// Storing individual sequences from each input file in a folder

• I. for each file F in the list FILES[] do

  • a. Read the genome sequence D from the file F

  • b. Remove all other characters and symbols from D except the ‘A’, ‘C’, ‘G’ and ‘T’ alphabets

  • c. Store the above obtained string S in SEQUENCES[] at individual index

• II. end for

  // Storing each 21-dimensional numerical vector in a two-dimensional array

• III. for i ← 0 to (TOTAL_FILES – 1) do

  • MAT[ ] ← COMPUTE(SEQUENCES[i])

  for j ← 0 to 20

  VECTOR[i][j] = MAT[j]

  end for

• IV. end for

  // Finding out the Distance Matrix

• V. for i ← 0 to (TOTAL_FILES – 1) do

  • PP ← i

    while (PP < (TOTAL_FILES - 2))

  • PP ← PP + 1

    sum ← 0

    for j ← 0 to 20 do

  • sum ← sum + (VECTOR[i][j] – VECTOR[PP][j])²

  end for

  • DIST_MAT[i][PP]←$\sqrt{\mathrm{sum}}$

    end while

• VI. end for

Time Complexity Analysis

In computer science, the time complexity of an algorithm indicates the amount of time taken by an algorithm to run till its completion. Here, the whole procedure is divided into two segments to compute time complexity.

In SEGMENT A, the 21-dimensional numerical vector is calculated depending on the Positional Matrix. Here, the time complexity of the Positional Matrix and the vector is O(6 × N) and O(21 × N) respectively. As, 6 and 21 both are finite numbers therefore the total time complexity becomes O(N) where ‘N’ refers to length of the genome sequence.

The SEGMENT B is divided into three partitions. Firstly, a one-dimensional array is used to store ‘M’ number of files containing genome sequences having a time complexity of O(M). Secondly, a two-dimensional array is used for storing the 21 vectors for all the input files that take O(21 × M) or O(M). But, as the vectors rely on the length of the sequence, the new time complexity becomes O(N × M). Finally, the distance matrix is computed among ‘M’ number of sequences possessing O({M × [M – 1]}/2) = O(M × M) = O(M²). Again, there is a dependency on the size of the sequence. Consequently, the complexity turns out to be O(N × M²). Hence, this segment produces O(N × M) + O(N × M²) = O(N × M²).

Therefore, the overall computational analysis becomes O(N) + O(N × M²) = O(N × M²) where the complexity of the algorithm is computationally fast. It is clear from this analysis that the size of the sequence and the frequency of genome sequence files are the principal factors for determining the time complexity analysis.

Moreover, the running time of our method is compared with the K-mer (K = 3) method and MSA(ClustalW) method mentioned in Table 5. It can also be seen that the MSA(ClustalW) method cannot even finish the alignment in Hepatitis C and SARS-CoV-2 data set whereas K-mer and our method produces result in a reasonable time. Moreover, our method is computationally faster as compared to K-mer method.

Table 5 Running time in minutes

Result Analysis

The new 21-dimensional numerical descriptor is applied to various datasets to calculate the distance matrix. It constitutes the complete coding sequences of the beta-globin gene for 11 species, the complete coding sequence datasets of 38 species of Influenza A viruses, the whole-genome sequences of 41 mammalian mitochondrial genes, the complete genome sequences of 81 species of Hepatitis C viruses, the whole-genome sequences of 59 Ebola viruses and the complete genome sequences of 942 species of the SARS-CoV-2 based on different geographical location and whole genome sequences of 21 Influenza A virus. The phylogenetic trees are constructed for these datasets using the UPGMA/NJ clustering method in MEGA11. The results from these datasets are compared with those of the formerly published methods that include the tri-nucleotide representation using J/J matrix method (Das et al. 2018a), the Graph-theoretic method (Das et al. 2020a), the Feature Frequency Profiles (FFP) method (Sims et al. 2009), the Fuzzy Integral Similarity (FIS) method (Saw et al 2019), the Positional Correlation Natural Vector (PCNV) method (He et al. 2020), the Multiple Encoding Vector (MEV) method (Li et al. 2017), the Accumulated Natural Vector (ANV) method (Dong et al. 2019). In most of the cases, it is observed that the appropriateness of the present results is better or equal to the results of the prior methods. The detailed result analysis of our proposed approach with other methodologies is given as follows.

Beta-Globin Gene Datasets of 11 Species

To verify our technique, the test is conducted on the coding sequence of 11 beta-globin genes from mammalian species that includes Woolly Monkey (AY279114.1), Tufted Monkey (AY279115.1), Opossum (J03642.1), Salmon (NM_001123672.1), Human (U01317.1), Gallus (V00409.1), Mouse (V00722.1), Rabbit (V00882.1), Rat (X06701.1), Duck (X15739.1), and Hare (Y00347.1). A similarity matrix is computed on these sequences shown in Table 4. Our result is compared with the results obtained in (Das et al. 2018a) and (He et al. 2020). In (Das et al. 2018a) the phylogenetic tree is drawn by the J/J matrix shown in Fig. 2b. It is observed that the Opossum is separated from Mouse and Rat. Also, the Human is clustered incorrectly. It should have been grouped with Woolly Monkey and Tufted Monkey belonging to the Primates group. Another comparison is made with the Positional Correlation Natural Vector method in He et al. (2020). In this case, the phylogenetic tree shown in Fig. 2c is almost similar to Fig. 2a with one exception. The Rat should be grouped with Mouse because they belong to the Rodentia group. The Opossum looks like a rodent, but it belongs to the Marsupial group. Further, the phylogenetic tree of our method is compared to the phylogenetic tree of the ClustalW shown in Fig. 2d. It is found that both the trees shows a clear and proper taxonomy of the 11 beta-globin genome sequences.

Fig. 2

a Phylogenetic tree of 11 species of Beta-globin gene using our proposed method constructed by UPGMA. b Phylogenetic tree of 10 species of Beta-globin genes using the J/J matrix. c Phylogenetic tree of 11 species of Beta-globin genes using the PCNV method. d Phylogenetic tree of 11 species of Beta-globin genes using the ClustalW (Colour figure online)

Mammalian Mitochondrial Gene Datasets of 41 Species

To verify our technique, a dataset that consists of whole mtDNAs of 41 mammalian species is chosen. The details of these species are mentioned in Table 6. The length of each sequence lies approximately between 16,200 and 17,400 nucleotides. In our procedure, the phylogenetic tree of 41 mammalian species is classified into nine clusters shown in Fig. 3a. They are: Artiodactyla (pink), Cetacea (green), Pachydermata (maroon), Carniformia (blue), Feliformia (olive), Primates (red), Lagomorpha (purple), Rodentia (black), and Erinaceomorpha (gray). In previous works, it has been seen that the researchers have used the same datasets in (Sims et al. 2009), (Saw et al. 2019), (He et al. 2020), (Li et al. 2017). But most of the approaches do not possess proper classifications. The Phylogenetic tree of the Feature Frequency Profiles method (Sims et al. 2009) using k = 7 is shown in Fig. 3c. Here, the Indus River Dolphin belongs to the Cetacea cluster, but it is alienated from the rest of the group. Even the Pachydermata (maroon) species classification is scattered throughout the figure. The Hedgehog, Erinaceomorpha (gray); should have been isolated from the other species. The Primates (red) are divided into two inaccurate sets. Therefore, the figure does not have the correct taxonomy of species. In the Fuzzy Integral Similarity method (Saw et al. 2019), as shown in Fig. 3b, it is observed that some of the clusters are improperly classified. The Hedgehog, Erinaceomorpha (gray); is clustered with Dormouse and Squirrel, Rodentia (black); which should have been separated from the rest of the species. Also, the Cat should be grouped with Tiger and Leopard instead, it is grouped with Artiodactyla (pink). The Rabbit is also misclassified. Even, the Carnivore (blue) clustered is erroneous because it cannot be sub-grouped into Caniformia and Feliformia. Overall, it shows only five appropriate classifications. According to the Positional Correlation Natural Vector method (He et al. 2020), many species are miscategorized in Fig. 3d. Only five classifications are appropriately clustered. The Fin Whale and the Blue Whale should have been grouped with Cetacea (green), the Dog and the Wolf with Carniformia (blue), the Cow with Artiodactyla (pink), and the Common Warthog with Pachydermata (maroon). The Indian Rhino and the White Rhino are branched separately. Also, the Human in Primates (red) is present with the Gibbon and Orangutan species instead, it should be in the other half of the cluster. Therefore, it is noticed that the construction of the phylogenetic tree is improper. Also, the phylogenetic tree of the proposed method is compared with the phylogenetic tree of the ClustalW mentioned in Fig. 3e. Here, most of the species classification is similar to the Fig. 3a with one difference, the Pig and the Common Warthog are separately clustered with other species under the Pachydermata classification in Fig. 3a. Moreover, the result obtained from our proposed method is consistent with the Multiple Encoding Vector method (Li et al. 2017) in Fig. 3f. Hence, it can be summarized that the proposed method and the Multiple Encoding Vector method are by far the best method among all other aforesaid methods for these 41 mtDNAs.

Table 6 Information of the mammalian mitochondrial genes of 41 species

Fig. 3

a Phylogenetic tree of 41 species of mammalian mitochondrial genes using our proposed method constructed by UPGMA. b Phylogenetic tree of 41 species of mammalian mitochondrial genes using the FIS method. c Phylogenetic tree of 41 species of mammalian mitochondrial genes using the FFP method. d Phylogenetic tree of 41 species of mammalian mitochondrial genes using the PCNV method. e Phylogenetic tree of 41 species of mammalian mitochondrial genes using the ClustalW method. f Phylogenetic tree of 41 species of mammalian mitochondrial genes using the MEV method (Colour figure online)

v

Hepatitis C Virus Datasets of 81 Species

To validate our proposed method, we consider 81 complete genome sequence datasets of Hepatitis C Virus (HCV) which has an average length of 9,300 nucleotides for our next experiment. The genomic details are given in Table 7. Here, the 81 Hepatitis C virus is appropriately grouped into six clusters, shown in Fig. 4a. They are denoted as type 1 (red), type 2 (olive), type 3 (purple), type 4 (blue), type 5 (black), and type 6 (pink). Our phylogenetic tree is compared with the results in (Sims et al. 2009), (He et al. 2020), (Li et al. 2017). The phylogenetic tree is obtained by the Feature Frequency Profiles (Sims et al. 2009) method as shown in Fig. 4b. It can be seen that the specie ‘JX227973’ of type 4(blue) is alienated from its group and incorrectly clustered with type 6 (pink). According to the Multiple Encoding Vector method (Li et al. 2017) in Fig. 4c, the specie ‘KM504118’ (pink) is separated from type 6 (pink) and grouped improperly with type 1 (red). Moreover, the result obtained from the Positional Correlation Natural Vector method (He et al. 2020), having the same number of datasets, is shown in Fig. 4d. It is observed that the phylogenetic tree is similar to that of our proposed method. Overall, it can be outlined that our method and Positional Correlation Natural Vector method give better results than the earlier methods.

Table 7 Information of the Hepatitis C Virus Datasets of 81 species

Fig. 4

a Phylogenetic tree of 81 species of HCV viruses using our proposed method constructed by NJ. b Phylogenetic tree of 81 species of HCV viruses using the FFP method. c Phylogenetic tree of 81 species of HCV viruses using the MEV method. d Phylogenetic tree of 81 species of HCV viruses using the PCNV method (Colour figure online)

Influenza A Virus Datasets of 38 Species

In this present work, 38 datasets of Influenza A viruses are used mentioned in Table 8. The average length of sequences runs up to 1400 nucleotides. Further, a phylogenetic tree is constructed in Fig. 5a. It can be grouped into five clusters; namely H1N1 (blue), H2N2 (pink), H5N1 (red), H7N9 (black), and H7N3 (green). Our result is compared with the results in (Das et al. 2020a), (Sims et al. 2009), (Dong et al. 2019). The phylogenetic tree constructed by the Graph-theoretic method (Das et al. 2020a) shows one misclassification where A/Turkey/VA/505472–18/2007 (H5N1) (red) is placed in the cluster of H1N1 (blue). This is shown in Fig. 5b. The same misclassification is also present in Fig. 5c. According, to the Feature Frequency Profiles method (Sims et al. 2009), lots of misclassifications of several viral species are clustered between H5N1 (red) and H1N1 (blue). This is shown in Fig. 5d. It is the worst choice method for this dataset as compared to others. The phylogenetic tree obtained by the Accumulated Natural Vector method (Dong et al. 2019), is the same as that of our proposed method as shown in Fig. 5e. Therefore, out of all these methods our proposed method is the best choice for the classification of viruses for this dataset.

Table 8 Information of the Influenza A Virus Datasets of 38 species

Fig. 5

a Phylogenetic tree of 38 species of Influenza A viruses using our proposed method constructed using NJ. b Phylogenetic tree of 38 species of Influenza A viruses using the Graph-theoretic method. c Phylogenetic tree of 38 Influenza A viruses using the ClustalW method. d Phylogenetic tree of 38 Influenza A viruses using the FFP method. e Phylogenetic tree of 38 Influenza A viruses using the ANV method (Colour figure online)

Ebola Virus Datasets of 59 Species

Next, the complete genome sequences of 59 Ebola Virus are considered. The length of the sequences is ranging from 18,700 to 19,000 nucleotides. All other dataset-related information is present in the Table 9. In our procedure, the phylogenetic tree of 59 Ebola viral datasets are divided in ten different groups that is shown in Fig. 6a. They include five different strains of Ebola viruses are: Bundibugyo virus (BDBV), 5 species indicated by purple; Reston virus (RESTV), 6 species indicated by light blue; Sudan virus (SUDV), 10 species indicated by pink; Tai Forest virus (TAFV), 1 species indicated by black and Ebola virus (EBOV), 37 species. Further, the Ebola viruses are grouped into six different clusters based on various location. One is EBOV of Guinea in 2014 indicated by red. Another type is known as DRC happened during 2007 indicated by green and its variant Zaire (DRC) occurred in 1995 indicated by blue, and in 1976–1977 indicated by light blue. The next type is Gabon occurred in 2002 indicated by gray, in 1994 and 1996 indicated by olive. In previous works, it has been seen that the authors have used the same datasets in (Sims et al. 2009), (Saw et al. 2019), (Li et al. 2017). Now, the phylogenetic tree of our method is compared with the phylogenetic tree of the Feature Frequency Profiles method (Sims et al. 2009). The Fig. 6b shows that the SUDV and the RESTV species are differently clustered. It should be grouped together in a single branch. Here, the consistency of the Ebola virus categorization is not maintained properly. The same type of misclassification is present in the method ClustalW in Fig. 6c. Further, in the Fuzzy Integral Similarity method (Saw et al. 2019), the EBOV_2007_KC242788 specie is clustered with the species of Zaire (DRC) 1976–1977 instead of DRC, 2007 as shown in Fig. 6d. Finally, the result of the Multiple Encoding Vector method (Li et al. 2017) in Fig. 6e, is compared with the phylogenetic tree of our proposed method where most of the species are not clustered properly. Here, the specie RESTV 2008 FJ621585 is separately clustered from rest of the RESTV species. Moreover, few species of Gabon, 1994/1996 and Zaire (DRC), 1976–1977 are clustered in single branch. It should have been grouped separately. Therefore, it can be concluded that the proposed method is by far the best method among all other methods for genome sequence comparison.

Table 9 Information of the Ebola Virus Datasets of 59 species

Fig. 6

a Phylogenetic tree of 59 species of Ebola viruses using our proposed method constructed using NJ. b Phylogenetic tree of 59 species of Ebola viruses using our FFP method. c Phylogenetic tree of 59 species of Ebola viruses using our ClustalW method. d Phylogenetic tree of 59 species of Ebola viruses using FIS method. e Phylogenetic tree of 59 species of Ebola viruses using MEV method (Colour figure online)

SARS-CoV-2 Based on Geographical Location Datasets of 942 Species

In our next experiment, a total of 942 numbers of whole-genome sequences of SARS-CoV-2 viruses based on the different geographical locations of the world is considered. Dataset consists of 1 sequence from Australia, 2 sequences from Brazil, 63 sequences from China and there different province, 1 sequence from France, 4 sequences from Greece, 9 sequences from Hongkong, 3 sequences from India, 1 sequence from Iran, 2 sequences from Israel, 2 sequences from Italy, 1 sequence from Nepal, 2 sequences from Pakistan, 1 sequence from Peru, 1 sequence from South Africa, 4 sequences from South Korea, 13 sequences from Spain, 1 sequence from Sweden, 3 sequences from Taiwan, 1 sequence from Turkey, 824 sequences from the USA and their different province, and 2 sequences from Vietnam. Now, using the entire dataset, a phylogenetic tree is constructed based on our methodology shown in Fig. 7. The phylogenetic tree helps us to find the evolutionary connection of the viruses based on their geographical location. From Fig. 7, it is noticed that most of the viruses that are collected from different provinces of the USA are clustered together (indicated in red color). Similarly, most of the viruses that are collected from Asian countries are clustered together and few are also combined with the viruses taken from Asian and American countries. Due to the mutation happened to viruses on different geographical location, viruses of different locations are clade together. This leads to special attention from pathogenesis for inventing the remedies from the virus. Therefore, our method provides satisfactory results using 942 number of whole-genome sequence datasets each having 29,500 nucleotides approximately.

Fig. 7

Phylogenetic tree of 942 species of SARS-CoV-2 viruses based on Geographical location (red color: North America, blue: Asia, green: Europe, yellow: Australia, black: South America) (Colour figure online)

Influenza A Viruses of 21 Species

In the present experiment, a total 21 number of species are considered which consist of 6 H1N1 virus genomes, 6 swine flu virus genomes, 6 avian virus genomes and 3 human seasonal flu virus genomes. The details are mentioned in the Table 10 and the phylogenetic result is obtained in the Fig. 8a. The comparative phylogenetic result of applying the maximum likelihood method with the proposed approach is demonstrated in Fig. 8b where the result shows that the swine flu virus genomes are not clustered correctly. On the contrary, the proposed approach shows no inconsistency that appears in clustering different types of viruses. In fact, 6 Influenza A(N1H1) viruses are now occupying the top position of the phylogenetic tree and they are clustered together. Thus, the phylogenetic tree of the proposed method provides better results compared to the maximum likelihood method.

Table 10 Information of the Influenza A Virus Datasets of 21 species

Fig. 8

a Phylogenetic tree of 21 species of Influenza A virus using our proposed method constructed by NJ. b Phylogenetic tree of 21 species of Influenza A virus using maximum likelihood method (Colour figure online)

Significance Test

In many cases, it is observed that the phylogenetic trees obtained by different methods are alike for some data sets. Naturally the question arises to see whether this happens by chance or significantly. As the phylogenetic trees are constructed based on the values of the descriptor, so the answer lies in the test of significance on paired of descriptor values of the same species taken in two methods. In the present case, the phylogenetic trees of 11 beta-globin genes from mammalian species are considered and the two methods for comparison are taken as our present method and the Positional Correlation Natural Vector (PCNV) method. At the start, the common species under consideration is Woolly Monkey. Subsequently other species of the beta-globin genes are taken one by one in pair. The length of the descriptor of our method is 21 vectors whereas that of Positional Correlation Natural Vector (PCNV) method is 18 vectors. As paired t-test for equality of means is not applicable, therefore the general t-test is considered. This is done under 0.05 level of significance error. It is noted that the expression for value of t is given by

t = $\frac{(\left( \overline{a } \right) - \left( \overline{b } \right))}{S.E.(\left( \overline{a } \right) - \left( \overline{b } \right))}$ , where $\left(\overline{a } \right), \left( \overline{b }\right)$ are the sample means and $S.E.\left(\left( \overline{a } \right) - \left( \overline{b }\right)\right)$, represents the standard error of $(\left( \overline{a } \right) - \left( \overline{b } \right))$

Now, $S.E.\left(\left( \overline{a } \right) - \left( \overline{b }\right)\right)$ = ${s}_{p} \sqrt{\frac{1}{{n}_{1}}+\frac{1}{{n}_{2}}}$, ${s}_{p}^{2}$ = $\frac{\left({n}_{1}*{s}_{1}^{2}\right) + \left({n}_{2}*{s}_{2}^{2}\right) }{{n}_{1}- {n}_{2}-2}$ which is the pulled variance; ${s}_{1}^{2}$, ${s}_{2}^{2}$ are the variances of first and second species; n₁, n₂ are their sample sizes.

Again this formula for ‘t’ is applicable only when the variances of the samples do not differ significantly. Otherwise a different formula works. Now the condition of equality of sample variances is determined by F-tests (Fisher’s F-statistics), which is given by F = $\frac{{s}_{1}^{2}}{{s}_{2}^{2}}$ where, ${s}_{1}^{2}$ = $\frac{{n}_{1}}{{n}_{1}-1}$ ${S}_{1}^{2}$ and ${s}_{2}^{2}$ = $\frac{{n}_{1}}{{n}_{2}-1}$ ${S}_{2}^{2}$ are the unbiased estimators of the variances; ${S}_{1}^{2}$, ${S}_{2}^{2}$ are the sample variances. The formula holds only when ${s}_{1}^{2}$ > ${s}_{2}^{2}$, otherwise F = $\frac{{s}_{2}^{2}}{{s}_{1}^{2}}$. The values of the datasets of Woolly Monkey species of Beta-globin gene using our method and PCNV method are mentioned in the Tables 11 and 12 respectively.

Table 11 Data set 1—vector values (D_i, i = 1 to 21) of Woolly Monkey species of Beta-globin gene using our proposed method

Table 12 Data set 2—vector values (D_i, i = 1 to 18) of Woolly Monkey species of Beta-globin gene using PCNV method

Hypothesis Testing for Equality of Sample Variances

H₀: There is no significance difference between the variances of the descriptors.

H_A: There is a significance difference between the variances of the descriptors.

Now, ${s}_{1}^{2}$ = $\frac{{n}_{1}}{{n}_{1}-1}$ ${S}_{1}^{2}$ = $\frac{21}{20}$ $\times$ 7558.84 = 7936.78; ${s}_{2}^{2}$ = $\frac{{n}_{1}}{{n}_{2}-1}$ ${S}_{2}^{2}$ = $\frac{18}{17}$ $\times$ 8284.20 = 8698.41; F = $\frac{{s_{2}^{2} }}{{s_{1}^{2} }}$ = 1.10.

But F = 1.10 < 2.62 = ${F}_{0.05\left(2\right), \mathrm{20,17}}$ So there is no significant difference between the variances.

Hence we can apply the aforesaid formula for calculation of ‘t’ statistics.

Hypothesis Testing for Equality of Sample Means

H₀: There is no significance difference between the means of the descriptors.

H_A: There is a significance difference between the means of the descriptors.

${s}_{p}^{2}$ = $\frac{\left({n}_{1}*{s}_{1}^{2}\right) + \left({n}_{2}*{s}_{2}^{2}\right) }{{n}_{1}- {n}_{2}-2}$  = 8736.32; ${s}_{p}$ = $\sqrt{8736.32}$  = 93.47, $S.E.\left(\left( \overline{a } \right) - \left( \overline{b }\right)\right)$ = ${s}_{p} \sqrt{\frac{1}{{n}_{1}}+\frac{1}{{n}_{2}}}$  = 30.02;

${t}_{0.05\left(2\right), 37}$ = $\frac{(\left( \overline{a } \right) - \left( \overline{b } \right))}{S.E.(\left( \overline{a } \right) - \left( \overline{b } \right))}$ = $\frac{35.84}{30.02}$  = 1.19 < 2.026 (prescribed value).

Thus H₀ holds. The conclusion is that there is no significance difference between the sample means.

In this way, the hypothesis testing is carried out for all the species separately with their descriptor values obtained from two methods. The results are listed below in Tables 13 and 14.

Table 13 F-test values of 11 species of Beta-globin gene

Table 14 t-test values of 11 species of beta-globin gene

In all cases it is found that F values and t values are less than the prescribed values. As all such values are obtained under the same level 0.05 of significance error, so there is no chance of Type I error. Thus the means of the descriptors of all the species do not vary significantly. As such, this is reflected in the corresponding Phylogenetic trees of the data sets under two different methods. In other words, the phylogenetic trees are similar significantly. This has not happened by chance. The same type of analysis works for comparing Phylogenetic trees obtained by other methods.

Bootstrap Approach

Bootstrap method is used to find the uncertainty in the means of different samples of the same data under replacement. To estimate the sample distribution for the desired estimator, it utilizes sampling with replacement. The uncertainty or confidence is determined by the length of the confidence interval; uncertainty increases or decreases with decrease and increase of the length. The reliability of the phylogenetic analysis is evaluated using this method. A phylogenetic tree's bootstrap values show how many times, out of 100, the same branch is shown when the construction of the tree is repeated using a resampled set of data. If this observation occurs 100 times out of 100, it supports the conclusion. A bootstrap score of 95% indicates that the node is well supported if the same node is recovered through 95 out of 100 iterations by removing one character and resampling the tree. If the value is less than 50% then the tree construction is not taken under consideration. Here, the Fig. 9a shows the original phylogenetic tree whereas the Fig. 9b shows the Bootstrap tree. It is clearly visible that the bootstrap tree’s values lie between 99 and 100%. Hence, this indicates that the tree is correctly constructed using our method.

Fig. 9

a The Original phylogenetic tree of 11 species of Beta-globin gene using our proposed method. b The Bootstrap phylogenetic tree of 11 species of Beta-globin gene using our proposed method (Colour figure online)

Comparison of the Phylogenetic Trees Under SD Values

The Robinson–Foulds (RF) or Symmetric Distance (SD) is used to calculate the distance between any two trees based on their topologies which can be obtained from the treedist program in the PHYLIP package (Kuhner and Felsenstein 1994). This method counts the number of partitions which are not shared by both the trees. Here, the SD values are calculated from phylogenetic trees of different methods in reference to the phylogenetic tree constructed by ClustalW method as shown in Table 15. It is clearly visible that the SD values of the proposed method are lesser than those of other methods applied for comparison of different species. Therefore, it can be considered that our method produces highly satisfactory results in the construction of the phylogenetic trees as compared to the other methods. Therefore, in comparison to other approaches, it can be said that our method generates highly satisfactory results in the construction of phylogenetic trees.

Table 15 SD values calculated from phylogenetic trees of different methods with ClustalW as the reference

Conclusion

The continuous evolution in genetic mutations has opened up significant realms for investigators in the field of bioinformatics. In this context, due to the rapid and steady growth in genome sequence datasets, it is most challenging to develop proper techniques for studying the evolutionary relationships of species. Consequently, several researchers have attempted to create new methods for genome sequence comparison. However, some of these methods do not produce suitable results for different multi-genome datasets. Therefore, a new method has been developed, in this paper, for the similarity/dissimilarity measures of many biological sequences which are analyzed based on the biochemical properties of nucleotides and the Positional Matrix. The frequency, positional average, variances, and co-variances are used as parameters to generate a simple 21-dimensional numerical descriptor. The method is tested on several species of mammals, influenza-A viruses, ebola viruses, hepatitis C viruses and SARS-CoV-2 viruses. The results of the proposed method are compared with those of the existing methods like the tri-nucleotide representation using J/J matrix method (Das et al. 2018a), the Graph-theoretic method (Das et al. 2020a), the Feature Frequency Profiles (FFP) method (Sims et al. 2009), the Fuzzy Integral Similarity (FIS) method (Saw et al. 2019), the Positional Correlation Natural Vector (PCNV) method (He et al. 2020), the Multiple Encoding Vector (MEV) method (Li et al. 2017), and the Accumulated Natural Vector (ANV) method (Dong et al. 2019), where the results are found to be highly satisfactory. The advantage of this method is that it is computationally fast, and it does not use any additional parameters to align genome sequences evenly, as is the case with traditional alignment-based methods. This numerical vector strategy relies on the alignment-free approach using large-scale datasets. However, it would be an interesting future study to apply a new distance metric (Ondov et al. 2016) for phylogenetic analysis. Therefore, it is concluded that an alternative and innovative approach has been proposed for comparing different biological species that can handle large volumes of genomic data effectively with minimal time complexity.