Abstract
This paper introduces the counterpart of strong bisimilarity for labelled transition systems extended with timeout transitions. It supports this concept through a modal characterisation, congruence results for a standard process algebra with recursion, and a complete axiomatisation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This is a contribution to classic untimed non-probabilistic process algebra, modelling systems that move from state to state by performing discrete, uninterpreted actions. A system is modelled as a process-algebraic expression, whose standard semantics is a state in a labelled transition system (LTS). An LTS consists of a set of states, with action-labelled transitions between them. The execution of an action is assumed to be instantaneous, so when any time elapses the system must be in one of its states. With “untimed” I mean that I will refrain from quantifying the passage of time; however, whether a system can pause in some state or not will be part of my model.
Following [33], I consider reactive systems that interact with their environments through the synchronous execution of visible actions \(a, b, c, \ldots \) taken from an alphabet A. At any time, the environment allows a set of actions \(X\subseteq A\), while blocking all other actions. At discrete moments, the environment can change the set of actions it allows. In a metaphor from [33], the environment of a system can be seen as a user interacting with it. This user has a button for each action \(a\in A\), on which it can exercise pressure. When the user exercises pressure and the system is in a state where it can perform action a, the action occurs. For the system, this involves taking an a-labelled transition to a following state; for the environment it entails the button going down, thus making the action occurrence observable. This can trigger the user to alter the set of buttons on which it exercises pressure.
The current paper considers two special actions that can occur as transition labels: the traditional hidden action \(\tau \) [33], modelling the occurrence of an instantaneous action from which we abstract, and the timeout action \(\mathrm{t}\), modelling the end of a time-consuming activity from which we abstract. The latter was introduced in [18] and constitutes the main novelty of the present paper with respect to [33] and forty years of research in process algebra. Both special actions are assumed to be unobservable, in the sense that their occurrence cannot trigger any state-change in the environment. Conversely, the environment cannot cause or block the occurrence of these actions.
Following [18], I model the passage of time in the following way. When a system arrives in a state P, and at that time X is the set of actions allowed by the environment, there are two possibilities. If P has an outgoing transition  with \(\alpha \in X\cup \{\tau \}\), the system immediately takes one of the outgoing transitions
with \(\alpha \in X\cup \{\tau \}\), the system immediately takes one of the outgoing transitions  with \(\alpha \in X\cup \{\tau \}\), without spending any time in state P. The choice between these actions is entirely nondeterministic. The system cannot immediately take a transition
with \(\alpha \in X\cup \{\tau \}\), without spending any time in state P. The choice between these actions is entirely nondeterministic. The system cannot immediately take a transition  with \(b\in A{\setminus }X\), because the action b is blocked by the environment. Neither can it immediately take a transition
with \(b\in A{\setminus }X\), because the action b is blocked by the environment. Neither can it immediately take a transition  , because such transitions model the end of an activity with a finite but positive duration that started when reaching state P.
, because such transitions model the end of an activity with a finite but positive duration that started when reaching state P.
In case P has no outgoing transition  with \(\alpha \in X\cup \{\tau \}\), the system idles in state P for a positive amount of time. This idling can end in two possible ways. Either one of the timeout transitions
with \(\alpha \in X\cup \{\tau \}\), the system idles in state P for a positive amount of time. This idling can end in two possible ways. Either one of the timeout transitions  occurs, or the environment spontaneously changes the set of actions it allows into a different set Y with the property that
occurs, or the environment spontaneously changes the set of actions it allows into a different set Y with the property that  for some \(a \in Y\). In the latter case, a transition
for some \(a \in Y\). In the latter case, a transition  occurs, with \(a \in Y\). The choice between the various ways to end a period of idling is entirely nondeterministic. It is possible to stay forever in state P only if there are no outgoing timeout transitions
occurs, with \(a \in Y\). The choice between the various ways to end a period of idling is entirely nondeterministic. It is possible to stay forever in state P only if there are no outgoing timeout transitions  .
.
The addition of timeouts enhances the expressive power of LTSs and process algebras. The process \(a.P + \mathrm{t}.b.Q\), for instance, models a choice between a.P and b.Q where the former has priority. In an environment where a is allowed it will always choose a.P and never b.Q; but in an environment that blocks a the process will, after some delay, proceed with b.Q. Such a priority mechanism cannot be modelled in standard process algebras without timeouts, such as CCS [33], CSP [6, 28] and ACP [2, 10]. Additionally, mutual exclusion cannot be correctly modelled in any of these standard process algebras [20], but adding timeouts makes it possible—see Sect. 11 for a more precise statement.
In [18], I characterised the coarsest reasonable semantic equivalence on LTSs with timeouts—the one induced by may testing, as proposed by De Nicola and Hennessy [8]. In the absence of timeouts, may testing yields weak trace equivalence, where two processes are defined equivalent iff they have the same weak traces: sequence of actions the system can perform, while eliding hidden actions. In the presence of timeouts weak trace equivalence fails to be a congruence for common process algebraic operators, and may testing yields its congruence closure, characterised in [18] as (rooted) failure trace equivalence.
The present paper aims to characterise one of the finest reasonable semantic equivalences on LTSs with timeouts—the counterpart of strong bisimilarity for LTSs without timeouts. Naturally, strong bisimilarity can be applied verbatim to LTSs with timeouts—and has been in [18]—by treating \(\mathrm{t}\) exactly like any visible action. Here, however, I aim to take into account the essence of timeouts, and propose an equivalence that satisfies some natural laws discussed in [18], such as \(\tau .P + \mathrm{t}.Q = \tau .P\) and \(a.P + \mathrm{t}.(Q + \tau .R + a.S) = a.P + \mathrm{t}.(Q + \tau .R)\). To motivate the last law, note that the timeout transition  can occur only in an environment that blocks the action a, for otherwise a would have taken place before the timeout went off. The occurrence of this transition is not observable by the environment, so right afterwards the state of the environment is unchanged, and the action a is still blocked. Therefore, the process \(Q + \tau .R + a.S\) will, without further ado, proceed with the \(\tau \)-transition to R, or any action from Q, just as if the a.S summand were not present.
can occur only in an environment that blocks the action a, for otherwise a would have taken place before the timeout went off. The occurrence of this transition is not observable by the environment, so right afterwards the state of the environment is unchanged, and the action a is still blocked. Therefore, the process \(Q + \tau .R + a.S\) will, without further ado, proceed with the \(\tau \)-transition to R, or any action from Q, just as if the a.S summand were not present.
Standard process algebras and LTSs without timeouts can model systems whose behaviour is triggered by input signals from the environment in which they operate. This is why they are called “reactive systems”. By means of timeouts, one can additionally model systems whose behaviour is triggered by the absence of input signals from the environment, during a sufficiently long period. This creates a greater symmetry between a system and its environment, as it has always been understood that the environment or user of a system can change its behaviour as a result of sustained inactivity of the system it is interacting with. Hence, one could say that process algebras and LTSs enriched with timeouts form a more faithful model of reactivity. It is for this reason that I use the name reactive bisimilarity for the appropriate form of bisimilarity on systems modelled in this fashion.
Section 2 introduces strong reactive bisimilarity as the proper counterpart of strong bisimilarity in the presence of timeout transitions. Naturally, it coincides with strong bisimilarity when there are no timeout transitions. Section 3 derives a modal characterisation; a reactive variant of the Hennessy–Milner logic. Section 4 offers an alternative characterisation of strong reactive bisimilarity that will be more convenient in proofs, although it is lacks the intuitive appeal to be used as the initial definition. Appendix C, reporting on work by Max Pohlmann [37], offers yet another characterisation of strong reactive bisimilarity; one that reduces it to strong bisimilarity in a context that models a system together with its environment.
Section 5 recalls the process algebra CCSP, a common mix of CCS and CSP, and adds the timeout action, as well as two auxiliary operators that will be used in the forthcoming axiomatisation. Section 6 states that in this process algebra one can express all countably branching transition systems, and only those, or all and only the finitely branching ones when restricting to guarded recursion.
Section 7 recalls the concept of a congruence, focusing on the congruence property for the recursion operator, which is commonly the hardest to establish. It then shows that the simple initials equivalence, as well as Milner’s strong bisimilarity, are congruences. Due to the presence of negative premises in the operational rules for the auxiliary operators, these proofs are not entirely trivial. Using these results as a stepping stone, Sect. 8 shows that strong reactive bisimilarity is a congruence for my extension of CCSP. Here, the congruence property for one of the auxiliary operators with negative premises is needed in establishing the result for the common CCSP operators, such as parallel composition.
Section 9 shows that guarded recursive specifications have unique solutions up to strong reactive bisimilarity. Using this, Sect. 10 provides a sound and complete axiomatisation for processes with guarded recursion. My completeness proof combines three innovations in establishing completeness of process algebraic axiomatisations. First of all, following [22], it applies to all processes in a Turing powerful language like guarded CCSP, rather than the more common fragment merely employing finite sets of recursion equations featuring only choice and action prefixing. Secondly, instead of the classic technique of merging guarded recursive equations [11, 30,31,32, 40], which in essence proves two bisimilar systems P and Q equivalent by equating both to an intermediate variant that is essentially a product of P and Q, I employ the novel method of canonical solutions [24, 29], which equates both P and Q to a canonical representative within the bisimulation equivalence class of P and Q—one that has only one reachable state for each bisimulation equivalence class of states of P and Q. In fact I tried so hard, and in vain, to apply the traditional technique of merging guarded recursive equations, that I came to believe that it fundamentally does not work for this axiomatisation. The third innovation is the use of the axiom of choice [41] in defining the transition relation on my canonical representative, in order to keep this process finitely branching.
Section 11 describes a worthwhile gain in expressiveness caused by the addition of timeouts, and presents an agenda for future work.
2 Reactive bisimilarity
A labelled transition system (LTS) is a triple  with
with  a set (of states or processes), Act a set (of actions) and
a set (of states or processes), Act a set (of actions) and  . In this paper, I consider LTSs with \(Act:= A\uplus \{\tau ,\mathrm{t}\}\), where A is a set of visible actions, \(\tau \) is the hidden action, and \(\mathrm{t}\) the timeout action. The set of initial actions of a process
. In this paper, I consider LTSs with \(Act:= A\uplus \{\tau ,\mathrm{t}\}\), where A is a set of visible actions, \(\tau \) is the hidden action, and \(\mathrm{t}\) the timeout action. The set of initial actions of a process  is
is  . Here
. Here  means that there is a Q with
means that there is a Q with  .
.
Definition 1
A strong reactive bisimulation is a symmetric relation  (meaning that
(meaning that  and
and  ), such that,
), such that,
-
if
 and
and  , then there exists a \(Q'\) such that
, then there exists a \(Q'\) such that  and
and  ,
, -
if
 then
then  for all \(X\subseteq A\),
for all \(X\subseteq A\),
and for all  ,
,
-
if
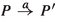 with \(a\in X\), then there exists a \(Q'\) such that
with \(a\in X\), then there exists a \(Q'\) such that  and
and  ,
, -
if
 , then there exists a \(Q'\) such that
, then there exists a \(Q'\) such that  and
and 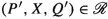 ,
, -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \), then
 , and
, and -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
 , then \(\exists Q'\) such that
, then \(\exists Q'\) such that  and
and  .
.
Processes  are strongly X-bisimilar, denoted
are strongly X-bisimilar, denoted  , if
, if  for some strong reactive bisimulation
for some strong reactive bisimulation  . They are strongly reactive bisimilar, denoted
. They are strongly reactive bisimilar, denoted  , if
, if  for some strong reactive bisimulation
for some strong reactive bisimulation  .
.
Intuitively,  says that processes P and Q behave the same way, as witnessed by the relation
says that processes P and Q behave the same way, as witnessed by the relation  , when placed in the environment X—meaning any environment that allows exactly the actions in X to occur—whereas
, when placed in the environment X—meaning any environment that allows exactly the actions in X to occur—whereas  says they behave the same way in an environment that has just been triggered to change. An environment can be thought of as an unknown process placed in parallel with P and Q, using the operator \({\Vert ^{}_{A}}\), enforcing synchronisation on all visible actions. The environment X can be seen as a process \(\sum _{i\in I}a_i.R_i + \mathrm{t}.R\) where \(\{a_i \mid i\in I\} = X\). A triggered environment, on the other hand, can execute a sequence of instantaneous hidden actions before stabilising as an environment Y, for \(Y\subseteq A\). During this execution, actions can be blocked and allowed in rapid succession. Since the environment is unknown, the bisimulation should be robust under any such environment.
says they behave the same way in an environment that has just been triggered to change. An environment can be thought of as an unknown process placed in parallel with P and Q, using the operator \({\Vert ^{}_{A}}\), enforcing synchronisation on all visible actions. The environment X can be seen as a process \(\sum _{i\in I}a_i.R_i + \mathrm{t}.R\) where \(\{a_i \mid i\in I\} = X\). A triggered environment, on the other hand, can execute a sequence of instantaneous hidden actions before stabilising as an environment Y, for \(Y\subseteq A\). During this execution, actions can be blocked and allowed in rapid succession. Since the environment is unknown, the bisimulation should be robust under any such environment.
The first clause for  is like the common transfer property of strong bisimilarity [33]: a visible a-transition of P can be matched by one of Q, such that the resulting processes \(P'\) and \(Q'\) are related again. However, I require it only for actions \(a\in X\), because actions \(b\in A{\setminus }X\) cannot happen at all in the environment X, and thus need not be matched by Q. Since the occurrence of a is observable by the environment, this can trigger the environment to change the set of actions it allows, so \(P'\) and \(Q'\) ought to be related in a triggered environment.
is like the common transfer property of strong bisimilarity [33]: a visible a-transition of P can be matched by one of Q, such that the resulting processes \(P'\) and \(Q'\) are related again. However, I require it only for actions \(a\in X\), because actions \(b\in A{\setminus }X\) cannot happen at all in the environment X, and thus need not be matched by Q. Since the occurrence of a is observable by the environment, this can trigger the environment to change the set of actions it allows, so \(P'\) and \(Q'\) ought to be related in a triggered environment.
The second clause is the transfer property for \(\tau \)-transitions. Since these are not observable by the environment, they cannot trigger a change in the set of actions allowed by it, so the resulting processes \(P'\) and \(Q'\) should be related only in the same environment X.
The first clause for  expresses the transfer property for \(\tau \)-transitions in a triggered environment. Here, it may happen that the \(\tau \)-transition occurs before the environment stabilises, and hence \(P'\) and \(Q'\) will still be related in a triggered environment. A similar transfer property for a-transitions is already implied by the next two clauses.
expresses the transfer property for \(\tau \)-transitions in a triggered environment. Here, it may happen that the \(\tau \)-transition occurs before the environment stabilises, and hence \(P'\) and \(Q'\) will still be related in a triggered environment. A similar transfer property for a-transitions is already implied by the next two clauses.
The second clause allows a triggered environment to stabilise into any environment X.
The first two clauses for  imply that if
imply that if  then \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \mathcal {I}(Q) \cap (X\cup \{\tau \})\). So
then \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \mathcal {I}(Q) \cap (X\cup \{\tau \})\). So  implies \(\mathcal {I}(P)=\mathcal {I}(Q)\). The condition \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) is necessary and sufficient for the system to remain a positive amount of time in state P when X is the set of allowed actions. The next clause says that during this time the environment may be triggered to change the set of actions it allows by an event outside our model, that is, by a timeout in the environment. So P and Q should be related in a triggered environment.
implies \(\mathcal {I}(P)=\mathcal {I}(Q)\). The condition \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) is necessary and sufficient for the system to remain a positive amount of time in state P when X is the set of allowed actions. The next clause says that during this time the environment may be triggered to change the set of actions it allows by an event outside our model, that is, by a timeout in the environment. So P and Q should be related in a triggered environment.
The last clause says that also a \(\mathrm{t}\)-transition of P should be matched by one of Q. Naturally, the \(\mathrm{t}\)-transition of P can be taken only when the system is idling in P, i.e. when \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \). The resulting processes \(P'\) and \(Q'\) should be related again, but only in the same environment allowing X.
Proposition 2
Strong X-bisimilarity and strong reactive bisimilarity are equivalence relations.
Proof
 ,
,  are reflexive, as
are reflexive, as  is a strong reactive bisimulation.
is a strong reactive bisimulation.
 and
and  are symmetric, since strong reactive bisimulations are symmetric by definition.
are symmetric, since strong reactive bisimulations are symmetric by definition.
 and
and  are transitive, for if
are transitive, for if  and
and  are strong reactive bisimulations, then so is
are strong reactive bisimulations, then so is

\(\square \)
Note that the union of arbitrarily many strong reactive bisimulations is itself a strong reactive bisimulation. Therefore, the family of relations  ,
,  for \(X\subseteq A\) can be seen as a strong reactive bisimulation.
for \(X\subseteq A\) can be seen as a strong reactive bisimulation.
To get a firm grasp on strong reactive bisimilarity, the reader is invited to check the two laws mentioned in the Introduction, and then to construct a strong reactive bisimulation between the two systems depicted in Fig. 1. Here, P, Q, R and S are arbitrary subprocesses.
The four processes that are targets of \(\mathrm{t}\)-transitions always run in an environment that blocks b. In an environment that allows a, the branch b.R disappears, so that the left branch of the first process can be matched with the left branch of the second process, and similarly for the two right branches. In an environment that blocks a, this matching won’t fly, as the branch b.R now survives. However, the branches a.Q will disappear, so that the left branch of the first process can be matched with the right branch of the second, and vice versa.
The processes U and V of Fig. 2 show that the pairs that occur in a strong reactive bisimulation are not completely determined by the triples. One has  for any \(X\subseteq A\), yet
for any \(X\subseteq A\), yet  . In particular, when \(a \in X\) the branch \(\mathrm{t}.R\) is redundant, and when \(a \notin X\) the branch a.Q is redundant.
. In particular, when \(a \in X\) the branch \(\mathrm{t}.R\) is redundant, and when \(a \notin X\) the branch a.Q is redundant.
Appendix C, reporting on work by Max Pohlmann [37], offers a context  with the property that
with the property that  iff
iff  , thereby reducing strong reactive bisimilarity to strong bisimilarity. The context
, thereby reducing strong reactive bisimilarity to strong bisimilarity. The context  places a system in a most general environment in which it could be running. This result allows any toolset for checking strong bisimilarity to be applicable for checking strong reactive bisimilarity.
places a system in a most general environment in which it could be running. This result allows any toolset for checking strong bisimilarity to be applicable for checking strong reactive bisimilarity.
2.1 A more general form of reactive bisimulation
The following notion of a generalised strong reactive bisimulation (gsrb) generalises that of a strong reactive bisimulation; yet it induces the same concept of strong reactive bisimilarity. This makes the relation convenient to use for further analysis. I did not introduce it as the original definition, because it lacks a strong motivation.
Definition 3
A gsrb is a symmetric relation  such that, for all
such that, for all  ,
,
-
if
 with \(\alpha \in A\cup \{\tau \}\), then there exists a \(Q'\) such that
with \(\alpha \in A\cup \{\tau \}\), then there exists a \(Q'\) such that  and
and  ,
, -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) with \(X\subseteq A\) and
 , then \(\exists Q'\) with
, then \(\exists Q'\) with  and
and  ,
,
and for all  ,
,
-
if
 with either \(a\in Y\) or \(\mathcal {I}(P)\cap (Y\cup \{\tau \})=\emptyset \), then \(\exists Q'\) with
with either \(a\in Y\) or \(\mathcal {I}(P)\cap (Y\cup \{\tau \})=\emptyset \), then \(\exists Q'\) with  and
and  ,
, -
if
 , then there exists a \(Q'\) such that
, then there exists a \(Q'\) such that  and
and  ,
, -
if \(\mathcal {I}(P)\cap (X\cup Y \cup \{\tau \})=\emptyset \) with \(X\subseteq A\) and
 then \(\exists Q'\) with
then \(\exists Q'\) with 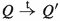 and
and  .
.
Unlike Definition 1, a gsrb needs the triples (P, X, Q) only after encountering a \(\mathrm{t}\)-transition; two systems without \(\mathrm{t}\)-transitions can be related without using these triples at all.
Proposition 4
 iff there exists a gsrb
iff there exists a gsrb  with
with  .
.
Likewise,  iff there exists a gsrb
iff there exists a gsrb  with
with  .
.
Proof
Clearly, each strong reactive bisimulation satisfies the five clauses of Definition 3 and thus is a gsrb. In the other direction, given a gsrb  , let
, let

It is straightforward to check that  satisfies the six clauses of Definition 1. \(\square \)
satisfies the six clauses of Definition 1. \(\square \)
The above proof has been formalised in [37], using the interactive proof assistant Isabelle. The formalisation takes up around 250 lines of code.
3 A modal characterisation of strong reactive bisimilarity
The Hennessy–Milner logic [27] expresses properties of the behaviour of processes in an LTS.
Definition 5
The class  of infinitary HML formulas is defined as follows, where I ranges over all index sets and \(\alpha \) over \(A\cup \{\tau \}\):
of infinitary HML formulas is defined as follows, where I ranges over all index sets and \(\alpha \) over \(A\cup \{\tau \}\):
\(\top \) abbreviates the empty conjunction, and \(\varphi _1\wedge \varphi _2\) stands for \(\bigwedge _{i\in \{1,2\}}\varphi _i\).
\(P\models \varphi \) denotes that process P satisfies formula \(\varphi \). The first two operators represent the standard Boolean operators conjunction and negation. By definition, \(P\models \langle \alpha \rangle \varphi \) iff  for some \(P'\) with \(P'\models \varphi \).
for some \(P'\) with \(P'\models \varphi \).
A famous result stemming from [27] states that

where  denotes strong bisimilarity [27, 33], formally defined in Sect. 7.2. It states that the Hennessy–Milner logic yields a modal characterisation of strong bisimilarity. I will now adapt this result to obtain a modal characterisation of strong reactive bisimilarity.
denotes strong bisimilarity [27, 33], formally defined in Sect. 7.2. It states that the Hennessy–Milner logic yields a modal characterisation of strong bisimilarity. I will now adapt this result to obtain a modal characterisation of strong reactive bisimilarity.
To this end, I extend the Hennessy–Milner logic with a new modality \(\langle X\rangle \), for \(X\subseteq A\), and auxiliary satisfaction relations  for each \(X \subseteq A\). The formula \(P \models \langle X\rangle \varphi \) says that in an environment X, allowing exactly the actions in X, process P can perform a timeout transition to a process that satisfies \(\varphi \). \(P \models _X \varphi \) says that P satisfies \(\varphi \) when placed in environment X. The relations \(\models \) and \(\models _X\) are the smallest ones satisfying:
for each \(X \subseteq A\). The formula \(P \models \langle X\rangle \varphi \) says that in an environment X, allowing exactly the actions in X, process P can perform a timeout transition to a process that satisfies \(\varphi \). \(P \models _X \varphi \) says that P satisfies \(\varphi \) when placed in environment X. The relations \(\models \) and \(\models _X\) are the smallest ones satisfying:

Note that a formula \(\langle a\rangle \varphi \) is less often true under \(\models _X\) than under \(\models \), due to the side condition \(a \in X\). This reflects the fact that a cannot happen in an environment that blocks it. The last clause in the above definition reflects the fifth clause of Definition 1. If \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \), then process P, operating in environment X, idles for a while, during which the environment can change. This ends the blocking of actions \(a \notin X\) and makes any formula valid under \(\models \) also valid under \(\models _X\).
Example 6
Both systems from Fig. 1 satisfy \(\langle \emptyset \rangle \langle \tau \rangle \langle b\rangle \top \wedge \langle \emptyset \rangle \langle \tau \rangle \lnot \langle b\rangle \top \wedge \langle \{a\}\rangle \langle a\rangle \top \wedge \langle \{a\}\rangle \lnot \langle a\rangle \top \) and neither satisfies  or
or  .
.
Theorem 7
Let  and \(X\subseteq A\). Then
and \(X\subseteq A\). Then  and
and  .
.
Proof
“\(\Rightarrow \)”: I prove by simultaneous structural induction on  that, for all
that, for all  and \(X\subseteq A\),
and \(X\subseteq A\),  and
and  . For each \(\varphi \), the converse implications (\(Q \models \varphi \Rightarrow P \models \varphi \) and \(Q \models _X \varphi \Rightarrow P \models _X \varphi \)) follow by symmetry. In particular, these converse directions may be used when invoking the induction hypothesis.
. For each \(\varphi \), the converse implications (\(Q \models \varphi \Rightarrow P \models \varphi \) and \(Q \models _X \varphi \Rightarrow P \models _X \varphi \)) follow by symmetry. In particular, these converse directions may be used when invoking the induction hypothesis.
-
Let
 .
.-
Let \(\varphi = \bigwedge _{i\in I}\varphi _i\). Then, \(P \models \varphi _i\) for all \(i\in I\). By induction \(Q \models \varphi _i\) for all i, so \(Q \models \bigwedge _{i\in I}\varphi _i\).
-
Let \(\varphi = \lnot \psi \). Then, \(P \not \models \psi \). By induction \(Q \not \models \psi \), so \(Q \models \lnot \psi \).
-
Let \(\varphi = \langle \alpha \rangle \psi \) with \(\alpha \in A\cup \{\tau \}\). Then,
 for some \(P'\) with \(P' \models \psi \). By Definition 3,
for some \(P'\) with \(P' \models \psi \). By Definition 3,  for some \(Q'\) with
for some \(Q'\) with  . So by induction \(Q' \models \psi \), and thus \(Q \models \langle \alpha \rangle \psi \).
. So by induction \(Q' \models \psi \), and thus \(Q \models \langle \alpha \rangle \psi \). -
Let \(\varphi = \langle X\rangle \psi \) for some \(X\subseteq A\). Then, \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \) and
 for some \(P'\) with \(P' \models _X \psi \). By Definition 3,
for some \(P'\) with \(P' \models _X \psi \). By Definition 3,  for some \(Q'\) with
for some \(Q'\) with 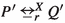 . So by induction \(Q' \models _X \psi \). Moreover, \(\mathcal {I}(Q)=\mathcal {I}(P)\), as
. So by induction \(Q' \models _X \psi \). Moreover, \(\mathcal {I}(Q)=\mathcal {I}(P)\), as  , so \(\mathcal {I}(Q)\cap (X\cup \{\tau \}) = \emptyset \). Thus, \(Q \models \langle X\rangle \psi \).
, so \(\mathcal {I}(Q)\cap (X\cup \{\tau \}) = \emptyset \). Thus, \(Q \models \langle X\rangle \psi \).
-
-
Let
 .
.-
Let \(\varphi = \bigwedge _{i\in I}\varphi _i\), and \(P \models _X \varphi _i\) for all \(i\in I\). By induction \(Q \models _X \varphi _i\) for all \(i\in I\), so \(q \models _X \bigwedge _{i\in I}\varphi _i\).
-
Let \(\varphi = \lnot \psi \), and \(P \not \models _X \psi \). By induction \(Q \not \models _X \psi \), so \(Q \models _X \lnot \psi \).
-
Let \(\varphi = \langle a\rangle \psi \) with \(a\in X\) and
 for some \(P'\) with \(P' \models \psi \). By Definition 1,
for some \(P'\) with \(P' \models \psi \). By Definition 1, 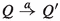 for some \(Q'\) with
for some \(Q'\) with  . By induction \(Q' \models \psi \), so \(Q \models _X \langle a\rangle \psi \).
. By induction \(Q' \models \psi \), so \(Q \models _X \langle a\rangle \psi \). -
Let \(\varphi = \langle \tau \rangle \psi \), and
 for some \(P'\) with \(P' \models _X \psi \). By Definition 1,
for some \(P'\) with \(P' \models _X \psi \). By Definition 1,  for some \(Q'\) with
for some \(Q'\) with  . By induction \(Q' \models _X \psi \), so \(Q \models _X \langle \tau \rangle \psi \).
. By induction \(Q' \models _X \psi \), so \(Q \models _X \langle \tau \rangle \psi \). -
Let \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \) and \(P \models \varphi \). By the fifth clause of Definition 1,
 . Hence, by the previous case in this proof, \(Q \models \varphi \). Moreover, \(\mathcal {I}(Q)\cap (X\cup \{\tau \}) =\mathcal {I}(P) \cap (X\cup \{\tau \})\), since
. Hence, by the previous case in this proof, \(Q \models \varphi \). Moreover, \(\mathcal {I}(Q)\cap (X\cup \{\tau \}) =\mathcal {I}(P) \cap (X\cup \{\tau \})\), since  . Thus, \(Q \models _X \varphi \).
. Thus, \(Q \models _X \varphi \).
-
“\(\Leftarrow \)”: Write \(P\! \equiv \!Q\) for  , and \(P\! \equiv _X \!Q\) for
, and \(P\! \equiv _X \!Q\) for  . I show that the family of relations \(\equiv \), \(\equiv _X\) for \(X\subseteq A\) constitutes a gsrb.
. I show that the family of relations \(\equiv \), \(\equiv _X\) for \(X\subseteq A\) constitutes a gsrb.
-
Suppose \(P \equiv Q\) and
 with \(\alpha \in A \cup \{\tau \}\). Let
with \(\alpha \in A \cup \{\tau \}\). Let  . For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let
. For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let  be a formula such that \(P'\models \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models \varphi _{Q^\dagger }\). (Such a formula always exists because
be a formula such that \(P'\models \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models \varphi _{Q^\dagger }\). (Such a formula always exists because  is closed under negation.) Define
is closed under negation.) Define  . Then, \(P' \models \varphi \), so \(P \models \langle a\rangle \varphi \). Consequently, also \(Q \models \langle a\rangle \varphi \). Hence, there is a \(Q'\) with
. Then, \(P' \models \varphi \), so \(P \models \langle a\rangle \varphi \). Consequently, also \(Q \models \langle a\rangle \varphi \). Hence, there is a \(Q'\) with  and \(Q' \models \varphi \). Since none of the \(Q^\dagger \in \mathcal {Q}^\dagger \) satisfies \(\varphi \), one obtains \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv Q'\).
and \(Q' \models \varphi \). Since none of the \(Q^\dagger \in \mathcal {Q}^\dagger \) satisfies \(\varphi \), one obtains \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv Q'\). -
Suppose \(P \equiv Q\), \(X\subseteq A\), \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \) and
 . Let
. Let 
For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let
 be a formula such that \(P'\models _X \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models _X \varphi _{Q^\dagger }\). Define \(\varphi := \bigwedge _{Q^\dagger \in \mathcal {Q}^\dagger } \varphi _{Q^\dagger }\). Then, \(P' \models _X \varphi \), so \(P \models \langle X\rangle \varphi \). Consequently, also \(Q \models \langle X\rangle \varphi \). Hence, there is a \(Q'\) with
be a formula such that \(P'\models _X \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models _X \varphi _{Q^\dagger }\). Define \(\varphi := \bigwedge _{Q^\dagger \in \mathcal {Q}^\dagger } \varphi _{Q^\dagger }\). Then, \(P' \models _X \varphi \), so \(P \models \langle X\rangle \varphi \). Consequently, also \(Q \models \langle X\rangle \varphi \). Hence, there is a \(Q'\) with  and \(Q' \models _X \varphi \). Again, \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv _X Q'\).
and \(Q' \models _X \varphi \). Again, \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv _X Q'\). -
Suppose \(P \equiv _Y Q\) and
 with \(a\in A\) and either \(a\in Y\) or \(\mathcal {I}(P)\cap (Y\cup \{\tau \})=\emptyset \). Let
with \(a\in A\) and either \(a\in Y\) or \(\mathcal {I}(P)\cap (Y\cup \{\tau \})=\emptyset \). Let  . For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let
. For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let  be a formula such that \(P'\models \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models \varphi _{Q^\dagger }\). Define
be a formula such that \(P'\models \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models \varphi _{Q^\dagger }\). Define  . Then, \(P' \models \varphi \), so \(P \models \langle a\rangle \varphi \), and also \(P \models _Y \langle a\rangle \varphi \), using either the third or last clause in the definition of \(\models _X\). Hence, also \(Q \models _Y \langle a\rangle \varphi \). Therefore, there is a \(Q'\) with
. Then, \(P' \models \varphi \), so \(P \models \langle a\rangle \varphi \), and also \(P \models _Y \langle a\rangle \varphi \), using either the third or last clause in the definition of \(\models _X\). Hence, also \(Q \models _Y \langle a\rangle \varphi \). Therefore, there is a \(Q'\) with  and \(Q' \models \varphi \), using the third clause of either \(\models _X\) or \(\models \). Since none of the \(Q^\dagger \in \mathcal {Q}^\dagger \) satisfies \(\varphi \), one obtains \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv Q'\).
and \(Q' \models \varphi \), using the third clause of either \(\models _X\) or \(\models \). Since none of the \(Q^\dagger \in \mathcal {Q}^\dagger \) satisfies \(\varphi \), one obtains \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv Q'\). -
The fourth clause of Definition 3 is obtained exactly like the first, but using \(\models _Y\) instead of \(\models \).
-
Suppose \(P \equiv _Y Q\),
 and \(\mathcal {I}(P)\cap (X \cup Y\cup \{\tau \}) = \emptyset \), with \(X \subseteq A\). Let
and \(\mathcal {I}(P)\cap (X \cup Y\cup \{\tau \}) = \emptyset \), with \(X \subseteq A\). Let 
For each \(Q^\dagger \in \mathcal {Q}^\dagger \), let
 be a formula such that \(P'\models _X \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models _X \varphi _{Q^\dagger }\). Define \(\varphi := \bigwedge _{Q^\dagger \in \mathcal {Q}^\dagger } \varphi _{Q^\dagger }\). Then, \(P' \models _X \varphi \), so \(P \models \langle X\rangle \varphi \), and thus \(P \models _Y \langle X\rangle \varphi \). Consequently, also \(Q \models _Y \langle X\rangle \varphi \) and therefore \(Q \models \langle X\rangle \varphi \). Hence, there is a \(Q'\) with
be a formula such that \(P'\models _X \varphi _{Q^\dagger }\) and \(Q^\dagger \not \models _X \varphi _{Q^\dagger }\). Define \(\varphi := \bigwedge _{Q^\dagger \in \mathcal {Q}^\dagger } \varphi _{Q^\dagger }\). Then, \(P' \models _X \varphi \), so \(P \models \langle X\rangle \varphi \), and thus \(P \models _Y \langle X\rangle \varphi \). Consequently, also \(Q \models _Y \langle X\rangle \varphi \) and therefore \(Q \models \langle X\rangle \varphi \). Hence, there is a \(Q'\) with  and \(Q' \models _X \varphi \). Again \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv _X Q'\).\(\square \)
and \(Q' \models _X \varphi \). Again \(Q' \notin \mathcal {Q}^\dagger \) and thus \(P' \equiv _X Q'\).\(\square \)
4 Timeout bisimulations
I will now present a characterisation of strong reactive bisimilarity in terms of a binary relation  on processes—a strong timeout bisimulation—not parametrised by the set of allowed actions X. To this end, I need a family of unary operators \(\theta _X\) on processes, for \(X\subseteq A\). These environment operators place a process in an environment that allows exactly the actions in X to occur. They are defined by the following structural operational rules.
on processes—a strong timeout bisimulation—not parametrised by the set of allowed actions X. To this end, I need a family of unary operators \(\theta _X\) on processes, for \(X\subseteq A\). These environment operators place a process in an environment that allows exactly the actions in X to occur. They are defined by the following structural operational rules.

The operator \(\theta _X\) modifies its argument by inhibiting all initial transitions (here including also those that occur after a \(\tau \)-transition) that cannot occur in the specified environment. When an observable transition does occur, the environment may be triggered to change, and the inhibiting effect of the \(\theta _X\)-operator comes to an end. The premises \(x \mathop {\nrightarrow }\limits ^{\beta }~\text{ for } \text{ all }~\beta \in X\cup \{\tau \}\) in the third rule guarantee that the process x will idle for a positive amount of time in its current state. During this time, the environment may be triggered to change, and again the inhibiting effect of the \(\theta _X\)-operator comes to an end.
Below I assume that  is closed under \(\theta \), that is, if
is closed under \(\theta \), that is, if  and \(X\subseteq A\) then
and \(X\subseteq A\) then  .
.
Definition 8
A strong timeout bisimulation is a symmetric relation  , such that, for
, such that, for  ,
,
-
if
 with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that
with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that  and
and  ,
, -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
 , then \(\exists Q'\) such that
, then \(\exists Q'\) such that  and
and  .
.
Proposition 9
 iff there exists a strong timeout bisimulation
iff there exists a strong timeout bisimulation  with
with  .
.
Proof
Let  be a gsrb on
be a gsrb on  . Define
. Define  by
by  iff either
iff either  or \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and
or \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and  . I show that
. I show that  is a strong timeout bisimulation.
is a strong timeout bisimulation.
-
Let
 and
and  with \(a\in A\). First suppose
with \(a\in A\). First suppose  . Then, by the first clause of Definition 3, there exists a \(Q'\) such that
. Then, by the first clause of Definition 3, there exists a \(Q'\) such that  and
and  . So
. So  . Next suppose \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and
. Next suppose \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and 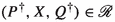 . Since
. Since  it must be that
it must be that  and either \(a\in X\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Hence, there exists a \(Q'\) such that
and either \(a\in X\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Hence, there exists a \(Q'\) such that  and
and  , using the third clause of Definition 3. Recall that
, using the third clause of Definition 3. Recall that  implies \(I(P^\dagger )\cap (X\cup \{\tau \}) = I(Q^\dagger )\cap (X\cup \{\tau \})\), and thus either \(a\in X\) or \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). It follows that
implies \(I(P^\dagger )\cap (X\cup \{\tau \}) = I(Q^\dagger )\cap (X\cup \{\tau \})\), and thus either \(a\in X\) or \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). It follows that  and
and  .
. -
Let
 and
and  . First suppose
. First suppose  . Then, using the first clause of Definition 3, there is a \(Q'\) with
. Then, using the first clause of Definition 3, there is a \(Q'\) with  and
and  . So
. So  . Next suppose \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and
. Next suppose \(P=\theta _{X}(P^\dagger )\), \(Q=\theta _{X}(Q^\dagger )\) and  . Since
. Since  , it must be that \(P'\) has the form \(\theta _{X}(P^\ddagger )\), and
, it must be that \(P'\) has the form \(\theta _{X}(P^\ddagger )\), and  . Thus, by the fourth clause of Definition 3, there is a \(Q^\ddagger \) with
. Thus, by the fourth clause of Definition 3, there is a \(Q^\ddagger \) with  and
and 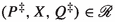 . Now
. Now  and
and  .
. -
Let
 , \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
, \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . First suppose
. First suppose  . Then, by the second clause of Definition 3, there is a \(Q'\) with
. Then, by the second clause of Definition 3, there is a \(Q'\) with  and
and  . So
. So  . Next suppose \(P=\theta _{Y}(P^\dagger )\), \(Q=\theta _{Y}(Q^\dagger )\) and
. Next suppose \(P=\theta _{Y}(P^\dagger )\), \(Q=\theta _{Y}(Q^\dagger )\) and 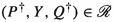 . Since
. Since  , it must be that
, it must be that  and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). Consequently, \(\mathcal {I}(P^\dagger )=\mathcal {I}(P)\) and thus \(\mathcal {I}(P^\dagger ) \cap (X\cup Y\cup \{\tau \}) = \emptyset \). By the last clause of Definition 3 there is a \(Q'\) such that
and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). Consequently, \(\mathcal {I}(P^\dagger )=\mathcal {I}(P)\) and thus \(\mathcal {I}(P^\dagger ) \cap (X\cup Y\cup \{\tau \}) = \emptyset \). By the last clause of Definition 3 there is a \(Q'\) such that  and
and  . So
. So  . From
. From 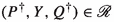 and \(\mathcal {I}(P^\dagger )\cap (Y\cup \{\tau \})=\emptyset \), I infer \(\mathcal {I}(Q^\dagger )\cap (Y\cup \{\tau \})=\emptyset \). So \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). This yields
and \(\mathcal {I}(P^\dagger )\cap (Y\cup \{\tau \})=\emptyset \), I infer \(\mathcal {I}(Q^\dagger )\cap (Y\cup \{\tau \})=\emptyset \). So \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). This yields 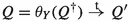 .
.
Now let  be a timeout bisimulation. Define
be a timeout bisimulation. Define  by
by  iff
iff  , and
, and  iff
iff  . I need to show that
. I need to show that  is a gsrb.
is a gsrb.
-
Suppose
 and
and  with \(\alpha \in A\cup \{\tau \}\). Then,
with \(\alpha \in A\cup \{\tau \}\). Then,  , so there is a \(Q'\) such that
, so there is a \(Q'\) such that  and
and  . Hence,
. Hence,  .
. -
Suppose
 , \(X\subseteq A\), \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
, \(X\subseteq A\), \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . Then,
. Then,  , so \(\exists Q'\) such that
, so \(\exists Q'\) such that  and
and  . Thus,
. Thus,  .
. -
Suppose
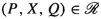 and
and 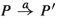 with either \(a\in X\) or \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \). Then,
with either \(a\in X\) or \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \). Then,  . Moreover,
. Moreover,  . Hence, there is a \(Q'\) such that
. Hence, there is a \(Q'\) such that  and
and  . It must be that
. It must be that  . Moreover,
. Moreover,  .
. -
Suppose
 and
and  . Then,
. Then,  . Since
. Since  , one has
, one has  . Hence, there is an R such that
. Hence, there is an R such that  and
and  . The process R must have the form \(\theta _X(Q')\) for some \(Q'\) with
. The process R must have the form \(\theta _X(Q')\) for some \(Q'\) with  . It follows that
. It follows that  .
. -
Suppose
 , \(X\subseteq A\), \(\mathcal {I}(P)\cap (X\cup Y \cup \{\tau \})=\emptyset \) and
, \(X\subseteq A\), \(\mathcal {I}(P)\cap (X\cup Y \cup \{\tau \})=\emptyset \) and  . Then,
. Then,  and
and  . Moreover, \(\mathcal {I}(\theta _Y(P))=\mathcal {I}(P)\), so by the second clause of Definition 8 there exists a \(Q'\) such that
. Moreover, \(\mathcal {I}(\theta _Y(P))=\mathcal {I}(P)\), so by the second clause of Definition 8 there exists a \(Q'\) such that  and
and  . So
. So  and
and  .\(\square \)
.\(\square \)
Note that the union of arbitrarily many strong timeout bisimulations is itself a strong timeout bisimulation. Consequently, the relation  is a strong timeout bisimulation.
is a strong timeout bisimulation.
5 The process algebra \(\text{ CCSP}_\mathrm{t}^\theta \)
Let A be a set of visible actions and \({ Var}\) an infinite set of variables. The syntax of \(\text{ CCSP}_\mathrm{t}^\theta \) is given by

with \(\alpha \in Act := A \uplus \{\tau ,\mathrm{t}\}\), \(S,I,U,L,X\subseteq A\), \(L \subseteq U\), \(\mathcal {R}\subseteq A \mathop \times A\), \(x \in { Var}\) and \({{\mathcal {S}}}\) a recursive specification: a set of equations \(\{y = {{\mathcal {S}}}_{y} \mid y \in V_{{\mathcal {S}}}\}\) with \(V_{{\mathcal {S}}}\subseteq { Var}\) (the bound variables of \({{\mathcal {S}}}\)) and each \({{\mathcal {S}}}_{y}\) a \(\text{ CCSP}_\mathrm{t}^\theta \) expression. I require that all sets \({\{b\mid (a,b)\in \mathcal {R}\}}\) are finite.
The constant 0 represents a process that is unable to perform any action. The process \(\alpha .E\) first performs the action \(\alpha \) and then proceeds as E. The process \(E+F\) behaves as either E or F. \({\Vert ^{}_{S}}\) is a partially synchronous parallel composition operator; actions \(a\in S\) must synchronise—they can occur only when both arguments are ready to perform them—whereas actions \(\alpha \notin S\) from both arguments are interleaved. \(\tau _I\) is an abstraction operator; it conceals the actions in I by renaming them into the hidden action \(\tau \). The operator \(\mathcal {R}\) is a relational renaming: it renames a given action \(a\in A\) into a choice between all actions b with \((a,b)\in \mathcal {R}\). The environment operators \(\theta _L^U\) and \(\psi _X\) are new in this paper and explained below. Finally,  represents the x-component of a solution of the system of recursive equations \({{\mathcal {S}}}\).
represents the x-component of a solution of the system of recursive equations \({{\mathcal {S}}}\).
The language CCSP is a common mix of the process algebras CCS [33] and CSP [6, 28]. It first appeared in [34], where it was named following a suggestion by M. Nielsen. The family of parallel composition operators \(\Vert _S\) stems from [35], and incorporates the two CSP parallel composition operators from [6]. The relation renaming operators \(\mathcal {R}(\_\!\_)\) stem from [39]; they combine both the (functional) renaming operators that are common to CCS and CSP, and the inverse image operators of CSP. The choice operator \(+\) stems from CCS, and the abstraction operator from CSP, while the inaction constant 0, action prefixing operators \(a.\_\!\_\,\) for \(a\in A\), and the recursion construct are common to CCS and CSP. The timeout prefixing operator \(\mathrm{t}.\_\!\_\,\) was added by me in [18]. The syntactic form of inaction 0, action prefixing \(\alpha .E\) and choice \(E+F\) follows CCS, whereas the syntax of abstraction \(\tau _I(\_\!\_)\) and recursion  follows ACP [2, 10]. The fragment of \(\text{ CCSP}_\mathrm{t}^\theta \) without \(\theta _L^U\) and \(\psi _X\) is called \(\hbox {CCSP}_\mathrm{t}\) [18].
follows ACP [2, 10]. The fragment of \(\text{ CCSP}_\mathrm{t}^\theta \) without \(\theta _L^U\) and \(\psi _X\) is called \(\hbox {CCSP}_\mathrm{t}\) [18].
An occurrence of a variable x in a \(\text{ CCSP}_\mathrm{t}^\theta \) expression E is bound iff it occurs in a subexpression  of E with \(x \in V_{{\mathcal {S}}}\); otherwise it is free. Here, each \({{\mathcal {S}}}_y\) for \(y \in V_{{\mathcal {S}}}\) counts as a subexpression of
of E with \(x \in V_{{\mathcal {S}}}\); otherwise it is free. Here, each \({{\mathcal {S}}}_y\) for \(y \in V_{{\mathcal {S}}}\) counts as a subexpression of  . An expression E is invalid if it has a subexpression \(\theta _L^U(F)\) or \(\psi _X(F)\) such that a variable occurrence in F is free in F but bound in E. Let
. An expression E is invalid if it has a subexpression \(\theta _L^U(F)\) or \(\psi _X(F)\) such that a variable occurrence in F is free in F but bound in E. Let  be the set of valid \(\text{ CCSP}_\mathrm{t}^\theta \) expressions. Furthermore,
be the set of valid \(\text{ CCSP}_\mathrm{t}^\theta \) expressions. Furthermore,  is the set of closed valid \(\text{ CCSP}_\mathrm{t}^\theta \) expressions, or processes; those in which every variable occurrence is bound.
is the set of closed valid \(\text{ CCSP}_\mathrm{t}^\theta \) expressions, or processes; those in which every variable occurrence is bound.
A substitution is a partial function  . The application \(E[\rho ]\) of a substitution \(\rho \) to an expression
. The application \(E[\rho ]\) of a substitution \(\rho \) to an expression  is the result of simultaneous replacement, for all \(x\in \text {dom}(\rho )\), of each free occurrence of x in E by the expression \(\rho (x)\), while renaming bound variables in E if necessary to prevent name clashes.
is the result of simultaneous replacement, for all \(x\in \text {dom}(\rho )\), of each free occurrence of x in E by the expression \(\rho (x)\), while renaming bound variables in E if necessary to prevent name clashes.
The semantics of \(\text{ CCSP}_\mathrm{t}^\theta \) is given by the labelled transition relation  , where the transitions
, where the transitions  are derived from the rules of Table 1. Here,
are derived from the rules of Table 1. Here,  for
for  and \({{\mathcal {S}}}\) a recursive specification denotes the result of substituting
and \({{\mathcal {S}}}\) a recursive specification denotes the result of substituting  for y in E, for all \(y \in V_{{\mathcal {S}}}\).
for y in E, for all \(y \in V_{{\mathcal {S}}}\).
The auxiliary operators \(\theta _L^U\) and \(\psi _X\) are added here to facilitate complete axiomatisation, similar to the left merge and communication merge of ACP [2, 10]. The operator \(\theta _X^X\) is the same as what was called \(\theta _X\) in Sect. 4. It inhibits those transitions of its argument that are blocked in the environment X, allowing only the actions from \(X\subseteq A\). It stops inhibiting as soon as the system performs a visible action or takes a break, as this may trigger a change in the environment. The operator \(\theta _L^U\) preserves those transitions that are allowed in some environment X with \(L\subseteq X \subseteq U\). The letters L and U stand for lower and upper bound. The operator \(\psi _X\) places a process in the environment X when a timeout transition occurs; it is inert if any other transition occurs. If  for \(\beta \in A\cup \{\tau \}\), then a timeout transition
for \(\beta \in A\cup \{\tau \}\), then a timeout transition  cannot occur in an environment that allows \(\beta \). Thus, the transition
cannot occur in an environment that allows \(\beta \). Thus, the transition  survives only when considering an environment that blocks \(\beta \), meaning \(\beta \notin X\cup \{\tau \}\). Taking the contrapositive, \(\beta \in X\cup \{\tau \}\) implies \(P \mathop {\nrightarrow }\limits ^{\beta }\).
survives only when considering an environment that blocks \(\beta \), meaning \(\beta \notin X\cup \{\tau \}\). Taking the contrapositive, \(\beta \in X\cup \{\tau \}\) implies \(P \mathop {\nrightarrow }\limits ^{\beta }\).
The operator \(\theta ^U_\emptyset \) features in the forthcoming law L3, which is a convenient addition to my axiomatisation, although only \(\psi _X\) and \(\theta _X\) (\(= \theta _X^X\)) are necessary for completeness.
Stratification.
Even though negative premises occur in Table 1, the meaning of this transition system specification is well-defined, for instance by the method of stratification explained in [15, 25]. Assign inductively to each expression  an ordinal \(\lambda _E\) that counts the nesting depth of recursive specifications: if
an ordinal \(\lambda _E\) that counts the nesting depth of recursive specifications: if  then \(\lambda _E\) is 1 more than the supremum of the \(\lambda _{S_y}\) for \(y \in V_{{\mathcal {S}}}\); otherwise \(\lambda _E\) is the supremum of
then \(\lambda _E\) is 1 more than the supremum of the \(\lambda _{S_y}\) for \(y \in V_{{\mathcal {S}}}\); otherwise \(\lambda _E\) is the supremum of  for all subterms
for all subterms  of E. Moreover
of E. Moreover  is the nesting depth of \(\theta _L^U\) and \(\psi _X\) operators in E that remain after replacing any subterm F of E with \(\lambda _F < \lambda _E\) by 0. Now the ordered pair \((\lambda _P,\kappa _P)\) constitutes a valid stratification for closed literals
is the nesting depth of \(\theta _L^U\) and \(\psi _X\) operators in E that remain after replacing any subterm F of E with \(\lambda _F < \lambda _E\) by 0. Now the ordered pair \((\lambda _P,\kappa _P)\) constitutes a valid stratification for closed literals  . Namely, whenever a transition
. Namely, whenever a transition  depends on a transition
depends on a transition  , in the sense that that there is a closed substitution instance \({\mathfrak {r}}\) of a rule from Table 1 with conclusion
, in the sense that that there is a closed substitution instance \({\mathfrak {r}}\) of a rule from Table 1 with conclusion  , and
, and  occurring in its premises, then either \(\lambda _Q < \lambda _P\), or \(\lambda _Q = \lambda _P\) and \(\kappa _Q \le \kappa _P\). Moreover, when
occurring in its premises, then either \(\lambda _Q < \lambda _P\), or \(\lambda _Q = \lambda _P\) and \(\kappa _Q \le \kappa _P\). Moreover, when  depends on a negative literal \(Q \mathop {\nrightarrow }\limits ^{\beta }\), then \(\lambda _Q = \lambda _P\) and \(\kappa _Q < \kappa _P\).
depends on a negative literal \(Q \mathop {\nrightarrow }\limits ^{\beta }\), then \(\lambda _Q = \lambda _P\) and \(\kappa _Q < \kappa _P\).
The above argument hinges on the exclusion of invalid \(\text{ CCSP}_\mathrm{t}^\theta \) expressions. The invalid expression  for instance, with \(\mathcal {R}= \{(b,a)\}\), does not have a well-defined meaning, since the transition
for instance, with \(\mathcal {R}= \{(b,a)\}\), does not have a well-defined meaning, since the transition  is derivable iff one has the premise \(P{\mathop {\nrightarrow }\limits ^{b}}\):
is derivable iff one has the premise \(P{\mathop {\nrightarrow }\limits ^{b}}\):

However, the meaning of the valid expression  , for instance, is entirely unproblematic.
, for instance, is entirely unproblematic.
6 Guarded recursion and finitely branching processes
In many process algebraic specification approaches, only guarded recursive specifications are allowed.
Definition 10
An occurrence of a variable x in an expression E is guarded if x occurs in a subexpression \(\alpha .F\) of E, with \(\alpha \in Act\). An expression E is guarded if all free occurrences of variables in E are guarded. A recursive specification \({{\mathcal {S}}}\) is manifestly guarded if all expressions \({{\mathcal {S}}}_y\) for \(y\in V_{{\mathcal {S}}}\) are guarded. It is guarded if it can be converted into a manifestly guarded recursive specification by repeated substitution of expressions \({{\mathcal {S}}}_y\) for variables \(y\in V_{{\mathcal {S}}}\) occurring in the expressions \({{\mathcal {S}}}_z\) for \(z\in V_{{\mathcal {S}}}\). Let guarded \(\text{ CCSP}_\mathrm{t}^\theta \) be the fragment of \(\text{ CCSP}_\mathrm{t}^\theta \) allowing only guarded recursion.
Definition 11
The set of processes reachable from a given process  is inductively defined by
is inductively defined by
-
(i)
P is reachable from P, and
-
(ii)
if Q is reachable from P and
 for some \(\alpha \in Act\) then R is reachable from P.
for some \(\alpha \in Act\) then R is reachable from P.
A process P is finitely branching if for all  reachable from P there are only finitely many pairs \((\alpha ,R)\) such that
reachable from P there are only finitely many pairs \((\alpha ,R)\) such that  . Likewise, P is countably branching if there are countably many such pairs. A process is finite iff it is finitely branching, has finitely many reachable states, and is loop-free, in the sense that there are no
. Likewise, P is countably branching if there are countably many such pairs. A process is finite iff it is finitely branching, has finitely many reachable states, and is loop-free, in the sense that there are no  with \(n>0\) and \(Q_0=Q_n\) reachable from P.
with \(n>0\) and \(Q_0=Q_n\) reachable from P.
Proposition 12
Each \(\text{ CCSP}_\mathrm{t}^\theta \) process is countably branching.
Proof
I show that for each \(\text{ CCSP}_\mathrm{t}^\theta \) process Q there are only countably many transitions  . Each such transition must be derivable from the rules of Table 1. So it suffices to show that for each Q there are only countably many derivations of transitions
. Each such transition must be derivable from the rules of Table 1. So it suffices to show that for each Q there are only countably many derivations of transitions  .
.
A derivation of a transition is a well-founded, upwardly branching tree, in which each node models an application of one of the rules of Table 1. Since each of these rules has finitely many positive premises, such a proof tree is finitely branching, and thus finite. Let \(d(\pi )\), the depth of \(\pi \), be the length of the longest branch in a derivation \(\pi \). If \(\pi \) derives a transition  , then I call Q the source of \(\pi \).
, then I call Q the source of \(\pi \).
It suffices to show that for each  there are only finitely many derivations of depth n with a given source. This I do by induction on n.
there are only finitely many derivations of depth n with a given source. This I do by induction on n.
In case \(Q=f(Q_1,\dots ,Q_k)\), with f an k-ary \(\text{ CCSP}_\mathrm{t}^\theta \) operator, a derivation \(\pi \) of depth n is completely determined by the concluding rule from Table 1, deriving a transition  , the subderivations of \(\pi \) with source \(Q_i\) for some of the \(i\in \{1,\dots ,k\}\), and the transition label \(\beta \). (For the purposes of this proof, Table 1 is understood to have only 15 rules, even if each of them can be seen as a template, with an instance for each choice of \(\mathcal {R}\), S, I, \({{\mathcal {S}}}\) etc., and for each fitting choice of a transition labels a, \(\alpha \) and/or \(\beta \).) The choice of the concluding rule depends on f, and for each f there are at most three choices. The subderivations of \(\pi \) with source \(Q_i\) have depth \(< n\), so by induction there are only finitely many. When f is not a renaming operator \(\mathcal {R}\), there is no further choice for the transition label \(\beta \), as it is completely determined by the premises of the rule, and thus by the subderivations of those premises. In case \(f=\mathcal {R}\), there are finitely many choices for \(\beta \) when faced with a given transition label \(\alpha \) contributed by the premise of the rule for renaming. Here, I use the requirement of Sect. 5 that all sets \({\{b\mid (a,b)\in \mathcal {R}\}}\) are finite. This shows there are only finitely many choices for \(\pi \).
, the subderivations of \(\pi \) with source \(Q_i\) for some of the \(i\in \{1,\dots ,k\}\), and the transition label \(\beta \). (For the purposes of this proof, Table 1 is understood to have only 15 rules, even if each of them can be seen as a template, with an instance for each choice of \(\mathcal {R}\), S, I, \({{\mathcal {S}}}\) etc., and for each fitting choice of a transition labels a, \(\alpha \) and/or \(\beta \).) The choice of the concluding rule depends on f, and for each f there are at most three choices. The subderivations of \(\pi \) with source \(Q_i\) have depth \(< n\), so by induction there are only finitely many. When f is not a renaming operator \(\mathcal {R}\), there is no further choice for the transition label \(\beta \), as it is completely determined by the premises of the rule, and thus by the subderivations of those premises. In case \(f=\mathcal {R}\), there are finitely many choices for \(\beta \) when faced with a given transition label \(\alpha \) contributed by the premise of the rule for renaming. Here, I use the requirement of Sect. 5 that all sets \({\{b\mid (a,b)\in \mathcal {R}\}}\) are finite. This shows there are only finitely many choices for \(\pi \).
In case  , the last step in \(\pi \) must be application of the rule for recursion, so \(\pi \) is completely determined by a subderivation \(\pi '\) of a transition with source
, the last step in \(\pi \) must be application of the rule for recursion, so \(\pi \) is completely determined by a subderivation \(\pi '\) of a transition with source  . By induction there are only finitely many choices for \(\pi '\), and hence also for \(\pi \). \(\square \)
. By induction there are only finitely many choices for \(\pi '\), and hence also for \(\pi \). \(\square \)
Proposition 13
Each \(\text{ CCSP}_\mathrm{t}^\theta \) process with guarded recursion is finitely branching.
Proof
A trivial structural induction shows that if P is a \(\text{ CCSP}_\mathrm{t}^\theta \) process with guarded recursion and Q is reachable from P, then also Q has guarded recursion. Hence, it suffices to show that for each \(\text{ CCSP}_\mathrm{t}^\theta \) process Q with guarded recursion there are only finitely many derivations with source Q.
Let \(\rightsquigarrow \) be the smallest binary relation on  such that (i) \(f(P_1,\dots ,P_k) \rightsquigarrow P_i\) for each k-ary \(\text{ CCSP}_\mathrm{t}^\theta \) operator f except action prefixing, and each \(i\in \{1,\dots ,k\}\), and (ii)
such that (i) \(f(P_1,\dots ,P_k) \rightsquigarrow P_i\) for each k-ary \(\text{ CCSP}_\mathrm{t}^\theta \) operator f except action prefixing, and each \(i\in \{1,\dots ,k\}\), and (ii)  . This relation is finitely branching. Moreover, on processes with guarded recursion, \(\rightsquigarrow \) has no forward infinite chains \(P_0 \rightsquigarrow P_1 \rightsquigarrow \dots \). In fact, this could have been used as an alternative definition of guarded recursion. Let, for any process Q with guarded recursion, e(Q) be the length of the longest forward chain \(Q \rightsquigarrow P_1 \rightsquigarrow \dots \rightsquigarrow P_{e(Q)}\). I show with induction on e(Q) that there are only finitely many derivations with source Q. In fact, this proceeds exactly as in the previous proof. \(\square \)
. This relation is finitely branching. Moreover, on processes with guarded recursion, \(\rightsquigarrow \) has no forward infinite chains \(P_0 \rightsquigarrow P_1 \rightsquigarrow \dots \). In fact, this could have been used as an alternative definition of guarded recursion. Let, for any process Q with guarded recursion, e(Q) be the length of the longest forward chain \(Q \rightsquigarrow P_1 \rightsquigarrow \dots \rightsquigarrow P_{e(Q)}\). I show with induction on e(Q) that there are only finitely many derivations with source Q. In fact, this proceeds exactly as in the previous proof. \(\square \)
Proposition 14
[13] Each finitely branching process in an LTS can be denoted by a closed \(\hbox {CCSP}_\mathrm{t}\) expression with guarded recursion. Here, I only need the operations inaction (0), action prefixing (\(\alpha .\_\!\_\,\)) and choice (\(+\)), as well as recursion  .
.
Proof
Let P be a finitely branching process in an LTS  . Let
. Let

For each Q reachable from P, let \(\textit{next}(Q)\) be the finite set of pairs  such that there is a transition
such that there is a transition  . Define the recursive specification \({{\mathcal {S}}}\) as \(\{x_Q = \sum _{(\alpha ,R)\in \textit{next}(Q)} \alpha .x_R \mid x_Q \in V_{{\mathcal {S}}}\}\). Here, the finite choice operator \(\sum _{i\in I}\alpha _i.P_i\) can easily be expressed in terms of inaction, action prefixing and choice. Now the \(\hbox {CCSP}_\mathrm{t}\) process
. Define the recursive specification \({{\mathcal {S}}}\) as \(\{x_Q = \sum _{(\alpha ,R)\in \textit{next}(Q)} \alpha .x_R \mid x_Q \in V_{{\mathcal {S}}}\}\). Here, the finite choice operator \(\sum _{i\in I}\alpha _i.P_i\) can easily be expressed in terms of inaction, action prefixing and choice. Now the \(\hbox {CCSP}_\mathrm{t}\) process  denotes P. \(\square \)
denotes P. \(\square \)
In fact,  , where
, where  denotes strong bisimilarity [33], formally defined in the next section.
denotes strong bisimilarity [33], formally defined in the next section.
Likewise, recursion-free \(\text{ CCSP}_\mathrm{t}^\theta \) processes are finite, and, up to strong bisimilarity, each finite process is denotable by a closed recursion-free \(\text{ CCSP}_\mathrm{t}^\theta \) expression, using only 0, \(\alpha .\_\!\_\,\) and \(+\).
Proposition 15
[13] Each countably branching process in an LTS can be denoted by a closed \(\hbox {CCSP}_\mathrm{t}\) expression. Again I only need the \(\hbox {CCSP}_\mathrm{t}\) operations inaction, action prefixing, choice and recursion.
Proof
The proof is the same as the previous one, except that \(\textit{next}(Q)\) now is a countable set, rather than a finite one, and consequently I need a countable choice operator  . The latter can be expressed in \(\hbox {CCSP}_\mathrm{t}\) with unguarded recursion by
. The latter can be expressed in \(\hbox {CCSP}_\mathrm{t}\) with unguarded recursion by  . \(\square \)
. \(\square \)
7 Congruence
Given an arbitrary process algebra with a collection of operators f, each with an arity n, and a recursion construct  as in Sect. 5, let
as in Sect. 5, let  and
and  be the sets of [closed] valid expressions, and let a substitution instance
be the sets of [closed] valid expressions, and let a substitution instance  for
for  and
and  be defined as in Sect. 5. Any semantic equivalence
be defined as in Sect. 5. Any semantic equivalence  extends to
extends to  by defining \(E \sim F\) iff \(E[\rho ] \sim F[\rho ]\) for each closed substitution
by defining \(E \sim F\) iff \(E[\rho ] \sim F[\rho ]\) for each closed substitution  . It extends to substitutions
. It extends to substitutions  by \(\rho \sim \nu \) iff \(\text {dom}(\rho ) = \text {dom}(\nu )\) and \(\rho (x) \sim \nu (x)\) for each \(x\in \text {dom}(\rho )\).
by \(\rho \sim \nu \) iff \(\text {dom}(\rho ) = \text {dom}(\nu )\) and \(\rho (x) \sim \nu (x)\) for each \(x\in \text {dom}(\rho )\).
Definition 16
[16] A semantic equivalence \({\sim }\) is a lean congruence if \(E[\rho ] \sim E[\nu ]\) for any expression  and any substitutions \(\rho \) and \(\nu \) with \(\rho \sim \nu \). It is a full congruence if it satisfies
and any substitutions \(\rho \) and \(\nu \) with \(\rho \sim \nu \). It is a full congruence if it satisfies


for all functions f of arity n, processes  , and recursive specifications \({{\mathcal {S}}},{{\mathcal {S}}}'\) with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\) and
, and recursive specifications \({{\mathcal {S}}},{{\mathcal {S}}}'\) with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\) and  .
.
Clearly, each full congruence is also a lean congruence, and each lean congruence satisfies (1). Both implications are strict, as illustrated in [16].
A main result of the present paper will be that strong reactive bisimilarity is a full congruence for the process algebra \(\text{ CCSP}_\mathrm{t}^\theta \). To achieve it, I need to establish first that strong bisimilarity [33],  , and initials equivalence [14, Section 16], \(=_\mathcal {I}\), are full congruences for \(\text{ CCSP}_\mathrm{t}^\theta \).
, and initials equivalence [14, Section 16], \(=_\mathcal {I}\), are full congruences for \(\text{ CCSP}_\mathrm{t}^\theta \).
7.1 Initials equivalence
Definition 17
Two \(\text{ CCSP}_\mathrm{t}^\theta \) processes P and Q are initials equivalent, denoted \(P =_\mathcal {I}Q\), if \(\mathcal {I}(P)=\mathcal {I}(Q)\).
Theorem 18
Initials equivalence is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \).
Proof
In Appendix A. \(\square \)
7.2 Strong bisimilarity
Definition 19
A strong bisimulation is a symmetric relation  on
on  , such that, whenever
, such that, whenever  ,
,
-
if
 with \(\alpha \in Act\) then
with \(\alpha \in Act\) then  for some \(Q'\) with
for some \(Q'\) with 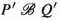 .
.
Two processes  are strongly bisimilar,
are strongly bisimilar,  , if
, if  for some strong bisimulation
for some strong bisimulation  .
.
Contrary to reactive bisimilarity, strong bisimilarity treats the timeout action \(\mathrm{t}\), as well as the hidden action \(\tau \), just like any visible action. In the absence of timeout actions, there is no difference between a strong bisimulation and a timeout bisimulation, so  and
and  coincide. In general, strong bisimulation is a finer equivalence relation than strong reactive bisimilarity and initials equivalence:
coincide. In general, strong bisimulation is a finer equivalence relation than strong reactive bisimilarity and initials equivalence:  , and both implications are strict.
, and both implications are strict.
Lemma 1
For each \(\text{ CCSP}_\mathrm{t}^\theta \) process P, there exists a \(\hbox {CCSP}_\mathrm{t}\) process Q only built using inaction, action prefixing, choice and recursion, such that  .
.
Proof
Immediately from Propositions 12 and 15. \(\square \)
Theorem 20
Strong bisimilarity is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \).
Proof
The structural operational rules for \(\hbox {CCSP}_\mathrm{t}\) (that is, \(\text{ CCSP}_\mathrm{t}^\theta \) without the operators \(\theta _L^U\) and \(\psi _X\)) fit the tyft/tyxt format with recursion of [16]. By [16, Theorem 3] this implies that  is a full congruence for \(\hbox {CCSP}_\mathrm{t}\). (In fact, when omitting the recursion construct, the operational rules for \(\hbox {CCSP}_\mathrm{t}\) fit the tyft/tyxt format of [26], and by the main theorem of [26],
is a full congruence for \(\hbox {CCSP}_\mathrm{t}\). (In fact, when omitting the recursion construct, the operational rules for \(\hbox {CCSP}_\mathrm{t}\) fit the tyft/tyxt format of [26], and by the main theorem of [26],  is a congruence for the operators of \(\hbox {CCSP}_\mathrm{t}\), that is, it satisfies (1) in Definition 16. The work of [16] extends this result of [26] with recursion.)
is a congruence for the operators of \(\hbox {CCSP}_\mathrm{t}\), that is, it satisfies (1) in Definition 16. The work of [16] extends this result of [26] with recursion.)
The structural operational rules for all of \(\text{ CCSP}_\mathrm{t}^\theta \) fit the ntyft/ntyxt format with recursion of [16]. By [16, Theorem 2] this implies that  is a lean congruence for \(\text{ CCSP}_\mathrm{t}^\theta \). (In fact, when omitting the recursion construct, the operational rules for \(\text{ CCSP}_\mathrm{t}^\theta \) fit the ntyft/ntyxt format of [25], and by the main theorem of [25],
is a lean congruence for \(\text{ CCSP}_\mathrm{t}^\theta \). (In fact, when omitting the recursion construct, the operational rules for \(\text{ CCSP}_\mathrm{t}^\theta \) fit the ntyft/ntyxt format of [25], and by the main theorem of [25],  is a congruence for the operators of \(\text{ CCSP}_\mathrm{t}^\theta \). The work of [16] extends this result of [25] with recursion.)
is a congruence for the operators of \(\text{ CCSP}_\mathrm{t}^\theta \). The work of [16] extends this result of [25] with recursion.)
To verify (2) for the whole language \(\text{ CCSP}_\mathrm{t}^\theta \), let \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) be recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that  and
and  for all \(y\in V_{{\mathcal {S}}}\). Let \(\{P_i \mid i \in I\}\) be the collection of processes of the form
for all \(y\in V_{{\mathcal {S}}}\). Let \(\{P_i \mid i \in I\}\) be the collection of processes of the form  or
or  , for some L, U, X, that occur as a closed subexpression of \({{\mathcal {S}}}_y\) or \({{\mathcal {S}}}'_y\) for one of the \(y\in V_{{\mathcal {S}}}\), not counting strict subexpressions of a closed subexpression R of
\({{\mathcal {S}}}_y\) or \({{\mathcal {S}}}'_y\) that is itself of the form
, for some L, U, X, that occur as a closed subexpression of \({{\mathcal {S}}}_y\) or \({{\mathcal {S}}}'_y\) for one of the \(y\in V_{{\mathcal {S}}}\), not counting strict subexpressions of a closed subexpression R of
\({{\mathcal {S}}}_y\) or \({{\mathcal {S}}}'_y\) that is itself of the form  or
or  . Pick a fresh variable
\(z_i\notin V_{{\mathcal {S}}}\) for each \(i\in I\), and let, for \(y\in V_{{\mathcal {S}}}\),
. Pick a fresh variable
\(z_i\notin V_{{\mathcal {S}}}\) for each \(i\in I\), and let, for \(y\in V_{{\mathcal {S}}}\),  be the result of replacing each occurrence of \(P_i\) in \({{\mathcal {S}}}_y\) by \(z_i\). Then,
be the result of replacing each occurrence of \(P_i\) in \({{\mathcal {S}}}_y\) by \(z_i\). Then,  does not contain the operators \(\theta _L^U(Q)\) or \(\psi _X(Q)\). In deriving this conclusion, it is essential that
does not contain the operators \(\theta _L^U(Q)\) or \(\psi _X(Q)\). In deriving this conclusion, it is essential that  is a valid expression, for this implies that the term
is a valid expression, for this implies that the term  , which may contain free occurrences of the variables \(y\in V_{{\mathcal {S}}}\), does not have a subterm of the form
, which may contain free occurrences of the variables \(y\in V_{{\mathcal {S}}}\), does not have a subterm of the form  or
or  that contains free occurrences of these variables. Let
that contains free occurrences of these variables. Let
 ; it is a recursive specification in the language \(\hbox {CCSP}_\mathrm{t}\). The recursive specification
; it is a recursive specification in the language \(\hbox {CCSP}_\mathrm{t}\). The recursive specification  is defined in the same way.
is defined in the same way.
For each \(i\in I\) there is, by Lemma 1, a process \(Q_i\) in the language \(\hbox {CCSP}_\mathrm{t}\) such that  . Now let
. Now let  be the substitutions defined by \(\rho (z_i)=P_i\) and \(\eta (z_i) = Q_i\) for all \(i \in I\). Then,
be the substitutions defined by \(\rho (z_i)=P_i\) and \(\eta (z_i) = Q_i\) for all \(i \in I\). Then,  . Since
. Since  is a lean congruence for \(\text{ CCSP}_\mathrm{t}^\theta \), one has
is a lean congruence for \(\text{ CCSP}_\mathrm{t}^\theta \), one has  and likewise
and likewise  . For the same reason, one has
. For the same reason, one has  for all \(y \in V_{{\mathcal {S}}}\). Since \({\widehat{{{\mathcal {S}}}}}[\eta ]\) and \({\widehat{{{\mathcal {S}}}}}'[\eta ]\) are recursive specifications over \(\hbox {CCSP}_\mathrm{t}\),
for all \(y \in V_{{\mathcal {S}}}\). Since \({\widehat{{{\mathcal {S}}}}}[\eta ]\) and \({\widehat{{{\mathcal {S}}}}}'[\eta ]\) are recursive specifications over \(\hbox {CCSP}_\mathrm{t}\),  . Hence,
. Hence,  . \(\square \)
. \(\square \)
The following lemmas on the relation between \(\theta _X\) and the other operators of \(\text{ CCSP}_\mathrm{t}^\theta \) deal with strong bisimilarity, but are needed in the congruence proof for strong reactive bisimilarity. Their proofs can be found in Appendix B.
Lemma 2
If \(P{{\mathop {\nrightarrow }\limits ^{\tau }}}\), \(\mathcal {I}(P) \cap X \subseteq S\) and \(Y=X\setminus (S\setminus \mathcal {I}(P))\), then 
 .
.
Lemma 3
 .
.
Lemma 4
 .
.
8 Strong reactive bisimilarity is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \)
The forthcoming proofs showing that  is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \) follow the lines of Milner [33], but are more complicated due to the nature of reactive bisimilarity. A crucial tool is Milner’s notion of bisimilarity up-to. The above three lemmas play an essential rôle. Even if we would not be interested in the operators \(\theta _L^U\) and \(\psi _X\), the proof needs to take the operator \(\theta _X\) (\(= \theta _X^X\)) along in order to deal with the other operators. This is a consequence of the occurrence of \(\theta _X\) in Definition 8.
is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \) follow the lines of Milner [33], but are more complicated due to the nature of reactive bisimilarity. A crucial tool is Milner’s notion of bisimilarity up-to. The above three lemmas play an essential rôle. Even if we would not be interested in the operators \(\theta _L^U\) and \(\psi _X\), the proof needs to take the operator \(\theta _X\) (\(= \theta _X^X\)) along in order to deal with the other operators. This is a consequence of the occurrence of \(\theta _X\) in Definition 8.
Definition 21
Given a relation  , a strong timeout bisimulation up to \(\sim \) is a symmetric relation
, a strong timeout bisimulation up to \(\sim \) is a symmetric relation  , such that, for
, such that, for  ,
,
-
if
 with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that
with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that  and
and  ,
, -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
 , then \(\exists Q'\) with
, then \(\exists Q'\) with  and
and  .
.
Here,  .
.
Proposition 22
If  for some strong timeout bisimulation
for some strong timeout bisimulation  up to
up to  , then
, then  .
.
Proof
Using the reflexivity of  it suffices to show that
it suffices to show that  is a strong timeout bisimulation. Clearly this relation is symmetric, and that it satisfies the first clause of Definition 8 is straightforward, using transitivity of
is a strong timeout bisimulation. Clearly this relation is symmetric, and that it satisfies the first clause of Definition 8 is straightforward, using transitivity of  . So assume
. So assume  , \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
, \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . Then, \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \). By the transfer property of
. Then, \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \). By the transfer property of  , there exists an \(R'\) with
, there exists an \(R'\) with  and
and  . Since
. Since  is a congruence for \(\theta _X\) it follows that
is a congruence for \(\theta _X\) it follows that  . By Definition 21, there exists a \(T'\) with
. By Definition 21, there exists a \(T'\) with  and
and  . Again using the transfer property of
. Again using the transfer property of  , there exists a \(Q'\) with
, there exists a \(Q'\) with  and
and  . Thus,
. Thus,  . \(\square \)
. \(\square \)
Theorem 23
Strong reactive bisimilarity is a lean congruence for \(\text{ CCSP}_\mathrm{t}^\theta \). In other words, if  are substitutions with
are substitutions with  , then
, then  for any expression
for any expression  .
.
Proof
It suffices to prove this theorem for the special case that  are closed substitutions; the general case then follows by means of composition of substitutions. Let
are closed substitutions; the general case then follows by means of composition of substitutions. Let  be the smallest relation satisfying
be the smallest relation satisfying
-
if
 , then
, then 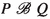 ,
, -
if
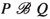 and \(\alpha \in A\cup \{\tau ,\mathrm{t}\}\), then
and \(\alpha \in A\cup \{\tau ,\mathrm{t}\}\), then  ,
, -
if
 and
and 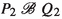 , then
, then  ,
, -
if
 , \(L\subseteq U \subseteq A\) and \(X \subseteq A\), then
, \(L\subseteq U \subseteq A\) and \(X \subseteq A\), then  and
and  ,
, -
if
 ,
,  and \(S\subseteq A\), then
and \(S\subseteq A\), then  ,
, -
if
 and \(I\subseteq A\), then
and \(I\subseteq A\), then 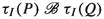 ,
, -
if
 and \(\mathcal {R}\subseteq A \times A\), then
and \(\mathcal {R}\subseteq A \times A\), then 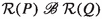 ,
, -
if \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and
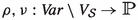 are substitutions satisfying
are substitutions satisfying  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\), then
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\), then  .
.
A straightforward induction on the derivation of  , employing Theorem 18, yields that
, employing Theorem 18, yields that

(For the last case, the assumption that  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\) implies \(\rho =_\mathcal {I}\nu \) by induction. Since \(=_\mathcal {I}\) is a lean congruence by Theorem 18, this implies
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\) implies \(\rho =_\mathcal {I}\nu \) by induction. Since \(=_\mathcal {I}\) is a lean congruence by Theorem 18, this implies  .)
.)
A trivial structural induction on  shows that
shows that

For \({{\mathcal {S}}}\) a recursive specification and  , let
, let  be the closed substitution given by
be the closed substitution given by  if \(x\in V_{{\mathcal {S}}}\) and \(\rho _{{\mathcal {S}}}(x):=\rho (x)\) otherwise. Then,
if \(x\in V_{{\mathcal {S}}}\) and \(\rho _{{\mathcal {S}}}(x):=\rho (x)\) otherwise. Then,  for all
for all  . Hence, an application of (
. Hence, an application of ( ) with \(\rho _{{\mathcal {S}}}\) and \(\nu _{{\mathcal {S}}}\) yields that under the conditions of the last clause for
) with \(\rho _{{\mathcal {S}}}\) and \(\nu _{{\mathcal {S}}}\) yields that under the conditions of the last clause for  above one even has
above one even has  for all expressions
for all expressions  .($)
.($)
It suffices to show that  is a strong timeout bisimulation up to
is a strong timeout bisimulation up to  , because then
, because then  , and (
, and ( ) implies that
) implies that  is a lean congruence. Because
is a lean congruence. Because  is symmetric, so is
is symmetric, so is  . So I need to show that
. So I need to show that  satisfies the two clauses of Definition 21.
satisfies the two clauses of Definition 21.
-
Let
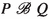 and
and  with \(\alpha \in A \cup \{\tau \}\). I have to find a \(Q'\) with
with \(\alpha \in A \cup \{\tau \}\). I have to find a \(Q'\) with  and
and  . In fact, I show that even
. In fact, I show that even  . This I will do by structural induction on the proof \(\pi \) of
. This I will do by structural induction on the proof \(\pi \) of  from the rules of Table 1. I make a case distinction based on the derivation of
from the rules of Table 1. I make a case distinction based on the derivation of  .
.-
Let
 . Using that the relation
. Using that the relation  is a strong timeout bisimulation, there must be a process \(Q'\) such that
is a strong timeout bisimulation, there must be a process \(Q'\) such that  and
and 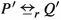 . Hence,
. Hence,  .
. -
Let \(P = \beta .P^\dagger \) and \(Q = \beta .Q^\dagger \) with \(\beta \in A\cup \{\tau ,\mathrm{t}\}\) and
 . Then, \(\alpha =\beta \) and \(P'=P^\dagger \). Take \(Q':=Q^\dagger \). Then,
. Then, \(\alpha =\beta \) and \(P'=P^\dagger \). Take \(Q':=Q^\dagger \). Then,  and
and  .
. -
Let \(P = P_1 + P_2\) and \(Q = Q_1 + Q_2\) with
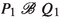 and
and  . I consider the first rule from Table 1 that could have been responsible for the derivation of
. I consider the first rule from Table 1 that could have been responsible for the derivation of 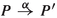 ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Then, by induction
. Then, by induction  for some \(Q'\) with
for some \(Q'\) with  . By the same rule from Table 1,
. By the same rule from Table 1,  .
. -
Let \(P=\theta _L^U(P^\dagger )\), \(Q=\theta _L^U(Q^\dagger )\) and
 . First suppose \(\alpha \in A\). Since
. First suppose \(\alpha \in A\). Since  , it must be that
, it must be that  and either \(\alpha \in U\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). In the latter case, \((\texttt {@})\) yields \(\mathcal {I}(P^\dagger ) = \mathcal {I}(Q^\dagger )\), and thus \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\mathop \cup \{\tau \}\). By induction there exists a \(Q'\) such that
and either \(\alpha \in U\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). In the latter case, \((\texttt {@})\) yields \(\mathcal {I}(P^\dagger ) = \mathcal {I}(Q^\dagger )\), and thus \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\mathop \cup \{\tau \}\). By induction there exists a \(Q'\) such that  and
and  . So, in both cases,
. So, in both cases,  . Now suppose \(\alpha =\tau \). Since
. Now suppose \(\alpha =\tau \). Since  it must be that \(P'\) has the form \(\theta _L^U(P^\ddagger )\), and
it must be that \(P'\) has the form \(\theta _L^U(P^\ddagger )\), and  . By induction, there exists a \(Q^\ddagger \) such that
. By induction, there exists a \(Q^\ddagger \) such that  and
and  . Now
. Now  and
and  .
. -
Let \(P=\psi _X(P^\dagger )\), \(Q=\psi _X(Q^\dagger )\) and
 . Since
. Since  , one has
, one has  . By induction there exists a \(Q'\) with
. By induction there exists a \(Q'\) with  and
and  . So
. So  .
. -
Let \(P = P_1 {\Vert ^{}_{S}} P_2\) and \(Q = Q_1 {\Vert ^{}_{S}} Q_2\) with
 and
and  . I consider the three rules from Table 1 that could have been responsible for the derivation of
. I consider the three rules from Table 1 that could have been responsible for the derivation of 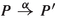 . First suppose that \(\alpha \notin S\),
. First suppose that \(\alpha \notin S\),  and \(P' = P'_1 {\Vert ^{}_{S}} P_2\). By induction,
and \(P' = P'_1 {\Vert ^{}_{S}} P_2\). By induction, 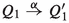 for some \(Q'_1\) with
for some \(Q'_1\) with  . Consequently,
. Consequently,  , and
, and  . Next suppose that \(\alpha \in S\),
. Next suppose that \(\alpha \in S\),  ,
,  and \(P' = P'_1 {\Vert ^{}_{S}} P'_2\). By induction,
and \(P' = P'_1 {\Vert ^{}_{S}} P'_2\). By induction, 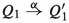 for some \(Q'_1\) with
for some \(Q'_1\) with  , and
, and  for some \(Q'_2\) with
for some \(Q'_2\) with  . Consequently,
. Consequently,  , and
, and  . The remaining case proceeds symmetrically to the first.
. The remaining case proceeds symmetrically to the first. -
Let \(P = \tau _I(P^\dagger )\) and \(Q= \tau _I(Q^\dagger )\) with \(I\subseteq A\) and
 . Then,
. Then,  for some \(P^\ddagger \) with \(P'= \tau _I(P^\ddagger )\), and either \(\beta = \alpha \notin I\), or \(\beta \in I\) and \(\alpha =\tau \). By induction,
for some \(P^\ddagger \) with \(P'= \tau _I(P^\ddagger )\), and either \(\beta = \alpha \notin I\), or \(\beta \in I\) and \(\alpha =\tau \). By induction,  for some \(Q^\ddagger \) with
for some \(Q^\ddagger \) with  . Consequently,
. Consequently,  and
and  .
. -
Let \(P = \mathcal {R}(P^\dagger )\) and \(Q= \mathcal {R}(Q^\dagger )\) with \(\mathcal {R}\subseteq A \times A\) and
 . Then,
. Then,  for some \(P^\ddagger \) with \(P'= \mathcal {R}(P^\ddagger )\), and either \((\beta ,\alpha ) \in \mathcal {R}\) or \(\beta =\alpha = \tau \). By induction,
for some \(P^\ddagger \) with \(P'= \mathcal {R}(P^\ddagger )\), and either \((\beta ,\alpha ) \in \mathcal {R}\) or \(\beta =\alpha = \tau \). By induction,  for some \(Q^\ddagger \) with
for some \(Q^\ddagger \) with  . Consequently,
. Consequently,  and
and  .
. -
Let
 and
and  where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and
where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and  satisfy
satisfy  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition  is provable by means of a strict subproof of the proof \(\pi \) of
is provable by means of a strict subproof of the proof \(\pi \) of  . By ($) above one has
. By ($) above one has  . So by induction there is a \(Q'\) such that
. So by induction there is a \(Q'\) such that  and
and  . By Table 1,
. By Table 1,  .
.
-
-
Let
 , \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
, \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . I have to find a \(Q'\) such that
. I have to find a \(Q'\) such that  and
and  . This I will do by structural induction on the proof \(\pi \) of
. This I will do by structural induction on the proof \(\pi \) of  from the rules of Table 1. I make a case distinction based on the derivation of
from the rules of Table 1. I make a case distinction based on the derivation of  .
.-
Let
 . Using that the relation
. Using that the relation  is a strong timeout bisimulation, there must be a process \(Q'\) such that
is a strong timeout bisimulation, there must be a process \(Q'\) such that  and
and  . Thus
. Thus  .
. -
Let \(P = \beta .P^\dagger \) and \(Q = \beta .Q^\dagger \) with \(\beta \in A\cup \{\tau ,\mathrm{t}\}\) and
 . Then, \(\beta =\mathrm{t}\) and \(P'=P^\dagger \). Take \(Q':=Q^\dagger \). Then,
. Then, \(\beta =\mathrm{t}\) and \(P'=P^\dagger \). Take \(Q':=Q^\dagger \). Then,  and
and  . Thus,
. Thus,  .
. -
Let \(P = P_1 + P_2\) and \(Q = Q_1 + Q_2\) with
 and
and  . I consider the first rule from Table 1 that could have been responsible for the derivation of
. I consider the first rule from Table 1 that could have been responsible for the derivation of  ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Since \(\mathcal {I}(P_1)\cap (X\cup \{\tau \})\subseteq \mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \), by induction
. Since \(\mathcal {I}(P_1)\cap (X\cup \{\tau \})\subseteq \mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \), by induction  for some \(Q'\) with
for some \(Q'\) with  . Hence,
. Hence,  .
. -
Let \(P=\theta _L^U(P^\dagger )\), \(Q=\theta _L^U(Q^\dagger )\) and
 . Since
. Since  it must be that
it must be that  and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Consequently,
and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Consequently,  iff
iff  , for all \(\alpha \in A \cup \{\mathrm{t}\}\). So \(\mathcal {I}(P^\dagger )\cap (X\cup \{\tau \}) = \emptyset \). By induction,
, for all \(\alpha \in A \cup \{\mathrm{t}\}\). So \(\mathcal {I}(P^\dagger )\cap (X\cup \{\tau \}) = \emptyset \). By induction,  for some \(Q'\) with
for some \(Q'\) with  . By \((\texttt {@})\), \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Hence
. By \((\texttt {@})\), \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Hence  .
. -
Let \(P=\psi _Y(P^\dagger )\), \(Q=\psi _Y(Q^\dagger )\) and
 . Since
. Since  one has
one has  for some \(P^\ddagger \) with \(P'=\theta _Y(P^\ddagger )\), and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\), i.e. \(\mathcal {I}(P^\dagger ) \cap (Y\cup \{\tau \}) = \emptyset \). By induction,
for some \(P^\ddagger \) with \(P'=\theta _Y(P^\ddagger )\), and \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\), i.e. \(\mathcal {I}(P^\dagger ) \cap (Y\cup \{\tau \}) = \emptyset \). By induction, 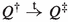 for a \(Q^\dagger \) with
for a \(Q^\dagger \) with  . By \((\texttt {@})\), \(\mathcal {I}(P^\dagger )=\mathcal {I}(Q^\dagger )\), so \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). Let \(Q' := \theta _Y(Q^\ddagger )\), so that
. By \((\texttt {@})\), \(\mathcal {I}(P^\dagger )=\mathcal {I}(Q^\dagger )\), so \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\). Let \(Q' := \theta _Y(Q^\ddagger )\), so that  . From
. From  , one obtains
, one obtains 
using that
 is a congruence for \(\theta _X\) (\(= \theta _X^X\)). Thus,
is a congruence for \(\theta _X\) (\(= \theta _X^X\)). Thus, 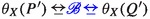 .
. -
Let \(P = P_1 {\Vert ^{}_{S}} P_2\) and \(Q = Q_1 {\Vert ^{}_{S}} Q_2\) with
 and
and  . I consider the last rule from Table 1 that could have been responsible for the derivation of
. I consider the last rule from Table 1 that could have been responsible for the derivation of  . The other proceeds symmetrically. So suppose that
. The other proceeds symmetrically. So suppose that  and \(P' = P_1 {\Vert ^{}_{S}} P'_2\). Let \(Y:=X\setminus (S\setminus \mathcal {I}(P_1))=(X\setminus S) \cup (X \cap S \cap \mathcal {I}(P_1))\). Then, \(\mathcal {I}(P_2)\cap (Y\cup \{\tau \})=\emptyset \). By induction,
and \(P' = P_1 {\Vert ^{}_{S}} P'_2\). Let \(Y:=X\setminus (S\setminus \mathcal {I}(P_1))=(X\setminus S) \cup (X \cap S \cap \mathcal {I}(P_1))\). Then, \(\mathcal {I}(P_2)\cap (Y\cup \{\tau \})=\emptyset \). By induction,  for some \(Q'_2\) with
for some \(Q'_2\) with  . Let \(Q':= Q_1 {\Vert ^{}_{S}} Q'_2\), so that
. Let \(Q':= Q_1 {\Vert ^{}_{S}} Q'_2\), so that  . From
. From  and
and  , one obtains
, one obtains  , using that
, using that  is a congruence for \({\Vert ^{}_{S}}\). Therefore, since
is a congruence for \({\Vert ^{}_{S}}\). Therefore, since  is also a congruence for \(\theta _X\) (\(= \theta _X^X\)),
is also a congruence for \(\theta _X\) (\(= \theta _X^X\)), 
Since \(\mathcal {I}(P_1{\Vert ^{}_{S}}P_2)\cap (X\cup \{\tau \})=\emptyset \), one has \(P_1 {{\mathop {\nrightarrow }\limits ^{\tau }}}\) and \(\mathcal {I}(P_1)\cap X \subseteq S\). Moreover, since
 , one has \(\mathcal {I}(P_1) = \mathcal {I}(Q_1)\). Hence
, one has \(\mathcal {I}(P_1) = \mathcal {I}(Q_1)\). Hence  by Lemma 2.
by Lemma 2. -
Let \(P = \tau _I(P^\dagger )\) and \(Q= \tau _I(Q^\dagger )\) with \(I\subseteq A\) and
 . Then,
. Then,  for some \(P^\ddagger \) with \(P'= \tau _I(P^\ddagger )\). Moreover, \(\mathcal {I}(P^\dagger ) \cap (X \cup I \cup \{\tau \}) = \emptyset \). By induction,
for some \(P^\ddagger \) with \(P'= \tau _I(P^\ddagger )\). Moreover, \(\mathcal {I}(P^\dagger ) \cap (X \cup I \cup \{\tau \}) = \emptyset \). By induction,  for some \(Q^\ddagger \) with
for some \(Q^\ddagger \) with  . Let \(Q' := \tau _I(Q^\ddagger )\), so that
. Let \(Q' := \tau _I(Q^\ddagger )\), so that  . From
. From  , one obtains
, one obtains 
using Lemma 3 and that
 is a congruence for \(\tau _I\) and \(\theta _X\). Thus,
is a congruence for \(\tau _I\) and \(\theta _X\). Thus, 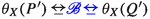 .
. -
Let \(P = \mathcal {R}(P^\dagger )\) and \(Q= \mathcal {R}(Q^\dagger )\) with \(\mathcal {R}\subseteq A \times A\) and
 . Then,
. Then,  for some \(P^\ddagger \) with \(P'= \mathcal {R}(P^\ddagger )\). Moreover, \(\mathcal {I}(P^\dagger ) \cap (\mathcal {R}^{-1}(X) \cup \{\tau \}) = \emptyset \). By induction,
for some \(P^\ddagger \) with \(P'= \mathcal {R}(P^\ddagger )\). Moreover, \(\mathcal {I}(P^\dagger ) \cap (\mathcal {R}^{-1}(X) \cup \{\tau \}) = \emptyset \). By induction,  for some \(Q^\ddagger \) with
for some \(Q^\ddagger \) with  . Let \(Q' := \mathcal {R}(Q^\ddagger )\), so that
. Let \(Q' := \mathcal {R}(Q^\ddagger )\), so that  . From
. From  , one obtains
, one obtains 
using Lemma 4 and that
 is a congruence for \(\mathcal {R}\) and \(\theta _X\). Thus,
is a congruence for \(\mathcal {R}\) and \(\theta _X\). Thus,  .
. -
Let
 and
and  where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and
where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and  satisfy
satisfy  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition  is provable by means of a strict subproof of the proof \(\pi \) of
is provable by means of a strict subproof of the proof \(\pi \) of  . The rule for recursion in Table 1 also implies that
. The rule for recursion in Table 1 also implies that  . Therefore,
. Therefore,  . By ($) above one has
. By ($) above one has 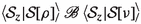 . So by induction there is a \(Q'\) such that
. So by induction there is a \(Q'\) such that  and
and  . By Table 1,
. By Table 1, 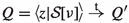 .\(\square \)
.\(\square \)
-
Proposition 24
If  for some strong timeout bisimulation
for some strong timeout bisimulation  up to
up to  , then
, then  .
.
Proof
Exactly as the proof of Proposition 22, now using that  is a congruence for \(\theta _X\). \(\square \)
is a congruence for \(\theta _X\). \(\square \)
Theorem 25
Strong reactive bisimilarity is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \).
Proof
Let  be the smallest relation satisfying
be the smallest relation satisfying
-
if \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\) and
 , such that
, such that  for all \(y\in V_{{\mathcal {S}}}\), then
for all \(y\in V_{{\mathcal {S}}}\), then  ,
,
in addition to the eight or nine clauses listed in the proof of Theorem 23. Again, a straightforward induction on the derivation of  , employing Theorem 18, yields that
, employing Theorem 18, yields that

(For the new case, the assumption that  for all \(y\in V_{{\mathcal {S}}}\) implies \({{\mathcal {S}}}_y =_\mathcal {I}{{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\). So by Theorem 18,
for all \(y\in V_{{\mathcal {S}}}\) implies \({{\mathcal {S}}}_y =_\mathcal {I}{{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\). So by Theorem 18,  .) A trivial structural induction on
.) A trivial structural induction on  shows again that
shows again that

This again implies that in the last clause for  one even has
one even has  for all
for all  ,($) and likewise, in the new clause,
,($) and likewise, in the new clause,  for all
for all  with variables from \(V_{{\mathcal {S}}}\). \((\#)\)
with variables from \(V_{{\mathcal {S}}}\). \((\#)\)
It suffices to show that  is a strong timeout bisimulation up to
is a strong timeout bisimulation up to  , because then
, because then  with Proposition 24, and the new clause for
with Proposition 24, and the new clause for  implies (2). By construction
implies (2). By construction  is symmetric.
is symmetric.
-
Let
 and
and  with \(\alpha \in A \cup \{\tau \}\). I have to find a \(Q'\) with
with \(\alpha \in A \cup \{\tau \}\). I have to find a \(Q'\) with  and
and 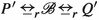 . In fact, I show that even
. In fact, I show that even  . This I will do by structural induction on the proof \(\pi \) of
. This I will do by structural induction on the proof \(\pi \) of  from the rules of Table 1. I make a case distinction based on the derivation of
from the rules of Table 1. I make a case distinction based on the derivation of  .
.-
Let
 and
and  where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that
where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that  for all \(y\in V_{{\mathcal {S}}}\), meaning that for all \(y\in W\) and
for all \(y\in V_{{\mathcal {S}}}\), meaning that for all \(y\in W\) and  one has
one has  . By Table 1 the transition
. By Table 1 the transition  is provable by means of a strict subproof of \(\pi \). By (#) above one has
is provable by means of a strict subproof of \(\pi \). By (#) above one has  . So by induction there is an
. So by induction there is an  such that
such that  and
and  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  , one has
, one has  . Hence, there is a \(Q'\) with
. Hence, there is a \(Q'\) with  and
and  . So
. So  . By Table 1,
. By Table 1,  .
. -
The remaining nine cases proceed just as in the proof of Theorem 23, but with
 substituted for the blue occurrences of
substituted for the blue occurrences of  . In the case for \(\theta _L^U\) with \(\alpha =\tau \), I conclude from
. In the case for \(\theta _L^U\) with \(\alpha =\tau \), I conclude from  that
that 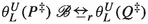 . Besides applying the definition of
. Besides applying the definition of  , this also involves the application of Theorem 23 that
, this also involves the application of Theorem 23 that 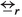 is already known to be a congruence for \(\theta _L^U\). The same reasoning applies in the cases for \({\Vert ^{}_{S}}\), \(\tau _I\) and \(\mathcal {R}\).
is already known to be a congruence for \(\theta _L^U\). The same reasoning applies in the cases for \({\Vert ^{}_{S}}\), \(\tau _I\) and \(\mathcal {R}\).
-
-
Let
 , \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
, \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . I will find a \(Q'\) such that
. I will find a \(Q'\) such that  and
and  . This I will do by structural induction on the proof \(\pi \) of
. This I will do by structural induction on the proof \(\pi \) of  from the rules of Table 1. I make a case distinction based on the derivation of
from the rules of Table 1. I make a case distinction based on the derivation of  .
.-
Let
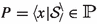 and
and 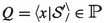 where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that for all \(y\in W\) and
where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that for all \(y\in W\) and  one has
one has  . By Table 1 the transition
. By Table 1 the transition  is provable by means of a strict subproof of the proof \(\pi \) of
is provable by means of a strict subproof of the proof \(\pi \) of  . The rule for recursion in Table 1 also implies that
. The rule for recursion in Table 1 also implies that  . Therefore,
. Therefore,  . By (#) above one has
. By (#) above one has  . So by induction there is an
. So by induction there is an  such that
such that  and
and  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  ,
,  . Using \((\texttt {@})\),
. Using \((\texttt {@})\),  . Hence, \(\exists Q'\) with
. Hence, \(\exists Q'\) with  and
and  , and thus
, and thus  , using Theorem 23. So
, using Theorem 23. So  . By Table 1,
. By Table 1,  .
. -
The remaining eight cases proceed just as in the proof of Theorem 23, but with
 substituted for the blue occurrences of
substituted for the blue occurrences of  . \(\square \)
. \(\square \)
-
9 The recursive specification principle
For \(W \subseteq { Var}\) a set of variables, a W-tuple of expressions is a function  . It has a component \(\vec {E}(x)\) for each variable \(x\in W\). Note that a W-tuple of expressions is nothing else than a substitution. Let \(\textit{id}_W\) be the identity function, given by \(\textit{id}_W(x)=x\) for all \(x\in W\). If
. It has a component \(\vec {E}(x)\) for each variable \(x\in W\). Note that a W-tuple of expressions is nothing else than a substitution. Let \(\textit{id}_W\) be the identity function, given by \(\textit{id}_W(x)=x\) for all \(x\in W\). If  and
and  then \(G[\vec {E}]\) denotes the result of simultaneous substitution of \(\vec {E}(x)\) for x in G, for all \(x\in W\). Likewise, if
then \(G[\vec {E}]\) denotes the result of simultaneous substitution of \(\vec {E}(x)\) for x in G, for all \(x\in W\). Likewise, if  and
and  then
then  denotes the V-tuple with components \(G(y)[\vec {E}]\) for \(y\in V\). Henceforth, I regard a recursive specification \({{\mathcal {S}}}\) as a \(V_{{\mathcal {S}}}\)-tuple with components \({{\mathcal {S}}}(y)={{\mathcal {S}}}_y\) for \(y\in V_{{\mathcal {S}}}\). If
denotes the V-tuple with components \(G(y)[\vec {E}]\) for \(y\in V\). Henceforth, I regard a recursive specification \({{\mathcal {S}}}\) as a \(V_{{\mathcal {S}}}\)-tuple with components \({{\mathcal {S}}}(y)={{\mathcal {S}}}_y\) for \(y\in V_{{\mathcal {S}}}\). If  and
and  , then
, then  is the W-tuple with components
is the W-tuple with components  for \(x\in W\).
for \(x\in W\).
For \({{\mathcal {S}}}\) a recursive specification and  a \(V_{{\mathcal {S}}}\)-tuple of expressions,
a \(V_{{\mathcal {S}}}\)-tuple of expressions,  states that \(\vec {E}\) is a solution of \({{\mathcal {S}}}\), up to strong reactive bisimilarity. The tuple
states that \(\vec {E}\) is a solution of \({{\mathcal {S}}}\), up to strong reactive bisimilarity. The tuple  is called the default solution.
is called the default solution.
In [2, 10], two requirements occur for process algebras with recursion. The recursive definition principle (RDP) says that each recursive specification must have a solution, and the recursive specification principle (RSP) says that guarded recursive specifications have at most one solution. When dealing with process algebras where the meaning of a closed expression is a semantic equivalence class of processes, these principles become requirements on the semantic equivalence employed.
Proposition 26
Let \({{\mathcal {S}}}\) be a recursive specification, and \(x\in V_{{\mathcal {S}}}\). Then  .
.
Proof
Let  be a closed substitution. I have to show that
be a closed substitution. I have to show that  . Equivalently I may show this for
. Equivalently I may show this for  . Now
. Now  and
and  . Consequently, it suffices to prove the proposition under the assumption that
. Consequently, it suffices to prove the proposition under the assumption that  . This follows immediately from the rule for recursion in Table 1 and Definition 8. \(\square \)
. This follows immediately from the rule for recursion in Table 1 and Definition 8. \(\square \)
Proposition 26 says that the recursive definition principle holds for strong reactive bisimulation semantics. The “default solution” of a recursive specification is in fact a solution. Note that the conclusion of Proposition 26 can be restated as  , and that
, and that  .
.
The following theorem establishes the recursive specification principle for strong reactive bisimulation semantics. Some aspects of the proof that are independent of the notion of bisimilarity employed are delegated to the following two lemmas.
Lemma 5
Let  be guarded and have free variables from \(W\subseteq { Var}\) only, and let
be guarded and have free variables from \(W\subseteq { Var}\) only, and let  . Then, \(\mathcal {I}(H[\vec {P}]) = \mathcal {I}(H[\vec {Q}])\).
. Then, \(\mathcal {I}(H[\vec {P}]) = \mathcal {I}(H[\vec {Q}])\).
Proof
In Appendix A. \(\square \)
Lemma 6
Let  be guarded and have free variables from \(W\subseteq { Var}\) only, and let
be guarded and have free variables from \(W\subseteq { Var}\) only, and let  . If
. If  with \(\alpha \in Act\), then \(R'\) has the form \(H'[\vec {P}]\) for some term
with \(\alpha \in Act\), then \(R'\) has the form \(H'[\vec {P}]\) for some term  with free variables in W only. Moreover,
with free variables in W only. Moreover,  .
.
Proof
By induction on the derivation of  , making a case distinction on the shape of H.
, making a case distinction on the shape of H.
Let \(H=\alpha .G\), so that \(H[\vec {P}] = \alpha .G[\vec {P}]\). Then, \(R' = G[\vec {P}]\) and  .
.
The case \(H=0\) cannot occur. Nor can the case \(H=x\in { Var}\), as H is guarded.
Let \(H = H_1 {\Vert ^{}_{S}} H_2\), so that \(H[\vec {P}] = H_1[\vec {P}]{\Vert ^{}_{S}} H_2[\vec {P}]\). Note that \(H_1\) and \(H_2\) are guarded and have free variables in W only. One possibility is that \(a\notin S\),  and \(R'= R_1 {\Vert ^{}_{S}} H_2[\vec {P}]\). By induction, \(R'_1\) has the form \(H'_1[\vec {P}]\) for some term
and \(R'= R_1 {\Vert ^{}_{S}} H_2[\vec {P}]\). By induction, \(R'_1\) has the form \(H'_1[\vec {P}]\) for some term  with free variables in W only. Moreover,
with free variables in W only. Moreover,  . Thus, \(R' = (H'_1 {\Vert ^{}_{S}} H_2)[\vec {P}]\), and \(H':= H'_1 {\Vert ^{}_{S}} H_2\) has free variables in W only. Moreover,
. Thus, \(R' = (H'_1 {\Vert ^{}_{S}} H_2)[\vec {P}]\), and \(H':= H'_1 {\Vert ^{}_{S}} H_2\) has free variables in W only. Moreover,  .
.
The other two cases for \({\Vert ^{}_{S}}\), and the cases for the operators \(+\), \(\tau _I\) and \(\mathcal {R}\), are equally trivial.
Let \(H= \theta _L^U(H^\dagger )\), so that \(H[\vec {P}] = \theta _L^U(H^\dagger [\vec {P}])\). Note that \(H^\dagger \) is guarded and has free variables in W only. The case \(\alpha = \tau \) is again trivial, so assume \(\alpha \ne \tau \). Then  and either \(\alpha \in X\) or \(H^\dagger [\vec {P}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). By induction, \(R'\) has the form \(H'[\vec {P}]\) for some term
and either \(\alpha \in X\) or \(H^\dagger [\vec {P}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). By induction, \(R'\) has the form \(H'[\vec {P}]\) for some term  with free variables in W only. Moreover,
with free variables in W only. Moreover,  . Since \(\mathcal {I}(H^\dagger [\vec {P}]) = \mathcal {I}(H^\dagger [\vec {Q}])\) by Lemma 5, either \(\alpha \in X\) or \(H^\dagger [\vec {Q}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Consequently,
. Since \(\mathcal {I}(H^\dagger [\vec {P}]) = \mathcal {I}(H^\dagger [\vec {Q}])\) by Lemma 5, either \(\alpha \in X\) or \(H^\dagger [\vec {Q}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). Consequently,  .
.
Let \(H= \psi _X(H^\dagger )\), so that \(H[\vec {P}] = \psi _X(H^\dagger [\vec {P}])\). Note that \(H^\dagger \) is guarded and has free variables in W only. The case \(\alpha \in A\cup \{\tau \}\) is trivial, so assume \(\alpha =\mathrm{t}\). Then,  for some \(R^\dagger \) such that \(R'=\theta _X(R^\dagger )\). Moreover, \(H^\dagger [\vec {P}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). By induction, \(R^\dagger \) has the form \(H'[\vec {P}]\) for some term
for some \(R^\dagger \) such that \(R'=\theta _X(R^\dagger )\). Moreover, \(H^\dagger [\vec {P}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). By induction, \(R^\dagger \) has the form \(H'[\vec {P}]\) for some term  with free variables in W only. Moreover,
with free variables in W only. Moreover,  . Since \(\mathcal {I}(H^\dagger [\vec {P}]) = \mathcal {I}(H^\dagger [\vec {Q}])\) by Lemma 5, \(H^\dagger [\vec {Q}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Consequently,
. Since \(\mathcal {I}(H^\dagger [\vec {P}]) = \mathcal {I}(H^\dagger [\vec {Q}])\) by Lemma 5, \(H^\dagger [\vec {Q}] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Consequently,  .
.
Finally, let  , so that
, so that  , where \(\vec {P}^\dagger \) is the \(W {\setminus } V_{{\mathcal {S}}}\)-tuple that is left of \(\vec {P}\) after deleting the y-components, for \(y\in V_{{\mathcal {S}}}\). The transition
, where \(\vec {P}^\dagger \) is the \(W {\setminus } V_{{\mathcal {S}}}\)-tuple that is left of \(\vec {P}\) after deleting the y-components, for \(y\in V_{{\mathcal {S}}}\). The transition  is derivable through a subderivation of the one for
is derivable through a subderivation of the one for  . Moreover,
. Moreover,  . So by induction, \(R'\) has the form \(H'[\vec {P}]\) for some term
. So by induction, \(R'\) has the form \(H'[\vec {P}]\) for some term  with free variables in W only, and
with free variables in W only, and  . Since
. Since  , it follows that
, it follows that  . \(\square \)
. \(\square \)
Theorem 27
Let \({{\mathcal {S}}}\) be a guarded recursive specification. If  and
and  with
with  , then
, then  .
.
Proof
It suffices to prove Theorem 27 under the assumptions that  and only the variables from \(V_{{\mathcal {S}}}\) occur free in the expressions \({{\mathcal {S}}}_x\) for \(x \in V_{{\mathcal {S}}}\). For in the general case I have to establish that
and only the variables from \(V_{{\mathcal {S}}}\) occur free in the expressions \({{\mathcal {S}}}_x\) for \(x \in V_{{\mathcal {S}}}\). For in the general case I have to establish that  for an arbitrary closed substitution
for an arbitrary closed substitution  . Let
. Let  be given by \({\hat{\sigma }}(x)=\sigma (x)\) for all \(x\in { Var}{\setminus }V_{{\mathcal {S}}}\). Then
be given by \({\hat{\sigma }}(x)=\sigma (x)\) for all \(x\in { Var}{\setminus }V_{{\mathcal {S}}}\). Then  implies
implies  . Hence, I merely have to prove the theorem with \(\vec {E}[\sigma ]\), \(\vec {F}[\sigma ]\)and \({{\mathcal {S}}}[{\hat{\sigma ]}}\) in place of \(\vec {E}\), \(\vec {F}\) and \({{\mathcal {S}}}\).
. Hence, I merely have to prove the theorem with \(\vec {E}[\sigma ]\), \(\vec {F}[\sigma ]\)and \({{\mathcal {S}}}[{\hat{\sigma ]}}\) in place of \(\vec {E}\), \(\vec {F}\) and \({{\mathcal {S}}}\).
It also suffices to prove Theorem 27 under the assumption that \({{\mathcal {S}}}\) is a manifestly guarded recursive specification. Namely, for a general guarded recursive specification \({{\mathcal {S}}}\), let \({{\mathcal {S}}}'\) be the manifestly guarded specification into which \({{\mathcal {S}}}\) can be converted. Then,  implies
implies  by Theorem 23.
by Theorem 23.
So let \({{\mathcal {S}}}\) be manifestly guarded with free variables from \(V_{{\mathcal {S}}}\) only, and let  be two of its solutions, that is,
be two of its solutions, that is,  and
and  . I will show that the symmetric closure of
. I will show that the symmetric closure of

is a strong timeout bisimulation up to  . Once I have that, taking \(H:= x\in V_{{\mathcal {S}}}\) yields
. Once I have that, taking \(H:= x\in V_{{\mathcal {S}}}\) yields  by Proposition 24, and thus
by Proposition 24, and thus  for all \(x\in V_{{\mathcal {S}}}\). So
for all \(x\in V_{{\mathcal {S}}}\). So  .
.
-
Let
 and
and  with \(\alpha \in A \cup \{\tau \}\). I have to find a \(T'\) with
with \(\alpha \in A \cup \{\tau \}\). I have to find a \(T'\) with  and
and  . Assume that \(R = H[{{\mathcal {S}}}[\vec {P}]]\) and \(T=H[{{\mathcal {S}}}[\vec {Q}]]\)—the case that \(R = H[{{\mathcal {S}}}[\vec {Q}]]\) will follow by symmetry. Note that \(H[{{\mathcal {S}}}[\vec {P}]]\) can also be written as \(H[{{\mathcal {S}}}][\vec {P}]\). Since the expressions \({{\mathcal {S}}}_x\) for \(x\in V_{{\mathcal {S}}}\) have free variables from \(V_{{\mathcal {S}}}\) only, so does \(H[{{\mathcal {S}}}]\). Moreover, since \({{\mathcal {S}}}\) is manifestly guarded, the expression \(H[{{\mathcal {S}}}]\) must be guarded. By Lemma 6, \(R'\) must have the form \(H'[\vec {P}]\), where
. Assume that \(R = H[{{\mathcal {S}}}[\vec {P}]]\) and \(T=H[{{\mathcal {S}}}[\vec {Q}]]\)—the case that \(R = H[{{\mathcal {S}}}[\vec {Q}]]\) will follow by symmetry. Note that \(H[{{\mathcal {S}}}[\vec {P}]]\) can also be written as \(H[{{\mathcal {S}}}][\vec {P}]\). Since the expressions \({{\mathcal {S}}}_x\) for \(x\in V_{{\mathcal {S}}}\) have free variables from \(V_{{\mathcal {S}}}\) only, so does \(H[{{\mathcal {S}}}]\). Moreover, since \({{\mathcal {S}}}\) is manifestly guarded, the expression \(H[{{\mathcal {S}}}]\) must be guarded. By Lemma 6, \(R'\) must have the form \(H'[\vec {P}]\), where  has free variables in \(V_{{\mathcal {S}}}\) only. Moreover,
has free variables in \(V_{{\mathcal {S}}}\) only. Moreover,  . Furthermore, by Theorem 23,
. Furthermore, by Theorem 23,  and
and  . Thus,
. Thus,  .
. -
Let
 , \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \) and
, \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \) and  . I have to find a \(T'\) such that
. I have to find a \(T'\) such that  and
and  . The proof for this case proceeds exactly as that of the previous case, up to the last sentence; the condition \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \) is not even used. Now from
. The proof for this case proceeds exactly as that of the previous case, up to the last sentence; the condition \(\mathcal {I}(R)\cap (X\cup \{\tau \})=\emptyset \) is not even used. Now from  it follows that
it follows that 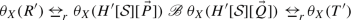
using Theorem 23 and the observation that \(\theta _X(H'[{{\mathcal {S}}}[\vec {P}]]) = \theta _X(H')[{{\mathcal {S}}}[\vec {P}]]\).\(\square \)
10 Complete axiomatisations
Let \(\textit{Ax}\) denote the collection of axioms from Tables 2, 3 and 4 , \(\textit{Ax}'\) the ones from Tables 2 and 3 , and \(\textit{Ax}''\) merely the ones from Table 2. Moreover, let \(\textit{Ax}_f\), resp. \(\textit{Ax}'_f\) and \(\textit{Ax}''_f\), be same collections without the two axioms using the recursion construct  , RDP and RSP. In this section, I establish the following.
, RDP and RSP. In this section, I establish the following.






In each of these cases, “\(\Leftarrow \)” states the soundness of the axiomatisation and “\(\Rightarrow \)” completeness.
Section 10.1 recalls (4), which stems from [22], and (3), which is folklore. Then, Sect. 10.2 extends the existing proofs of (4) and (3) to obtain (6) and (5). In Sect. 10.3, I move from strong bisimilarity to strong reactive bisimilarity; I discuss the merits of the axiom RA from Table 4 and establish its soundness, thereby obtaining direction “\(\Leftarrow \)” of (8) and (7). I prove the completeness of \(\textit{Ax}_f\) for recursion-free processes—direction “\(\Rightarrow \)” of (7)—in Sect. 10.4. Sections 10.5–10.7 deal with the completeness of \(\textit{Ax}\) for guarded \(\text{ CCSP}_\mathrm{t}^\theta \)—direction “\(\Rightarrow \)” of (8). Section 10.8 explains why I need the axiom of choice for the latter result.
10.1 A complete axiomatisation of strong bisimilarity on guarded \(\hbox {CCSP}_\mathrm{t}\)
The well-known axioms of Table 2 are sound for strong bisimilarity, meaning that writing  for \(=\), and substituting arbitrary expressions for the free variables x, y, z, or the meta-variables \(P_i\) and \(Q_j\), turns them into true statements. In these axioms \(\alpha ,\beta \) range over Act and a, b over A. All axioms involving variables are equations. The axiom involving P and Q is a template that stands for a family of equations, one for each fitting choice of P and Q. This is the \(\hbox {CCSP}_\mathrm{t}\) version of the expansion law from [33]. The axiom RDP (
for \(=\), and substituting arbitrary expressions for the free variables x, y, z, or the meta-variables \(P_i\) and \(Q_j\), turns them into true statements. In these axioms \(\alpha ,\beta \) range over Act and a, b over A. All axioms involving variables are equations. The axiom involving P and Q is a template that stands for a family of equations, one for each fitting choice of P and Q. This is the \(\hbox {CCSP}_\mathrm{t}\) version of the expansion law from [33]. The axiom RDP ( ) says that recursively defined processes
) says that recursively defined processes  satisfy their set of defining equations \({{\mathcal {S}}}\). As discussed in the previous section, this entails that each recursive specification has a solution. The axiom RSP [2, 10] is a conditional equation with the equations of a guarded recursive specification \({{\mathcal {S}}}\) as antecedents. It says that the x-component of any solution of \({{\mathcal {S}}}\)—a vector of processes substituted for the variables \(V_{{\mathcal {S}}}\)—equals
satisfy their set of defining equations \({{\mathcal {S}}}\). As discussed in the previous section, this entails that each recursive specification has a solution. The axiom RSP [2, 10] is a conditional equation with the equations of a guarded recursive specification \({{\mathcal {S}}}\) as antecedents. It says that the x-component of any solution of \({{\mathcal {S}}}\)—a vector of processes substituted for the variables \(V_{{\mathcal {S}}}\)—equals  . In other words, each solution of \({{\mathcal {S}}}\) equals the default solution. This is a compact way of saying that solutions of guarded recursive specifications are unique.
. In other words, each solution of \({{\mathcal {S}}}\) equals the default solution. This is a compact way of saying that solutions of guarded recursive specifications are unique.
Theorem 28
For \(\hbox {CCSP}_\mathrm{t}\) processes  with guarded recursion, one has
with guarded recursion, one has  , that is, P and Q are strongly bisimilar, iff \(P=Q\) is derivable from the axioms of Table 2.
, that is, P and Q are strongly bisimilar, iff \(P=Q\) is derivable from the axioms of Table 2.
In this theorem, “if”, the soundness of the axiomatisation of Table 2, is an immediate consequence of the soundness of the individual axioms. “Only if” states the completeness of the axiomatisation.
A crucial tool in its proof is the simple observation that the axioms from the first box of Table 2 allow any \(\hbox {CCSP}_\mathrm{t}\) process with guarded recursion to be brought in the form \(\sum _{i\in I}\alpha _i.P_i\)—a head normal form. Using this, the rest of the proof is a standard argument employing RSP, independent of the choice of the specific process algebra. It can be found in [2, 10, 31, 33] and many other places. However, in the literature this completeness theorem was always stated and proved for a small fragment of the process algebra, allowing only guarded recursive specifications with a finite number of equations, and whose right-hand sides \({{\mathcal {S}}}_y\) involve only the basic operators inaction, action prefixing and choice. Since the set of true statements  , with P and Q processes in a process algebra like guarded \(\hbox {CCSP}_\mathrm{t}\), is well known to be undecidable, and even not recursively enumerable, it was widely believed that no sound and complete finitely presented axiomatisation of strong bisimilarity could exist. Only in March 2017, Kees Middelburg observed (in the setting of the process algebra ACP [2, 10]) that the standard proof applies almost verbatim to arbitrary processes with guarded recursion, although one has to be a bit careful in dealing with the infinite nature of recursive specifications. The argument has been carefully documented in [22], in the setting of the process algebra ACP. This result does not contradict the non-enumerability of the set of true statements
, with P and Q processes in a process algebra like guarded \(\hbox {CCSP}_\mathrm{t}\), is well known to be undecidable, and even not recursively enumerable, it was widely believed that no sound and complete finitely presented axiomatisation of strong bisimilarity could exist. Only in March 2017, Kees Middelburg observed (in the setting of the process algebra ACP [2, 10]) that the standard proof applies almost verbatim to arbitrary processes with guarded recursion, although one has to be a bit careful in dealing with the infinite nature of recursive specifications. The argument has been carefully documented in [22], in the setting of the process algebra ACP. This result does not contradict the non-enumerability of the set of true statements  , due to the fact that RSP is a proof rule with infinitely many premises.
, due to the fact that RSP is a proof rule with infinitely many premises.
A well-known simplification of Theorem 28 and its proof also yields completeness without recursion:
Theorem 29
For \(\hbox {CCSP}_\mathrm{t}\) processes  without recursion, one has
without recursion, one has  iff \(P=Q\) is derivable from the axioms of Table 2 minus RDP and RSP.
iff \(P=Q\) is derivable from the axioms of Table 2 minus RDP and RSP.
10.2 A complete axiomatisation of strong bisimilarity on guarded \(\text{ CCSP}_\mathrm{t}^\theta \)
Table 3 extends Table 2 with axioms for the auxiliary operators \(\theta _L^U\) and \(\psi _X\). With Table 1 it is straightforward to check the soundness of these axioms. The fourth axiom, for instance, follows from the second or third rule for \(\theta _L^U\) in Table 1, depending on whether \(\beta \in L\cup \{\mathrm{t}\}\). Moreover, a straightforward induction shows that these axioms suffice to convert each \(\text{ CCSP}_\mathrm{t}^\theta \) process with guarded recursion into the form \(\sum _{I\in I}\!\alpha _i.P_i\)—a head normal form. The below proposition sharpens this observation by pointing out that one can take the processes \(P_i\) for \(i\in I\) to be exactly the ones that are reachable by one \(\alpha _i\)-labelled transition from P.
Definition 30
Given a \(\text{ CCSP}_\mathrm{t}^\theta \) process  , let
, let  .
.
By Proposition 12, P is countably branching, so using Proposition 15\({\widehat{P}}\) is a valid \(\text{ CCSP}_\mathrm{t}^\theta \) process. In case  is a process with only guarded recursion, then P is finitely branching by Proposition 13, so also \({\widehat{P}}\) is a valid \(\text{ CCSP}_\mathrm{t}^\theta \) process with only guarded recursion.
is a process with only guarded recursion, then P is finitely branching by Proposition 13, so also \({\widehat{P}}\) is a valid \(\text{ CCSP}_\mathrm{t}^\theta \) process with only guarded recursion.
Proposition 31
Let  have guarded recursion only. Then, \(\textit{Ax}' \vdash P = {\widehat{P}}\). The conditional equation RSP is not even needed here.
have guarded recursion only. Then, \(\textit{Ax}' \vdash P = {\widehat{P}}\). The conditional equation RSP is not even needed here.
Proof
The proof is by induction on the measure e(P), defined in the proof of Proposition 13.
Let  . Axiom RDP yields
. Axiom RDP yields  . Moreover,
. Moreover,  . So by induction,
. So by induction,  . Moreover,
. Moreover,  , so
, so  . Thus \(\textit{Ax} \vdash P = {\widehat{P}}\).
. Thus \(\textit{Ax} \vdash P = {\widehat{P}}\).
Let \(P= \theta _L^U(P')\). Using that \(e(P')<e(P)\), by induction \(\textit{Ax} \vdash P' = \widehat{P'}\) so \(\textit{Ax} \vdash P = \theta _L^U(\widehat{P'})\). Let
where \(a_i\in L\) for all \(i \in I\), \(b_j\in U{\setminus }L\) for all \(j \in J\), and \(\gamma _k\notin U\cup \{\tau \}\) for all \(k \in K\). (So \(\gamma _k\) may be \(\mathrm{t}\).)
In case \(H\cup I=\emptyset \), one has \(\textit{Ax} \vdash P = \theta _L^U(\widehat{P'}) = \widehat{P'} = {\widehat{P}}\), using the first axiom for \(\theta _L^U\). Otherwise
by the remaining four axioms for \(\theta _L^U\). The right-hand side is \({\widehat{P}}\).
The cases for the remaining operators are equally straightforward. \(\square \)
In the special case that P is a recursion-free process, also the axiom RDP is not needed for this result.
Once we have head normalisation, the proofs of Theorems 28 and 29 are independent of the precise syntax of the process algebra in question. Using Proposition 31, we immediately obtain (6) and (5):
Theorem 32
For \(\text{ CCSP}_\mathrm{t}^\theta \) processes  with guarded recursion, one has
with guarded recursion, one has  iff \(P=Q\) is derivable from the axioms of Tables 2 and 3. \(\square \)
iff \(P=Q\) is derivable from the axioms of Tables 2 and 3. \(\square \)
Theorem 33
For \(\text{ CCSP}_\mathrm{t}^\theta \) processes  without recursion, one has
without recursion, one has  iff \(P=Q\) is derivable from the axioms of Tables 2 and 3 minus RDP and RSP.
iff \(P=Q\) is derivable from the axioms of Tables 2 and 3 minus RDP and RSP.
A law that turns out to be particularly useful in verifications modulo strong reactive bisimilarity is

Note that the right-hand side only exists if \((K\cup L)\subseteq (V\cap U)\). This law is sound for strong bisimilarity, as demonstrated by the following proposition. Yet it is not needed to add it to Table 3, as all its closed instances are derivable. In fact, this is a consequence of the above completeness theorems.
Proposition 34
 , provided \((K\cup L)\subseteq (V\cap U)\) and either \(U=V\) or \(K=L\) or \(K\subseteq L \subseteq U \subseteq V\) or \(L\subseteq K \subseteq V \subseteq U\).
, provided \((K\cup L)\subseteq (V\cap U)\) and either \(U=V\) or \(K=L\) or \(K\subseteq L \subseteq U \subseteq V\) or \(L\subseteq K \subseteq V \subseteq U\).
Proof
For given \(K,L,U,V\subseteq A\) with \((K\cup L)\subseteq (V\cap U)\) and either \(U=V\) or \(K=L\) or \(K\subseteq L \subseteq U \subseteq V\) or \(L\subseteq K \subseteq V \subseteq U\), let

It suffices to show that the symmetric closure  of
of  is a strong bisimulation. So let
is a strong bisimulation. So let  and
and  with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with
with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with  and
and  .
.
-
The case that \(R = T\) is trivial.
-
Let \(R = \theta _K^V(\theta _L^U(P))\) and \(T = \theta _{K\cup L}^{V\cap U}(P)\). First assume \(\alpha =\tau \). Then,
 for some \(P'\) such that \(R' = \theta _K^V(\theta _L^U(P'))\). Hence,
for some \(P'\) such that \(R' = \theta _K^V(\theta _L^U(P'))\). Hence,  , and
, and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,  and either \(\alpha \in V\) or \(\theta _L^U(P)\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup \{\tau \}\). Using that \(K\subseteq U\), this implies that either \(\alpha \in V\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup \{\tau \}\). Moreover,
and either \(\alpha \in V\) or \(\theta _L^U(P)\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup \{\tau \}\). Using that \(K\subseteq U\), this implies that either \(\alpha \in V\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup \{\tau \}\). Moreover,  and either \(\alpha \in U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). It follows that either \(\alpha \in V\cap U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup L\cup \{\tau \}\). (Here I use that either \(U=V\) or \(K=L\) or \(K\subseteq L \subseteq U \subseteq V\) or \(L\subseteq K \subseteq V \subseteq U\).) Consequently,
and either \(\alpha \in U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). It follows that either \(\alpha \in V\cap U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup L\cup \{\tau \}\). (Here I use that either \(U=V\) or \(K=L\) or \(K\subseteq L \subseteq U \subseteq V\) or \(L\subseteq K \subseteq V \subseteq U\).) Consequently,  .
. -
Let \(R = \theta _{K\cup L}^{V\cap U}(P)\) and \(T = \theta _K^V(\theta _L^U(P))\). First assume \(\alpha =\tau \). Then,
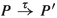 for some \(P'\) such that \(R' =\theta _{K\cup L}^{V\cap U}(P')\). Hence,
for some \(P'\) such that \(R' =\theta _{K\cup L}^{V\cap U}(P')\). Hence,  , and
, and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,  and either \(\alpha \in V\cap U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup L\cup \{\tau \}\). Consequently, \('\) and thus
and either \(\alpha \in V\cap U\) or \(P\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in K\cup L\cup \{\tau \}\). Consequently, \('\) and thus  . \(\square \)
. \(\square \)
The side condition to L1 cannot be dropped, for  , yet \(\theta _{\{c\}}^{\{c\}}(a.0+c.0) {\mathop {\nrightarrow }\limits ^{a}}\).
, yet \(\theta _{\{c\}}^{\{c\}}(a.0+c.0) {\mathop {\nrightarrow }\limits ^{a}}\).
10.3 A complete axiomatisation of strong reactive bisimilarity on guarded \(\text{ CCSP}_\mathrm{t}^\theta \)
To obtain a sound and complete axiomatisation of strong reactive bisimilarity for \(\text{ CCSP}_\mathrm{t}^\theta \) with guarded recursion, one needs to combine the axioms of Tables 2, 3 and 4. These axioms are useful only in combination with the full congruence property of strong reactive bisimilarity, Theorem 25. This is what allows us to apply these axioms within subexpressions of a given expression. Since  , the soundness of all equational axioms for strong reactive bisimilarity follows from their soundness for strong bisimilarity. The soundness of RSP has been established as Theorem 27. The soundness of RA, the reactive approximation axiom, is contributed by the following proposition.
, the soundness of all equational axioms for strong reactive bisimilarity follows from their soundness for strong bisimilarity. The soundness of RSP has been established as Theorem 27. The soundness of RA, the reactive approximation axiom, is contributed by the following proposition.
Proposition 35
Let  . If
. If  for all \(X\subseteq A\), then
for all \(X\subseteq A\), then  .
.
Proof
Given  with
with  for all \(X\subseteq A\), I show that
for all \(X\subseteq A\), I show that  is a strong timeout bisimulation.
is a strong timeout bisimulation.
Let  with \(\alpha \in A\cup \{\tau \}\). Take any \(X\subseteq A\). Then,
with \(\alpha \in A\cup \{\tau \}\). Take any \(X\subseteq A\). Then,  . Since
. Since  , this implies
, this implies  for some \(Q'\) with
for some \(Q'\) with  , and hence
, and hence  .
.
Let  and \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \). Then, \(\psi _X(P)\mathrm{t}\theta _X(P')\) and \(\mathcal {I}(\psi _X(P)) \cap (X\cup \{\tau \}) = \emptyset \). Since
and \(\mathcal {I}(P)\cap (X\cup \{\tau \}) = \emptyset \). Then, \(\psi _X(P)\mathrm{t}\theta _X(P')\) and \(\mathcal {I}(\psi _X(P)) \cap (X\cup \{\tau \}) = \emptyset \). Since  , this implies
, this implies  for some \(Q''\) with
for some \(Q''\) with  . It must be that
. It must be that  for some \(Q'\) with \(Q'' = \theta _X(Q')\). By Proposition 34,
for some \(Q'\) with \(Q'' = \theta _X(Q')\). By Proposition 34,  for all
for all  . Thus,
. Thus,  , which had to be shown. \(\square \)
, which had to be shown. \(\square \)
At first sight, it appears that axiom RA is not very handy, as, in case the alphabet A of visible actions is finite, the number of premises to verify is exponential in the size A. In case A is infinite, there are even uncountably many premises. However, in practical verifications this is hardly an issue, as one uses a partition of the premises into a small number of equivalence classes, each of which requires only one common proof. This technique will be illustrated on three examples below. Furthermore, one could calculate the set of visible actions \(\mathcal {J}(P)\) of a process P that can be encountered as initial actions after one \(\mathrm{t}\)-transition followed by a sequence of \(\tau \)-transitions. For large classes of processes, \(\mathcal {J}(P)\) will be a finite set. Now axiom RA can be modified by changing \(X \subseteq A\) into \(X \subseteq \mathcal {J}(P)\cup \mathcal {J}(Q)\). This preserves the soundness of the axiom, because only the actions in \(\mathcal {J}(P)\) play any rôle in evaluating \(\psi _X(P)\).
A crucial property of strong reactive bisimilarity was mentioned in the Introduction:

It is an immediate consequence of RA, since \(\psi _X(\tau .P + \mathrm{t}.Q) = \psi _X(\tau .P)\) for any \(X\subseteq A\), by Table 3. Another useful law in verifications modulo strong reactive bisimilarity is

Its soundness is intuitively obvious: the \(\mathrm{t}\)-transition to y will be taken only in an environment X with \(X \cap { In} = \emptyset \). Hence, one can just as well restrict the behaviour of y to those transitions that are allowed in one such environment. This law was one of the prime reasons for extending the family of operators \(\theta _X\) (\(= \theta _X^X\)), which were needed to establish the key theorems of this paper, to the larger family \(\theta _L^U\). Law L3 for finite I is effortlessly derivable from its simple instance

in combination with L1. I now show how to derive L3 from RA. For this proof, I need to partition the set of premises of RA in only two equivalence classes.
First let \(X\cap { In} \ne \emptyset \). Then, \(\psi _X(\sum _{i\in I}a_i. x_i + \mathrm{t}.y) = \sum _{i\in I}a_i. x_i = \psi _X(\sum _{i\in I}a_i .x_i + \mathrm{t}.\theta _\emptyset ^{A\setminus In}(y))\).
Next let \(X\cap { In} = \emptyset \). Then \(\psi _X(\sum _{i\in I}a_i. x_i + \mathrm{t}.y) \begin{array}{@{~=~}l}\sum _{i\in I}a_i. x_i + \mathrm{t}.\theta _X(y) \\ \sum _{i\in I}a_i .x_i + \mathrm{t}.\theta _X(\theta _\emptyset ^{A\setminus In}(y)) \\ \psi _X(\sum _{i\in I}a_i .x_i + \mathrm{t}.\theta _\emptyset ^{A\setminus In}(y))\;, \end{array}\) where the second step is an application of L1.
As an application of L3\('\), one obtains the law from [18] that was justified in the Introduction:
As a third illustration of the use of RA, I derive an equational law that does not follow from L1, L2 and L3, namely

These are the systems depicted in Fig. 1. These systems are surely not strongly bisimilar. Moreover, L3 does not help in proving them equivalent, as applying  to any of the four targets of a \(\mathrm{t}\)-transition does not kill any of the transitions of those processes. In particular,
to any of the four targets of a \(\mathrm{t}\)-transition does not kill any of the transitions of those processes. In particular,  . To derive this law from RA, I partition
. To derive this law from RA, I partition  into three equivalence classes.
into three equivalence classes.
First, let \(b \in X\). Then,
Next, let \(b\notin X\) and \(a \in X\). Then,

Finally, let \(a,b \notin X\). Then,

10.4 Completeness for finite processes
Theorem 36
Let P and Q be closed recursion-free \(\text{ CCSP}_\mathrm{t}^\theta \) expressions. Then,  .
.
Proof
Let the length of a path  of a processes P be n. Let d(P), the depth of P, be the length of its longest path; it is guaranteed to exist when P is a closed recursion-free \(\text{ CCSP}_\mathrm{t}^\theta \) expression. I prove the theorem with induction on \(\max (d(P),d(Q))\).
of a processes P be n. Let d(P), the depth of P, be the length of its longest path; it is guaranteed to exist when P is a closed recursion-free \(\text{ CCSP}_\mathrm{t}^\theta \) expression. I prove the theorem with induction on \(\max (d(P),d(Q))\).
Suppose  . By Proposition 31 one has \(\textit{Ax}_f \vdash P = {\widehat{P}}\) and \(\textit{Ax}_f \vdash Q = {\widehat{Q}}\). I will show that \(\textit{Ax}_f \vdash \psi _X({\widehat{P}}) = \psi _X({\widehat{Q}})\) for all \(X\subseteq A\). This will suffice, as then Axiom RA yields \(\textit{Ax}_f \vdash {\widehat{P}} = {\widehat{Q}}\) and thus \(\textit{Ax}_f \vdash P = Q\). So pick \(X \subseteq A\). Let
. By Proposition 31 one has \(\textit{Ax}_f \vdash P = {\widehat{P}}\) and \(\textit{Ax}_f \vdash Q = {\widehat{Q}}\). I will show that \(\textit{Ax}_f \vdash \psi _X({\widehat{P}}) = \psi _X({\widehat{Q}})\) for all \(X\subseteq A\). This will suffice, as then Axiom RA yields \(\textit{Ax}_f \vdash {\widehat{P}} = {\widehat{Q}}\) and thus \(\textit{Ax}_f \vdash P = Q\). So pick \(X \subseteq A\). Let
with \(\alpha _j,\beta _k \in A\cup \{\tau \}\) for all \(i\in I\) and \(k\in K\). The following two claims are the crucial part of the proof.
Claim 1: For each \(i \in I\), there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(\textit{Ax}_f \vdash P'_i = Q'_k\).
Claim 2: If \(\mathcal {I}(P) \cap (X \cup \{\tau \}) = \emptyset \), then for each \(j \in J\) there is a \(h \in H\) with \(\textit{Ax}_f \vdash \theta _X(P''_j) = \theta _X(Q''_h)\).
With these claims, the rest of the proof is straightforward. Since  , one has \(\mathcal {I}(P) = \mathcal {I}(\widehat{P}) = \{\alpha _i \mid i \in I\} =\ \{\beta _k \mid k \in K\} = \mathcal {I}({\widehat{Q}}) = \mathcal {I}(Q)\). First suppose that \(\mathcal {I}(P) \cap (X \cup \{\tau \}) = \emptyset \). Then,
, one has \(\mathcal {I}(P) = \mathcal {I}(\widehat{P}) = \{\alpha _i \mid i \in I\} =\ \{\beta _k \mid k \in K\} = \mathcal {I}({\widehat{Q}}) = \mathcal {I}(Q)\). First suppose that \(\mathcal {I}(P) \cap (X \cup \{\tau \}) = \emptyset \). Then,
Claim 1 yields \(\textit{Ax}_f \vdash \psi _X({\widehat{Q}}) = \psi _X({\widehat{Q}}) + \alpha _i.P'_i\) for each \(i \in I\). Likewise, Claim 2 yields \(\textit{Ax}_f \vdash \psi _X({\widehat{Q}}) = \psi _X({\widehat{Q}}) + \mathrm{t}.\theta _X(P''_j)\) for each \(j \in J\). Together this yields \(\textit{Ax}_f \vdash \psi _X({\widehat{Q}}) = \psi _X(\widehat{Q}) + \psi _X({\widehat{P}})\). By symmetry, one obtains \(\textit{Ax}_f \vdash \psi _X({\widehat{P}}) = \psi _X({\widehat{P}}) + \psi _X({\widehat{Q}})\) and thus \(\textit{Ax}_f \vdash \psi _X({\widehat{P}}) = \psi _X(\widehat{Q})\).
Next suppose \(\mathcal {I}(P) \cap (X \cup \{\tau \}) \ne \emptyset \). Then, \(\psi _X({\widehat{P}}) = \sum _{i\in I} \alpha _i.P'_i\) and \(\psi _X({\widehat{Q}}) = \sum _{k\in K} \beta _k.Q'_k\). The proof proceeds just as above, but without the need for Claim 2.
Proof of Claim 1: Pick \(i \in I\). Then  . So
. So  for some \(Q'\) with
for some \(Q'\) with  . Hence there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(Q'=Q'_k\). Using that \(d(P'_i) < d(P)\) and \(d(Q'_i) < d(Q)\), by induction \(\textit{Ax}_f \vdash P'_i = Q'_k\).
. Hence there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(Q'=Q'_k\). Using that \(d(P'_i) < d(P)\) and \(d(Q'_i) < d(Q)\), by induction \(\textit{Ax}_f \vdash P'_i = Q'_k\).
Proof of Claim 2: Pick \(j \in J\). Then  . Since \(\mathcal {I}({\widehat{P}}) \cap (X \cup \{\tau \}) = \emptyset \), there is a \(Q''\) such that
. Since \(\mathcal {I}({\widehat{P}}) \cap (X \cup \{\tau \}) = \emptyset \), there is a \(Q''\) such that  and
and  . Hence, there is a \(h \in H\) with \(Q''=Q''_h\). Using that \(d(\theta _X(P''_j)) \le d(P''_j) < d(P)\) and \(d(\theta _X(Q''_h)) \le d(Q''_h) < d(Q)\), by induction \(\textit{Ax}_f \vdash \theta _X(P''_j) = \theta _X(Q''_h)\). \(\square \)
. Hence, there is a \(h \in H\) with \(Q''=Q''_h\). Using that \(d(\theta _X(P''_j)) \le d(P''_j) < d(P)\) and \(d(\theta _X(Q''_h)) \le d(Q''_h) < d(Q)\), by induction \(\textit{Ax}_f \vdash \theta _X(P''_j) = \theta _X(Q''_h)\). \(\square \)
10.5 The method of canonical representatives
The classic technique of proving completeness of axiomatisations for process algebras with recursion involves merging guarded recursive equations [11, 30,31,32, 40]. In essence, it proves two bisimilar systems P and Q equivalent by equating both to an intermediate variant that is essentially a product of P and Q. I tried so hard, and in vain, to apply this technique to obtain (8), that I came to believe that it fundamentally does not work for this axiomatisation.
The problem is illustrated in Fig. 3. Here, similar to the example of Fig. 1, the processes 1 and 6 are strongly reactive bisimilar. The merging technique constructs a transition system whose states are pairs of states reachable from 1 and 6. There is a transition  iff both
iff both  and
and  . Normally, only those pairs (s, t) satisfying
. Normally, only those pairs (s, t) satisfying  are included. Here, the requirement
are included. Here, the requirement  would be to strong. Namely, although
would be to strong. Namely, although  , one has neither
, one has neither  nor
nor  nor
nor  nor
nor  , so there would be no outgoing \(\mathrm{t}\)-transitions from (1, 6). Hence, one has to include states (s, t) with
, so there would be no outgoing \(\mathrm{t}\)-transitions from (1, 6). Hence, one has to include states (s, t) with  for some set X. Note that
for some set X. Note that  and
and  when \(a\in X\) and \(b \notin X\), whereas
when \(a\in X\) and \(b \notin X\), whereas  and
and  when \(a\notin X\). This yields the product depicted in Fig. 3.
when \(a\notin X\). This yields the product depicted in Fig. 3.
In the reactive bisimulation game, the transition  will be matched by
will be matched by  only in an environment X with \(a \not \in X\). Hence, intuitively the state (2, 8) in the product should only be visited in such an environment. Yet, when aiming to show that
only in an environment X with \(a \not \in X\). Hence, intuitively the state (2, 8) in the product should only be visited in such an environment. Yet, when aiming to show that  , one cannot prevent taking the transition
, one cannot prevent taking the transition  in an environment X with \(a\in X\) and \(b \notin X\). However, since \((2,8) \mathop {\nrightarrow }\limits ^{a}\), this \(\mathrm{t}\)-transition cannot be simulated by process 2.
in an environment X with \(a\in X\) and \(b \notin X\). However, since \((2,8) \mathop {\nrightarrow }\limits ^{a}\), this \(\mathrm{t}\)-transition cannot be simulated by process 2.
It may be possible to repair the construction, for instance by adding a transition  or
or  after all, but not both. However, each such ad hoc repair that I tried gave raise to further problems, making the solution more and more complicated without sight on success.
after all, but not both. However, each such ad hoc repair that I tried gave raise to further problems, making the solution more and more complicated without sight on success.
Therefore, I here employ the novel method of canonical solutions [24, 29], which equates both P and Q to a canonical representative within the bisimulation equivalence class of P and Q—one that has only one reachable state for each bisimulation equivalence class of states of P and Q. Moreover, my proof employs the axiom of choice [41] in defining the transition relation on my canonical representative, in order to keep this process finitely branching.
To illustrate his technique on the example from Fig. 3, the states 1 and 6, being strongly reactive bisimilar, form one new state \(\{1,6\}\) of the canonical representative. Likewise, there will be states \(\{4,9\}\) and \(\{5,10\}\). However, the states 2, 3, 7 and 8 remain separate. Within the new state \(\{1,6\}\), my construction chooses an arbitrary element, say 1. Based on this choice, the outgoing transitions of \(\{1,6\}\) are dictated by 1, and thus go to P, \(\{2\}\) and \(\{3\}\). As a result, the canonical representative will look just like the left-hand process. It could however be the case that  , in which case the initial states of these subprocesses are merged in the canonical representative, and again an element in the resulting equivalence class will be chosen that dictates its outgoing transitions.
, in which case the initial states of these subprocesses are merged in the canonical representative, and again an element in the resulting equivalence class will be chosen that dictates its outgoing transitions.
10.6 The canonical representative
Let  denote the set of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion. Let
denote the set of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion. Let  be the strong reactive bisimulation equivalence class of a process
be the strong reactive bisimulation equivalence class of a process  . Below, by “abstract process” I will mean such an equivalence class. Choose a function \(\chi \) that selects an element out of each
. Below, by “abstract process” I will mean such an equivalence class. Choose a function \(\chi \) that selects an element out of each  -equivalence class of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion—this is possible by the axiom of choice [41]. Define the transition relations
-equivalence class of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion—this is possible by the axiom of choice [41]. Define the transition relations  , for \(\alpha \in Act\), between abstract processes by
, for \(\alpha \in Act\), between abstract processes by

I will show that  for all
for all  . Formally,
. Formally,  has been defined only between processes belonging to the same LTS
has been defined only between processes belonging to the same LTS  , and here
, and here  . However, this restriction is not material: two processes
. However, this restriction is not material: two processes  and
and  from different LTSs can be compared by considering
from different LTSs can be compared by considering  on the disjoint union
on the disjoint union  .
.
Lemma 7
Let \(\alpha \in A \cup \{\tau \}\). Then,  iff
iff  for some \(P'\) with \(R'=[P']\).
for some \(P'\) with \(R'=[P']\).
Proof
Let  with \(\alpha \in A \cup \{\tau \}\). Since
with \(\alpha \in A \cup \{\tau \}\). Since  , by Definition 8 there is a \(Q'\) such that
, by Definition 8 there is a \(Q'\) such that  and
and  . Hence,
. Hence,  by (9). Moreover, \(P' \in [Q']{=}[P']\).
by (9). Moreover, \(P' \in [Q']{=}[P']\).
Let  with \(\alpha \in A \cup \{\tau \}\). Then,
with \(\alpha \in A \cup \{\tau \}\). Then,  for some \(Q'\in R'\). Since
for some \(Q'\in R'\). Since  , there is a \(P'\) such that
, there is a \(P'\) such that  and
and  . Hence, \(P'\in R'\) and thus \(R'=[P']\). \(\square \)
. Hence, \(P'\in R'\) and thus \(R'=[P']\). \(\square \)
Corollary 37
\(\mathcal {I}([P]) = \mathcal {I}(P)\) for all  .
.
Lemma 8
If \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  then
then  for a \(Q'\) with
for a \(Q'\) with  . Moreover, if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
. Moreover, if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  then
then  for a \(P'\) with
for a \(P'\) with  .
.
Proof
Let \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . Since
. Since  , by Definition 8 there is a \(Q'\) such that
, by Definition 8 there is a \(Q'\) such that  and
and  . Hence,
. Hence,  by (9).
by (9).
Let \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and  . Then,
. Then,  for some \(R'\in [Q']\). Since
for some \(R'\in [Q']\). Since  (so \(\mathcal {I}(\chi ([P])) = \mathcal {I}(P)\)), there is a \(P'\) such that
(so \(\mathcal {I}(\chi ([P])) = \mathcal {I}(P)\)), there is a \(P'\) such that  and
and  . As
. As  is a congruence for \(\theta _X\), one has
is a congruence for \(\theta _X\), one has  , and thus
, and thus  . \(\square \)
. \(\square \)
Definition 38
Let  denote the reflexive and transitive closure of a binary relation
denote the reflexive and transitive closure of a binary relation  . A strong timeout bisimulation up to reflexivity and transitivity is a symmetric relation
. A strong timeout bisimulation up to reflexivity and transitivity is a symmetric relation  , such that, for
, such that, for  ,
,
-
if
 with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that
with \(\alpha \in A\cup \{\tau \}\), then \(\exists Q'\) such that 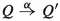 and
and  ,
, -
if \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
 , then \(\exists Q'\) with
, then \(\exists Q'\) with  and
and  .
.
Proposition 39
If  for a strong timeout bisimulation
for a strong timeout bisimulation  up to reflexivity and transitivity, then
up to reflexivity and transitivity, then  .
.
Proof
It suffices to show that  is a strong timeout bisimulation. Clearly this relation is symmetric.
is a strong timeout bisimulation. Clearly this relation is symmetric.
-
Suppose
 for some \(n\ge 0\) and
for some \(n\ge 0\) and  with \(\alpha \in A\cup \{\tau \}\). I have to find an
with \(\alpha \in A\cup \{\tau \}\). I have to find an  such that
such that  and
and  . I proceed with induction on n. The case \(n=0\) is trivial. Fixing an \(n>0\), by Definition 38 there is an
. I proceed with induction on n. The case \(n=0\) is trivial. Fixing an \(n>0\), by Definition 38 there is an  such that
such that  and
and  . Now, by induction there is an \(R'_n\) such that
. Now, by induction there is an \(R'_n\) such that  and
and  . Hence,
. Hence, 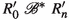 .
. -
Suppose
 for some \(n\ge 0\), \(\mathcal {I}(R_0)\cap (X\cup \{\tau \})=\emptyset \) and
for some \(n\ge 0\), \(\mathcal {I}(R_0)\cap (X\cup \{\tau \})=\emptyset \) and 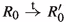 . By Definition 38\(\mathcal {I}(R_0) = \mathcal {I}(R_1) = \dots = \mathcal {I}(R_n)\). I have to find an \(R'_n\) such that
. By Definition 38\(\mathcal {I}(R_0) = \mathcal {I}(R_1) = \dots = \mathcal {I}(R_n)\). I have to find an \(R'_n\) such that  and
and  . This proceeds exactly as for the case above.\(\square \)
. This proceeds exactly as for the case above.\(\square \)
Lemma 9
 for all
for all  and \(X \subseteq A\).
and \(X \subseteq A\).
Proof
I show that the symmetric closure of  is a strong timeout bisimulation up to reflexivity and transitivity.
is a strong timeout bisimulation up to reflexivity and transitivity.
-
Let
 . Then,
. Then,  for some \(Q'\) with \(R'=\theta _X(Q')\). By Lemma 7,
for some \(Q'\) with \(R'=\theta _X(Q')\). By Lemma 7,  for some \(P'\) with \(Q'=[P']\). Hence,
for some \(P'\) with \(Q'=[P']\). Hence,  and thus
and thus  by Lemma 7. Moreover,
by Lemma 7. Moreover,  .
. -
Let
 . By Lemma 7,
. By Lemma 7, 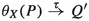 for some \(Q'\) with \(R'=[Q']\). Thus,
for some \(Q'\) with \(R'=[Q']\). Thus,  for some \(P'\) with \(Q'=\theta _X(P')\). Now
for some \(P'\) with \(Q'=\theta _X(P')\). Now  by Lemma 7, and thus
by Lemma 7, and thus  . Moreover,
. Moreover,  .
. -
Let
 with \(a \in A\). Then,
with \(a \in A\). Then,  and either \(a \in \mathcal {I}([P])\) or \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Thus, either \(a \in \mathcal {I}(P)\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37. By Lemma 7,
and either \(a \in \mathcal {I}([P])\) or \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Thus, either \(a \in \mathcal {I}(P)\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37. By Lemma 7,  for some \(P'\) with \(R'=[P']\). Hence,
for some \(P'\) with \(R'=[P']\). Hence,  and thus
and thus  .
. -
Let
 with \(a \in A\). By Lemma 7,
with \(a \in A\). By Lemma 7,  for some \(P'\) with \(R'=[P']\). Thus,
for some \(P'\) with \(R'=[P']\). Thus,  and either \(a \in \mathcal {I}(P)\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Therefore, either \(a \in \mathcal {I}([P])\) or \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37. Moreover,
and either \(a \in \mathcal {I}(P)\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Therefore, either \(a \in \mathcal {I}([P])\) or \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37. Moreover,  by Lemma 7. It follows that
by Lemma 7. It follows that  .
. -
Let \(\mathcal {I}(\theta _X([P])) \cap (X \cup \{\tau \})=\emptyset \) and
 . Then,
. Then,  and \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Thus, \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37, so \(\mathcal {I}(P) \cap (X \cup \{\tau \})=\emptyset \) and \(\mathcal {I}(\theta _X(P)) \cap (X \cup \{\tau \})=\emptyset \). By Lemma 8,
and \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Thus, \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), using Corollary 37, so \(\mathcal {I}(P) \cap (X \cup \{\tau \})=\emptyset \) and \(\mathcal {I}(\theta _X(P)) \cap (X \cup \{\tau \})=\emptyset \). By Lemma 8, 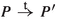 for some \(P'\) with
for some \(P'\) with  . Hence
. Hence  and thus, again applying Lemma 8,
and thus, again applying Lemma 8,  for some \(T'\) with
for some \(T'\) with  . Moreover,
. Moreover,  .
. -
Let \(\mathcal {I}([\theta _X(P)])\cap (X\cup \{\tau \})=\emptyset \) and
 . By Lemma 8,
. By Lemma 8,  for a \(P'\) with
for a \(P'\) with  . Hence
. Hence  and \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), so \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \). Hence, by Lemma 8,
and \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\), so \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \). Hence, by Lemma 8,  for a \(T'\) with
for a \(T'\) with  . By Corollary 37, \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). So
. By Corollary 37, \([P] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). So  . Moreover,
. Moreover,  .\(\square \)
.\(\square \)
Proposition 40
 for all
for all  .
.
Proof
Using Proposition 24, I show that the symmetric closure of the relation  is a strong timeout bisimulation up to
is a strong timeout bisimulation up to  . Here, the right-hand side processes come from an LTS that is closed under \(\theta \) and contains the processes [P] for
. Here, the right-hand side processes come from an LTS that is closed under \(\theta \) and contains the processes [P] for  .
.
-
Let
 with \(\alpha \in A \cup \{\tau \}\). Then,
with \(\alpha \in A \cup \{\tau \}\). Then,  by Lemma 7, and
by Lemma 7, and  .
. -
Let
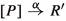 with \(\alpha \in A \cup \{\tau \}\). Then, by Lemma 7,
with \(\alpha \in A \cup \{\tau \}\). Then, by Lemma 7, 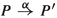 for some \(P'\) with \(R'=[P']\). Moreover,
for some \(P'\) with \(R'=[P']\). Moreover,  .
. -
Let \(\mathcal {I}(P)\cap (X\cup \{\tau \})=\emptyset \) and
 . By Lemma 8,
. By Lemma 8,  for some \(Q'\) such that
for some \(Q'\) such that  . Moreover, using Lemma 9,
. Moreover, using Lemma 9,  .
. -
Let \(\mathcal {I}([P])\cap (X\cup \{\tau \})=\emptyset \) and
 . Then, by Lemma 8,
. Then, by Lemma 8,  for some \(P'\) with
for some \(P'\) with 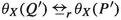 . By Lemma 9,
. By Lemma 9,  .
.
\(\square \)
By Proposition 13, each  is finitely branching. By construction, so is [P].
is finitely branching. By construction, so is [P].
No two states reachable from [P] are strongly reactive bisimilar. Hence, the process [P] with its above-generated transition relation can be seen as a version of P where each equivalence class of reachable states is collapsed into a single state—a kind of minimisation. But it is not exactly a minimisation, as not all states reachable from [P] need be strongly reactive bisimilar with reachable states of P. This is illustrated by Process 6 of Fig. 3, when \(\chi (\{1,6\})=1\). Now \(\{2\}\) and \(\{3\}\) are reachable from [P], but not strongly reactive bisimilar with reachable states of 6.
10.7 Completeness for finitely branching processes
I will now give a syntactic representation of each process [P], for  , as a \(\text{ CCSP}_\mathrm{t}^\theta \) process with guarded recursion. Take a different variable \(x_R\) for each
, as a \(\text{ CCSP}_\mathrm{t}^\theta \) process with guarded recursion. Take a different variable \(x_R\) for each  -equivalence class R of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion. Let \(V_{{\mathcal {S}}}\) be the set of all those variables and define the recursive specification \({{\mathcal {S}}}\) by
-equivalence class R of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion. Let \(V_{{\mathcal {S}}}\) be the set of all those variables and define the recursive specification \({{\mathcal {S}}}\) by

By construction,  , that is, the process
, that is, the process  is strongly bisimilar to [P]. In fact, the symmetric closure of the relation
is strongly bisimilar to [P]. In fact, the symmetric closure of the relation  is a strong bisimulation. Thus, \(\mathbf [ P\mathbf ] \) serves as a normal form within the
is a strong bisimulation. Thus, \(\mathbf [ P\mathbf ] \) serves as a normal form within the  -equivalence class of
-equivalence class of  .
.
The above construction will not work when there are not as many variables as equivalence classes of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion. Note that each real number in the interval [0, 1) can be represented as an infinite sequence of 0s and 1s, and thus as \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion employing the finite alphabet \(A=\{0,1\}\). Hence, there are uncountably many equivalences classes of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion.
To solve this problem, one starts here already with the proof of (8), and fixes two processes \(P_0\) and  with
with  . The task is to prove \(\textit{Ax} \vdash P_0 = Q_0\). Now call an equivalence class R of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion relevant if either R is reachable from \([P_0] = [Q_0]\), or a member of R is reachable from \(P_0\) or \(Q_0\). There are only countably many relevant equivalence classes. It suffices to take a variable \(x_R\) only for relevant R. Below, I will call a process
. The task is to prove \(\textit{Ax} \vdash P_0 = Q_0\). Now call an equivalence class R of \(\text{ CCSP}_\mathrm{t}^\theta \) processes with guarded recursion relevant if either R is reachable from \([P_0] = [Q_0]\), or a member of R is reachable from \(P_0\) or \(Q_0\). There are only countably many relevant equivalence classes. It suffices to take a variable \(x_R\) only for relevant R. Below, I will call a process  relevant if it is a member of a relevant equivalence class; in case we had enough variables to start with, all processes
relevant if it is a member of a relevant equivalence class; in case we had enough variables to start with, all processes  may be called relevant.
may be called relevant.
Lemma 10
Let  be relevant. Then,
be relevant. Then,  .
.
Proof
Suppose  . Then,
. Then,  , so \([P]=[Q]\), and hence \(\mathbf [ P\mathbf ] =\mathbf [ Q\mathbf ] \). \(\square \)
, so \([P]=[Q]\), and hence \(\mathbf [ P\mathbf ] =\mathbf [ Q\mathbf ] \). \(\square \)
Lemma 11
Let  be relevant. Then,
be relevant. Then,  .
.
Proof
I show that  is a strong bisimulation.
is a strong bisimulation.
Suppose  . Then, \(\mathbf [ P\mathbf ] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\) iff \(\mathbf [ Q\mathbf ] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\), since \(\mathcal {I}(\mathbf [ P\mathbf ] ) \cap (X\cup \{\tau \}) = \mathcal {I}(\theta _X(\mathbf [ P\mathbf ] )) \cap (X\cup \{\tau \}) = \mathcal {I}(\theta _X(\mathbf [ Q\mathbf ] )) \cap (X\cup \{\tau \}) = \mathcal {I}(\mathbf [ Q\mathbf ] ) \cap (X\cup \{\tau \})\).
. Then, \(\mathbf [ P\mathbf ] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\) iff \(\mathbf [ Q\mathbf ] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\), since \(\mathcal {I}(\mathbf [ P\mathbf ] ) \cap (X\cup \{\tau \}) = \mathcal {I}(\theta _X(\mathbf [ P\mathbf ] )) \cap (X\cup \{\tau \}) = \mathcal {I}(\theta _X(\mathbf [ Q\mathbf ] )) \cap (X\cup \{\tau \}) = \mathcal {I}(\mathbf [ Q\mathbf ] ) \cap (X\cup \{\tau \})\).
First consider the case that \(\mathbf [ P\mathbf ] \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Then,  and
and  . Hence,
. Hence,  . So by Lemma 10, \(\mathbf [ P\mathbf ] = \mathbf [ Q\mathbf ] \), and thus \(\theta _X(\mathbf [ P\mathbf ] ) \mathrel {\textit{Id}} \theta _X(\mathbf [ Q\mathbf ] )\).
. So by Lemma 10, \(\mathbf [ P\mathbf ] = \mathbf [ Q\mathbf ] \), and thus \(\theta _X(\mathbf [ P\mathbf ] ) \mathrel {\textit{Id}} \theta _X(\mathbf [ Q\mathbf ] )\).
Henceforth, I suppose that  for some \(\beta \in X\cup \{\tau \}\). So \(\mathbf [ P\mathbf ] {{\mathop {\nrightarrow }\limits ^{\mathrm{t}}}}\) and \(\mathbf [ Q\mathbf ] {{\mathop {\nrightarrow }\limits ^{\mathrm{t}}}}\).
for some \(\beta \in X\cup \{\tau \}\). So \(\mathbf [ P\mathbf ] {{\mathop {\nrightarrow }\limits ^{\mathrm{t}}}}\) and \(\mathbf [ Q\mathbf ] {{\mathop {\nrightarrow }\limits ^{\mathrm{t}}}}\).
-
Let
 with \(a \in A\). Then,
with \(a \in A\). Then,  for some \(Q''\) with
for some \(Q''\) with  . One has
. One has  and
and  . The process \(P''\) must have the form \(\mathbf [ P'\mathbf ] \), and likewise \(Q''=\mathbf [ Q'\mathbf ] \). Since
. The process \(P''\) must have the form \(\mathbf [ P'\mathbf ] \), and likewise \(Q''=\mathbf [ Q'\mathbf ] \). Since  , Lemma 10 yields \(\mathbf [ P'\mathbf ] = \mathbf [ Q'\mathbf ] \).
, Lemma 10 yields \(\mathbf [ P'\mathbf ] = \mathbf [ Q'\mathbf ] \). -
Let
 . Then,
. Then,  for some \(Q''\) with
for some \(Q''\) with 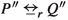 . The process \(P''\) must have the form \(\theta _X(\mathbf [ P'\mathbf ] )\), and likewise \(Q''=\theta _X(\mathbf [ Q'\mathbf ] )\). Hence
. The process \(P''\) must have the form \(\theta _X(\mathbf [ P'\mathbf ] )\), and likewise \(Q''=\theta _X(\mathbf [ Q'\mathbf ] )\). Hence  .\(\square \)
.\(\square \)
Definition 41
Given a relevant \(\text{ CCSP}_\mathrm{t}^\theta \) process  , let
, let  .
.
Thus, \({\widetilde{P}}\) is defined like the head-normal form \(\widehat{P}\) of  , except that all processes Q reachable from P by performing one transition are replaced by the normal form within their
, except that all processes Q reachable from P by performing one transition are replaced by the normal form within their  -equivalence class.
-equivalence class.
So  . Note that \(\mathbf [ P\mathbf ] = \widetilde{\chi ([P])}\) is provable through a single application of the axiom RDP.
. Note that \(\mathbf [ P\mathbf ] = \widetilde{\chi ([P])}\) is provable through a single application of the axiom RDP.
The following step is the only one where the reactive approximation axiom (RA) is used.
Proposition 42
Let  be relevant. Then,
be relevant. Then,  .
.
Proof
Suppose  . Then,
. Then,  .With Axiom RA it suffices to show that \(\textit{Ax}_f \vdash \psi _X({\widetilde{P}}) = \psi _X(\widetilde{Q})\) for all \(X\subseteq A\). So pick \(X \subseteq A\). Let
.With Axiom RA it suffices to show that \(\textit{Ax}_f \vdash \psi _X({\widetilde{P}}) = \psi _X(\widetilde{Q})\) for all \(X\subseteq A\). So pick \(X \subseteq A\). Let
with \(\alpha _j,\beta _k \in A\cup \{\tau \}\) for all \(i\in I\) and \(k\in K\). As for Theorem 36, the following two claims are crucial.
Claim 1: For each \(i \in I\), there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(\textit{Ax} \vdash P'_i = Q'_k\).
Claim 2: If \(\mathcal {I}(P) \cap (X \cup \{\tau \}) = \emptyset \), then for each \(j \in J\) there is a \(h \in H\) with \(\textit{Ax} \vdash \theta _X(P''_j) = \theta _X(Q''_h)\).
With these claims the proof proceeds exactly as the one of Theorem 36.
Proof of Claim 1: Pick \(i \in I\). Then,  . So
. So  for some \(Q'\) with
for some \(Q'\) with  . Hence there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(Q'=Q'_k\). The processes \(P'_i\) and \(Q'_k\) must have the form \(\mathbf [ P'\mathbf ] \) and \(\mathbf [ Q'\mathbf ] \) for some
. Hence there is a \(k \in K\) with \(\alpha _i=\beta _k\) and \(Q'=Q'_k\). The processes \(P'_i\) and \(Q'_k\) must have the form \(\mathbf [ P'\mathbf ] \) and \(\mathbf [ Q'\mathbf ] \) for some  . Hence, by Lemma 10, \(P'_i = Q'_k\), and thus certainly \(\textit{Ax} \vdash P'_i = Q'_k\).
. Hence, by Lemma 10, \(P'_i = Q'_k\), and thus certainly \(\textit{Ax} \vdash P'_i = Q'_k\).
Proof of Claim 2: Pick \(j \in J\). Then,  . Since \(\mathcal {I}({\widetilde{P}}) \cap (X \cup \{\tau \}) = \emptyset \), there is a \(Q''\) such that
. Since \(\mathcal {I}({\widetilde{P}}) \cap (X \cup \{\tau \}) = \emptyset \), there is a \(Q''\) such that  and
and  . Hence, there is a \(h \in H\) with \(Q''=Q''_h\). The processes \(P''_j\) and \(Q''_h\) have the form \(\mathbf [ P''\mathbf ] \) and \(\mathbf [ Q''\mathbf ] \) for some
. Hence, there is a \(h \in H\) with \(Q''=Q''_h\). The processes \(P''_j\) and \(Q''_h\) have the form \(\mathbf [ P''\mathbf ] \) and \(\mathbf [ Q''\mathbf ] \) for some  . So by Lemma 11,
. So by Lemma 11,  . The completeness of Ax for strong bisimilarity (Theorem 32) now yields \(\textit{Ax} \vdash \theta _X(P''_j) = \theta _X(Q'')\). \(\square \)
. The completeness of Ax for strong bisimilarity (Theorem 32) now yields \(\textit{Ax} \vdash \theta _X(P''_j) = \theta _X(Q'')\). \(\square \)
Theorem 43
Let  be relevant. Then, \(\textit{Ax} \vdash P = \mathbf [ P\mathbf ] \).
be relevant. Then, \(\textit{Ax} \vdash P = \mathbf [ P\mathbf ] \).
Proof
Let \(\textit{reach}(P)\) be the set of processes reachable from P. Take a different variable \(z_R\) for each \(R \in \textit{reach}(P)\), and define the recursive specification \({{\mathcal {S}}}'\) by \(V_{{{\mathcal {S}}}'} := \{z_R\mid R \in \textit{reach}(P)\}\) and

By construction,  . In fact, the symmetric closure of
. In fact, the symmetric closure of  is a strong bisimulation. To establish Theorem 43 through an application of RSP, I show that both P and \(\mathbf [ P\mathbf ] \) are \(x_P\)-components of solutions of \({{\mathcal {S}}}'\). So I show
is a strong bisimulation. To establish Theorem 43 through an application of RSP, I show that both P and \(\mathbf [ P\mathbf ] \) are \(x_P\)-components of solutions of \({{\mathcal {S}}}'\). So I show

for all \(R \in \textit{reach}(P)\). The first of these statements is a direct application of Proposition 31. The second statement can be reformulated as \(\textit{Ax} \vdash \mathbf [ R\mathbf ] = {\widetilde{R}}\). As remarked above, \(\textit{Ax} \vdash \mathbf [ R\mathbf ] = \widetilde{\chi ([R])}\) through a single application of RDP. Hence, I need to show that \(\textit{Ax} \vdash \widetilde{\chi ([R])} = {\widetilde{R}}\). Considering that  , this is a consequence of Proposition 42. \(\square \)
, this is a consequence of Proposition 42. \(\square \)
Corollary 44
Let  be relevant. Then,
be relevant. Then,  .
.
Proof
Let  . Then, \(\mathbf [ P\mathbf ] =\mathbf [ Q\mathbf ] \) by Lemma 10, so \(\textit{Ax} \vdash P = \mathbf [ P\mathbf ] = \mathbf [ Q\mathbf ] = Q\). \(\square \)
. Then, \(\mathbf [ P\mathbf ] =\mathbf [ Q\mathbf ] \) by Lemma 10, so \(\textit{Ax} \vdash P = \mathbf [ P\mathbf ] = \mathbf [ Q\mathbf ] = Q\). \(\square \)
10.8 Necessity of the axiom of choice
At first glance, it may look like the above proof can be simplified so as to avoid using the axiom of choice, namely by changing (9) into

However, this would make some processes [P] infinitely branching, even when P is finitely branching. Figure 4 shows an uncountable collection of strongly reactive bisimilar finitely branching processes. Here, each pair of a dashed b-transition and the dotted one right below it constitutes a design choice: either the dashed or the dotted b-transition is present, but not both. Since there is this binary choice for infinitely many pairs of b-transitions, this figure represents an uncountable collection of processes. All of them are strongly reactive bisimilar, because the \(\mathrm{t}\)-transition will only be taken in an environment that blocks b. In case a is blocked as well, all the a-transitions from a state with an outgoing \(\tau \)-transition can be dropped, and the difference between these processes disappears. In case a is allowed by the environment, all b transitions can be dropped, and again the difference between these processes disappears. Hence, the above alternative definition would yield uncountably many outgoing \(\mathrm{t}\)-transitions from the equivalence class of all these processes. This would make it impossible to represent such a “minimised” process in \(\text{ CCSP}_\mathrm{t}^\theta \).
11 Concluding remarks
This paper laid the foundations of the proper analogue of strong bisimulation semantics for a process algebra with timeouts. This makes it possible to specify systems in this setting and verify their correctness properties. The addition of timeouts comes with considerable gains in expressive power. An illustration of this is mutual exclusion.
As shown in [20], it is fundamentally impossible to correctly specify mutual exclusion protocols in standard process algebras, such as CCS [33], CSP [6, 28], ACP [2, 10] or CCSP, unless the correctness of the specified protocol hinges on a fairness assumption. The latter, in the view of [20], does not provide an adequate solution, as fairness assumptions are in many situations unwarranted and lead to false conclusions. In [9], a correct process-algebraic rendering of mutual exclusion is given, but only after making two important modifications to standard process algebra. The first involves making a justness assumption. Here, justness [21] is an alternative to fairness, in some sense a much weaker form of fairness—meaning weaker than weak fairness. Unlike (strong or weak) fairness, its use typically is warranted and does not lead to false conclusions. The second modification is the addition of a new construct—signals—to CCS, or any other standard process algebra. Interestingly, both modifications are necessary; just using justness, or just adding signals, is insufficient. Bouwman [4, 5] points out that since the justness requirement was fairly new, and needed to be carefully defined to describe its interaction with signals anyway, it is possible to specify mutual exclusion without adding signals to the language at all, instead reformulating the justness requirement in such a way that it effectively turns some actions into signals. Yet justness is essential in all these approaches. This may be seen as problematic, because large parts of the foundations of process algebra are incompatible with justness, and hence need to be thoroughly reformulated in a justness-friendly way. This is pointed out in [17].
The addition of timeouts to standard process algebra makes it possible to specify mutual exclusion without assuming justness! Instead, one should make the assumption called progress in [21], which is weaker than justness, uncontroversial, unproblematic, and made (explicitly or implicitly) in virtually all papers dealing with issues like mutual exclusion. This claim is substantiated in [19].
Besides applications to protocol verification, future work includes adapting the work done here to a form of reactive bisimilarity that abstracts from hidden actions, that is, to provide a counterpart for process algebras with timeouts of, for instance, branching bisimilarity [23], weak bisimilarity [33] or coupled similarity [3, 12, 36]. Other topics worth exploring are the extension to probabilistic processes, and especially the relations with timed process algebras. Davies & Schneider in [7], for instance, added a construct with a quantified timeout to the process algebra CSP [6, 28], elaborating the timed model of CSP presented by Reed & Roscoe in [38].
Notes
Pohlmann [37] follows the original, 2020, version of this paper; this appendix was added in September 2021.
References
Baeten, J.C.M., Bergstra, J.A., Klop, J.W.: Syntax and defining equations for an interrupt mechanism in process algebra. Fundam. Inform. 9(2), 127–168 (1986). https://doi.org/10.3233/FI-1986-9202
Baeten, J.C.M., Weijland, W.P.: Process Algebra. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge (1990). https://doi.org/10.1017/CBO9780511624193
Bisping, B., Nestmann, U., Peters, K.: Coupled similarity: the first 32 years. Acta Inform. 57(3–5), 439–463 (2020). https://doi.org/10.1007/s00236-019-00356-4
Bouwman, M.S.: Liveness analysis in process algebra: simpler techniques to model mutex algorithms. Technical Report, Eindhoven University of Technology (2018). http://www.win.tue.nl/~timw/downloads/bouwman_seminar.pdf
Bouwman, M.S., Luttik, B., Willemse, T.A.C.: Off-the-shelf automated analysis of liveness properties for just paths. Acta Inform. 57(3–5), 551–590 (2020). https://doi.org/10.1007/s00236-020-00371-w
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984). https://doi.org/10.1145/828.833
Davies, J., Schneider, S.: Recursion induction for real-time processes. Formal Aspects Comput. 5(6), 530–553 (1993). https://doi.org/10.1007/BF01211248
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theor. Comput. Sci. 34, 83–133 (1984). https://doi.org/10.1016/0304-3975(84)90113-0
Dyseryn, V., van Glabbeek, R.J., Höfner, P.: Analysing Mutual Exclusion using Process Algebra with Signals. In: Peters, K., Tini, S. (eds.). Proceedings Combined 24th International Workshop on Expressiveness in Concurrency and 14th Workshop on Structural Operational Semantics, Electronic Proceedings in Theoretical Computer Science, vol. 255. Open Publishing Association, pp. 18–34. https://doi.org/10.4204/EPTCS.255.2 (2017)
Fokkink, W.J.: Introduction to Process Algebra. Texts in Theoretical Computer Science, An EATCS Series. Springer, Berlin (2000). https://doi.org/10.1007/978-3-662-04293-9
van Glabbeek, R.J.: A complete axiomatization for branching bisimulation congruence of finite-state behaviours. In: Borzyszkowski, A.M., Sokołowski, S. (eds.). Proceedings 18th International Symposium on Mathematical Foundations of Computer Science, MFCS ’93, LNCS 711. Springer, pp. 473–484 (1993). https://doi.org/10.1007/3-540-57182-5_39
van Glabbeek, R.J.: The Linear Time—Branching Time Spectrum II; The semantics of sequential systems with silent moves. In: Best, E. (ed.). Proceedings 4th International Conference on Concurrency Theory, CONCUR’93, LNCS 715. Springer, pp. 66–81 (1993). https://doi.org/10.1007/3-540-57208-2_6
van Glabbeek, R.J.: On the expressiveness of ACP (extended abstract). In: Ponse, A., Verhoef, C., van Vlijmen, S.F.M. (eds.). Proceedings First Workshop on the Algebra of Communicating Processes, ACP’94, Workshops in Computing. Springer, pp. 188–217 (1994). https://doi.org/10.1007/978-1-4471-2120-6_8
van Glabbeek, R.J.: The Linear Time—Branching Time Spectrum I; The Semantics of Concrete, Sequential Processes. In: Bergstra, J.A., Ponse, A., S.A. Smolka, editors: Handbook of Process Algebra, chapter 1, Elsevier, pp. 3–99 (2001). https://doi.org/10.1016/B978-044482830-9/50019-9
van Glabbeek, R.J.: The meaning of negative premises in transition system specifications II. J. Logic Algebr. Program. 60–61, 229–258 (2004). https://doi.org/10.1016/j.jlap.2004.03.007
van Glabbeek, R.J.: Lean and full congruence formats for recursion. In: Proceedings 32nd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS’17. IEEE Computer Society Press (2017). https://doi.org/10.1109/LICS.2017.8005142
van Glabbeek, R.J.: Ensuring liveness properties of distributed systems: open problems. J. Log. Algebr. Methods Program. 109, 100480 (2019)
van Glabbeek, R.J.: Failure trace semantics for a process algebra with time-outs. Log. Methods Comput. Sci. 17(2), 11 (2021). https://doi.org/10.23638/LMCS-17(2:11)2021
van Glabbeek, R.J.: Modelling Mutual Exclusion in a Process Algebra with Time-outs. https://arxiv.org/abs/2106.12785 (2021)
van Glabbeek, R.J., Höfner, P.: CCS: It’s not fair! Fair schedulers cannot be implemented in CCS-like languages even under progress and certain fairness assumptions. Acta Inform. 52(2–3), 175–205 (2015)
van Glabbeek, R.J., Höfner, P.: Progress, justness and fairness. ACM Comput. Surv. 52(4), 69 (2019). https://doi.org/10.1145/3329125
van Glabbeek, R.J., Middelburg, C.A.: On Infinite Guarded Recursive Specifications in Process Algebra (2020). http://arxiv.org/abs/2005.00746
van Glabbeek, R.J., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. J. ACM 43(3), 555–600 (1996). https://doi.org/10.1145/233551.233556
Grabmayer, C., Fokkink, W.J.: A complete proof system for 1-free regular expressions modulo bisimilarity. In: Hermanns, H., Zhang, L., Kobayashi, N., Miller, D. (eds.). Proceedings of 35th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS’20. ACM, pp. 465–478 (2020). https://doi.org/10.1145/3373718.3394744
Groote, J.F.: Transition system specifications with negative premises. Theor. Comput. Sci. 118, 263–299 (1993). https://doi.org/10.1016/0304-3975(93)90111-6
Groote, J.F., Vaandrager, F.W.: Structured operational semantics and bisimulation as a congruence. Inf. Comput. 100(2), 202–260 (1992). https://doi.org/10.1016/0890-5401(92)90013-6
Hennessy, M., Milner, R.: Algebraic laws for nondeterminism and concurrency. J. ACM 32(1), 137–161 (1985). https://doi.org/10.1145/2455.2460
Hoare, C.A.R.: Communicating Sequential Processes. Prentice Hall, Englewood Cliffs (1985)
Liu, X., Yu, T.: Canonical solutions to recursive equations and completeness of equational axiomatisations. In: Konnov, I., Kovacs, L. (eds.). Proceedings 31st International Conference on Concurrency Theory (CONCUR 2020), Leibniz International Proceedings in Informatics (LIPIcs) 171, Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2020). https://doi.org/10.4230/LIPIcs.CONCUR.2020.35
Lohrey, M., D’Argenio, P.R., Hermanns, H.: Axiomatising divergence. Inf. Comput. 203(2), 115–144 (2005). https://doi.org/10.1016/j.ic.2005.05.007
Milner, R.: A complete inference system for a class of regular behaviours. J. Comput. Syst. Sci. 28, 439–466 (1984). https://doi.org/10.1016/0022-0000(84)90023-0
Milner, R.: A complete axiomatisation for observational congruence of finite-state behaviors. Inf. Comput. 81(2), 227–247 (1989). https://doi.org/10.1016/0890-5401(89)90070-9
Milner, R.: Operational and algebraic semantics of concurrent processes. In: van Leeuwen, J. (ed.). Handbook of Theoretical Computer Science, chapter 19, Elsevier Science Publishers B.V. (North-Holland), pp. 1201–1242. Alternatively see Communication and Concurrency, Prentice-Hall, Englewood Cliffs, 1989, of which an earlier version appeared as A Calculus of Communicating Systems, LNCS 92, Springer (1990). https://doi.org/10.1007/3-540-10235-3
Olderog, E.-R.: Operational Petri net semantics for CCSP. In: Rozenberg, G. (ed.). Advances in Petri Nets 1987, LNCS 266. Springer, pp. 196–223 (1987). https://doi.org/10.1007/3-540-18086-9_27
Olderog, E.-R., Hoare, C.A.R.: Specification-oriented semantics for communicating processes. Acta Inform. 23, 9–66 (1986). https://doi.org/10.1007/BF00268075
Parrow, J., Sjödin, P.: Multiway synchronization verified with coupled simulation. In: Cleaveland, W.R. (ed.). Proceedings CONCUR 92, Stony Brook, NY, USA, LNCS 630. Springer, pp. 518–533 (1992). https://doi.org/10.1007/BFb0084813
Pohlmann, M.: Reducing strong reactive bisimilarity to strong bisimilarity. Bachelor’s thesis, TU Berlin. https://maxpohlmann.github.io/Reducing-Reactive-to-Strong-Bisimilarity/thesis.pdf (2021)
Reed, G.M., Roscoe, A.W.: A timed model for communicating sequential processes. Theor. Comput. Sci. 58, 249–261 (1988). https://doi.org/10.1016/0304-3975(88)90030-8
Vaandrager, F.W.: Expressiveness results for process algebras. In: de Bakker, J.W., de Roever, W.P., Rozenberg, G. (eds.). Proceedings REX Workshop on Semantics: Foundations and Applications, Beekbergen, The Netherlands, 1992, LNCS 666. Springer, pp. 609–638 (1993). https://doi.org/10.1007/3-540-56596-5_49
Walker, D.J.: Bisimulation and divergence. Inf. Comput. 85(2), 202–241 (1990). https://doi.org/10.1016/0890-5401(90)90048-M
Zermelo, E.: Untersuchungen über die Grundlagen der Mengenlehre I. Math. Ann. 65(2), 261–281 (1908). https://doi.org/10.1007/bf01449999
Acknowledgements
I thank the CONCUR’20 and Acta Informatica referees for helpful feedback.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
An extended abstract of this paper appears in the proceedings of CONCUR 2020. https://doi.org/10.4230/LIPIcs.CONCUR.2020.6.
Appendices
A Initials congruence
This appendix contains the proofs of two facts about initials equivalence I need in this paper, namely that it is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \) and that it is not affected by which processes are substituted for variables whose free occurrences are guarded.
Theorem 18
Initials equivalence is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \).
Proof
Let  be the smallest relation satisfying
be the smallest relation satisfying
-
if \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\) and
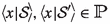 , such that \({{\mathcal {S}}}_y =_I {{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\), then
, such that \({{\mathcal {S}}}_y =_I {{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\), then  ,
, -
if \(P =_\mathcal {I}Q\), then
 ,
, -
if
 and \(\alpha \in A\cup \{\tau ,\mathrm{t}\}\), then
and \(\alpha \in A\cup \{\tau ,\mathrm{t}\}\), then  ,
, -
if
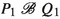 and
and  , then
, then  ,
, -
if
 ,
,  and \(S\subseteq A\), then
and \(S\subseteq A\), then  ,
, -
if
 and \(I\subseteq A\), then
and \(I\subseteq A\), then  ,
, -
if
 and \(\mathcal {R}\subseteq A \times A\), then
and \(\mathcal {R}\subseteq A \times A\), then  ,
, -
if
 , \(L\subseteq U \subseteq A\) and \(X\subseteq A\), then
, \(L\subseteq U \subseteq A\) and \(X\subseteq A\), then  and
and  ,
, -
if \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and
 are substitutions satisfying
are substitutions satisfying  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\), then
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\), then 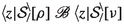 .
.
A trivial structural induction on  (not using the first two clauses) shows that if
(not using the first two clauses) shows that if  satisfy
satisfy  for all \(x\in { Var}\), then
for all \(x\in { Var}\), then  .(
.( )
)
For \({{\mathcal {S}}}\) a recursive specification and  , let
, let  be the closed substitution given by
be the closed substitution given by  if \(x\in V_{{\mathcal {S}}}\) and \(\rho _{{\mathcal {S}}}(x):=\rho (x)\) otherwise. Then,
if \(x\in V_{{\mathcal {S}}}\) and \(\rho _{{\mathcal {S}}}(x):=\rho (x)\) otherwise. Then,  for all
for all  . Hence, an application of (
. Hence, an application of ( ) with \(\rho _{{\mathcal {S}}}\) and \(\nu _{{\mathcal {S}}}\) yields that under the conditions of the last clause for
) with \(\rho _{{\mathcal {S}}}\) and \(\nu _{{\mathcal {S}}}\) yields that under the conditions of the last clause for  above one even has
above one even has  for all expressions
for all expressions  ,($)
,($)
and likewise, in the first clause,  for all
for all  with variables from \(V_{{\mathcal {S}}}\).(#)
with variables from \(V_{{\mathcal {S}}}\).(#)
It suffices to show that  , because then
, because then  , and (
, and ( ) implies that
) implies that  is a lean congruence. Moreover, the clauses for
is a lean congruence. Moreover, the clauses for  (not needing the last) then imply that \(=_\mathcal {I}\) is a full congruence. This I will do by induction on the stratum \((\lambda _R,\kappa _R)\) of processes
(not needing the last) then imply that \(=_\mathcal {I}\) is a full congruence. This I will do by induction on the stratum \((\lambda _R,\kappa _R)\) of processes  , as defined in Sect. 5. So pick a stratum \((\lambda ,\kappa )\) and assume that
, as defined in Sect. 5. So pick a stratum \((\lambda ,\kappa )\) and assume that  for all
for all  with \((\lambda _P,\kappa _P) < (\lambda ,\kappa )\) and \((\lambda _Q,\kappa _Q) < (\lambda ,\kappa )\). I need to show that
with \((\lambda _P,\kappa _P) < (\lambda ,\kappa )\) and \((\lambda _Q,\kappa _Q) < (\lambda ,\kappa )\). I need to show that  for all
for all  with \((\lambda _P,\kappa _P) \le (\lambda ,\kappa )\) and \((\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\).
with \((\lambda _P,\kappa _P) \le (\lambda ,\kappa )\) and \((\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\).
Because \(=_I\) is symmetric, so is  . Hence, it suffices to show that
. Hence, it suffices to show that  for all
for all  with \((\lambda _P,\kappa _P), (\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\) and all \(\alpha \in A \cup \{\tau \}\). This I will do by structural induction on the proof \(\pi \) of
with \((\lambda _P,\kappa _P), (\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\) and all \(\alpha \in A \cup \{\tau \}\). This I will do by structural induction on the proof \(\pi \) of  from the rules of Table 1. I make a case distinction based on the derivation of
from the rules of Table 1. I make a case distinction based on the derivation of  . So assume
. So assume  , \((\lambda _P,\kappa _P), (\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\), and
, \((\lambda _P,\kappa _P), (\lambda _Q,\kappa _Q) \le (\lambda ,\kappa )\), and  with \(\alpha \in A \cup \{\tau \}\).
with \(\alpha \in A \cup \{\tau \}\).
-
Let
 and
and  where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that \({{\mathcal {S}}}_y =_\mathcal {I}{{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\), meaning that for all \(y\in V_{{\mathcal {S}}}\) and
where \({{\mathcal {S}}}\) and \({{\mathcal {S}}}'\) are recursive specifications with \(x \in V_{{\mathcal {S}}}= V_{{{\mathcal {S}}}'}\), such that \({{\mathcal {S}}}_y =_\mathcal {I}{{\mathcal {S}}}'_y\) for all \(y\in V_{{\mathcal {S}}}\), meaning that for all \(y\in V_{{\mathcal {S}}}\) and  one has \({{\mathcal {S}}}_y[\sigma ] =_\mathcal {I}{{\mathcal {S}}}'_y[\sigma ]\). By Table 1, the transition
one has \({{\mathcal {S}}}_y[\sigma ] =_\mathcal {I}{{\mathcal {S}}}'_y[\sigma ]\). By Table 1, the transition 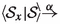 is provable by means of a strict subproof of \(\pi \). By (#) above, one has
is provable by means of a strict subproof of \(\pi \). By (#) above, one has  . So by induction
. So by induction  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  , one has
, one has  . Hence,
. Hence,  . By Table 1,
. By Table 1,  .
. -
The case \(P =_\mathcal {I}Q\) is trivial.
-
Let \(P = \beta .P^\dagger \) and \(Q = \beta .Q^\dagger \) with \(\beta \in A\cup \{\tau ,\mathrm{t}\}\) and
 . Then, \(\alpha =\beta \) and
. Then, \(\alpha =\beta \) and  .
. -
Let \(P = P_1 + P_2\) and \(Q = Q_1 + Q_2\) with
 and
and  . I consider the first rule from Table 1 that could have been responsible for the derivation of
. I consider the first rule from Table 1 that could have been responsible for the derivation of  ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Then, by induction
. Then, by induction  . By the same rule,
. By the same rule,  .
. -
Let \(P = P_1 {\Vert ^{}_{S}} P_2\) and \(Q = Q_1 {\Vert ^{}_{S}} Q_2\) with
 and
and  . I consider the three rules from Table 1 that could have been responsible for the derivation of
. I consider the three rules from Table 1 that could have been responsible for the derivation of  . First suppose that \(\alpha \notin S\), and
. First suppose that \(\alpha \notin S\), and  . By induction,
. By induction,  . Consequently,
. Consequently,  . Next suppose that \(\alpha \in S\),
. Next suppose that \(\alpha \in S\),  and
and  . By induction,
. By induction,  and
and  . So
. So  . The remaining case proceeds symmetrically to the first.
. The remaining case proceeds symmetrically to the first. -
Let \(P = \tau _I(P^\dagger )\) and \(Q= \tau _I(Q^\dagger )\) with \(I\subseteq A\) and
 . Then,
. Then,  and either \(\beta = \alpha \notin I\), or \(\beta \in I\) and \(\alpha =\tau \). By induction,
and either \(\beta = \alpha \notin I\), or \(\beta \in I\) and \(\alpha =\tau \). By induction,  . Consequently,
. Consequently,  .
. -
Let \(P = \mathcal {R}(P^\dagger )\) and \(Q= \mathcal {R}(Q^\dagger )\) with \(\mathcal {R}\subseteq A \times A\) and
 . Then,
. Then,  and either \((\beta ,\alpha ) \in \mathcal {R}\) or \(\beta =\alpha = \tau \). By induction,
and either \((\beta ,\alpha ) \in \mathcal {R}\) or \(\beta =\alpha = \tau \). By induction,  . Consequently,
. Consequently,  .
. -
Let \(P=\theta _L^U(P^\dagger )\), \(Q=\theta _L^U(Q^\dagger )\) and
 . Then, \((\lambda _{P^\dagger },\kappa _{P^\dagger }) < (\lambda ,\kappa )\) and \((\lambda _{Q^\dagger },\kappa _{Q^\dagger }) < (\lambda ,\kappa )\), as remarked in Sect. 5. So by induction \(P^\dagger =_\mathcal {I}Q^\dagger \). (This is the only use of stratum induction.) Since
. Then, \((\lambda _{P^\dagger },\kappa _{P^\dagger }) < (\lambda ,\kappa )\) and \((\lambda _{Q^\dagger },\kappa _{Q^\dagger }) < (\lambda ,\kappa )\), as remarked in Sect. 5. So by induction \(P^\dagger =_\mathcal {I}Q^\dagger \). (This is the only use of stratum induction.) Since  , it must be that
, it must be that  and either \(\alpha \in U\cup \{\tau \}\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). In the latter case, \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\mathop \cup \{\tau \}\). Moreover,
and either \(\alpha \in U\cup \{\tau \}\) or \(P^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\cup \{\tau \}\). In the latter case, \(Q^\dagger \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in L\mathop \cup \{\tau \}\). Moreover,  . So, in both cases,
. So, in both cases,  .
. -
Let \(P=\psi _X(P^\dagger )\), \(Q=\psi _X(Q^\dagger )\) and
 . Since
. Since  , one has
, one has  . By induction
. By induction 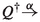 . So
. So  .
. -
Let
 and
and  where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and
where \({{\mathcal {S}}}\) is a recursive specification with \(z \in V_{{\mathcal {S}}}\), and  satisfy
satisfy  for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition
for all \(x\in { Var}\setminus V_{{\mathcal {S}}}\). By Table 1 the transition  is provable by means of a strict subproof of the proof \(\pi \) of
is provable by means of a strict subproof of the proof \(\pi \) of  . By ($) above one has
. By ($) above one has  . So by induction,
. So by induction,  . By Table 1,
. By Table 1,  .\(\square \)
.\(\square \)
Lemma 5
Let  be guarded and have free variables from \(W\subseteq { Var}\) only, and let
be guarded and have free variables from \(W\subseteq { Var}\) only, and let  . Then, \(\mathcal {I}(H[\vec {P}]) = \mathcal {I}(H[\vec {Q}])\).
. Then, \(\mathcal {I}(H[\vec {P}]) = \mathcal {I}(H[\vec {Q}])\).
Proof
Lemma 5 can be strengthened as follows.
Let
be such that all free occurrences of variables from \(W\subseteq { Var}\) in H are guarded, and let
. Then, \(H[\vec {P}] =_\mathcal {I}H[\vec {Q}]\).
The proof proceeds with structural induction on H.
-
Let
 , so that
, so that  , where \(\vec {P}^\dagger \) is the \(W {\setminus } V_{{\mathcal {S}}}\)-tuple that is left of \(\vec {P}\) after deleting the y-components, for \(y\in V_{{\mathcal {S}}}\), and
, where \(\vec {P}^\dagger \) is the \(W {\setminus } V_{{\mathcal {S}}}\)-tuple that is left of \(\vec {P}\) after deleting the y-components, for \(y\in V_{{\mathcal {S}}}\), and  . For each \(y \in V_{{\mathcal {S}}}\), all free occurrences of variables from \(W{\setminus } V_{{\mathcal {S}}}\) in \({{\mathcal {S}}}_y\) are guarded. Thus, by induction, \({{\mathcal {S}}}_y[\vec {P}^\dagger ] =_\mathcal {I}{{\mathcal {S}}}_y[\vec {Q}^\dagger ]\). Since \(=_\mathcal {I}\) is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \), it follows that
. For each \(y \in V_{{\mathcal {S}}}\), all free occurrences of variables from \(W{\setminus } V_{{\mathcal {S}}}\) in \({{\mathcal {S}}}_y\) are guarded. Thus, by induction, \({{\mathcal {S}}}_y[\vec {P}^\dagger ] =_\mathcal {I}{{\mathcal {S}}}_y[\vec {Q}^\dagger ]\). Since \(=_\mathcal {I}\) is a full congruence for \(\text{ CCSP}_\mathrm{t}^\theta \), it follows that 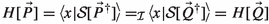 .
. -
Let \(H = \alpha .H'\) for some \(\alpha \in Act\). Then, \(\mathcal {I}(H[\vec {P}]) = \mathcal {I}(H[\vec {Q}])\) (namely \(\emptyset \) if \(\alpha =\mathrm{t}\) and \(\{ \alpha \}\) otherwise).
-
Let \(H = H_1 {\Vert ^{}_{S}} H_2\). Since all free occurrences of variables from \(W\subseteq { Var}\) in H are guarded, so are those in \(H_1\) and \(H_2\). Thus, by induction, \(H_1[\vec {P}] =_\mathcal {I}H_1[\vec {Q}]\) and \(H_2[\vec {P}] =_\mathcal {I}H_2[\vec {Q}]\). Since \(=_\mathcal {I}\) is a full congruence for \( {S}\), it follows that \(H[\vec {P}] =_\mathcal {I}H[\vec {Q}]\).
-
The cases for all other operators go exactly like the case for \({\Vert ^{}_{S}}\). \(\square \)
B Proofs of lemmas on \(\theta _X\) and strong bisimilarity from Sect. 7.2
The following lemmas on the relation between \(\theta _X\) and the other operators of \(\text{ CCSP}_\mathrm{t}^\theta \) deal with strong bisimilarity, but are needed in the congruence proof for strong reactive bisimilarity.
Lemma 12
If \(\mathcal {I}(Q)\cap (Y\cup \{\tau \}) = \emptyset \) then  .
.
Proof
This follows immediately from the operational rules for \(\theta _Y\). \(\square \)
Lemma 2
If \(P{{\mathop {\nrightarrow }\limits ^{\tau }}}\), \(\mathcal {I}(P) \cap X \subseteq S\) and \(Y=X\setminus (S\setminus \mathcal {I}(P))\), then  .
.
Proof
Let  and \(S,X,Y \subseteq A\) be as indicated in the lemma. Let
and \(S,X,Y \subseteq A\) be as indicated in the lemma. Let

It suffices to show that the symmetric closure  of
of  is a strong bisimulation.
is a strong bisimulation.
So let  and
and  with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with
with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with  and
and  .
.
-
The case that
 is trivial.
is trivial. -
Let \(R = \theta _X(P {\Vert ^{}_{S}} Q)\) and \(T = \theta _X(P {\Vert ^{}_{S}}\theta _Y(Q))\), for some
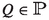 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(Q'\) with \(R' = \theta _X(P{\Vert ^{}_{S}}Q')\). Consequently,
for some \(Q'\) with \(R' = \theta _X(P{\Vert ^{}_{S}}Q')\). Consequently,  and
and  . Now assume \(\alpha \in A\cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A\cup \{\mathrm{t}\}\). Then,  . I first deal with the case that \(\alpha \in X\), and consider the three rules from Table 1 that could have derived
. I first deal with the case that \(\alpha \in X\), and consider the three rules from Table 1 that could have derived 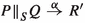 .
.-
The case that \(\alpha \notin S\) and
 cannot occur, because \(\mathcal {I}(P) \cap X \subseteq S\).
cannot occur, because \(\mathcal {I}(P) \cap X \subseteq S\). -
Let \(\alpha \in S\),
 ,
,  and \(R' = P' {\Vert ^{}_{S}} Q'\). Then, \(\alpha \in \mathcal {I}(P)\), so \(\alpha \notin S\setminus \mathcal {I}(P)\) and thus \(\alpha \in Y\). Hence,
and \(R' = P' {\Vert ^{}_{S}} Q'\). Then, \(\alpha \in \mathcal {I}(P)\), so \(\alpha \notin S\setminus \mathcal {I}(P)\) and thus \(\alpha \in Y\). Hence,  . Now
. Now  .
. -
Let \(\alpha {\notin } S\),
 and \(R'= P {\Vert ^{}_{S}} Q'\). Then, \(\alpha \in Y\), so
and \(R'= P {\Vert ^{}_{S}} Q'\). Then, \(\alpha \in Y\), so  . Therefore,
. Therefore,  and thus
and thus  .
.
Finally, assume \(\alpha \in (A\cup \{\mathrm{t}\})\setminus X\). In that case \(P{\Vert ^{}_{S}}Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Therefore, \(Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in (X\setminus S)\cup \{\tau \}\), and for all \(\beta \in X\cap S \cap \mathcal {I}(P)\), and thus for all \(\beta \in Y\cup \{\tau \}\). By Lemma 12, \(\theta _Y(Q) =_\mathcal {I}Q\), and hence \(P{\Vert ^{}_{S}}\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Again, I consider the three rules from Table 1 that could have derived
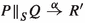 .
.-
Let \(\alpha {\notin } S\),
 and \(R'= P' {\Vert ^{}_{S}} Q\). Then,
and \(R'= P' {\Vert ^{}_{S}} Q\). Then,  and thus
and thus  . By Lemma 12,
. By Lemma 12,  . Since
. Since  is a congruence for \({\Vert ^{}_{S}}\), it follows that
is a congruence for \({\Vert ^{}_{S}}\), it follows that  .
. -
Let \(\alpha \in S\),
 ,
, 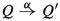 and \(R' = P' {\Vert ^{}_{S}} Q'\). Then,
and \(R' = P' {\Vert ^{}_{S}} Q'\). Then, 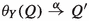 and therefore
and therefore  and
and  .
. -
Let \(\alpha {\notin } S\),
 and \(R'= P {\Vert ^{}_{S}} Q'\). Then,
and \(R'= P {\Vert ^{}_{S}} Q'\). Then,  , so
, so 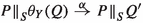 and thus
and thus  .
.
-
-
Let \(R = \theta _X(P {\Vert ^{}_{S}}\theta _Y(Q))\) and \(T = \theta _X(P {\Vert ^{}_{S}} Q)\), for some
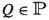 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(Q'\) with \(R' = \theta _X(P{\Vert ^{}_{S}}\theta _Y(Q'))\). Consequently,
for some \(Q'\) with \(R' = \theta _X(P{\Vert ^{}_{S}}\theta _Y(Q'))\). Consequently,  and
and  . Now assume \(\alpha \in A\cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A\cup \{\mathrm{t}\}\). Then,  and either \(\alpha \in X\) or \(P{\Vert ^{}_{S}}\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). In the latter case, one obtains \(\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\) (as above), and thus \(Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\), that is, \(\mathcal {I}(Q)\cap (Y\cup \{\tau \}) = \emptyset \). Furthermore, this implies that \(P{\Vert ^{}_{S}}Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). I consider the three rules from Table 1 that could have derived
and either \(\alpha \in X\) or \(P{\Vert ^{}_{S}}\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). In the latter case, one obtains \(\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\) (as above), and thus \(Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in Y\cup \{\tau \}\), that is, \(\mathcal {I}(Q)\cap (Y\cup \{\tau \}) = \emptyset \). Furthermore, this implies that \(P{\Vert ^{}_{S}}Q \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). I consider the three rules from Table 1 that could have derived  .
.-
Let \(\alpha {\notin } S\),
 and \(R'= P' {\Vert ^{}_{S}} \theta _Y(Q)\). Then, \(a \notin X\), because \(\mathcal {I}(P) \cap X \subseteq S\). Hence, \(P{\Vert ^{}_{S}}\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\), so \(\mathcal {I}(Q)\cap (Y\cup \{\tau \}) = \emptyset \). Now
and \(R'= P' {\Vert ^{}_{S}} \theta _Y(Q)\). Then, \(a \notin X\), because \(\mathcal {I}(P) \cap X \subseteq S\). Hence, \(P{\Vert ^{}_{S}}\theta _Y(Q) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\), so \(\mathcal {I}(Q)\cap (Y\cup \{\tau \}) = \emptyset \). Now  and
and  , using Lemma 12.
, using Lemma 12. -
Let \(\alpha \in S\),
 ,
, 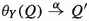 and \(R' = P' {\Vert ^{}_{S}} Q'\). Then,
and \(R' = P' {\Vert ^{}_{S}} Q'\). Then,  . Hence,
. Hence,  and thus
and thus  .
. -
Let \(\alpha \notin S\),
 and \(R'= P {\Vert ^{}_{S}} Q'\). Then,
and \(R'= P {\Vert ^{}_{S}} Q'\). Then,  . Consequently,
. Consequently,  and thus
and thus  .\(\square \)
.\(\square \)
-
Lemma 3
 .
.
Proof
For given X and I, let  . It suffices to show that the symmetric closure
. It suffices to show that the symmetric closure  of
of  is a strong bisimulation. So let
is a strong bisimulation. So let  and
and  with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with
with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with  and
and  .
.
-
The case that \(R = T\) is trivial.
-
Let \(R = \theta _X(\tau _I(P))\) and \(T = \theta _X(\tau _I(\theta _{X\cup I}(P)))\), for some
 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(R''\) such that \(R' = \theta _X(R'')\). Therefore,
for some \(R''\) such that \(R' = \theta _X(R'')\). Therefore,  for some \(\beta \in I \cup \{\tau \}\) and some \(P'\) with \(R''=\tau _I(P')\). In case \(\beta =\tau \), it turns out that
for some \(\beta \in I \cup \{\tau \}\) and some \(P'\) with \(R''=\tau _I(P')\). In case \(\beta =\tau \), it turns out that  . Moreover,
. Moreover,  . In case \(\beta \in I\),
. In case \(\beta \in I\),  , so
, so  and
and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,  and either \(\alpha \in X\) or \(\tau _I(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). It follows that \(\alpha \notin I\) and
and either \(\alpha \in X\) or \(\tau _I(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). It follows that \(\alpha \notin I\) and  for some \(P'\) with \(R'=\tau _I(P')\). Moreover, in case \(\alpha \notin X\) one has \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\), and hence also \(\theta _{X\cup I}(P)\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\), and thus \(\tau _I(\theta _{X\cup I}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Now
for some \(P'\) with \(R'=\tau _I(P')\). Moreover, in case \(\alpha \notin X\) one has \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\), and hence also \(\theta _{X\cup I}(P)\mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\), and thus \(\tau _I(\theta _{X\cup I}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup \{\tau \}\). Now  , so
, so  and thus
and thus  .
. -
Let \(R = \theta _X(\tau _I(\theta _{X\cup I}(P)))\) and \(T = \theta _X(\tau _I(P))\), for some
 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(R''\) such that \(R' = \theta _X(R'')\). Therefore,
for some \(R''\) such that \(R' = \theta _X(R'')\). Therefore,  for some \(\beta \in I \cup \{\tau \}\) and some \(P'\) with \(R''=\tau _I(P')\). In case \(\beta =\tau \), it turns out that
for some \(\beta \in I \cup \{\tau \}\) and some \(P'\) with \(R''=\tau _I(P')\). In case \(\beta =\tau \), it turns out that  for some \(P''\) such that \(P' = \theta _{X\cup I}(P'')\). So
for some \(P''\) such that \(P' = \theta _{X\cup I}(P'')\). So  , and
, and  . In case \(\beta \in I\), one has
. In case \(\beta \in I\), one has  , so
, so  and
and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,  , so \(\alpha \notin I\) and
, so \(\alpha \notin I\) and  for some \(P'\) such that \(R' = \tau _I(P')\). Thus,
for some \(P'\) such that \(R' = \tau _I(P')\). Thus,  and either \(\alpha \in X\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\). In the latter case, \(\tau _I(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Now
and either \(\alpha \in X\) or \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X\cup I \cup \{\tau \}\). In the latter case, \(\tau _I(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Now  and consequently
and consequently  .\(\square \)
.\(\square \)
Lemma 4
 .
.
Proof
For given \(X\subseteq A\) and \(\mathcal {R}\subseteq A\times A\), let  . It suffices to show that the symmetric closure
. It suffices to show that the symmetric closure  of
of  is a strong bisimulation. So let
is a strong bisimulation. So let  and
and  with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with
with \(\alpha \in A \cup \{\tau ,\mathrm{t}\}\). I have to find a \(T'\) with  and
and  .
.
-
The case that \(R = T\) is trivial.
-
Let \(R= \theta _X(\mathcal {R}(P))\) and \(T=\theta _X(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)))\), for some
 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(P'\) such that \(R' = \theta _X(\mathcal {R}(P'))\). Hence,
for some \(P'\) such that \(R' = \theta _X(\mathcal {R}(P'))\). Hence,  , and
, and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then,  , and either \(\alpha \in X\) or \(\mathcal {R}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). In the latter case, \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\). Moreover,
, and either \(\alpha \in X\) or \(\mathcal {R}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). In the latter case, \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\). Moreover,  , for some \(\gamma \) with \(\gamma =\mathrm{t}=\alpha \) or \((\gamma ,\alpha )\in \mathcal {R}\), and some \(P'\) with \(R' = \mathcal {R}(P')\). In case \(\alpha \in X\), one has \(\gamma \in \mathcal {R}^{-1}(X)\). Therefore,
, for some \(\gamma \) with \(\gamma =\mathrm{t}=\alpha \) or \((\gamma ,\alpha )\in \mathcal {R}\), and some \(P'\) with \(R' = \mathcal {R}(P')\). In case \(\alpha \in X\), one has \(\gamma \in \mathcal {R}^{-1}(X)\). Therefore,  , and thus
, and thus  . Either \(\alpha {\in } X\) or \(\theta _{\mathcal {R}^{-1}(X)}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), in which case \(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Consequently,
. Either \(\alpha {\in } X\) or \(\theta _{\mathcal {R}^{-1}(X)}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), in which case \(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Consequently,  .
. -
Let \(R= \theta _X(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)))\) and \(T = \theta _X(\mathcal {R}(P))\), for some
 . First assume \(\alpha =\tau \). Then,
. First assume \(\alpha =\tau \). Then,  for some \(P'\) such that
for some \(P'\) such that  . Hence,
. Hence,  , and
, and  . Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then
. Now assume \(\alpha \in A \cup \{\mathrm{t}\}\). Then  and either \(\alpha \in X\) or \(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Therefore,
and either \(\alpha \in X\) or \(\mathcal {R}(\theta _{\mathcal {R}^{-1}(X)}(P)) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in X \cup \{\tau \}\). Therefore,  for some \(\gamma \) with \(\gamma =\mathrm{t}=\alpha \) or \((\gamma ,\alpha )\in \mathcal {R}\), and some \(P'\) such that \(R' = \mathcal {R}(P')\). Hence,
for some \(\gamma \) with \(\gamma =\mathrm{t}=\alpha \) or \((\gamma ,\alpha )\in \mathcal {R}\), and some \(P'\) such that \(R' = \mathcal {R}(P')\). Hence,  , and thus
, and thus  . In case \(\alpha \notin X\), one has \(\theta _{\mathcal {R}^{-1}(X)}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), and thus \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), so
. In case \(\alpha \notin X\), one has \(\theta _{\mathcal {R}^{-1}(X)}(P) \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), and thus \(P \mathop {\nrightarrow }\limits ^{\beta }\) for all \(\beta \in \mathcal {R}^{-1}(X) \cup \{\tau \}\), so 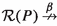 for all \(\beta \in X \cup \{\tau \}\). Hence,
for all \(\beta \in X \cup \{\tau \}\). Hence,  . \(\square \)
. \(\square \)
C Reducing strong reactive bisimilarity to strong bisimilarity
Pohlmann [37] introduces unary operators \(\vartheta \) and \(\vartheta _X\) for \(X\subseteq A\) that model placing their argument process in an environment that is triggered to change, or allows exactly the actions in X, respectively. Although inspired by my operators \(\theta _X\) from Sect. 4,Footnote 1 their semantics is different, and given by the following structural operational rules (for all \(X \subseteq A\)).

Here, the actions \(\mathrm{t}_\varepsilon \notin A\) and \(\varepsilon _X\notin A\) for \(X \subseteq A\) are generated by the new operators, but may not be used by processes substituted for their arguments x. They model a timeout action taken by the environment, and the stabilisation of an environment into one that allows exactly the set of actions X, respectively.
These rules mirror the clauses of Definition 1 of a strong reactive bisimulation.
-
\(\tau \)-transitions can be performed regardless of the environment,
-
triggered environments can stabilise into arbitrary stable environments X for \(X \subseteq A\),
-
allowed visible transitions can be performed and can trigger a change in the environment,
-
\(\tau \)-transitions cannot be observed by the environment and hence cannot trigger a change,
-
if the underlying system is idle, the environment may timeout and become triggered to change,
-
if the underlying system is idle, it can perform a \(\mathrm{t}\)-transition, not observed by the environment.
The main result from [37] reduces strong reactive bisimilarity to strong bisimilarity:
Theorem 45
Let  , \(X\subseteq A\). Then,
, \(X\subseteq A\). Then,  iff
iff  , and
, and  iff
iff  .
.
Proof
If  is a strong reactive bisimulation, then
is a strong reactive bisimulation, then

is a strong bisimulation. Moreover,

is a strong reactive bisimulation. Both statements follow directly from the definitions, and they imply the theorem. This proof stems from [37], where it is formalised in Isabelle. \(\square \)
Another notable result from [37] is a function \(\varsigma \) that turns any formula \(\varphi \) from my extension of the Hennessy–Milner logic into a formula \(\varsigma (\varphi )\) in the regular Hennessy–Milner logic, such that \(P \models \varphi \) iff \(\vartheta (P) \models \varsigma (\varphi )\) and \(P \models _X \varphi \) iff \(\vartheta _X(P) \models \varsigma (\varphi )\).
Interestingly, the operators \(\vartheta \) and \(\vartheta _X\) from [37] can be expressed in terms of (fairly) standard process algebra operators. Define the universal environment \(\mathcal {E}\) as the recursive specification
In case A is infinite, this requires an infinite choice operator \(\sum \), which was not included in the syntax of \(\hbox {CCSP}_\mathrm{t}\) used in Sect. 5. Here, \(V_\mathcal {E}= \{U\}\cup \{X \mid X \subseteq A\}\) are the bound variables of \(\mathcal {E}\). The process  denotes an environment that is triggered to change, and
denotes an environment that is triggered to change, and  one that allows exactly the actions in X. The only actions that
one that allows exactly the actions in X. The only actions that  can do are stabilising into any
can do are stabilising into any  . The process
. The process  can either synchronise on any action \(a \in X\) or perform a timeout, in both cases returning to the state
can either synchronise on any action \(a \in X\) or perform a timeout, in both cases returning to the state  .
.
If we now drop the negative premises from the structural operational rules of the operators \(\vartheta _X\), and add a rule  , then
, then  and
and  . Here, the operator \(\Vert _A\) enforces synchronisation on all visible actions \(a\in A\), although actions \(\varepsilon _X\) and \(\mathrm{t}_\varepsilon \) can occur when the environment is ready do do them, and actions \(\tau \) and \(\mathrm{t}\) can be triggered by just the process P. Checking strong bisimilarity between \(\vartheta (P)\) and
. Here, the operator \(\Vert _A\) enforces synchronisation on all visible actions \(a\in A\), although actions \(\varepsilon _X\) and \(\mathrm{t}_\varepsilon \) can occur when the environment is ready do do them, and actions \(\tau \) and \(\mathrm{t}\) can be triggered by just the process P. Checking strong bisimilarity between \(\vartheta (P)\) and  , and between \(\vartheta _X(P)\) and
, and between \(\vartheta _X(P)\) and  , is straightforward.
, is straightforward.
To obtain the real process \(\vartheta (P)\) from  , or \(\vartheta _X(P)\) from
, or \(\vartheta _X(P)\) from  , all one has to do is to inhibit any \(\mathrm{t}\)- or \(\mathrm{t}_\varepsilon \)-transition when a transition with a label in \(A \cup \{\tau \} \cup \{\varepsilon _X\mid X \subseteq A\}\) is possible. This can be achieved with the priority operator of Baeten, Bergstra & Klop [1]. This unary operator \(\Theta \) is parametrised by a partial order < on the set of actions, the priority order, and passes through a transition of its argument process only if no transition with a higher priority is possible. Its operational semantic is given by
, all one has to do is to inhibit any \(\mathrm{t}\)- or \(\mathrm{t}_\varepsilon \)-transition when a transition with a label in \(A \cup \{\tau \} \cup \{\varepsilon _X\mid X \subseteq A\}\) is possible. This can be achieved with the priority operator of Baeten, Bergstra & Klop [1]. This unary operator \(\Theta \) is parametrised by a partial order < on the set of actions, the priority order, and passes through a transition of its argument process only if no transition with a higher priority is possible. Its operational semantic is given by

For the present application, I take \({<} := \{(\mathrm{t},\alpha ),(\mathrm{t}_\varepsilon ,\alpha )\mid \alpha \in Act{\setminus }\{\mathrm{t},\mathrm{t}_\varepsilon \}\}\), thus giving \(\mathrm{t}\) and \(\mathrm{t}_\varepsilon \) a lower priority than all other actions. This yields the desired properties

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van Glabbeek, R. Reactive bisimulation semantics for a process algebra with timeouts. Acta Informatica 60, 11–57 (2023). https://doi.org/10.1007/s00236-022-00417-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-022-00417-1





 and
and  , then there exists a
, then there exists a  and
and  ,
, then
then  for all
for all 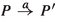 with
with  and
and  ,
, , then there exists a
, then there exists a  and
and 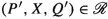 ,
, , and
, and , then
, then  and
and  .
.

 with
with  and
and  ,
, , then
, then  and
and  ,
, with either
with either  and
and  ,
, , then there exists a
, then there exists a  and
and  ,
, then
then 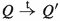 and
and  .
. .
. for some
for some  for some
for some  . So by induction
. So by induction  for some
for some  for some
for some 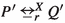 . So by induction
. So by induction  , so
, so  .
. for some
for some 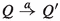 for some
for some  . By induction
. By induction  for some
for some  for some
for some  . By induction
. By induction  . Hence, by the previous case in this proof,
. Hence, by the previous case in this proof,  . Thus,
. Thus,  with
with  . For each
. For each  be a formula such that
be a formula such that  is closed under negation.) Define
is closed under negation.) Define  . Then,
. Then,  and
and  . Let
. Let 
 be a formula such that
be a formula such that  and
and  with
with  . For each
. For each  be a formula such that
be a formula such that  . Then,
. Then,  and
and  and
and 
 be a formula such that
be a formula such that  and
and  with
with  and
and  ,
, , then
, then  and
and  .
. and
and  with
with  . Then, by the first clause of Definition
. Then, by the first clause of Definition  and
and  . So
. So  . Next suppose
. Next suppose 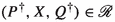 . Since
. Since  it must be that
it must be that  and either
and either  and
and  , using the third clause of Definition
, using the third clause of Definition  implies
implies  and
and  .
. and
and  . First suppose
. First suppose  . Then, using the first clause of Definition
. Then, using the first clause of Definition  and
and  . So
. So  . Next suppose
. Next suppose  . Since
. Since  , it must be that
, it must be that  . Thus, by the fourth clause of Definition
. Thus, by the fourth clause of Definition  and
and 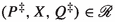 . Now
. Now  and
and  .
. ,
,  . First suppose
. First suppose  . Then, by the second clause of Definition
. Then, by the second clause of Definition  and
and  . So
. So  . Next suppose
. Next suppose 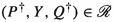 . Since
. Since  , it must be that
, it must be that  and
and  and
and  . So
. So  . From
. From 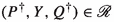 and
and 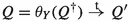 .
. and
and  with
with  , so there is a
, so there is a  and
and  . Hence,
. Hence,  .
. ,
,  . Then,
. Then,  , so
, so  and
and  . Thus,
. Thus,  .
. and
and 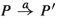 with either
with either  . Moreover,
. Moreover,  . Hence, there is a
. Hence, there is a  and
and  . It must be that
. It must be that  . Moreover,
. Moreover,  .
. and
and  . Then,
. Then,  . Since
. Since  , one has
, one has  . Hence, there is an R such that
. Hence, there is an R such that  and
and  . The process R must have the form
. The process R must have the form  . It follows that
. It follows that  .
. ,
,  . Then,
. Then,  and
and  . Moreover,
. Moreover,  and
and  . So
. So  and
and  .
. for some
for some  with
with  for some
for some 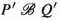 .
. with
with  and
and  ,
, , then
, then  and
and  .
. , then
, then 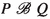 ,
,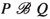 and
and  ,
, and
and 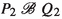 , then
, then  ,
, ,
,  and
and  ,
, ,
,  and
and  ,
, and
and 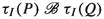 ,
, and
and 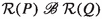 ,
,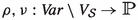 are substitutions satisfying
are substitutions satisfying  for all
for all  .
.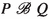 and
and  with
with  and
and  . In fact, I show that even
. In fact, I show that even  . This I will do by structural induction on the proof
. This I will do by structural induction on the proof  from the rules of Table
from the rules of Table  .
. . Using that the relation
. Using that the relation  is a strong timeout bisimulation, there must be a process
is a strong timeout bisimulation, there must be a process  and
and 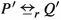 . Hence,
. Hence,  .
. . Then,
. Then,  and
and  .
.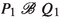 and
and  . I consider the first rule from Table
. I consider the first rule from Table 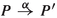 ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Then, by induction
. Then, by induction  for some
for some  . By the same rule from Table
. By the same rule from Table  .
. . First suppose
. First suppose  , it must be that
, it must be that  and either
and either  and
and  . So, in both cases,
. So, in both cases,  . Now suppose
. Now suppose  it must be that
it must be that  . By induction, there exists a
. By induction, there exists a  and
and  . Now
. Now  and
and  .
. . Since
. Since  , one has
, one has  . By induction there exists a
. By induction there exists a  and
and  . So
. So  .
. and
and  . I consider the three rules from Table
. I consider the three rules from Table 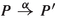 . First suppose that
. First suppose that  and
and 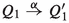 for some
for some  . Consequently,
. Consequently,  , and
, and  . Next suppose that
. Next suppose that  ,
,  and
and 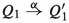 for some
for some  , and
, and  for some
for some  . Consequently,
. Consequently,  , and
, and  . The remaining case proceeds symmetrically to the first.
. The remaining case proceeds symmetrically to the first. . Then,
. Then,  for some
for some  for some
for some  . Consequently,
. Consequently,  and
and  .
. . Then,
. Then,  for some
for some  for some
for some  . Consequently,
. Consequently,  and
and  .
. and
and  where
where  satisfy
satisfy  for all
for all  is provable by means of a strict subproof of the proof
is provable by means of a strict subproof of the proof  . By ($) above one has
. By ($) above one has 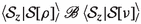 . So by induction there is a
. So by induction there is a  and
and  . By Table
. By Table  .
. ,
,  . I have to find a
. I have to find a  and
and  . This I will do by structural induction on the proof
. This I will do by structural induction on the proof  from the rules of Table
from the rules of Table  .
. . Using that the relation
. Using that the relation  is a strong timeout bisimulation, there must be a process
is a strong timeout bisimulation, there must be a process  and
and  . Thus
. Thus  .
. . Then,
. Then,  and
and  . Thus,
. Thus,  .
. and
and  . I consider the first rule from Table
. I consider the first rule from Table  ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Since
. Since  for some
for some  . Hence,
. Hence,  .
.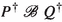 . Since
. Since  it must be that
it must be that  and
and  iff
iff  , for all
, for all  for some
for some  . By
. By  .
. . Since
. Since  one has
one has  for some
for some 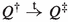 for a
for a  . By
. By  . From
. From  , one obtains
, one obtains 
 is a congruence for
is a congruence for 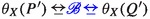 .
. and
and  . I consider the last rule from Table
. I consider the last rule from Table  . The other proceeds symmetrically. So suppose that
. The other proceeds symmetrically. So suppose that  and
and  for some
for some  . Let
. Let  . From
. From  and
and  , one obtains
, one obtains  , using that
, using that  is a congruence for
is a congruence for  is also a congruence for
is also a congruence for 
 , one has
, one has  by Lemma
by Lemma  . Then,
. Then,  for some
for some  for some
for some  . Let
. Let  . From
. From  , one obtains
, one obtains 
 is a congruence for
is a congruence for 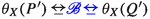 .
. . Then,
. Then,  for some
for some  for some
for some  . Let
. Let  . From
. From  , one obtains
, one obtains 
 is a congruence for
is a congruence for  .
. and
and  where
where  satisfy
satisfy  for all
for all  is provable by means of a strict subproof of the proof
is provable by means of a strict subproof of the proof  . The rule for recursion in Table
. The rule for recursion in Table  . Therefore,
. Therefore,  . By ($) above one has
. By ($) above one has 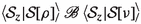 . So by induction there is a
. So by induction there is a  and
and  . By Table
. By Table 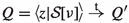 .
. , such that
, such that  for all
for all  ,
, and
and  with
with  and
and  . In fact, I show that even
. In fact, I show that even  . This I will do by structural induction on the proof
. This I will do by structural induction on the proof  from the rules of Table
from the rules of Table  .
. and
and  where
where  for all
for all  one has
one has  . By Table
. By Table  is provable by means of a strict subproof of
is provable by means of a strict subproof of  . So by induction there is an
. So by induction there is an  such that
such that  and
and  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  , one has
, one has  . Hence, there is a
. Hence, there is a  and
and  . So
. So  . By Table
. By Table  .
. substituted for the blue occurrences of
substituted for the blue occurrences of  . In the case for
. In the case for  that
that 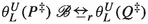 . Besides applying the definition of
. Besides applying the definition of  , this also involves the application of Theorem
, this also involves the application of Theorem  is already known to be a congruence for
is already known to be a congruence for  ,
,  . I will find a
. I will find a  and
and  . This I will do by structural induction on the proof
. This I will do by structural induction on the proof  from the rules of Table
from the rules of Table  .
.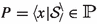 and
and 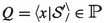 where
where  one has
one has  . By Table
. By Table  is provable by means of a strict subproof of the proof
is provable by means of a strict subproof of the proof  . The rule for recursion in Table
. The rule for recursion in Table  . Therefore,
. Therefore,  . By (#) above one has
. By (#) above one has  . So by induction there is an
. So by induction there is an  such that
such that  and
and  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  ,
,  . Using
. Using  . Hence,
. Hence,  and
and  , and thus
, and thus  , using Theorem
, using Theorem  . By Table
. By Table  .
. substituted for the blue occurrences of
substituted for the blue occurrences of  .
.  and
and  with
with  and
and  . Assume that
. Assume that  has free variables in
has free variables in  . Furthermore, by Theorem
. Furthermore, by Theorem  and
and  . Thus,
. Thus,  .
. ,
,  . I have to find a
. I have to find a  and
and  . The proof for this case proceeds exactly as that of the previous case, up to the last sentence; the condition
. The proof for this case proceeds exactly as that of the previous case, up to the last sentence; the condition  it follows that
it follows that 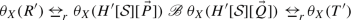
 for some
for some  , and
, and  . Now assume
. Now assume  and either
and either  and either
and either  .
.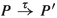 for some
for some  , and
, and  . Now assume
. Now assume  and either
and either  .
. 
 with
with 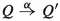 and
and  ,
, , then
, then  and
and  .
. for some
for some  with
with  such that
such that  and
and  . I proceed with induction on n. The case
. I proceed with induction on n. The case  such that
such that  and
and  . Now, by induction there is an
. Now, by induction there is an  and
and  . Hence,
. Hence, 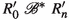 .
. for some
for some 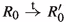 . By Definition
. By Definition  and
and  . This proceeds exactly as for the case above.
. This proceeds exactly as for the case above. . Then,
. Then,  for some
for some  for some
for some  and thus
and thus  by Lemma
by Lemma  .
. . By Lemma
. By Lemma 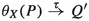 for some
for some  for some
for some  by Lemma
by Lemma  . Moreover,
. Moreover,  .
. with
with  and either
and either  for some
for some  and thus
and thus  .
. with
with  for some
for some  and either
and either  by Lemma
by Lemma  .
. . Then,
. Then,  and
and 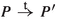 for some
for some  . Hence
. Hence  and thus, again applying Lemma
and thus, again applying Lemma  for some
for some  . Moreover,
. Moreover,  .
. . By Lemma
. By Lemma  for a
for a  . Hence
. Hence  and
and  for a
for a  . By Corollary
. By Corollary  . Moreover,
. Moreover,  .
. with
with  by Lemma
by Lemma  .
.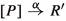 with
with 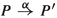 for some
for some  .
. . By Lemma
. By Lemma  for some
for some  . Moreover, using Lemma
. Moreover, using Lemma  .
. . Then, by Lemma
. Then, by Lemma  for some
for some 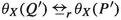 . By Lemma
. By Lemma  .
. with
with  for some
for some  . One has
. One has  and
and  . The process
. The process  , Lemma
, Lemma  . Then,
. Then,  for some
for some 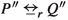 . The process
. The process  .
.
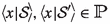 , such that
, such that  ,
, ,
, and
and  ,
,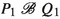 and
and  , then
, then  ,
, ,
,  and
and  ,
, and
and  ,
, and
and  ,
, ,
,  and
and  ,
, are substitutions satisfying
are substitutions satisfying  for all
for all 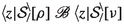 .
. and
and  where
where  one has
one has 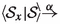 is provable by means of a strict subproof of
is provable by means of a strict subproof of  . So by induction
. So by induction  . Since
. Since  is the application of a substitution of the form
is the application of a substitution of the form  , one has
, one has  . Hence,
. Hence,  . By Table
. By Table  .
.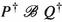 . Then,
. Then,  .
. and
and  . I consider the first rule from Table
. I consider the first rule from Table  ; the other proceeds symmetrically. So suppose that
; the other proceeds symmetrically. So suppose that  . Then, by induction
. Then, by induction  . By the same rule,
. By the same rule, 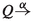 .
. and
and  . I consider the three rules from Table
. I consider the three rules from Table  . First suppose that
. First suppose that  . By induction,
. By induction,  . Consequently,
. Consequently,  . Next suppose that
. Next suppose that  and
and  . By induction,
. By induction,  and
and  . So
. So  . The remaining case proceeds symmetrically to the first.
. The remaining case proceeds symmetrically to the first. . Then,
. Then,  and either
and either  . Consequently,
. Consequently,  .
. . Then,
. Then,  and either
and either  . Consequently,
. Consequently,  .
. . Then,
. Then,  , it must be that
, it must be that  and either
and either  . So, in both cases,
. So, in both cases,  .
. . Since
. Since  , one has
, one has  . By induction
. By induction 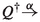 . So
. So  .
. and
and  where
where  satisfy
satisfy  for all
for all  is provable by means of a strict subproof of the proof
is provable by means of a strict subproof of the proof  . By ($) above one has
. By ($) above one has  . So by induction,
. So by induction,  . By Table
. By Table  .
. be such that all free occurrences of variables from
be such that all free occurrences of variables from  . Then,
. Then,  , so that
, so that  , where
, where  . For each
. For each 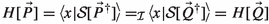 .
. is trivial.
is trivial.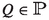 . First assume
. First assume  for some
for some  and
and  . Now assume
. Now assume  . I first deal with the case that
. I first deal with the case that 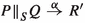 .
. cannot occur, because
cannot occur, because  ,
,  and
and  . Now
. Now  .
. and
and  . Therefore,
. Therefore,  and thus
and thus  .
.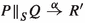 .
. and
and  and thus
and thus  . By Lemma
. By Lemma  . Since
. Since  is a congruence for
is a congruence for  .
. ,
, 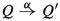 and
and 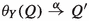 and therefore
and therefore  and
and  .
. and
and  , so
, so 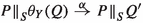 and thus
and thus  .
.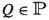 . First assume
. First assume  for some
for some  and
and  . Now assume
. Now assume  and either
and either  .
. and
and  and
and  , using Lemma
, using Lemma  ,
, 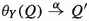 and
and  . Hence,
. Hence,  and thus
and thus  .
. and
and  . Consequently,
. Consequently,  and thus
and thus  .
. . First assume
. First assume  for some
for some  for some
for some  . Moreover,
. Moreover,  . In case
. In case  , so
, so 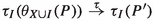 and
and  . Now assume
. Now assume  and either
and either  for some
for some  , so
, so  and thus
and thus  .
. . First assume
. First assume 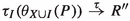 for some
for some  for some
for some  for some
for some  , and
, and  . In case
. In case  , so
, so  and
and  . Now assume
. Now assume  , so
, so  for some
for some  and either
and either  and consequently
and consequently  .
. . First assume
. First assume  for some
for some  , and
, and  . Now assume
. Now assume  , and either
, and either  , for some
, for some  , and thus
, and thus  . Either
. Either  .
. . First assume
. First assume  for some
for some  . Hence,
. Hence,  , and
, and  . Now assume
. Now assume  and either
and either  for some
for some  , and thus
, and thus  . In case
. In case  for all
for all  .
.