On Huang and Wong’s algorithm for generalized binary split trees

Abstract

Huang and Wong (Acta Inform 21(1):113–123, 1984) proposed a polynomial-time dynamic-programming algorithm for computing optimal generalized binary split trees. We show that their algorithm is incorrect. Thus, it remains open whether such trees can be computed in polynomial time. Spuler (Optimal search trees using two-way key comparisons, PhD thesis, 1994) proposed modifying Huang and Wong’s algorithm to obtain an algorithm for a different problem: computing optimal two-way comparison search trees. We show that the dynamic program underlying Spuler’s algorithm is not valid, in that it does not satisfy the necessary optimal-substructure property and its proposed recurrence relation is incorrect. It remains unknown whether the algorithm is guaranteed to compute a correct overall solution.

1 Introduction

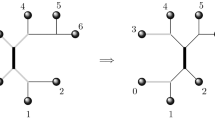
Given an ordered set $\mathsf {K}$ of n keys, a generalized binary split tree T is a form of binary search tree where each node N has two associated keys in $\mathsf {K}$: an equality-test key and a split key [8]. For any query $v\in \mathsf {K}$, a search for v in T starts at the root. If v equals the root’s equality-test key, then the search halts. Otherwise, the search recurses in the left or right subtree, depending on whether or not v is less than the root’s split key. A correct tree T must have n nodes, and the search for each query $v\in \mathsf {K}$ must halt at the node whose equality-test key is v. (There must be exactly one such node for each $v\in \mathsf {K}$.) Given also a probability distribution p on $\mathsf {K}$, the cost of a tree T is the expected number of nodes visited when searching in T for a random query v drawn from p. The goal, given $\mathsf {K}$ and p, is to compute a tree T of minimum cost (thus minimizing, over any tree T of this form, the expected number of two-way comparisons made when searching in T). We denote this problem gbsplit. See Fig. 1 for an example. Following Huang and Wong, here we focus on the so-called successful-queries variant, in which all queries are guaranteed to be in $\mathsf {K}$. (In the general variant, arbitrary queries are allowed.)

Fig. 1

The picture on the left shows an example of a generalized binary split tree for key interval $\{{{\mathsf {A}}},{{\mathsf {B}}},{{\mathsf {C}}},{{\mathsf {D}}},{{\mathsf {E}}},{{\mathsf {F}}}\}$. Each node is labeled with its equality key and its probability, as well as the node’s split key (except that split keys are omitted at leaves, where they are irrelevant). The total cost of this tree is $0.3\cdot 1 + 2\cdot (0.2\cdot 2) + 3\cdot (0.1\cdot 3) = 2$. In all figures in the paper we use a more compact representation, shown on the right, where split keys are omitted. (Each node’s split key can be any key that separates the equality keys in the left subtree from those in the right subtree.)

Huang and Wong [8] proposed a polynomial-time algorithm for gbsplit. We show (in Theorem 1, Sect. 2) that their algorithm and claimed proof of correctness are wrong. The reason is that their dynamic program does not satisfy the claimed optimal-substructure property. Consequently, as far as we know, it is not known whether gbsplit has a polynomial-time algorithm.

A closely related problem is to find an optimal two-way comparison search tree, in which each node is associated with just one key and one binary comparison operator—equality or less-than. We use 2wcst to denote this problem. (See Fig. 4 for an example.) Spuler [14, 15] proposed several 2wcst algorithms. He described two of his proposed 2wcst algorithms (for the successful-queries and general variants, respectively) as “straightforward” modifications of Huang and Wong’s gbsplit algorithm, but he gave no formal proof of correctness, explaining only that correctness follows from the dynamic-programming formulation, in particular from the underlying recurrence relation.

We show (Theorem 3, Sect. 3) that this recurrence relation is wrong, and his algorithm computes incorrect solutions to some subproblems in the dynamic program. Here also the dynamic program does not satisfy the assumed optimal-substructure property. This counter-example is only for a subproblem, not a full instance, so the overall correctness of his proposed algorithm remains open. (Here also we focus on the successful-queries variant only.)

Historical context. The study of optimal binary search trees began with three-way comparison search trees. These have only one key associated with each node, and comparing the given query to that key has three possible outcomes—less than, equal to, or greater than. Knuth’s classical dynamic-programming algorithm computes a minimum-cost tree of this kind (supporting both successful and unsuccessful queries) in time $O(n^2)$ [10].

Following Knuth’s suggestion [11, §6.2.2 ex. 33], various authors began exploring trees based on two-way (binary) comparisons. Sheil [13] introduced median split trees—generalized binary split trees where the split key at each node N must be a median key among the set $\mathsf {K}_N$ of keys whose search visits node N, and the equality-test key must be a most likely key among $\mathsf {K}_N$. He gave an $O(n\log n)$-time algorithm to compute a median split tree (for the successful-queries variant). Other authors [7, 9, 12] then introduced binary split trees—generalized binary split trees with the added restriction that the equality-test key at each node must be a most likely key among keys reaching the node. These trees can be thought of as a relaxation of median split trees, without the restriction that the split key has to be a median key. Their algorithms compute minimum-cost binary split trees in $O(n^5)$ time for both the successful-queries and general variants. (See also the note at the end of this paper.) Huang and Wong [8] then introduced gbsplit (generalized binary split trees) as defined above, and proposed an $O(n^5)$-time algorithm for the problem, the one we show here to be incorrect.

Subsequently, the algorithm was extended by Chen and Liu to multiway gbsplit, a variant of gbsplit that requires multiple split keys per node [2]. Chen and Liu’s algorithm and proof of correctness are directly patterned on Huang and Wong’s. Their proof is invalid (and we believe their algorithm to be incorrect) for the same reason that Huang and Wong’s proof and algorithm fail. (See the remark at the end of Sect. 2.)

As mentioned above, Spuler [14, 15] proposed several 2wcst algorithms without proof of correctness. Anderson et al. [1] gave the first proof that 2wcst is in polynomial time. Their algorithm runs in time $O(n^4)$ and is restricted to the successful-queries variant. Chrobak et al. [3,4,5] gave a somewhat simpler $O(n^4)$-time algorithm for the general variant.

Beyond pointing out errors in the literature on binary search trees, we hope that the constructions underlying our counter-examples will contribute to a better understanding of the difficulties involved in designing algorithms for gbsplit and 2wcst, leading to better algorithms or even new hardness results.

2 Huang and Wong’s gbsplit algorithm is incorrect

This section gives our first main result: a proof that Huang and Wong’s proposed gbsplit algorithm [8] has a fundamental flaw.

Theorem 1

Huang and Wong’s gbsplit algorithm [8] is incorrect. There is a gbsplit instance $(\mathsf {K}, p)$ for which it returns a non-optimal tree.

We summarize their algorithm and analysis, give the intuition behind the failure, then prove the theorem. The basic intuition is that, for the dynamic program that Huang and Wong define, the optimal-substructure property fails. The proof gives a specific counter-example and verifies it. The counter-example can also be verified computationally by running the Python code for Huang and Wong’s algorithm in Appendix A.

Fix any gbsplit instance $(\mathsf {K}, p)$. Assume without loss of generality that the keys are $\mathsf {K}=\{1,2,\ldots ,n\}$. Regarding the probability vector p, for convenience, throughout the paper we drop the constraint that the probabilities must sum to 1, and we use “probabilities” and “weights” synonymously, allowing their values to be arbitrary non-negative reals. (To represent probabilities, these values can be appropriately normalized.)

During a search, the outcome of each less-than comparison narrows the current search interval, while the outcome of each (failed) equality test removes one key within the interval from consideration. Thus, at each node in any search tree, the set of keys reaching the node consists of some interval of keys, minus some so-called holes—keys removed from consideration by previous equality tests. Next, we formally define an exponentially large (!) class of subproblems that arise in this way, along with a natural recurrence relation for their cost. We then discuss how Huang and Wong attempt to reduce the number of subproblems to $O(n^3)$.

Abusing notation, a query interval $I=[i,j]$ is the set of contiguous keys $\{i,i+1,\ldots ,j\}$. Given any query interval I and any subset $H\subseteq I$ of “hole” keys, consider the subproblem (I, H) formed by the subset of keys $I\setminus H$, with the weight distribution obtained from p by restricting to $I\setminus H$. Let $\mathsf {opt}(I,H)$ denote the minimum cost of any generalized binary split tree for this subproblem. Let $p(I\setminus H) = \sum _{k\in I\setminus H} p_k$ denote the total weight of its keys.

If $H = I$ then the subproblem can be handled by an “empty” tree, so $\mathsf {opt} ({I,H}) = 0$. Otherwise, letting $I=[i,j]$, the definition of generalized binary split trees gives the recurrence

where $H_{e} = H \cup \{e\}$. (Here $s\in [i, j+1]$ ranges over the possible split keys;¹$e\in I \setminus H$ ranges over the possible equality keys.)

The goal is to compute $\mathsf {opt} ({\mathsf {K},\emptyset })$. The recurrence above allows arbitrary equality keys $e$, so it gives rise to exponentially many hole sets H, resulting in a dynamic program with exponentially many subproblems. Huang and Wong propose a dynamic program with $O(n^3)$ subproblems (I, h), one for each interval I and integer $h\le |I|$. Specifically, they define

which is the minimum cost of any tree for interval I minus any hole set of size h. Each such tree will have $|I|-h$ nodes. (Their paper uses “$p[i-1,j,h]$” to denote $\mathsf {opt}^{*} ({[i,j],h})$.) We refer to any such subproblem (I, h) as an HW-subproblem.

They develop a recurrence for $\mathsf {opt}^*({I, h})$ as follows. For any node N in an optimal tree, define N’s interval $I_N$ and hole set $H_N$ in the natural way so that interval $I_N$ contains those key values that, if searched for in T with the equality tests ignored, would reach N, and $H_N\subseteq I_N$ contains those keys in interval $I_N$ that are equality keys at ancestors of N. Hence, the set of keys reaching N is $I_N\setminus H_N$, and the subtree rooted at N is a solution for the subproblem $(I_N, H_N)$, as well as the HW-subproblem $(I_N, |H_N|)$, which we refer to as the HW-subproblem arising at N. Huang and Wong’s Lemma 1 states:

Lemma 1

(From [8] (ambiguous)) “Subtrees of an optimal generalized binary split tree are optimal generalized binary split trees.”

This statement is ambiguous in that it doesn’t specify for which subproblem the subtree is optimal. Consider any subtree $T'$ of an optimal tree $T^*$. Let $T'$ have root N, interval $I_N$ and hole set $H_N$. The first interpretation of their Lemma 1 is that $T'$ must be an optimal solution for $({I_N, H_N})$. With this interpretation (following the first recurrence above), the lemma is indeed true. But another interpretation is that $T'$ must be an optimal solution for the HW-subproblem $({I_N, |H_N|})$ arising at N. This interpretation is not the same—the HW-subproblem specifies only the number of holes, and choosing different holes can give a cheaper tree, so it can be that $\mathsf {opt}^*({I_N, |H_N|}) < \mathsf {opt}({I_N, H_N})$. As we shall see below, it is the second interpretation that underlies the recurrence relation that Huang and Wong propose, but, with that interpretation, as our Theorem 2 shows, the above lemma is false because the HW-subproblems do not have optimal substructure.

The ambiguity in Lemma 1 appears to be their first misstep. They follow it with the following (correct) observation:

Lemma 2

(From [8] (correct)) Let N be the root of a subtree $T'$ with interval I in an optimal generalized binary split tree $T^*$. The equality-test key $e_N$ of N must be the least frequent key among those in N’s interval $I_N$ that do not occur (as an equality-test key) in the left and right subtrees of N.²

Proof

The proof is a simple exchange argument. Suppose for contradiction that $e_N$ is more likely than some key k in $I_N$ and k does not occur as an equality-test key in the left and right subtrees of N. Then k is a hole at N, so it must be the equality-test key $k=e_{N'}$ of some ancestor $N'$ of N. A contradiction is obtained by observing that exchanging $e_N$ and $e_{N'}$ gives a correct tree cheaper than $T^*$. $\square$

Huang and Wong’s Lemma 2 above (with the second, incorrect interpretation of their Lemma 1) suggests the following idea. To find a hopefully optimal tree ${\tau }(I,h)$ for the HW-subproblem (I, h), consider each possible root split key and each possible split of the h hole slots. For each, first find optimal left and right subtrees for their respective subproblems, and then take the equality key at the root to be the least-likely key in I that is not an equality test in either subtree. Among trees obtained in this way, take ${\tau }(I,h)$ to be one of minimum cost. Following this idea, their algorithm (as detailed on pages 118–120 of their paper) solves any given HW-subproblem (I, h), where $I=[i,j]$ is non-empty, as follows:

1.  For each triple $(s, h_{1}, h_{2})$ where $s\in [i, j+1]$ (the split key), and $h_{1}$ and $h_{2}$ (the

numbers of holes in the left and right subtrees) are non-negative integers such that

$h_{1}+ h_{2}= h+1$, $h_{1}\le |[i, s-1]| = s-i$, and $h_{2}\le |[s, j]| = j-s+1$,

construct one possible candidate tree $T(s, h_{1}, h_{2})$ as follows:

1.1.   Give $T(s, h_{1}, h_{2})$ left and right subtrees ${\tau }([i, s-1], h_{1})$ and ${\tau }([s, j], h_{2})$.

1.2.   Give the root of $T(s, h_{1}, h_{2})$ split key $s$ and equality-test key $e$,

where $e$ is a least-likely key in I that is not an equality-test key in either subtree.

2.   Among trees $T(s, h_{1}, h_{2})$ so constructed, take ${\tau }(I,h)$ to be one of minimum cost.

The algorithm is not hard to implement. Appendix A gives Python code for it (30 lines).

Note that, by their Lemma 2, the choice for e in Line 1.2 would be correct if the second interpretation of their Lemma 1 was correct. We surmise that this line of thinking led Huang and Wong to their algorithm.

To justify the algorithm, Huang and Wong proceed as follows. Fix any execution of the algorithm (breaking ties arbitrarily; see the remarks below). For any HW-subproblem (I, h) that it solves, let $\mathsf {opt}^*({I, h})$ denote the minimum cost of any tree for the subproblem. Recall that ${\tau }(I, h)$ denotes the algorithm’s solution (tree) for the subproblem, presumably of cost $\mathsf {opt}^*({I, h})$. Huang and Wong first state a correct base case:

Lemma 3

(From [8] (correct))

$$\begin{aligned} \mathsf {opt}^*({\emptyset , 0}) = 0. \end{aligned}$$

But their Lemma 4 then claims that, for any non-empty interval $I=[i,j]$ and any number of holes $h \le |I|$, the following recurrence relation holds:

Lemma 4

(From [8] (incorrect))

$$\begin{aligned} \displaystyle {\mathsf {opt}}^*({I, h}) \,=\, \min _{s,h_{1}}~\big (p(T(s, h_{1}, h_{2})) \,+\, \mathsf {opt}^*({ [i,s-1], h_{1}}) \,+\, \mathsf {opt}^*({ [s,j], h_{2}}) \big ) \end{aligned}$$

where the minimum is over all legal combinations of $s$ and $h_{1}$, and $h_{2}= h-h_{1}+1$, and $p(T(s, h_{1}, h_{2}))$ is the weight of keys in the tree $T(s, h_{1}, h_{2})$ as defined above.

Ambiguities in Lemma 4. During the execution of the algorithm, in Steps 1.2 and 2, ties may arise in choosing a minimizer. Different choices can lead to different subtrees for any given $T(s, h_{1}, h_{2})$, with different hole sets. Huang and Wong do not explicitly discuss tie-breaking, and in the absence of such a rule $p(T(s, h_{1}, h_{2}))$ is not uniquely determined by the subproblem (I, h) and the parameters $(s, h_{1}, h_{2})$. But the refutations we give here hold no matter how ties are broken.

More significantly, our statement of their Lemma 4 corrects what we believe is an error. Namely, their statement of the lemma has “w(I, h)” where we have “$p(T(s, h_{1}, h_{2}))$”, with w(I, h) (on their page 118) defined as the “total weight of the optimal GBST for” the HW-subproblem (I, h). We believe that they had in mind the recurrence as we give it (using $p(T(s, h_{1}, h_{2}))$), mainly because this recurrence is the one that their algorithm, as defined on pages 118–120 of their paper, actually uses.

Our Theorem 2, next, refutes their Lemma 4 regardless of this issue—it refutes any recurrence based on the class of HW-subproblems $\{(I, h)\}$, by showing that the class doesn’t have the optimal-substructure property. In Theorem 1 and elsewhere, by “Huang and Wong’s algorithm”, we mean the algorithm as defined in pages 118–120 of their paper (independently of their statement of Lemma 4). Our refutation of that algorithm, after Theorem 2 below, gives an instance on which it fails.

Theorem 2

There exists a gbsplit instance $({\mathsf {K}},\textit{p})$ with the following property. In every optimal tree $T^*$ for $({\mathsf {K}},\textit{p})$, there is at least one node N such that the subtree $T^*_N$ rooted at N in $T^*$ is not optimal for the HW-subproblem $(I_N,|H_N|)$ arising at N. (The tree $T^*_N$ has cost strictly larger than $\mathsf {opt}^*({I_N, |H_N|})$.)

Proof

Before we describe $(\mathsf {K},\textit{p})$, we first describe an HW-subproblem for which using a minimum-cost tree $T'$ can be a bad choice globally. The HW-subproblem is $(I_9, 2)$, with $h=2$ holes and interval $I_9$ consisting of nine keys $I_9 = \{{{\mathsf {A1}}}$, ${{\mathsf {A2}}}$, ${{\mathsf {A3}}}$, ${{\mathsf {B0}}}$, ${{\mathsf {B4}}}$, ${{\mathsf {C0}}}$, ${{\mathsf {D0}}}$, ${{\mathsf {D1}}}$, ${{\mathsf {E0}}}\}$, ordered lexicographically, with weights as follows:

Fig. 2

Subtrees $T_{2{a}}$ and $T_{2{b}}$ for 9-key interval $I_9$ with $h=2$. $T_{2{a}}$ is missing the two keys ${{\mathsf {A3}}}, {{\mathsf {B4}}}$; $T_{2{b}}$ is missing ${{\mathsf {A3}}}, {{\mathsf {D1}}}$. Each node shows its equality key and the frequency of that key; split keys are not shown. (For each node, take the split key to be any key that separates the keys in the left and right subtrees.) The costs of $T_{2{a}}$ and $T_{2{b}}$ are 209 and 210, respectively, but in $T_{2{a}}$, the total weight of the keys is larger by 2

Figure 2 shows two possible subtrees $T_{2{a}}$ and $T_{2{b}}$ for $(I_9, 2)$, each with seven nodes. By calculation, subtree $T_{2{b}}$ costs 1 more than subtree $T_{2{a}}$ for $(I_9, 2)$. (Indeed, key ${{\mathsf {C0}}}$ contributes 5 units more to $T_{2{b}}$ than to $T_{2{a}}$, while key ${{\mathsf {B4}}}$ contributes 4 units less to $T_{2{b}}$ than key ${{\mathsf {D1}}}$ contributes to $T_{2{a}}$.)

Although $T_{2{b}}$ costs 1 more than $T_{2{a}}$, choosing subtree $T_{2{b}}$ instead of $T_{2{a}}$ can decrease the cost of the overall tree! To see why, suppose that $T_{2{a}}$ occurs as a subtree of some tree $T^*$, in which $T_{2{a}}$ has parent ${{\mathsf {A3}}}$ and grandparent ${{\mathsf {B4}}}$ as shown in the figure. (See also Fig. 3.) Consider replacing $T_{2{a}}$ and its two hole keys ${{\mathsf {A3}}}$ and ${{\mathsf {B4}}}$ by $T_{2{b}}$ and its two hole keys ${{\mathsf {A3}}}$ and ${{\mathsf {D1}}}$. This replacement decreases the cost of the entire tree by 1 unit, because the contribution of ${{\mathsf {C0}}}$ increases by 5, swapping ${{\mathsf {B4}}}$ and ${{\mathsf {D1}}}$ decreases the cost by 6, and the contributions of other nodes do not change. But a different calculation gives better intuition why Huang and Wong’s algorithm fails. The contribution of the subtree $T_{2{a}}$ to the overall cost equals the cost of $T_{2{a}}$ in isolation plus twice the weight of keys in $T_{2{a}}$ (because $T_{2{a}}$ has two ancestors). The modification increases the cost of the subtree by 1 (so it is no longer optimal for its subproblem) but decreases the total weight of its keys by 2. Thus, the subtree’s contribution to the overall cost changes by $+1 - 2\cdot 2 = -3$. This decrease of 3 is more than the increase of 2 that comes from changing the key ${{\mathsf {B4}}}$ at the overall root to ${{\mathsf {D1}}}$, which is 2 units heavier.

Fig. 3

Trees $T_{3{a}}$ and $T_{3{b}}$ for an instance of gbsplit with 31-key interval $I_{31}$. Key order is lexicographic: ${{\mathsf {A0}}}< {{\mathsf {A1}}}< {{\mathsf {A2}}}< {{\mathsf {A3}}}< {{\mathsf {B0}}}< \cdots$. As in Fig. 2, split keys are not shown. Huang and Wong’s algorithm gives a tree of cost 1763, such as $T_{3{a}}$, but tree $T_{3{b}}$ costs 1762

Next we use this HW-subproblem to obtain the complete instance $(\mathsf {K},\textit{p})$ for Theorem 2. The instance has a 31-key interval $I_{31}$, which extends the previously considered interval $I_9$ by appending two “neutral” subintervals, with 7 and 15 keys. Figure 3 shows two trees $T_{3{a}}$ and $T_{3{b}}$ for $(\mathsf {K},\textit{p})$. As shown there, the new keys are given weights so that each of the two added subintervals (without any holes) has a self-contained, optimal balanced subtree. To finish proving Theorem 2, we prove that $(\mathsf {K}, p)$ has the necessary properties:

Lemma 5

Let $T^*$ be any optimal tree for this gbsplit instance $(\mathsf {K},\textit{p})$. At some node N of $T^*$ the HW-subproblem $(I_9, 2)$ arises, but the subtree $T^*_N$ rooted at N has cost at least 210 for $(I_9, 2)$, while $\mathsf {opt}^*({I_9, 2}) \le 209$.

To bound tree costs, define a key placement (for a tree T) to be an assignment of the equality-test keys in T to distinct nodes in the infinite rooted binary tree $T_\infty$. Define the cost of the placement to be the average weighted depth of the placed keys, weighted according to the key weight-vector p. Each correct gbsplit tree T yields a placement of equal cost by placing each equality-test key in the same place in $T_\infty$ that it occupies in T. The converse does not hold, partly because placements can ignore the ordering of keys.

By an exchange argument, a placement has minimum cost if and only if it puts the weight-22 key ${{\mathsf {D1}}}$ at depth 0, the fourteen weight-20 keys at depths 1–3, and the sixteen remaining (weight-10 and weight-5) keys at depth 4. By calculation, such a placement costs 1757. No placement costs less, so no tree costs less. Tree $T_{3{b}}$ almost achieves a minimum-cost placement—it fails only in that it places the weight-5 key at depth 5, so costs 1762, just 5 units more than the minimum placement cost.

Claim 6

$T^*$ has the following structure:

• (i) It places the fifteen keys of weight 20 or more at depths 0–3.

• (ii) It places the fifteen weight-10 keys at depth 4.

Next we prove the claim. Since $T^*$ is optimal it costs at most 1762 (the cost of $T_{3{b}}$), so its placement also costs at most 1762. Suppose for contradiction that (i) doesn’t hold. Then $T^*$ places a key k of weight 20 or more at depth at least 4. Also, in depths 1–3, it either places at least one key $k'$ of weight 10, or places fewer than fifteen keys. In either case, by exchanging k and $k'$, or just re-placing k in depth 1–3, we can obtain a key placement that costs at least 10 units less than 1762. But this is impossible, as the minimum placement cost is 1757. So (i) holds. Now suppose for contradiction that (ii) doesn’t hold. Then there is a weight-10 key $k'$ at depth 5 or more, and at most fifteen keys at depth 4, so $k'$ can be re-placed in depth 4, yielding a key placement that costs 10 less, which is impossible. This proves the claim.

Key placements ignore the ordering of keys. The following order property captures the restrictions on key placements due to the ordering.

Let T be any correct gbsplit tree. Let P and $P'$ be nodes in T with equality-test keys k and $k'$. Let Q be the least-common ancestor of P and $P'$. If P is in Q’s left subtree, and $P'$ is in Q’s right subtree, then $k<k'$.

The property holds simply because k and $k'$ are separated by M’s split key.

Fix any optimal tree $T^*$ for $(\mathsf {K},\textit{p})$. Claim 6 imposes stringent constraints on the depth of all keys in $T^*$, except for the weight-5 key ${{\mathsf {C0}}}$. There are two cases:

Case 1: $T^*$ places ${{\mathsf {C0}}}$ at depth 4. With Claim 6, this implies that $T^*$ is a complete balanced binary tree of depth 4 (like $T_{3{a}}$), whose sixteen depth-4 nodes hold the fifteen weight-10 keys and ${{\mathsf {C0}}}$. By the order property, these depth-4 keys are ordered left to right, just as they are in $T_{3{a}}$, with the left-most four nodes at depth 4 having keys ${{\mathsf {B0}}}$, ${{\mathsf {C0}}}$, ${{\mathsf {D0}}}$ and ${{\mathsf {E0}}}$.

The left spine has only five nodes. By the order property, all five keys less than ${{\mathsf {C0}}}$ cannot be elsewhere than on the spine. So ${{\mathsf {D1}}}$ is not on the left spine.

Let M be the parent of sibling leaves ${{\mathsf {D0}}}$ and ${{\mathsf {E0}}}$. Since ${{\mathsf {D0}}}< {{\mathsf {D1}}}< {{\mathsf {E0}}}$, by the order property, ${{\mathsf {D1}}}$ must lie on the path from M to the root. Since ${{\mathsf {D1}}}$ is not on the left spine, and M is the only node on this path that is not on the left spine, ${{\mathsf {D1}}}$ must be M. So ${{\mathsf {D1}}}$ has depth 3 in $T^*$. Now exchanging ${{\mathsf {D1}}}$ with the root key gives a placement that costs at least 6 less, that is, at most $1762-6 < 1757$, which is impossible as the minimum placement cost is 1757. So Case 1 cannot happen.

Case 2: $T^*$ places ${{\mathsf {C0}}}$ at depth 5. Let $L_0, L_1, \ldots , L_\ell$ be the left spine of $T^*$, starting at the root. Take $T'$ to be the subtree of $T^*$ rooted at $L_2$. By Claim 6, $T^*$ has fifteen depth-4 nodes, holding the fifteen weight-10 keys. By the order property, these depth-4 keys are ordered left to right within their level and at most twelve of them are not in $T'$. This implies that the weight-10 keys ${{\mathsf {B0}}}$, ${{\mathsf {D}}}0$ and ${{\mathsf {E0}}}$ must be in $T'$.

The next larger weight-10 key, ${{\mathsf {N0}}}$, cannot be in $T'$. Indeed, if it were, then by the order property, all keys less than or equal to ${{\mathsf {N0}}}$ would be in $T'\cup \{L_1, L_0\}$. But there are twelve keys less than or equal to ${{\mathsf {N0}}}$ and at most eight keys in $T'$.

We now focus on the cost of $T'$. By the previous two paragraphs, $T'$ has exactly three keys at depth 2, namely ${{\mathsf {B0}}}$, ${{\mathsf {D0}}}$ and ${{\mathsf {E0}}}$. By the order property and the assumption for Case 2, ${{\mathsf {C0}}}$ must be (the only key) at depth 3 in $T'$ (as the child of either ${{\mathsf {B0}}}$ or ${{\mathsf {D0}}}$). By Lemma 8, the three keys at depths 0 and 1 in $T'$ have weight 20 or 22. Therefore, by calculation, the cost of $T'$ is at least 210 (see Fig. 2).

Since ${{\mathsf {E0}}}$ is in $T'$, by the order property, all eight keys less than ${{\mathsf {E0}}}$ are in $T' \cup \{L_0, L_1\}$. That is, $T'\cup \{L_0, L_1\}$ contains at least the 9 keys in $I_{9}$. But (as observed above) $T'$ has seven nodes. So $T'\cup \{L_0, L_1\}$ contains exactly the 9 keys in $I_{9}$, and the HW-subproblem solved by $T'$ must be $(I_9, 2)$. As observed above, $T'$ costs at least 210. But tree $T_{2{a}}$ (Fig. 2) of cost 209 also solves $(I_9, 2)$, so $\mathsf {opt}^{*}({I_9, 2}) \le 209$.

This proves Lemma 5 and Theorem 2. $\square$

Table 1 The HW-subproblems used to solve HW-subproblem $(I_9, 2)$, with $I_9=[1, 9]$

We prove one final utility lemma before we prove Theorem 1. Consider any execution of Huang and Wong’s algorithm on the input $(\mathsf {K}, p)$ defined in the proof of Theorem 2. Let $T = {\tau }(I_{31}, 0)$ be the algorithm’s solution.

Lemma 7

If T contains a node N whose HW-subproblem is $(I_9, 2)$, then the subtree ${\tau }(I_9, 2)$ rooted at N costs at most 209 for $(I_9, 2)$.

Proof

Abusing notation, for $1\le i < j \le 9$, let [i, j] denote the ith through jth keys in interval $I_9$, as shown in Fig. 3. (See also Fig. 2 for intuition.) Consider Table 1:

Each row of the table is for one HW-subproblem (I, h) (shown in the leftmost column) and demonstrates that the cost of the tree ${\tau }(I,h)$ computed by the algorithm for that subproblem is as shown in the fifth column (“cost for ${\tau }(I,h)$”). The last column lists the keys that are holes in ${\tau }(I, h)$. The first four rows are singleton cases (key sets of size one), and their correctness and optimality can be verified by straightforward inspection. For each subsequent row, the second column gives one of the triples $(s, h_1, h_2)$ considered by the algorithm for the given HW-subproblem (I, h), where s is the split key, and $h_1$ and $h_2$ are the numbers of holes allocated to the left and right subtrees. Columns “left” and “right” show the left and right HW-subproblems that follow from that choice of $(s, h_1, h_2)$, and column “cost for ${\tau }(I,h)$” gives the cost of tree $T(s, h_{1}, h_{2})$ resulting from that choice. Likewise, the final column “holes” describes the possible hole sets (in order to achieve the given cost,covering all ways to break ties). For the HW-subproblems in rows five and six, the choices of $(s, h_1, h_2)$ in the table are optimal. For the seventh subproblem, the cost of 209 is an upper bound (in fact it is optimal, but we don’t need that here). Each row can be verified by manual computation assuming inductively that the previous rows are correct.

To illustrate how to verify the rows, we explain the information included in the 5th row, for HW-subproblem $(I,h) = ([1,6],3)$. This subproblem involves interval [1, 6] that consists of keys ${{\mathsf {A1}}}$, ${{\mathsf {A2}}}$, ${{\mathsf {A3}}}$, ${{\mathsf {B0}}}$, ${{\mathsf {B4}}}$, ${{\mathsf {C0}}}$, with 3 of the keys being holes. For the choice $(s,h_1,h_2) = ({{\mathsf {C0}}},4,0)$ in the algorithm (the 2nd column), the left and right HW-subproblems will be ([1, 5], 4) and ([6, 6], 0) (the 3rd and 4th column). Their solutions are summarized in the 1st and 2nd row of the table. (These solutions are: ${\tau }([1,5],4)$ contains only node ${{\mathsf {B0}}}$, and ${\tau }([6,6],0)$ contains only node ${{\mathsf {C0}}}$.) The algorithm will then choose any key from ${{\mathsf {A1}}}$, ${{\mathsf {A2}}}$, ${{\mathsf {A3}}}$, ${{\mathsf {B0}}}$, as the equality key in the root of tree $T({{\mathsf {C0}}},4,0)$, since they all have the same weight 20. The weight of $T({{\mathsf {C0}}},4,0)$ is then 35, so its cost will be 50, and the holes will be any three keys among ${{\mathsf {A1}}}$, ${{\mathsf {A2}}}$, ${{\mathsf {A3}}}$, ${{\mathsf {B0}}}$. (Note: another choice in the algorithm that gives the same tree is $(s,h_1,h_2) = ({{\mathsf {B4}}},3,1)$.) As claimed in the paragraph above, this tree $T({{\mathsf {C0}}},4,0)$ is an optimal solution for HW-subproblem ([1, 6], 3), that is $T({{\mathsf {C0}}},4,0) = {\tau }([1,6],3)$. Indeed, $T({{\mathsf {C0}}},4,0)$ is the only tree for ([1, 6], 3) that contains only one key of weight 20, and any tree that has two keys of weight 20 will have cost at least 60. $\square$

By Lemmas 5 and 7, the tree T computed by Huang and Wang’s algorithm for $(\mathsf {K}, p)$ cannot be optimal: Lemma 5 states that all optimal trees for $(\mathsf {K}, p)$ contain a node with a certain property, while Lemma 7 states that T does not contain such a node. This proves Theorem 1.

For empirical verification, note that executing the algorithm on $(\mathsf {K}, p)$, via the Python code in Appendix A,³ returns a tree of cost 1763. This tree is not optimal, as $T_{3{b}}$ costs 1762. The tree does have the HW-subproblem $(I_9,2)$, and executing the algorithm directly on that subproblem does return a tree of cost 209.

Remark on Chen and Liu’s algorithm for multiway gbsplit [2]. Chen and Liu’s algorithm [2] and analysis are patterned directly on Huang and Wong’s, and the proofs they present also conflate (their equivalents of) $\mathsf {opt}^*({I,h})$ and $\mathsf {opt}({I,H})$, leading to the same problems with optimal substructure. For example, Property 1 of [2] states “Any subtree of an optimal $(m+1)$-way generalized split tree is optimal.” They do not define “optimal”, so their Property 1 has the same problem as Huang and Wong’s Lemma 1: it is true if “optimal” means “with respect to their equivalent of $\mathsf {opt}({I,H})$”, but does not necessarily hold if “optimal” means “with respect to their equivalent of $\mathsf {opt}^*({I,h})$”. Lemmas 2, 3 and 4 of [2], which state the recurrence relations for their dynamic program, are direct generalizations of Huang and Wong’s Lemma 4. Their recurrence chooses equality keys by first finding optimal subtrees for the children, then taking the equality keys to be the least-likely keys that are not equality keys in the children’s subtrees. As pointed out in the proof of Theorem 1, correctness of this approach requires the optimal-substructure property to hold with respect to $\mathsf {opt}^*({I,h})$. But it does not. For these reasons, their proof of correctness is not valid. We believe that their algorithm for multiway gbsplit is also incorrect, but describing their algorithm and analysis in detail, and giving a complete counter-example, are out of the scope of this paper.

3 A 2wcst algorithm by Spuler fails on some subproblems

This section concerns 2wcst, the problem of computing an optimal two-way comparison search tree, given a set $\mathsf {K}$ of n keys and their weight distribution p. Such a tree T is a rooted binary tree, where each non-leaf node N has two children, as well as a key $k_N\in \mathsf {K}$ and a binary comparison operator (equality or less-than). Denote such a node by ${ \left\langle v \mathbin {=} k_N \right\rangle }$ or ${ \left\langle v \mathbin {<} k_N \right\rangle }$, depending on which comparison operator is used. The tree T has n leaves, each labeled with a unique key in $\mathsf {K}$.

Fig. 4

A two-way-comparison search tree with keys $\mathsf {K}=\{1,2,3,4,5,6\}$. Below each leaf is its weight. The cost of this tree is $0.6\cdot 1 + 0.1\cdot 3 + 0.1\cdot 3 + 0.05\cdot 4 + 0.05\cdot 4 + 0.1\cdot 3 = 1.9$

The search for a query v in T starts at the root. If the root is a leaf, the search halts. Otherwise, it compares v to the root’s key using the root’s comparison operator, then recurses left if the comparison succeeds, and right otherwise. For the tree to be correct,⁴ the search for any query $v\in \mathsf {K}$ must end at the leaf that is labeled with v. Given an instance $(\mathsf {K}, p)$, the problem is to find a tree that minimizes the weighted average depth of the leaves (in the case that p is a probability distribution, this is the expected number of comparisons in a search for a query v drawn randomly according to p). Figure 4 shows an example.

Spuler’s thesis proposed various algorithms for 2wcst and for gbsplit, for both the successful-queries variant and the general variant [15].⁵ Here we discuss the (successful-queries) 2wcst algorithm that Spuler presented as a modification of Huang and Wong’s gbsplit algorithm in Section 6.4.1 of his thesis [15, Section 6.4.1]. That section starts with the following remark:

“The changes to the optimal generalized binary split tree algorithm of Huang and Wong [8] to produce optimal generalized two-way comparison trees are quite straight forward.”

(“Generalized two-way comparison trees” in the thesis are two-way comparison search trees as defined herein.) The remainder of his Section 6.4.1 sketches the code for the algorithm. His Appendix A.4.1. gives complete code. Spuler does not explicitly define the dynamic program or recurrence that he has in mind; however, it is implicitly defined by his algorithm as described below. In addition to lacking proofs of correctness, these algorithms have not appeared in any peer-reviewed publication, although Spuler did refer to them in his journal paper [14], and they have been cited in the literature as the first polynomial-time algorithms for 2wcst [1].

Following Huang and Wong, Spuler’s algorithms are based on a dynamic program where each subproblem is specified by an interval of keys and a number of holes, and each subproblem is solved using a recurrence relation. In the remainder of the section, we prove that the dynamic program is flawed:

Theorem 3

There is an instance $(\mathsf {K},\textit{p})$ of 2wcst for which the dynamic program used by Spuler’s 2wcst algorithm [15, Section 6.4.1] has the following flaws: for some subproblems, the recurrence relation is incorrect and the algorithm computes non-optimal solutions.

Note that Theorem 3 does not imply that the algorithm is incorrect, in the sense that it gives an incorrect solution to some full instance (where the number h of holes is 0).

Following Huang and Wong, the dynamic program implicit in Spuler’s algorithm has a subproblem (I, h) for each query interval I and number of holes h. In what follows we call any such subproblem (I, h) an S-subproblem. The definition of a correct tree for an S-subproblem is a natural extension of the definition for full instances: a correct tree for (I, h) must have exactly $|I| - h$ leaves, each labeled with a unique key from I; however, all keys in I can be used as inequality-comparison keys. We use $\mathsf {opt}^*({I,h})$ to denote the minimum cost of any tree for S-subproblem (I, h). The underlying flaw is the same as in Huang and Wong’s dynamic program—S-subproblems do not have optimal substructure.

Given any S-subproblem (I, h), where $I=[i,j]$ and the subproblem size $|I|-h$ is more than one, Spuler’s algorithm computes a tree $\tau (I,h)$ for S-subproblem (I, h) by combining trees $\tau (I',h')$ that it has computed for smaller S-subproblems, as follows:

1. Construct one candidate tree with an equality test at the root, as follows:

1.1.   Let $e$ be a least-likely key in I that is not a leaf in $\tau (I, h+1)$.

1.2.  The candidate tree has root ${ \left\langle v \mathbin {=} e \right\rangle }$ and right subtree $\tau (I, h+1)$.

2. For $s\in [i+1, j]$ and $(h_{1}, h_{2})$ s.t. $h_{1}+ h_{2}= h$, $s-i - h_{1}\ge 1$ and $j-s+1-h_{2}\ge 1$:

2.1.   Make a candidate tree with root ${ \left\langle v \mathbin {<} s \right\rangle }$ and subtrees $\tau ([i, s-1], h_{1})$, $\tau ([s, j], h_{2})$.

3.   Among the candidate trees so constructed, let $\tau (I,h)$ be one of minimum cost.

Remarks. The algorithm is not hard to implement. Appendix B gives Python code (42 lines). As noted earlier, Spuler does not explicitly define his dynamic program or recurrence relation for $\mathsf {opt}^*({I,h})$; however, it is implicitly defined by his algorithm and his assumption that each tree $\tau (I,h)$ is optimal for S-subproblem (I, h) (so has cost $\mathsf {opt}^*({I, h})$).

Although ties may arise in choosing the minimizers in Lines 1.1 and 3, Spuler does not discuss ties. We’ll show that his recurrence relation is incorrect no matter how ties are broken.

Given an S-subproblem (I, h), Spuler’s algorithm constructs its tree $\tau (I, h)$ out of trees $\tau (I', h')$ that it built for smaller S-subproblems. This only works if S-subproblems have optimal substructure. To complete the proof of Theorem 3, we show that they do not:

Theorem 4

There exists a 2wcst S-subproblem (I, h) with the following property. In every optimal tree $T^*$ for (I, h), there is at least one node N such that, for the S-subproblem $(I_N,h')$ arising at N, the subtree $T^*_N$ rooted at N in $T^*$ does not have minimum cost, $\mathsf {opt}^*({I_N,h'})$, for that S-subproblem.⁶

Proof

Before we describe the full S-subproblem (I, h), we describe one smaller S-subproblem $(I',h')$ for which using a minimum-cost tree $T'$ can be a bad choice globally. It is $(I_{8}, 1)$, with one hole and interval $I_8$ having keys $\{1,2,\ldots ,8\}$ whose weights are as follows:

Fig. 5

Three trees (circled and lightly shaded) for S-subproblem $(I_8, 1)$. $T_{5a}$ has cost 49 and weight 22. $T_{5b}$ and $T_{5c}$ have cost 50 but weight 20. $T_{5a}$ is optimal for $(I_8, 1)$. Among trees that don’t contain the weight-7 key 1, trees $T_{5b}$ and $T_{5c}$ have minimum cost. Subtrees marked with 0 (dark shaded) contain keys of weight 0

Figure 5 shows three possible subtrees $T_{5a}$, $T_{5b}$ and $T_{5c}$ for $(I_8, 1)$. By inspection, $T_{5a}$ has cost 49 for S-subproblem $(I_{8}, 1)$, while $T_{5b}$ and $T_{5c}$ cost 50 but weigh 2 units less. Suppose, in a larger tree, that $T_{5a}$ occurs as the left child of a node N, as shown in Fig. 5. Let $T_N$ be the subtree rooted at N. Suppose that the interval of the left child of $T_N$ (that is, the root of $T_{5a}$) contains all keys $1,2,\ldots ,8$. (For example, N might be ${ \left\langle v \mathbin {<} 9 \right\rangle }$.) Then replacing $T_{5a}$ by $T_{5b}$ would reduce the overall cost by at least 1 unit. This is because the contribution of $T_{5a}$ to the cost of $T_N$ is not the cost of $T_{5a}$; rather, it is its cost plus its weight, and the cost plus weight of $T_{5b}$ is 1 unit less.

Next we construct the full S-subproblem $(I, h)=(I_{15},2)$ for Theorem 4. It has two holes, and extends the above S-subproblem $(I_{8}, 1)$ to a larger interval $I_{15} = \{1,2,\ldots ,15\}$ with the following symmetric weights:

We use the following terminology to distinguish the different types of keys in a subtree. Given an S-subproblem $(I',h')$ of (I, h), and a tree $T'$ for $(I', h')$, the keys of $I'$ that appear in the leaves of $T'$ are $T'$-queries. The other keys in interval $I'$, which are holes in $T'$, are $T'$-holes. (We don’t introduce new terminology for the comparison keys in $T'$.) We drop the prefix $T'$ from these terms when it is understood from context.

To analyze $(I_{15},2)$ we need some utility lemmas. We start with one that will help us characterize how weight-0 queries increase costs. This lemma (Lemma 8 below) is in fact general and it holds for S-subproblems of an arbitrary instance of 2wcst. Define two integer sequences ${ \left\{ d_m \right\} }$ and ${ \left\{ e_m \right\} }$, as follows: $d_1 = 0$, $d_2 = 3$, $e_1 = 0$, $e_2 = 2$, $e_3 = 6$ and

$$\begin{aligned} d_m&~=~ m\, + \,\min \,\{d_i + d_{m-i} : 1\le i< m \}\,\quad \text {for} \,m\ge 3, \\ e_m&~=~ m\, + \,\min \,\{d_i + e_{m-i} : 1\le i < m \}\,\quad \text {for}\, m\ge 4. \end{aligned}$$

By calculation, $d_3 = 6$, $d_4 = 10$, $d_5 = 14$, $e_4 = 9$, $e_5 = 13$ and $e_6 = 18$.

Consider a tree $T'$ for an S-subproblem of some arbitrary instance of 2wcst (not necessarily our specific instance $(\mathsf {K},\textit{p})$). A subset Q of $T'$-queries will be called $T'$-separated (or simply separated, if $T'$ is understood from context) if for any two $k,k'\in Q$, with $k < k'$, there is a $T'$-query $k''$ that separates them, that is $k< k'' < k'$. Also, if $Q\setminus { \left\{ f \right\} }$ is $T'$-separated for some $f\in Q$, then we say that Q is nearly $T'$-separated.

Lemma 8

Let T be a tree for an S-subproblem of some arbitrary instance of 2wcst. Let Q be a set of T-queries and $m=|Q|$. (i) If Q is T-separated then the total depth (i.e., the sum of the depths) in T of the keys in Q is at least $d_m$. (ii) If Q is nearly T-separated then the total depth in T of the keys in Q is at least $e_m$.

The proof of Lemma 8 is a straightforward induction—we postpone it to the end of this section and proceed with our analysis.

Now we focus our attention on our instance $(\mathsf {K},\textit{p})$, and we characterize the weights and costs of optimal subtrees for certain subproblems. For $1\le \ell \le 14$, let $I_\ell =\{1,2,\ldots ,\ell \}$ denote the subinterval of $I_{15}$ containing its first $\ell$ keys. These keys have $\ell$ weights (in order) $\{7, 5, 0, 5, \ldots \}$: one key of weight 7, then $\lfloor \ell /2\rfloor$ even keys of weight 5, separated by odd keys of weight 0. Let ${\ell _{\scriptscriptstyle {+}}} = 1+\lfloor \ell /2\rfloor$ be the number of positive-weight keys in $I_\ell$. Note that each S-subproblem $(I_\ell , h')$ can be solved by a tree with ${\ell _{\scriptscriptstyle {+}}}-h'$ positive-weight queries, having $h'$ (positive-weight) hole keys.

Lemma 9

Consider any S-subproblem $(I_\ell , h')$ with $\ell \le 14$ and ${\ell _{\scriptscriptstyle {+}}}-h' = 4$. Let $T'$ be an optimal tree for $(I_\ell , h')$. Then $T'$ has weight 22 and cost 49 (like $T_{5a}$).

Proof

As $T'$ is fixed throughout the proof, the terms holes, queries, and separated, mean $T'$-holes, $T'$-queries and $T'$-separated as defined earlier, unless otherwise specified.

Let $h_0$ be the number of weight-0 holes and ${q_{\scriptscriptstyle {+}}}$ the number of queries with positive weight. We use the following facts about $T'$.

• (F1) $T'$ costs at most 49. Indeed, one way to solve $(I_\ell ,h')$ is as follows: take the $h'$ rightmost weight-5 keys in $I_\ell$ to be the holes, then handle the remaining ${\ell _{\scriptscriptstyle {+}}}-h'=4$ queries with positive weight (queries 1, 2, 4, 6), along with any weight-0 queries $3,5,7,\ldots$, using tree $T_{5a}$, at cost 49.

• (F2) ${q_{\scriptscriptstyle {+}}} = 4+h_0$. This follows by simple calculation: ${q_{\scriptscriptstyle {+}}} = {\ell _{\scriptscriptstyle {+}}}-(h'-h_0) = 4+h_0$.

• (F3) $T'$ does not contain four separated weight-5 queries. Indeed, otherwise, by Lemma 8, $T'$ would cost at least $5\cdot d_4 = 50 > 49$, contradicting (F1).

To finish we show that $T'$ costs at least 49. Along the way we show it has weight 22.

Case 1: First consider the case that $h_0 = 0$. By (F2), there are 4 positive-weight queries in $T'$. Since $h_0=0$, all weight-0 keys are queries in $T'$, so the set of all weight-5 queries in $T'$ is separated, and by (F3), there are at most three such queries. The fourth positive-weight query must be the weight-7 query, query 1. So the positive-weight queries in $T'$ are the weight-7 query and three separated weight-5 queries.

So $T'$ has total weight 22, as desired. Further, by Lemma 8, the four positive-weight queries in $T'$ have total depth at least $e_4$ in $T'$. So $T'$ costs at least $5\cdot e_4 + (7-5)\cdot j = 45+2j$, where j is the depth of the weight-7 query. If $j\ge 2$, by the previous bound, $T'$ costs at least 49, and we are done. In the remaining case we have $j = 1$ (as $j=0$ is impossible), so the weight-7 query is a child of the root. The three weight-5 queries are in the other child’s subtree (and are a separated subset there), so by Lemma 8 have total depth at least $d_3=6$ in that subtree, and therefore total depth at least 9 in $T'$. So the total cost of $T'$ is at least $7 + 5\cdot 9 > 49$, contradicting (F1).

Case 2: In the remaining case $h_0 \ge 1$. By (F2), there are ${q_{\scriptscriptstyle {+}}} = 4+ h_0$ positive-weight queries in $T'$. Let $q_5 \ge {q_{\scriptscriptstyle {+}}}-1$ be the number of weight-5 queries in $T'$. Since all but $h_0$ of the weight-0 queries are in $T'$, there is a separated set of $q_5-h_0$ weight-5 queries in $T'$. By (F3), $q_5 - h_0 \le 3$.

This (with ${q_{\scriptscriptstyle {+}}} = 4+h_0$ and $q_5\ge {q_{\scriptscriptstyle {+}}}-1$) implies $q_5 = h_0 + 3 = {q_{\scriptscriptstyle {+}}} - 1$. This implies that the weight-7 query is in $T'$, along with some $q_5-h_0 = 3$ separated weight-5 queries. Reasoning as in Case 1, the cost of these four queries alone is at least 49. But $T'$ contains at least one additional weight-5 query (as $q_5 = 3+h_0 > 3$), so $T'$ costs strictly more than 49, contradicting (F1). Thus Case 2 cannot actually occur. $\square$

Fig. 6

Trees $T_{6a}$ and $T_{6b}$, with five positive weight queries. Tree $T_{6a}$ has cost 69 and weight 27. Tree $T_{6b}$ has cost 70 and weight 25

Lemma 10

Consider any S-subproblem $(I_\ell , h')$ with $\ell \le 14$ and ${\ell _{\scriptscriptstyle {+}}}-h' = 5$. Let $T'$ be an optimal tree for $(I_\ell , h')$. Then $T'$ has weight 27 and cost 69 (like $T_{6a}$ in Fig. 6).

Proof

Again, throughout the proof, unless otherwise specified, the terms holes, queries, and separated, are all with respect to $T'$. Let $h_0$ be the number of weight-0 holes and ${q_{\scriptscriptstyle {+}}}$ the number of queries with positive weight. We use the following facts about $T'$.

• (F4) $T'$ costs at most 69. Indeed, one can solve $(I_\ell ,h')$ as follows: take the $h'$ rightmost weight-5 keys in $I_\ell$ to be the holes, then handle the remaining ${\ell _{\scriptscriptstyle {+}}}-h'=5$ queries with positive weight (queries 1, 2, 4, 6, 8), along with any weight-0 queries $3,5,7,\ldots$, using tree $T_{6a}$ at cost 69.

• (F5) ${q_{\scriptscriptstyle {+}}} = 5+h_0$. This follows by straightforward calculation: ${q_{\scriptscriptstyle {+}}} = {\ell _{\scriptscriptstyle {+}}}-(h'-h_0) = 5+h_0$.

• (F6) $T'$ does not contain five separated weight-5 queries. Indeed, otherwise, by Lemma 8, $T'$ would cost at least $5\cdot d_5 = 70 > 69$, a contradiction.

To finish, we show that $T'$ has cost at least 69. Along the way we show it has weight 27.

Case 1: First consider the case that $h_0 = 0$. By (F5), there are 5 positive-weight queries in $T'$. Also, since $h_0=0$, all weight-0 keys are queries in $T'$, so the set of all weight-5 queries in $T'$ is separated, and by (F6), there are at most four of them. The fifth positive-weight query must be the weight-7 query, query 1. So the positive-weight queries in $T'$ are the weight-7 query and four separated weight-5 queries.

So $T'$ has total weight 27. Further, by Lemma 8, the five positive-weight queries in $T'$ have total depth at least $e_5$ in $T'$. So $T'$ costs at least $5\cdot e_5 + (7-5)\cdot j = 65+2j$, where j is the depth of the weight-7 query. If $j\ge 2$ then, by the previous bound, $T'$ costs at least 69, and we are done. In the remaining case we have $j = 1$ (as $j=0$ is impossible), so the weight-7 query is a child of the root. The four weight-5 queries are in the other child’s subtree (and form a separated set there), so by Lemma 8 have total depth at least $d_4=10$ in that subtree, and therefore total depth at least 14 in $T'$. So the total cost of $T'$ is at least $7 + 5\cdot 14 > 69$, contradicting (F4).

Case 2: In the remaining case, $h_0 \ge 1$. By (F5), there are ${q_{\scriptscriptstyle {+}}} = 5+ h_0$ positive-weight queries in $T'$. Let $q_5 \ge {q_{\scriptscriptstyle {+}}}-1$ be the number of weight-5 queries in $T'$. Since all but $h_0$ of the weight-0 queries are in $T'$, there is a separated set of $q_5-h_0$ weight-5 queries in $T'$. By (F6), $q_5 - h_0 \le 4$.

This (with ${q_{\scriptscriptstyle {+}}} = 5+h_0$ and $q_5\ge {q_{\scriptscriptstyle {+}}}-1$) implies $q_5 = h_0 + 4 = {q_{\scriptscriptstyle {+}}} - 1$. This implies that the weight-7 query is in $T'$, along with some separated set of $q_5-h_0 = 4$ weight-5 queries. Reasoning as in Case 1, the cost of these five queries alone is at least 69. But $T'$ contains at least one additional weight-5 query (as $q_5 = 4+h_0 > 4$), so $T'$ costs strictly more than 69, contradicting (F4). Thus, Case 2 cannot actually occur. $\square$

To conclude the proof of Theorem 4, we prove that $(I_{15}, 2)$ has the necessary properties:

Lemma 11

Let $T^*$ be any optimal tree for S-subproblem $(I_{15}, 2)$. Then $T^*$ has at least one node N such that, for the S-subproblem $(I_N,|H_N|)$ arising at N, the subtree $T^*_N$ rooted at N in $T^*$ does not have minimum cost, $\mathsf {opt}({I_N,|H_N|})$, for that S-subproblem.

Fig. 7

Spuler’s algorithm fails on the S-subproblem $(I_{15}, 2)$. The algorithm computes a tree of cost 116, such as $T_{7a}$ above, but there are trees, such as $T_{7b}$, of cost 115. The two trees’ left subtrees are $T_{5a}$ and $T_{5c}$

Throughout the proof, unless otherwise specified, the terms holes, queries and separated are all with respect to $T^*$. We use the following properties of $T^*$:

• (P1) $T^*$ costs at most 115. Indeed, one way to solve $(I_{15}, 2)$ is to take the two weight-7 keys as holes, then use tree $T_{7b}$ in Fig. 7, of cost 115. As $T^*$ is optimal, it costs at most 115.

• (P2) The root of $T^*$ does a less-than comparison. Indeed, by [1, Theorem 5], since $T^*$ is optimal for its queries, if $T^*$ does an equality-test at the root, then the total query weight in $T^*$ is at most four times the maximum query weight. But the total query weight in $T^*$ is at least $7\cdot 5 = 35$, while the maximum query weight is at most 7.

• (P3) In $T^*$ there are seven positive-weight queries, and the set of weight-5 queries is separated (by weight-0 queries). To show this, we show that no weight-0 key is a hole. Suppose otherwise for contradiction. Let $k'$ be a weight-0 hole. We can assume without loss of generality that $k'$ is not used in any node of $T^*$ as an inequality key, for otherwise we can modify $T^*$ to not use it, without changing its cost, by replacing it with the weight-5 key $k'' = k'+1$ (which could be a hole or a query). Since $k'$ is a $T^*$-hole, by definition, $k'$ also cannot be used as an equality key. So we can assume that $k'$ does not appear as a comparison key in $T^*$. Let $k\in \{k'\pm 1\}$ be a weight-5 query in $T^*$. (Query k exists in $T^*$—otherwise $\{k'-1, k', k'+1\}$ would all be holes.) Replace k throughout $T^*$ by $k'$. As $k'$ and k are adjacent keys and $k'$ does not occur in $T^*$, the resulting tree ${\bar{T}}$ still solves $(I_{15}, 2)$, and ${\bar{T}}$ costs less than $T^*$ (as ${\bar{T}}$ uses the weight-0 key $k'$ instead of the weight-5 key k). This contradicts the optimality of $T^*$.

By (P3), $T^*$ has seven positive-weight queries. Using condition (P2) and left-right symmetry of subproblem $(I_{15}, 2)$, we can assume that the left subtree of $T^*$ has at least four of the seven. (Note that “flipping” the tree, namely replacing each key k by $16-k$ and swapping the yes and no-subtrees, would map each inequality comparison ${ \left\langle v \mathbin {<} k \right\rangle }$ to ${ \left\langle v \mathbin {\le } 16-k \right\rangle }$, while our model uses only strict inequalities. However, this latter comparison is equivalent to ${ \left\langle v \mathbin {<} 17-k \right\rangle }$.) Let $T'$ be the left subtree. Denote the S-subproblem that $T'$ solves by $(I_\ell , h')$. To prove the lemma, assume for contradiction that $T'$ is optimal for its S-subproblem, and proceed by cases:

Case 1: $T'$ has four positive-weight queries. That is, $T'$ solves an S-subproblem $(I_\ell , h')$ where ${\ell _{\scriptscriptstyle {+}}}-h' = 4$. By Lemma 9, $T'$ has cost 49 and weight 22. The right subtree $T''$ of $T^*$ has the three remaining positive-weight queries, the leftmost two of which are separated in $T''$ by a zero-weight query (using (P3)). By Lemma 8 (ii), $T''$ has cost at least $5\cdot e_3 = 30$ and weight at least 15. The cost of $T^*$ is its weight plus the costs of $T'$ and $T''$. By the above observations, this is at least $(22+15)+49+30 = 116$, contradicting (P1).

Case 2: $T'$ has five positive-weight queries. That is, $T'$ solves an S-subproblem $(I_\ell , h')$ where ${\ell _{\scriptscriptstyle {+}}}-h' = 5$. By Lemma 10, $T'$ has cost 69 and weight 27. The right subtree $T''$ of $T^*$ has the two other positive-weight queries, which have total depth at least $1+1=2$ in $T''$, and each has weight at least 5. So $T''$ has cost, and weight, at least $5\cdot 2 = 10$. The cost of $T^*$ is its weight plus the costs of $T'$ and $T''$. By the above observations, this is at least $(27+10) + 69 + 10 = 116$, contradicting (P1).

Case 3: $T'$ has six or seven positive-weight queries. Let set S consist of just the first six of these queries. Since $T'$ is the left subtree of $T^*$ (which has seven positive-weight queries) S does not contain the last key, 15. So (using (P3)) all queries in S, except possibly $\{1, 2\}$, are separated by weight-zero queries in $T'$. By Lemma 8 (ii), $T'$ has cost at least $5\cdot e_6 = 90$. The cost of $T^*$ is its weight (at least $7\cdot 5 = 35$), plus the cost of its left and right subtrees (at least 90, counting $T'$ alone). So $T^*$ costs at least $35+90=125$, contradicting (P1).

This proves the lemma and Theorem 4. $\square$

Finally we prove Theorem 3.

Proof

(Theorem 3) Consider any execution of Spuler’s algorithm on the S-subproblem (I, h) from Theorem 4, breaking ties arbitrarily. Let T be the tree it computes for that S-subproblem. By Theorem 4, either T is not optimal for (I, h), or some subtree $T'$ of T is not optimal for its S-subproblem $(I', h')$. So Spuler’s algorithm must compute a non-optimal solution to at least one S-subproblem. $\square$

In fact, for this instance (I, h), Spuler’s algorithm (as implemented via the Python code in Appendix B) computes a non-optimal tree of cost 116, such as $T_{7a}$ in Fig. 7. By inspection, tree $T_{7b}$ in that figure costs 115, so $T_{7a}$ is not optimal.

Discussion. As mentioned earlier, this counter-example is just for a subproblem. This subproblem has $h=2$ holes, so it does not represent a complete instance of 2wcst for which Spuler’s algorithm would give an incorrect final result. However, this counter-example does demonstrate that Spuler’s algorithm solves some subproblems incorrectly, so that the recurrence relation underlying its dynamic program is incorrect. At a minimum, this suggests that any proof of correctness for Spuler’s algorithm would require a more delicate approach. Anderson et al. [1] establish some conditions on the weights of equality-test keys in optimal trees. It may be possible to leverage the bounds from [1] to show that bad subproblems—those that are not solved correctly by the algorithm—never appear as subproblems of an optimal complete tree. For example, per Anderson et al’s Theorem 5 for any equality-test node in any optimal tree, the weight of the node’s key must be at least one quarter of the total weight of the keys that reach the node. Hence, if a subproblem $(I', h')$ is solved by some subtree $T'$ of an optimal tree $T^*$, then each hole key in $T'$ must have weight at least one third of the total weight of the queries in $T'$. This implies that the subproblem $(I_{15}, 2)$ in the proof of Theorem 3 cannot actually occur in any optimal tree for $(I_{15}, 0)$.

While the question of correctness of Spuler’s algorithm is somewhat intriguing, it should be noted that showing its correctness will not improve known complexity bounds for 2wcst, as there are faster 2wcst algorithms that are known to be correct [1, 3].

3.1 Proof of Lemma 8

Here is the promised proof of Lemma 8.

Proof

(Lemma 8) Recall that T is a tree for some S-subproblem and Q is a subset of the queries in T, with $m = |Q|$.

Part (i). Assume that Q is separated. Our goal is to show that the total depth in T of queries in Q is at least $d_m$, as defined before Lemma 8. It is convenient to recast the problem as follows. Change the weight of each query in Q to 1. Change the weight of each query not in Q to 0. We will refer to the resulting cost of a tree as modified cost. Now we need to show that the modified cost of T is at least $d_m$. The proof is by induction on m.

The base cases (when $m = 1,2$) are easily verified, so consider the inductive step, for some given $m \ge 3$. We assume that T and Q are chosen to minimize the modified cost of T, subject to $|Q|=m$. Call this the minimality assumption.

Suppose T does an inequality test at the root. Let $T_1$ and $T_2$ be the left and right subtrees of T, and for $a\in { \left\{ 1,2 \right\} }$ let $Q_a\subseteq Q$ contain the queries in Q that fall in $T_a$. Let $i = |Q_1|$, so that $|Q_2| = m-i$. For $a\in { \left\{ 1,2 \right\} }$, query set $Q_a$ is $T_a$-separated. By the minimality assumption, $0\not \in \{i, m-i\}$. The modified cost of T is its weight (m), plus the modified costs of $T_1$ and $T_2$. By the inductive assumption, this is at least $m+d_{i} + d_{m-i} \ge d_m$, as desired.

Suppose T does an equality test at the root. The minimality assumption implies that the equality-test key has nonzero (modified) weight. (This follows via the argument given for Property (P2) in the proof of Lemma 11, using Anderson et al’s Theorem 5 or Corollary 3.) So the equality-test key is in Q. Let $T_1$ be the no-subtree of T and let $Q_1\subseteq Q$ contain the queries in Q that fall in $T_1$; so we have $|Q_1|=m-1$. Set $Q_1$ is $T_1$-separated, so by the inductive assumption, $T_1$ has modified cost at least $d_{m-1}$. So the modified cost of T is at least $m+ d_{m-1} = m + d_1 + d_{m-1} \ge d_m$, as desired.

Part (ii). The proof of Part (ii) follows the same inductive argument as above. The base cases for $m=1,2$ are trivial. The verification of the base case for $m=3$ is by straightforward case analysis. In the inductive step, the only significant difference is in the case when T does an inequality test at the root. Since Q is now only nearly separated, $Q_1$ will be $T_1$-separated while $Q_2$ will be nearly $T_2$-separated (or vice versa), giving us that the modified cost of T is at least $m+d_{i} + e_{m-i} \ge e_m$. $\square$

Note: We would like to use this opportunity to acknowledge yet another error in the literature on binary split trees, this one in our own paper [3]. In that paper we introduced a perturbation method that can be used to extend algorithms for binary search trees with keys of distinct weights to instances where key-weights need not be distinct, and we claimed that this method can be used to speed up the computation of optimal binary split trees to achieve running time $O(n^4)$. (Recall that in binary split trees from [7, 9, 12], the equality-test key in each node must be a most likely key among keys reaching the node.) As it turns out, this claim is not valid. In essence, the perturbation approach from [3] does not apply to binary split trees because such perturbations affect the choice of the equality-test key and thus also the validity of some trees. See [4, 5] for an erratum, full proofs of the remaining results, and pointers to follow-up work.

Appendices

Appendix A

Python code for Huang and Wong’s gbsplit algorithm

See Fig. 8.

Fig. 8

Python code for Huang and Wong’s gbsplit algorithm

Appendix B

Python code for Spuler’s 2wcst algorithm

See Fig. 9.

Fig. 9

Python code for Spuler’s 2wcst algorithm