Abstract
Interface theories based on Interface Automata (IA) are formalisms for the component-based specification of concurrent systems. Extensions of their basic synchronization mechanism permit the modelling of data, but are studied in more complex settings involving modal transition systems or do not abstract from internal computation. In this article, we show how de Alfaro and Henzinger’s original IA theory can be conservatively extended by shared memory data, without sacrificing simplicity or imposing restrictions. Our extension IA for shared Memory (IAM) decorates transitions with pre- and post-conditions over algebraic expressions on shared variables, which are taken into account by IA’s notion of component compatibility. Simplicity is preserved as IAM can be embedded into IA and, thus, accurately lifts IA’s compatibility concept to shared memory. We also provide a ground semantics for IAM that demonstrates that our abstract handling of data within IA’s open systems view is faithful to the standard treatment of data in closed systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Behavioural types [4, 17] play an increasingly important role when developing and verifying software systems. For object-oriented software, behavioural types are specified as contracts [25], annotating methods and classes with pre- and post-conditions and invariants, respectively. For distributed software, session types are employed [10, 19] to specify permitted and prohibited interactions. For concurrent software, component compatibility has been studied by interface theories, such as de Alfaro and Henzinger’s Interface Automata (IA) [12, 13]. Although IA is a well-studied theory, it does not directly reflect modern IT architectures that rely on networked, distributed clusters of multi-core/-processor computers. In these architectures, communication between clusters is via message passing, and communication within a cluster is typically via shared variables. Holik et al. have studied the IA paradigm for message passing in [18], but the treatment of shared variables in the context of IA has so far been unsatisfactory.
This article is addressed to concurrency theoreticians and studies an IA-based setting where data are communicated via shared memory while activities, or operations, are triggered by synchronizing actions. In this introduction, we first summarize IA and related works on extensions of IA with data, both of which is elaborated in Sects. 2 and 3, respectively. This allows us to spell out our contributions and advances over the state-of-the-art in interface theories.
Background Interface Automata (IA) [12, 13] model system components as labelled transition systems that distinguish a component’s input and output actions. Parallel component composition assumes that a component may wait on inputs but never on outputs, implying that a component’s output must be consumed immediately, or a communication error occurs. In case no system environment may restrict the components’ behaviour so that all errors are avoided, the components are deemed to be incompatible.
To support refinement during software development, IA is equipped with a branching-time behavioural preorder called alternating simulation; it allows one to substitute an abstract component by a concrete one, provided the concrete component offers no fewer inputs and no more outputs than the abstract one. As this implies that outputs cannot be enforced in IA, researchers have frequently based IA-inspired interface theories on the more expressive Modal Transition Systems (MTS) and modal refinement [3, 5, 15, 22, 29]. As an aside, a linear-time semantics respecting communication errors as in IA was proposed by Dill [14] and more recently adapted for variations of IA in [6, 8].
To enable the modelling of richer classes of concurrent systems and software, IA has been extended in various ways to capture data in addition to control [1, 2, 9, 11, 18, 27]. Except for [18], these works focus on shared memory. The work of Mouelhi et al. [9, 27] is closest to ours and adopts a paradigm well-known from structured programming. It considers an output of one IA to trigger an operation in another IA. The guaranteed data state resulting upon executing the operation on the input side is expected to meet the trigger’s assumption; otherwise, an error occurs. While Mouelhi et al. stick to the IA-setting and express assumptions and guarantees on data states by decorating actions with pre- and post-conditions, respectively, none of the essential results that we treat in Sects. 3–7 are shown.
For an interface theory built upon the more expressive MTS setting, Bauer et al. [1, 2] also introduce data via pre- and post-conditions with the idea of operation calls. But counter to the optimistic view on component compatibility adopted by IA, they restrict themselves to a pessimistic view, whereby components are already deemed to be incompatible if there exists a system environment that causes a communication error. De Alfaro et al.’s Sociable Interfaces [11] employs scoping and non-interference conditions to ensure that interfaces can participate in sophisticated n-to-n communication schemes on global variables. The semantics of sociable interfaces is not directly based on a behavioural preorder but uses a related phrasing in terms of game semantics. This semantics, however, does not abstract from internal computation, which is also a limitation for [1, 2].
Contributions This article demonstrates that IA permits a simple and faithful extension where data are communicated via shared memory while activities are triggered by synchronizing actions. To do so, we develop Interface Automata for Shared Memory (IAM) which, similarly to [1, 2, 9, 27], specify operation calls via pre- and post-conditions attached to transitions (see Sect. 3).
Naturally, pre-conditions act as transition guards. As in [9, 27], the post-condition of an output-transition and that of a matching input-transition describe an assumption and guarantee, respectively, on the data state obtained after the synchronization. Thus, an output-transition may be understood as invoking an operation associated with the transition’s action, whereas the matching input-transition describes how this operation manipulates the system’s data state. One may think of the input-transition to actually perform the operation. This approach contrasts the one in [11], where the inputs contain only assumptions about the change of data values and the outputs determine which values are produced. We adopt the point-to-point, handshake communication model of IA that is inspired by the process algebra CCS [26]. A communication error occurs if either, as in IA, a matching input is not provided for an output, or if the new data state set by the input after synchronization does not obey the output’s assumption.
We conservatively extend IA’s concepts of parallel composition and alternating refinement to IAM, while preserving compositionality and abstracting from internal computation (see Sects. 3, 4). Then, we formally prove that IAM can be embedded into IA, which implies that, using IAM, one can reason finitely about component compatibility in IA, even when infinite data domains are involved (see Sect. 6); this is an important aspect not considered in related work. We also connect our abstract treatment of data via pre- and post-conditions, where data states are implicit, to the concrete treatment known from ground semantics for (data-)closed systems (see Sect. 7). Such ground semantics naturally encode data values into control states, leading to infinite presentations in the presence of infinite data domains. For establishing the connection, we define a reduction on IAM such that—under some restrictions—ground semantics and finiteness are preserved. The key result is that this ground semantics is bisimilar to the structure of the reduced IAM. Hence, we arrive at a finite presentation of the usually infinite ground semantics, which we consider as our most original and interesting result. The result shows that a cluster, as introduced above, externally behaves as an IA, i.e. as a message passing system, so that our ground semantics provides the user with an often finite description of the cluster’s behaviour.
This article expands the published extended abstract [16] in multiple ways. First, a detailed introduction to IA and discussion of closely related work on extending IA with data is given here (see Sect. 2), in order to make the article accessible to an as broad audience of concurrency theoreticians as possible. Further, we extend the IAM setting with the possibility to refer to the previous data state in post-conditions by distinguishing between ‘primed’ and ‘unprimed’ variables. Thus, it is now possible to specify that a value is preserved or changed by some operation. The setting in [16] is equivalent to the current one if we refrain from unprimed variables in post-conditions. Additionally, this article technically justifies the pruning employed in parallel composition, includes all proofs of our results, and applies our theory to an illustrative example. The latter also testifies to the practical importance of primed variables (see Sect. 5.1). To testify that our theoretical research may eventually lead to tool-supported interface checkers employed in software engineering practice, we have built a first, prototypic, open-source IAM toolset that consists of a textual modelling language, implements interface composition, allows for simulating interfaces and debugging them for communication errors, automates refinement checking for simple data theories, and offers the interactive exploration of counterexamples in case a refinement check fails (see Sect. 5.2). Last but not least, we have improved the article’s presentation in particular regarding, but not limited to, our ground semantics (see Sect. 7).
2 The IA setting
We start off with a brief technical introduction to the classical setting of Interface Automata (IA) by de Alfaro and Henzinger [13]. This makes it easier to understand our extension with data, and the concepts and results for IA are technically needed in Sects. 6 and 7 for our shared-memory extension IAM. An interface automaton specifies a system component as a labelled transition system over some input and output alphabets I and O, respectively.
Definition 1
(Interface Automata) An Interface Automaton (IA) is a tuple \((P, I, O,\xrightarrow {}, p_0)\), where
-
P is the set of states with \(p_0 \in P\) being the initial state.
-
\(A =_{\text {df}}I \cup O\) is the alphabet consisting of disjoint sets I and O of input and output actions, respectively, not containing the distinguished internal action \(\tau \); (I, O) is the signature of the IA.
-
\(\xrightarrow {} \; \subseteq P \times (A \cup \{\tau \}) \times P\) is the transition relation, and \(p \xrightarrow {\alpha } q\) is written for \((p,\alpha ,q) \in \,\xrightarrow {}\). The IA is required to be input-deterministic, i.e. \(p'=p''\) whenever \(p \xrightarrow {a?}p'\) and \(p \xrightarrow {a?}p''\) for some \(p\in P\) and \(a?\in I\).
We use a, a?, a!, \(\alpha \), \(\alpha ?\) and \(\alpha !\) as representatives of the sets A, I, O, \(A \cup \{\tau \}\), \(I\cup \{\tau \}\) and \(O\cup \{\tau \}\) and simply write P for an IA \((P, I, O, \xrightarrow {}, p_0)\), and similarly for IAM below. According to the above definition, a transition is labelled either with an input action a?, an output action a! or the internal action \(\tau \). Here, ? and ! are just comments showing whether an action is an input or an output. The actual name of the action is a; thus, two components of a parallel composition can share an action a, which then necessarily is an input of one and an output of the other component (see below). The two IAs synchronize on such actions a, resulting in internal \(\tau \)-transitions; the IAs interleave on all other actions. In general, an a?-labelled transition shows that the component is willing to synchronize on a. In contrast, an action a! (like \(\tau \)) is locally controlled (or local for short) and can always be performed disregarding the environment. Thus, a! initiates a synchronization, and this requires an environment with input a? to be ready to receive a with a corresponding transition. As an aside note that, in [13], there can be several internal actions and the refinement does not allow one to rename these. We avoid this issue by having a single internal action \(\tau \) only.
Definition 2
(Parallel Product) IAs \((P, I_P, O_P, \xrightarrow {}_P, p_0)\) and \((Q, I_Q, O_Q, \xrightarrow {}_Q, q_0)\) are composable if \(O_P \cap O_Q = \emptyset = I_P \cap I_Q\). The product \(P \,{{\overline{\otimes }}}\,Q\) of such composable IAs is defined as \((P \times Q, I, O, \xrightarrow {}, (p_0,q_0))\), where \(I =_{\text {df}}(I_P \cup I_Q) {\setminus } (A_P \cap A_Q)\), \(O =_{\text {df}}(O_P \cup O_Q) {\setminus } (A_P \cap A_Q)\), and the transition relation \(\xrightarrow {}\) is the least relation satisfying the following rules:
-
\(\langle {p},{q}\rangle \xrightarrow {\alpha } \langle {p'},{q}\rangle \) if \(p \xrightarrow {\alpha }_P p'\) and \(\alpha \notin A_Q\);
-
\(\langle {p},{q}\rangle \xrightarrow {\alpha }\langle {p},{q'}\rangle \) if \(q \xrightarrow {\alpha }_Q q'\) and \(\alpha \notin A_P\);
-
\(\langle {p},{q}\rangle \xrightarrow {\tau } \langle {p'},{q'}\rangle \) if \(p \xrightarrow {a?}_P p'\), \(q \xrightarrow {a!}_Q q'\) for some a;
-
\(\langle {p},{q}\rangle \xrightarrow {\tau }\langle {p'},{q'}\rangle \) if \(p \xrightarrow {a!}_P p'\), \(q \xrightarrow {a?}_Q q'\) for some a.
Note that we often drop the index from a transition relation whenever it is clear from the context.
If IA P outputs an action shared with IA Q at a state p but Q cannot receive it in its current state q, a communication error occurs in state \(\langle {p},{q}\rangle \). The parallel composition prunes all illegal states, i.e. all error states \(\langle {p},{q}\rangle \) as well as those states from which an error state can be reached autonomously via local transitions; these are the states where the environment can no longer prevent the composition of P and Q from entering an error state. This consideration of errors makes the IA interface theory suitable for reasoning about component compatibility and provides a means of error-awareness.
Interface Automata apply an open systems view with optimistic compatibility, assuming that a composed system runs in a so-called helpful environment. Such an environment obeys the operation guideline as given by the parallel composition \(P{\parallel }Q\) (see below) and avoids communication mismatches by controlling the composed component’s input actions. Other theories such as [1, 3] take a pessimistic view, where no assumptions about the environment are made: any occurrence of a reachable error state leads to an incompatibility of the components.
Definition 3
(Parallel Composition) Given a parallel product \(P \,{{\overline{\otimes }}}\,Q\) of IAs P and Q, a state \(\langle {p},{q}\rangle \) is an error state if there is some \(a \in A_P \cap A_Q\) s.t.
-
\(p \xrightarrow {a!}p'\) with \(a\in I_Q\), but there is no transition \(q \xrightarrow {a?}q'\);
-
\(q \xrightarrow {a!}q'\) with \(a\in I_P\), but there is no transition \(p \xrightarrow {a?}p'\).
The set \(E \subseteq P \times Q\) of illegal states is the least set containing all error states and those states \(\langle {p},{q}\rangle \) for which there is a transition \(\langle {p},{q}\rangle \xrightarrow {\alpha !}\langle {p'},{q'}\rangle \) with \(\langle {p'},{q'}\rangle \in E\). The parallel composition \(P{\parallel }Q\) is then computed by pruning the illegal states, i.e. by removing all states in E and their incoming and outgoing transitions. If \(\langle {p},{q}\rangle \in P {\parallel }Q\), then states p and q are compatible, written \(p{\parallel }q\); one also says that \(p{\parallel }q\) is defined. Furthermore, P and Q are compatible if their initial states are compatible; otherwise, \(P{\parallel }Q\) is undefined.
Proposition 4
(Associativity & Commutativity) If P, Q and R are pairwise composable IAs, then \((P {\parallel }Q) {\parallel }R\) and \(P {\parallel }(R {\parallel }Q)\) are either both undefined or \((P {\parallel }Q) {\parallel }R\) and \(P {\parallel }(R {\parallel }Q)\) are isomorphic. Analogously, \({\parallel }\) is commutative.
IA supports the compositional refinement of systems via a notion of alternating simulation: P refines Q if the input-transitions of Q can be simulated by P and, vice versa, the output-transitions of P can be simulated by Q. By simply following this pattern, new communication errors cannot be introduced during refinement. The pattern prevents the removal of specified inputs needed to synchronize with outputs of an environment as well as the addition of unspecified outputs, which would create new needs of synchronization. A weak transition  stands for a finite and possibly empty sequence of \(\tau \)-transitions.
stands for a finite and possibly empty sequence of \(\tau \)-transitions.
Definition 5
(Alternating Simulation) For IAs P, Q with the same signature, a relation \({\mathcal {R}}\subseteq P\times Q\) is an alternating simulation if the following conditions hold for all \(p{\mathcal {R}} q\) and actions a:
-
(i)
\(q \xrightarrow {a?} q'\) implies \(\exists p'.\) \(p \xrightarrow {a?} p'\) and \(p' {\mathcal {R}} q'\)
-
(ii)
\(p \xrightarrow {a!} p'\) implies \(\exists q', q''.\) \(q'' \xrightarrow {a!} q'\) with
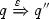 and \(p' {\mathcal {R}} q'\).
and \(p' {\mathcal {R}} q'\). -
(iii)
\(p \xrightarrow {\tau } p'\) implies \(\exists q'.\)
 and \(p' {\mathcal {R}} q'\).
and \(p' {\mathcal {R}} q'\).
We write \(P\sqsubseteq _{\textit{IA}}Q\) to say that P IA-refines Q, if there exists an alternating simulation \({\mathcal {R}}\) s.t. \(p_0 {\mathcal {R}} q_0\). Further, P is IA-equivalent to Q if P and Q IA-refine each other.
Intuitively, a state p refines q if it matches all inputs of q and, conversely, if q matches all outputs of p. Note that p may have additional inputs in which q cannot engage and which may be followed by arbitrary behaviour afterwards. It is not hard to show that the IA-refinement \(\sqsubseteq _{\textit{IA}}\) is a preorder and, as motivated above, a pre-congruence for parallel composition. It is also easy to see that, for the latter result, an input of q must immediately be matched by p, i.e. without preceding \(\tau \)s; neither trailing \(\tau \)s are allowed.
Theorem 6
(Compositionality of IA) Let P, Q, R be IAs and \(P \sqsubseteq _{\textit{IA}}Q\). Further assume that Q and R are composable. We have: (i) P and R are composable; (ii) \(P {\parallel }R\) is defined if \(Q {\parallel }R\) is, and then \(P {\parallel }R \sqsubseteq _{\textit{IA}}Q {\parallel }R\).
We illustrate the concepts of IA with a simple vending machine example that consists of two components, the machine—offering coffee and tea—and the customer (see Figs. 1, 2).
The machine M waits for the customer C to select coffee or tea (inputs selC? and selT?). In the case of coffee, the machine accepts a positive number of coins (transitions labelled coin?), while tea is free of charge. Eventually, coffee or resp. tea is released (outputs relC! and relT!). If the customer approaches the vicinity of the machine and is thirsty for coffee or tea (inputs \(\hbox {atVM}_C\)? and \(\hbox {atVM}_T\)?), she or he presses the appropriate selection button (outputs selC! and selT!) and makes a selfie of her or him at the machine afterwards (output selfie!). In case of tea, a British customer would also accept the drink without taking the selfie. She or he then inserts some coins (output coin!) and waits for the drink to be dispensed (inputs relC? and relT?).
For the parallel composition of M and C, one determines the product shown in Fig. 3. Here, \(\langle {m_3},{c_6}\rangle \) is an error state, because \(m_3\) does not accept the coin offered in \(c_6\). Therefore, also states \(\langle {m_3},{c_5}\rangle \) and \(\langle {m_0},{c_4}\rangle \) are illegal, because they can locally reach \(\langle {m_3},{c_6}\rangle \). Thus, \(M {\parallel }C\) is \(M \,{{\overline{\otimes }}}\,C\) without the tea vending cycle in the right half of the figure.
An IA-refinement \(C'\) of C that accommodates the taste of Italian customers is shown in Fig. 4. Customer \(C'\) has an additional input relC? at state \(c_2\), because he or she would also accept coffee earlier. Moreover, \(C'\) has learned from M, seen as an ‘operating guideline,’ not to pay for tea. The product \(M \,{{\overline{\otimes }}}\,C'\) is the same as \(M \,{{\overline{\otimes }}}\,C\) except that \(\langle {m_3},{c_6}\rangle \) is no longer an error state. Hence, \(M {\parallel }C' = M \,{{\overline{\otimes }}}\,C'\). Note that the additional input at \(c_2\) has no effect on the composition.
3 The IAM setting
To capture shared memory in IA, our extension IAM additionally labels transitions by pre- and post-conditions, similar to [1, 2, 9, 27]. These allow us to abstractly specify and reason about manipulations of global variables without modelling data states explicitly, i.e. as functions from variables to values. Formally, the shared memory is represented by a set V of variables, ranged over by x, y, etc., and all IAMs, as defined below, have the same set V of variables. Pre-conditions are predicates over V, i.e. first-order formulas with interpreted function and predicate symbols. Besides the propositional operators \(\lnot \), \(\vee \), \(\wedge \) and \(\xrightarrow {}\), we employ the usual arithmetic operators and predicate symbols such as <, \(=\) and \(\ge \). The universe of our predicates is denoted by \(\textit{Pred}({V})\), with representatives \(\varphi \), \({{\overline{\varphi }}}\), \(\varphi _1\), etc. In order to represent also post-values of variables, we introduce the set \(V'\) of fresh primed variables \(x'\) for each \(x \in V\). While x represents the value of x before executing the respective transition, the value after is referenced by \(x'\). We write \(\varphi '\) for \(\varphi \) where each x is replaced by \(x'\). Post-conditions are ranged over by \(\psi \), \(\psi _1\), etc. and taken from the set \(\textit{Pred}({V,V'})\) of predicates over \(V \cup V'\).
A data state over V, often represented by \(\sigma \) or \({{\overline{\sigma }}}\), is a valuation \(\sigma {:}\,V \rightarrow \mathbb {D}\) over a fixed, possibly infinite domain \(\mathbb {D}\) of values. The set of all these data states is denoted by \(\llbracket {V}\rrbracket \). To take a transition, now also its pre-condition \(\varphi \) must be satisfied by the current data state \(\sigma \), and we write \(\sigma \models \varphi \) in this case; further, we define \(\llbracket {\varphi }\rrbracket =_{\text {df}}\{\sigma \in \llbracket {V}\rrbracket \,|\, \sigma \models \varphi \}\), and similarly for predicates over \(V'\). The post-condition \(\psi \) must be satisfied by \(\sigma \) together with the new data state \({{\overline{\sigma }}}\) applied to the primed variables, and we write \(\sigma ,{{\overline{\sigma }}}' \models \psi \). Here, \({{\overline{\sigma }}}{:}\,V \rightarrow \mathbb {D}\) is a valuation like \(\sigma \): because the post-condition refers to the next state with primed variables, we introduce \({{\overline{\sigma }}}'{:}\,V' \rightarrow \mathbb {D}\) defined by \({{\overline{\sigma }}}'(x') = {{\overline{\sigma }}}(x)\) for all \(x \in V\).
Intuitively, a pre-condition acts as a guard for a transition. An output-transition labelled \((\varphi , a!, \psi )\) specifies that it is only executable when the system’s data state satisfies pre-condition \(\varphi \) and expects that the system environment, upon synchronizing on a, leaves the system in a data state such that post-condition \(\psi \) is satisfied. Similarly, an input-transition labelled \((\varphi , a?, \psi )\) is executable in data states satisfying \(\varphi \) and guarantees that it implicitly manipulates variables only in ways such that the post-condition \(\psi \) is satisfied. This corresponds to an operation call: the caller performs an output-transition; this requires the callee to execute a respective input-transition in each data state satisfying \(\varphi \), or otherwise a communication mismatch arises; the callee modifies the memory according to the post-condition of the input-transition and requires the caller to accept this. A violation of the caller’s assumption gives rise to a (data-)error in the parallel composition (see Sect. 4). These mutual requirements are very different from the one-way requirement in an IA; thus, it is quite surprising that we can nevertheless embed IAM into IA below (see Sect. 6).
Interface Automata for Shared Memory We can now formally define the notion of IAM:
Definition 7
(Interface Automata for Shared Memory) An Interface Automaton for Shared Memory (IAM) is a tuple \((P, I, O, \xrightarrow {}, p_0)\), where P, I, O, \(p_0\) and the related notations are as for IA (cf. Definition 1) and \(\xrightarrow {} \; \subseteq P \times \textit{Pred}({V}) \times (A\cup \{\tau \} ) \times \textit{Pred}({V,V'}) \times P\) is the transition relation. The states in P are also called control states.
For a transition \((p, \varphi , \alpha , \psi , p') \in \, \xrightarrow {}\), written \({p\,{-\!\!\left( \varphi , \alpha , \psi \right) \!\!\!\rightarrow _{\,}}p'}\) for simplicity, its pre-condition \(\varphi \) must be satisfiable, i.e. \(\llbracket {\varphi }\rrbracket \not = \emptyset \) and denoted by \(\varphi \) sat. There is a stricter requirement for the post-condition: if one assigns values to the unprimed variables in \(\psi \) according to some data state \(\sigma \) satisfying \(\varphi \), the resulting predicate \(\psi (\sigma )\) must be satisfiable.Footnote 1 This requirement can also be written as \(\varphi \Rightarrow \exists X'.\, \psi \), where \(\exists X'\) existentially quantifies over all primed variables in \(\psi \) and symbol \(\Rightarrow \) denotes logical entailment.
Moreover, the transition relation \(\xrightarrow {}\) is required to be data-deterministic for input actions, i.e. for all \(p \in P\) and different transitions \({p\,{-\!\!\left( \varphi _1, a?, \psi _1\right) \!\!\!\rightarrow _{\,}}p'}\) and \({p\,{-\!\!\left( \varphi _2, a?, \psi _2\right) \!\!\!\rightarrow _{\,}}p''}\) with \(a? \in I\), the conjunction \(\varphi _1 \wedge \varphi _2\) is unsatisfiable.
In figures, pre- and post-conditions are set in square brackets. Note that the above definition coincides with the one of IA [13] in case only the tautology true, written tt, is allowed as pre- and post-condition. In particular, the normally finer notion of data-determinism is then the same as input-determinism, which is needed to achieve compositionality for parallel composition (see Theorem 6). Data-determinism is needed in our approach for the respective result (see Corollary 18).
Figure 5 shows two simple IAMs P and Q, where P can call operation a (output action a!) in initial state \(p_0\), provided that variable x has value \(-1\) (pre-condition \(x=-1\)). IAM P assumes that operation a adjusts the value of x to a positive one (post-condition \(x'>0\)), and transitions to state \(p_1\). Alternatively, if x is non-negative (pre-condition \(x \ge 0\)), P can serve a call to operation b in \(p_0\) (input action b?), guarantees that the value of x remains unchanged (post-condition \(x'=x\)), and transitions to state \(p_2\). Similarly, IAM Q offers to execute operation a in state \(q_0\) (input action a?), provided that x has a non-zero value (pre-condition \(x\not =0\)), and transitions to state \(q_1\) while guaranteeing that the value of x is set to 1 (post-condition \(x'=1\)). The resulting synchronization on action a in the parallel composition of P and Q can only take place if \(x=-1\) and then updates the value of x to 1. The post-condition of Q’s transition always meets the assumption of P’s transition due to \(x'=1 \Rightarrow x'>0\). Parallel composition for IAM is fully introduced and discussed in Sect. 4.
Alternating simulation We now adapt alternating simulation from IA to IAM. First observe that a single IAM transition may represent many transitions when explicitly considering the underlying data state. This implies that the behaviour of a transition in one IAM might need to be matched by multiple transitions in another IAM, i.e. by a family—an indexed collection—of transitions. For example, the behaviour of a transition labelled with pre-condition \(x \ge 0\) may only be covered in the other IAM by two transitions with pre-conditions \(x=0\) and \(x>0\), respectively, where the former transition matches the behaviour for data states in which x has value 0 and the latter in which x has a strictly positive value. Employing such families makes our approach more flexible and sophisticated than the one in [9, 27]. In the following, families of transitions are indexed over some implicit index set with representative i. Such a family could even be infinite, e.g. when encoding local data states with infinite domains; the meaning of \(\varphi \Rightarrow {\bigvee _i\,} \varphi _i\) is clear also in such a case.
A weak transition  stands for a finite and possibly empty sequence of \(\tau \)-transitions labelled with arbitrary satisfiable pre- and post-conditions. This is because an environment component can always change a data state satisfying a post-condition to a data state satisfying the next pre-condition. This also explains why pre- and post-conditions are simply ignored in Item (iii) of the following definition.
stands for a finite and possibly empty sequence of \(\tau \)-transitions labelled with arbitrary satisfiable pre- and post-conditions. This is because an environment component can always change a data state satisfying a post-condition to a data state satisfying the next pre-condition. This also explains why pre- and post-conditions are simply ignored in Item (iii) of the following definition.
Definition 8
(Alternating Simulation) For IAMs P and Q with the same signature, \({\mathcal {R}} \subseteq P \times Q\) is an alternating simulation if the following conditions hold for all \(p {\mathcal {R}} q\) and \(\varphi \), a, \(\psi \):
-
(i)
\({q\,{-\!\!\left( \varphi , a?, \psi \right) \!\!\!\rightarrow _{\,}}q'}\) implies that there exists a family of \({p\,{-\!\!\left( \varphi _i, a?, \psi _i\right) \!\!\!\rightarrow _{\,}}p'_i}\) with \(\varphi \Rightarrow {\bigvee _i\,} \varphi _i\) and, for all i and all \(\sigma \), \(\sigma \models \varphi \wedge \varphi _i\) implies \(\psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p'_i {\mathcal {R}} q'\).
-
(ii)
\({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\) implies that there exists a family of \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) with \(\varphi \Rightarrow {\bigvee _i\,} \varphi _i\) and, for every \(\sigma \) with \(\sigma \models \varphi \), there is at least one transition \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) of the family satisfying \(\sigma \models \varphi _i\),
 , \(\psi _i (\sigma )\Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} q'_i\).
, \(\psi _i (\sigma )\Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} q'_i\). -
(iii)
\({p\,{-\!\!\left( \varphi , \tau , \psi \right) \!\!\!\rightarrow _{\,}}p'}\) implies that there exists a \(q'\) with
 and \(p' {\mathcal {R}} q'\).
and \(p' {\mathcal {R}} q'\).
We write \(P \sqsubseteq _{\textit{IAM}}Q\) and say that P IAM-refines Q, if there exists an alternating simulation \({\mathcal {R}}\) such that \(p_0 {\mathcal {R}} q_0\). Further, P is IAM-equivalent to Q if P and Q IAM-refine each other. Note that “for all \(\sigma \) with \(\sigma \models \varphi \wedge \varphi _i\), \(\psi _i (\sigma ) \Rightarrow \psi (\sigma )\)” is equivalent to \(\varphi \wedge \varphi _i \wedge \psi _i \Rightarrow \psi \).
As for alternating simulation in IA and motivated in Sect. 2, inputs must be matched immediately for IAM, i.e. leading and trailing \(\tau \)s are not allowed. Additionally, Cond. (i) shows that pre-conditions are weakened while post-conditions are strengthened. The weakening of a pre-condition keeps in line with IA in that refinement may introduce additional inputs. The strengthening in the post-conditions ensures that refinement does not loosen guarantees, i.e. strengthening prevents the refined system from generating more data states than specified. Note that, as Cond. (i) covers input actions, the pre-conditions \(\varphi _i\) are pairwise disjoint due to data-determinism.
Outputs are matched the other way around, as specified in Cond. (ii), which is analogous to Cond. (i) except that, as in \(\sqsubseteq _{\textit{IA}}\), leading \(\tau \)s are permitted when matching output-transitions. The matching runs show that the same output can occur in the specification, at least in an environment causing the appropriate changes of data states; this time, the post-condition of the specification is stricter because it is a requirement. Cond. (iii) has been explained above.
Despite the fact that \(\sqsubseteq _{\textit{IA}}\) does not consider families when matching transitions, our alternating simulation \(\sqsubseteq _{\textit{IAM}}\) for IAM coincides with \(\sqsubseteq _{\textit{IA}}\) when considering only IAMs where all pre- and post-conditions are equivalent to tt. For such IAMs, it does not matter with which family member a transition is matched, any one family member would do.
An example illustrating alternating refinement is depicted in Fig. 6, where IAMs P, Q, R are defined over shared variable sets \(V = \{x\}\) and \(V' = \{x'\}\) with domain \(\mathbb {R}\) such that \(P \sqsubseteq _{\textit{IAM}}Q \sqsubseteq _{\textit{IAM}}R\). The input-transition \({r_0\,{-\!\!\left( x > 0, a?, \textit{tt}\right) \!\!\!\rightarrow _{\,}}r_1}\) of the most abstract IAM R is matched by transition \({q_0\,{-\!\!\left( x \ne 0, a?, x' \ne 0\right) \!\!\!\rightarrow _{\,}}q_1}\) of Q, where the pre-condition is weakened and the post-condition is strengthened. In turn, this transition is matched in P by the transitions \({p_0\,{-\!\!\left( x>0, a?, x'<0\right) \!\!\!\rightarrow _{\,}}p_1}\) and \({p_0\,{-\!\!\left( x<0, a?, x'>0\right) \!\!\!\rightarrow _{\,}}p_3}\). The internal transition of \(q_1\) is matched by \(r_1\) staying put.
For output-transitions, leading \(\tau \)s are allowed when refining. Transition \({q_2\,{-\!\!\left( x \ge -1, b!, x' \ge -3\right) \!\!\!\rightarrow _{\,}}q_4}\) of Q is matched in R by the family consisting of \({r_2\,{-\!\!\left( x \le 0, b!, -2 \le x' \le 2\right) \!\!\!\rightarrow _{\,}}r_4}\) and \({r_3\,{-\!\!\left( x \ge 0, b!, x'=1\right) \!\!\!\rightarrow _{\,}}r_5}\); observe that  and
and  . Note that R has overlapping pre-conditions in \(r_1\); unlike for inputs, data-determinism is not required for local actions in IAM.
. Note that R has overlapping pre-conditions in \(r_1\); unlike for inputs, data-determinism is not required for local actions in IAM.
Theorem 9
(Preorder) \(\sqsubseteq _{\textit{IAM}}\) is a preorder.
Proof
Reflexivity immediately follows from the fact that the identity relation is an alternating simulation. For transitivity, we let \(P \sqsubseteq _{\textit{IAM}}Q\) and \(Q \sqsubseteq _{\textit{IAM}}R\) due to \({\mathcal {R}}_1\) and \({\mathcal {R}}_2\), respectively. We show that \({\mathcal {R}} =_{\text {df}}\{(p,r) \mid \exists q \in Q.\; p {\mathcal {R}}_1 q \text { and } q {\mathcal {R}}_2 r\}\) is an alternating simulation, too, implying \(P \sqsubseteq _{\textit{IAM}}R\). Obviously, \(p_0 {\mathcal {R}} r_0\). Let \(p {\mathcal {R}} r\) due to q with \(p {\mathcal {R}}_1 q\) and \(q {\mathcal {R}}_2 r\), and distinguish Cases (i)–(iii) according to Definition 8. Because Cases (i) and (iii) are easier than Case (ii), we focus on the latter only. A transition \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\) implies the existence of a family \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) with \(\varphi \Rightarrow {\bigvee _i\,}\varphi _i\) and, for every \(\sigma \) with \(\sigma \models \varphi \), there is at least one transition \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) of the family such that \(\sigma \models \varphi _i\),  , \(\psi _i (\sigma )\Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}}_1 q'_i\).
, \(\psi _i (\sigma )\Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}}_1 q'_i\).
For every \(q_i\), we provide a state \(r_i\) for which  and \(q_i {\mathcal {R}}_2 r_i\). Consider the given sequence \({q{=}q_i^1\,{-\!\!\left( \varphi _i^1, \tau , \psi _i^1\right) \!\!\!\rightarrow _{\,}}q_i^2} \dots {q_i^n\,{-\!\!\left( \varphi _i^n, \tau , \psi _i^n\right) \!\!\!\rightarrow _{\,}}q_i^{n+1}}\) \(=q_i\) for some \(n \ge 0\). Starting from \(r_i^1 =_{\text {df}}r\), we iteratively find \(r_i^2, \ldots r_i^{n+1}\) by Definition 8 (iii) such that
and \(q_i {\mathcal {R}}_2 r_i\). Consider the given sequence \({q{=}q_i^1\,{-\!\!\left( \varphi _i^1, \tau , \psi _i^1\right) \!\!\!\rightarrow _{\,}}q_i^2} \dots {q_i^n\,{-\!\!\left( \varphi _i^n, \tau , \psi _i^n\right) \!\!\!\rightarrow _{\,}}q_i^{n+1}}\) \(=q_i\) for some \(n \ge 0\). Starting from \(r_i^1 =_{\text {df}}r\), we iteratively find \(r_i^2, \ldots r_i^{n+1}\) by Definition 8 (iii) such that  and \(q_i^{k+1} {\mathcal {R}}_2 r_i^{k+1}\) for \(1 \le k \le n\). We conclude that
and \(q_i^{k+1} {\mathcal {R}}_2 r_i^{k+1}\) for \(1 \le k \le n\). We conclude that  and \(q_i {\mathcal {R}}_2 r_i\) for \(r_i =_{\text {df}}r_i^{n+1}\).
and \(q_i {\mathcal {R}}_2 r_i\) for \(r_i =_{\text {df}}r_i^{n+1}\).
For every transition of the family \({q_i\,{-\!\!\left( \varphi _i , a!,\psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\), there exists a family of transitions \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) with \(\varphi _i \Rightarrow {\bigvee _j\,}\varphi _{i,j}\) and, for every \(\sigma \) with \(\sigma \models \varphi _i\), there is at least one transition \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) of the family such that \(\sigma \models \varphi _{i,j}\),  , \(\psi _{i,j} (\sigma ) \Rightarrow \psi _i (\sigma )\) and \(q'_i {\mathcal {R}}_2 r'_{i,j}\). Thus, we have a family \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) with \(\varphi \Rightarrow {\bigvee _i\,}\varphi _i \Rightarrow {\bigvee _i\,} {\bigvee _j\,} \varphi _{i,j}\) and, for every \(\sigma \) with \(\sigma \models \varphi \), there exists a transition \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) with \(\sigma \models \varphi _i\) and a transition \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) of the family of transitions of R such that \(\sigma \models \varphi _{i,j}\),
, \(\psi _{i,j} (\sigma ) \Rightarrow \psi _i (\sigma )\) and \(q'_i {\mathcal {R}}_2 r'_{i,j}\). Thus, we have a family \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) with \(\varphi \Rightarrow {\bigvee _i\,}\varphi _i \Rightarrow {\bigvee _i\,} {\bigvee _j\,} \varphi _{i,j}\) and, for every \(\sigma \) with \(\sigma \models \varphi \), there exists a transition \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) with \(\sigma \models \varphi _i\) and a transition \({r_{i,j}\,{-\!\!\left( \varphi _{i,j}, a!, \psi _{i,j}\right) \!\!\!\rightarrow _{\,}}r'_{i,j}}\) of the family of transitions of R such that \(\sigma \models \varphi _{i,j}\),  , \(\psi _{i,j} (\sigma ) \Rightarrow \psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} r'_{i,j}\). This family matches \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\). \(\square \)
, \(\psi _{i,j} (\sigma ) \Rightarrow \psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} r'_{i,j}\). This family matches \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\). \(\square \)
Note that the decidability of alternating simulation for finite-state IAMs depends on the logic chosen for expressing pre- and post-conditions. Above we picked first-order logic, for which implication is known to be undecidable. We leave the question as to which logic is most suitable for future work.
Related work We close this section by discussing the differences of our IAM setting to the most closely related work, namely the publications of Mouelhi et al. [27], Bauer et al. [2] (which extends [1]) and de Alfaro et al. [11]:
Mouelhi et al. The paper [27] has served as our original motivation for IAM. We adopted Mouelhi et al.’s symbolic handling of data and their intuition of outputs triggering operations, with the exception that they fix a pre- and post-condition for each action, while we do so for each action instance. This results in larger expressiveness by being able to consider different caller states, as does our addition of primed variables. However, the notion of communication error—due to a missing input or because the pre- or post-conditions of caller and callee do not fit—are the same in IAM as in [27]. The latter should be checked statically for each action a, and in case of a misfit, each state with an a-output directly gives rise to an error. Otherwise, only the presence of input a has to be checked. Additionally, the variation of alternating refinement studied in [27] does not consider transition families when matching and, thus, is unnecessarily limited. Mouelhi et al. also do not prove the precongruence result wrt. parallel composition, and leave important terms such as compatibility open to interpretation.
Moreover, ideas such as extending the set of variables when refining are neither explained nor intuitive; we cannot see how then a pre-condition in the specification could imply one in the refinement. As an aside, note that Mouelhi et al. base their work on an early version of IA [12] and not [13], which uses a variation of alternating simulation but appropriately abstracts from internal actions; in particular, output transitions are matched with weak transitions.
Bauer et al. In [2], shared memory is considered for an IA-inspired variation of modal transition systems [21], which increases expressiveness wrt. IA by allowing one to specify outputs that are compulsory and cannot be refined away. Parallel composition is, however, different from IA in that Bauer et al. adopt the pessimistic view of compatibility, as explained in Sect. 1: if a communication error is possible, then parallel composition is undefined. This makes technicalities much easier, e.g. when proving a precongruence result. But it also disregards many meaningful compositions. Therefore, we advocate the optimistic compatibility of IA, where the description of a parallel composition can also be seen as an operating guideline that tells the system environment how to use the components such that errors are avoided.
As in IAM, Bauer et al. use pre- and post-conditions for modelling operation calls and their effect on shared-memory data, and adopt the same notion of communication error. Moreover, the memory available to a component is subdivided in [2] into local variables and external variables. A local variable can be read and written by the component, and it can only be read by another component provided the variable is declared to be visible. An external variable is a local visible variable of another component. Additionally, each operation has a list of parameters with values set by the caller. In case of a synchronization, the operation and the shared variables are internalized but operations keep their names. Hence, such a variable only allows a one-way information flow between only two components; this is not what is usually called shared memory. Moreover, refinement does not abstract from internal computation: each transition, even if is invisible, has to be matched by a single step with the same operation, which is quite restrictive in practice.
A further study of Bauer et al. concerns the comparison of systems via inclusion of their sets of implementations. Such a refinement is often called thorough and shown to be implied by the refinement preorder adopted in [2]. Here, a state of an implementation consists of a control state and a data state for the local variables. This is not unlike our ground semantics (see Sect. 7), but the implementation is still open since the values of external variables are not fixed. Instead, such a valuation is part of each transition label.
In addition, there is no discussion in [2] that one transition can end in some concrete data state for the external variables, while the next transition might be performed from a different data state. Surprisingly, there is also no requirement that pre- and post-conditions must be satisfiable: if a data state \(\sigma \) satisfies some pre-condition but there is no \(\sigma '\) satisfying the new data state, then there might be no implementation for such a specification.
De Alfaro et al. Sociable interfaces [11] also employ automata, called modules, but in contrast to IA, de Alfaro et al. allow a module to use the same action both as input and as output, consider a multicast parallel operator, and do not abstract from internal actions for refinement. Each module has local and global variables, where local variables describe the module’s state. Further, for each action a, a module has a set W(a) of variables that it can modify, which interestingly might contain none of the local variables; in the latter case, a cannot change the state, which is a bit peculiar. In a parallel composition, W(a) always contains all local variables, and an output a modifies the values of W(a), while the input requires that these are acceptable. Hence, sociable interfaces are not meant to model operation calls.
Sociable interfaces are equipped with a semantics in terms of a two-player game, where one player controls input actions and the other controls output actions. Moreover, the module states are partitioned into the two sets iSet (called \(\varphi ^I\) in [11]) and oSet, with the aim of the input (output) player being that the game does not leave iSet (oSet). In the product of two modules, the good states are defined, in standard terms, as the non-error states. On the basis of the good states, the old iSets and the winning states for input, the iSet of the product is modified and this gives the parallel composition. However, the relation of this construction to standard pruning is not clarified in any way in [11], and this is not obvious to us.
To conclude, we point out that it might well be useful to add local variables to IAM in the future, similar to [2, 11]. But, for the time being, this would only obscure our issue, namely to study an IA-like setting where data is communicated by shared memory while operations are triggered by synchronizing actions. From the perspective of the present article, local variables are just syntactic sugar: if an interface has local variables x and y, we can choose states of the form \(s_{xy}\), where the index gives the current variable values. For this to work, it is important that our IAM theory treats infinite state systems.
4 Parallel composition
This section extends the parallel operator of IA, as outlined above, to IAM.Footnote 2 Two IAMs P and Q can be composed, if each action that is in the alphabets of both is an output action in one IAM and an input action in the other. When the overall system composed of P and Q is in data state \(\sigma \) and P is in control state p with \({p\,{-\!\!\left( \varphi _p , a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\) such that \(\sigma \models \varphi _p\), then P can perform action a!. If Q is in state q and \(a \in I_Q\), a transition \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) such that \(\sigma \models \varphi _q\) is required, i.e. Q has to perform the operation invoked: such a transition provides a new data state \({{\overline{\sigma }}}\) with \(\sigma ,{{\overline{\sigma }}}' \models \psi _q\). If each such \({{\overline{\sigma }}}\) meets the expectation of P, i.e. \(\sigma , {{\overline{\sigma }}}' \models \psi _p\) (and \(\psi _q (\sigma ) \Rightarrow \psi _p (\sigma )\) in Definition (P!?)), the data state changes from \(\sigma \) to \({{\overline{\sigma }}}\) and the components jointly move from \(\langle {p},{q}\rangle \) to \(\langle {p'},{q'}\rangle \). Otherwise, we have a communication mismatch, and \(\langle {p},{q}\rangle \) is an error state. This also holds if there is no transition \({q\,{-\!\!\left( \varphi _q,a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) with \(\sigma \models \varphi _q\). As for IA, all error states are pruned in the parallel composition of P and Q; the same applies for those states from which reaching an error cannot be prevented by any system environment.
Definition 10
(Parallel Product) IAMs \((P, I_P, O_P, \xrightarrow {}_P, p_0)\), \((Q, I_Q, O_Q,\) \(\xrightarrow {}_Q, q_0)\) are composable if \(O_P \cap O_Q = \emptyset = I_P \cap I_Q\). The product \(P \otimes Q\) of composable IAMs is defined as \((P \times Q, I, O, \xrightarrow {},\langle {p_0},{q_0}\rangle )\), where \(I =_{\text {df}}(I_P \cup I_Q) {\setminus } (A_P \cap A_Q)\), \(O =_{\text {df}}(O_P \cup O_Q) {\setminus } (A_P \cap A_Q)\), and the transition relation \(\xrightarrow {}\) is the least relation satisfying the following rules:

The asynchronous interleaving of autonomous transitions of P and Q is modelled by Rules (Pl) and (Pr). Rules (P!?) and (P?!) govern synchronization between P and Q. The pre-condition of the synchronized transition is the conjunction of the pre-conditions of the two involved transitions, as both must be fulfilled in the system’s current data state for P and Q to engage in their transitions. To model the invocation of an operation, the input-transition may alter the data state; accordingly, the synchronized transition is labelled with the post-condition \(\psi _q\). This requires that the post-condition of the output-transition is respected, leading to the implication \(\psi _q(\sigma ) \Rightarrow \psi _p(\sigma )\) as explained above. The text “\(\psi _q (\sigma ) \Rightarrow \psi _p (\sigma )\) for all \(\sigma \) with \(\sigma \models \varphi _p \wedge \varphi _q\)” could be replaced by \(\varphi _p \wedge \varphi _q \wedge \psi _q \Rightarrow \psi _p\).
Here, as already announced above, we deviate from the IA-approach—as do the authors of [9, 27]—in order to model operation calls properly as follows. A synchronization has two phases: it is triggered by the caller’s output in the first phase, which requires a matching input; in the second phase, the new data state is produced on the input side (i.e. by the callee), requiring the outputting component (i.e. the caller) to accept it. Violation of one of the requirements leads to an error.
Definition 11
(Parallel Composition) Given a parallel product \(P \otimes Q\) of IAMs P and Q, a state \(\langle {p},{q}\rangle \) is an error state if at least one of the following conditions is satisfied:

The set \(E \subseteq P \times Q\) of illegal states is the least set containing all error states and the states \(\langle {p},{q}\rangle \) satisfying \({\langle {p},{q}\rangle \,{-\!\!\left( \varphi , \alpha !,\psi \right) \!\!\!\rightarrow _{\,}}\langle {p'},{q'}\rangle }\) with \(\langle {p'},{q'}\rangle \in E\); this is also called Rule (Epb).
The parallel composition \(P{\parallel }Q\) is obtained by pruning the illegal states. We also refer to the set of illegal states of \(P \otimes Q\) as its E-set. The notions of state and component compatibility are as in IA.
Rule (E!?\(\varphi \)) describes a situation where p performs a! in some data state \(\sigma \) where q has no a?-transition enabled by \(\sigma \). If (E!?\(\psi \)) applies, q has such an enabled a?-transition and it is unique by data-determinism; but this transition can update the shared memory in a way that violates the assumption of the a!-transition.
Note that the above definition coincides with the corresponding one for IA, if we consider IAMs where only tt occurs as pre- and post-condition. The latter guarantees that the side conditions of the parallel product, i.e. \(\varphi _p \wedge \varphi _q\) sat and \(\psi _q (\sigma ) \Rightarrow \psi _p (\sigma )\) for all \(\sigma \) with \(\sigma \models \varphi _p \wedge \varphi _q\) are satisfied trivially. Rule (E!?\(\varphi \)) states that q has no a?-transition, giving rise to an error as for IA, and Rule (E!?\(\psi \)) is never applicable.
Figure 7 shows an example of a parallel product \(P \otimes Q\) and the effect of pruning. IAMs P, Q synchronize on a where, e.g. \({p_0\,{-\!\!\left( x=2, a!, x' \ne 2\right) \!\!\!\rightarrow _{\,}}p_1}\) can only synchronize with the upper transition \({q_0\,{-\!\!\left( x>0, a?, x'<0\right) \!\!\!\rightarrow _{\,}}q_1}\) of Q: data state \(\sigma \) with \(\sigma (x)=2\) satisfies both pre-conditions, and \(x' < 0 \Rightarrow x' \ne 2\) for the post-conditions. Note that the pre-condition \(x<0\) of the lower a?-transition from \(q_0\) contradicts \(x=2\). The synchronization results in transition \({\langle {p_0},{q_0}\rangle \,{-\!\!\left( x=2, \tau , x'<0\right) \!\!\!\rightarrow _{\,}}\langle {p_1},{q_1}\rangle }\) in \(P \otimes Q\). IAM P can perform its b?-transition independently. Transition \({p_3\,{-\!\!\left( x \ge 0, a!, x' = 0\right) \!\!\!\rightarrow _{\,}}p_4}\) cannot be matched by an a?-transition of \(q_0\) for \(x=0\), so (E!?\(\varphi \)) applies to \(\langle {p_3},{q_0}\rangle \). For \(x>0\), the upper transition from \(q_0\) has a fitting pre-condition, but the new value of x could be \(-1\); this contradicts \(x'=0\), so (E!?\(\psi \)) applies, too. Hence, \(\langle {p_3},{q_0}\rangle \) is an error state so that transitions \({\langle {p_0},{q_0}\rangle \,{-\!\!\left( \textit{tt}, b?, \textit{tt}\right) \!\!\!\rightarrow _{\,}}\langle {p_3},{q_0}\rangle }\) and \({\langle {p_3},{q_0}\rangle \,{-\!\!\left( x=2, \tau , x'<0\right) \!\!\!\rightarrow _{\,}}\langle {p_5},{q_1}\rangle }\) in \(P \otimes Q\) are pruned and not part of \(P {\parallel }Q\).
It is important to observe that, in contrast to IA, an error may arise in a parallel composition due to an output enabled in some data state, although a \(\tau \)-transition in which the output participates may still exist in the product due to some different data state. For example, an output a! might be offered when variable x has value 1 or 2, while the communication partner only has input a? if x has value 1. This results in an error due to (E!?\(\varphi \)), but the product still has a synchronizing \(\tau \)-transition with pre-condition \(x=1\).
Clearly, one expects parallel composition to be associative and commutative. While the latter is obvious, the former is not trivial in IA-like approaches. For our IAM-setting, the associativity proof is given in Sect. 6.
Proposition 12
(Associativity & Commutativity) If P, Q and R are pairwise composable IAMs, then \((P {\parallel }Q) {\parallel }R\) and \(P {\parallel }(R {\parallel }Q)\) are undefined or \((P {\parallel }Q) {\parallel }R\) and \(P {\parallel }(R {\parallel }Q)\) are isomorphic. Analogously, parallel composition is commutative.
Preorder \(\sqsubseteq _{\textit{IAM}}\) is compositional wrt. parallel composition, which follows directly from the properties of our embedding of IAM to IA in the next section (see Corollary 18). Before showing this embedding, we wish to technically justify the notion of pruning which realizes IAM’s optimistic notion of compatibility that it inherits from IA. We follow the approach adopted by us for Modal Interface Automata (MIA) in [5], which is based on so-called legal, or helpful, environments as first introduced for IA in [13].
Definition 13
(Legal Environment) A legal environment for IAMs P, Q is an IAM U such that
-
(i)
U is composable with \(P \otimes Q\);
-
(ii)
The reachable states of \((P \otimes Q) \otimes U\) contain no error states, where \(((r_1,r_2),r_3)\) is an error state, if some \((r_i,r_j)\) with \(i \ne j\) is an error state according to Definition 11.
Intuitively, U prevents \(P \otimes Q\) from reaching an error state, so that one can think of a legal environment as modelling a user with whom each desired system assembled from concurrently running IAMs is composed at the end. Technically, our definition of legal environment is more general than the one of de Alfaro and Henzinger in [13], because we only demand composability for the signature. In the IA setting, de Alfaro and Henzinger showed that two IAs are compatible if and only if there is a legal environment for them. As in MIA, we can give a better justification for pruning:
Proposition 14
(Pruning Justification) Let P, Q be IAMs.
-
(i)
P and Q are compatible if and only if there exists a legal environment for them.
-
(ii)
\((P \otimes Q) \otimes U = (P {\parallel }Q) \otimes U\), for any legal environment U for P and Q.
Hence, pruning only removes behaviour from \(P \otimes Q\) that is never reached in any legal environment, i.e. when the composition is used properly.
Proof
-
(i)
-
“\(\Rightarrow \)”: If P and Q are compatible, then \(P \otimes Q\) has no locally reachable error states. Composing it with an IAM U that has only one state, no transitions, no inputs, and all inputs of \(P\otimes Q\) as outputs, yields essentially only those states that are locally reachable from \((p_0,q_0)\). Thus, U is a legal environment for P and Q.
-
“\(\Leftarrow \)”: Assume towards a contradiction that P and Q are incompatible, i.e. \(P \otimes Q\) has a locally reachable error state (p, q). Then, for any IAM U, the IAM \((P\otimes Q)\otimes U\) either has a locally reachable error state ((p, q), u), or there is a first output transition on the path to (p, q) that U prevents by not providing the corresponding input transition. This also results in a locally reachable error state in \((P\otimes Q)\otimes U\). Either way, U is no legal environment.
-
-
(ii)
The claim can only fail if there is a state \((p,q) \in P \otimes Q\) that is illegal due to error \((p',q')\) but exists in \((P \otimes Q) \otimes U\) in the form of some ((p, q), u). As just argued, the path from (p, q) to \((p',q')\) still exists in \((P \otimes Q) \otimes U\), or is prevented by U at some stage leading to another error state. Either way, U is not a legal environment.
\(\square \)
The correctness of pruning has also been investigated in the context of a linear-time semantics for IA in [6], where a problem with the original version of IA [12] in the presence of input-nondeterminism is pointed out and fixed.
5 Example
This section first illustrates the handling of data in IAM using a variation of the vending machine example of Sect. 2. It then briefly introduces an initial, prototypic toolset-based around our IAM theory, which supports modelling and simulating IAMs, debugging communication errors, as well as checking and reasoning about model refinements.
5.1 The vending machine example, expanded with shared memory
The variation of our vending machine example (see Figs. 8, 9) considers, in particular, the payment operation coin and the change giving operation relCh, the latter of which is supplemented with action done in case no change is given. Variable \(\textit{th}\) stores whether customer C is thirsty for coffee (value C) or tea (value T); hence, this information is no longer encoded in action atVM. Variable v stores the payment that the customer has made so far. Upon receiving a selection selC or selT, machine M sets this value to 0. Variable v is updated in operation coin; for coffee (tea), the machine never lowers (always raises) the value, while the customer always expects an increase. Variable c holds the value of the inserted coin, which can be 50¢, 1€ or 2€. Note that, implicitly, c is set by the customer when selecting a coin. The drink is dispensed (operation relC) when v reaches the resp. price of 2€ for coffee and 1€ for tea. Finally, the change computed in \(\textit{ch}\) is returned in operation relCh.
The product \(M \otimes C\) is shown in Fig. 10. We discuss some of the transitions. In the \(\tau \)-transition from \(\langle {m_0},{c_4}\rangle \), actions selT! and selT? synchronize and M sets v to 0, while C does not care about the value. The \(\tau \)-transition from \(\langle {m_4},{c_6}\rangle \) originating from the synchronization on done is triggered by M if \(v=1\); customer C would also accept a lesser value. The pre-condition of the \(\tau \)-loop at \(\langle {m_3},{c_5}\rangle \) is the conjunction of the pre-conditions of the underlying coin-loops. But coin! is also triggered when the customer has chosen a 50¢ coin for the cheaper drink. Because the machine does not accept such a coin, \(\langle {m_3},{c_5}\rangle \) is an error state according to Rule (E?!\(\varphi \)). The coin-transitions at \(m_1\) and \(c_2\) do not give rise to a \(\tau \)-loop because M might keep the value of v, violating the assumption \(v' > v\) of C. Also \(\langle {m_1},{c_2}\rangle \) is an error state since \(v' \ge v\) does not imply \(v'>v\). Consequently, \(M {\parallel }C\) just consists of \(\langle {m_0},{c_0}\rangle \). While M and C are formally compatible, this is only the case if the environment ensures that the customer is never thirsty in the vicinity of the machine.
To improve the situation, we IAM-refine M and C to \(M'\) and \(C'\), respectively. Refinement \(C'\) (not shown) is obtained from C by deleting the 0.5-option in the offending pre-condition. Analogously to the IA-example, the customer has learned that 50¢ coins are never accepted. On the machine side, refinement \(M'\) (see Fig. 11) computes the correct payment \(v'=v+c\) instead of \(v'>v\) at \(m_3\). A similar change is made at \(m_1\), but here we have a new feature, showing the splitting of the input selC? at \(m_0\). The refined machine \(M'\) is configurable to give a discount if variable disc is true. In this case, payment v is incremented by one additional Euro for each coin, which actually happens exactly once. Observe that data-determinism is maintained since \(\textit{disc} \wedge \lnot \textit{disc}\) unsat, while Definition 8(i) is satisfied because \(\textit{disc} \vee \lnot \textit{disc}\) implies tt. With these changes, we obtain \(M' \otimes C' = M' {\parallel }C'\), as displayed in Fig. 12. Because \(M' \sqsubseteq _{\textit{IAM}}M\) and \(C' \sqsubseteq _{\textit{IAM}}C\), we also have \(M' {\parallel }C' \sqsubseteq _{\textit{IAM}}M {\parallel }C\) and, indeed, \(\langle {m_0},{c_0}\rangle \) only has additional inputs in \(M' {\parallel }C'\). Note that the behaviour after a new input can be arbitrary, because inputs of the refinement do not have to be matched according to Definition 8.
5.2 A prototypic IAM toolset
In order to demonstrate that tool support for the IAM interface theory is conceivable, we have developed an initial, prototypical toolset, to which we refer as IAM Toolset. The toolset is developed using various open-source technologies described below, is itself open source and available for download and further development via GitHub [28] and comprises approx. 12,000 lines of code. It runs on Windows, Linux and macOS with installed JDK11. We have used the toolset to check small examples that we had developed by pencil and paper, such as the vending machine example above. Note that we do neither claim that the IAM Toolset is fit for practical use by software engineers as is, nor that it scales to real-world examples of concurrent systems.
Textual language To specify interfaces, we have developed a textual syntax for IAM, have used the popular Xtext framework (https://www.eclipse.org/Xtext/) to realize this domain-specific modelling language, and written an extension for Microsoft’s Visual Studio Code (VS Code) editor (https://code.visualstudio.com). This has led to a state-of-the-art IDE for IAM, with a modern editor that supports features such as syntax highlighting and code completion, and a compiler—actually, more of an interpreter—for transforming the textual language into IAM automata.
The textual language allows one to specify the underlying universe of global actions (keyword actions), the shared global variables (keyword var) that are typed using built-in primitive types such as int and bool or custom-defined enumeration types (keyword type), and the templates of interface processes (keyword proc). It also has an initialization section (keyword init), where processes can be instantiated from templates (keyword sys), composed in parallel (keywords product and composition for the parallel product and composition, respectively) and checked for refinement (keyword refinement). In fact, there is also an explicit pruning operator (keyword prune) such that composition is simply product followed by prune. While Xtext assist us in realizing our language interpreter’s front-end (approx. 1100 lines of code), the backend and, thus, all IAM operators are implemented solely in the Kotlin programming language (approx. 9400 lines of code). The various commands for instantiation, composition and refinement can also be executed directly from VS Code (approx. 1350 lines of code in TypeScript) or the command line. For checking static semantics constraints, we frequently call the Z3 SMT solver (https://github.com/Z3Prover/z3), which we also use in the context of the product operator and IAM refinement for checking logic implications that involve arithmetic expressions over shared variables.
Figure 13 shows, in the rightmost two columns, snippets of the machine and customer specifications of our vending machine example of the previous section, now cast in the syntax of the IAM Toolset. The process template Machine first defines its input and output alphabet and then defines interface behaviour via a guarded-command language enriched with control structures such as while loops (with optional breaks), case statements, sequential composition (via newlines or semicolons), or goto (jump to a label). Guards are on the left of symbol -> and constitute the pre-condition of the first action following symbol -> . Post-conditions immediately follow an action and are labelled with keyword assume for post-conditions of output actions and guarantee for post-conditions of input actions; the rationale is that a post-condition of an output action a! abstractly specifies how the called operation a may modify the global variables, while a post-condition of an input a? abstractly specifies how the global variables are modified when operation a is executed. Missing pre- and post-conditions around an action are simply assumed to be true.
Debugging The left column in Fig. 13 reveals (see the section labelled Call Stack) that this screenshot has been taken after instantiating machine and customer and computing their product, which revealed a communication error between the interfaces. This error relates to the highlighted lines 17 and 54, i.e. on the synchronization on action coin. The detailed error message in the red box explains that the assumption is not met by the guarantee, and the section labelled Product in the left column provides information via which series of actions the error state is reached from the products initial state. As an aside, we wish to note here that the IAM toolset has standard debugging features, including the setting of breakpoints, that allow engineers the interactive tracing through interface processes, parallel products and parallel compositions.
Refinement checking IAM’s notion of refinement, alternating simulation, has a convenient characterization in terms of a two-player game [13], which we exploit so that users can interactively explore in the IAM Toolset whether two processes are related under refinement. A snapshot of such an exploration is shown in Fig. 14 where, in a first move of the game, the initial selC? input action of the specification side (right-hand side), i.e. of Machine, was chosen. The toolset now highlights the available selC? families on the implementation side (left-hand side), i.e. of MachinePrimed; in this case, there is a single family consisting of two selC? transitions, one with pre-condition disc and one with its negation. In general, our tool displays every family (i) consisting of members that have pre- and post-conditions that match the requirements of alternating simulation (cf. Definition 8) and (ii) not including a member already covered by others. The engineer now, in the matching move, picks the only available family and continues the game by investigating the two transitions of the family.
The IAM Toolset also prototypes an automated refinement checker which reduces the refinement problem between two IAMs to solving a Boolean equation system; note that all IAMs specified in the toolset’s textual language are finite-state. The reduction is rather straightforward and follows the lines proposed by Mateescu and Oudot in [24] who proposed such a reduction for bisimulation [26]. We then employ the mCRL2 toolset [7] (https://www.mcrl2.org) for solving the resulting Boolean equation system. In case a refinement does not hold, the IAM Toolset synthesizes an attacking strategy so that an engineer might play a game against the computer to gain understanding as to why refinement between the given two processes is violated.
6 Embedding IAM into IA
This section shows that, while IAM adds shared memory to the IA theory, it does not alter IA’s concept of component compatibility and refinement. IAM is rather an intuitive and possibly finite abstraction for reasoning about possibly infinite data, which maintains the simplicity that has made IA popular. In the following, we develop a behaviour-preserving translation from IAM to IA such that our parallel composition and refinement match exactly those of IA.
While our formal semantics of IAM is based on alternating simulation, we wish to foster intuition here by considering an IAM P to have runs of the form \((\sigma _0,p_0) \xrightarrow {\alpha _0} ({{\overline{\sigma }}}_0,p_1)(\sigma _1,p_1) \xrightarrow {\alpha _1} ({{\overline{\sigma }}}_1,p_2) \,\ldots \, (\sigma _{n-1},p_{n-1}) \xrightarrow {\alpha _{n-1}} ({{\overline{\sigma }}}_{n-1},p_n)\), for transitions \({p_i\,{-\!\!\left( \varphi _i, \alpha _i, \psi _i\right) \!\!\!\rightarrow _{\,}}p_{i+1}}\) with \(\sigma _i \models \varphi _i\) and \(\sigma _i,{{\overline{\sigma }}}'_i \models \psi _i\), for all \(0 \le i < n\). Note that \({{\overline{\sigma }}}_i\) and \(\sigma _{i+1}\) might be different, because interface theories consider open systems and P’s environment can always interleave and arbitrarily modify the data state; we study and define closed systems in Sect. 7.Footnote 3
For our translation, one might consider to integrate data states into actions, so that the above run gives rise to \(\alpha _0 (\sigma _0, {{\overline{\sigma }}}'_0) \,\ldots \, \alpha _{n-1} (\sigma _{n-1},{{\overline{\sigma }}}'_{n-1})\) as a sequence of actions, i.e. each \(\alpha _i (\sigma _i, {{\overline{\sigma }}}'_i)\) is taken to be an (atomic) action. This idea is similar to, e.g. the translation of full CCS into basic CCS in [26].
However, this translation does not work in general. Consider IAMs P, Q of Fig. 15, where \(V = \{x\}\), \(V' = \{x'\}\) and \(\mathbb {D} = \{1,2\}\). By the above idea, P would have transition \(p_0 \xrightarrow {a(x=1,x'=2)!} p_1\) in its corresponding IA, as shown in Fig. 16. The best match \(q_0 \xrightarrow {a(x=1,x'=1)?} q_1\) in the IA for Q is not good enough; thus, \(\langle {p_0},{q_0}\rangle \in E\), i.e. the IAs of P and Q are incompatible. But there is no error according to Rule (E!?\(\psi \)) in the operational reality: Q decides about the new data state when answering the request of P. In other words, P would take the transition \(p_0 \xrightarrow {a(x=1,x'=1)!} p_1\).
As a remedy, we translate an output-transition \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\) of IAM P to multiple IA transitions \(\{p \xrightarrow {a(\sigma , M)!} p' \mid \sigma \models \varphi , \; \llbracket {\psi (\sigma )}\rrbracket \subseteq M \subseteq \llbracket {V'}\rrbracket \}\), and analogously for input-transitions. Pre- and post-conditions of \(\tau \)-transitions are simply suppressed. The reasons for this choice are as follows. The first idea would be to use \(p \xrightarrow {a(\sigma , M)!} p'\) with \(M = \llbracket {\psi (\sigma )}\rrbracket \), because it is really the set of acceptable new data states that counts. To get a matching input-transition, the same translation should be applied there. But such an input-transition could have a smaller set according to its post-condition as in the example. To get the same input action as the output, we allow all \(M \supseteq \llbracket {\psi (\sigma )}\rrbracket \) for inputs; such an M can be understood as the guarantee that the new data state will be in M. This way, the IAs do not produce false errors, and the real errors still occur in the translation if the output with \(M = \llbracket {\psi (\sigma )}\rrbracket \) cannot be matched.
Another issue is that, if we refine some \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\), we could weaken the assumption, i.e. the corresponding \(a(\sigma , M)!\) would be refined by \(a(\sigma , M')!\) with \(M \subsetneq M'\). To make this possible, we also include supersets on the output side. This does not disturb the correct handling of errors: if there is a matching input for \(a(\sigma , M)!\), there is also one for \(a(\sigma , M')!\). Observe that taking supersets for inputs actually also allows for correct refinements, because we have the same entailment \(\psi _i (\sigma )\Rightarrow \psi (\sigma )\) in Definition 8(i) and (ii).
To reflect on this translation scheme for our example IAMs P, Q, consider their translations \(\textit{IA}({P})\), \(\textit{IA}({Q})\) in Fig. 17, where \(\sigma _i\) stands for \(\sigma (x) = i\). Due to pre-condition tt, the transition of P is split into two transitions in \(\textit{IA}({P})\), one each for the possible values of x in the given domain. Because \(\psi (\sigma _1) = \psi (\sigma _2) = (x' \in \{1,2\})\), the only choice for M is \(\{\sigma '_1, \sigma '_2\}\). Similarly, the translation scheme splits Q’s transition into two; each of these is again split into two transitions, because \(\psi (\sigma _1) = \psi (\sigma _2) = (x'=1)\) allows for choosing \(M = \{\sigma '_1\}\) and also \(M = \{\sigma '_1, \sigma '_2\}\). This way, the resulting \(\textit{IA}({P})\) and \(\textit{IA}({Q})\) do not produce false errors on action \(a(\sigma _1, \{\sigma '_1, \sigma '_2\})\) when being composed. In other words, our translation ensures that the weaker post-condition of P is taken care of by allowing the according weakening of Q’s post-condition, while maintaining the semantics of Q by also including transitions for Q’s original post-condition.
In such a scenario, more generally speaking, \(a(\sigma ,M)!\) is present for \(\sigma \) satisfying the pre-conditions of both P and Q whenever \(\llbracket {\psi _P(\sigma )}\rrbracket \subseteq M\), and \(a(\sigma ,M')?\) whenever \(\llbracket {\psi _Q(\sigma )}\rrbracket \subseteq M'\), where \(\psi _P\) and \(\psi _Q\) refer to the according post-conditions in P and Q, resp. If no error arises for \(\sigma \), i.e. if \(\llbracket {\psi _Q(\sigma )}\rrbracket \subseteq \llbracket {\psi _P(\sigma )}\rrbracket \), each \(a(\sigma ,M)!\) is matched by \(a(\sigma ,M)?\). Otherwise, \(a(\sigma ,\llbracket {\psi _P(\sigma )}\rrbracket )!\) does not have a match and the error arises in the translation as well.
We now formalize our translation and then work towards proving the correctness of the induced embedding of IAM into IA.
Definition 15
(Embedding IAM into IA) IAM P is translated to the IA \(\textit{IA}({P}) =_{\text {df}}(P, I', O', \xrightarrow {}', p_0)\), where \(I' =_{\text {df}}\{a(\sigma ,M) \mid a \in I,\,\sigma \in \llbracket {V}\rrbracket \text { and}\) \(M \subseteq \llbracket {V'}\rrbracket \}\), \(O' =_{\text {df}}\{a(\sigma ,M) \mid a \in O,\, \sigma \in \llbracket {V}\rrbracket \text { and } M \subseteq \llbracket {V'}\rrbracket \}\), and \(\xrightarrow {}'\) is obtained from \(\xrightarrow {}\) of P according to the following rules:
-
\({p\,{-\!\!\left( \varphi , a, \psi \right) \!\!\!\rightarrow _{\,}}p'}\) implies \(p \xrightarrow {a(\sigma ,M)}\!'\, p'\), for \(\sigma \models \varphi \) and \(M \supseteq \llbracket {\psi (\sigma )}\rrbracket \);Footnote 4
-
\({p\,{-\!\!\left( \varphi , \tau , \psi \right) \!\!\!\rightarrow _{\,}}p'}\) implies \(p \xrightarrow {\tau }\!'\, p'\).
This embedding satisfies two important properties: it is a homomorphism for parallel composition, as indicated in Figs. 15 and 17, and monotonic wrt. alternating refinement.
Theorem 16
(Homomorphism) IAMs P, Q are composable (compatible, resp.) iff \(\textit{IA}({P})\) and \(\textit{IA}({Q})\) are. Then, \(\textit{IA}({P {\parallel }Q})\) and \(\textit{IA}({P}) {\parallel }\textit{IA}({Q})\) are identical.
Proof
Composability only depends on the signature, and inputs (outputs, resp.) of an IAM R give rise to inputs (outputs, resp.) of \(\textit{IA}({R})\), so the first claim follows. Obviously, \(P \otimes Q\) and \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\) have the same state sets. The initial states also coincide. We proceed as follows:
-
1.
We show that \(P \otimes Q\) has the same error states as \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\):
-
\(\langle {p},{q}\rangle \) is an error state in \(P \otimes Q\) due to Definition 11 (\(E!?\varphi \)) or (\(E?!\varphi \)). W.l.o.g., P has a transition \({p\,{-\!\!\left( \varphi _p, a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\), and some \(\sigma \) with \(\sigma \models \varphi _p\) satisfies \(\sigma \not \models \varphi _q\) for all transitions \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\). The p-transition gives rise to some \(p \xrightarrow {a(\sigma ,M)!} p'\) in \(\textit{IA}({P})\) but, due to the condition \(\sigma \not \models \varphi _q\), state q has no input-transition with any \(a(\sigma , X)?\). As a result, \(\langle {p},{q}\rangle \) is also an error state in \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\).
-
\(\langle {p},{q}\rangle \) is an error state in \(P \otimes Q\) due to Definition 11 (\(E!?\psi \)) or (\(E?!\psi \)). W.l.o.g., P has a transition \({p\,{-\!\!\left( \varphi _p, a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\) and, for some transition \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) and data state \(\sigma \), \(\sigma \models \varphi _p \wedge \varphi _q\) and \(\psi _q (\sigma ) \not \Rightarrow \psi _p (\sigma )\). The latter means \(\llbracket {\psi _q (\sigma )}\rrbracket \not \subseteq \llbracket {\psi _p (\sigma )}\rrbracket \). Now, \(\textit{IA}({P})\) contains the transition \(p \xrightarrow {a(\sigma , \llbracket {\psi _p (\sigma )}\rrbracket )!} p'\). Due to data-determinism, the \(a(\sigma ,M)?\)-transitions of q result from transition \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\), i.e. \(M \supseteq \llbracket {\psi _q (\sigma )}\rrbracket \) and M cannot be \(\llbracket {\psi _p (\sigma )}\rrbracket \). Again, \(\langle {p},{q}\rangle \) is also an error in \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\).
-
\(\langle {p},{q}\rangle \) is an error state in \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\). W.l.o.g., \(\textit{IA}({P})\) has a transition \(p \xrightarrow {a(\sigma ,M)!} p'\) that \(\textit{IA}({Q})\) cannot match in state q. Thus, P has a transition \({p\,{-\!\!\left( \varphi _p, a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\) with \(\sigma \models \varphi _p\) and \(\llbracket {\psi _p (\sigma )}\rrbracket \subseteq M\). By the definition of our translation, p can also perform \(a(\sigma ,\llbracket {\psi _p (\sigma )}\rrbracket )\), while q cannot:
-
If \(\textit{IA}({Q})\) does not contain any \(a(\sigma ,X)?\)-transition at q, then there is no \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) with \(\sigma \models \varphi _q\) in Q. Thus, \(\langle {p},{q}\rangle \) is an error in \(P \otimes Q\) due to Definition 11 (\(E!?\varphi \)).
-
Otherwise, there exists only one transition \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) with \(\sigma \models \varphi _q\) in Q, due to data-determinism. Because q does not have the action \(a(\sigma ,\llbracket {\psi _p (\sigma )}\rrbracket )\), we get \(\llbracket {\psi _p (\sigma )}\rrbracket \not \supseteq \llbracket {\psi _q (\sigma )}\rrbracket \). Again, \(\langle {p},{q}\rangle \) is an error in \(P \otimes Q\) due to Definition 11 (\(E!?\psi \)).
-
-
-
2.
We show that \(\textit{IA}({P \otimes Q})\) is isomorphic to \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\), except for outgoing transitions of error states, and consider synchronized transitions first:
-
If \({p\,{-\!\!\left( \varphi _p, a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\) and \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\), \(\varphi _p \wedge \varphi _q\) sat and \(\psi _q (\sigma ) \Rightarrow \psi _p (\sigma )\) holds for all \(\sigma \) with \(\sigma \models \varphi _p \wedge \varphi _q\), then the transitions synchronize to \({\langle {p},{q}\rangle \,{-\!\!\left( \varphi _p \wedge \varphi _q, \tau ,\psi _q\right) \!\!\!\rightarrow _{\,}}\langle {p'},{q'}\rangle }\) in \(P \otimes Q\). We get \(\langle {p},{q}\rangle \xrightarrow {\tau } \langle {p'},{q'}\rangle \) on the left.
Choose \(\sigma \) with \(\sigma \models \varphi _p \wedge \varphi _q\) and \(M \supseteq \llbracket {\psi _p (\sigma )}\rrbracket \supseteq \llbracket {\psi _q (\sigma )}\rrbracket \). Then, we have \(p \xrightarrow {a(\sigma ,M)!} p'\) and \(q \xrightarrow {a(\sigma ,M)?} q'\), resulting in \(\langle {p},{q}\rangle \xrightarrow {\tau }\langle {p'},{q'}\rangle \) on the right. Note that all transitions \(p\xrightarrow {a(\sigma , X)!} p'\) are dealt with in this way, but possibly not all transitions \(q \xrightarrow {a(\sigma , X)?} q'\) stemming from the q-transition in Q; these are inputs and do not arise on the right.
-
If \(\langle {p},{q}\rangle \xrightarrow {\tau }\langle {p'},{q'}\rangle \) arises due to \(p\xrightarrow {a(\sigma , M)!} p'\) and \(q \xrightarrow {a(\sigma , M)?} q'\) on the right, then there are \({p\,{-\!\!\left( \varphi _p, a!, \psi _p\right) \!\!\!\rightarrow _{\,}}p'}\) and \({q\,{-\!\!\left( \varphi _q, a?, \psi _q\right) \!\!\!\rightarrow _{\,}}q'}\) with \(\sigma \models \varphi _p \wedge \varphi _q\). In case \(\psi _q (\sigma ) \not \Rightarrow \psi _p (\sigma )\), state \(\langle {p},{q}\rangle \) is an error state in \(P \otimes Q\). Otherwise, \({\langle {p},{q}\rangle \,{-\!\!\left( \varphi _p \wedge \varphi _q, \tau , \psi _q\right) \!\!\!\rightarrow _{\,}}\langle {p'},{q'}\rangle }\) in \(P \otimes Q\), and we get \(\langle {p},{q}\rangle \xrightarrow {\tau }\langle {p'},{q'}\rangle \) on the left, for all \(\sigma \) such that \(\sigma \models \varphi _p \wedge \varphi _q\).
Unsynchronized transitions of P are “copied” into \(P \otimes Q\) and replaced by a bundle of transitions on the left, and replaced by the same bundle that is copied into the product on the right. The same holds for unsynchronized transitions of Q.
-
-
3.
Due to Item (1), \(P \otimes Q\) and \(\textit{IA}({P}) \,{{\overline{\otimes }}}\,\textit{IA}({Q})\) have the same error states. Each illegal state has a path of local actions reaching an error state at the end only. Hence, we can conclude from Item (2) that both systems have the same illegal states, and \(\textit{IA}({P}) {\parallel }\textit{IA}({Q})\) is defined iff \(P {\parallel }Q\) is. Applying Item (2) again, we get that \(\textit{IA}({P {\parallel }Q})\) is isomorphic to \(\textit{IA}({P}) {\parallel }\textit{IA}({Q})\).
\(\square \)
Theorem 17
(Monotonicity) \(P\sqsubseteq _{\textit{IAM}}Q\) iff \(\textit{IA}({P})\sqsubseteq _{\textit{IA}}\textit{IA}({Q})\), for all IAMs P, Q.
Proof
-
“\(\Rightarrow \)”: Assume \(P \sqsubseteq _{\textit{IAM}}Q\) due to the alternating simulation \({\mathcal {R}}\). We show that \({\mathcal {R}}\) is also an alternating simulation for \(\textit{IA}({P})\) and \(\textit{IA}({Q})\). First, \(p_0 {\mathcal {R}} q_0\) holds for the IAMs and, thus, also for the IAs. Let \(p{\mathcal {R}}q\) and consider the following cases:
-
\(q \xrightarrow {a({{\overline{\sigma }}}, M)?} q'\) due to \({q\,{-\!\!\left( \varphi , a?, \psi \right) \!\!\!\rightarrow _{\,}}q'}\). Then, there is a family of transitions \({p\,{-\!\!\left( \varphi _i, a?, \psi _i\right) \!\!\!\rightarrow _{\,}}p_i}\) with \(\varphi \Rightarrow {\bigvee _i\,} \varphi _i\) such that, for all i and \(\sigma \) with \(\sigma \models \varphi \wedge \varphi _i\), we have \(\psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p_i {\mathcal {R}} q'\). Further, \({{\overline{\sigma }}}\models \varphi \) and \(\llbracket {\psi ({{\overline{\sigma }}})}\rrbracket \subseteq M\) due to our translation. Hence, \({{\overline{\sigma }}} \models {\bigvee _i\,}\varphi _i\) and there is a unique i with \({{\overline{\sigma }}} \models \varphi _i\). Because \(\llbracket {\psi _i ({{\overline{\sigma }}})}\rrbracket \subseteq \llbracket {\psi ({{\overline{\sigma }}})}\rrbracket \subseteq M\), we get \(p \xrightarrow {a({{\overline{\sigma }}}, M)?} p_i\) in \(\textit{IA}({P})\) and \(p_i {\mathcal {R}} q'\).
-
\(p \xrightarrow {a(\sigma ,M)!} p'\) due to \({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\), \(\sigma \models \varphi \) and \(\llbracket {\psi (\sigma )}\rrbracket \subseteq M\). Then, there is a suitable family of \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) with \(\varphi \Rightarrow {\bigvee _i\,}\varphi _i\), and at least one of these transitions \({q_i\,{-\!\!\left( \varphi _i, a!, \psi _i\right) \!\!\!\rightarrow _{\,}}q'_i}\) satisfies \(\sigma \models \varphi _i\),
 , \(\psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} q'_i\). Now,
, \(\psi _i (\sigma ) \Rightarrow \psi (\sigma )\) and \(p' {\mathcal {R}} q'_i\). Now,  also in \(\textit{IA}({Q})\), \(q_i \xrightarrow {a(\sigma , M)!} q'_i\) due to \(\llbracket {\psi _i (\sigma )}\rrbracket \subseteq \llbracket {\psi (\sigma )}\rrbracket \subseteq M\), and \(p' {\mathcal {R}} q'_i\).
also in \(\textit{IA}({Q})\), \(q_i \xrightarrow {a(\sigma , M)!} q'_i\) due to \(\llbracket {\psi _i (\sigma )}\rrbracket \subseteq \llbracket {\psi (\sigma )}\rrbracket \subseteq M\), and \(p' {\mathcal {R}} q'_i\). -
\(p \xrightarrow {\tau } p'\). This obviously leads to
 in \(\textit{IA}({Q})\), for some \(q'\) with \(p' {\mathcal {R}} q'\).
in \(\textit{IA}({Q})\), for some \(q'\) with \(p' {\mathcal {R}} q'\).
-
-
“\(\Leftarrow \)”: Assume \(\textit{IA}({P}) \sqsubseteq _{\textit{IA}}\textit{IA}({Q})\) due to the alternating simulation \({\mathcal {R}}\). We claim that \({\mathcal {R}}\) is also an alternating simulation for P and Q. Note that \(p_0 {\mathcal {R}} q_0\) holds for the IAs and, thus, also for the IAMs. Let \(p{\mathcal {R}} q\) and distinguish the following cases:
-
\({q\,{-\!\!\left( \varphi , a?, \psi \right) \!\!\!\rightarrow _{\,}}q'}\). Consider some \(\sigma \) with \(\sigma \models \varphi \). So, \(q \xrightarrow {a(\sigma , \llbracket {\psi (\sigma )}\rrbracket )?} q'\) and there is some \(p \xrightarrow {a(\sigma , \llbracket {\psi (\sigma )}\rrbracket )?} p'_{\sigma }\) with \(p'_{\sigma } {\mathcal {R}} q'\). The latter is due to a unique transition \({p\,{-\!\!\left( \varphi _{\sigma }, a?, \psi _{\sigma }\right) \!\!\!\rightarrow _{\,}}p'_{\sigma }}\) with \(\sigma \models \varphi _{\sigma }\), which also satisfies \(\llbracket {\psi _{\sigma } (\sigma )}\rrbracket \subseteq \llbracket {\psi (\sigma )}\rrbracket \).Footnote 5 The family of all these transitions satisfies \(\varphi \Rightarrow {\bigvee _{\sigma }\,} \varphi _{\sigma }\) and, for all \(\sigma \) with \(\sigma \models \varphi \), we have \(\sigma \models \varphi \wedge \varphi _{\sigma }\) and \(\psi _{\sigma } (\sigma ) \Rightarrow \psi (\sigma )\).
-
\({p\,{-\!\!\left( \varphi , a!, \psi \right) \!\!\!\rightarrow _{\,}}p'}\). Consider some \(\sigma \) with \(\sigma \models \varphi \). So, \(p \xrightarrow {a(\sigma ,\llbracket {\psi (\sigma )}\rrbracket )!} p'\) and there is some \(q_{\sigma }\) with
 and \(q_{\sigma }\xrightarrow {a(\sigma ,\llbracket {\psi (\sigma )}\rrbracket )!} q'_{\sigma }\) such that \(p' {\mathcal {R}} q'_{\sigma }\). The latter is due to some \({q_{\sigma }\,{-\!\!\left( \varphi _{\sigma }, a!, \psi _{\sigma }\right) \!\!\!\rightarrow _{\,}}q'_{\sigma }}\) with \(\sigma \models \varphi _{\sigma }\) and \(\llbracket {\psi _{\sigma } (\sigma )}\rrbracket \subseteq \llbracket {\psi (\sigma )}\rrbracket \). The family of all these transitions in Q satisfies \(\varphi \Rightarrow {\bigvee _{\sigma }\,} \varphi _{\sigma }\) and, for each \(\sigma \) with \(\sigma \models \varphi \), the resp. transition satisfies \(\sigma \models \varphi _{\sigma }\),
and \(q_{\sigma }\xrightarrow {a(\sigma ,\llbracket {\psi (\sigma )}\rrbracket )!} q'_{\sigma }\) such that \(p' {\mathcal {R}} q'_{\sigma }\). The latter is due to some \({q_{\sigma }\,{-\!\!\left( \varphi _{\sigma }, a!, \psi _{\sigma }\right) \!\!\!\rightarrow _{\,}}q'_{\sigma }}\) with \(\sigma \models \varphi _{\sigma }\) and \(\llbracket {\psi _{\sigma } (\sigma )}\rrbracket \subseteq \llbracket {\psi (\sigma )}\rrbracket \). The family of all these transitions in Q satisfies \(\varphi \Rightarrow {\bigvee _{\sigma }\,} \varphi _{\sigma }\) and, for each \(\sigma \) with \(\sigma \models \varphi \), the resp. transition satisfies \(\sigma \models \varphi _{\sigma }\),  and \(\psi _{\sigma }(\sigma ) \Rightarrow \psi (\sigma )\).
and \(\psi _{\sigma }(\sigma ) \Rightarrow \psi (\sigma )\). -
\({p\,{-\!\!\left( \varphi , \tau , \psi \right) \!\!\!\rightarrow _{\,}}p'}\). We get the transition \(p\xrightarrow {\tau } p'\). Due to \({\mathcal {R}}\), we obtain some \(q'\) with
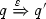 in \(\textit{IA}({Q})\) and \(p' {\mathcal {R}} q'\). Hence,
in \(\textit{IA}({Q})\) and \(p' {\mathcal {R}} q'\). Hence,  also holds in Q.
also holds in Q.
-
\(\square \)
Using the last two theorems and Proposition 4, we can now prove the associativity of parallel composition as stated in Proposition 12:
Proof
\(\textit{IA}({(P {\parallel }Q) {\parallel }R}) = (\textit{IA}({P}) {\parallel }\textit{IA}({Q})) {\parallel }\textit{IA}({R})\) is IAM-equivalent to \(\textit{IA}({P}) {\parallel }(\textit{IA}({Q}) {\parallel }\textit{IA}({R})) = \textit{IA}({P {\parallel }(Q {\parallel }R)})\) \(\square \)
Example showing \(P \ne P'\) but \(\textit{IA}({P}) = \textit{IA}({P'})\), for IAM P of Fig. 15
The embedding of IAM into IA is not injective due to at least two possible reasons, although these are somewhat pathological. The first reason is that pre- and post-conditions of \(\tau \)-transitions in an IAM are omitted in the translation. Hence, \(\textit{IA}({P})\) cannot distinguish between \(\tau \)-transitions with the same source and target but different pre- or post-conditions in P. The second reason is that two different IAMs can have the same translation because of visible parallel transitions. IAM \(P'\) in Fig. 18 is not equal to P, but \(\textit{IA}({P'})\) is the same automaton as \(\textit{IA}({P})\) shown in Fig. 17. Observe that, in general, two IAMs that are mapped to the same IA are at least IAM-equivalent due to Theorem 17.
The compositionality of parallel composition for IAM now follows from the corresponding property for IA [13] (see Theorem 6) and the above theorems:
Corollary 18
(Compositionality) Let P, Q, R be IAMs and \(P \sqsubseteq _{\textit{IAM}}Q\). Further, assume that Q and R are composable. We have: (i) P and R are composable; (ii) \(P {\parallel }R\) is defined if \(Q {\parallel }R\) is, and then \(P {\parallel }R \sqsubseteq _{\textit{IAM}}Q {\parallel }R\).
Proof
By Theorems 16 and 17, the assumptions hold for \(\textit{IA}({P})\), \(\textit{IA}({Q})\) and \(\textit{IA}({R})\), and also the assumption in (ii) carries over. For these, the result is known (see Theorem 6). Hence, also P and R are composable (compatible, resp.) by Theorem 16. Further, \(\textit{IA}({P}) {\parallel }\textit{IA}({R}) \sqsubseteq _{\textit{IA}}\textit{IA}({Q}){\parallel }\textit{IA}({R})\) implies \(\textit{IA}({P {\parallel }R}) \sqsubseteq _{\textit{IA}}\textit{IA}({Q {\parallel }R})\) by Theorem 16. Now, \(P {\parallel }R \sqsubseteq _{\textit{IAM}}Q {\parallel }R\) follows by Theorem 17. \(\square \)
7 Ground semantics: data-closed IAM
Communication via shared memory works efficiently only for a limited number of components that are locally close to each other. In practical applications, one has a group of components that communicate among each other via shared memory and with their environment via, e.g. message passing [18]. The group is modelled as a parallel composition of IAMs with the understanding that the shared memory is local to this group. Technically, the composition is itself an IAM that is data-closed as defined below. Informally, we speak of a cluster to keep in mind that it represents a group closely connected by common data. To sketch the use of our framework for designing shared-memory systems, we assume that the communication with the system environment is just by synchronizing on common actions, i.e. the environment is an IA and sees the cluster as an IA that is originally specified by some IA Spec.
As the first step for implementing Spec, it has to be translated to an IAM Spec’, and we demonstrate how this can be done towards the end of this section. Spec’ is developed with the IAM design-process into a final cluster P. Now, the system environment needs an IA as a behavioural description of P. As the main result, we show how to represent P by an IA that refines Spec; under some restrictions, the construction even gives a finite IA if P is finite. Due to the symbolic handling of possibly infinite data, this is not obvious. After Proposition 30, when having obtained all formal results, we describe the design process from Spec to the representation of P in greater detail. Until then, we concentrate on the representation of P.
In the previous sections, we have assumed that a control state p of P can be entered while being in some data state \(\sigma \), and then left because of a data state \({{\overline{\sigma }}}\) different from \(\sigma \). In a data-closed system, such a change cannot happen since the shared memory is inaccessible from the outside. To describe the behaviour of such a system, we present a ground semantics where p can only be left via a transition whose pre-condition is satisfied by data state \(\sigma \). In particular, pre- and post-conditions are now also relevant for \(\tau \)-transitions.
More formally, states of the ground semantics are pairs \(\langle {p},{\sigma }\rangle \), where p is a control state and \(\sigma \) a data state. A transition of p with pre-condition \(\varphi \) is only kept for \(\langle {p},{\sigma }\rangle \) if \(\sigma \models \varphi \). Note that, in case of infinite data, there are usually infinitely many states, even if P is finite.
The ground semantics of a data-closed IAM P, denoted by \(\textit{gs}({P})\), describes the behaviour of P as seen from its environment, given some initial data state \(\sigma _0\). Such an initial state would not make much sense for an IAM since it could be changed immediately by the environment. Automaton \(\textit{gs}({P})\) is essentially an IA without pre- and post-conditions, but it might violate input-determinism if several data states satisfy the post-condition of an input-transition. Figure 19 shows an example with \(V=\{x\}\), \(\mathbb {D}=\{1,2\}\) and an initial data state where \(x=1\). In this section, we call such IA-like systems quasi-IAs. Similarly, a system that is an IAM except for data-determinism is called a quasi-IAM.
Definition 19
(Ground Semantics) A data-closed IAM P is a tuple \((P, I, O, \xrightarrow {}_P, p_0, \sigma _0)\), where \((P,I,O,\xrightarrow {}_P,p_0)\) is an IAM and \(\sigma _0\) is the initial data state. The ground semantics of such a P is the quasi-IA \(\textit{gs}({P}) =_{\text {df}}(P \times \llbracket {V}\rrbracket , I, O, \xrightarrow {}_{\textit{gs}({P})}, \langle {p_0},{\sigma _0}\rangle )\) such that \(\langle {p},{\sigma }\rangle \xrightarrow {\alpha }_{\textit{gs}({P})} \langle {p'},{{{\overline{\sigma }}}}\rangle \) if there is a transition \({p\,{-\!\!\left( \varphi , \alpha , \psi \right) \!\!\!\rightarrow _{P\,}}p'}\) with \(\sigma \models \varphi \) and \(\sigma , {{\overline{\sigma }}}' \models \psi \).
7.1 Reduction of a data-closed IAM
To fit the development of a shared-memory cluster into the IA-approach, we first define a quasi-IA that properly reflects the behaviour of the final data-closed IAM P wrt. the ground semantics, but is finite whenever P is (cf. Theorem 25). In turn, this quasi-IA is based on a quasi-IAM to which we refer as the reduction of P; it has the same ground semantics as P. Recall that state \(\langle {p},{\sigma }\rangle \) of the ground semantics inherits those transitions of p whose pre-conditions are satisfied by \(\sigma \). If another data state \({{\overline{\sigma }}}\) satisfies the same pre-conditions as \(\sigma \), then \(\langle {p},{{{\overline{\sigma }}}}\rangle \) inherits the same transitions as \(\langle {p},{\sigma }\rangle \). The main idea is to merge such states. Each merged state is essentially characterized by a conjunction of pre-conditions, written \(\varphi _{J}\) in the following definition.
Definition 20
(Reduction) Given a data-closed IAM \((P, I, O, \xrightarrow {}_P, p_0, \sigma _0)\), assume that each \(p \in P\) has outgoing transitions indexed over some \(K_p\) with pre-conditions \(\varphi _j\), \(j \in K_p\). For each \(J \subseteq K_p\), let \(\varphi _{J}\) be \(\bigwedge _{j\in J}\,\varphi _j \wedge \bigwedge _{j\notin J}\,\lnot \varphi _j\). Set J is called a p-index set if \(\varphi _{J}\) is satisfiable.
The reduction of P is the data-closed quasi-IAM \((\textit{red}({P}), I, O, \xrightarrow {}_{\textit{red}({P})}, \langle {p_0},{\varphi _0}\rangle ,\sigma _0)\) with the following properties:
-
The set \(\textit{red}({P}) \subseteq P {\times } \textit{Pred}({V})\) of states consists of all pairs \(\langle {p},{\varphi _{J}}\rangle \) with J being a p-index set.
-
If \({p\,{-\!\!\left( \varphi _j, \alpha , \psi \right) \!\!\!\rightarrow _{P\,}}p'}\) and there are p- and \(p'\)-index sets J and \(J'\), resp., with \(j{\in }J\) and \(\varphi _J \wedge \psi \wedge \varphi '_{J'}\) sat, then \({\langle {p},{\varphi _J}\rangle \,{-\!\!\left( \varphi _J, \alpha , \varphi _J{\wedge }\psi {\wedge }\varphi '_{J'}\right) \!\!\!\rightarrow _{\textit{red}({P})\,}}\langle {p'},{\varphi _{J'}}\rangle }\).
-
Predicate \(\varphi _0\) in the initial state \(\langle {p_0},{\varphi _0}\rangle \) is \(\varphi _{J_0}\), where \(J_0\) is the \(p_0\)-index set \(\{j \mid \sigma _0 \models \varphi _j\}\).
State \(\langle {p},{\varphi _{J}}\rangle \) of \(\textit{red}({P})\) represents all \(\langle {p},{\sigma }\rangle \) in \(\textit{gs}({P})\) where \(\sigma \models \varphi _J\). Given p and \(\sigma \), there is a unique p-index set J with \(\sigma \models \varphi _J\); for this J, data state \(\sigma \) satisfies \(\varphi _j\) iff \(j \in J\). A state \(\langle {p},{\varphi _{\emptyset }}\rangle \) corresponds to the data states that do not satisfy any pre-condition attached to p; so all such states of \(\textit{red}({P})\) have no outgoing transitions and could be identified with a new state dead. Observe that there are finitely many formulas \(\varphi _J\) for a finite P; thus:
Lemma 21
(Finiteness) For any finite, data-closed IAM P, the quasi-IAM \(\textit{red}({P})\) is finite.
Given the transition from p in Definition 20, consider some \(\sigma \) with \(\sigma \models \varphi _J\). Because \(j \in J\), we have \(\sigma \models \varphi _j\), \(\psi (\sigma )\) is satisfiable and, for each feasible new data state \({{\overline{\sigma }}}\) at \(p'\), one identifies the proper \(p'\)-index set \(J'\). Then, \({{\overline{\sigma }}}'\) (which is applied to \(V'\)) satisfies \(\psi (\sigma )\) and \(\varphi '_{J'}\) (obtained from the resp. pre-conditions, replacing each x by \(x'\) first). Together, \(\sigma , {{\overline{\sigma }}}' \models \varphi _J{\wedge }\psi {\wedge }\varphi '_{J'}\). This explains the details of the transition of \(\textit{red}({P})\) in the above definition. It also shows that each transition from p gives rise to a transition from \(\langle {p},{\varphi _{J}}\rangle \) for each suitable J; we refer to this in the proof of Theorem 29. Examples of reductions can be found in Figs. 20 and 21.
Now, we show that \(\textit{gs}({\textit{red}({P})})\) is essentially the same as \(\textit{gs}({P})\). This means that \(\textit{red}({P})\) and P have the same behaviour as seen from the environment. We call a state \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \) of \(\textit{gs}({\textit{red}({P})})\) data consistent if \(\sigma \models \varphi _J\). In other words, \(\varphi _J\) is an invariant for data consistent states \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \). All reachable states in \(\textit{gs}({\textit{red}({P})})\) are data consistent: the initial state is data consistent, because \(\varphi _0\) is defined such that \(\sigma _0 \models \varphi _0\). Furthermore, if \(\sigma \) and \({{\overline{\sigma }}}'\) satisfy the post-condition of a transition leading to \(\langle {p'},{\varphi _{J'}}\rangle \) in \(\textit{red}({P})\), then \({{\overline{\sigma }}} \models \varphi _{J'}\), i.e. the resp. state \(\langle {\langle {p'},{\varphi _{J'}}\rangle },{{{\overline{\sigma }}}}\rangle \) of \(\textit{gs}({\textit{red}({P})})\) is data consistent.
Similarly, we remark that only data consistent states of \(\textit{gs}({\textit{red}({P})})\) have outgoing transitions. All transitions in \(\textit{gs}({\textit{red}({P})})\) are based on transitions of \(\textit{red}({P})\) and the data states have to fulfill the pre-conditions of the outgoing transitions; these pre-conditions coincide with the \(\varphi _J\) of the state of \(\textit{red}({P})\).
Theorem 22
(Data consistency) Let P be a data-closed IAM. Each reachable state of \(\textit{gs}({\textit{red}({P})})\) is data consistent. The quasi-IA induced by data consistent states is isomorphic to \(\textit{gs}({P})\) due to the isomorphism \(\iota {:}\,\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \mapsto \langle {p},{\sigma }\rangle \); note that \(\sigma \models \varphi _J\). The reachable parts of \(\textit{gs}({\textit{red}({P})})\) and \(\textit{gs}({P})\) are isomorphic due to the resp. restriction of \(\iota \).
Proof
After the above observations, it only remains to show that \(\iota \) is an isomorphism. Because the initial state of \(\textit{gs}({\textit{red}({P})})\) is data consistent and mapped to \(\langle {p_0},{\sigma _0}\rangle \), this implies the last claim. Let \(\iota (\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle ) = \langle {p},{\sigma }\rangle \):
-
Let \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \xrightarrow {\alpha }_{\textit{gs}({\textit{red}({P})})} \langle {\langle {p'},{\varphi _{J'}}\rangle },{{{\overline{\sigma }}}}\rangle \) be a transition from \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \). This exists due to transition \({\langle {p},{\varphi _J}\rangle \,{-\!\!\left( \varphi _J, \alpha , \varphi _J \wedge \psi \wedge \varphi '_{J'}\right) \!\!\!\rightarrow _{\textit{red}({P})\,}}\langle {p'},{\varphi _{J'}}\rangle }\) with \(\sigma ,{{\overline{\sigma }}}' \models \varphi _J \wedge \psi \wedge \varphi '_{J'}\). In turn, this has arisen from a transition \({p\,{-\!\!\left( \varphi _j, \alpha , \psi \right) \!\!\!\rightarrow _{P\,}}p'}\) with \(j \in J\) in P. Hence, \(\sigma \models \varphi _j\) and \(\sigma ,{{\overline{\sigma }}}' \models \psi \), implying that there is the transition \(\langle {p},{\sigma }\rangle \xrightarrow {\alpha }_{\textit{gs}({P})} \langle {p'},{{{\overline{\sigma }}}}\rangle \) in \(\textit{gs}({P})\).
-
Let \(\langle {p},{\sigma }\rangle \xrightarrow {\alpha }_{\textit{gs}({P})} \langle {p'},{{{\overline{\sigma }}}}\rangle \) be a transition from \(\langle {p},{\sigma }\rangle \), which has resulted from some transition \({p\,{-\!\!\left( \varphi _i,\alpha ,\psi \right) \!\!\!\rightarrow _{P\,}}p'}\) with \(\sigma \models \varphi _i\) and \(\sigma , {{\overline{\sigma }}}' \models \psi \). This is the ith outgoing transition of p, and since \(\sigma \) also fulfills \(\varphi _J\), we must have \(i \in J\) as observed above. Also as observed, there is a unique \(p'\)-index set \(J'\) with \({{\overline{\sigma }}} \models \varphi _{J'}\). Thus, \(\sigma \) and \({{\overline{\sigma }}}'\) show \(\varphi _J \wedge \psi \wedge \varphi '_{J'}\) sat, and \(\textit{red}({P})\) has the transition \({\langle {p},{\varphi _J}\rangle \,{-\!\!\left( \varphi _J, \alpha , \varphi _J{\wedge }\psi {\wedge }\varphi '_{J'}\right) \!\!\!\rightarrow _{\textit{red}({P})\,}}\langle {p'},{\varphi _{J'}}\rangle }\). Hence, \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \xrightarrow {\alpha }_{\textit{gs}({\textit{red}({P})})} \langle {\langle {p'},{\varphi _{J'}}\rangle },{{{\overline{\sigma }}}}\rangle \) in \(\textit{gs}({\textit{red}({P})})\) and \(\iota (\langle {\langle {p'},{\varphi _{J'}}\rangle },{{{\overline{\sigma }}}}\rangle ) = \langle {p'},{{{\overline{\sigma }}}}\rangle \).
\(\square \)
We now define a simple translation of an IAM Q to a quasi-IA \(\textit{ia}({Q})\). It turns out that \(\textit{ia}({\textit{red}({P})})\) has essentially the same behaviour as \(\textit{gs}({P})\), if P’s post-conditions do not contain any unprimed variables.
Definition 23
(Quasi-IA Function) Quasi-IA \(\textit{ia}({Q})\) results from IAM Q by deleting all pre- and post-conditions.
The quasi-IA \(\textit{ia}({Q})\) is only IA-like as we do not necessarily get an input-deterministic system. Input-determinism is implied by data-determinism in combination with another property (see below). Obviously, \(\textit{ia}({Q})\) is finite if Q is. The notion of similar behaviour, as used here, is (strong) bisimilarity. On IAs, this is much stronger than mutual IA-refinement.
Definition 24
(Bisimulation) A bisimulation for quasi-IAs P, Q is a relation \({\mathcal {R}} \subseteq P \times Q\) if the following conditions hold for all \(p {\mathcal {R}} q\) and \(\alpha \):
-
(i)
\(p \xrightarrow {\alpha } p'\) implies \(\exists q'.\; q \xrightarrow {\alpha } q'\) and \(p' {\mathcal {R}} q'\);
-
(ii)
\(q \xrightarrow {\alpha } q'\) implies \(\exists p'.\; p \xrightarrow {\alpha } p'\) and \(p' {\mathcal {R}} q'\).
States p and q are called bisimilar if \(p {\mathcal {R}} q\) for a bisimulation \({\mathcal {R}}\). Further, P and Q are bisimilar if the initial states \(p_0\) and \(q_0\) are bisimilar.
If P has no unprimed variables in its post-conditions, one obtains directly from Definitions 19 and 20 that data consistent states \(\langle {\langle {p},{\varphi _J}\rangle },{\sigma }\rangle \) and \(\langle {\langle {p},{\varphi _J}\rangle },{{{\overline{\sigma }}}}\rangle \) in \(\textit{gs}({\textit{red}({P})})\) have the same transitions, i.e. actions and target states coincide. Relating all such pairs results in a bisimulation \({\mathcal {R}}\) on \(\textit{gs}({\textit{red}({P})})\) that is an equivalence. It is well known that merging such equivalence classes gives a bisimilar system [20]. If we denote each class by the resp. \(\langle {p},{\varphi _J}\rangle \), this system is \(\textit{ia}({\textit{red}({P})})\). With Theorem 22 and the above observation that \(\textit{ia}({Q})\) is finite if Q is, we have:
Theorem 25
Let P be a data-closed IAM. If P is finite, then \(\textit{ia}({\textit{red}({P})})\) is finite, too. If P has no unprimed variables in its post-conditions, then \(\textit{ia}({\textit{red}({P})})\) and \(\textit{gs}({\textit{red}({P})})\), as well as \(\textit{ia}({\textit{red}({P})})\) and \(\textit{gs}({P})\), are bisimilar. They are IA-equivalent, if they are IAs.
Remark 26
The example in Fig. 20 shows that the restriction wrt. unprimed variables cannot be dropped for this result; here, we do not show conjuncts tt in the post-conditions of \(\textit{red}({P})\). The ground semantics of data-closed IAM P, with \(\sigma _0\) mapping x and y to 0, has the sequence \(ab^1ab^2ab^3\dots \) of outputs as visible behaviour. On the resp. unique run, \(\tau \)-transitions and visible transitions alternate. The states connected by \(\tau \) are bisimilar; each pair is characterized by the number of bs before the next a and the number of bs after the next but before the next but one a. Thus, no other states are bisimilar, and no finite quasi-IA is bisimilar to \(\textit{gs}({P})\). Although the ground semantics of the reduction \(\textit{red}({P})\) is infinite, \(\textit{red}({P})\) is finite, and so is \(\textit{ia}({\textit{red}({P})})\). Hence, \(\textit{ia}({\textit{red}({P})})\) and \(\textit{gs}({P})\) cannot be bisimilar.
Even worse, when we consider only quasi-IAs where outputs a and b are the only visible actions, then the quasi-IAs are actually IAs. Taking all states as final states, we can regard them as ‘possibly infinite finite automata,’ which are language equivalent if they are equivalent wrt. \(\sqsubseteq _{\textit{IA}}\). The language of \(\textit{gs}({P})\) consists of all finite prefixes of \(ab^1ab^2ab^3\dots \); this language is not regular, so no finite IA is equivalent to the IA \(\textit{gs}({P})\) wrt. \(\sqsubseteq _{\textit{IA}}\).
The restriction regarding unprimed variables is clearly uncomfortable; we plan to study how to weaken it in future work. \(\square \)
7.2 Fitting the reduction to the IA-approach
As indicated above, we want to use a data-closed IAM P in a design process developing an IA. For this, we would like \(\textit{red}({P})\) to be an IAM and \(\textit{ia}({P})\) and \(\textit{ia}({\textit{red}({P})})\) to be IAs. This only holds under some restrictions. We first characterize those \(\textit{red}({P})\) that violate data-determinism.
Definition 27
(Transition ambiguity) Input-transition \({p\,{-\!\!\left( \varphi , a?, \psi \right) \!\!\!\rightarrow _{\,}}p'}\) of data-closed IAM P is ambiguous if, for some p-index set J containing the index of this transition, \(\varphi _J \wedge \psi \wedge \varphi '_{J'}\) is satisfiable for more than one \(p'\)-index set \(J'\).
A predicate that is satisfied exactly by one data state \(\sigma \) is called univalent and denoted by \(\varphi _{\sigma }\); w.l.o.g. we assume that a univalent post-condition is written without unprimed variables.
Concerning the input-transitions of some state p in a data-closed IAM P, we observe the following: if two transitions from p numbered i and j concern the same input a?, the pre-conditions \(\varphi _i\) and \(\varphi _j\) contradict each other due to data-determinism. Thus, a p-index set J can contain at most one index of an a?-transition for a fixed a?, i.e. there is at most one \({p\,{-\!\!\left( \varphi , a?, \psi \right) \!\!\!\rightarrow _{P\,}}p'}\) that gives rise to a?-transitions from \(\langle {p},{\varphi _J}\rangle \). Still, \(\textit{red}({P})\) might only be a quasi-IAM: if a were an input in the example shown in Fig. 20, \(\textit{red}({P})\) would otherwise look the same and would violate data-determinism in state \(\langle {p_1},{\textit{tt}}\rangle \).
Because every p-index set can contain at most one index of an a?-transition for a fixed a?, a violation of data-determinism at some \(\langle {p},{\varphi _J}\rangle \) can only arise from a single input-transition at p, which is then ambiguous. Conversely, if p has an outgoing ambiguous a?-transition as in the definition, \(\textit{red}({P})\) has more than one outgoing a?-transition from \(\langle {p},{\varphi _J}\rangle \) by the definition of reduction. Hence, \(\textit{red}({P})\) is not data-deterministic, because every outgoing transition of \(\langle {p},{\varphi _J}\rangle \) has the pre-condition \(\varphi _J\). The latter also shows that data-determinism at each \(\langle {p},{\varphi _J}\rangle \) implies input-determinism and that \(\textit{ia}({\textit{red}({P})})\) is an IA.
We summarize, noting also that a transition with a univalent post-condition is unambiguous, because the \(\varphi _{J'}\) at some state \(p'\) contradict each other:
Proposition 28
Let P be a data-closed IAM.
-
(i)
P has no ambiguous input-transitions iff \(\textit{red}({P})\) is an IAM.
-
(ii)
If \(\textit{red}({P})\) is an IAM, then \(\textit{ia}({\textit{red}({P})})\) is an IA.
-
(iii)
If all input post-conditions in P are univalent, then P has no ambiguous input-transitions.
Obviously, \(\textit{ia}({P})\) is input-deterministic, i.e. an IA, if every state of P has at most one outgoing a?-transition for each input a. Due to data-determinism, this is guaranteed if all pre-conditions of input-transitions are equivalent to true. The latter condition also allows us to relate a data-closed IAM P and \(\textit{red}({P})\) on the IA-level:
Theorem 29
(Reduction and IA-refinement) Let P be a data-closed IAM without ambiguous input-transitions, where all pre-conditions of input-transitions are equivalent to true. Then, \(\textit{ia}({\textit{red}({P})})\) and \(\textit{ia}({P})\) are IAs and, moreover, \(\textit{ia}({\textit{red}({P})}) \sqsubseteq _{\textit{IA}}\textit{ia}({P})\).
Proof
As noted above and by Proposition 28(i) and (ii), \(\textit{ia}({\textit{red}({P})})\) and \(\textit{ia}({P})\) are IAs. We show that \({\mathcal {R}} =_{\text {df}}\{(\langle {p},{\varphi _J}\rangle ,p) \mid p \in P\}\) is an alternating simulation for \(\textit{ia}({\textit{red}({P})})\) and \(\textit{ia}({P})\). Clearly, \(\langle {p_0},{\varphi _0}\rangle {\mathcal {R}} p_0\) holds for the initial states. Let \(\langle {p},{\varphi _J}\rangle {\mathcal {R}} p\) and consider the following cases:
-
\(p\xrightarrow {a?}_{\textit{ia}({P})} p'\). For some \(\varphi \) and \(\psi \), the transition \({p\,{-\!\!\left( \varphi ,a?,\psi \right) \!\!\!\rightarrow _{P\,}}p'}\) is a transition of P, and \(\varphi \) is equivalent to tt by assumption, implying that the index of the transition is in each p-index set. As argued after Definition 20, there is some \(p'\)-index set \(J'\) such that \({\langle {p},{\varphi _J}\rangle \,{-\!\!\left( \varphi _J, a?, \varphi _J \wedge \psi \wedge \varphi '_{J'}\right) \!\!\!\rightarrow _{\textit{red}({P})\,}}\langle {p'},{\varphi _{J'}}\rangle }\). (Actually, \(J'\) is unique by unambiguity.) This implies \(\langle {p},{\varphi _J}\rangle \xrightarrow {a?}_{\textit{ia}({\textit{red}({P})})} \langle {p'},{\varphi _{J'}}\rangle \) with \(\langle {p'},{\varphi _{J'}}\rangle {\mathcal {R}} p'\).
-
\(\langle {p},{\varphi _J}\rangle \xrightarrow {\alpha !}_{\textit{ia}({\textit{red}({P})})} \langle {p'},{\varphi _{J'}}\rangle \). The IAM \(\textit{red}({P})\) has a corresponding transition \({\langle {p},{\varphi _J}\rangle \,{-\!\!\left( \varphi _J, \alpha !, \varphi _J\wedge \psi \wedge \varphi '_{J'}\right) \!\!\!\rightarrow _{\textit{red}({P})\,}}\langle {p'},{\varphi _{J'}}\rangle }\) for some \(\psi \). Hence, P has some transition \({p\,{-\!\!\left( \varphi _j, \alpha !, \psi \right) \!\!\!\rightarrow _{P\,}}p'}\) with \(j \in J\), implying \(p\xrightarrow {\alpha !}_{\textit{ia}({P})} p'\) with \(\langle {p'},{\varphi _{J'}}\rangle {\mathcal {R}} p'\).
\(\square \)
The following, final result shows how IAM-refinement fits together with IA-refinement:
Proposition 30
(IAM-refinement fits IA-refinement) Let \(P \sqsubseteq _{\textit{IAM}}Q\) due to an alternating simulation \({\mathcal {R}}\). Then, \({\mathcal {R}}\) also satisfies the conditions of an alternating simulation for \(\textit{ia}({P})\) and \(\textit{ia}({Q})\).
Proof
Let \(p{\mathcal {R}}q\). The case of \(\tau \)-transitions is obvious, because we ignore their conditions in the IAMs anyway. An input-transition of q is matched by a family of input-transitions from p. Each of these results in a transition in \(\textit{ia}({P})\) that matches the resp. transition in \(\textit{ia}({Q})\). The case of outputs is similar. \(\square \)
We now describe in detail how one can implement a given IA specification Spec as a shared memory cluster; explanations and the correctness proof are given afterwards. The inputs and outputs of Spec are the external actions for the IAM-design. In the first step, we translate Spec into an IAM Spec\('\) by decorating each transition with tt as pre- and post-condition, except for the post-conditions of output-transitions. As first design choices, we select an initial data state \(\sigma _0\) and, for each output-transition, a single expected \(\sigma \), i.e. the post-condition is the univalent predicate \(\varphi '_{\sigma }\). A possible resulting IAM Spec\('\) is given in Fig. 21.
To obtain a working implementation, one typically refines Spec\('\) by a parallel composition. While developing this cluster in the IAM-framework, the overall system keeps the external actions, and we require that the pre-condition of a transition with an external input is always tt. Introducing new components introduces new actions; there are no restrictions for the resp. transitions, and they are hidden after synchronization. Refining the new components, which are not data-closed, demands IAM-refinement in order to have a precongruence.
We require the final cluster P to not have any unprimed variables in its post-conditions. Furthermore, it must not have any ambiguous transitions, e.g. due to all post-conditions of external input-transitions being univalent (cf. Definition 27). Then, \(\textit{ia}({\textit{red}({P})})\) IA-refines Spec; as a faithful behavioural description of the data-closed IAM P, \(\textit{ia}({\textit{red}({P})})\) can be given to the user of the shared memory cluster as an operating guideline. Preferably, P is finite so that \(\textit{ia}({\textit{red}({P})})\) is finite as well, even if the common ground semantics of P and \(\textit{red}({P})\) were infinite.
This concludes the description of the design process. In order to demonstrate the technical steps, we give a small example and, as we aim to keep things simple, we do not show any components here. Instead, Fig. 21 depicts a realization P of Spec\('\), which has to be understood as the parallel composition of the final cluster. Spec\('\), P and \(\textit{red}({P})\) have the external inputs and outputs as signature. Most interestingly, state \(p_2\) in P has transitions with overlapping pre-conditions. This leads to three satisfiable conditions \(\varphi _J\), which are equivalent to \(x<0\), \(x>0\) and \(x=0\). As \(x<0\) is always invalid after the \(\tau \)-transition in P, state \(p_2\) results in two reachable states in \(\textit{red}({P})\); the post-conditions of the two \(\tau \)-transitions are suitably adapted. The left-hand state inherits the two c-transitions where \(x>0\) is allowed, and the right-hand state inherits only the c-transition where \(x=0\) is allowed; the pre-conditions are adapted.
We close this section by motivating the initial choices for Spec\('\) and proving the correctness of our method. Predicate tt is chosen as pre-condition for output-transitions, because this is the most general choice. These pre-conditions can be made stricter during refinement. Dually, the post-conditions can be made broader, so we start from a minimal post-condition. The conditions of \(\tau \)-transitions do only matter for the final cluster. Post-conditions tt for input-transitions are again most general. The pre-conditions of input-transitions being tt is only necessary for the final P, where we have to apply Theorem 29, but it seems conceptually easiest to require this throughout. This condition guarantees that the environment, which does not have access to the shared memory, can really rely on the operation calls being accepted as promised in the operating guideline. Obviously, \(\textit{ia}({\textit{Spec}'})\) is Spec.
As an aside, we note that Spec\('\) is isomorphic to \(\textit{red}({Spec'})\); simply replace each p by \(\langle {p},{\textit{tt}}\rangle \). Furthermore, Spec\('\) has no post-conditions with unprimed variables. Hence, the behaviour of the data-closed IAM Spec\('\) properly reflects \(\textit{ia}({\textit{red}({\textit{Spec}'})})\) by Theorem 25, and the latter is isomorphic to Spec. Therefore, the choice of Spec\('\) is intuitively well motivated.
The final cluster P is obtained from Spec\('\) by IAM-refinement. By Theorem 29, \(\textit{ia}({P})\) and \(\textit{ia}({\textit{red}({P})})\) are IAs and \(\textit{ia}({\textit{red}({P})}) \sqsubseteq _{\textit{IA}}\textit{ia}({P})\). From \(P \sqsubseteq _{\textit{IAM}}\textit{Spec}'\) and Proposition 30, we derive \(\textit{ia}({P}) \sqsubseteq _{\textit{IA}}\textit{ia}({\textit{Spec}'})\), where the latter is Spec. Together, we have \(\textit{ia}({\textit{red}({P})}) \sqsubseteq _{\textit{IA}}\textit{Spec}\). So, \(\textit{ia}({\textit{red}({P})})\) is an IA-refinement of Spec, and it faithfully shows the behaviour of P by Theorem 25. Finally, \(\textit{ia}({\textit{red}({P})})\) is finite by Lemma 21, if P is.
IAM \(\textit{red}({P})\) for IAM P of Fig. 22
Remark 31
One might think that these considerations could be simplified. The idea would be to conclude \(\textit{red}({P}) \sqsubseteq _{\textit{IAM}}\textit{Spec}'\) from \(\textit{red}({P}) \sqsubseteq _{\textit{IAM}}P\). The IAM P in Fig. 22 and \(\textit{red}({P})\) in Fig. 23 show that the latter can fail in various ways. In this example, we have \(\mathbb {D} = \{1,2\}\), \(V=\{x,y\}\) and \(\sigma _0\) maps x and y to 1. We write \(\varphi _{i,j}\) instead of \(x=i \wedge y=j\) and, therefore, \(\varphi '_{i,j}\) instead of \(x'=i \,\wedge \, y'=j\), for \(i, j \in \mathbb {D}\). In some of the post-conditions in \(\textit{red}({P})\), we have omitted some redundant conjuncts like \(\textit{tt}\). We assume that each of \(p_2\), \(p_3\), \(p_4\) and \(p_5\) has a characteristic behaviour that is omitted in the figures, e.g. each has an input-transition not occurring elsewhere. This way, no alternating simulation can relate any \(\langle {p_i},{\varphi _J}\rangle \in \textit{red}({P})\) to some \(p_j \in P\) with \(i, j \in \{2,3,4,5\}\) and \(i \ne j\).
Suppose that \(\textit{red}({P}) \sqsubseteq _{\textit{IAM}}P\) due to some alternating simulation that relates \(\langle {p_0},{x=1}\rangle \) to \(p_0\). Due to the o-transition from \(\langle {p_0},{x=1}\rangle \) to \(\langle {p_1},{\varphi _{1,1}}\rangle \), the simulation also relates \(\langle {p_1},{\varphi _{1,1}}\rangle \) to \(p_1\). Now, the first problem is that \({p_1\,{-\!\!\left( x=2, i?, \varphi '_{2,1}\right) \!\!\!\rightarrow _{P\,}}p_5}\) must be matched by an i-transition from \(\langle {p_1},{\varphi _{1,1}}\rangle \) to \(\langle {p_5},{\textit{tt}}\rangle \). But there is no such transition, because the common pre-condition \(\varphi _{1,1}\) of the transitions from \(\langle {p_1},{\varphi _{1,1}}\rangle \) contradicts \(x=2\). More generally speaking, the index of the i-transition above is not in the \(p_1\)-index set giving rise to \(\varphi _{1,1}\). Such a contradiction cannot occur if all pre-conditions of input-transitions in P are tautologies, which implies input-determinism.
The second problem is similar. Transition \({p_1\,{-\!\!\left( x=1, i?, \varphi '_{1,1}\right) \!\!\!\rightarrow _{P\,}}p_2}\) must be matched by the only i-transition from \(\langle {p_1},{\varphi _{1,1}}\rangle \). However, due to transition \({p_1\,{-\!\!\left( y=1, o!, \varphi '_{1,1}\right) \!\!\!\rightarrow _{P\,}}p_3}\) and the construction of \(\textit{red}({P})\), we have the pre-condition \(\varphi _{1,1}\) in the latter IAM, and this is not implied by \(x=1\). This effect can also occur if all pre-conditions of input-transitions in P are tautologies.
Consider the transition \({\langle {p_0},{x=1}\rangle \,{-\!\!\left( x=1, o!, x=1 \wedge \varphi '_{1,1}\right) \!\!\!\rightarrow _{\,}}\langle {p_1},{\varphi _{1,1}}\rangle }\) in \(\textit{red}({P})\) to see the last problem. This must be matched by the only o-transition from \(p_0\). By the construction of \(\textit{red}({P})\), the post-condition of the given transition has an additional conjunct that makes the post-condition stricter than \(x'=1\). This also contradicts the definition of alternating simulation. \(\square \)
Finally, observe that also \(\textit{ia}({P}) \sqsubseteq _{\textit{IA}}\textit{Spec}\), but \(\textit{ia}({P})\) should not be used in place of \(\textit{ia}({\textit{red}({P})})\). It might have outputs that cannot ever occur in the data-closed P, i.e. outputs for which the environment does not have to care.
8 Conclusions and future work
Interface Automata (IA) [12, 13] have laid the foundation for reasoning about the compatibility of concurrent system components and been extended in the literature in various ways by shared variables for modelling data manipulating operations [1, 2, 9, 11, 27]. However, all these works consider a more complex setting than IA [1, 2], do not relate their proposed semantics to an intuitive ground semantics [1, 2, 9, 11, 27], or do not abstract from internal computation [1, 2, 9, 11, 27]. Thus, it has remained an open question whether IA permits a simple and faithful extension to shared memory.
This article answered this question positively. Our interface theory IAM is a conservative extension of IA by shared memory. Similar to [1, 2, 9, 27], we decorated action-labelled transitions with pre- and post-conditions constraining data states. A pre-condition acts as the transition’s guard, and a post-condition of an output (input) transition specifies an assumption (guarantee) on the data state reached when executing the transition. We extended IA’s concepts of compatibility, refinement and parallel composition to this setting, and provided a translation from IAM to IA. The latter shows that IAM accurately lifts IA’s concepts to shared memory. In this sense, IAM keeps the simplicity that has made IA increasingly popular in the formal methods community. But the clear advantage is that IAM attains finiteness even when reasoning about infinite data domains. For our IAM theory, we implemented an initial, prototypic toolset [28] using open-source technologies and applied it to a simple example, thereby demonstrating that practical tool support is conceivable.
To prove that IAM treats shared variables as intuitively expected and that a cluster of IAMs can be abstracted to an IA, we provided a ground semantics for data-closed IAMs. This makes the data states, which are implicit in an IAM, explicit, and is not unlike the implementation semantics of [2]. Most importantly, our presentation of the usually infinite ground semantics is often finite. Data-closed IAMs may occur as a cluster of IAMs that communicate among each other by shared memory, but via message passing with the system environment. Thus, the cluster looks externally similar to an IA. We sketched an approach, where under some restrictions, an IA as a specification is transformed into an IAM, which in turn can be implemented by a cluster according to IAM-refinement. Then, the ground semantics of the cluster IA-refines the specification, and it can be turned into a bisimilar finite IA obtained from a reduction of data-closed IAMs.
Future work We propose to extend IAM with operators enhancing its practicality, namely a conjunction operator that is needed when a component must satisfy several interfaces, as well as operators for action scoping and variable scoping. The former is not as easy as for IA [23], where two interfaces always have a common refinement since contradictions cannot occur. In IAM, contradictions may arise due to transitions with conflicting post-conditions. Action scoping can be realized by pruning inputs and hiding outputs [8]. Variable scoping requires the introduction of an access control to IAM’s global variables [1, 2, 11].
Further, we plan to attach data invariants to IAM states. The idea is that, while a component is in a state, a compatible system environment can only alter data in ways respecting the invariant. This restricts the environments with which a component can be composed, thus making shared variables more meaningful wrt. an open systems view. Variations like this bring our theory closer to practical application; we then have to adapt our cluster result accordingly, while replacing IA by message-passing systems.
Last, but not least, we wish to investigate the extent to which our prototypic IAM toolset scales to realistic systems and whether it can cope with the variety of concurrent systems developed in engineering practice. Certainly, scalability also depends on the logic chosen for expressing pre- and post-conditions, which effects the computational complexity for deciding alternating simulation.
Notes
For example, given \(\sigma \) with \(\sigma (y) = 1\) and the predicate \(x'+y=3\), the result is \(x'+1=3\). In other words, \(\psi (\sigma )\) results from \(\psi \) by replacing any unprimed variable x with the syntactical element representing \(\sigma (x)\).
Recall that all IAMs have the same set V of variables.
Note that infinite branching may occur in case the domain of variables is infinite and, thus, \(I'\) and \(O'\) are infinite. This may be unusual in interface theories, but the embedding exercise is rather a theoretical one aimed at demonstrating that the IAM setting is not more expressive than the IA setting in principle.
The notation \(\varphi _{\sigma }\) used in this proof does not stand for a univalent predicate as introduced in the next section.
References
Bauer, S.S., Hennicker, R., Bidoit, M.: A modal interface theory with data constraints. In: SBMF, volume 6527 of LNCS, pp. 80–95. Springer, Berlin (2010)
Bauer, S.S., Hennicker, R., Wirsing, M.: Interface theories for concurrency and data. Theoret. Comput. Sci. 412(28), 3101–3121 (2011)
Bauer, S.S., Mayer, P., Schroeder, A., Hennicker, R.: On weak modal compatibility, refinement, and the MIO Workbench. In: TACAS, volume 6015 of LNCS, pp. 175–189. Springer, Berlin (2010)
Benveniste, A., Caillaud, B., Nickovic, D., Passerone, R., Raclet, J.-B., Reinkemeier, P., Sangiovanni-Vincentelli, A., Damm, W., Henzinger, T.A., Larsen, K.G.: Contracts for system design. Found. Trends Electr. Des. Autom. 12(2–3), 124–400 (2018)
Bujtor, F., Fendrich, S., Lüttgen, G., Vogler, W.: Nondeterministic modal interfaces. Theoret. Comput. Sci. 642(C), 24–53 (2016)
Bujtor, F., Vogler, W.: Error-pruning in interface automata. Theoret. Comput. Sci. 597, 18–39 (2015)
Bunte, O., Groote, J.F., Keiren, J.J.A., Laveaux, M., Neele, T., de Vink, E.P., Wesselink, W., Wijs, A., Willemse, T.A.C.: The mCRL2 toolset for analysing concurrent systems–improvements in expressivity and usability. In: TACAS, volume 11428 of LNCS, pp. 21–39. Springer, Berlin (2019)
Chilton, C., Jonsson, B., Kwiatkowska, M.: An algebraic theory of interface automata. Theoret. Comput. Sci. 549, 146–174 (2014)
Chouali, S., Mountassir, H., Mouelhi, S.: An I/O automata-based approach to verify component compatibility: application to the CyCab car. ENTCS 238(6), 3–13 (2010)
Dardha, O., Giachino, E., Sangiorgi, D.: Session types revisited. Inf. Comput. 256, 253–286 (2017)
de Alfaro, L., da Silva, L.D., Faella, M., Legay, A., Roy, P., Sorea, M.: Sociable interfaces. In: FroCoS, volume 3717 of LNCS, pp. 81–105. Springer, Berlin (2005)
de Alfaro, L., Henzinger, T.A.: Interface automata. In: ESEC/FSE, pp. 109–120. ACM (2001)
de Alfaro, L., Henzinger, T.A.: Interface-based design. In: ETSIS, volume 195 of NAII, pp. 83–104. Springer, Berlin (2005)
Dill, D.L.: Trace Theory for Automatic Hierarchical Verification of Speed-Independent Circuits. MIT Press, Cambridge (1989)
Fendrich, S., Lüttgen, G.: A generalised theory of interface automata, component compatibility and error. Acta Inf. 56(4), 298–319 (2019)
Gareis, J., Lüttgen, G., Schinko, A., Vogler, W.: Interface automata for shared memory. In: Models, Mindsets, Meta: The What, the How, and the Why Not?—Essays Dedicated to Bernhard Steffen on the Occasion of His 60th Birthday, volume 11200 of LNCS, pp. 151–166. Springer, Berlin (2018)
Hatcliff, J., Leavens, G.T., Leino, K.R.M., Müller, P., Parkinson, M.: Behavioral interface specification languages. ACM Comput. Surv. 44(3), 16:1-16:58 (2012)
Holik, L., Isberner, M., Jonsson, B.: Mediator synthesis in a component algebra with data. In: Correct System Design, volume 9360 of LNCS, pp. 238–259. Springer, Berlin (2015)
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. SIGPLAN Not. 43(1), 273–284 (2008)
Kanellakis, P.C., Smolka, S.A.: CCS expressions, finite state processes, and three problems of equivalence. Inf. Comput. 86(1), 43–68 (1990)
Larsen, K.G.: Modal specifications. In: Automatic Verification Methods for Finite State Systems, volume 407 of LNCS, pp. 232–246. Springer, Berlin (1989)
Larsen, K.G., Nyman, U., Wasowski, A.: Modal I/O automata for interface and product line theories. In: ESOP, volume 4421 of LNCS, pp. 64–79. Springer, Berlin (2007)
Lüttgen, G., Vogler, W.: Modal interface automata. Log. Methods Comput. Sci. 9(3:4), 1–28 (2013)
Mateescu, R., Oudot, E.: Improved on-the-fly equivalence checking using boolean equation systems. In: SPIN, volume 5156 of LNCS, pp. 196–213. Springer, Berlin (2008)
Meyer, B.: Applying “Design by Contract”. IEEE Comput. 25(10), 40–51 (1992)
Milner, R.: Communication and Concurrency. Prentice Hall, Englewood Cliffs (1989)
Mouelhi, S., Chouali, S., Mountassir, H.: Refinement of interface automata strengthened by action semantics. ENTCS 253(1), 111–126 (2009)
Nguyen, N.T., Lüttgen, G. The IAM Toolset, 2021. Available at GitHub: https://github.com/uniba-swt/ia-toolset
Raclet, J.-B., Badouel, E., Benveniste, A., Caillaud, B., Legay, A., Passerone, R.: A modal interface theory for component-based design. Fundam. Inform. 108(1–2), 119–149 (2011)
Schinko, A., Vogler, W.: Fault-free refinements for interface automata. Sci. Ann. Comp. Sci. 28, 289–337 (2018)
Vogler, W., Lüttgen, G.: A linear-time branching-time perspective on interface automata. Acta Inform. 57(3), 513–550 (2020)
Acknowledgements
We thank the anonymous reviewers and also the reviewers of the extended abstract of this article [16] for their helpful comments and suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research support provided by the DFG (German Research Foundation) under Grant Nos. LU 1748/3-2 and VO 615/12-2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schinko, A., Vogler, W., Gareis, J. et al. Interface Automata for Shared Memory. Acta Informatica 59, 521–556 (2022). https://doi.org/10.1007/s00236-021-00408-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-021-00408-8





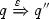 and
and  and
and 




 ,
,  and
and 











 ,
,  also in
also in  in
in  and
and  and
and 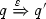 in
in  also holds in Q.
also holds in Q.




