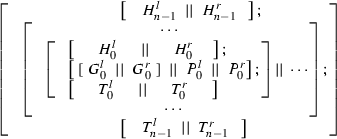Formal communication elimination and sequentialization equivalence proofs for distributed system models

Abstract

Equivalence reasoning with distributed system models, expressed directly as imperative programs with explicit parallelism, communication operations, storage variables and boolean conditions, remains virtually unexplored. Only reasoning with models expressed as process algebras has been amply dealt with in literature. However, these formalisms do not contemplate either storage variables or Boolean conditions as fundamental items, although these items become essential in most situations. This article develops the foundation of the until now non existent theory of equivalence reasoning with the aforementioned imperative notation and two novel equivalence proof techniques: communication elimination and sequentialization. The development is grounded on state systems and transition interleavings, as treated by Manna and Pnueli. Equivalence proofs safely transform a model via the application of a sequence of equivalence laws; aiming to obtain an equivalent model which is purely sequential, free from internal communication operations and parallelism, as a simplification of the initial model. After this, verification of the original model can be carried out, indirectly, in the simplified model, thus reducing complexity. Some of the presented novel notions are: (1) modular procedure for decomposition of both models and proofs, (2) interface behavior for statement semantics, (3) interface equivalence between behaviors, between statements and between procedures, (4) a set of communication elimination laws and (5) substitution rules of procedure references by their bodies or by references to equivalent procedures. An elimination proof construction algorithm is also presented; when it terminates, deadlock freedom of the original model can be decided. The main design lines of a computer aided equivalence reasoning tool are outlined as well. This is the foundation for a more widely applicable tool. As an illustration, the sequentialization proof of a simplified pipelined processor is overviewed. It is modeled as a distributed system with procedures and two levels of parallelism. The model obtained at the end of the equivalence proof is the sequential loop of a Von Neumann processor. This result establishes that the original model is deadlock-free, behaves as a processor and, as a consequence, the partition of processor functions among parallel processes is correct. The ratio of the upper bounds on the number of states of the final over the initial models, $\frac{final}{initial}$, is $\frac{1}{2^{672}}$.

Appendices

Appendix A: Grounding notions and notation semantics

The work reported in this article is based on fair transition systems and transition interleaving semantics, as presented in [37, 38]. This appendix introduces the necessary concepts for the unfamiliar reader. For instance, the notions of computation, set of observed variables, reduced behavior, congruence, etc., assumed to be known in Sect. 2, are covered.

Many variants of SPL are discussed in [37, 38]. The SPL used in this article is a specific variant. For instance, the selection and the communications selection statements are used here in a different form. Also, nil and stop have been introduced here. Therefore, the presentation of the semantics of the specific SPL variant of this work is mandatory. This is accomplished in this appendix as well.

1.1 A.1  Fair transition systems

An interleaving semantics of parallelism is adopted. Informally, each statement is associated with atomic state transitions. Parallel statements denote all possible interleavings of the transitions of each of their top parallel statements. A model (program) denotes a fair transition system (FTS), which includes the transitions of each of its substatements. All this is introduced in this subsection. For more elaboration, the reader is referred to [37, 38].

The specific FTS associated with a model will become clear after the introduction of these notions. This FTS will define the transitions, the runs and the behaviors of the model which are required in Sect. 2.

A fair transition system (FTS) $S$ is the tuple $\langle V, \varSigma , \varTheta , \mathcal{T}, \mathcal{J}, \mathcal{C}\rangle$, where

• $V$ is a finite set of system variables, expressible as $V = Y \cup \{\pi \}$, where $\pi$ is the control variable, and $Y = \{ y_{1},\ldots ,y_{m}\}$ is the set of data variables.

• $\varSigma$ is the set of states.

• $\varTheta$, a satisfiable assertion, is the initial condition satisfied by any initial state of $S$.

• $\mathcal T$ is a finite set of transitions.

• $\mathcal J$ is the set of just (weakly fair) transitions.

• $\mathcal C$ is the set of compassionate (strongly fair) transitions.

The control variable $\pi$ contains the values of the program counters of each parallel process, which are control locations, defined below.

A transition $\tau \in \mathcal{T}$ is a relation on pairs of states $(s, s')$. $s'$ is a $\tau$-successor of $s$. $\tau (s)$ denotes the set of successors of $s$ in the relation. The relation will be specified by a transition relation $\rho _{\tau }(V,V')$, a first order formula which evaluates to true for each state pair of the transition. $V$ and $V'$ correspond to the sets of state variables evaluated at $s$ and at $s'$, respectively. It has the general form

$$\begin{aligned} \rho _{\tau }(V,V') : E_{\tau }(V) \wedge D_{\tau }(V, V') \end{aligned}$$

where conjunct $E_{\tau }$ depends only on the initial state $s$, and conjunct $D_{\tau }$ depends on both states $s$ and $s'$, and specifies the changes made on the variables by the transition. Transitions correspond to atomic actions associated with statements.

A transition is enabled or disabled on state $s$ when $E_{\tau }(V)$ evaluates to true or false on $s$, respectively. One of the transitions $\tau _{I} \in \mathcal{T}$ is the idling transition. It is such that $s'=s$ for every state $s$.

A run of a FTS is an infinite sequence of states $\; \sigma :\; s_{0},\; s_{1},\; s_{2},\; \dots \;$ satisfying

• initiation ($s_{0} \models \varTheta$) and

• consecution ($s_{j+1}\in \tau (s_{j})$).

Whenever required, the unbounded length of a run is attained with idle transitions.

A transition is just (weakly fair) when being continuously enabled in a run, it is eventually taken in the run. Hence, it will be taken an indefinite number of times as well.

A transition is compassionate (strongly fair) when being enabled an indefinite number of times in a run, it is eventually taken in the run. Hence, it will be taken an indefinite number of times as well.

A computation of a FTS is a run all of whose transitions satisfy their corresponding fairness requirements, expressed by the sets $\mathcal J$ and $\mathcal C$.

Runs and computations may be represented as tables, such as Tables 1 and 2 in Sect. 2. Each row of a table corresponds to a state $s_{i}$. Each column corresponds to a variable.

1.2 A.2  Auxiliary notions for statement semantics

Before going into the semantics, which will detail the transitions associated to each statement of the SPL variant, some auxiliary notions are needed. These are explained in this subsection.

A statement $S$ may have labels, as in $l$:$S$;$\hat{l}$ where $l$ and $\hat{l}$ are the pre and post labels of $S$, respectively. A finite set of transitions, and a finite set of control locations is associated with each statement $S$.

An equivalence relation $\sim _{L}$, defined on statement labels, will put together labels which denote the same control location.

A location is an equivalence class of the label relation $\sim _{L}$. The location corresponding to label $\ell$ will be denoted by $[\ell ]$. It stands for the equivalence class containing $\ell$ and all the labels that are $\sim _{L}$-equivalent to $\ell$. The pre and post control locations of $S, [\ell ]$ and $[\hat{\ell }]$, are also written as $pre(S)$ and $post(S)$, respectively.

The special variable $\pi$, introduced above, will range over sets of locations. Its value on a state denotes all the locations in the program that are active on that state. A state such that $[\ell ]\in \pi$ will be referred to as an $\ell$-state.

Predicates $\; pres(U):\bigwedge _{u \in \; U} (u'= u)$ and $move(L,\hat{L}):L\subseteq \pi \wedge \pi ' =( \pi - L ) \cup \hat{L}\;$ express preservation of the values of the variables in $U$ and movement of control from set $L$ to $\hat{L}$. pres specifies the data variables which are not changed by the transition. move specifies also the set $L$ of control locations which should be active in order for the transition to be enabled and the set of locations that are active at the end of the transition, those in $\hat{L}$ are amongst them.

As a shortcut, the expression $move(\ell ,\hat{\ell })$ will be used instead of $move(\{ [\ell ] \}, \{[\hat{\ell }]\} )$. A transition $\tau _{\ell }$ whose transition relation is of the form $\;\rho _{\ell }:\; \; move(L,\hat{L}) \wedge pres(Y)\;$ will be referred to as a skip-type transition. It changes control but does not modify data variables.

1.3 A.3  Statement formal semantics

Statement	Transition relations	Labels
$\ell : \mathbf{{skip}}; \hat{\ell }:$	$\rho _{\ell }:\; move(\ell ,\hat{\ell }) \wedge pres(Y)$
$\ell :\; \mathbf{nil}; \hat{\ell }:$		$\ell \sim _{L} \hat{\ell }$
$\ell :\; \mathbf{stop}; \hat{\ell }:$
$\ell : \bar{u}\,{:=}\,\; \bar{e}; \hat{\ell }:\; \;$	$\rho _{\ell }:\; move(\ell ,\hat{\ell }) \; \wedge \; \bar{u}'= \bar{e} \; \wedge \; pres(Y-\{ \bar{u}\} )$
$\ell : \alpha \Leftarrow e ; \hat{\ell }:\; \; m: \alpha \Rightarrow u ; \hat{m}: \;$	$\rho _{<\ell , m >}: \; move(\{ [\ell ],[m]\},\{[\hat{\ell }],[\hat{m}]\}) \wedge \; u' = e \; \wedge \; pres(Y-\{ u\} )\;$

The table gives the semantics of the basic statements.

skip involves a transition in the underlying fair transition system, but without any effect on the data variables. It moves control and preserves the values of all the variables. The transition is in the justice set $\mathcal J$.

nil can be characterized by contributing no transition, but only the equivalence between its pre and post labels.

stop has neither transitions nor label relation. Control remains at $l$ forever.

The variables $\bar{u}'$ after the assignment take the values of their corresponding expressions in $\bar{e}$. The rest of model variables conserve their values. The transition is in $\mathcal J$.

The above table last row states that the execution of a pair of matching communication operations is atomic and simultaneous. Thus, it corresponds to a single joint transition which belongs to $\mathcal J$ as required for the laws to be sound [14]. A synchronous communication event occurs when the transition is taken. Its effect is equivalent to the assignment $u\,{:=}\, e$. Matching communication operations should be parallel, as in Definition 31 of Sect. 3.

Statement	Transition relations
$\ell :[\ell _{1}:S_{1};\hat{\ell _{1}}\; \dots \; ;\ell _{m}:S_{m};\hat{\ell _{m}}];\hat{\ell }:$
$\ell : [\;[\ell _{1}: S_{1}; \hat{\ell _{1}}] \;|| \dots ||\; [\ell _{m}: S_{m}; \hat{\ell _{m}}]\; ]; \hat{\ell }:$	$\rho _{\ell }^{E}: move(\{[\ell ]\},\{[\ell _{1}],\ldots ,[\ell _{m}]\}) \wedge pres(Y)$
	$\rho _{\ell }^{X}: move(\{[\hat{\ell _{1}}],\ldots ,[\hat{\ell _{m}}]\},\{[\hat{\ell }]\}) \wedge pres(Y)$
$\ell :[\; c_{1} ; S_{1} \mathbf{{ or }}\; \dots \; \mathbf{{ or }}c_{m} ; S_{m}\; ] ; \hat{\ell }:$	$\rho _{i}: move(\{ \ell \},\{ \ell _{i}\}) \wedge c_{i} \wedge pres(Y)$
$\ell :[\; c_{1} , c(\alpha _{1}) ; S_{1} \mathbf{{ or }}\; \dots \; \mathbf{{ or }}c_{m}, c(\alpha _{m}) ; S_{m}\; ] ; \hat{\ell }:$	$\rho _{< i , n >}: move(\{ \ell , n \},\{ \ell _{i},\hat{n} \}) \wedge c_{i} \wedge u' = e \wedge pres(Y-\{ u\} )\;$

The transition relations of the semantics of compound statements are given in the above table. This semantics is completed in the following paragraphs, where $\ell _{i}$ and $\hat{\ell _{i}}$ are the pre and post labels of substatements $S_{i}$. These labels are not always represented explicitly in the table.

No transition is directly associated with concatenation (sequential composition). All its transitions are associated with its substatements. The concatenation label relations are $\hat{\ell _{i}} \sim _{L} \ell _{i+1}$ for $\; i=1,\ldots ,m-1\;, \; \ell \sim _{L} \ell _{1}\; \;$ and $\; \; \hat{\ell } \sim _{L} \hat{\ell _{m}}$.

Cooperation (parallel composition) has an entry $\tau ^{E}$ and an exit $\tau ^{X}$ transition. They are in $\mathcal J$. In addition, cooperation has the transitions of its substatements.

The label relations of selection are $\ell \sim _{L} \ell _{1} \sim _{L}\; \cdots \; \sim _{L} \ell _{m}$ and $\hat{\ell } \sim _{L} \hat{\ell _{1}} \sim _{L}\; \cdots \; \sim _{L} \hat{\ell _{m}}$.

Labels $n$ and $\hat{n}$ of the communication selection transitions $\tau _{<i,n>}$ are the pre and post labels of the operation which forms the matching pair with $c(\alpha _{i})$. This operation is within some statement which is parallel to the communication selection. $u$ and $e$ are the variable and the expression, respectively, which are associated with the pair of operations. $\tau _{<i,n>}$ belongs to $\mathcal J$ in agreement with what was said above.

Pre labels $\bar{\ell _{i}}$ of the communication operations $c(\alpha _{i})$ are not shown explicitly in the table. The label relations associated with communication selection are $\ell \sim _{L} \bar{\ell _{1}} \sim _{L}\; \cdots \; \sim _{L} \bar{\ell _{m}}$ and $\hat{\ell } \sim _{L} \hat{\ell _{1}} \sim _{L}\; \cdots \; \sim _{L} \hat{\ell _{m}}$.

1.4 A.4  Equivalences

Equivalence between statements reduces to equivalence between their transition systems. In order to define a practical notion of equivalence between transition systems it is enough to consider observable parts. Then, a reduced behavior $\sigma ^{r}$ is obtained from a computation $\sigma$ by retaining an observable part, relative to a set of observed variables (observation set) $\mathcal{O}$, where $\pi \not \in \mathcal{O}$, and eliminating from it stuttering steps (equivalent to idling transitions). In other words, deleting any state which equals its predecessor but not all its successors. $\mathcal{R}_\mathcal{O}(S)$ denotes the set of all reduced behaviors of a transition system $S$ with respect to the set $\mathcal{O}$ of observed variables.

Remark 13

(Control is never observed) Program counters are never observed, i.e., $\pi \not \in \mathcal{O}$.

Transition systems $S_{1}$ and $S_{2}$ are equivalent relative to set of observed variables $\mathcal O$, written $\; S_{1} \sim _\mathcal{O} S_{2}\;$, if $\; \; \mathcal{R}_\mathcal{O}(S_{1}) \equiv \mathcal{R}_\mathcal{O}(S_{2})$. Transition system $S_{c}$ refines transition system $S_{a}$, written $\; S_{c} \sqsubseteq _\mathcal{O} S_{a} \;$, if every reduced behavior of $S_{c}$ is also a reduced behavior of $S_{a}$.

A program context $P[\cdot ]$ is a program $P$ one of whose statements is highlighted as a hole to be filled-in with an arbitrary statement $S$. With some abuse of notation $P[S]$ will denote a program context, where $S$ denotes the arbitrary statement placed in the hole. The notion of statement context is defined in a similar way.

The reduced behaviors of statements are, by definition, the reduced behaviors of their transition systems. Statement $S_{1}$ refines $S_{2}$, written $S_{1} \sqsubseteq _\mathcal{{O}} S_{2}$, when for any program context $P[\cdot ]$, any reduced behavior of $P[S_{1}]$ is also a reduced behavior of $P[S_{2}]$.

Statement $S_{1}$ is congruent to $S_{2}$, written $S_{1}\approx _\mathcal{{O}} S_{2}$, when $S_{1} \sqsubseteq _\mathcal{{O}} S_{2}$ and $S_{2} \sqsubseteq _\mathcal{{O}} S_{1}$. Observe that these relations are defined with respect to a set of observed variables $\mathcal {O}$.

Appendix B: Communication elimination laws and their applicability conditions

The communication elimination laws of Sect. 3 reduce the parallelism of the statement on which they are applied. Some substatements that are parallel in the left sides of these laws are composed in sequence in their right sides. When the substatements which match these left side substatements are communicating, as in Definition 4, deadlock may appear after the law is applied. Thus, applicability conditions are needed to guarantee deadlock freedom conservation.

This appendix derives the elimination laws and their applicability conditions. They are gathered in Theorems 6 and 7. Theorem 8 states the conditions of Theorem 7 in another form. Theorem 9 on the elimination of a communication pair from a statement in standard form corresponds to Theorem 1 of Sect. 3.3. Its justification, which was not included in the main text, is included in this appendix.

$G^{l}$ and $G^{r}$ have the same meaning as in Lemma 14 of Sect. 3.1 throughout the appendix. The outer form of a law given in Sect. 3.2 transforms the statement which matches its left side when it is applied from left to right. This transformation is recursively repeated for a law of order $k_{0}>1$ as it has been explained in the same subsection. In order to start the derivations of this appendix, the transformation step of the recursion is split into the two equivalences of Lemmas 23 and 24.

Lemma 23

(G-statement pairing equivalence) Assume that none of the statements below have the problematic ending statements of Lemma 8 and that the statement pairs which are parallel are also disjoint.

Let $\mathcal{O}$ be the union of all variables and channel variables in them.

Let $H^{l}$ and $H^{r}$ contain no communication statements over internal channels.

Assume that in each of the statement pairs ($P^{l},T^{r}$), ($P^{r},T^{l}$), ($G^{l},T^{r}$) and ($G^{r},T^{l}$) no operation channel of a statement of the pair is also the channel of some operation of the other statement of the pair. Then,

and either both sides are deadlock-free or none of them is.

Justification The assumptions imply that the four pairs of the lemma do not communicate, as in Definition 4. $T^{l}$ is parallel to $H^{r}, G^{r},$ and $P^{r}$ in the left but concatenated with the same statements in the right. However, it remains parallel to $T^{r}$ in both sides. Similarly with $T^{r}$. The lemma follows by a twofold application of Lemma 17 of Sect. 4.1 which is valid due to the assumptions of our lemma.$\square$

$[G^{l}||G^{r}]$ at the right side of the equivalence of Lemma 23 has to be isolated and matched with the parallel statement of the left side of the same equivalence, considered now at the next recursion level. Afterwards, this equivalence is applied from left to right to transform the binary parallelism into the statement denoted by $\bar{G}$ in the right side of the equivalence of Lemma 24. (see also the outer form of the law given in Sect. 3.2). But in this transformation, the substatements which are sequentialized are parallel to $P^{l}$ and $P^{r}$. Lemma 24 formulates the additional conditions which are required by this fact. A notion needed in the lemma is introduced before in the following

Definition 35

(Communication precedence) Let $A$ and $B$ be parallel to $C$, a statement which is clear in a given context. Then, $cw(A)\le cw(B)$ will mean that, in the concatenation order of $C$, the communication operations which may form matching pairs with those of $A$ precede or are unordered with all the operations of $C$ which may form pairs with those of $B$.

Lemma 24

(Reduction of G-statement parallelism) Let $\; \bar{G}^{l}||\bar{G}^{r} =_\mathcal{O} \bar{G} \;$ represent the equivalence of Lemma 23, where the substatements of the three $\bar{G}$’s and the statements below satisfy the conditions stated in it. Assume that, within $\bar{P}^{l}$ and $\bar{P}^{r}$,

$$\begin{aligned} cw(P^{l}) \le cw(T^{r})\;\!\!,\;\; cw(P^{r}) \le cw(T^{l})\;\!\!,\;\; cw(G^{l}) \le cw(T^{r})\;\;\hbox { and }\;\; cw(G^{r}) \le cw(T^{l}) \end{aligned}$$

Then,

$$\begin{aligned} \left[ \begin{array}{c} \left[ \bar{H}^{l} || \bar{H}^{r}\right] ; \\ \left[ \bar{G}^{l} \ \ || \ \ \bar{G}^{r} \ \ || \ \ \bar{P}^{l} \ \ || \ \ \bar{P}^{r}\right] ; \\ \left[ \bar{T}^{l} || \bar{T}^{r} \right] \end{array}\right] =_{\mathcal{O}} \quad \left[ \begin{array}{c} \left[ \bar{H}^{l} || \bar{H}^{r}\right] ; \\ \left[ \bar{G} \ \ || \ \ \bar{P}^{l} \ \ || \ \ \bar{P}^{r}\right] ; \\ \left[ \bar{T}^{l} || \bar{T}^{r}\right] \end{array}\right] \end{aligned}$$

and either both sides are deadlock-free or none of them is.

Justification In order to obtain the right side of the equivalence of this lemma, the equivalence of Lemma 23 is applied to the inner parallelism between $\bar{G}^{l}$ and $\bar{G}^{r}$. The only statements which are parallel to $\bar{G}^{l}$ and $\bar{G}^{r}$ in the left side statement are $\bar{P}^{l}$ and $\bar{P}^{r}$. Also, they are the only ones which are parallel to $\bar{G}$ in the right side statement. But, in the equivalence of Lemma 23, the statement pairs ($P^{l},T^{r}$), ($P^{r},T^{l}$), ($G^{l},T^{r}$) and ($G^{r},T^{l}$) are parallel in the left side. But, in the right side, they are concatenated in the same order as they stand in each one of the pairs. Therefore, the communication operations with these statements within $\bar{P}^{l}$ and $\bar{P}^{r}$, should they exist, must have the same order restrictions required by the lemma, which follows from Lemma 23. $\square$

The restrictions of Lemmas 23 and 24 have to be fulfilled in all the iterations needed to obtain the law of order $n$. Theorems 6 and 7 put them together, respectively.

Theorem 6

(Non-communication restrictions for eliminability) A necessary condition for the elimination of a pair $p$:$(l,r)$ from $\;[G^{l}_{n+1}||G^{r}_{n+1}]\;$ without introducing deadlock, via the application of the law which was defined in Sect. 3.2, is that no operation channel of a statement of any of the following pairs is also the channel of some operation of the other statement of the same pair.

• 1. $(P^{l}_{i},T^{r}_{k})$ and $(P^{r}_{i},T^{l}_{k})$ for $i\in [0,k], k\in [0,n]$ and

• 2. $(T^{r}_{i},T^{l}_{j})$ for $i,j\in [0,n]$, $i\ne j$.

Justification In order to obtain the elimination law defined recursively in Sect. 3.2, the equivalence of Lemma 23 is applied from left to right for $\; k=n\;$ first. At this outermost level, its restrictions apply to the statement pairs $(P^{l}_{n},T^{r}_{n})$ and $(G^{l}_{n},T^{r}_{n})$, and the two symmetric ones $(P^{r}_{n},T^{l}_{n})$ and $(G^{r}_{n},T^{l}_{n})$. But $G^{l}_{n}$ of the second pair does not exist as such and has to be split, for $n>0$, into all of its substatements of its recursive definition of Sect. 3.2. This leads to the restrictions $(P^{l}_{i},T^{r}_{n}), (T^{l}_{i},T^{r}_{n})$, for $i=n-1, n-2, \ldots , 1, 0$. The $H$’s do not intervene since they have no inner communication operations. These pairs together with $(P^{l}_{n},T^{r}_{n})$ give the set

$$\begin{aligned} (P^{l}_{i},T^{r}_{n}),\quad \hbox {for} \quad i=0,\ldots ,n, \quad \hbox {and}\quad (T^{l}_{i},T^{r}_{n}), \quad \hbox {for}\quad i=0,\ldots ,n-1, \quad \hbox {for}\quad n>0. \end{aligned}$$

Proceeding similarly with the two symmetric pairs $(P^{r}_{n},T^{l}_{n})$ and $(G^{r}_{n},T^{l}_{n})$, the following additional pairs are obtained, which have to be added to the restricted set.

$$\begin{aligned} (P^{r}_{i},T^{l}_{n}),\quad \hbox {for}\quad i=0,\ldots ,n, \hbox {and}\quad (T^{r}_{i},T^{l}_{n}), \quad \hbox {for}\quad i=0,\ldots ,n-1, \quad \hbox {for} \quad n>0. \end{aligned}$$

But the equivalence of Lemma 23 has to be applied again at levels $k=n-1,\ldots ,1$. Thus, similar restrictions have to hold at these levels. For $n=0$ we have still the restricted pairs $(P_{0}^{l},T_{0}^{r})\;\!\!,\;\;(G_{0}^{l},T_{0}^{r})\;\!\!,\;\; (P_{0}^{r},T_{0}^{l})\;$ and $\;\;(G_{0}^{r},T_{0}^{l})$. Pairs $\;(G_{0}^{l},T_{0}^{r})\;$ and $\;(G_{0}^{r},T_{0}^{l})\;$ can be ignored since $G_{0}^{l}$ and $G_{0}^{r}$, which form a matching pair, communicate among themselves only. Putting together all the $P$-$T$ restrictions, Point 1 of the lemma is obtained. Point 2 follows when all the $T$-$T$ restrictions are gathered together.$\square$

Theorem 7

(Broad communication order restrictions) A necessary condition for the elimination of a pair $p$:$(l,r)$ from $\;[G^{l}_{n+1}||G^{r}_{n+1}]\;$ without introducing deadlock, via the application of the law which was defined in Sect. 3.2, is that for $i\in [0,k-1]$, $k\in [1,n]$ and within $P^{l}_{k}$ and $P^{r}_{k}$,

$$\begin{aligned} cw(P^{l}_{i}) \le cw(T^{r}_{i})\;\!\!, \;\;cw(P^{r}_{i}) \le cw(T^{l}_{i})\;\!\!, \;\;cw(G^{l}_{i}) \le cw(T^{r}_{i})\;\; \hbox {and} \;\;cw(G^{r}_{i}) \le cw(T^{l}_{i}). \end{aligned}$$

Justification Consider again, as in the justification of Theorem 6, the recursive application of the equivalence of Lemma 23 in order to obtain the elimination law of order $n$ starting from $\;[G^{l}_{n+1}||G^{r}_{n+1}]$. The restrictions of Lemma 24 are not required at the first application, $k=n$. However, they should be fulfilled at the application levels of orders $k=n-1,\ldots ,1$. Thus, at level $k=n-1$ the restrictions

$$\begin{aligned} cw(P^{l}_{n-1})&\le cw(T^{r}_{n-1}), \;cw(P^{r}_{n-1})\le cw(T^{l}_{n-1}), \;\\ cw(G^{l}_{n-1})&\le cw(T^{r}_{n-1})\; \hbox {and} \;cw(G^{r}_{n-1})\le cw(T^{l}_{n-1}) \end{aligned}$$

should hold within $P^{l}_{n}$ and $P^{r}_{n}$. At level $k=n-2$, the statement pairs $\;(P_{n-2}^{l},T_{n-2}^{r}),(P_{n-2}^{r},T_{n-2}^{l}), \;(G_{n-2}^{l},T_{n-2}^{r})\;$ and $\;(G_{n-2}^{r},T_{n-2}^{l})\;$ are sequentialized and are parallel to $P^{l}_{n-1}$ and $P^{r}_{n-1}$ but still to $P^{l}_{n}$ and $P^{r}_{n}$. Thus, up to and including level $k=n-2$ the restrictions of the lemma should hold for $i\in [n-2,k-1]$, $k\in [n-1,n]$. Continuing up to $k=1$, the complete set of restrictions of the lemma is obtained.$\square$

Theorem 8

(Communication order restrictions for eliminability) Under the same framework and aim of Theorem 7, its set of restrictions can be expressed equivalently as follows: for all $k\in [2,n]$, within $P^{l}_{k}$ and $P^{r}_{k}$,

$$\begin{aligned} cw(P_{j}^{l})&\le cw(T_{i}^{r})\;\hbox {and}\;\;cw(P_{j}^{r})\le cw(T_{i}^{l})\;\; \hbox {for} \;\;j\in [0,i],\;i\in [0,k-1],\\ cw(T_{j}^{l})&\le cw(T_{i}^{r})\;\hbox {and}\;\;cw(T_{j}^{r})\le cw(T_{i}^{l})\;\; \hbox {for} \;\;j\in [0,i-1],\;i\in [1,k-1] \end{aligned}$$

and for $k=1$, within $P_{1}^{l}$ and $P_{1}^{r}, \;cw(P_{0}^{l})\le cw(T_{0}^{r})\;$and$\;\;cw(P_{0}^{r})\le cw(T_{0}^{l})$.

Justification $G_{i}^{l}$ and $G_{i}^{r}$ in the last two restrictions of Theorem 7 can be replaced by all their $P$ and $T$ substatements, $G_{0}^{l}$ and $G_{0}^{r}$. This process follows the recursive definition given in Sect. 3.2, i.e., $G_{k}^{x}$:$[H_{k-1}^{x};[G_{k-1}^{x}||P_{k-1}^{x}];T_{k-1}^{x}]$ where $x$ stands for either $l$ or $r$. Recall that the $H$’s have no internal communications, that all the $G$’s disappear in the recursive process with the exception of $G_{0}^{l}$ and $G_{0}^{r}$ which form a matching pair of communication operations. Thus, each one of them communicates with the other only. In order to illustrate the process, for $k=n,i=2$ the restrictions $\;cw(P_{j}^{l}) \le cw(T_{2}^{r})\;$ and $\;cw(T_{j}^{l}) \le cw(T_{2}^{r})\;$ for $j\in [1,2]$ within $P^{l}_{n}$ and $P^{r}_{n}$, together with their symmetricals in $l$ and $r$, are obtained.

The recursive substitution process leads to the following equivalent restrictions: for $k\in [2,n]$ within $P^{l}_{k}$ and $P^{r}_{k}$, and for $j\in [0,i-1], \;i\in [1,k-1]$

$$\begin{aligned} cw(P_{j}^{l})\le cw(T_{i}^{r}),\;cw(T_{j}^{l})\le cw(T_{i}^{r}), \;cw(P_{j}^{r})\le cw(T_{i}^{l})\; \hbox {and} \;cw(T_{j}^{r})\le cw(T_{i}^{l}); \end{aligned}$$

for $\;k\in [2,n],\;i=0$, within $P_{k}^{l}$ and $P_{k}^{r}, \;cw(G_{0}^{l}) \le cw(T_{0}^{r}), cw(G_{0}^{r}) \le cw(T_{0}^{l})\;$ which need not be included since ($G_{0}^{l},G_{0}^{r}$) is a pair of communication operations communicating between themselves only; for $k=1,i=0$ one has again the above two restrictions which can be ignored, but also $\;cw(P_{0}^{l}) \le cw(T_{0}^{r})\;$ and $\;cw(P_{0}^{r}) \le cw(T_{0}^{l})$, within $P^{l}_{1}$ and $P^{r}_{1}$, which are included in the theorem under $k=1$. With that, the $T$-$T$ restrictions of the theorem have been also obtained.

The remaining $P$-$T$ restrictions of the theorem follow by gathering together the above $P$-$T$ restrictions and the ones of Theorem 7 since, for $k=1, cw(G_{0}^{l})\le cw(T_{0}^{r})\;$ and $\;cw(G_{0}^{r})\le cw(T_{0}^{l})\;$ can be ignored again.$\square$

Theorem 9

(Elimination from a standard form binary cooperation) Let statement $\;S:[G^{l}_{n}||G^{r}_{n}]\;$ be selection-free BC as in Definition 34, its two top statements have the standard form given in Lemma 15 of Sect. 3.1, and $S$ satisfy the applicability conditions of Theorems 6 and 7.

Let $\mathcal{O}$ be an interface set of $S, \;G_{0}$:$[u\,{:=}\,e]\;,\;G_{0}^{l}$:$l\;,\;G_{0}^{r}$:$r\;, \;p$:$(l,r)$ over channel $c\not \in \mathcal{O}$ be the pair to be eliminated and, for $k= 1, 2,\ldots ,n$,

$$\begin{aligned} G_{k}:[H_{k-1}^{l}||H_{k-1}^{r}] ;[G_{k-1}||P_{k-1}^{l}||P_{k-1}^{r}]; [T_{k-1}^{l}||T_{k-1}^{r}]. \end{aligned}$$

Then, $\;G_{n}\; =_\mathcal{O} \;[ G_{n}^{l} || G_{n}^{r} ]\;$ and either both sides are deadlock-free or none of them is.

Justification The equivalence is obtained with the following steps:

• 1. Iterative application of the equivalence of Lemma 23, starting from $[G_{n}^{l}||G_{n}^{r}]$. This process has been explained in connection with Lemmas 23 and 24 and in Sect. 3.2. The following statement is obtained at its end:

  

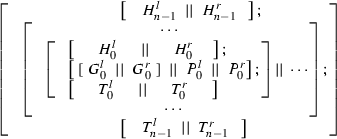
• 2. Application of $[G_{0}^{l}||G_{0}^{r}]\approx G_{0}$, given in Sect. 3.2, to its inner substatement.

The theorem follows by transitivity and monotonicity of equivalence, as well as Theorems 6 and 7 provided that their assumptions are satisfied. Their applicability conditions are sufficient since all deadlock introduction possibilities are captured between both theorems. This is due to the fact that, in the framework of this work, the only possible cause of deadlock is waiting at communications that can never take place and, in the present situation, this can only happen with communications within substatements that change from being parallel in $\;[G_{n}^{l}||G_{n}^{r}]\;$ to being concatenated in $G_{n}$.

Notice that monotonicity of equivalence is a consequence of the substitution Lemmas 10 and 12.$\square$

Appendix C: Special laws for the parallel processor proof

Under certain conditions, the following laws allow for the order change of assignments which contain references to an array $r(\cdot )$. This array models the register file in the processor proof. The left side of these laws captures what remains, in the sequentialized model, of the forwarding circuit of the original pipelined processor model.

Lemma 25

(Array reference commutation) Let $a \notin \mathcal{O}$ and $S$ be free from references to $a, r(j)$ and r(k), and from write references to $q$. Then,

Justification There are two cases. Assuming first that $j=k$, the left side is equivalent to $[ \ a\,{:=}\,r(k); r(k)\,{:=}\,q; S; a\,{:=}\,q \ ]$. The first statement is useless and can be deleted, leading to $[ \ r(k)\,{:=}\,q; S; a\,{:=}\,q \ ]$. This is valid since $a\not \in \mathcal{O}$ and $S$ has no reference to $a$. But this is also equivalent to $[ \ r(k)\,{:=}\,q; S; a\,{:=}\,r(k) \ ]$ since $r(k)$ does not appear within $S$ and its value equals $q$ after the first assignment. $S$ can be moved to the end due to the assumptions imposed on it. This leads to $[ \ r(k)\,{:=}\,q; a\,{:=}\,r(k); S \ ]$ which is the right side of the equivalence to be proved in the case $j=k$. In the second case $j\ne k$ the left side becomes $[ \ a\,{:=}\,r(j); r(k)\,{:=}\,q; S; nil \ ]$ which is equivalent to the right side since the first two statements are disjoint and can be interchanged.$\square$

Lemma 26

(Double array reference commutation) Let $a, b \notin \mathcal{O}$, as in Lemma 25. Then,

Justification The multiple assignment is equivalent to

$$\begin{aligned}{}[a\,{:=}\,r(i);b\,{:=}\,r(j);(c,d,e,f)\,{:=}\,(i,j,t,s)] \end{aligned}$$

whose third assignment can be moved to the end of the left side statement. All this can be done since the elementary assignments are disjoint among themselves and the last multiple assignment is disjoint with the rest of the left side. The result follows after two applications of Lemma 25. In the first application $S$ is identified with the first if substatement, and $b$ plays the role of the $a$ of Lemma 25. The following equivalent statement is obtained:

$$\begin{aligned}{}[a\,{:=}\,r(i);r(k)\,{:=}\,q;b:=r(j);\mathbf{if}\; i=k\; \mathbf{then}\; a\,{:=}\,q \; \mathbf{else}\; nil;(c,d,e,f)\,{:=}\,(i,j,t,s)] \end{aligned}$$

In the second application, $S$ is identified with $[b\,{:=}\,r(j)]$ and the three last assignments of the resulting statement are combined into a single multiple assignment.