Finite regular semigroups with permutations that map elements to inverses

Abstract

We give an account on what is known on the subject of permutation matchings, which are bijections of a finite regular semigroup that map each element to one of its inverses. This includes partial solutions to some open questions, including a related novel combinatorial problem.

1 Introduction and background

The author published three papers [3, 4], and [5] in Semigroup Forum relating to the question of when a finite regular semigroup S has a bijection $\phi$ such that $\phi (a)\in V(a)$, which is to say that $\phi$ maps elements to their inverses. Some simple observations will occur to the reader: if S is an inverse semigroup, then there is a unique such permutation $\phi$, and if S is a union of groups, the mapping $a\mapsto a^{-1}$, where $a^{-1}$ denotes the group inverse of a in S, defines a permutation matching, as these bijections are called (we shall sometimes abbreviate the term to matching). Indeed in both cases these matchings are involutions. Rectangular bands are exactly the semigroups where every bijection of S is a matching, as they are characterised by the identity $x=xyx$, while the identity mapping is a matching if and only if S satisfies the identity $x=x^{3}$.

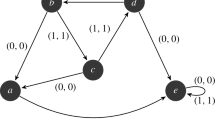
It does not take long however to locate examples of finite regular semigroups that have no matching. A minimal example is given by the 7-element orthodox 0-rectangular band $B=\{(i,j):1\le i\le 2,1\le j\le 3\}\cup \{0\}$, where $E(B)=\{(1,2),(1,3),(2,1)\}\cup \{0\}$. The pairs (2, 2) and (2, 3) have only one inverse element between them, that being (1, 1), and so no permutation matching exists for B. Proposition 1.5 of [3] gives an example of an orthodox 0-rectangular band, with an involution matching, but which has B as a retract. It follows from this that the class of semigroups that possess a permutation matching is not closed under the taking of regular subsemigroups, nor the taking of homomorphic images. The class is closed however under the taking of direct products.

The nature of the example represented by B suggests that the existence of permutation matchings will correspond to the satisfaction of Hall’s condition in the bipartite graph featuring two copies of S with edges joining mutually inverse pairs. Indeed we see this as part (iii) of the following theorem.

Theorem 1.1

([3, Theorem 1.6]) For a finite regular semigroup S the following are equivalent:

• (i) S has a permutation matching;

• (ii) S is a transversal of $\{V(a)\}_{a\in S}$;

• (iii) $|A|\le |V(A)|$ for all $A\subseteq S$;

• (iv) S has a permutation matching $(\cdot ')$ that preserves the $\mathscr {H}$-relation; (meaning that $a\,\mathscr {H}\,b\rightarrow a'\,\mathscr {H}\,b'$);

• (v) each principal factor $D_{a}\cup \{0\}$ $(a\in S)$ has a permutation matching;

• (vi) each 0-rectangular band $(D_{a}\cup \{0\})/{\mathscr {H}}$ has a permutation matching.

This theorem was applied to show that the full transformation semigroup $T_{n}$ has a matching [3, Theorem 2.12]. The argument also extends to the partial transformation semigroup, $PT_{n}$.

The proof shows that each $\mathscr {D}$-class D of $T_{n}$ has a matching, and this was done by partitioning D into so-called $\mathscr {Q}$-classes, which are themselves unions of $\mathscr {R}$-classes. To each $\mathscr {R}$-class $R\subseteq D$, (remembering that $\alpha \,\mathscr {R}\,\beta$ in $T_{n}$ if and only if $\ker \alpha =\ker \beta$), we associate an increasing sequence of positive integers $s_{R}=(k_{1},k_{2},\ldots ,k_{t})$ where the $k_{i}$ run over the cardinalities of the kernel classes of the members of R, so that t is the rank of the members of D. The ${\mathscr {Q}}$-class defined by R is then the union of all $\mathscr {R}$-classes $R'$ such that $s_{R'}=s_{R}$.

We then show the existence of a permutation matching for each ${\mathscr {Q}}$-class Q of $T_{n}$. To do this, we consider the bipartite graph G consisting of two copies, Q and $Q'$, of Q, where $ab'$ is an edge in G if (and only if) a and b are mutual inverses in $T_{n}$. It is then proved that G is a regular graph, which is to say each vertex is of a common degree $m\ge 1$, whence each member of Q has exactly m inverses in Q. It then follows by a standard result from graph theory that G has a perfect matching, which is a set of disjoint edges covering all vertices of G.

This perfect matching may then be used to generate a permutation matching of Q as follows. Begin with any vertex $a_{1}$ of Q and consider the sequence of vertices $a_{1},b_{1}',b_{1}:=a_{2},b_{2}',b_{2}:=a_{3},\dotsc$, which will eventually yields a cycle $a_{1},a_{2},\dots ,a_{r}$ say, where $a_{i}$ and $a_{i+1}$ are mutual inverses (and where we take $r+1=1)$. Since the edges of G form a perfect matching, no vertex $a_{i}$ of Q can be followed in the Q-sequence by a previous vertex of Q, other than $a_{1}$, as that would result in the contradiction of two edges of the perfect matching having a common vertex in $Q'$. We then repeat the process for a new vertex not contained in any of the previous cycles of inverses, culminating in a permutation matching of Q.

However the following question remains open.

Question 1

Does the semigroup $O_{n}$ of all order-preserving mappings on a finite n-chain have a permutation matching?¹

2 Involution matchings

We have already noted that the two classes of Inverse semigroups and Completely regular semigroups possess involution matchings. The class ${\mathscr {O}}\!\mathscr {P}_{n}$ of all semigroups of orientation-preserving mappings is another collection whose members have a natural involution matching (Example 2.6 of [3]), and the technique found there extends to the class $\mathscr {P}_{n}$ of all semigroups of orientation-preserving and orientation-reversing mappings (Sect. 3.2 of [3]). For background on these classes of semigroups see [2, 6, 7]. A natural question is then:

Question 2

Does $T_{n}$ have an involution matching?

By a result of Schein [9], $T_{n}$ is covered by its inverse subsemigroups. If $T_{n}$ possessed an inverse cover with the additional property that the non-empty intersection of any pair of subsemigroups in the cover were regular (and hence inverse), it would be possible to use that cover to construct an involution matching. However, it was shown in [5, Theorem 4.2.3] that for $n\ge 4$, no such cover exists. Moreover for $n\ge 8$, $T_{n}$ does not have a permutation matching in which each element is mapped to a strong inverse $a'$, which is an inverse with the property that the subsemigroup $\langle a,a'\rangle$ is an inverse subsemigroup of $T_{n}$.

The case of $T_{n}$ is however only a particular instance of the general question, which has not been resolved.

Question 3

Does every finite regular semigroup with a permutation matching possess an involution matching?

In [5, Theorems 3.7 and 3.1] it was proved that any (finite) orthodox semigroup with a permutation matching has an involution matching. Moreover an orthodox semigroup possesses a permutation matching if and only if each 0-rectangular band $B=(D_{a}\cup \{0\})/\mathscr {H}$ $(a\in S)$ has the property that the maximal rectangular subbands of B are pairwise similar, meaning that the ratio of their number of $\mathscr {L}$- to $\mathscr {R}$-classes is a constant throughout $D_{a}$.

A broader class of regular semigroups is defined by the condition on the arrangement of idempotents within ${\mathscr {D}}$-classes: for all idempotents $e,f,g\in E(S)$,

$$\begin{aligned} e{\,\mathscr {L}}\,f\,\mathscr {R}g\Rightarrow \exists h\in E(S)\,\text {such that}\,e\,{\mathscr {R}}\,h\,{\mathscr {L}\,}g, \end{aligned}$$

giving an egg-box picture where the four idempotents in question form a ‘solid’ rectangle within their ${\mathscr {D}}$-class, which lead to the name E-solid semigroups. Equivalently, a regular semigroup S is E-solid if and only if the idempotent generated subsemigroup $\langle E(S)\rangle$ of S is a union of groups. Using the fact that each 0-rectangular band $B = (D_{a}\cup \{0\})/\mathscr {H}$ $(a\in S)$ of a finite E-solid semigroup is orthodox, we may extend the previous results from orthodox to E-solid semigroups [5, Theorem 1.3.5].

We can attempt to build an involution matching from a given permutation matching as follows. Consider the graph G(S) with vertices corresponding to the members of S and edges joining each pair of mutual inverses. Next suppose that S possesses a permutation matching and consider the subgraph of G(S) consisting of the vertices and edges of some permutation matching, which is a set of disjoint cycles. Any even cycle may then be split into mutually inverse pairs. On the other hand if an odd cycle contains an idempotent, e, we may pair e with itself and pair the remaining members of this odd cycle in mutually inverse pairs. It follows that if S has a permutation matching, but no involution matching, then every permutation matching of S must contain an odd cycle that is idempotent-free.

Suppose then that S is an example of a semigroup of minimum cardinality that has a matching but no involution matching. Then every principal factor $D_{a}\cup \{0\}$ of S (or simply $D_{a}$, if $D_{a}$ is the minimum ideal of S) has a permutation matching, mapping $D_{a}$ onto itself. If each of these principal factors had an involution matching, then the union of these involution matchings on the ${\mathscr {D}}$-classes $D_{a}$ would define an involution matching of S. Since we are assuming that no such involution matching exists, it follows that some principal factor has a permutation matching but no involution matching. Therefore by minimality of the cardinal of S, it follows that S is a completely 0-simple semigroup. (Every completely simple semigroup, being a union of groups, has an involution matching.)

By Theorem 1.1(vi), we have that $B=S/\mathscr {H}$ also has a permutation matching. If S contained proper subgroups, it would follow by the minimality of the cardinal of S that B possessed an involution matching, $\phi$. However this would allow the construction of an involution matching $\overline{\phi }$ on S as follows.

We identify the non-zero members of B with the $\mathscr {H}$-classes $H_{a}$ of S. We then define $a\overline{\phi }=a'$, where $a'$ is the unique inverse of a in $H_{a}\phi$. Then $a'\overline{\phi }$ is the unique inverse of $a'$ in $H_{a'}\phi$, and since $H_{a'}\phi =H_{a}$, we infer that $\overline{\phi }$ would indeed be an involution matching on S. Since this is a contradiction, we reach the conclusion that any minimal example S is a 0-rectangular band, thereby establishing the following fact.

Proposition 2.1

Suppose that S is a finite regular semigroup of minimum cardinality with the property that S possesses a permutation matching but no involution matching. Then S is a 0-rectangular band.

In this way we are led to consider 0-rectangular bands S. Let the non-zero $\mathscr {D}$-class D of S have m rows and n columns. Without loss we may take $3 \le m \le n$, as if $m\le 2$, then any odd cycle of any permutation matching must contain an idempotent. We therefore arrive at the question:

Question 4

Does there exist a 0-rectangular band S that has a permutation matching but no involution matching?

We may prove that if this is the case then m cannot be a divisor of n, and so in particular our major $\mathscr {D}$-class D of S cannot be square. In what follows we let R and C respectively stand for the set of m rows and n columns of D. Let us write $n=am$ for some positive integer a.

Lemma 2.2

Suppose that S has a permutation matching $\phi$. Then for any collection T of t rows of D $(1\le t\le m)$

$$\begin{aligned} |\{c\in C:c\cap E(T)\ne \emptyset \}|\ge ta. \end{aligned}$$

(1)

And for any collection T of t columns of D $(1\le t\le n)$

$$\begin{aligned} |\{r\in R:r\cap E(T)\}|\ge \frac{t}{a}. \end{aligned}$$

(2)

Proof

The t rows contain nt members. These are mapped by $\phi$ into s columns say, which collectively contain ms members. Hence $nt\le ms$ and so

$$\begin{aligned} s\ge t\cdot \frac{n}{m}=t\cdot \frac{am}{m}=ta. \end{aligned}$$

Since the set on the left hand side of (1) contains the set of s columns, the inequality (1) now follows.

Similarly, any set of t columns $(1\le t\le n)$ is mapped by $\phi$ into s rows of D and the t columns collectively contain mt members. Hence $mt\le ns$ and so

$$\begin{aligned} s\ge t\cdot \frac{m}{n}=t\cdot \frac{m}{am}=\frac{t}{a}, \end{aligned}$$

and then (2) follows. $\square$

Proposition 2.3

Let S be a 0-rectangular band with m rows and $n=am$ $(a\ge 1)$ columns in its non-zero $\mathscr {D}$-class D. If S has a permutation matching $\phi$, then S has an involution matching.

Proof

Consider the bipartite graph G with vertex set $R\,\dot{\cup }\,C$, the disjoint union of the respective sets of rows and columns of D, with an edge connecting a row and a column if that row and column intersect in an idempotent. Note in particular that if $a\phi =b$, then an edge connects $R_{a}$ to $L_{b}$ (and $R_{b}$ to $L_{a}$).

From (1) and (2) we see that any set of t rows of R is collectively adjacent to at least at columns of C in D, and any set of t columns is collectively adjacent to at least $\frac{t}{a}$ rows of D. By Hall’s Harem theorem, (see Sect. III.3 of [1]) there exist a injective functions, $\pi _{0},\pi _{1},\ldots ,\pi _{a-1}$ from R into C with pairwise disjoint ranges, whose union is C. We label the m columns in the range of $\pi _{t}$ as $tm,tm+1,\ldots ,(t+1)m-1$.

We may then define an involution matching on D as follows. Let $(i,j)\in D$ with $j=tm+r$, where $0\le r\le m-1$. We define

$$\begin{aligned} (i,j)\pi =(j\pi _{t}^{-1},i\pi _{t}). \end{aligned}$$

(3)

Then

$$\begin{aligned} (i,j)\pi ^{2}=(j\pi _{t}^{-1},i\pi _{t})\pi =(i\pi _{t}\pi _{t}^{-1},j\pi _{t}^{-1}\pi _{t})=(i,j), \end{aligned}$$

so that $\pi$ defines an involution on D (which extends to S by putting $0\pi =0$). Moreover, by definition of adjacency in G we have that $(i,i\pi _{t})\in E(D)$, and also $(j\pi _{t}^{-1},j)\in E(D)$ as $j\pi _{t}^{-1}\pi _{t}=j$. It now follows from (3) that (i, j) and $(i,j)\pi$ are mutual inverses in D. Therefore $\pi$ is indeed an involution matching of S. $\square$

There have been lively exchanges on a problem related to ours, some of which have been recorded on Mathoverflow [8]. The conversation was initiated by Fedya Petrov who explains that our question (matching implies involution matching), would be settled in the affirmative if the same were true of the following purely combinatorial problem.

A set of m girls have mn balls so that each girl has n balls. There are m balls of each of n colours. Two girls may exchange the balls (1 ball for 1 ball, so each girl still has n balls), but no ball may participate in more than one exchange. The goal is to achieve a situation where each girl has balls of all n colours (and so exactly one of each colour). This question we shall call the $m \times n$ Colour distribution problem.

The participants in the discussion then claim proofs of results that subsume Proposition 2.3 in that the problem may be solved if $n\equiv 0,\pm 1,\pm 2$ (mod m). However, at the time of writing, the general question remains open.

Theorem 2.4

(F. Petrov, private communication) A positive solution of the Colour distribution problem implies a positive solution of the involution matching problem.

Proof

Suppose that the Colour distribution problem may always be solved. (The exchanges may include vacuous exchanges where a girl exchanges a ball with itself: in this way we may claim that in our solution every ball is exchanged exactly once.) Let S be an $m\times n$ 0-rectangular band with a permutation matching $\phi$. We identify the set of n columns with the set of n colours, and the set of balls is identified with the set of elements of D, the non-zero $\mathscr {D}$-class of S. For the ball $x= (i,j)$ we write $x_{1} = i$ and $x_{2 } = j$.

Each of the m girls is not identified with a row of D but with the image of a row under $\phi$, in that these images constitute the starting position of an $m \times n$ Colour distribution problem K, where girl a is assigned balls $\phi (a, \alpha )$ ($1 \le \alpha \le n$). This assigns n balls to each girl. Moreover, since $\phi$ is bijective, one ball is assigned for each entry of D. In particular the requirement that there are exactly m balls of each colour is satisfied. We let T denote a fixed solution of this Colour distribution problem K.

In what follows mappings are written on the left. We construct our involution matching $\varPhi$ on D as follows. Suppose that $(a, \phi (a, \alpha )_2)$ and $(b, \phi (b, \beta )_2)$ represents an exchange in T. Then we put

$$\begin{aligned} \varPhi (a,\phi (b,\beta )_{2})=(b,\phi (a,\alpha )_{2}). \end{aligned}$$

(4)

This is a well-defined function action, for if not there would be an equality of the form $\phi (b,\beta )_{2}=\phi (b',\beta ')_{2}$, with an exchange in T of the form $(a,\phi (a, \alpha ')_2)$ and $(b', \phi (b', \beta '))$. But then, since $\phi (b,\beta )_{2}=\phi (b',\beta ')_{2}$ represents equality of colours, in T girl a would finish with two balls of this one colour, contradicting that T is a solution to K. Hence $\varPhi$ is a function. Moreover, by (4) it follows that $\varPhi (b,\phi (a,\alpha )_{2})=(a,\phi (b,\beta )_{2})$, so that $\varPhi$ is an involution.

It remains to check that the domain of $\varPhi$ is the complete array, D. For a given $(a,\alpha )\in D$, since $\phi$ is a bijection of D, there exists a unique $(b,\beta )\in D$ such that $(a,\alpha )=\phi (b,\beta )$. Then $(a,\alpha )=(a,\phi (b,\beta )_{2})$, and so from (4) it follows that $(a,\alpha )$ belongs to the domain of $\varPhi$.

To conclude the proof, we need only note that the pairs on either side of (4) are mutual inverses as both $(a,\phi (a,\alpha )_{2})$ and $(b,\phi (b,\beta ){}_{2})$ are idempotents because $(a,\alpha )$ and $\phi (a,\alpha )$ are mutual inverses, as are $(b,\beta )$ and $\phi (b, \beta )$. Therefore $\varPhi \cup \{(0,0)\}$ is an involution matching for our semigroup S. $\square$