Orientation-preserving and orientation-reversing mappings: a new description

Abstract

We characterise the respective semigroups of mappings that preserve, or that preserve or reverse orientation of a finite cycle, in terms of their actions on oriented triples and oriented quadruples. This leads to a proof that the latter semigroup coincides with the semigroup of all mappings that preserve intersections of chords on the corresponding circle.

1 Orientation-preserving and orientation-reversing mappings on a cycle

This section presents definitions and some known results; it is based mainly on Catarino and Higgins [1] and also on McAlister [4]. Let [n] denote the set $\{0,1,\ldots ,n-1\}$. Consider a sequence $S=(a_{0},a_{1},\ldots ,a_{t-1})$ drawn from [n]. A cyclic variant of S is a sequence $(a_{i+1},a_{i+2},\ldots ,a_{i})$, where $0\le i<t$, and subscripts are taken modulo t. We say S is cyclic if there is at most one subscript i such that $a_{i}>a_{i+1}$ (subscripts taken modulo t). Equivalently, S is cyclic if and only if at least one of its cyclic variants is non-decreasing $a_{i+1}\le a_{i+2}\le \cdots \le a_{i}$. We say S is anti-cyclic if there is at most one subscript i such that $a_{i}<a_{i+1}$. Equivalently, S is anti-cyclic if and only if at least one of its cyclic variants is non-increasing $a_{i+1}\ge a_{i+2}\ge \cdots \ge a_{i}$. We shall say that S is oriented if S is cyclic or S is anti-cyclic. Orientation, that is, being cyclic or anti-cyclic, is a property inherited by subsequences of an oriented sequence. We say that S is uniquely oriented if S is cyclic and not anti-cyclic or anti-cyclic and not cyclic. Let |S| denote the number of distinct elements of S, that is, $|S|=|\{a_{0},\dots ,a_{t-1}\}|$. It is easy to see that if $|S|\le 2$ then S is either both cyclic and anti-cyclic (for example, $S=(0,1)$) or neither (for example, $S=(0,1,0,1)$). As we will show below, non-trivial and useful examples of oriented sequences are those with $|S|=3$ and $|S|=4$.

We introduce an equivalence relation $\sim$ on the set of uniquely oriented sequences whereby $S\sim T$ if S and T have the same orientation. For example, if $S'$ is a cyclic variant of S, then $S\sim S'$.

We write $\mathcal {T}_{n}$ for the full transformation semigroup on [n]. For $\alpha \in \mathcal {T}_{n}$ and a sequence $S=(a_{0},a_{1},\ldots ,a_{t-1})$ with entries drawn from [n] we shall write $S\alpha$ for the sequence $(a_{0}\alpha ,a_{1}\alpha ,\ldots ,a_{t-1}\alpha )$.

Definition 1

A mapping $\alpha \in \mathcal {T}_{n}$ is orientation-preserving (resp. orientation-reversing) if the sequence $(0,1,\ldots ,n-1)\alpha$ is cyclic (resp. anti-cyclic); these names are justified by Lemma 2. The collection of all orientation-preserving (resp. orientation-reversing) mappings in $\mathcal {T}_{n}$ is denoted by $\mathcal {OP}_{n}$ (resp. $\mathcal {OR}_{n}$), while $\mathcal {P}_{n}$ is defined as $\mathcal {P}_{n}=\mathcal {OP}_{n}\cup \mathcal {OR}_{n}$.

If S is a sequence, we denote the reversed sequence by $S^{R}$.

Lemma 2

Let $\alpha \in \mathcal {OP}_{n}$ (resp. $\alpha \in \mathcal {OR}_{n}$) and let S be an oriented sequence such that $|S\alpha |\ge 3$. Then $S\alpha \sim S$ (resp. $S\alpha \sim S^{R}$).

Since a sequence S is cyclic (resp. anti-cyclic) if and only if $S^{R}$ is anti-cyclic (resp. cyclic), it follows that we may equally define $\mathcal {OP}_{n}$ as the set of all members of $\mathcal {T}_{n}$ that map anti-cyclic sequences to anti-cyclic sequences.

That $\mathcal {OP}_{n}$ is a semigroup is now easily proved (Lemma 2.1 of [1]). However $\mathcal {OR}_{n}$ is not a semigroup: $\mathcal {OR}_{n}\cdot \mathcal {OR}_{n}=\mathcal {OP}_{n}$, $\mathcal {OR}_{n}\cdot \mathcal {OP}_{n}=\mathcal {OP}_{n}\cdot \mathcal {OR}_{n}=\mathcal {OR}_{n}$, and $\mathcal {OP}_{n}\cap \mathcal {OR}_{n}=\{\alpha \in \mathcal {P}_{n}:\,|\text {im}(\alpha )|\le 2\}$. It follows that $\mathcal {P}_{n}$ is a semigroup.

2 Describing $\mathcal {OP}_{n}$ and $\mathcal {OR}_{n}$ with oriented triples

This result was stated but not proved in [3, Proposition 1.1], so here it is proved for the first time.

Theorem 3

Let $\alpha \in \mathcal {T}_{n}$. Then $\alpha \in \mathcal {OP}_{n}$ (resp. $\alpha \in \mathcal {OR}_{n})$ if and only if for every triple $S=(i,j,k)$ of members of [n], $S\alpha$ has the same (resp. the opposite) orientation as S.

Proof

($\Rightarrow )$ Follows from inheritance of orientation by subsequences.

($\Leftarrow )$ First, assume $\alpha \not \in \mathcal {OP}_{n}$. We find a cyclic triple (r, s, t) such that $(r\alpha ,s\alpha ,t\alpha )$ is not cyclic. Since $\alpha$ is not orientation-preserving there exist distinct integers i, j such that $i\alpha >(i+1)\alpha$ and $j\alpha >(j+1)\alpha$.

Case 1 $i\alpha \ne j\alpha$. Without loss we assume that $i\alpha >j\alpha$. Put $r=i,s=j,t=j+1$. Then (r, s, t) is cyclic but since $i\alpha>j\alpha >(j+1)\alpha$, $(r\alpha ,s\alpha ,t\alpha )$ is anti-cyclic (and not cyclic as the three entries are pairwise distinct).

Case 2 $(i+1)\alpha \ne (j+1)\alpha .$ Without loss we assume that $(i+1)\alpha >(j+1)\alpha$. Put $r=i,s=i+1,t=j+1$. Then (r, s, t) is cyclic but since $i\alpha>(i+1)\alpha >(j+1)\alpha$, $(r\alpha ,s\alpha ,t\alpha )$ is anti-cyclic.

Case 3 $i\alpha =j\alpha$ and $(i+1)\alpha =(j+1)\alpha$. Since $|\text {im}{\alpha }{|\ge 3}$ there exists k such that $k\alpha \not \in \{i\alpha ,(i+1)\alpha \}$. It follows that the members of the list $i,i+1,k,j,j+1$ are pairwise distinct and, by interchanging the symbols i and j if necessary, we may assume that $(i,i+1,k,j,j+1)$ is cyclic.

• (1) Suppose that $k\alpha >i\alpha .$ Put $r=k,s=i,t=i+1$. Then (r, s, t) is cyclic but since $k\alpha>i\alpha >(i+1)\alpha$, $(r\alpha ,s\alpha ,t\alpha )$ is anti-cyclic.

• (2) Suppose $i\alpha>k\alpha >(i+1)\alpha$. Put $r=i,s=k,t=j+1$. Then (r, s, t) is cyclic but $(r\alpha ,s\alpha ,t\alpha )$ is anti-cyclic.

• (3) Suppose $(i+1)\alpha >k\alpha$. Put $r=i,s=i+1,t=k$. Then (r, s, t) is cyclic but since $i\alpha>(i+1)\alpha >k\alpha$, $(r\alpha ,s\alpha ,t\alpha )$ is anti-cyclic.

This completes a proof of the reverse implication in the case where $\alpha \not \in \mathcal {OP}_{n}$. For the case where $\alpha \not \in \mathcal {OR}_{n}$ let $\gamma$ be the permutation of order reversal: $i\gamma =n-1-i$ $(0\le i\le n-1)$. Then $\gamma \in \mathcal {OR}_{n}$ so that $\alpha \gamma \not \in \mathcal {OP}_{n}$ as otherwise $\alpha \gamma ^{2}=\alpha \in \mathcal {OR}_{n}$. We then apply the previous argument to conclude that there exist three pairwise distinct integers forming a cyclic triple (r, s, t) such that $(r\alpha \gamma ,s\alpha \gamma ,t\alpha \gamma )$ is anti-cyclic. But then $(r\alpha \gamma ^{2},s\alpha \gamma ^{2},t\alpha \gamma ^{2})=(r\alpha ,s\alpha ,t\alpha )$ is cyclic, and noting this completes the proof. $\square$

3 Describing $\mathcal {P}_{n}$ with oriented quadruples and with chord intersections

We introduce a new characterization of $\mathcal {P}_{n}$ in terms of the preservation of a single geometric property. This stems from the study of Gauss diagrams in knot theory, which consist of a circle and chords. The paper [2] first described Gauss diagrams satisfying an important property known as being realizable, and now we know that one can describe realizable Gauss diagrams by only using the information stating, for every pair of chords, whether or not they intersect [5].

Definition 4

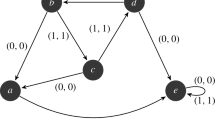
Consider the integers $0,1,\ldots ,n-1$ positioned clockwise around a circle. A mapping $\alpha \in \mathcal {T}_{n}$ has the chord property if whenever the chords ac and bd intersect $(a,b,c,d\in [n])$ then so do the chords $a\alpha c\alpha$ and $b\alpha d\alpha$. (See Figure 1.)

Fig. 1

Diagram a shows two intersecting chords 13 and 02 as a dotted line and dashed line. If we apply a mapping $0\mapsto 0$, $1\mapsto 0$, $2\mapsto 3$, $3\mapsto 2$, the rearranged chords still intersect, see diagram b. If, instead, we apply a mapping $0\mapsto 0$, $1\mapsto 1$, $2\mapsto 3$, $3\mapsto 2$, the rearranged chords do not intersect, see diagram c

This definition makes allowance for one point chords. If there is repetition among the a, b, c, d due to the chords having a common endpoint, then chord intersection is preserved by any mapping $\alpha$ by virtue of the image of that common endpoint. We shall denote the clockwise arc of the circle R that runs from a to c as $\overrightarrow{ac}$.

Lemma 5

Let $a,b,c,d\in [n]$ be four points on the circumference of a circle on which the members of [n] are placed clockwise. The chords ac and bd meet if and only if the quadruple $S=(a,b,c,d)$ is oriented.

Proof

Suppose the chords ac and bd meet. Suppose that our four points are distinct. If b lies on the arc $\overrightarrow{ac}$ then d lies on $\overrightarrow{ca}$ and (a, b, c, d) is oriented clockwise on the circle, whence (a, b, c, d) is cyclic. Alternatively b lies on the arc $\overrightarrow{ca}$, and d does not, in which case d lies on $\overrightarrow{ac}$ and (a, d, c, b) is cyclic. But then $(a,d,c,b)^{R}=(b,c,d,a)\sim (a,b,c,d)$ is anti-cyclic. In either event, S is oriented.

On the other hand, suppose that S has a repeated entry. If $a=c$, then since ac meets bd, it follows that $a=b=c$ or $a=d=c$, in which case S is oriented; the same conclusion follows if $b=d$. Otherwise two cyclically adjacent entries in S, for instance a and b, are equal, in which case it also follows that S is oriented.

Conversely, if (a, b, c, d) is cyclic, then b lies on $\overrightarrow{ac}$ and d lies on $\overrightarrow{ca}$ so that the chords ac and bd meet. On the other hand if (a, b, c, d) is anti-cyclic then $(a,b,c,d)^{R}=(d,c,b,a)$ is cyclic and so the chord $db=bd$ meets the chord $ca=ac$, as required. $\square$

Proposition 6

A mapping $\alpha \in \mathcal {T}_{n}$ has the chord property if and only if for every oriented quadruple $S=(a,b,c,d$), the image sequence $S\alpha$ is also oriented.

Proof

Suppose that $\alpha$ has the chord property and let $S=(a,b,c,d$) be an oriented sequence. Let $S\alpha =(A,B,C,D)$. By Lemma 5, the chords ac and bd intersect, and hence by hypothesis so do the chords AC and BD. Again by Lemma 5 it follows that $S\alpha$ is oriented.

Conversely, suppose that the image of every oriented quadruple under $\alpha$ is oriented and let chords ac and bd meet. By Lemma 5 (a, b, c, d) is oriented and so by hypothesis so is (A, B, C, D). Again by Lemma 5, it follows that chords AC and BD meet, whence we conclude that $\alpha$ has the chord property. $\square$

Theorem 7

• (a) $\alpha \in \mathcal {P}_{n}$ if and only if for every oriented quadruple $S=(a,b,c,d)$, $S\alpha$ is also oriented.

• (b) $\alpha$ has the chord property if and only if $\alpha \in \mathcal {P}_{n}$.

Proof

(b) follows from Proposition 6 together with (a).

(a) ($\Rightarrow )$ Follows from inheritance of orientation by subsequences.

(a) ($\Leftarrow$) We again argue the contrapositive, like in Theorem 3, so suppose that $\alpha \not \in \mathcal {P}_{n}$. Let $m=$ min$(\text {im}(\alpha )).$ Choose i such that $i\alpha =m$ but $i\alpha <(i+1)\alpha$. Consider the cyclic sequence $I:i+1,i+2,\ldots ,i+n-2$ and let j be the first listed member of I such that $j\alpha >(j+1)\alpha$; since $\alpha \not \in \mathcal {OP}_{n}$, j occurs in I, as there are at least 2 integers t such that $t\alpha >(t+1)\alpha$. Similarly let $M=$ max$(\text {im}(\alpha )).$ Choose $i'$ such that $i' \alpha =M$ but $i' \alpha >(i'+1)\alpha$. Consider the cyclic sequence $I':i'+1,i'+2,\ldots ,i'+n-2$ and let $j'$ be the first listed member of $I'$ such that $j' \alpha <(j'+1)\alpha$; since $\alpha \not \in \mathcal {OR}_{n}$, $j'$ occurs in $I'$ as there are at least 2 integers t such that $t\alpha <(t+1)\alpha$. Note that $(i+1)\alpha \le j\alpha$ and $(i'+1)\alpha \ge j' \alpha .$

Case 1 $(i+1)\alpha =j\alpha$ or $(i'+1)\alpha =j' \alpha$. First suppose $(i+1)\alpha =j\alpha$, whence by definition of j and the assumption that $(i+1)\alpha =j\alpha$ it follows that

$$\begin{aligned} m=i\alpha <(i+1)\alpha =\cdots =j\alpha >(j+1)\alpha . \end{aligned}$$

(3.1)

Consider the subsequence J of I given by $J:j+1,j+2,\ldots ,i+n-2$. Since $\alpha \not \in \mathcal {OR}_{n}$, there exists k in J such that $k\alpha <(k+1)\alpha$, (for otherwise the first such k is $k=i+n-1$, but then $k+1=i$, contradicting $(k+1)\alpha >k\alpha \ge i\alpha$). By choosing the first listed such k in J we have by (3.1) that $j\alpha >k\alpha$ and so

$$\begin{aligned} m=i\alpha<(i+1)\alpha =j\alpha>k\alpha <(k+1)\alpha >i\alpha =m. \end{aligned}$$

(3.2)

From (3.2) we infer that $S=(i,i+1,k,k+1)$ is a cyclic quadruple of pairwise distinct integers but, by (3.2), $S\alpha$ is not oriented.

Similarly if $(i'+1)\alpha =j' \alpha$ the dual argument obtained by reversing all inequalities and interchanging $\mathcal {OP}_{n}$ and $\mathcal {OR}_{n}$ throughout yields a cyclic sequence $S'=(i',i'+1,k',k'+1)$ such that $S' \alpha$ is not oriented as

$$\begin{aligned} M=i' \alpha>(i'+1)\alpha =j' \alpha<k'\alpha >(k'+1)\alpha <i'\alpha =M. \end{aligned}$$

Case 2: $(i+1)\alpha <j\alpha$ and $(i'+1)\alpha >j'\alpha$. From the given inequalities we now have

$$\begin{aligned} m=i\alpha<(i+1)\alpha <M=i'\alpha>(i'+1)\alpha >m=i\alpha , \end{aligned}$$

which implies that $T=(i,i+1,i',i'+1)$ is a cyclic sequence of pairwise distinct integers such that $T\alpha =(i\alpha ,(i+1)\alpha ,i'\alpha ,(i'+1)\alpha )$ is not oriented. $\square$