The word problem for one-relation monoids: a survey

Abstract

This survey is intended to provide an overview of one of the oldest and most celebrated open problems in combinatorial algebra: the word problem for one-relation monoids. We provide a history of the problem starting in 1914, and give a detailed overview of the proofs of central results, especially those due to Adian and his student Oganesian. After showing how to reduce the problem to the left cancellative case, the second half of the survey focuses on various methods for solving partial cases in this family. We finish with some modern and very recent results pertaining to this problem, including a link to the Collatz conjecture. Along the way, we emphasise and address a number of incorrect and inaccurate statements that have appeared in the literature over the years. We also fill a gap in the proof of a theorem linking special inverse monoids to one-relation monoids, and slightly strengthen the statement of this theorem.

1 Introduction

The word problem for one-relation monoids is one of the most fundamental open problem in combinatorial algebra. The problem itself is deceptively simple to state.

Question

Is the word problem decidable for every one-relation monoid?

The fact that this problem has remained open since its conception more than a century ago is in stark contrast to the same situation in the theory of one-relator groups; among the first known results in this latter case was Magnus’ 1932 theorem proving that the word problem is decidable for all one-relator groups. P. S. Novikov is quoted as saying that the word problem for one-relation monoids “contains something transcendental”, and part of the aim of this survey is to illustrate this. Although A. I. Maltsev [106] wrote in his 1965 monograph on the theory of algorithms that the problem “has nearly been solved by Adian”, we shall see that the mysterious and complex world in which the problem lives had only just begun to unfurl at that point. This survey is intended to provide a history of the above question, and the numerous attempts to attack, simplify, and solve it. It is intended to be readable by researchers with a graduate level of experience in combinatorial algebra.

An overview of the structure of the survey is as follows. In §1, we first present a brief rundown on some elementary concepts necessary to appreciate the statement of the question and some of terminology of the methods by which it will be attacked. Then, in §2, an exposition of the early history of the problem and early results of decidability is presented, in which the special and cancellative cases are treated. In §3, we then present the two types of compression, which together with a further reduction theorem can be used to prove a reduction result of the problem to some particular difficult cases. In §4, we present Adian’s algorithm ${\mathfrak {A}}$, which, if its behaviour could be properly understood, would solve the word problem for all one-relation monoids. We also discuss the ramifications of a result of Sarkisian’s which was thought to be proved, but where a gap was later discovered. In §5, we present some sporadic results that have appeared in various publications and contexts. Finally, in §6, we present some modern and future directions for the problem, including links with inverse monoids, in which a gap in a proof of a theorem from 2001 by Ivanov, Margolis and Meakin is fixed, as well as links with undecidability and the Collatz conjecture.

There have been some other surveys on the word problem for one-relation monoids, which we begin by mentioning. The 1984 survey by Adian and Makanin [14] deals with general algorithmic questions in algebra, and mentions some results on the one-relation case. There is also a 1988 survey by Lallement [95], which later appeared with only minor modifications in a conference proceedings [96] and as part of lecture notes [97]. However, this survey is rather brief, and does not detail much of the history or ideas behind many of the proofs; furthermore, it includes some results which are now only considered conjecture (as we shall see in §4.4). Adian’s 1993 brief survey [9] suffers from this too, giving many statements which are conditional. That survey additionally focuses primarily on the algorithm ${\mathfrak {A}}$. The only survey the author is aware of which addresses the now-conjectural results is the 2000 survey by Adian and Durnev [13]. The scope of this survey is general decision problems, and the word problem for one-relation monoids only occupies a comparatively small part. Finally, Cain and Maltcev [35] have produced an extensive and excellent collection on the status of various miscellaneous decision problems for one-relation monoids, but it gives no details whatsoever regarding the word problem.

The contributions of authors writing in Russian to the area are numerous. For this reason, we make a linguistic remark. For the reader unfamiliar with Russian-to-English transliteration conventions, certain names which are written in the Cyrillic alphabet can and have been transliterated to the Roman alphabet in several different ways. This is generally done phonetically, with many different standard methods of transliteration existing. As Schein notes, “it is like transliterating the name Poincaré, written in Russian, as Puankare in the Roman alphabet” [157]. This means that one person can at times be split into several in the literature; this notoriously happened to the famous semigroup theorist V. V. Wagner, who himself preferred the German spelling of his name, although standard transliteration dictates that it ought to be Vagner. Personal preference of the author is also important; for example, S. I. Adian published under Adian, Adjan, and Adyan, but seems to have favoured Adian in later years. We give below, for reference, a fixed set of spellings used in the survey of author names who are affected by the above issues. The alternative transliterations of the same names can be used to inform the reader of the correct pronunciation of the names.

Transliteration used	Alternative transliteration(s)
Adian	Adjan, Adyan
Anisimov	Anīsīmov, Anisimoff
Greendlinger$^\mathrm{a}$	Grindlinger
Maltsev	Malcev, Mal’cev, Mal’tsev
Markov	Markoff
Matiyasevič	Matijasevich, Matijasevic
Novikov	Novikoff
Oganesian	Hovhannisyan, Oganessjan, Oganesyan
Sarkisian	Sarkisjan, Sarkisyan
Sushkevič	Sushkevich, Suschkewitsch
Tseitin	Ceitin, Tseĭtin, Tsejtin
Wagner	Vagner

1. $^\mathrm{a}$Martin Greendlinger was born in the US, but defected to the USSR in the 1960s, and his name was transcribed in a non-involutive way between English and Russian

A remark on the source material that forms the backbone of this survey is necessary. In general, most articles on the word problem for one-relation monoids are rather self-contained, and not difficult to read on their own. On the contrary, the English translations of certain Russian articles are rather poor, and at times completely change theorems as written. Remarks have been added in this survey to alert the reader of this. The author wishes to emphasise the contributions of S. I. Adian in this area of research. His results and general interest in this problem, and related areas, have been influential beyond measure. Even a cursory glance through the survey or its bibliography will make this clear. This survey does not aspire to replace its sources; the original proofs are all perfectly readable, and particular care has been taken to make precise attributions of theorems and results. However, an overview of the main ideas behind a given proof has been given at times, to aid in exposition. This has been done in part for reasons of brevity, and in part because there is little to add to the original proofs. The author hopes that the interested reader will pursue these articles and experience these excellent proofs for themselves. After all, as N. H. Abel said, one should study the masters and not the pupils.

The author wishes to express his gratitude to R. D. Gray, V. Guba, D. Jackson, J. Meakin, M. Volkov, and the reviewer for many helpful comments. Finally, a special thanks is extended to G. Watier for his detailed and careful reading of an early version of the survey, and comments which significantly improved the exposition in numerous places.

2 Preliminaries

In this section, we shall give some background information, including defining all terms used later and some remarks on the notation used.

2.1 Arghmgog

A finite set of symbols A is called an alphabet. Then $A^*$ denotes the free monoid on A, which consists of all words of finite length over the alphabet A, together with the operation of word concatenation. For example, using the charming example given by A. Turing [173], if $u, v \in A^*$ are two such words (e.g. arghm and gog), then uv represents the result of writing one after the other (i.e. arghmgog). The empty word in $A^*$, being the identity element, is denoted interchangeably either by $\varepsilon$ or 1, depending on the context. For two words $u, v \in A^*$, the expression $u \equiv v$ indicates graphical equality, i.e. that the words are spelled the same. The length |u| of a word $u \in A^*$ is defined inductively by setting $|\varepsilon | = 0$, and $|u \cdot a| = |u| + 1$ for $a \in A$ and $u \in A^*$. For $u \in A^*$ the reversal $u^\text {rev}$ is just u written backwards.

A rewriting system T (also called a semi-Thue system, named after the Norwegian mathematician A. Thue [171]) on an alphabet A is a subset of $A^*~\times ~A^*$. All rewriting systems considered, as well as the presentations associated to them (see below), will be assumed to be finite unless explicitly stated otherwise. A rewriting system T induces a relation $\xrightarrow {}_T$ on $A^*$ as follows: if $u, v \in A^*$, then $u \xrightarrow {}_{T} v$ if and only if there exist $x, y \in A^*$ and some rule $(\ell , r) \in T$ such that $u \equiv x\ell y$ and $v \equiv x r y$. The reflexive and transitive closure of is denoted . The symmetric and transitive closure of is denoted . If $(\ell , r) \in T$, then replacing an occurrence of $\ell$ by r (or vice versa) in some word $u \in A^*$ is called an elementary transformation in T.

A rewriting system T on A is called terminating (also sometimes called Noetherian) if there exists no infinite chain . The system is called locally confluent if for all $u, v, w \in A^*$, we have and together imply that there exists some $z \in A^*$ such that and . The system is called confluent if for all $u, v, w \in A^*$, we have and together imply that there exists some $z \in A^*$ such that and . If a rewriting system T is terminating and confluent, then we say that T is complete (also sometimes called convergent). A word is $w \in A^*$ is irreducible (modulo T) if it does not contain any subword that is a left-hand side of some rule of T. The set of irreducible elements of T is denoted ${\text {Irr}}(T)$. If T is terminating, we can for every word $w \in A^*$ find an element $w' \in {\text {Irr}}(T)$ such that by “rewriting” w, i.e. continuously removing any left-hand sides of rules we find as subwords of w until this cannot be done any further. In a complete rewriting system, there exists a unique such $w'$. Hence any complete rewriting system has unique normal forms for all elements. The word problem for a rewriting system T over A is the decision problem of, given any two words $u, v \in A^*$, deciding in finite time whether . Naturally, for a finite complete rewriting system, this problem can be solved by computing the normal forms of the input words, followed by graphical comparison.¹

A monoid presentation $\text {Mon} \langle A \mid u_i = v_i \, (1 \le i \le p) \rangle = \text {Mon} \langle A \mid T \rangle$ is the ordered pair (A, T), where T is a rewriting system on A. We will abuse notation and take such a monoid presentation to denote the monoid . This quotient, called the monoid defined by the presentation $\text {Mon} \langle A \mid T \rangle$ is well-defined, as is clearly the smallest congruence containing T. We will abuse notation and substitute “let $M = \text {Mon} \langle A \mid u_i = v_i \, (1 \le i \le p) \rangle$” for “let M be the monoid defined by the presentation $\text {Mon} \langle A \mid u_i = v_i \, (1 \le i \le p) \rangle$”. We say that M is finitely presented. If two words $u, v \in A^*$ are equal in , then we say that $u=v$ in M. If $u, v \in A^*$ are such that u can be obtained from v by an elementary transformation in T, then we shall say that u can be obtained from v by an elementary transformation in $M = \text {Mon} \langle A \mid T \rangle$.

We shall also speak of a group presentation $\text {Gp} \langle A \mid T \rangle$, which is a shorthand for the monoid presentation $\text {Mon} \langle A \cup A^{-1} \mid T \cup \{ a_ia_i^{-1} = 1, a_i^{-1}a_i = 1 \mid a_i \in A \} \rangle$, where $A^{-1}$ is a set in bijective correspondence with A such that $A \cap A^{-1} = \varnothing$, and T is a subset of $(A \cup A^{-1})^*\times (A \cup A^{-1})^*$.

Unless explicitly specified, all (monoid or group) presentations in this survey will be assumed to be finite.

Let $M = \text {Mon} \langle A \mid T \rangle$. We say that a word $u \in A^*$ is right invertible in M if there exists some $v \in A^*$ such that $uv = 1$ in M. We define left invertibility analogously. We say that $u \in A^*$ is invertible in M if it is left and right invertible. We say that u is right divisible by v if there exists $w \in A^*$ such that $u = wv$ in M, and left divisibility is defined analogously. We say that M is right cancellative if for all $u, v, x \in A^*$ we have that $ux = vx$ in M implies $u = v$ in M. We define left cancellative analogously. We say that M is cancellative if it is left and right cancellative. Note that every group is cancellative.

2.2 Notational remarks

We make some remarks on the notation used in this survey in contrast to other notation for the same concepts found elsewhere in the literature. As mentioned, we use $\equiv$, to denote equality of words, i.e. equality in the free monoid. This is sometimes denoted $\eqcirc$ in older articles, particularly Soviet ones. We sometimes use $:=$ to denote a “definitional” equality, i.e. that the equality in question is also a definition. This is sometimes denoted $\rightleftharpoons$ in older articles, particularly Soviet ones. We use |u| to denote the length of a word in the free monoid. This is sometimes denoted $[u^\partial$ or $\partial (u)$ in older articles, particularly Soviet ones, where $\partial$ is used to represent the first letter in the Russian word dlina, meaning length. We denote the empty word as 1 or $\varepsilon$, depending on notational convenience. This is sometimes denoted $\Lambda$ in older articles, as well as articles in theoretical computer science and set theory, with $\Lambda$ indicating the first letter of the German leer, meaning empty.

2.3 Decision problems

We give some examples of decision problems which are of central importance to this survey. Let $M = \text {Mon} \langle A \mid R \rangle$. Then the word problem for M has as input two words $u,v \in A^*$, and outputs yes if $u = v$ in M, and otherwise outputs no. The left divisibility problem for M has as input two words $u, v \in A^*$ and outputs yes if u is left divisible by v in M, and otherwise outputs no. The right divisibility problem is defined entirely analogously. In general, these three problems are pairwise independent from one another; indeed, the divisibility problems are trivially solvable whenever M is a group. However, if M is given by a presentation in which all defining relations are non-empty, and such that M is left cancellative, then it is not hard to show that decidability of the left divisibility problem implies decidability of the word problem, by induction on word length and noting that no non-empty word is equal to the empty word in such a monoid. The analogous statement is true substituting right for left.

We note that as, in the context of this survey, a monoid M is always assumed to be given by a finite presentation, say $\text {Mon} \langle A \mid R \rangle$, we have that if two words $u, v \in A^*$ are equal in M, then we can find a sequence of single applications of relations from R which transforms u into v. Thus, if the left (right) divisibility problem is decidable for M, and one finds that the word u is left divisible by the word v, then one can always effectively construct a “witness” word w such that $u = vw$ in M (resp. $u = wv$ in M).

We also introduce the following useful piece of notation. Let $M = \text {Mon} \langle A \mid R \rangle$. Let $R^\text {rev}~\subseteq ~A^*\times A^*$ be the rewriting system with rules $(u^\text {rev}, v^\text {rev})$ whenever $(u, v) \in R$. Let

$$\begin{aligned} M^\text {rev}= \text {Mon} \langle A \mid R^\text {rev} \rangle . \end{aligned}$$

Then it is easy to see that the word problem for M reduces to the word problem for $M^\text {rev}$, and vice versa; for $u = v$ in M if and only if $u^\text {rev}= v^\text {rev}$ in $M^\text {rev}$. More importantly, the left divisibility problem for M reduces to the right divisibility problem for $M^\text {rev}$, for given $u, v \in A^*$, there exists a word $w \in A^*$ such that $u = wv$ in M if and only if $u^\text {rev}= v^\text {rev}w^\text {rev}$ in $M^\text {rev}$. This trick will often be used.

In 1947, and almost simultaneously, Markov [111, 112] and Post [149] proved the existence of a finitely presented monoid with undecidable word problem. This was quite a remarkable theorem, and can be, as noted by Crvenkovič [46], considered the first undecidability result outside the foundations of mathematics. Providing monoids with an undecidable word problem is also no mere idle pursuit if one is interested in providing groups with an undecidable word problem, which was at times seen as a primary motivation. Indeed, A. Turing’s famous proof [173] of the existence of a finitely presented cancellative monoid with undecidable word problem plays a key rôle in Novikov’s 1955 detailed proof of the existence of a finitely presented group with undecidable word problem.² Turing’s proof is at times rather inaccurate, and should best be read with the accompanying 1958 analysis of these issues by Boone [27]. We note that because of the large number of alterations required to make Turing’s proof correct, Adian and Novikov [15] gave an argument in 1958 which modifies Novikov’s original argument to circumvent any reference to cancellative monoids with an undecidable word problem.

A contrasting theorem had been known for decades. This was a decidability result by W. Magnus [99], a student of M. Dehn’s, who translated Dehn’s geometric intuition about the structure of one-relator groups into a purely combinatorial result [39].

Theorem 1.1

(Magnus, 1932) The word problem is decidable for every one-relator group.

Here a one-relator group is one that can be defined by a group presentation with a single defining relation $\text {Gp} \langle A \mid w=1 \rangle$. By contrast, the best known undecidability result for groups is, to this day, a 12-relator group with undecidable word problem due to Borisov [28], and the word problem for k-relator groups when $2 \le k \le 11$ remains open in general. On the other hand, a much smaller gap is known for monoids. In the sequel to his 1947 paper, Markov provided an example of a monoid with 33 defining relations and undecidable word problem [112]. This was subsequently improved, in 1956 and 1958, respectively, by D. Scott and G. S. Tseitin, who both provided examples of monoids with seven very short defining relations and undecidable word problem [158, 172]. Tseitin’s example remains the shortest, with respect to total length of the defining relations, known example.

The number of defining relations sufficient for presenting a monoid with undecidable word problem continued to creep down. In 1966, G. S. Makanin provided an example showing that five (short!) defining relations suffice [102]; Ju. V. Matiyasevič [114] provided an example with the same number of relations (one of which is rather long) in 1967. This record would not last for long; that same year, Matiyasevič improved this to give an example of a monoid with only three defining relations and with undecidable word problem [113].³ The first two relations of this monoid are very short; the third is very long (several hundred letters in either word). Three relations remains the smallest number of defining relations known to suffice to present a monoid with undecidable word problem. In this way, we have at this point arrived at the question at the heart of this survey.

Question

Is the word problem decidable for every one-relation monoid?

The deceptively simple nature of the question is a large part of what makes the word problem for one-relation monoids such a fascinating problem; the fact that it remains open even today makes it all the more intriguing.

3 Early results (1914–1960)

When one is presented with a one-relation monoid $\text {Mon} \langle A \mid u=v \rangle$ and faced with the task of solving its word problem, one of the first questions one ought to ask is: what are the trivial cases? We shall begin with these, and then present the theory of cancellative and special one-relation monoids, two classes which were quickly dealt with. The “father of semigroup theory”, A. K. Sushkevič, considered a problem about semigroups—or indeed monoids—solved if it could be reduced to a problem about groups [168, §38] (see also [54]). We shall see that this theme is very much present in these early results, in which reductions to Magnus’ result on the word problem for one-relator groups are made.

3.1 Equal length and self-overlap free words

The first observation one might make when presented with a one-relation monoid $\text {Mon} \langle A \mid u=v \rangle$ is that if $|u| = |v|$, then any elementary transformation of any word will keep its length fixed. In particular, two words are equal only if their lengths are equal; hence one can effectively enumerate all finitely many words equal to a given word, giving an immediate solution to the word problem.⁴ This observation was already made by Thue in 1914, in the very paragraph following his introduction of the word problem for monoids [171, Problem I].

In fact, that same paragraph by Thue provides another trivial case. Suppose $|u| > |v|$, and that u is self-overlap free, i.e. no non-trivial prefix of u is also a suffix of u (such a word is often called a hypersimple word in the Soviet literature). Then the rewriting system with the single rule $u \rightarrow v$ is locally confluent, as there are no critical pairs; furthermore, it is terminating as $|u| > |v|$. By Newman’s lemma [122], it is a finite complete rewriting system for the monoid, thus solving the word problem. This is essentially the idea behind Thue’s proof, although this obviously has no reference to the 1942 Newman’s lemma.

We pause at this moment to address a potentially misleading comment which has appeared in the literature. In 1984, Book and Squier [26] proved that “almost all” one-relation monoids have decidable word problem. This claim is made specific in the following sense: for a positive integer k, fix an alphabet A of size k. For a positive integer $n>1$ let $u_k(n)$ be the number of self-overlap free words in $A^*$. Then Book and Squier proved that the ratio $u_k(n) / k^n$ tends to 1 as $k, n \rightarrow \infty$ (though note that this result was already observed by Nielsen [123], outside the context of one-relation monoids). A quick thought together with this result yields that “almost all” one-relation monoids have decidable word problem.

This result is less exciting than it first appears, as the following analysis will indicate. Indeed, for fixed k, the ratio $u_k(n) / k^n$ does not tend to 1 as $n \rightarrow \infty$. Indeed, for $k=2$, the ratio is approximately 0.2677868 (see OEIS sequence A094536 [1], and also Nielsen [123] for other values of k). Hence this argument can only be used to yield that around 27% of two-generated one-relation monoids $\text {Mon} \langle a,b \mid u=v \rangle$ have decidable word problem, which is not quite as exciting—by comparison, the fraction of two-generated one-relation monoids $\text {Mon} \langle a,b \mid u=v \rangle$ satisfying $|u|=|v|$ is quickly seen, by summing a geometric series, to be $\frac{1}{3}$. The asymptotic argument by Book and Squier (as beautiful as the statement might be) also ignores the wild and complex behaviour of one-relation monoids that we shall detail presently. It is hence not particularly useful as a tool for gaining insight into the word problem for all one-relation monoids. In spite of this, Book [24] frames the above density result as strong evidence that the word problem is decidable for all one-relation monoids; we reiterate that, in view of the above analysis, this framing is not accurate.⁵

Outside these trivial cases,⁶ the word problem for one-relation monoids appears to have laid untouched for some decades, with seemingly little interest in the problem. However, in the early 1960s, the Soviet mathematician S. I. Adian would begin working on this problem, and would thus begin the development that would transform the area into its modern form.

3.2 Cancellativity and embeddability

The study of cancellativity of monoids and their embeddability into groups goes back to the very beginning of semigroup theory. Any submonoid of a group is cancellative, and in the commutative case it is not hard to see (analogous to constructing a field of fractions) that a cancellative monoid can be embedded in a group. Furthermore, it is clear by universal considerations that if $M = \text {Mon} \langle A \mid R \rangle$ is group-embeddable, then M can be embedded in $\text {Gp} \langle A \mid R \rangle$, i.e. the group with the “same presentation” as M, by the identity map $a \mapsto a$. For example, the cancellative commutative monoid $\text {Mon} \langle a,b \mid ab=ba \rangle$, isomorphic with ${\mathbb {N}} \times {\mathbb {N}}$, can be embedded by the identity map in $\text {Gp} \langle a,b \mid ab=ba \rangle$, isomorphic with ${\mathbb {Z}} \times {\mathbb {Z}}$.

Sushkevič studied the problem of embedding cancellative monoids in groups, and in 1935, he published a “proof” that being cancellative is also sufficient for embeddability into a group [169]!⁷ This “proof”, however, would not be long-lived; in 1937, Maltsev found a counterexample to Sushkevič’s “theorem”, i.e. an example of a cancellative monoid which is not group-embeddable [103]. Sushkevič later that same year wrote a monograph⁸ on the theory of generalised groups, in which he (unsuccessfully) attempts to fix his erroneous proof, while simultaneously, slightly perplexingly, acknowledging Maltsev’s counterexample [170]. Maltsev was correct, and would later produce a countable list of necessary and sufficient conditions for a monoid to embed in a group, such that no finite sublist is also necessary and sufficient [104, 105]. Later, Adian would provide a monoid which is finitely presented as a cancellative monoid, but which is not finitely presented as a monoid [4, Theorem 1]. Hollings has written an excellent and thorough overview of the history of embedding monoids into groups, to which we refer the interested reader [68].

As concluded above, being cancellative is not in general sufficient for a monoid to embed in a group. One might instead ask what conditions are sufficient. S. I. Adian seems to be have become interested in this problem—and cancellativity in general—at an early stage; indeed, in 1955, in one of his first published papers, he proved the existence of a finitely presented cancellative semigroup with undecidable divisibility problems [3, Theorem 1]. Five years later, Adian [5] introduced a very simple criterion which is sufficient for group-embeddability, and which furthermore can easily be read off a presentation for the monoid. We now present this criterion.

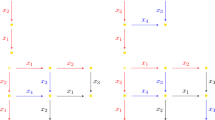
Let $M = \text {Mon} \langle A \mid R \rangle$. The left graph ${\mathcal {L}}(M)$ of M is defined as the undirected (not necessarily simple) graph with vertex set A, and an edge $(a_i, a_j)$ for $a_i, a_j \in A$ in ${\mathcal {L}}(M)$ for every occurrence of a relation $r=s$ in R in which $a_i$ is the initial letter of r, and $a_j$ is the initial letter of s. We define the right graph ${\mathcal {R}}(M)$ in an analogous way, substituting terminal letters for initial letters. We emphasise that we permit both loops and multiple edges; see the examples below. We say that (the presentation for) M is left cycle-free if ${\mathcal {L}}(M)$ is a forest, i.e. a disjoint union of trees, and otherwise we say that M has left cycles.⁹ We define right cycle-free analogously, and we say that M is cycle-free if it has no left or right cycles. We extend this definition to group presentations in which the defining relations are all written over a positive alphabet. Thus we may speak of e.g. the cycle-free group $\text {Gp} \langle a,b \mid ab=ba \rangle$.

Example 2.1

Let $M_1 = \text {Mon} \langle a,b,c \mid ab = ba^2, ac = c^2b \rangle$. Then the left and right graphs of $M_1$ are given below.

Hence $M_1$ is both left and right cycle-free. In particular (see Theorem 2.5 below), $M_1$ is cancellative and embeds in the cycle-free group $G_1 = \text {Gp} \langle a, b, c \mid ab = ba^2, ac=c^2b \rangle$. By a simple Tietze transformation, this latter group is a one-relator group isomorphic with an HNN-extension of a free group of rank three, and the word problem is hence straightforward to solve using the Britton-Novikov lemma and the Nielsen procedure for decidability of the membership problem for subgroups of free groups; alternatively, one can use Magnus’ breakdown procedure (cf. e.g. [115]). In either case, having solved the word problem in $G_1$ we hence conclude that $M_1$ has decidable word problem, as $M_1 \le G_1$.

Example 2.2

Let $M_2 = \text {Mon} \langle a,b,c \mid b^2ca = bca b, a^2b = ba^2 c, ac^2 = cb^2a \rangle$. Then the left and right graphs of $M_2$ are given below.

Hence $M_2$ has both left and right cycles. We can conclude nothing about the cancellativity of $M_2$ based on these graphs, nor anything about its group-embeddability. Solving the word problem in this monoid is left as a potentially somewhat interesting challenge.

Example 2.3

Let $M_3 = \text {Mon} \langle a,b,c,d \mid ab = cd, aeb = ced \rangle$. Then the left and right graphs of $M_3$ are

Hence $M_3$ has both left and right cycles. We can conclude nothing about its cancellativity based on these graphs; however, it can be shown that it is simultaneously both cancellative and not group-embeddable (see below).

Example 2.4

Let $\Gamma$ be an (undirected) finite graph with vertex set $a_1, \ldots , a_k$. Let

$$\begin{aligned} A(\Gamma ) = \text {Gp} \langle a_1, \ldots , a_k \mid a_i a_j = a_j a_i \, \text {whenever} \, (a_i, a_j) \in E(\Gamma ) \rangle . \end{aligned}$$

Then $A(\Gamma )$ is called a right-angled Artin group (RAAG). Evidently, the left and right graphs of $A(\Gamma )$ are both isomorphic to $\Gamma$, and hence the above presentation for $A(\Gamma )$ is a cycle-free presentation if and only if $\Gamma$ is a finite forest. Hence, given any $\Gamma$, as the left and right divisibility problems are trivially decidable in the monoid presentation with the same generators and defining relations (often called a trace monoid), it follows by a result due to Sarkisian [154, Theorem 3] that the word problem is decidable for the RAAG $A(\Gamma )$ whenever $\Gamma$ is a finite forest. We remark that this is quite a contorted method of solving the word problem; in fact the word problem is relatively straightforward to solve in $A(\Gamma )$ for arbitrary finite graphs $\Gamma$ (see especially Crisp et al. [45]). Furthermore, it is a consequence of a more general due to Paris [145] that any trace monoid embeds in its corresponding right-angled Artin group; this is also easy to prove using the theory of rewriting systems, cf. Chouraqui [41]. Right-angled Artin groups play a key rôle in modern geometric group theory due to their rich subgroup structure, as demonstrated in the work of Wise and Haglund on special cube complexes (an area far beyond the scope of this survey; the reader is directed to Wise’s monograph [178]) and the recent interest in solving equations over right-angled Artin groups, cf. e.g. [38, 159, 160].

We emphasise that, given a presentation, it is easily decidable whether it has left or right cycles, or indeed whether it is cycle-free. The key property of cycle-free monoids is that one can show that any such monoids are in fact group-embeddable.

Theorem 2.5

([5, Theorem 5]) Let $M = \text {Mon} \langle A \mid R \rangle$ be a finitely presented monoid. If M is left (right) cycle-free, then M is left (right) cancellative. If M is cycle-free, then M is cancellative and can furthermore be embedded in $\text {Gp} \langle A \mid R \rangle$ via the identity map.

We make some remarks on this theorem before proceeding, and some developments following the work by Adian. The theorem has been generalised to all cycle-free monoids (not just finitely presented), by Remmers [152], who used used the diagram method of geometric semigroup theory. See Higgins [66, 1.§7 and 5.§3] for an excellent overview of these methods. Recently, these diagram methods have been used to generalise Adian’s theorem to certain situations in which some relations of the form $w=1$ (see §2.3) are also permitted [83]. Diagram methods have also been used for studying left or right cycle-free monoids from the point of view of asphericity e.g. in the work by Kilibarda [87] (see also the monograph by Guba and Sapir [64]). A. I. Valitskas also strengthened the second half of Theorem 2.5 to prove that if a monoid $M = \text {Mon} \langle A \mid R \rangle$ is (1) left (right) cycle-free; and (2) right (left) cancellative; then M is group-embeddable. This is a non-trivial strengthening, as being right cycle-free implies being right cancellative, but the converse does not hold. Valitskas’ proof of the strengthening was never published; a proof was given later by Guba [61, Theorem 4]. Gerasimov [53] has also given some necessary and sufficient conditions for a monoid to embed in a group. For a broad overview of various embeddability criteria for monoids and general algebra, we refer the reader to the survey by Bokut’ [22].

Returning to cycle-free presentations and their relation to the word problem, we note that as it is decidable whether or not a monoid (presentation) is cycle-free, being cycle-free is not a necessary condition for cancellativity; indeed, it the problem of deciding whether a given finitely presented monoid is cancellative is undecidable in general. However, this can also be seen by way of concrete example, as provided by Adian [5]¹⁰ as follows

$$\begin{aligned} \text {Mon} \langle a,b,c,d,e \mid ab=cd, aeb=ced \rangle . \end{aligned}$$

As witnessed above in Example 2.3, it has both left and right cycles, but it is not hard to show that it is cancellative. One can also check that $ae^2b \ne ce^2d$ in this monoid, and so it cannot possibly embed in the group with the same presentation.

Thus we have three properties for monoids, which in general are not equivalent:

• (1) being cancellative;

• (2) being group-embeddable;

• (3) being cycle-free.

Hence, as the examples above show, we only have $(3) \implies (2) \implies (1)$, and the reverse implications can fail already in the case of two defining relations. However, in the case of one-relation monoids, it is not very hard to show that $(1) \implies (3)$, by induction on the number of elementary transitions required. Hence these three properties are all equivalent in the class of one-relation monoids. Summarising, we have the following theorem.

Theorem 2.6

([5, Corollary 4 & 5]) Let $M = \text {Mon} \langle A \mid u=v \rangle$ be a one-relation monoid. Then the following are equivalent:

• (1) M is cancellative;

• (2) M embeds in $\text {Gp} \langle A \mid u=v \rangle$;

• (3) M is cycle-free.

Hence, if M is cycle-free then M has decidable word problem.

As a concrete example, any monoid of the form $\text {Mon} \langle a,b \mid aub = bva \rangle$ is cancellative, and the word problem is decidable in any such monoid.¹¹ This monoid embeds in $\text {Gp} \langle a,b \mid auba^{-1}v^{-1}b^{-1} = 1 \rangle$, to which we can readily apply Magnus’ procedure for solving the word problem. We hence see that our first example of a non-trivial solvable word problem comes about as an example of Sushkevič’s principle of reducing a semigroup problem to a group problem. With one non-trivial class of one-relation taken care of, there is one class that stands out among the rest as being particularly special.

3.3 Special monoids

A monoid is called special if it admits a monoid presentation having the form $\text {Mon} \langle A \mid r_1 = 1, r_2 = 1, \ldots , r_k =1 \rangle$. Of course, all groups are special monoids; in fact, given a k-relator group, it always admits a $(k+1)$-relation special monoid presentation by a simple trick introduced already by von Dyck [50]: if G is given by the presentation $\text {Gp} \langle a_1, \ldots , a_n \mid r_1 = 1, \ldots , r_k = 1 \rangle$, where the $r_i$ are words in the $a_j$ and their inverses, we can add a single generator x and a defining relation $a_1 a_2 \ldots a_{n} x a_{n} \ldots a_2 a_1 = 1$. We can now clearly rewrite the $w_i$ as words over the positive alphabet; for example, $a_1^{-1}$ is equal to $a_2 \ldots a_{n} x a_{n} \ldots a_2 a_1$. The resulting special monoid is isomorphic with G. There are, however, k-relator groups which are not k-relation special monoids (see §5.2).

Now, not all special monoids are groups; the simplest example is the bicyclic monoid $\text {Mon} \langle b,c \mid bc=1 \rangle$. There b is right (but not left) invertible, and c is left (but not right) invertible. It is, in fact, not too hard to show that M has no non-trivial invertible elements. Special monoids were first properly¹² introduced to the literature and given their name by G. S. Tseitin in 1958, who named them special associative systems (spetsialnaia assotsiativnaia sistema). However, the first systematic study of special monoids came 2 years later, by Adian [6].

We say that a special monoid $\text {Mon} \langle A \mid r_1 = 1, r_2 = 1, \ldots , r_k=1 \rangle$ is $\ell$-homogeneous if there exists $\ell \in {\mathbb {N}}$ such that $|r_i| = \ell$ for all $1 \le i \le k$. One defines $\ell$-homogeneous groups in precisely the same manner. In his paper, Adian gives a very thorough overview of the proofs of the following central result regarding homogeneous special monoids; the full proofs were provided 2 years later in his celebrated monograph, see [7, III.Theorem 1].

Theorem 2.7

(Adian, 1960) Let $M = \text {Mon} \langle A \mid r_1 = 1, r_2 = 1, \ldots , r_k=1 \rangle$ be an $\ell$-homogeneous special monoid. If the word problem is decidable for all k-relator $\ell$-homogeneous groups, then the word problem and the divisibility problems are decidable for M.

Note that for fixed k and $\ell$, there are only finitely many k-relator $\ell$-homogeneous groups (up to a free factor of a free group). Furthermore, every one-relation special monoid is $\ell$-homogeneous, yielding the following immediate corollary by applying Magnus’ result.

Corollary 2.8

(Adian, 1960) Let $M = \text {Mon} \langle A \mid w=1 \rangle$. Then the word problem and divisibility problems for M is decidable.

Adian also proves certain undecidability results for $\ell$-homogeneous special monoids. In particular, he proves that for every $\ell > 3$, there exists an $\ell$-homogeneous special monoid with undecidable word problem. Note that in the case $\ell =2$, the word problem is trivially decidable, as every 2-homogeneous group is a free product of finitely many cyclic groups (cf. [7, III.§5, Theorem 11]). The subgroup U(M) of a monoid M consisting of all invertible elements of M is called the group of units of M. When giving the full proofs in his monograph, Adian also proves (see [7, III.§4, Theorem 8]) that the group of units of an $\ell$-homogeneous k-relation special monoid M is isomorphic with an $\ell$-homogeneous k-relator group, and that the word and divisibility problems for M reduce to the word problem for U(M) (though this latter reduction is not in general constructive). In particular, this gives the following beautiful result.

Theorem 2.9

(Adian, 1966) Let $M = \text {Mon} \langle A \mid w=1 \rangle$. Then the group of units U(M) of M is a one-relator group.

In fact, Adian gives an algorithm for computing a presentation for the group of units of a one-relation special monoid [7, III.§4, Theorem 7] which Zhang [186] noticed had unnecessary steps (this is discussed in greater detail below). We give a brief overview of the simplified algorithm here, following Kobayashi [90]. Let $M = \text {Mon} \langle A \mid w=1 \rangle$. Let $C_0 = \{ w \}$, and suppose, for induction, that $C_i$ has been defined for some $i \ge 0$. Let $x, y \in C_i$. If $x \equiv vu$ and $y \equiv uw$ for some words $u, v, w \in A^+$ (i.e. if x and y overlap in the word u) then we set

$$\begin{aligned} C_{i+1} = (C_i \setminus \{x, y \} ) \cup \{ u, v, w \}. \end{aligned}$$

As the lengths of u, v and w are all less than the lengths of x and y, we must have that this process will stabilise eventually, giving us a finite (but not uniquely determined) sequence $C_0, C_1, \ldots , C_k$. In this case, $C_k$ is a biprefix code (i.e. none of the words of $C_k$ overlap), and in fact it is not difficult to see that although the sequence is not, the set $C_k$ is uniquely determined by w. We set C(w) to be this set, and call this the self-overlap free code generated by w. In an entirely analogous fashion we can define the self-overlap free code C(W) generated instead by a set of words W.

Example 2.10

Let $w \equiv abbaab$. Let $C_0 = \{ abbaab\}$. Then choosing $x \equiv abbaab$ and $y \equiv abbaab$, we find that we can take $x \equiv (ab)(baab)$ and $y \equiv (abba)(ab)$, so we set

$$\begin{aligned} C_1 = (C_0 \setminus \{ abbaab \}) \cup \{ ab, baab, abba\} = \{ ab, baab, abba\}. \end{aligned}$$

Now we can pick $x \equiv ab$ and $y \equiv baab$, and find $x \equiv (a)(b)$ and $y \equiv (b)(aab)$, so we set

$$\begin{aligned} C_2 = (C_1 \setminus \{ ab, baab \}) \cup \{ a, b, aab\} = \{ a, b, aab, abba\}. \end{aligned}$$

Now we can repeatedly pick $x \equiv a$ followed by repeatedly picking $x \equiv b$ to remove both aab and abba, and we eventually end up with a set

$$\begin{aligned} C(w) = \{ a, b \}. \end{aligned}$$

Thus $C(w) = \{ a, b \}$ is the self-overlap free code generated by $w \equiv abbaab$.

Example 2.11

Let $w \equiv abcabdab$. Then the self-overlap free code generated by w is

$$\begin{aligned} C(w) = \{ ab, cabd\}. \end{aligned}$$

In particular, C(w) is not an infix code in general, i.e. one might find words in C(w) appearing as subwords of other words in C(w).

Returning to our given one-relation monoid $\text {Mon} \langle A \mid w=1 \rangle$, if $C(w) = \{ w_1, w_2, \ldots , w_n\}$, then let $X = \{ x_1, \ldots , x_n \}$ be a set in bijective correspondence with C(w) via the map $\varphi :w_i \mapsto x_i$. As C(w) is a biprefix code, this can be uniquely extended to a homomorphism

$$\begin{aligned} \varphi :C(w)^*\rightarrow X^*. \end{aligned}$$

As w is clearly a word in $C(w)^*$, we can consider the word $\varphi (w)$, and the monoid

$$\begin{aligned} \text {Mon} \langle X \mid \varphi (w) = 1 \rangle . \end{aligned}$$

It is not hard to see that this monoid is, in fact, a (one-relator) group. Clearly, every word in $C(w)^*$ is invertible, but the key insight by Adian is that every invertible word is equal in M to some word from $C(w)^*$. In particular, U(M) is isomorphic with the group with the above presentation.

Example 2.12

Let $M = \text {Mon} \langle a,b,c,d \mid abcabdab = 1 \rangle$. Then

$$\begin{aligned} C(w) = \{ ab, cabd\} = \{ w_1, w_2 \}. \end{aligned}$$

We factor abcabdab uniquely as (ab)(cabd)(ab), and hence find that

$$\begin{aligned} U(M) \cong \text {Mon} \langle x_1, x_2 \mid x_1x_2x_1 = 1 \rangle \cong \text {Gp} \langle x_1, x_2 \mid x_1x_2x_1 = 1 \rangle \cong {\mathbb {Z}}. \end{aligned}$$

Thus the group of units of M is infinite cyclic, and the word and divisibility problems are rather straightforward to solve in M (see below).

This algorithm is very simple to use in practice. We shall present the main idea of why the word problem can be reduced to the word problem for the group of units below, in the general setting of k-relation special monoids.

Makanin [101] in his Ph.D. thesis extended Adian’s results from $\ell$-homogeneous special monoids to all special monoids (the results were announced in a bulletin article [102]). Specifically, he proved that the group of units of a k-relation special monoid M is a k-relator group, and that the word problem and divisibility problems for a k-relation special monoid in which all defining relations have length $\le \ell$ reduce to the word problem for all k-relator groups in which all defining relators have length $\le \ell$. This solution is constructive, but Makanin also proves that the word and divisibility problems in M reduce non-constructively to the word problem for U(M). The non-constructibility comes from the difficulty of actually computing a presentation for U(M). The author of the survey clarifies this issue in a forthcoming expository article on the subject [128]. We also remark that the author has recently translated Makanin’s Ph.D. thesis into English [129]. We summarise the key theorem below.

Theorem 2.13

(Makanin, 1966) Let $M = \text {Mon} \langle A \mid r_1 = 1, r_2 = 1, \ldots , r_k=1 \rangle$ be a special monoid. If the word problem is decidable for U(M), then the word problem and the divisibility problems are decidable for M.

The fundamental idea behind the study of special monoids (not just the one-relation case) can be heuristically explained as follows: suppose that we have a word w containing $r_1$ and $r_2$ as subwords, where $r_1=1$ and $r_2=1$ are some two defining relations of a special monoid. Suppose that these two occurrences have a non-trivial overlap. Then we can write $w \equiv w' r_1' s r_2'' w''$, where $r_1 \equiv r_1' s$ and $r_2 \equiv s r_2''$. As s is a suffix of $r_1$, it is left invertible, and as it is a prefix of $r_2$, it is right invertible. Hence any overlap of defining relations must be invertible: in particular, if we factor $r_1$ and $r_2$ (necessarily uniquely) into minimal invertible factors as $r_1 \equiv \delta _1 \ldots \delta _k$ and $r_2 \equiv \delta _1' \ldots \delta _\ell '$, then we must have

$$\begin{aligned} s \equiv \delta _i \delta _{i+1} \ldots \delta _k \delta _1' \delta _2' \ldots \delta _j' \end{aligned}$$

for some $i, j \ge 1$. Hence, all resolutions of overlaps in a special monoid are actually resolutions of equalities of invertible words. Because of this crucial point, the reader familiar with the importance of resolving overlaps when solving the word problem in rewriting systems will at this point, perhaps, feel more confident in accepting that the word problem of a special monoid could somehow be reduced to the same problem for its group of units (while noting that the above heuristic is far from a proof!).

A little more rigorously, there is certainly always a way one can factorise any relator word $r_i$ into certain minimal invertible pieces, i.e. words which do not have any left or right factors which are invertible. To find this set, Adian and Makanin use certain extension operations to compute this set, starting from $C(\cup _i \{ r_i \})$ (i.e. the self-overlap free code generated by the set of left-hand sides of the defining relations). These operations are based on using equalities in the group with the k-relator presentation obtained from factorising the pieces into words from $C(\cup _i \{ r_i \})$, which can produce new, shorter invertible words, giving a presentation for another group, and the process repeats. Eventually, one finds that this process terminates (though of course not constructively, unless the word problem is decidable in all groups one encounters along the way). This results in a finite set $\Delta$ consisting of all invertible words w with no non-trivial left or right factors in $\Delta$ with the property that w is equal to some invertible factor of some relation word $r_i$, and such that additionally $|w| \le |r_i|$.¹³ One can then factor the relation words into words from $\Delta$ uniquely, and obtain a presentation for a group. This group turns out to be isomorphic with the group of units of M.

Let us say we now wish to solve the word problem for M. We do this by finding normal forms of words in the following manner. Let $w \in A^*$ be a word. The key point in Adian’s and Makanin’s proofs is to find subwords of w in $\Delta ^*$ and replace them with equal and shorter words in $\Delta ^*$, until this cannot be done anymore. They prove that the resulting form is unique, and hence reduce the word problem for M to the comparison of words in $\Delta ^*$. By construction, this is the word problem for comparison of words in $\Lambda ^*$, which is just the word problem for U(M).

At this point, it is important to discuss the contributions to this area by L. Zhang in the 1990s, coming from theoretical computer science and the theory of rewriting systems. He noticed that the extension operations of Adian and Makanin, used to compute the set $\Delta$, is not necessary in the one-relation case. This observation reduces to the fact that given a one-relation monoid $\text {Mon} \langle A \mid w=1 \rangle$, it is not possible to have non-trivial equalities of distinct pieces with one another, cf. [186, Lemma 1]. This follows from Magnus’ Freiheitssatz for the one-relator group $\text {Gp} \langle X \mid \varphi (w) = 1 \rangle$. Beyond this, the proof—which is now phrased in terms of rewriting systems—is identical.

Zhang would thereafter write several other papers on special monoids, rephrasing many of the old results using rewriting systems. This brought the attention of Adian [9], who writes:

I was surprised recently seeing several papers of L. Zhang [...] published in well known mathematical journals. The large part of these papers looks like a result of rewriting from [Adian’s monograph] in a direct meaning of the word. Of course, to refresh the ideas and the technique of [the monograph] may be useful, but it should be done in a more decent way.

The papers referenced by Adian are [182, 183, 185, 186]; also relevant to this discussion are [144, 184, 187]. There is merit to Adian’s criticism. For example, none of the results appearing in [186] are new. They are all rather straightforward corollaries of Makanin’s work, whether they appear implicitly or explicitly therein. For example, Zhang proves that the submonoid of right invertible elements of a special monoid is isomorphic with a free product of a free monoid by the group of units; this observation, though not phrased algebraically, is precisely what is used by Makanin to reduce the right divisibility problem to the word problem for the group of units [101, I.§3].

One feature common to Zhang’s papers on special monoids (especially [186]) is that they may appear succinct and elegant when compared to the difficult and lengthy inductive arguments of Adian and Makanin. This characterisation is also not entirely accurate; the difficult and lengthy inductive arguments are still included in Zhang’s approach, but are hidden in the references to various confluence lemmas and results for general rewriting systems. On the contrary, the work by Adian and Makanin on special monoids is extensively self-contained. This can, of course, make a cursory reading of the material rather difficult: the chapter of Adian’s monograph [6] which deals with the word problem for special monoids ends with Lemma 111 (!), and the corresponding chapter of Makanin’s Ph.D. thesis, which is rather streamlined by comparison, ends with Lemma 31. Thus the main benefit of reading [186] comes from its expository nature.

The other papers by Zhang on the topic do, however, contain some new results for special monoids, including the one-relation case. To this end we only expand on the conjugacy problem. There are a number of generally inequivalent ways to define this problem for special monoids; Zhang [183] proved that several natural such definitions coincide in the special case. The one we shall adopt here is the following: decide for two given words $u, v \in A^*$ whether $ux = xv$ holds for some $x \in A^*$. Using rewriting techniques, Zhang reduces the conjugacy problem to the same problem for the group of units. In particular, this shows that the conjugacy problem is decidable in $\text {Mon} \langle A \mid w^n=1 \rangle$, when $n >1$, as the conjugacy problem is decidable for one-relator groups with torsion by applying the B. B. Newman Spelling Theorem [121] (cf. also [127]).

We mention briefly that special monoids have recently been investigated by the author from the point of view of their geometry and formal language theory, cf. [124, 126].

In summary, we have thus seen two examples (special and cycle-free) of families of one-relation monoids with decidable word problem, in which the solution to the word problem reduces fairly directly to Magnus’ result that the word problem is decidable in one-relator groups. At this point, however, there yet remained many cases and difficult reductions to make, which began to illustrate the complex nature of the problem.

4 Compression and reductions (1974–1987)

Following the initial success of Adian’s work on cycle-free and special one-relation monoids, Adian and his doctoral student G. U. Oganesian would provide the next major step forward in the form of (weak) compression in 1978. However, this method had in fact been discovered independently several years earlier by G. Lallement, for slightly different (but closely related) purposes; the authors seem to have been unaware of the others’ work. The method allows one to reduce each of the word and divisibility problems for one-relation monoids with left and right cycles to the same problem for a one-relation monoid with a shorter defining relation. Lallement focused on the case when this resulting monoid was special—this case would later be called subspecial one-relation monoids by Kobayashi. The methods in this section ultimately lead to the situation of reducing the word and divisibility problems to one-relation monoids without left cycles or without right cycles.

There are two types of compression. One is “weak”, and is based on finding a self-overlap free word as a prefix and suffix of both words in the defining relation. This method has been used and analysed in-depth by Lallement [94], a 1978 paper by Adian and Oganesian [16], Kobayashi [90], Gray and Steinberg [57], and Nyberg-Brodda [125]. There is also another, more general, form of compression, which bears some similarity to the first, and is “stronger” in the sense it only requires that the two words in the defining relation have some shared prefix and some shared suffix; this is featured only in a 1987 paper by Adian and Oganesian [17] and the surveys by Lallement [95,96,97]. The titles of the two papers [16, 17] are very similar, and their years of publications are, for obvious reasons, rather easy to mistake for one another. For this reason, it is not uncommon to see references in the literature to the two papers confused. We remark that the terminology “weak” resp. “strong” compression does not appear elsewhere in the literature.

4.1 Weak compression

We shall present the theory of weak compression essentially as it appears in the work of Adian and Oganesian [16], while blending in some notation from Kobayashi [90] (see §6 for more details on Kobayashi’s work). We remark that compression can easily be defined for arbitrary monoids, not necessarily one-relation, but for brevity we only deal with the one-relation case below; see [125] for full details.

Let $M = \text {Mon} \langle A \mid u=v \rangle$ be a one-relation monoid. Let $\alpha \in A^+$ be a self-overlap free word. If $u, v \in \alpha A^*\cap A^*\alpha$, then we say that M is (weakly) compressible. Suppose that M is compressible. Consider the language $\Sigma (\alpha ) = \alpha (A^*\setminus A^*\alpha A^*)$. Let

$$\begin{aligned} X(\alpha ) = \{ x_{w_1}, x_{w_2}, \ldots , x_{w_i}, x_{w_{i+1}}\ldots , \} \end{aligned}$$

be a set of new symbols in bijective correspondence with the (infinitely many) elements of $\Sigma (\alpha )$ via the bijection $\alpha w_i \mapsto x_{w_i}$. It is not hard to show that $\Sigma (\alpha )$ is a suffix code (see Kobayashi [90, Lemma 3.4] and Lallement [94] for details), i.e. no element of $\Sigma (\alpha )$ is a suffix of any other; thus, for any word in $\alpha A^*$, we can decode it uniquely, moving from left to right, as a product of elements of $\Sigma (\alpha )$. In particular, as $u, v \in \alpha A^*$, we can uniquely factor the words in the defining relation as

$$\begin{aligned} u&\equiv w_{1,1} w_{1,2} \ldots w_{1,n} \alpha , \\ v&\equiv w_{2,1} w_{2,2} \ldots w_{2,m} \alpha \end{aligned}$$

where $w_{i, j} \in \Sigma (\alpha )$. We define the compressor function $\psi _\alpha$ on the defining relation as:

$$\begin{aligned} \psi _{\alpha }(u)&= x_{w_{1,1}} x_{w_{1,2}} \ldots x_{w_{1,n}}, \\ \psi _{\alpha }(v)&= x_{w_{2,1}} x_{w_{2,2}} \ldots x_{w_{2,m}}. \end{aligned}$$

Let $X \subseteq X(\alpha )$ be the (finite) set of all $x_{i, j}$ which appear in one of the above two factorisations. Then we define the left monoid L(M) associated to M to be

$$\begin{aligned} L(M) = \text {Mon} \langle X \mid \psi _{\alpha }(u) = \psi _{\alpha }(v) \rangle . \end{aligned}$$

This definition looks rather abstract, but in practice it is very simple to find.

Example 3.1

Consider the one-relation monoid

$$\begin{aligned} M = \text {Mon} \langle a,b \mid ab ba ab bb ab bb ab = abbaab \rangle . \end{aligned}$$

Then the self-overlap free word $\alpha = ab$ is both a prefix and a suffix of each word in the defining relation, and obviously it is the unique such word. We factor each word uniquely into elements from $\Sigma (ab) = ab (A^*\setminus A^*ab A^*)$ as:

$$\begin{aligned} abbaabbbabbbab&\equiv ab{\underline{ba}} \cdot ab{\underline{bb}} \cdot ab{\underline{bb}} \cdot ab, \\ abbaab&\equiv ab{\underline{ba}} \cdot ab. \end{aligned}$$

Thus, the compressor $\psi _{ab}$ as applied to each word gives:

$$\begin{aligned} \psi _{ab}(abbaabbbabbbab)&= x_{ba} x_{bb} x_{bb}, \\ \psi _{ab}(abbaab)&= x_{ba}. \end{aligned}$$

The left monoid of M thus has the presentation

$$\begin{aligned} L(M) = \text {Mon} \langle x_{ba}, x_{bb} \mid x_{ba} x_{bb} x_{bb} = x_{ba} \rangle \cong \text {Mon} \langle c,d \mid cdd = c \rangle . \end{aligned}$$

The word problem in L(M) is now easily decidable by using the complete rewriting system $(cdd \rightarrow c)$; as we shall see below (Theorem 3.2), this implies that the word problem for M is decidable.

We note some immediate properties of L(M). The defining relation $\psi _{\alpha }(u) = \psi _{\alpha }(v)$ is shorter than the defining relation $u=v$, so there is basis for the name compression. The relation $\psi _{\alpha }(u) = \psi _{\alpha }(v)$ could itself, of course, be compressible. There is also a natural way to extend $\psi _\alpha$ to other words than just the defining relations; this behaves similarly to a homomorphism, there is a close connection between words equal in M and words equal in L(M). We do not give the full details of this here, as it is already very well written in Adian and Oganesian’s [16] original paper.

Theorem 3.2

(Lallement 1974, Adian and Oganesian 1978) Let M be a compressible one-relation monoid. Then each of the word problem and the divisibility problems reduces to the respective problem in L(M).

The proof of this theorem, while occasionally notationally somewhat technical, is not conceptually difficult at all, and bears some similarity to the situation of special monoids (see §2.3). Indeed, a resolution of an overlap of defining relations in M will clearly be a resolution of an overlap of defining relations in L(M)—as $\alpha$ is self-overlap free and $u, v \in \alpha A^*\cap A^*\alpha$—and the proof heuristic given for special monoids applies in this case too. We do not give the full details of the proof here, but give an instructive example.

Example 3.3

Let $M = \text {Mon} \langle a,b \mid abaabbab = abbabaab \rangle$. Then M is weakly compressible with respect to $\alpha \equiv ab$, and we find that

$$\begin{aligned} \psi _\alpha (abaabbab)&= x_a x_b, \\ \psi _\alpha (abbabaab)&= x_b x_a. \end{aligned}$$

Hence we expect M to behave as the free commutative monoid

$$\begin{aligned} L(M) = \text {Mon} \langle x_a, x_b \mid x_a x_b = x_b x_a \rangle . \end{aligned}$$

Indeed, it is not hard to find a structure coarsely resembling the right Cayley graph of the free commutative monoid on two generators inside that of M. The geometric aspects of weak compression are interesting in their own right, but are beyond the scope of the present survey. Full details will soon appear in work by the author.

We remark that Theorem 3.2 and the general method of weak compression as it appears in Adian and Oganesian’s article [16, Theorem 3] appears to have been solely due to Adian; a footnote on the first page of the article specifies precisely which of the two authors contributed which theorem.

The astute reader will have noticed the partial attribution of Theorem 3.2 to Lallement. We give a brief overview of weak compression as used by him. Lallement’s primary interest appears to have been in characterising which one-relation monoids have non-trivial elements of finite order, similar to Fischer et al.’s 1972 characterisation in the one-relator group case [51]. Lallement considered monoids of the form

$$\begin{aligned} \text {Mon} \langle A \mid u = v \rangle \quad \text {such that } u \in v A^*\cap A^*v, \end{aligned}$$

and proved that the word problem and divisibility problems in this case reduce to the word problem for a special monoid. The monoids of the above form are called subspecial. The special monoid obtained from this reduction is just the left monoid of the monoid in question, although Lallement’s compression technique, which is in a “single step”, differs slightly from the method using $\psi _\alpha$ as detailed above, and is rather technical in nature. Clearly, a subspecial monoid (with v non-empty) can be weakly compressed in the earlier sense, by considering the maximal self-overlap free word which is a prefix and a suffix of v. By repeatedly compressing in the usual sense, one eventually obtains the same monoid as described by Lallement; see Gray and Steinberg’s treatment [57] of compression for this connection. We do not detail this method here, but mention that Zhang [185] rewrote Lallement’s proof using the language of rewriting system, and used this to solve the conjugacy problem in many cases of one-relation monoids with non-trivial elements of finite order.

As mentioned, one of the reasons for Lallement’s interest in subspecial monoids came from characterising the one-relation monoids which have non-trivial elements of finite order. First, the following result (see [94, Corollary 2.5]) completely characterises the existence of non-trivial (i.e. $\ne 1$) idempotents in one-relation monoids.

Theorem 3.4

(Lallement, 1974) Let $M = \text {Mon} \langle A \mid u=v \rangle$. Then M has a non-trivial idempotent if and only if M is subspecial or special, but not a group.

Using this, he is able to completely characterise the one-relation monoids with elements of finite order as the subspecial monoids of a particular form, see [94, Theorem 2.7].

Theorem 3.5

(Lallement, 1974) A one-relation monoid has non-trivial elements of finite order if and only if its presentation is of the form $\text {Mon} \langle A \mid (uv)^mu = (uv)^nu \rangle$, where uv is not a proper power in the free monoid, and $m > n \ge 0$.

Lallement’s goal is clearly algebraic in nature, as opposed to Adian and Oganesian, who focused on the decision problems for the monoids involved. He also proves many statements regarding the residual finiteness of one-relation monoids, which we shall not expand on here, beyond mentioning that one can derive many more powerful algebraic statements and properties regarding one-relation monoids using weak compression. This algebraic connection has been exploited by Kobayashi [90] (see §6 and Gray and Steinberg [57]. The author of the present survey has also investigated the language-theoretic aspects of compression [125]. For example, it is decidable whether a one-relation monoid with a non-trivial idempotent has context-free word problem (see [125] for the relevant definitions).

At this point, we make the crucial point that weak compression is not enough to reduce the word problem for all one-relation monoids to the left cancellative case. Indeed, the one-relation monoid

$$\begin{aligned} \text {Mon} \langle a,b \mid aab = ab \rangle \end{aligned}$$

is not (weakly) compressible, but it has both left and right cycles. To deal with these cycles, we therefore need a more powerful tool.

4.2 Strong compression

For strong compression, we shall use an encoding function $\tau _k$, which is applicable to any one-relation monoid with left and right cycles, unlike weak compression. This encoding function already (rather confusingly) appeared in the 1978 paper by Adian and Oganesian. We follow the definition as given by Adian and Oganesian in their 1987 article introducing this encoding [17]. Let $E_1, E_2, \ldots , E_n$ be all words of length $k>0$ in an alphabet A with $|A|=m$; note that $n = m^k$. Let $e_1, e_2, \ldots , e_n$ be letters in some new alphabet. We shall define $\tau _k(w)$ for words $w \in A^*$. If $|w| < k$, then we set $\tau _k(w) = 1$. If $w \equiv E_i$ for some $1 \le i \le n$, then we set $\tau _k(w) = e_i$. If w begins with $E_i$, and $w \equiv aw'$ for some letter $a \in A$, then we set $\tau _k(w) \equiv e_i \tau _k(w')$.

Example 3.6

Let $A = \{ a, b\}$ and $k = 2$. Let $E_1 \equiv aa, E_2 \equiv ab, E_3 \equiv ba, E_4 \equiv bb$. Then we consider the encoding function $\tau _2$, which operates as follows:

$$\begin{aligned} \tau _2(aababab)&\equiv e_1 \tau _2(ababab) \\&\equiv e_1 e_2 \tau _2(babab) \\&\equiv e_1 e_2 e_3 \tau _2(abab) \\&\equiv e_1 e_2 e_3 e_2 \tau _2(bab) \\&\equiv e_1 e_2 e_3 e_2 e_3 \tau _2(ab) \\&\equiv e_1 e_2 e_3 e_2 e_3 e_2. \end{aligned}$$

Obviously, the particular ordering chosen on $\{ aa, ab, ab, bb \}$ is of no significance.

Now the encoding function $\tau _k$ is not, in general, a homomorphism, but it has many similar properties: let $u, v \in A^*$ be arbitrary words such that $|v| \ge k-1$. Write $v \equiv v' v''$ such that $|v'| = k-1$. Then we clearly have

$$\begin{aligned} \tau _k(uv) \equiv \tau _k(uv') \tau _k(v''), \end{aligned}$$

and a similar statement is easy to make regarding $\tau _k(uv)$ when $|u| \ge k-1$. Using this property of $\tau _k$, one finds the following quite striking lemma, which is almost (see the remark following the lemma) the statement of [17, Lemma 1].

Lemma 3.7

Suppose $M = \text {Mon} \langle A \mid u=v \rangle$ has both left and right cycles. Let C be the maximal common prefix of u and v, and let D be the maximal common suffix of u and v. Let $k = 1 + \min (|C|, |D|)$. Then the word problem and the divisibility problems for M can be reduced to the corresponding problems for the monoid

$$\begin{aligned} M_\tau := \text {Mon} \langle e_1, e_2, \ldots , e_n \mid \tau _k(u) = \tau _k(v) \rangle , \end{aligned}$$

The relation $\tau _k(u) = \tau _k(v)$ has no left cycles if $|C| \le |D|$, and no right cycles if $|C| \ge |D|$. If $|C| = |D|$, then the word problem for M is decidable.

Remark 3.8

The statement of [17, Lemma 1] concludes that in the case $|C| = |D|$ the divisibility problems for M are decidable, as in this case $M_\tau$ is cycle-free. It was, at the time, believed that there was a proof that any cycle-free monoid has decidable divisibility problems; as we shall expand on in §4.4, this belief should be regarded as conjecture.

The monoid $M_\tau$ in the statement of Lemma 3.7 is said to be obtained from M by strong compression; this terminology is justified by the fact that any weakly compressible monoid is also strongly compressible. The proof of the lemma is not particularly difficult or long, and is self-contained enough that there is little value in reproducing it here. The interested reader may find the original proof repeated word for word in Adian and Durnev’s survey [13, Lemma 4.5]. We remark that (just as in the case of weak compression) there is an interesting language-theoretic interpretation of strong compression. This will appear in future work by the author.

Example 3.9

Let $M = \text {Mon} \langle a,b \mid abaababb = abbaabb \rangle$. Then M has left and right cycles. The maximal common prefix of abaababb and abbaabb is ab, and the maximal common suffix is abb. Thus we will consider the encoding function $\tau _k$, where $k = 1 + \min (|ab|, |abb|) = 3$. Suppose we enumerate the $2^3$ words of length 3 as

$$\begin{aligned} (E_1, E_2, E_3, E_4, E_5, E_6, E_7, E_8) = (aaa, aab, aba, abb, baa, bab, bba, bbb). \end{aligned}$$

Using this, we apply the encoding function $\psi _k$ to the defining relation to find

$$\begin{aligned} \psi _3(abaababb)&= e_3 \psi _3(baababb) \\&= e_3 e_5 \psi _3(aababb) \\&= e_3 e_5 e_2 \psi _3(ababb) \\&= e_3 e_5 e_2 e_3 \psi _3(babb) \\&= e_3 e_5 e_2 e_3 e_6 \psi _3(abb) \\&= e_3 e_5 e_2 e_3 e_6 e_4, \end{aligned}$$

and, with the details assigned to the diligent reader, also

$$\begin{aligned} \psi _3(abbaabb) = e_4 e_7 e_5 e_2 e_4. \end{aligned}$$

Thus the weakly compressed monoid $M_\tau$ has the presentation

$$\begin{aligned} M_\tau = \text {Mon} \langle e_1, \ldots , e_7 \mid e_3 e_5 e_2 e_3 e_6 e_4 = e_4 e_7 e_5 e_2 e_4 \rangle , \end{aligned}$$

which obviously has no left cycles. The word problem and the divisibility problems for M reduce to the same problems for $M_\tau$. Note that the word problem is trivially solvable in $M_\tau$, as the left-hand side of the relation is self-overlap free. Hence the word problem is decidable in M. In fact, the left divisibility problem is also decidable in $M_\tau$, by a result of Oganesian (see §4.3).

By using Lemma 3.7 one easily sees that the word problem for any one-relation monoid can be reduced to the word problem for a one-relation monoid with no left cycles or to one with no right cycles. By using the standard symmetry argument, we hence have the following theorem.

Theorem 3.10

(Adian and Oganesian 1978) The word problem resp. the left divisibility problem for an arbitrary one-relation monoid reduces to the same problem for a one-relation monoid of the form

$$\begin{aligned} \text {Mon} \langle A \mid bua = ava \rangle \end{aligned}$$

or of the form

$$\begin{aligned} \text {Mon} \langle A \mid bua = a \rangle , \end{aligned}$$

where $a, b \in A$ are distinct letters and u and v are arbitrary words.

We remark that the statement of this theorem already appears as [16, Theorem 5], and is proved by a method devised by Oganesian.¹⁴ As the above formulation using Lemma 3.7 becomes significantly cleaner and quicker, we use this instead. Theorem 3.10 is also (essentially) presented by Howie and Pride [69, Corollary 4], though without a detailed proof and with some non-essential cases included. The paper of Howie and Pride uses geometric techniques of diagrams, and their results were arrived at independently of the work by Adian and Oganesian.

4.3 Two generators

We now have two types of compression, with strong compression being the more general, and allowing us to reduce the word problem for all one-relation monoids to the same problem for left-cycle free one-relation monoids. However, there is a further significant reduction that can be made, which is to reduce to the two-generator case.

Now, a priori it is not difficult to reduce the word problem for a finitely presented k-generator monoid to the word problem for a two-generator monoid; indeed, if one has a finitely presented monoid on the generators $a_1, \ldots , a_k$, then the mapping

$$\begin{aligned} a_i \mapsto aba^{i+1}b^{i+1} \end{aligned}$$

will define an injective homomorphism into a finitely presented monoid given by the generators a, b. Thus the word problem for a k-generator monoid reduces to the word problem for a two-generator monoid, as decidability of the word problem is inherited by submonoids. However, even if one starts with a left cycle-free one-relation monoid, the embedding is not necessarily into a left cycle-free monoid, the defining relations of the resulting monoid might be significantly longer, and decidability of the divisibility problems is not inherited by taking submonoids. Thus we will require a more careful reduction if we are to reduce the word and divisibility problems to two-generated one-relation monoids without left cycles. This is precisely what is provided in the first part of Adian and Oganesian’s article [17].

Theorem 3.11

(Adian and Oganesian, 1987) Suppose that

$$\begin{aligned} M = \text {Mon} \langle A \mid u_1 = v_1, \ldots , u_n = v_n \rangle \end{aligned}$$

is a left cycle-free monoid. Then one can find a monoid

$$\begin{aligned} {\overline{M}} = \text {Mon} \langle a_1, \ldots , a_{n+1} \mid {\overline{u}}_1 = {\overline{v}}_1, \ldots , {\overline{u}}_n = {\overline{v}}_n \rangle \end{aligned}$$

such that $|u_i| = |{\overline{u}}_i|$ and $|v_i| = |{\overline{v}}_i|$ for all $1 \le i \le n$, and each of the equality and left divisibility problems for M reduces to the same problem for ${\overline{M}}$.

We shall not give a proof of this theorem, as it uses the algorithm ${\mathfrak {A}}$ (see §4.1) and is in any case already very clearly written in Adian and Oganesian’s article [17]. However, we will give the method by which one finds the words ${\overline{u}}_i$ and ${\overline{v}}_i$.

Let M be as given in the statement of Theorem 3.11. Consider the left graph ${\mathcal {L}}(M)$ of M (see §2.2). By assumption ${\mathcal {L}}(M)$ has no cycles. If the letter a appears at the beginning of some $u_i$ or $v_i$, then we say that the letter a is leftist. Of course, any non-leftist letter is isolated. Denote the connected components of ${\mathcal {L}}(M)$ as $L_1, \ldots , L_k$. For every $L_j$ we will choose one letter $c_j$ appearing in this component. Then, for every word $w \in A^*$, we let ${\overline{w}}$ be the result of replacing in w every occurrence of the letter $c_j$ by $c_1$. Then obviously $|w| = |{\overline{w}}|$, and as ${\mathcal {L}}(M)$ has no cycles, the monoid ${\overline{M}}$ with presentation as in the statement of Theorem 3.11 will clearly have that ${\mathcal {L}}({\overline{M}})$ is cycle-free. In fact ${\mathcal {L}}({\overline{M}})$ consists of a single component, and so clearly has $n+1$ letters.

Example 3.12

We continue our example given in Example 3.9. Recall that

$$\begin{aligned} M_\tau = \text {Mon} \langle e_1, \ldots , e_7 \mid e_3 e_5 e_2 e_3 e_6 e_4 = e_4 e_7 e_5 e_2 e_4 \rangle . \end{aligned}$$

Now ${\mathcal {L}}(M)$ has a single edge between the two leftist vertices $e_3$ and $e_4$. We choose $c_3 \equiv e_3$ (though of course the choice $c_3 \equiv e_4$ works the same), and all other choices of $c_j$ are forced, as all other vertices are isolated. Thus replacing the letters $c_j$ by $c_1$, we find

$$\begin{aligned} \overline{M_\tau } = \text {Mon} \langle c_1, e_4 \mid c_1 c_1 c_1 c_1 c_1 e_4 = e_4 c_1 c_1 c_1 e_4 \rangle \cong \text {Mon} \langle a,b \mid bbbbba = abbba \rangle . \end{aligned}$$

Each of the word problem and left divisibility problems for $M_\tau$ reduces to the same problem for $\overline{M_\tau }$ (and both problems are easily decidable).

In summary, by combining the two techniques of strong compression and Theorem 3.11 to pass to the 2-generated case, we find the following theorem.

Theorem 3.13

(Adian and Oganesian, 1987) The word problem resp. the left divisibility problem for an arbitrary one-relation monoid reduces to the same problem for a one-relation monoid of the form

$$\begin{aligned} \text {Mon} \langle a,b \mid bua = ava \rangle \end{aligned}$$

or of the form

$$\begin{aligned} \text {Mon} \langle a,b \mid bua = a \rangle , \end{aligned}$$

where u and v are arbitrary words.

We remark that Adian and Durnev [13, p. 242] incorrectly claim that Theorem 3.13 was first proved in 1978, referencing Adian and Oganesian’s 1978 article [16]. However, the only theorem of the sort proved in this article is Theorem 3.10, as discussed above, which does not reduce to the 2-generated case. Instead, Theorem 3.13 first occurs in the literature as precisely the statement of [17, Theorem 2], if one accounts for the fact that the monadic case $\text {Mon} \langle a,b \mid bua = a \rangle$ was at that point believed to have been solved (see §4.4 for further discussion).

Example 3.14

We give a full example of combining several reduction techniques for a rather difficult-looking one-relation monoid. Consider the one-relation monoid

$$\begin{aligned} M_4 = \text {Mon} \langle a,b,c,d \mid abdadadacbaca = abdadabdaca \rangle . \end{aligned}$$

Then $M_4$ is both weakly and strongly compressible; as weak compression reduces relation length significantly quicker, and is a bit more fun to use, we first use this. The (unique) self-overlap free word $\alpha$ such that both words in the relation begin and end with $\alpha$ is $\alpha \equiv a$. We find

$$\begin{aligned} abdadadacbaca&\equiv a{\underline{bd}} \cdot a{\underline{d}} \cdot a{\underline{d}} \cdot a{\underline{cb}} \cdot a{\underline{c}} \cdot a, \\ abdadabdaca&\equiv a{\underline{bd}}\cdot a{\underline{d}} \cdot a{\underline{bd}} \cdot a{\underline{c}} \cdot a, \end{aligned}$$

and hence, when applying the compressor function $\psi _a$ we have

$$\begin{aligned} \psi _a(abdadadacbaca)&= x_{bd} x_d x_d x_{cb} x_c \\ \psi _a(abdadabdaca)&= x_{bd} x_{d} x_{bd} x_c. \end{aligned}$$

Hence the divisibility problems and word problem for $M_4$ reduce to the same problems for

$$\begin{aligned} M_4'&= \text {Mon} \langle x_{bd}, x_d, x_{cb}, x_c \mid x_{bd} x_d x_d x_{cb} x_c =x_{bd} x_{d} x_{bd} x_c \rangle \\&\cong \text {Mon} \langle a,b,c,d \mid abbcd = abad \rangle . \end{aligned}$$

This one-relation monoid still has left and right cycles. It is strongly (but not weakly) compressible with respect to the maximal common prefix ab and suffix d. Hence we find $k = 1 + \min (2,1) = 2$, and we are using the function $\tau _2$. There are $4^2 = 16$ words of length 2 in the alphabet $\{ a, b, c, d\}$, which we order as

$$\begin{aligned} (aa, ab, ac, ad, ba, bb, bc, bd, ca, cb, cc, cd, da, db, dc, dd) \end{aligned}$$

where the index $1 \le i \le 16$ of each word in this sequence indicates that it is word $E_i$. Thus

$$\begin{aligned} \psi _2(abbcd)&= e_2 \psi _2(bbcd) = e_2 e_6 \psi _2(bcd) = e_2 e_6 e_7 \psi _2(cd) = e_2 e_6 e_7 e_{12}, \\ \psi _2(abad)&= e_2 \psi _2(bad) = e_2 e_5 \psi _2(ad) = e_2 e_5 e_4. \end{aligned}$$

Hence the word problem and divisibility problems for $M_4'$ (and hence also for $M_4$) reduce to the same problems for

$$\begin{aligned} M_4''&= \text {Mon} \langle e_2, e_4, e_5, e_6, e_7, e_{12} \mid e_2 e_6 e_7 e_{12} = e_2 e_5 e_4 \rangle \\&\cong \text {Mon} \langle a,b,c,d,e,f \mid adef = acb \rangle , \end{aligned}$$

where the redundant generators have not been included, as these split off in a free factor. This is now a right cycle-free one-relation monoid, but it has left cycles. Of course, the word problem and the left/right divisibility problem for $M_4''$ reduces to the word problem and the right/left divisibility problem for

$$\begin{aligned} M_4''' = \text {Mon} \langle a,b,c,d,e,f \mid feda = bca \rangle , \end{aligned}$$

by reading the words backwards. This is now a one-relation monoid without left cycles. We now apply Theorem 3.11 to reduce the word and divisibility problems to a two-generated one-relation monoid without left cycles. The only leftist letters are f and b. We choose b to represent this component in ${\mathcal {L}}(M_4''')$. This finally reduces the word and divisibility problems for $M_4$ to the same problems for

$$\begin{aligned} M_4'''' = \text {Mon} \langle c_1, f \mid fc_1c_1c_1 = c_1 c_1 c_1 \rangle \cong \text {Mon} \langle a,b \mid baaa = aaa \rangle . \end{aligned}$$

In this monoid, solving these aforementioned problems is not hard, and so we have a solution to the same problems for our original (rather complicated-looking) monoid $M_4$.

We have thus found our desired reduction theorem. The above Theorem 3.13 is still, at the time of the writing of this survey, the strongest general reduction theorem for one-relation monoids. There are a number of important cases of left cycle-free one-relation monoids for which the word and left divisibility problems are known to be decidable. One of the major sources of such results is Adian’s algorithm ${\mathfrak {A}}$, which we shall now present.

5 Adian’s algorithm ${\mathfrak {A}}$ (1976–2001)

From the reductions we have seen, the word problem for all one-relation monoids has been reduced to the left divisibility problem for one-relation monoids without left cycles. The algorithm ${\mathfrak {A}}$ was devised by Adian¹⁵ in 1976 as an attempt to solve this latter problem.

5.1 Two generators, one relation

The algorithm ${\mathfrak {A}}$ is very general, and will be defined for all left cycle-free monoids; to get a feel for how the algorithm operates, we shall begin by considering how the algorithm operates on left cycle-free two-generated one-relation monoids. In view of Theorem 3.13, this is no (direct) restriction if one wishes to solve the word problem in one-relation monoids using the algorithm ${\mathfrak {A}}$. We borrow some aspects of the excellent exposition of the algorithm ${\mathfrak {A}}$ by Lallement [96]. Let

$$\begin{aligned} M = \text {Mon} \langle a,b \mid u=v \rangle \end{aligned}$$

be a left cycle-free one-relation monoid. Let $w \in \{a, b\}^+$. As M has no left cycles, we can uniquely factor w from the left into a product of maximal prefixes of u and v. Using this, we describe the prefix decomposition of w. We factor w from the left into maximal prefixes of u and v. If at some point during this factorisation a prefix happens to be u or v, then the decomposition stops, and we call this prefix the head of the prefix decomposition. A prefix decomposition without a head is called a headless prefix decomposition.

We illustrate this by an example. Let $M = \text {Mon} \langle a,b \mid babba = aba \rangle$, and consider the word $w_1 \equiv abbababab$. Then $w_1$ has ab as a prefix, which is the maximal prefix that is also a prefix of either babba or aba. Thus the decomposition begins with this prefix, which we denote as $ab \mid bababab$. The decomposition now continues on the word bababab. There, the next prefix is bab, so the decomposition continues as $ab \mid bab \mid abab$. Finally, the next prefix is aba, which is one of the words in the defining relation. This ends the decomposition. Thus aba is the head, and we denote the prefix decomposition of $w_1$ as

Similarly, we can find the prefix decomposition of $w_2 \equiv abbabbba$ to be

$$\begin{aligned} ab \mid babb \mid ba \end{aligned}$$

which is hence a headless prefix decomposition. Using the prefix decomposition, we can describe the algorithm ${\mathfrak {A}}$. Let $x \in \{ a, b \}$ be a letter. The algorithm ${\mathfrak {A}}$ attempts to decide whether w is left divisible by x as follows.

• (1) If w begins with x, then stop.

• (2) Otherwise, compute the prefix decomposition of w.

  • (a) If this prefix decomposition is headless, then stop.

  • (b) Otherwise, replace the head by the other side of the defining relation, obtaining a new word $w'$, and goto (1) with the new word $w'$ and the letter x.

It is not a priori clear that this algorithm should do any better than the naïve procedure for checking if two words are equal in a monoid by successively attempting all possible elementary transformations. However, there is much more power in ${\mathfrak {A}}$ than it first appears. We first give a straightforward example of using this algorithm below.

Example 4.1

( [96, Example 2.1]) Let $M = \text {Mon} \langle a,b \mid baababa = aba \rangle$. We may ask the question: is $w \equiv abbaaababab$ left divisible by b? The prefix decomposition of w is:

As the defining relation is $aba = baababa$, we replace the head aba by baababa, and repeat. This gives the sequence:

Thus the algorithm has terminated with a witness for the fact that z is left divisible by b, i.e. in M we have $w = b \cdot aabababaababababab$.

It is not always the case that ${\mathfrak {A}}$ terminates. For this reason, it is perhaps slightly abusive to use the term “algorithm” for ${\mathfrak {A}}$. We give an easy example of this non-terminating behaviour happening below.

Example 4.2

( [97, Example 29]) Let $M = \text {Mon} \langle a,b \mid baabbaa = a \rangle$, and consider the word $w \equiv bbaaa$. Applying ${\mathfrak {A}}$, we find:

Thus we have entered a loop, for we have found an occurrence of the first prefix decomposition inside the decomposition .

It seems as if this looping behaviour would be difficult to deal with, as one might not know whether falling into an infinite loop would imply divisibility by a letter or not. However, the remarkable result obtained by Adian regarding ${\mathfrak {A}}$ is the following theorem, which is a combination of the arguments given in [8, §6].

Theorem 4.3

(Adian, 1976) The result of applying the algorithm ${\mathfrak {A}}$ to a word w and a letter x will be exactly one of the following three cases:

• (1) ${\mathfrak {A}}$ transforms w into a word $xw'$ after finitely many steps.

• (2) ${\mathfrak {A}}$ ends in a headless prefix decomposition after finitely many steps.

• (3) ${\mathfrak {A}}$ loops indefinitely.

The word w is left divisible by x if and only if we are in case (1).

Furthermore, in this case ${\mathfrak {A}}$ produces the shortest proof of this.

As an example of how this theorem deals with loops, we see that as ${\mathfrak {A}}$ loops in Example 4.2 on input w and a, we can conclude that w is not left divisible by a.

Now a solution to the left divisibility problem by a letter is easily equivalent to a solution to the left divisibility problem in left cancellative monoids, by induction on the length of the word by which one divides. Thus we almost have a solution to the left divisibility problem for all two-generated left cycle-free one-relation monoids, and hence almost have a solution to the word problem for all one-relation monoids by Theorem 3.13! Of course, the difficulty comes from the fact that there is at present no known general algorithm which detects when case (3) of Theorem 4.3 occurs. Adian, however, conjectured that such an algorithm (which he calls ${\mathfrak {B}}$) exists, and therefore indirectly conjectures that the word problem is decidable for all one-relation monoids. This conjecture appears throughout his published works, and was repeated by Adian as late as 2018 at a conference at the Euler International Mathematical Institute in Saint Petersburg.

There have been some attempts to derive general methods for detecting loops in ${\mathfrak {A}}$ (i.e. attempts at producing ${\mathfrak {B}}$). For example, Lallement [97, pp. 38–39] provides an algorithm which can always detect whether or not ${\mathfrak {A}}$ loops on an input word in the monoid given in Example 4.2, thus solving the word (and left divisibility) problem for this monoid. This detection is via regular languages and finite state automata. These methods of detecting loops have been expanded by Lallement’s student J. Bouwsma in her Ph.D. thesis [29], solving a number of more cases of the form $\text {Mon} \langle a,b \mid bua=a \rangle$. In fact, Lallement [96] conjectures that their methods (using finite state automata) might be sufficient to detect all loops that can appear when applying ${\mathfrak {A}}$ to $\text {Mon} \langle a,b \mid bua = a \rangle$. If this is true, then this would imply decidability of the word problem for such monoids, which remains open (see §4.4).

5.2 The general case

We now describe the algorithm ${\mathfrak {A}}$ in the general case, as it is presented by Adian [8]. Let $M = \text {Mon} \langle A \mid T \rangle$ be a finitely presented monoid without left cycles. For all triples (a, b, aW), where $a, b \in A$ are distinct letters and $W \in A^*$ is an arbitrary word, we will define the prefix decomposition $R_\ell (aW, b)$ of aW with respect to b inductively on the length of aW. This prefix decomposition will not always exist. We will first reduce the definition of $R_\ell (aW, b)$ to when a and b are adjacent in ${\mathcal {L}}(M)$, and then present a definition similar to the two-generator one-relation case. For expositional reasons, we will simultaneously with the general case present the material in the special case of the left cycle-free monoid

$$\begin{aligned} \Pi = \text {Mon} \langle \alpha , \beta , \gamma , \delta \mid \alpha \gamma = \gamma \delta \alpha , \gamma \gamma \beta = \beta \alpha \beta \delta \gamma \rangle , \end{aligned}$$

which has left graph ${\mathcal {L}}(\Pi )$ as below.

First of all, if the left graph ${\mathcal {L}}(M)$ contains no path from the vertex a to b, then we say that the prefix decomposition $R_\ell (aW, b)$ does not exist. Thus, for example, $R_\ell (\alpha \beta \gamma \delta , \delta )$ is not defined (for $\Pi$ as above). On the other hand, if there is such a path, then there is a unique shortest such path, as M is left cycle-free. Let c be the letter adjacent to a on the shortest path joining a to b in ${\mathcal {L}}(M)$. Let $aE = cD$ be the defining relation corresponding to the edge between a and c on the specified path, accommodating an interchange of the left- and right-hand sides of the relation. We define

$$\begin{aligned} R_\ell (aW, b) := R_\ell (aW, c). \end{aligned}$$

For example, we have $R_\ell (\alpha \gamma ^3 \delta ^2, \beta ) := R_\ell (\alpha \gamma ^3 \delta ^2, \gamma )$, as the unique shortest path joining $\alpha$ and $\beta$ in ${\mathcal {L}}(\Pi )$ has $\alpha$ adjacent to $\gamma$.

We must now define $R_\ell (aW, c)$, which will eventually be a definition quite familiar to the reader who is accustomed to the two-generator one-relation case. Let aF be the maximal common prefix of the words aE and aW. Write

$$\begin{aligned} aE&\equiv (aF)E_1 \\ aW&\equiv (aF)W_1. \end{aligned}$$

We will now define $R_\ell (aW, c)$ based on the properties of the words $E_1, W_1$.

• (1) If $E_1 \equiv \varepsilon$, i.e. if $aE \equiv aF$, we then define

  

  and we say that aE is the head of the prefix decomposition, which is indicated by the box. Note that a head is always one side of a defining relation! We say that this head aE is associated to the relation $aE = cD$. For example,

  

  and the heads are associated to the relations $\alpha \gamma = \gamma \delta \alpha$ resp. $\gamma \delta \alpha = \alpha \gamma$.

• (2) If $E_1 \not \equiv \varepsilon$ but $W_1 \equiv \varepsilon$, we then define

  $$\begin{aligned} R_\ell (aW, c) := aE \mid \end{aligned}$$

  where $\mid$ indicates that aE is the first prefix in the prefix decomposition. This decomposition is headless, i.e. it has no head. For example,

  $$\begin{aligned} R_\ell (\beta \alpha \beta , \gamma )&= \beta \alpha \beta \mid \\ R_\ell (\gamma \delta , \alpha )&= \gamma \delta \mid \end{aligned}$$

  as $\beta \alpha \beta$ and $\gamma \delta$ are proper prefixes of their corresponding relation words (i.e. $\beta \alpha \beta \delta \gamma$ resp. $\gamma \delta \alpha$).

• (3) If¹⁶$E_1 \not \equiv \varepsilon$ and $W_1 \not \equiv \varepsilon$, then we can write

  $$\begin{aligned} E_1&\equiv qE_2 \\ W_1&\equiv d W_2, \end{aligned}$$

  for some letters $q, d \in A$ and words $E_2, W_2 \in A^*$. Then d and q are distinct. As $|dW_2| < |aW|$, we can by the inductive hypothesis determine whether or not $R_\ell (dW_2, q)$ exists.

  • (i) If $R_\ell (dW_2, q)$ does not exist, then we say that $R_\ell (aW, c)$, and consequently also $R_\ell (aW, b)$, does not exist.

  • (ii) If $R_\ell (dW_2, q)$ exists, and is of the form

    

    where the $H_i$ are the prefix components of the decomposition, and the head R is associated to the relation $R=S$, then we define

    

This completes the description of the prefix decomposition $R_\ell (aW, b)$. It is not difficult to check that this is uniquely defined. Note that the prefix decomposition $R_\ell (aW, b)$ can always be algorithmically computed for any pair of letters a, b and any word $W \in A^*$, regardless of whether we have e.g. a solution to the word problem or not.

Example 4.4

Continuing our example with $\Pi$ as above, which for ease of access was defined by

$$\begin{aligned} \Pi = \text {Mon} \langle \alpha , \beta , \gamma , \delta \mid \alpha \gamma = \gamma \delta \alpha , \gamma \gamma \beta = \beta \alpha \beta \delta \gamma \rangle \end{aligned}$$

we give a complete computation of a prefix decomposition below. The reader is encouraged to follow along (perhaps with their own example).

We can also compute

$$\begin{aligned} R_\ell (\gamma \beta \gamma \delta \gamma \delta , \beta )&= \gamma \mid R_\ell (\beta \gamma \delta \gamma \delta , \gamma ) \\&= \gamma \mid \beta \mid R_\ell (\gamma \delta \gamma \delta , \alpha ) \\&= \gamma \mid \beta \mid \gamma \delta \mid R_\ell (\gamma \delta , \alpha ) \\&= \gamma \mid \beta \mid \gamma \delta \mid \gamma \delta \mid \end{aligned}$$

which is a headless decomposition. On the other hand,

$$\begin{aligned} R_\ell (\beta \alpha \beta \alpha , \gamma ) = \beta \alpha \beta \mid R_\ell (\alpha , \delta ) \end{aligned}$$

and as $R_\ell (\alpha , \delta )$ is not defined, it follows that $R_\ell (\beta \alpha \beta \alpha , \gamma )$ is not defined.

We emphasise that it is not hard to check that the prefix decomposition $R_\ell$ as defined here coincides with the earlier defined prefix decomposition for two generators and one relation. We may now state Adian’s algorithm ${\mathfrak {A}}$ in full generality for a left cycle-free monoid $M = \text {Mon} \langle A \mid R \rangle$. Let $w \in A^+$ be an arbitrary word, and let $b \in A$ be any letter. The algorithm ${\mathfrak {A}}$ will attempt to decide if w is left divisible by b in M.

• (1) If w begins with b, then stop.

• (2) Otherwise, determine if the prefix decomposition $R_\ell (w, x)$ exists.

  • (a) If $R_\ell (w, x)$ does not exist, then stop.

  • (b) If $R_\ell (w, x)$ exists, but is headless, then stop.

  • (c) If $R_\ell (w, x)$ exists and has a head, let $R=S$ be the relation associated to its head R. Replace the head R by the word S in w, obtaining a new word $w'$, and goto (1) with the new word $w'$ and the letter x.

This is very similar to the algorithm ${\mathfrak {A}}$ presented earlier in the two-generated one-relation case; the only difference is the added step of ensuring that the prefix decomposition exists. Note that—obviously!—for every transformation $w \longrightarrow w'$ done by a step of ${\mathfrak {A}}$, we have $w = w'$ in M. We can now state Adian’s Theorem 4.3 in full generality.

Theorem 4.5

(Adian, 1976) The result of applying the algorithm ${\mathfrak {A}}$ to a word w and a letter x will be exactly one of the following four cases:

• (1) ${\mathfrak {A}}$ transforms w into a word $xw'$ (after finitely many steps).

• (2) ${\mathfrak {A}}$ transforms w into a word $w'$ for which $R_\ell (w', x)$ does not exist.

• (3) ${\mathfrak {A}}$ transforms w into a word $w'$ for which $R_\ell (w', x)$ is headless.

• (4) ${\mathfrak {A}}$ does not terminate.

The word w is left divisible by x if and only if we are in case (1).

Furthermore, in this case ${\mathfrak {A}}$ produces the shortest proof of this.

The proof is rather short, and does not depend on any significant results not contained in the paper itself. We direct the reader to the paper for the proof (and pleasant reading).

Example 4.6

We again consider

$$\begin{aligned} \Pi = \text {Mon} \langle \alpha , \beta , \gamma , \delta \mid \alpha \gamma = \gamma \delta \alpha , \gamma \gamma \beta = \beta \alpha \beta \delta \gamma \rangle . \end{aligned}$$

We provide a few fully worked examples of applying the algorithm ${\mathfrak {A}}$. We begin with $w \equiv \alpha \beta \alpha \gamma \gamma \beta \alpha \delta \delta$ and the letter $\beta$. That is, we will try and decide whether or not w is left divisible in $\Pi$ by $\beta$. Now as computed in Example 4.4, we have

as the head $\gamma \gamma \beta$ corresponds to the relation $\gamma \gamma \beta = \beta \alpha \beta \delta \gamma$. We now apply ${\mathfrak {A}}$ to the word $\alpha \beta \beta \alpha \beta \delta \gamma \alpha \delta \delta$ and the (same as before!) letter $\beta$.

We compute

$$\begin{aligned} R_\ell (\alpha \beta \alpha \beta \alpha \beta \delta \gamma \alpha \delta \delta , \beta ) = \alpha \mid \beta \alpha \beta \mid R_\ell (\alpha \beta \delta \gamma \alpha \delta \delta , \delta ) \end{aligned}$$

and since $R_\ell (\alpha \beta \delta \gamma \alpha \delta \delta , \delta )$ is not defined—as $\alpha$ and $\delta$ are in distinct connected components of ${\mathcal {L}}(\Pi )$—it follows that $R_\ell (\alpha \beta \alpha \beta \alpha \beta \delta \gamma \alpha \delta \delta , \beta )$ is not defined. By Theorem 4.5 we conclude that in $\Pi$ the word $w \equiv \alpha \beta \alpha \gamma \gamma \beta \alpha \delta \delta$ is not left divisible by $\beta$.

The other two examples in Example 4.4 are quicker to find conclusions about. As $R_\ell (\gamma \beta \gamma \delta \gamma \delta , \beta )$ is headless, it follows that $\gamma \beta \gamma \delta \gamma \delta$ is not left divisible by $\beta$. Similarly, as $R_\ell (\beta \alpha \beta \alpha , \gamma )$ does not exist, it follows that $\beta \alpha \beta \alpha$ is not left divisible by $\gamma$.

Now, if we wish to decide whether $\gamma \gamma \beta \delta \alpha$ is left divisible by $\beta$, we simply compute

and thus applying a step of ${\mathfrak {A}}$, we transform $\gamma \gamma \beta \delta \alpha$ into $\beta \alpha \beta \delta \gamma \delta \alpha$. Hence, we conclude that $\gamma \gamma \beta \delta \alpha$ is left divisible by $\beta$ in $\Pi$.

We leave as an exercise to the reader a proof that the algorithm ${\mathfrak {A}}$ always terminates for $\Pi$, solving the left divisibility problem for this monoid.

Example 4.7

We can adapt the one-relation monoid $\text {Mon} \langle a,b \mid baabbaa = a \rangle$ from Example 4.2 to give the left cycle-free monoid

$$\begin{aligned} \Pi ' = \text {Mon} \langle \alpha , \beta , \gamma \mid \beta \alpha \gamma \alpha \gamma \beta \beta \alpha \gamma \alpha \gamma = \alpha \gamma , \gamma = \alpha \gamma \rangle . \end{aligned}$$

We leave the reader to check that ${\mathfrak {A}}$ will loop when checking whether $\beta \beta \alpha \gamma \alpha \gamma \alpha \gamma$ is left divisible by $\alpha$, just as ${\mathfrak {A}}$ loops in the monoid of Example 4.2 when checking whether bbaaa is left divisible by a.

What is remarkable is that this algorithm ${\mathfrak {A}}$ has the potential to solve the left divisibility problem and the word problem in any finitely presented monoid without left cycles—not just the one-relation case. If this potential turns out to be fulfillable, this would indicate that the class of left cycle-free monoids is significantly more well-behaved than simply being left cancellative (as left cancellative monoids can have undecidable word problem). However, no criterion is yet known for deciding when ${\mathfrak {A}}$ loops; the general case is thus, in a sense, at present understood to approximately the same degree as the one-relation case.

5.3 Applications of ${\mathfrak {A}}$

There have been a number of appearances of the algorithm ${\mathfrak {A}}$ in the literature, and it has spurred a good deal of research, having appeared in a large number of publications [10, 16, 17, 29, 89, 131,132,133,134,135, 153,154,155, 176, 177]. It is also present in the brief articles by Adian [9, 11], but no new results are presented therein. In this section, we shall mention some major classical results, the proofs of which depend critically on the algorithm ${\mathfrak {A}}$. The first concerns “monadic one-relation monoids with torsion”, and was proved (see [131]) only two years after the introduction of ${\mathfrak {A}}$.

Theorem 4.8

(Oganesian, 1978) Let $M = \text {Mon} \langle a,b \mid (bu)^na = a \rangle$ for some $n>1$ and u arbitrary. Then the left divisibility (and hence the word) problem for M is decidable.

A result in the non-monadic case was proved by the same author in the same year (see [132, Theorem 1]), but does not appear to have received much attention in the literature. Let $\sigma _a$ be the function which counts the number of occurrences of the letter a in a word.

Theorem 4.9

(Oganesian, 1978) Let $M = \text {Mon} \langle a,b \mid bua = ava \rangle$. If either

$$\begin{aligned} \sigma _a(bua)&= \sigma _a(ava), \quad \text {or if} \\ \sigma _b(bua)&= \sigma _b(ava) \end{aligned}$$

then the left divisibility problem (and hence also the word problem) is decidable for M.

As an example, this shows that the word problem is decidable for the one-relation monoid $\text {Mon} \langle a,b \mid ababa = baba \rangle$, as both sides have equally many occurrences of the letter b. The above theorem is one of the most general results in the non-monadic case.

There are two further important contributions in the non-monadic case, both due to G. Watier. Consider $\text {Mon} \langle a,b \mid bua=ava \rangle$. The case when bua is self-overlap free received some attention by Adian and Oganesian [17]. In fact, a proof was claimed that whenever bua is a factor of ava, the word problem is decidable; this result, however, should be regarded as conditional (see §4.4). Nevertheless, Watier [176] studies this case in his first of two articles on the subject, and is able to prove the following remarkable theorem.

Theorem 4.10

(Watier, 1996) Let $M = \text {Mon} \langle a,b \mid bua=ava \rangle$. If the leftmost sequence of b’s in bua is strictly longer than the others, then the word problem is decidable for M.

This is a very general theorem. As noted by Watier, this solves the word problem in $\text {Mon} \langle a,b \mid b^ma^n = ava \rangle$ for $m, n > 0$, with no conditions on the word ava. Note that bua is always self-overlap free in the cases that the above theorem applies. The second article¹⁷ by Watier on the subject again concerns the case when bua is self-overlap free. As mentioned, the case when bua is a factor of ava has been studied to some extent; Watier’s article studies the case when bua is not a factor of ava. He is then able to show the following very general result.

Theorem 4.11

(Watier, 1997) Let $M = \text {Mon} \langle a,b \mid bua = ava \rangle$. Suppose that bua is self-overlap free and not a subword of ava. If $|ava| \ge |bua|^2$, then the word problem for M is decidable.

The article itself makes for very pleasant reading, and many of the results are phrased in terms of formal language theory and the theory of codes, while still being centered on the algorithm ${\mathfrak {A}}$. Watier’s two results, along with the results by Oganesian mentioned above, represent the bulk of the progress hitherto made on the case $\text {Mon} \langle a,b \mid bua=ava \rangle$. We mention in passing that Kashintsev [86] proved that if u is self-overlap free, and $|u| > |v|$, then the conjugacy problem is decidable in $\text {Mon} \langle A \mid u=v \rangle$. Unlike for groups, however, decidability of the conjugacy problem is not sufficient for decidability of the word problem.

5.4 An incorrect proof

Up to this point, all results mentioned have been unconditional. However, around the early 1990s a gap was discovered in the proof of a theorem that had up to that point been generally accepted. The “theorem” was a result by O. A. Sarkisian, another doctoral student of Adian’s, and is simple to state.

Claim

(Sarkisian, 1981) The divisibility problems are decidable for all cycle-free monoids.

This is a rather remarkable result; indeed, outside of the above claim, even the word problem is not known to be decidable for cycle-free monoids. There are many remarkable consequences of the result, which we shall list below. However, Oganesian discovered a gap in Sarkisian’s proof [63]. The presence of this gap is first mentioned in 1994 by Adian [10], but by then the result had already been used in the proofs of a number of further results. As we shall see, this has led to a number of results in the literature either being entirely conditional, or else needing a repair (see e.g. §6.2 where such a repair is done in connection with one-relation special inverse monoids).

The author has collected all results known to him to be conditional on this result. We define the Sarkisian hypothesis sh to be the above claim, i.e. that the divisibility problems are decidable for all cycle-free monoids.

Theorem 4.12

Suppose $\textsc {sh}$ holds. Then:

• (1) The word problem is decidable for every cycle-free semigroup.

• (2) The word problem is decidable for every cycle-free group [155].¹⁸

• (3) The isomorphism problem for one-relation monoids is decidable [135].

• (4) The word problem for $\text {Mon} \langle a,b \mid bua = a \rangle$ is decidable [134].

• (5) Suppose M is a strongly compressible one-relation monoid. If $|C|=|D|$, then the divisibility problems are decidable for M (see §3.2) [17].

• (6) If u, v are such that v is self-overlap free and v is a factor of u, then the word and at least one of the divisibility problems are decidable for $\text {Mon} \langle A \mid u=v \rangle$ [17].

Without sh, all of the above results should only be regarded as conditional, as no other proof of them is known. Note also that (6) in the above theorem generalises (4) in virtue of the fact that the word and divisibility problems are easily decidable for $\text {Mon} \langle a,b \mid b^n = a \rangle$. We remark that there are other statements which are highly specialised (see e.g. [9, Theorem 7]) and rather involved to state, which are also conditional on sh. We instead refer the reader to Adian and Durnev [13], in which slightly detailed corrections that can be made to such statements.¹⁹

V. S. Guba [62, p. 1142] has stated that, in his opinion, decidability of the divisibility problems for cycle-free monoids “is likely to be still more complicated than the word problem for one-relator semigroups”. We shall see some results by Guba in §6.3 which illustrates the potential difficulty in solving the word problem for monadic one-relation monoids (and thereby also indirectly the difficulty in proving that sh holds).

6 Sporadic results

In this section, we shall present some approaches to the word problem for one-relation monoid which are “sporadic” in nature, in that they are not necessarily founded in an attempt to solve the word problem for all one-relation monoids, but have nevertheless been fruitfully applied to many classes. One quick example is that Magnus’ Freiheitssatz²⁰, which was integral in solving the word problem for one-relator groups, can with little difficulty be generalised to one-relation monoids; an elementary proof is given by Squier and Wrathall [164]. However, this does not yet appear to have led to any direct new insights regarding the word problem. We mention one related insight.

Magnus classified all one-relator groups satisfying some non-trivial identity [100], and Adian classified all special one-relation monoids satisfying some non-trivial identity [7].²¹ Using the Freiheitssatz and the work by Adian and Magnus, L. Shneerson [162, 163] was able to completely classify the one-relation monoids which satisfy some non-trivial identity.²² Using this classification, Vazhenin [174] proved that a non-special one-relation monoid has decidable first-order theory if and only if it is monogenic, or else generated by a, b and with defining relation one of

$$\begin{aligned} ab = ba \, \mid \, ab = b^k \, (k \ge 1) \, \mid \, ba = aba \, \mid \, ab = bab^2 \, \mid \, a = bab \, \mid \, a^2 = b^2, \end{aligned}$$

or the right cycle-free equivalent of one of the above defining relations. This coincides with the class of non-special one-relation monoids satisfying some non-trivial identity. Cain et al [36, Proposition 9.1] showed that the above cases are also precisely the cases in which a one-relation monoid admits an automatic presentation. This gives an efficient solution to the word problem in all the above cases, and is of independent interest (though note that directly solving the word problem in any of the above specified one-relation monoids requires very little effort).

We shall now present some families of one-relation monoids which have been studied in a rather detailed manner using normal forms in a more or less “sporadic” fashion.

6.1 Normal forms

One example of using normal forms to solve the word problem comes from Jackson [72] who, seemingly inspired by the example $\text {Mon} \langle a,b \mid baaba = a \rangle$ which escaped the methods of Howie and Pride [69], proved that the one-relation monoids

$$\begin{aligned} \text {Mon} \langle a,b \mid ba^nba = a \rangle \quad (n \ge 0) \end{aligned}$$

admit a particular nice solution to their word problem via normal forms; the article is only two pages long, and consists of a quick proof via van der Waerden’s trick that the normal forms as specified are correct. We remark that although Jackson modestly notes that “the result here should be regarded as a special case of a more general result of Oganesian”, this modesty is unfounded, in view of the gap mentioned in §4.4. Zhang [183, §6] later remarked that the one can solve the word problem in any monoid as above by considering its right cancellative analogue $\text {Mon} \langle a,b \mid aba^nb = a \rangle$ and noting that this admits a finite complete rewriting system with the two rules

$$\begin{aligned} \{ (aba^nb \rightarrow a), (a^{n+1}b \rightarrow aba^n)\}. \end{aligned}$$

A similar result regarding certain infinite families comes from Lallement and Rosaz [98], who prove that the monoids

$$\begin{aligned} \text {Mon} \langle a,b \mid ba = a(ba)^na \rangle \quad (n \ge 0) \end{aligned}$$

have decidable word problem, again using normal forms. The special case with $n=1$, i.e. $\text {Mon} \langle a,b \mid ba = abaa \rangle$ was then studied by Jackson [73], who proved that such monoids even have decidable submonoid membership problem. Jackson [74] also studied the submonoid membership problem for the Baumslag-Solitar semigroups

$$\begin{aligned} \text {Mon} \langle a,b \mid ab^k = b^\ell a \rangle \quad (k, \ell > 0) \end{aligned}$$

and proved that this problem is decidable. Note, however, that the word problem is easily solvable in such monoids as they are all cycle-free.

Finally, Yasuhara [181] proved that the word problem for one-relation monoids

$$\begin{aligned} \text {Mon} \langle A \cup \{ t \} \mid u = vtw \rangle \end{aligned}$$

where t does not appear in u, v, or w, and $|u| > \max (|v|, |w|)$. This result was strengthened by Oganesian [133] to solve the word problem in the above situation, with no condition on the lengths |u|, |v| and |w|. However, Yasuhara’s proof shows that the equivalence class of any word is finite when the length condition holds, which can be used to solve a number of other decision problems in this case (such as the membership problem). We note that in the two-generator case, the above monoids are all of the form

$$\begin{aligned} \text {Mon} \langle a,b \mid a^n = a^p b a^q \rangle , \quad n > p + q. \end{aligned}$$

Normal form results are closely connected to rewriting systems by a result of Squier [165], see also Brown [30]. Thus, we shall give some brief remarks regarding the interface between the theory of rewriting systems and the word problem for one-relation monoids.

6.2 Rewriting systems

While the theory of rewriting systems has often been limited to solving the word problem for very particular examples of one-relation monoids, there are some important points to be made on their general applicability. We begin by noting that occasionally, the algebraic structure of the rewriting systems in question seems to be somewhat unduly ignored. For example, the Jantzen monoid $\text {Mon} \langle a,b \mid abbaab = 1 \rangle$ has been the subject of a number of investigations after its 1981 introduction by Jantzen [75]. An explicit linear representation for it is found, and it is proved that no congruence class of words is a context-free language. However, it is not hard to see that this monoid is a group: ab is a prefix and a suffix of abbaab, and hence ab and ba are invertible. Furthermore, this group is easily seen to be the Baumslag-Solitar group ${\text {BS}}(1, -2)$, by using the free group automorphism induced by $a \mapsto ab^{-1}$ and $b \mapsto b$. Seeing that no congruence class of words is a context-free language in ${\text {BS}}(1, -2)$ is very straightforward. The “Jantzen monoid” has, however, been studied to good effect from the point of view of admitting a finite complete rewriting system, where the situation has been seen to be similar to the same for the Greendlinger group $\text {Gp} \langle a,b,c \mid abc = cba \rangle$, see [59, 60, 140].

Similarly, using rewriting techniques, Otto [141] proves in 1988 that there exists a one-relator group that is not a one-relation monoid. This group is just ${\mathbb {Z}} \times {\mathbb {Z}}$, but Magnus [100]—in the very first paper on one-relator group theory—uses the Hauptform des Freiheitssatzes to prove that the only one-relator group presentation for this group is $\text {Gp} \langle a,b \mid [a,b]=1 \rangle$. Hence it is already clear that there can be no one-relation monoid presentation for ${\mathbb {Z}} \times {\mathbb {Z}}$, for such a presentation would also be a one-relator group presentation for the group, but the defining relation would be a positive word.

However, one of the major benefits of rewriting is that their techniques can often provide a strong link between formal language theory and monoids. A full description of this is certainly beyond the scope of this survey, but we point the reader to some articles which the author found to be of particular relevance to the word problem for one-relation monoids, viz. [23, 31, 40, 77, 91, 116, 117, 120, 139, 142, 143, 150, 179, 180]. We also refer to the excellent survey by Book, Jantzen and Wrathall [25] and to the monograph by Jantzen [77] for a general introduction to the interface between these areas. We remark that the author of the present survey has also studied the language-theoretic properties of special monoids (see §2.3), and proved that a special monoid has context-free word problem if and only if its group of units is virtually free [126], generalising the Muller-Schupp theorem from groups to all special monoids.

Regarding obtaining finite complete rewriting systems for one-relation monoids, Pedersen [146, 147] introduced morphocompletion. This is a method that automatically introduces new generators, and can be regarded as a rather powerful completion procedure. The idea is to attempt standard completion (e.g. Knuth-Bendix completion) and, if a confluent system is not thereby attained, it backtracks, and adds new generators to stop the non-confluent branching from appearing. His morphocompletion solves the word problem in a number of one-relation monoids. For example, he solves the word problem in the cases

$$\begin{aligned} \text {Mon} \langle a,b \mid buba^m = a^n \rangle \quad (n \ge m+3) \end{aligned}$$

when the word $buba^m$ is self-overlap free. Pedersen’s morphocompletion seems to be one of few methods that also applies to the case $\text {Mon} \langle a,b \mid bua=ava \rangle$ when bua is not self-overlap free. Even for small examples, it generally produces finite complete rewriting systems with around 30–50 rules. It also seems rather unlikely that his methods will generalise to all one-relation monoids. For a thorough survey on other forms of completion, see Dershowitz [49].

6.3 Small overlap conditions

We shall briefly mention a particularly general method for solving many decision problems, which has some use also in the one-relation case. Consider a monoid presentation with alphabet A and with defining relations $(u_i, v_i)$, where the relation words $u_i, v_i \in A^+$ are assumed non-empty. A non-empty subword p of a relation word is called a piece if it appears in at least two distinct ways as a subword of relation words. For $n \ge 1$, we say that the presentation satisfies the small overlap hypothesis C(n) if no relation word can be written as a product of fewer than n pieces. Remmers [152] proved that the word problem is decidable in any monoid presentation satisfying C(3). In fact, this has been greatly extended; C(3) is sufficient to imply decidability of the conjugacy problem [47], and Kambites [79] has shown that C(4) is sufficient to solve even the rational subset membership problem, which greatly generalises the divisibility problems, submonoid membership problem, and the word problem. In fact, in C(4) monoids, the word problem can be solved in linear time by a result of Kambites [78], cf. also the recent normal form algorithm for C(4)-monoids devised by Mitchell and Tsalakou [118]. Kashintsev [84] has explored connections between small overlap conditions and embeddability of monoids into groups, as well as using small overlap techniques for solving the word problem in some classes of special monoids [82, 85].

It follows from Kambites’ work on genericity in small overlap monoids (see [80]²³) work that for any $n \ge 1$, the probability that a two-generated one-relation monoid satisfies the small overlap condition C(n) tends to 1 as the length of the relation increases. Hence all of the problems mentioned above are decidable for almost all one-relation monoids. It follows that the small overlap argument provides a reasonable argument for conjecturing that the word problem (even the rational subset membership problem) is decidable for all one-relation monoids. We remark that a parallel definition of small overlap monoids was given by V. A. Osipova. She proved that in certain monoids (so-called $\ge \frac{1}{2}$-monoids) satisfying a type of overlap condition the word problem is decidable [136]. These methods were also applied by her to partially understand the solvability of equations (the Diophantine problem) in $\ge \frac{1}{3}$-monoids [137, 138]. This latter problem is beyond the scope of this survey, but has very recently been investigated in the special one-relation case by Garreta and Gray [52].

7 Modern and future results (1997–present)

This section will give a high-level overview of some modern results related to the word problem for one-relation monoids. For obvious reasons of space, we will not be giving detailed proofs (or sometimes definitions) of the results and concepts mentioned here, but pointers to further reading will be amply provided.

7.1 Finite complete rewriting systems

It is an open problem whether every one-relation monoid admits a finite complete rewriting system, i.e. whether for every one-relation monoid $M = \text {Mon} \langle A \mid u=v \rangle$ there exists an alphabet²⁴B and a finite complete rewriting system $T \subseteq B^*\times B^*$ such that M is isomorphic with . In general, this property is stronger than having decidable word problem. In this section, we will briefly present two finiteness properties which are closely connected to finite complete rewriting systems, and what is known about these in the one-relation case.

Kobayashi [89] investigated homotopy finiteness properties for one-relation monoids. One central such property is finite derivation type (${{\,\mathrm{FDT}\,}}$), which was introduced in 1987 by Squier [165] (and, independently, Pride [151]), though Kobayashi notes that the idea appears implicitly in work by Adian [7, 8]. The central idea behind ${{\,\mathrm{FDT}\,}}$ is as a homotopy finiteness property for equivalence classes of derivations in monoids, and is independent of the particular finite presentation chosen for a monoid. While the full details of ${{\,\mathrm{FDT}\,}}$ are beyond the scope of the current article, our main interest comes from the following result due to Squier: if a monoid admits a finite complete rewriting system, then it has ${{\,\mathrm{FDT}\,}}$. This gives a potential venue for proving that a monoid does not admits a finite complete rewriting system (which otherwise is a very difficult task), or indeed for providing supporting evidence that, say, a given one-relation monoid admits a finite complete rewriting system.

Kobayashi [89] first used the algorithm ${\mathfrak {A}}$ in 1998 to prove that every one-relation monoid presented by a non-subspecial relation has ${{\,\mathrm{FDT}\,}}$. In a subsequent paper, he then proves that subspecial one-relation monoids have ${{\,\mathrm{FDT}\,}}$, by using weak compression to reduce it to the special one-relation case, which can then be reduced to ${{\,\mathrm{FDT}\,}}$ for one-relator groups [90]. As one-relator groups have ${{\,\mathrm{FDT}\,}}$ by a 1994 result of Cremanns [43], it then follows that all one-relation monoids have ${{\,\mathrm{FDT}\,}}$. Further to this, if a monoid admits a finite complete rewriting system, it also satisfies a certain homological finiteness property ${{\,\mathrm{FP}\,}}_\infty$ (by Kobayashi [88] and Squier [165]). It is known that any monoid with ${{\,\mathrm{FDT}\,}}$ also has ${{\,\mathrm{FP}\,}}_3$ by Cremanns and Otto [44], and for some time it was an open problem whether every one-relation monoid has ${{\,\mathrm{FP}\,}}_\infty$. This was very recently answered affirmatively by Gray and Steinberg [57] in 2019. This can be regarded as supporting the conjecture that every one-relation monoid admits a finite complete rewriting system. The proofs leading up to these results are also notable in their usage of (weak) compression and the algorithm ${\mathfrak {A}}$ not to solve the word problem, but to derive strong structural results.

We end this section by noting that some partial progress has also recently been made in constructing explicit finite complete rewriting systems for certain one-relation monoids. To this end, the results by Cain and Maltcev [33, 34] bear mentioning, as they show that all one-relation monoids of the form $\text {Mon} \langle a,b \mid b^\alpha a^\beta b^\gamma a^\delta b^\varepsilon a^\varphi = a \rangle$ admit finite complete rewriting systems, where $\alpha , \beta , \gamma , \delta , \varepsilon , \varphi \ge 0$, i.e. where the “relative length” of the left-hand side is at most 6. This result provides quite explicit solutions to the word problem for such monoids, but their methods do not seem to be easily generalisable to all monoids $\text {Mon} \langle a,b \mid bua = a \rangle$. We note in passing that the smallest monadic one-relation monoid to which no result in the literature appears to be available to solve the word problem for is $\text {Mon} \langle a,b \mid bababbbabba = a \rangle$. The author has not found a finite complete rewriting system for this monoid, but has solved the word problem for this monoid by other means.

7.2 Special inverse monoids

In 2001, a landmark paper by Ivanov, Margolis and Meakin appeared; this discovered a strong link between the word problem for one-relation monoids and special one-relator inverse monoids. We give a brief summary of this link here.

A monoid M is said to be inverse if for every $x \in M$ there exists a unique $y \in M$ such that $xyx = x$ and $yxy = y$. This “inverse” (which need not be a group inverse) is usually denoted $x^{-1}$. The existence of free inverse monoids was first proved in 1961 by V. V. Wagner [175], although the word problem for free inverse monoids was not proved to be decidable until the 1974 groundbreaking paper by D. Munn [119]. It bears remarking that free inverse monoids on a non-empty finite set of generators are not finitely presented²⁵ as ordinary monoids [156], even though they are (of course!) finitely presented as inverse monoids. Every inverse monoid admits an inverse monoid presentation. Such presentations are commonly written as $\text {Inv} \langle A \mid R \rangle$, where, as for group presentations, one considers words over $A \cup A^{-1}$. Of course, one defines special inverse monoids as is done for ordinary monoids (see §2.3). Arguably the most useful tool for studying inverse monoid presentations comes from Stephen’s procedure, defined in J. B. Stephen’s Ph.D. thesis [166].²⁶ This is a graphical procedure defined entirely analogously to M. Dehn’s Gruppenbild (see Dehn [48] and Chandler and Magnus [39, pp. 24–25]). We refer the reader to subsequent publications by Stephen [167] for more details.

Stephen’s procedure is often useful for solving the word problem in finitely presented inverse monoids, and has been used to solve the word problem in a number of cases (see e.g. [21, 65, 109]). In the case of special monoids, the main interest in solving this problem comes from the following fascinating link proved by Ivanov et al. [71]. A word is reduced if it does not contain a subword of the form $aa^{-1}$ or $a^{-1}a$, where a is some letter.

Theorem 6.1

(Ivanov et al. 2001) If the word problem is decidable for all inverse monoids of the form $\text {Inv} \langle A \mid w=1 \rangle$ where w is some reduced word, then the word problem is also decidable for every one-relation monoid.

We make an important remark that the proof of this theorem as given by Ivanov et al. is incomplete. This fact does not appear to have been observed in the literature before. Their proof begins by reducing the word problem for M to the word problem for the right cancellative case $\text {Mon} \langle a,b \mid aub = ava \rangle$, before embedding this monoid in the special one-relator inverse monoid $\text {Inv} \langle a,b \mid aub(ava)^{-1} = 1 \rangle$, from which the result follows. However, this does not account for the fact that the word problem remains open for the monadic case $\text {Mon} \langle a,b \mid aub = a \rangle$ (as seen in §4.4). Fortunately, the only property of $\text {Mon} \langle a,b \mid aub = ava \rangle$ used to produce such an embedding as above is that it is right cancellative; in particular, by adding the case $\text {Mon} \langle a,b \mid aub=a \rangle$ and embedding this into $\text {Mon} \langle a,b \mid auba^{-1}=1 \rangle$, one finds that the proof of the above theorem is fixed.

As the word problem is decidable for all one-relator groups $\text {Gp} \langle A \mid w=1 \rangle$ and all special one-relation monoids $\text {Mon} \langle A \mid w=1 \rangle$ (see §2.3), one might view the above result with optimism by conjecturing that the word problem is decidable for all one-relator special inverse monoids $\text {Inv} \langle A \mid w=1 \rangle$. However, the following recent and astounding result by Gray [55] demonstrates that this optimism is unfounded.

Theorem 6.2

(Gray, 2020) There exists a special one-relator inverse monoid

$$\begin{aligned} I_B = \text {Inv} \langle A \mid w_B = 1 \rangle \end{aligned}$$

such that the word problem for $I_B$ is undecidable.

However, the word $w_B$ constructed by Gray is not reduced, so the implication in Theorem 6.1 remains a valid path to solving the word problem for all one-relation monoids. Of course, the word problem for special one-relator inverse monoids defined by a reduced word could potentially be significantly harder than that for one-relation monoids. However, the author of the present survey has reasons to suspect that the word problem for all one-relation monoids is equivalent to the word problem for all types of special one-relator inverse monoids occurring in the proof of Theorem 6.1.

The author notes that it is very straightforward to show that any special one-relator inverse monoid occurring in the proof of Theorem 6.1 will have trivial group of units. If special inverse monoids behaved anything like ordinary special monoids (see § 2.3), we might expect this to be strong evidence in favour of decidability. However, very recently, Gray and Ruškuc [56] have demonstrated that the group of units of even one-relator special inverse monoids can exhibit rather exotic behaviour when compared to the monoid itself; it need not, for example, be a one-relator group. There is, at present, not even an algorithm known for decomposing the relator word w in $\text {Inv} \langle A \mid w=1 \rangle$ into minimal invertible pieces. Adian’s overlap algorithm for ordinary special monoids (see §2.3) fails spectacularly here, as is demonstrated by the O’Hare monoid with presentation

$$\begin{aligned} \text {Inv} \langle a,b,c,d \mid (abcd)(acd)(ad)(abbcd)(acd) = 1 \rangle , \end{aligned}$$

where the defining relation word has no self-overlaps, but the factorisation into minimal invertible pieces is indicated by the parentheses [110]. The author of the present survey has recently found a smaller counterexample, namely

$$\begin{aligned} \text {Inv} \langle a,b \mid aabbaabab = 1 \rangle , \end{aligned}$$

which is a group (the trefoil knot group), despite the fact that the defining relation word has no self-overlaps. Gray and Ruškuc [56] propose an improved algorithm (the “Benois algorithm”) for computing the minimal invertible pieces of a special one-relator inverse monoid, and which correctly computes the pieces of the above two examples. However, the author of the present survey has recently found an example showing that this algorithm does not always produce the minimal invertible pieces. This will appear in future work by the author. Thus, until the word problem for one-relator special inverse monoids is better understood, this seems a difficult avenue for tackling the word problem for one-relation monoids.

7.3 The monadic case

As mentioned, cf. §4.4, the word problem for monadic one-relation monoids $\text {Mon} \langle a,b \mid bua=a \rangle$ remains an open problem, conditional on the decidability of the divisibility problems for cycle-free monoids. However, two major results have since appeared for the monadic case, and both were proved in 1997 by Guba.

The first concerns the equivalence of decision problems for such monoids. While it is clear that decidability of the left divisibility problem (even by a single letter) implies decidability of the word problem, it is not a priori true that the converse holds. Furthermore, the rôle of the right divisibility problems seems unclear at first. However—surprisingly—Guba showed that these problems are all, in fact, equivalent in the monadic case. The corresponding statement for general left cycle-free one-relation monoids is not known to hold or not.

Theorem 6.3

(Guba, 1997) Let $M = \text {Mon} \langle a,b \mid bua=a \rangle$. The following are equivalent:

• (1) The word problem for M is decidable;

• (2) The left divisibility problem for M is decidable;

• (3) The right divisibility problem for M is decidable.

Furthermore, each of these problems is equivalent to its restricted variant of considering equality with (resp. left/right divisibility by) the single letter a.

The proof uses diagrammatic methods, and are rather involved; we refer the reader to [62, Theorem 4.1] to begin navigating the proof, and do not expound on it any further.

We now present Guba’s second major result. Consider a monadic one-relation monoid $\text {Mon} \langle a,b \mid bua=a \rangle$. Oganesian considered the submonoid $S_M$ generated by all suffixes of the word bua in $\text {Mon} \langle a,b \mid bua = a \rangle$. He then reduces, by a very general result, the left divisibility problem for M to the left divisibility problem for $S_M$ ( [134, Theorem 1]). He then proves the quite remarkable (and non-trivial!) fact that $S_M$ can be defined by a cycle-free presentation ( [134, Theorem 2]). This makes the implication regarding sh and the word problem for monadic one-relation monoids clear (see §4.4).

Guba, however, studied $S_M$ in more depth. In general, $S_M$ can be shown to not always be a one-relation monoid. However, as it is cycle-free, it is of course group-embeddable (see §2.2), and so one might reasonably ask questions about the group $G_M$ with the same defining relations. Guba, remarkably, shows that $G_M$ is always isomorphic with a one-relator group (which he denotes ${\overline{G}}(\Pi )$). Furthermore, this one-relator group is a positive one-relator group; recall that a one-relator group $\text {Gp} \langle A \mid w=1 \rangle$ is positive if no inverse symbols appear in the word w (these have been studied by Baumslag [20]). He then shows that the left divisibility problem reduces to deciding membership in $S_M$ inside $G_M$. This provides the following astounding statement, which is [62, Corollary 2.1].

Theorem 6.4

(Guba, 1997) The word problem for $\text {Mon} \langle a,b \mid bua=a \rangle$ reduces to the membership problem for a certain submonoid of a positive one-relator group.

Perrin and Schupp [148] have proved that a one-relator group is a special one-relator monoid if and only if it admits a presentation $\text {Gp} \langle A \mid w=1 \rangle$ where w is a positive word. Hence, we have the following remarkable statement: if the submonoid membership problem is decidable for all special one-relator monoids $\text {Mon} \langle A \mid w=1 \rangle$, then the word problem is decidable for all one-relation monoids of the form $\text {Mon} \langle a,b \mid bua = a \rangle$. We do not know of a special one-relator monoid with undecidable submonoid membership problem. However, there is some indication that it might be undecidable, which we discuss below.

Theorem 6.5

( [55, Theorem B]) The cycle-free one-relator group

$$\begin{aligned} B = \text {Gp} \langle a,b \mid abba=baab \rangle \end{aligned}$$

has undecidable submonoid membership problem.

The proof is almost immediate, and so we reproduce it here: consider the right-angled Artin group $A(P_4)$ with defining graph the path on 4 vertices. Then $A(P_4)$ has generators $a_1, \ldots , a_4$ and defining relations $[a_i, a_j] = 1$ whenever $j = i + 1$. It is well-known, and follows quickly from results of Aalbersberg and Hoogeboom [2], that the submonoid membership problem for $A(P_4)$ is undecidable. Consider the HNN-extension B of $A(P_4)$ with stable letter t and associated subgroups $\langle a_1, a_2, a_3 \rangle \cong \langle a_2, a_3, a_4 \rangle$. Then by a few quick Tietze transformations, one finds

$$\begin{aligned} B \cong \text {Gp} \langle a, b \mid [a, bab^{-1}] = 1 \rangle \cong \text {Gp} \langle a, b \mid abba = baab \rangle . \end{aligned}$$

Hence $A(P_4)$ embeds in B, and the result follows.²⁷ However, we note that by [108, Corollary 2.6] the membership problem for all positively generated submonoids of B (with respect to the latter of the two presentations) is decidable. Here a submonoid is positively generated if it admits a generating set with only positive words. Furthermore, the subgroup membership problem is decidable, as B can easily be shown to be an HNN-extension of ${\mathbb {Z}}^2$ conjugating one generator to the other; thus this problem is decidable by using the results in e.g. Kapovich et al [81]. We also note that the monoid $\text {Mon} \langle a,b \mid abba=baab \rangle$ trivially has solvable submonoid membership problem.

7.4 The Collatz conjecture

In recent years, an interesting connection due to Guba between the word problem for monadic one-relation monoids $\text {Mon} \langle a,b \mid bua=a \rangle$ and the Collatz conjecture has appeared. The author is not aware of any place in the literature where this connection has been written down, and so it is fully expanded on here.

The Collatz conjecture (or the $3x+1$ problem) is a famous problem concerning the function $f :{\mathbb {N}} \rightarrow {\mathbb {N}}$ defined as

$$\begin{aligned} f(x)= {\left\{ \begin{array}{ll} \frac{x}{2} &{} \text {if } x \equiv 0 \mod 2\\ 3x+1 &{} \text {if } x \equiv 1 \mod 2. \end{array}\right. } \end{aligned}$$

Let $f^{(i)}(x)$ denote the result of applying f i times to x. The conjecture states that the sequence $(x, f(x), f^{(2)}(x), \ldots )$ eventually reaches 1, at which point it cycles as $(1, 4, 2, 1, \ldots )$. The conjecture has been verified for very large x. Occasionally, the time taken to reach 1 is very long, and has a large degree of unpredictability; for example, even starting with something as small as $x=27$, one has the sequence

$$\begin{aligned} (27, 82, 41, \ldots , 3077, 9232, 4616, \ldots , 5, 16, 8, 4, 2, 1) \end{aligned}$$

taking 111 steps to reach 1. We refer to the survey by Lagarias [93] for an excellent overview.

The connection between the Collatz conjecture (and its generalisations) and decision problems has been studied in the past. J. H. Conway [42] proved that certain generalisations of the Collatz conjecture are undecidable (this has subsequently been strengthened by Kurtz and Simon [92]). We say that a function $g :{\mathbb {N}} \rightarrow {\mathbb {N}}$ is a Collatz function if there is some integer m together with some non-negative rational numbers $a_i, b_i$ $(i < m)$ such that

$$\begin{aligned} g(x)= {\left\{ \begin{array}{ll} a_0 x + b_0 &{} \text {if } x \equiv 0 \mod m,\\ a_1 x + b_1 &{} \text {if } x \equiv 1 \mod m,\\ \quad \vdots \\ a_{m-1} x + b_{m-1} &{} \text {if } x \equiv -1 \mod m.\\ \end{array}\right. } \end{aligned}$$

The usual Collatz function is of the above form for $m=2, a_0 = \frac{1}{2}, b_0 = 0, a_1 = 3, b_1 = 1$.

Theorem 6.6

(Conway, 1972) There exists a fixed Collatz function $g_e :{\mathbb {N}} \rightarrow {\mathbb {N}}$ such that it is undecidable (with input $x \in {\mathbb {N}}$) whether $g_e^{(i)}(x) = 1$ for some $i \ge 1$.

Thus the iterative behaviour of Collatz functions is enough to encode undecidability statements. See Margenstern’s survey [107] for further details on connections between computability and the Collatz conjecture.

Guba realised that there is a connection between Collatz-like functions and the word problem for monadic one-relation monoids. We shall consider the right cancellative case $\text {Mon} \langle a,b \mid aub=a \rangle$, rather than the usual left cancellative case, as this makes the formulation of the problem easier. We shall not detail how (the non-general form of) ${\mathfrak {A}}$ works in this case; it is entirely analogous to the left cancellative case, where prefix is replaced by suffix, etc.

Let $M = \text {Mon} \langle a,b \mid aub = a \rangle$. Let us say we have a pair of words (X, Y), and we wish to decide whether $X = Y$ in M. We shall describe an iterative procedure on such pairs using the way Adian’s algorithm ${\mathfrak {A}}$ operates. We shall indicate this action by $\longrightarrow ^{{\mathfrak {A}}}$. We first describe the base cases. If one of X and Y is empty, then we terminate, and conclude that $X = Y$ in M if and only if $X \equiv Y \equiv \varepsilon$. If both X and Y are non-empty, then we terminate if $X \equiv Y$, and conclude $X = Y$ in M. Otherwise, if $X \not \equiv Y$, and if X (resp. Y) is a single letter which is a suffix of Y (resp. X), then we terminate and conclude that $X \ne Y$ in M.

Now, if $X \equiv X'a$ and $Y \equiv Y'a$, or $X \equiv X'b$ and $Y \equiv Y'b$, then we cancel these letters. This defines transformations

$$\begin{aligned} (X'a, Y'a)&\longrightarrow ^{{\mathfrak {A}}} (X', Y') \\ (X'b, Y'b)&\longrightarrow ^{{\mathfrak {A}}} (X', Y') \end{aligned}$$

If instead X and Y end in different letters, then we flip the pair (X, Y), if necessary, such that it is a pair of the form $(X'b, Y'a)$. We then (as ${\mathfrak {A}}$ tells us to) replace the rightmost a by aub, and cancel the right-most b, resulting in a transformation

$$\begin{aligned} (X'b, Y'a) \longrightarrow ^{{\mathfrak {A}}} (X', Y'au). \end{aligned}$$

We now iterate this process, which completes the description. We conclude by Adian’s theorem regarding ${\mathfrak {A}}$ (cf. Theorem 4.3) that $X = Y$ in M if and only if the process terminates successfully; hence, to solve the word problem is equivalent to be able to decide if the above procedure terminates on a given input (X, Y). Of course, this can also be used to study the right divisibility problem, but these two problems are equivalent for M by Guba’s earlier result.

The insight by Guba is that one can consider the binary representation of words via $a \mapsto 1$ and $b \mapsto 0$, and that the above procedure thus produces a Collatz-like function ${\mathbb {N}}\times {\mathbb {N}} \rightarrow {\mathbb {N}}$.

Example 6.7

Let $M = \text {Mon} \langle a,b \mid abaab = a \rangle$. Let $X \equiv aabaab$ and $Y \equiv a$. This gives the sequence

$$\begin{aligned} (aabaab, a) \rightarrow ^{\mathfrak {A}} (aabaa, abaa) \rightarrow ^{\mathfrak {A}} (aaba, aba) \rightarrow ^{\mathfrak {A}} (aab, ab) \rightarrow ^{\mathfrak {A}} (aa, a). \end{aligned}$$

We terminate unsuccessfully, and conclude that $X \ne Y$ in M. Using the dyadic representation $a \mapsto 1$ and $b \mapsto 0$, we have that the above sequence is a sequence of transformations

$$\begin{aligned} (110110_2, 1_2) \rightarrow ^{\mathfrak {A}} (11011_2, 1011_2) \rightarrow ^{\mathfrak {A}} (1101_2, 101_2) \rightarrow ^{\mathfrak {A}} (110_2, 10_2) \rightarrow ^{\mathfrak {A}} (11_2, 1_2) \end{aligned}$$

Considered as a sequence of natural numbers, the above sequence is

$$\begin{aligned} (54, 1) \rightarrow ^{\mathfrak {A}} (27, 11) \rightarrow ^{\mathfrak {A}} (13, 5) \rightarrow ^{\mathfrak {A}} (6, 2) \rightarrow ^{\mathfrak {A}} (3, 1). \end{aligned}$$

In fact, it can be shown that no input word will give an infinite loop.

The process induced by $\rightarrow ^{\mathfrak {A}}$ is not hard to see to be Collatz-like. Note that the cancelling of final letters corresponds to removing the final bit of a binary digit, which is the same as division by 2 and rounding down, which we hence carry out if the two words map to binary digits that are congruent ${\text {mod}} 2$. Similarly, the transformation

$$\begin{aligned} (X'b, Y'a) \longrightarrow ^{{\mathfrak {A}}} (X', Y'au) \end{aligned}$$

is carried out when the last bits differ, and when considered in its dyadic representation the transformation corresponds to removing the final bit of the dyadic representation of $X'b$ resp. multiplying the dyadic representation of $Y'a$ by $2^{|u|}$ and adding the binary number corresponding to u. Finally, we map $(X, Y) \rightarrow ^{\mathfrak {A}} (Y, X)$ when the last bits differ and the last bit of the word corresponding to X is 0.

Hence, given a one-relation monoid $\text {Mon} \langle a,b \mid aub=a \rangle$, let K be the natural number corresponding to the dyadic representation of u. Then the word problem for M is decidable if and only if the termination problem is decidable for $G :{\mathbb {N}} \times {\mathbb {N}} \rightarrow {\mathbb {N}}$ defined by

$$\begin{aligned} G(x, y)= {\left\{ \begin{array}{ll} \left( \lfloor \frac{x}{2}\rfloor , \lfloor \frac{y}{2}\rfloor \right) &{} \text {if } x \equiv y \mod 2,\\ \left( \frac{x}{2}, 2^{|u|}y + K\right) &{} \text {if } x \not \equiv y \text { and } x \equiv 0 \mod 2, \\ (y, x) &{} \text {if } x \not \equiv y \text { and } x \equiv 1 \mod 2.\\ \end{array}\right. } \end{aligned}$$

That is, we can solve the word problem for M if and only if we can decide, for arbitrary input (x, y), whether or not the sequence $((x, y), G(x, y), G^{(2)}(x, y), \ldots )$ eventually terminates.

Example 6.8

Continuing the example $M_1 = \text {Mon} \langle a,b \mid abaab = a \rangle$ from earlier, we find that as $baa \mapsto 011_2$, we have $K = 3$, so

$$\begin{aligned} G_1(x, y)= {\left\{ \begin{array}{ll} \left( \lfloor \frac{x}{2}\rfloor , \lfloor \frac{y}{2}\rfloor \right) &{} \text {if } x \equiv y \mod 2,\\ \left( \frac{x}{2}, 8y + 3\right) &{} \text {if } x \not \equiv y \text { and } x \equiv 0 \mod 2, \\ (y, x) &{} \text {if } x \not \equiv y \text { and } x \equiv 1 \mod 2.\\ \end{array}\right. } \end{aligned}$$

Similarly, in the (right cancellative analogue of the) monoid from Example 4.2, which is given by $M_2 = \text {Mon} \langle a,b \mid aabbaab = a \rangle$, we find that $u \equiv abbaa \mapsto 10011_2$, so $K = 19$. Thus we can solve the word problem in this monoid if and only if we can decide when the function

$$\begin{aligned} G_2(x, y)= {\left\{ \begin{array}{ll} \left( \lfloor \frac{x}{2}\rfloor , \lfloor \frac{y}{2}\rfloor \right) &{} \text {if } x \equiv y \mod 2,\\ \left( \frac{x}{2}, 32y + 19 \right) &{} \text {if } x \not \equiv y \text { and } x \equiv 0 \mod 2, \\ (y, x) &{} \text {if } x \not \equiv y \text { and } x \equiv 1 \mod 2\\ \end{array}\right. } \end{aligned}$$

terminates. Note that this function loops on input (aaabb, a), as indicated by the (reversal) of the transitions given in this example; this corresponds to the infinite loop starting in (28, 1), given by

$$\begin{aligned} (28, 1) \rightarrow ^{\mathfrak {A}} (14, 51) \rightarrow ^{\mathfrak {A}} (7, 1651) \rightarrow ^{\mathfrak {A}} (3, 825) \rightarrow ^{\mathfrak {A}} (1, 412) \rightarrow ^{\mathfrak {A}} (412, 1). \end{aligned}$$

Now note that $412 \equiv 28 \mod 2^5$, i.e. $1100\mathbf{11100} _2 = \mathbf{11100} _2 \mod 2^5$, so this process will now loop indefinitely to produce the binary numbers $(1100)^n11100_2$ for $n \ge 0$, which gives the non-terminating sequence

$$\begin{aligned} (28,1) \rightarrow ^{\mathfrak {A}} \cdots \rightarrow ^{\mathfrak {A}} (412,1) \rightarrow ^{\mathfrak {A}} \cdots \rightarrow ^{\mathfrak {A}} (6556, 1) \rightarrow ^{\mathfrak {A}} \cdots \rightarrow ^{\mathfrak {A}} (104860, 1) \rightarrow ^{\mathfrak {A}} \cdots \end{aligned}$$

Hence we conclude that $aaabb \ne a$ in M (we can also conclude that aaabb is not right divisible by a). To be clear, if we could detect this looping behaviour for $G_2(x, y)$, we could conclude $aaabb \ne a$ in M simply by checking if $G_2(x, y)$ loops on input (28, 1).

Guba suspects that Conway’s undecidability result indicates that it is probable that the word problem or one of its generalisations for monadic one-relation monoids is undecidable. The problem comes down to understanding poor behaviour of the algorithm ${\mathfrak {A}}$. Of particular interest is the following question.²⁸

Question

(Guba, 1997) Is there some $M = \text {Mon} \langle a,b \mid bua = a \rangle$ and a word w such that w is left²⁹ divisible by $a^k$ in M for every $k \ge 0$?

If this question has an affirmative answer, then this indicates that the algorithm ${\mathfrak {A}}$ has quite complicated behaviour. Of course, the right cancellative analogue of the question above, i.e. does there exist some $M = \text {Mon} \langle a,b \mid aub = a \rangle$ and a word w such that w is right divisible by $a^k$ in M for every $k \ge 0$, can be directly translated to a statement about the above functions by asking for the existence of $m \in {\mathbb {N}}$ such that the monadic Collatz-like function of M when applied to the initial word $(m, 2^k-1)$ always terminates successfully for $k \ge 1$. Demonstrating the existence of such an M and m would indicate that ${\mathfrak {A}}$ (and by extension, the Collatz-like function) can behave rather poorly, and, although there is no direct implication of any kind, this would be an important first step if one intends to construct an undecidable Collatz-like function as above.

8 Concluding remarks

This survey has hopefully given the reader a good feel for the many intricacies, connections to other areas, and beautiful results that combine to make the word problem for one-relation monoids the fascinating problem that it continues to be. Although the many positive decidability results proved over the years seems to indicate that the problem will one day be proved to be decidable, the newly discovered links to undecidable problems by e.g. Gray and Guba might one day come to prove just the opposite. In any case, it seems fair to say that the problem has turned out to be significantly more difficult than the early positive results in the 1960s might have suggested. The question of decidability of the word problem for one-relation monoids might be compared to the question of whether or not Thompson’s group F is amenable. At the door to the office of my M.Sc. advisor C. Bleak there was printed an introduction to F by Cannon and Floyd (see [37]), which I occasionally would glance at while waiting to be let in. One line stood out: “at a recent conference devoted to the group a poll was taken. Is F amenable? Twelve participants voted yes and twelve voted no.” Perhaps the situation would be similar at a conference devoted to the word problem for one-relation monoids?

Given the overwhelming extent of the contributions by S. I. Adian to this area, it would not be appropriate to end this survey with such an anecdote of my own. Instead, I will mention that at a conference long ago, following a talk on the word problem for one-relation monoids, it is reported that Adian was asked: if a Western mathematician were to solve the problem, would Soviet journals publish the solution in English? Adian’s response was: “before the problem is solved, everybody will publish in English in the Soviet Union”. As Almeida and Perrin remark, he seems to have been right [18]. There is likely no more fitting final sentence for this survey than that given by Adian in 2018 at a conference at the Euler International Mathematical Institute in Saint Petersburg, regarding the word problem for one-relation monoids: its solution is a task for the future generations of mathematicians.