Avoid common mistakes on your manuscript.
1 Correction to: Semigroup Forum (2016) 92:361–376 https://doi.org/10.1007/s00233-015-9739-8
Abstract In this corrigendum, we correct the statement and the proof of Proposition 4.11, where the word “lower” is stated instead of “upper,” and vice versa.
Proposition 1
(Proposition 4.11) Let S be a skew lattice such that \(S/{{\mathcal {D}}}\) is a distributive lattice.
-
(i)
Let S be upper symmetric. Then, S is upper cancellative, if and only if \(M\vee x\vee M= M\vee x'\vee M \Leftrightarrow B \vee x \vee B= B \vee x'\vee B\) holds for all skew diamonds
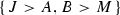 in S and all \(x,x'\in A\).
in S and all \(x,x'\in A\). -
(ii)
Let S be lower symmetric. Then, S is lower cancellative, if and only if \(B\wedge x \wedge B=B\wedge x' \wedge B \Leftrightarrow J\wedge x \wedge J=J\wedge x' \wedge J\) holds for all skew diamonds
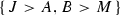 in S and all \(x,x'\in A\).
in S and all \(x,x'\in A\).
Proof
(i). A skew lattice is upper cancellative if and only if it is upper symmetric and simply cancellative. Assume first that S is not upper cancellative, i.e., it is not simply cancellative. By a result of [5], it follows that S contains a subalgebra \({S}'\) isomorphic to \({{\mathbf {N}}}{{\mathbf {C}}}_5\), given by the diagram below:

In \({{\mathbf {N}}}{{\mathbf {C}}}_5\) operations on \(\{x_1, x_2\}\) are defined in one of the following ways: either \(x_i\wedge x_j=x_j\) and \(x_i\vee x_j=x_i\) which yields a right-handed structure; or \(x_i\wedge x_j=x_i\) and \(x_i\vee x_j=x_j\) yielding a left-handed structure. Let A, B, M and J denote the \({{\mathcal {D}}}\)-classes of elements \(x_1\), y, u and v in S, respectively. Note that \(x_2\in A\). Since \(x_1\) and \(x_2\) are both contained in the image of u in A, they cannot lie in the same coset of M in A, i.e., we obtain \(M\vee x_1\vee M\ne M\vee x_2\vee M\). On the other hand, the cosets \(B\vee x_1\vee B\) and \(B\vee x_2\vee B\) both contain v (because \(y\vee x_1\vee y=v=y\vee x_2\vee y\)) and hence coincide by Theorem 2.4. Therefore, the implication \(B\vee x_1\vee B=B\vee x_2\vee B \Rightarrow M\vee x_1\vee M=M\vee x_2\vee M\) fails.
Assume next that S is upper cancellative and let  be a skew diamond in S. Given any \(x,x'\in A\), the direct implication \(M\vee x\vee M=M\vee x'\vee M \Rightarrow B\vee x\vee B=B\vee x'\vee B\) holds by Remark 4.8. Assume that there exist \(x_1,x_2\in A\) such that \(B \vee x_1 \vee B= B \vee x_2\vee B\), but \(M\vee x_1\vee M\ne M\vee x_2\vee M\). Take any \(m\in M\) and consider \(a_1=m \vee x_1\vee m\), \(a_2=m \vee x_2\vee m\). Note that \(a_1,a_2\in A\), \(m<a_1\) and \(m<a_2\). Take \(b\in B\) such that \(b>m\). Since \(m<a_1\) and \(m<b\), it follows that \(a_1\wedge b=m=b\wedge a_1\), and likewise \(a_2\wedge b=m=b\wedge a_2\). By upper symmetry, \(a_1\vee b=b\vee a_1\) and \(a_2\vee b=b\vee a_2\) follow. Denote \(j_1=a_1\vee b\) and \(j_2=a_2\vee b\). The assumption \(B \vee x_1 \vee B= B \vee x_2\vee B\) together with \(m<b\) implies \(b\vee a_1 \vee b=b\vee m\vee x_1\vee m\vee b=b\vee x_1\vee b=b\vee x_2\vee b=b\vee m\vee x_2\vee m\vee b=b\vee a_2\vee b\). It follows that \(j_1=j_2\), and the set \(S'=\{m,a_1,a_2, b,j_1\}\) forms a subalgebra of S, given by the following diagram:
be a skew diamond in S. Given any \(x,x'\in A\), the direct implication \(M\vee x\vee M=M\vee x'\vee M \Rightarrow B\vee x\vee B=B\vee x'\vee B\) holds by Remark 4.8. Assume that there exist \(x_1,x_2\in A\) such that \(B \vee x_1 \vee B= B \vee x_2\vee B\), but \(M\vee x_1\vee M\ne M\vee x_2\vee M\). Take any \(m\in M\) and consider \(a_1=m \vee x_1\vee m\), \(a_2=m \vee x_2\vee m\). Note that \(a_1,a_2\in A\), \(m<a_1\) and \(m<a_2\). Take \(b\in B\) such that \(b>m\). Since \(m<a_1\) and \(m<b\), it follows that \(a_1\wedge b=m=b\wedge a_1\), and likewise \(a_2\wedge b=m=b\wedge a_2\). By upper symmetry, \(a_1\vee b=b\vee a_1\) and \(a_2\vee b=b\vee a_2\) follow. Denote \(j_1=a_1\vee b\) and \(j_2=a_2\vee b\). The assumption \(B \vee x_1 \vee B= B \vee x_2\vee B\) together with \(m<b\) implies \(b\vee a_1 \vee b=b\vee m\vee x_1\vee m\vee b=b\vee x_1\vee b=b\vee x_2\vee b=b\vee m\vee x_2\vee m\vee b=b\vee a_2\vee b\). It follows that \(j_1=j_2\), and the set \(S'=\{m,a_1,a_2, b,j_1\}\) forms a subalgebra of S, given by the following diagram:

(Again, with the operations on \(\{a_1,a_2\}\) defined either in a right-handed or in a left-handed fashion.) Subalgebra \(S'\) is isomorphic to \({{\mathbf {N}}}{{\mathbf {C}}}_5\). By a result of [5], it follows that S is not simply cancellative and thus not upper cancellative, which is a contradiction.
The proof of (ii) is similar. \(\square \)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Victoria Gould.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Costa, J.P., Cvetko-Vah, K. Correction to: Flat coset decompositions of skew lattices. Semigroup Forum 99, 522–523 (2019). https://doi.org/10.1007/s00233-019-10043-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00233-019-10043-y


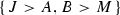 in S and all
in S and all 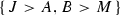 in S and all
in S and all