On properties of square-free elements in commutative cancellative monoids

Abstract

We discuss various square-free factorizations in monoids in the context of: atomicity, ascending chain condition for principal ideals, decomposition, and a greatest common divisor property. Moreover, we obtain a full characterization of submonoids of factorial monoids in which all square-free elements of a submonoid are square-free in a monoid. We also present a factorial property implying that all atoms of a submonoid are square-free in a monoid.

1 Introduction

Throughout this paper by a monoid we mean a commutative cancellative monoid. We adopt the notation from [11].

Let H be a monoid. We denote by $H^{\times }$ the group of all invertible elements of H. Two elements $a,b\in H$ are called relatively prime if they have no common non-invertible divisors, what we denote by $a{\mathrm{rpr}}b$. The set of all atoms in H will be denoted by $\mathcal{A}(H)$. Recall that an element $a\in H$ is called square-free if it cannot be presented in the form $a = b^2c$, where $b, c\in H$ and $b\not \in H^{\times }$. The set of all square-free elements in H we will denote by $\mathcal{S}(H)$.

The main motivation of this paper is connected with the following two properties concerning a submonoid $M\subset H$. The first one is that all atoms of M are square-free in H:

$$\begin{aligned} \mathcal{A}(M)\subset \mathcal{S}(H). \end{aligned}$$

(1.1)

The second one is that all square-free elements of M are square-free in H:

$$\begin{aligned} \mathcal{S}(M)\subset \mathcal{S}(H). \end{aligned}$$

(1.2)

These properties are related to the famous Jacobian conjecture (for details see Sect. 2).

If H is a factorial monoid and a submonoid $M\subset H$ satisfies $M^{\times }=H^{\times }$ and ${\textsf {q}}(M)\cap H=M$, then condition (1.2) can be expressed in a factorial way (see [14], Theorem 3.4—formulated in terms of rings, but in fact valid for monoids):

$$\begin{aligned} \hbox {for every }a\in H\hbox {, }b\in \mathcal{S}(H), \quad \hbox {if }a^2b\in M, \quad \hbox {then }a,b\in M. \end{aligned}$$

(1.3)

Recall also (see [14], Theorem 3.6) that under these assumptions a submonoid M satisfying (1.2) is root closed in H. Recently Angermüller showed in [4], Theorem 3, that under the same assumptions a submonoid M satisfying (1.1) is root closed in H. A submonoid $M\subset H$ is called root closed in H if, for every $a\in H$ and $n\ge 1$, $a^n\in M$ implies $a\in M$.

Recall two questions concerning the conditions (1.1) and (1.2) in the case of a UFD, stated in [13]. We have asked if they are equivalent under some natural assumptions (like $M^{\times }=H^{\times }$), and if not, can the condition (1.1) be expressed in a form of factoriality, similarly to (1.3)?

In Sect. 4 we present a factorial property implying (1.1), weaker than (1.3), namely:

$$\begin{aligned} \hbox {for every }a\in H\hbox {, }b\in \mathcal{S}(H), \quad \hbox {if }a^2b\in M, \quad \hbox {then }a,ab\in M. \end{aligned}$$

(1.4)

In Theorem 4.3 we show that property (1.4) has natural equivalent forms with respect to various square-free factorizations.

In Theorem 5.1 we obtain full description of submonoids of a factorial monoid, satisfying (1.2), as factorial submonoids generated (up to irreducibles) by any set of pairwise relatively prime square-free non-units. We also obtain the answer to a question, when (1.1) and (1.2) are equivalent, expressing (1.2) as a conjunction of (1.1) and the property that any two non-associated atoms of M are relatively prime in H. Moreover, we refer in Theorem 5.1 to various square-free factorizations, in particular equivalence between (1.2) and (1.3) holds without the assumption ${\textsf {q}}(M)\cap H=M$.

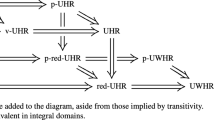
Section 6 is devoted to properties of radical elements. Reinhart in [21] introduced the notions of radical element and radical factoriality of a monoid. An element $a\in H$ is called radical if its principal ideal aH is a radical ideal. A monoid H is called radical factorial if every element is a product of radical elements. As we already observed in [15], Lemma 3.2 (b), every radical element is square-free. So we have the following diagram of relations on elements of a monoid:

$$\begin{aligned} \begin{array}{ccc} \text {prime}&{}\Rightarrow &{}\text {atom} \\ \Downarrow &{} &{} \Downarrow \\ \text {radical}&{}\Rightarrow &{}\text {square-free} \\ \end{array} \end{aligned}$$

(1.5)

A radical element is an analog of a square-free one in the same way as a prime element is an analog of an atom. Moreover, a radical element is a generalization of a prime in the same way as a square-free element is a generalization of an atom.

How these analogies and generalizations work, we show in Sect. 6. In Propositions 6.5– 6.7 we study the uniqueness of factorizations. In Proposition 6.4 we prove that in a decomposition monoid all square-free elements are radical. Recall that a monoid H is called a decomposition monoid if every element $a\in H$ is primal, that is, for every $b,c\in H$ such that $a\mid bc$ there exist $a_1,a_2\in H$ such that $a=a_1a_2$, $a_1\mid b$ and $a_2\mid c$. A domain R is pre-Schreier if the multiplicative monoid $R \setminus \{0\}$ is a decomposition monoid. The notion of a pre-Schreier domain was introduced by Zafrullah in [24], see also [6] and the references given there.

In Sects. 2 and 7 we discuss square-free factorizations in monoids in the context of the following properties: atomicity, ACCP, decomposition, GCD. We collect all relationships in Proposition 3.4. This is a generalization and extension of Proposition 1 from [16]. In Sect. 7 we consider possible classifications of monoids with respect to square-free factorizations and we state questions about existence of monoids. Some examples are presented in Sect. 8.

We refer to the following diagram of relations of monoids:

(1.6)

Remember that

$$\begin{aligned} \text {atomic}\;\wedge \;\text {atoms are primes}\;\;\Rightarrow \;\; \text {factorial} \end{aligned}$$

(1.7)

Finally, in Sect. 9 we concern a natural question about the possible number of square-free elements in a monoid.

2 Connections with the Jacobian conjecture

The Jacobian conjecture, stated by Keller [17] in 1939 is one of the most important open problems stimulating modern mathematical research (see [22]), with long lists of false proofs and equivalent formulations. For more information we refer the reader to van den Essen’s book [23].

Jacobian conjecture Let k be a field of characteristic 0. For every polynomials $f_1,\ldots ,f_n\in k[x_1,\ldots ,x_n]$ with $n\ge 2$, if

$$\begin{aligned} \left| \begin{array}{c@{\quad }c@{\quad }c} \dfrac{\partial f_1}{\partial x_1}&{}\cdots &{} \dfrac{\partial f_1}{\partial x_n}\\ \vdots &{}&{}\vdots \\ \dfrac{\partial f_n}{\partial x_1}&{}\cdots &{} \dfrac{\partial f_n}{\partial x_n} \end{array}\right| \in k\setminus \{0\}, \end{aligned}$$

(2.1)

then $k[f_1,\ldots ,f_n]=k[x_1,\ldots ,x_n]$.

Now, we will describe some topics of an approach to the conjecture in terms of irreducibility and square-freeness. For more details we refer the reader to our survey article [13].

Under the assumption that $f_1,\ldots ,f_n$ are algebraically independent over k, the Jacobian condition (2.1) is equivalent to any of the following ones [8, 12, 14]:

$$\begin{aligned}&\hbox {every atom of }k[f_1,\ldots ,f_n]\hbox { is square-free in }k[x_1,\ldots ,x_n], \end{aligned}$$

(2.2)

$$\begin{aligned}&\hbox {every square-free element of }k[f_1,\ldots ,f_n]\hbox { is square-free in }k[x_1,\ldots ,x_n].\nonumber \\ \end{aligned}$$

(2.3)

Under the same assumption, the assertion of the conjecture: $k[f_1,\ldots ,f_n]=k[x_1,\ldots ,x_n]$ is equivalent to the following one [1, 5, 12]:

$$\begin{aligned} \hbox {every atom of }k[f_1,\ldots ,f_n]\hbox { is an atom of }k[x_1,\ldots ,x_n]. \end{aligned}$$

(2.4)

Hence, in particular, the existence of a non-trivial example for (2.2), where by “non-trivial” we mean “not satisfying (2.4)”, is equivalent to the negation of the Jacobian conjecture.

Recall a generalization of the Jacobian conjecture formulated in [14].

Conjecture Let k be a field of characteristic 0. For every polynomials $f_1,\ldots ,f_r\in k[x_1,\ldots ,x_n]$ with $n\ge 2$ and $r\in \{2,\ldots ,n\}$, if

$$\begin{aligned} \gcd \left( \left| \begin{array}{c@{\quad }c@{\quad }c} \dfrac{\partial f_1}{\partial x_{j_1}}&{}\cdots &{} \dfrac{\partial f_1}{\partial x_{j_r}}\\ \vdots &{}&{}\vdots \\ \dfrac{\partial f_r}{\partial x_{j_1}}&{}\cdots &{} \dfrac{\partial f_r}{\partial x_{j_r}} \end{array}\right| ,\; 1\le j_1<\ldots <j_r\le n\right) \in k\setminus \{0\}, \end{aligned}$$

(2.5)

then $k[f_1,\ldots ,f_r]$ is algebraically closed in $k[x_1,\ldots ,x_n]$.

By Nowicki’s characterization ([19], Theorem 5.4, [18], Theorem 4.1.4, [7], 1.4) the assertion above is equivalent to: “R is a ring of constants for some k-derivation of $k[x_1,\ldots ,x_n]$”.

Under the assumption that $f_1,\ldots ,f_r$ are algebraically independent over k, the generalized Jacobian condition (2.5) is equivalent to any of the following ones ([14]):

$$\begin{aligned}&\hbox {every atom of }k[f_1,\ldots ,f_r]\hbox { is square-free in }k[x_1,\ldots ,x_n], \end{aligned}$$

(2.6)

$$\begin{aligned}&\hbox {every square-free element of }k[f_1,\ldots ,f_r]\hbox { is square-free in }k[x_1,\ldots ,x_n].\nonumber \\ \end{aligned}$$

(2.7)

3 Square-free factorizations in monoids

The aim of this section is to recall and extend some observations from [16]. The statements in that paper were formulated for rings, but the arguments are valid for monoids, since we were working only with the multiplicative structure of rings. In particular, Lemma 1 and Lemma 2 e) of [16] take the following form.

Lemma 3.1

Let H be a monoid. If $a\in \mathcal{S}(H)$ and $a=b_1b_2\ldots b_n$, then $b_1$, $b_2$, $\ldots$, $b_n\in \mathcal{S}(H)$ and $b_i{\mathrm{rpr}}b_j$ for $i\ne j$.

Lemma 3.2

Let H be a decomposition monoid. If $a_1,\ldots ,a_n\in \mathcal{S}(H)$ and $a_i{\mathrm{rpr}}a_j$ for all $i\ne j$, then $a_1\ldots a_n\in \mathcal{S}(H)$.

As an immediate consequence we obtain.

Corollary 3.3

If H is a decomposition monoid and $a_1,\ldots ,a_n\in \mathcal{A}(H)$, $a_i\not \sim a_j$ for $i\ne j$, then $a_1\ldots a_n\in \mathcal{S}(H)$.

In [16], Proposition 1, we considered three types of square-free factorizations—(ii), (iii), (iv) in Proposition 3.4 below. In [16] we did not consider condition denoted (i) below as a separate one, as well as atomicity implying it. Moreover, we considered in [16], Proposition 1, only one type of square-free extraction—(vi) in Proposition 3.4 below. Here we add a second type of square-free extraction—(v) as easily following from (ii) for an arbitrary monoid. Finally, implications $\mathrm{(vi)}\Rightarrow \mathrm{(ii)}$ and $\mathrm{(vi)}\Rightarrow \mathrm{(iv)}$ in [16], Proposition 1 (b) were formulated for GCD-domains, but the proofs were based only on [16], Lemma 2 e). This is why implications $\mathrm{(iii)}\Rightarrow \mathrm{(ii)}$ and $\mathrm{(iii)}\Rightarrow \mathrm{(iv)}$ below hold for arbitrary decomposition monoids. In part (c) of Proposition 3.4 we take into account the following remark of the reviewer.

Reviewer’s remark

Since every square-free element of a GCD-monoid is radical, we have every GCD-monoid that satisfies property (i) is radical factorial. Therefore, [20], Theorem 3.10 and Corollary 4.5, imply that every GCD-monoid that satisfies property (i), satisfies property (ii), since every principal ideal is a product of finitely many pairwise comparable radical principal ideals.

Proposition 3.4

Let H be a monoid. Consider the following conditions:

(i) for every $a\in H$ there exist $n\ge 1$ and $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$ such that $a=s_1s_2\ldots s_n$,

(ii) for every $a\in H$ there exist $n\ge 1$ and $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$ such that $s_i\mid s_{i+1}$ for $i=1,\ldots ,n-1$, and $a=s_1s_2\ldots s_n$,

(iii) for every $a\in H$ there exist $n\ge 1$ and $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$ such that $s_i{\mathrm{rpr}}s_j$ for $i\ne j$, and $a=s_1s_2^2s_3^3\ldots s_n^n$,

(iv) for every $a\in H$ there exist $n\ge 0$ and $s_0,s_1,\ldots ,s_n\in \mathcal{S}(H)$ such that $a=s_0s_1^2s_2^{2^2}\ldots s_n^{2^n}$,

(v) for every $a\in H$ there exist $b\in H$ and $c\in \mathcal{S}(H)$ such that $a=bc$ and $a\mid c^n$ for some $n\ge 1$,

(vi) for every $a\in H$ there exist $b\in H$ and $c\in \mathcal{S}(H)$ such that $a=b^2c$.

(a) The following implications hold:

(b) If H is a decomposition monoid, then

$$\begin{aligned} \begin{array}{ccccc} \mathrm{(ii)}\Leftrightarrow & {} \mathrm{(iii)}\Rightarrow & {} \mathrm{(iv)}. \end{array} \end{aligned}$$

(c) If H is a GCD-monoid, then

$$\begin{aligned} \begin{array}{ccccccc} \mathrm{(i)}\Leftrightarrow & {} \mathrm{(ii)}\Leftrightarrow & {} \mathrm{(iii)}\Leftrightarrow & {} \mathrm{(iv)}. \end{array} \end{aligned}$$

Note that, according to (v), under the assumption $a=bc$ the condition “$a\mid c^n$ for some $n\ge 1$” is equivalent to “$b\mid c^n$ for some $n\ge 1$”.

Recall that every radical element is square-free ([15], Lemma 3.2 (b), so radical factorial monoids studied by Reinhart in [21] satisfy condition (i).

Remark 3.5

The statement that there are (in general) no other implications than the ones stated above is equivalent to the existence of the following counter-examples.

• 1. Non-factorial GCD-monoids satisfying: $\mathrm{(v)}\wedge \lnot \mathrm{(vi)}$, $\mathrm{(vi)}\wedge \lnot \mathrm{(v)}$.

• 2. Decomposition non-GCD monoids satisfying: $\mathrm{(i)}\wedge \lnot \mathrm{(vi)}$, $\mathrm{(iv)}\wedge \lnot \mathrm{(v)}$.

• 3. Non-decomposition monoids satisfying: $\mathrm{(ii)}\wedge \lnot \mathrm{(vi)}$, $\mathrm{(iii)}\wedge \lnot \mathrm{(v)}$.

• 4. Non-factorial ACCP-monoids satisfying: $\lnot \mathrm{(iii)}$, $\lnot \mathrm{(v)}$.

• 5. An atomic non-ACCP monoid satisfying $\lnot \mathrm{(vi)}$.

• 6. A non-atomic monoid satisfying $\mathrm{(ii)}$.

4 Sufficient conditions for $\mathcal{A}(M)\subset \mathcal{S}(H)$

In this section we study a factorial property (1.4) implying that all atoms of a submonoid are square-free in a monoid. We show that this property is, in general, not a necessary one. However, it is interesting by itself since it has natural equivalent forms with respect to several square-free factorizations, what we obtain in Theorem 4.3.

Proposition 4.1

Let H be a monoid satisfying condition (vi) of Proposition  3.4. Let M be a submonoid of H such that for every $a\in H$, $b\in \mathcal{S}(H)$,

$$\begin{aligned}a^2b\in M\Rightarrow a,ab\in M.\end{aligned}$$

Then $\mathcal{A}(M)\subset \mathcal{S}(H)$.

Proof

Suppose that there exists some $c\in \mathcal{A}(M)$ such that $c\notin \mathcal{S}(H)$. Then $c=a^2b$ for some $a\in H$, $b\in \mathcal{S}(H)$. Since $a^2b\in M$, then $a,ab\in M$. Note that $a\notin H^{\times }$, because $c\notin \mathcal{S}(H)$, so $a,ab\notin M^{\times }$, a contradiction. $\square$

The converse implication is not valid:

Example 4.2

Consider a monoid $H={\mathbb N}_{\ge 0}^3$ and its submonoid $M=\langle (1,1,0),$$(1,0,1) \rangle$. Then $\mathcal{A}(M)=\{(1,1,0),(1,0,1)\}$, so $\mathcal{A}(M)\subset \mathcal{S}(H)$, but for $a=(1,0,0)\in H$, $b=(0,1,1)\in \mathcal{S}(H)$ we have $2a+b\in M$ and $a,a+b\notin M$.

Observe that in the above example the monoid M satisfies ${\textsf {q}}(M)\cap H=M$, and under this condition properties (1.3) and (1.4) are equivalent.

The most difficult part of Theorem’s 4.3 proof is the connection between $\mathrm{(i)}\Leftrightarrow \mathrm{(ii)}$ and $\mathrm{(iii)}\Leftrightarrow \mathrm{(iv)}\Leftrightarrow \mathrm{(v)}$, i.e. the equivalence of (ii) and (iii).

Theorem 4.3

Let H be a factorial monoid. Let $M\subset H$ be a submonoid such that $M^{\times }=H^{\times }$. The following conditions are equivalent:

(i) for every $a\in H$ and $b\in \mathcal{S}(H)$,

$$\begin{aligned} a^2b\in M\Rightarrow a,ab\in M, \end{aligned}$$

(ii) for every $n\ge 0$ and $s_0, s_1, \ldots , s_n\in \mathcal{S}(H)$,

$$\begin{aligned} s_0s_1^2s_2^{2^2}\ldots s_n^{2^n}\!\!\in \!M\Rightarrow s_is_{i+1}s_{i+2}^2s_{i+3}^{2^2}\ldots s_n^{2^{n-i-1}}\!\!\in \!M, i=0,\ldots ,n-1, \text{ and }\; s_n\!\in \!M, \end{aligned}$$

(iii) for every $n\ge 1$ and $s_1, s_2, \ldots , s_n\in \mathcal{S}(H)$ such that $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$,

$$\begin{aligned}s_1s_2^2s_3^3\ldots s_n^n\in M\Rightarrow s_n, s_{n-1}s_n, s_{n-2}s_{n-1}s_n, \ldots , s_1s_2\ldots s_n\in M,\end{aligned}$$

(iv) for every $n\ge 1$ and $s_1, s_2, \ldots , s_n\in \mathcal{S}(H)$ such that $s_i\mid s_{i+1}$ for $i=1, \ldots , n-1$,

$$\begin{aligned} s_1s_2\ldots s_n\in M\Rightarrow s_{1}, s_2,\ldots , s_n\in M, \end{aligned}$$

(v) for every $a\in H$ and $b\in \mathcal{S}(H)$ such that $a\mid b^n$ for some $n\ge 1$,

$$\begin{aligned}ab\in M\Rightarrow a,b\in M.\end{aligned}$$

Proof

$\mathrm{(i)}\Rightarrow \mathrm{(ii)}$

Assume (i). Consider elements $s_0, \ldots , s_n\in \mathcal{S}(H)$ such that $s_0s_1^2s_2^{2^2}\ldots s_n^{2^n}\in M$. Since $\big (s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}}\big )^2s_0\in M$, from (i) we obtain

$$\begin{aligned} s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}},\;\; \big (s_1s_2^2s_3^{2^2} \ldots s_n^{2^{n-1}}\big )s_0 \in M. \end{aligned}$$

Then, since $\big (s_2s_3^2s_4^{2^2}\ldots s_n^{2^{n-2}}\big )^2s_1\in M$, from (i) we obtain

$$\begin{aligned} s_2s_3^2s_4^{2^2}\ldots s_n^{2^{n-2}},\;\; \big (s_2s_3^2s_4^{2^2} \ldots s_n^{2^{n-2}}\big )s_1 \in M. \end{aligned}$$

Continuing, finally we receive:

$$\begin{aligned} \big (s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}} \big ) s_0,\, \big (s_2s_3^2s_4^{2^2}\ldots s_n^{2^{n-2}} \big )s_1, \ldots ,\, s_{n-1}s_n^2s_{n-2},\, s_ns_{n-1},\, s_n\in M. \end{aligned}$$

$\mathrm{(ii)}\Rightarrow \mathrm{(i)}$

Assume (ii). Consider $a\in H, b\in \mathcal{S}(H)$ such that $a^2b\in M$. We can express a in the form $a=s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}}$, where $s_i\in \mathcal{S}(H)$ for $i=1, \ldots , n$. Put $s_0=b$. Thus we receive:

$$\begin{aligned} s_0s_1^2s_2^{2^2}\ldots s_n^{2^n}=a^2b\in M. \end{aligned}$$

Using the assumption we obtain:

$$\begin{aligned} s_0s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}},\; s_1s_2s_3^2s_4^{2^2}\ldots s_n^{2^{n-2}}, \ldots ,\; s_{n-2}s_{n-1}s_n^2,\; s_{n-1}s_n,\; s_n\in M. \end{aligned}$$

We see that $ab=s_0s_1s_2^2s_3^{2^2}\ldots s_n^{2^{n-1}}\in M$. Moreover:

$$\begin{aligned} a=s_n(s_{n-1}s_n)\big (s_{n-2}s_{n-1}s_n^2\big ) \big (s_{n-3}s_{n-2}s_{n-1}^2s_n^{2^2}\big )\ldots \big (s_1s_2s_3^2s_4^{2^2}\ldots s_n^{2^{n-2}}\big )\in M. \end{aligned}$$

$\mathrm{(ii)}\Rightarrow \mathrm{(iii)}$

Assume (ii). We write ${\lceil x \rceil }$ and ${\lfloor x \rfloor }$ for respectively the ceiling and the floor of a real number x.

Step I. If$s_1s_2^2s_3^3\ldots s_n^n\in M$, where$s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$for$i\ne j$, then$s_1s_2s_3^2s_4^2\ldots s_n^{\lceil \frac{n}{2} \rceil },\; s_2s_3s_4^2s_5^2\ldots s_n^{\lfloor \frac{n}{2} \rfloor }\in M.$

Let $a=s_1s_2^2s_3^3\ldots s_n^n\in M$, where $s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$. Then the element a can be presented in the form $a=t_0t_1^2t_2^{2^2}\ldots t_r^{2^r}$, where $t_i=s_1^{c^{(1)}_i}\ldots s_n^{c^{(n)}_i}\in \mathcal{S}(H)$, $i=0,\ldots , r$ and $k=\sum _{i=0}^r c_i^{(k)}2^i$ with $c_i^{(k)}\in \{0,1\}$, $k=1,\ldots ,n$ (see the proof of (vi)$\Rightarrow$(ii) in [16], Proposition 1). From (ii) we get $t_it_{i+1}t_{i+2}^2t_{i+3}^{2^2}\ldots t_r^{2^{r-i-1}}\in M$, $i=0,\ldots ,r-1$ and $t_r\in M$. In particular, $t_0t_1t_2^2\ldots t_r^{2^{r-1}}\in M$. Moreover:

$$\begin{aligned} t_1t_2^2t_3^{2^2}\ldots t_r^{2^{r-1}}= \left( \prod _{i=1}^{r-1}t_it_{i+1}t_{i+2}^2t_{i+3}^{2^2}\ldots t_r^{2^{r-i-1}}\right) t_r\in M. \end{aligned}$$

By the definition of $c^{(j)}_i$, we have

$$\begin{aligned}&s_1s_2s_3^2s_4^2\ldots s_n^{\left\lceil \frac{n}{2} \right\rceil }= t_0t_1t_2^2\ldots t_r^{2^{r-1}}\in M,\\&s_2s_3s_4^2s_5^2\ldots s_n^{\lfloor \frac{n}{2} \rfloor }= t_1t_2^2t_3^{2^2}\ldots t_r^{2^{r-1}}\in M. \end{aligned}$$

Step II. If$s_1s_2^2s_3^3\ldots s_n^n\in M$, where$s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$for$i\ne j$, then$s_1s_2s_3\ldots s_n,\; s_2s_3^2s_4^3\ldots s_n^{n-1}\in M.$

Assume that $s_1s_2^2s_3^3\ldots s_n^n\in M$, where $s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$. We prove by induction on l that

$$\begin{aligned} s_1^{\left\lceil \frac{1}{2^l} \right\rceil } s_2^{\left\lceil \frac{2}{2^l} \right\rceil }\ldots s_{n-1}^{\left\lceil \frac{n-1}{2^l} \right\rceil } s_n^{\left\lceil \frac{n}{2^l} \right\rceil },\;\; s_1^{1-\left\lceil \frac{1}{2^l} \right\rceil } s_2^{2-\left\lceil \frac{2}{2^l} \right\rceil }\ldots s_{n-1}^{n-1-\left\lceil \frac{n-1}{2^l} \right\rceil } s_n^{n-\left\lceil \frac{n}{2^l} \right\rceil } \in M. \end{aligned}$$

Put $q={\lceil \frac{n}{2^l} \rceil }$. Then $(q-1)2^l<n\le q2^l$. Put $s_i'=s_{(i-1)2^l+1}s_{(i-1)2^l+2}\ldots s_{i2^l}$ for $i=1,\ldots ,q-1$ and $s_q'=s_{(q-1)2^l+1}s_{(q-1)2^l+2}\ldots s_n$. Note that $s_1',s_2',\ldots , s_q'\in \mathcal{S}(H)$ and $s_i'{\mathrm{rpr}}_H s_j'$ for $i\ne j$, because $s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$. We have $s_1^{\lceil \frac{1}{2^l} \rceil } s_2^{\lceil \frac{2}{2^l} \rceil }\ldots s_{n-1}^{\lceil \frac{n-1}{2^l} \rceil } s_n^{\lceil \frac{n}{2^l} \rceil }= s_1'(s_2')^2\ldots (s_q')^q.$ If $s_1^{\lceil \frac{1}{2^l} \rceil } s_2^{\lceil \frac{2}{2^l} \rceil }\ldots s_{n-1}^{\lceil \frac{n-1}{2^l} \rceil } s_n^{\lceil \frac{n}{2^l} \rceil }\in M$, then by step I we obtain that

$$\begin{aligned} s_1^{\left\lceil \frac{1}{2^{l+1}} \right\rceil } s_2^{\left\lceil \frac{2}{2^{l+1}} \right\rceil }\ldots s_{n-1}^{\left\lceil \frac{n-1}{2^{l+1}} \right\rceil } s_n^{\left\lceil \frac{n}{2^{l+1}} \right\rceil } =s_1's_2'(s_3')^2(s_4')^2\ldots (s_q')^{\left\lceil \frac{q}{2} \right\rceil } \in M \end{aligned}$$

and

$$\begin{aligned} s_1^{\left\lceil \frac{1}{2^l} \right\rceil -\left\lceil \frac{1}{2^{l+1}} \right\rceil } s_2^{\left\lceil \frac{2}{2^l} \right\rceil -\left\lceil \frac{2}{2^{l+1}} \right\rceil } \ldots s_n^{\left\lceil \frac{n}{2^l} \right\rceil -\left\lceil \frac{n}{2^{l+1}} \right\rceil } =s_2's_3'(s_4')^2(s_5')^2\ldots (s_q')^{\lfloor \frac{q}{2} \rfloor } \in M. \end{aligned}$$

If moreover $s_1^{1-\lceil \frac{1}{2^l} \rceil } s_2^{2-\lceil \frac{2}{2^l} \rceil }\ldots s_n^{n-\lceil \frac{n}{2^l} \rceil }\in M$, then also

$$\begin{aligned}&s_1^{1-\left\lceil \frac{1}{2^{l+1}} \right\rceil } s_2^{2-\left\lceil \frac{2}{2^{l+1}} \right\rceil }\ldots s_n^{n-\left\lceil \frac{n}{2^{l+1}} \right\rceil }\\&\quad =s_1^{1-\left\lceil \frac{1}{2^l} \right\rceil } s_2^{2-\left\lceil \frac{2}{2^l} \right\rceil }\ldots s_n^{n-\left\lceil \frac{n}{2^l} \right\rceil }\cdot s_1^{\left\lceil \frac{1}{2^l} \right\rceil -\left\lceil \frac{1}{2^{l+1}} \right\rceil } s_2^{\left\lceil \frac{2}{2^l} \right\rceil -\left\lceil \frac{2}{2^{l+1}} \right\rceil } \ldots s_n^{\left\lceil \frac{n}{2^l} \right\rceil -\left\lceil \frac{n}{2^{l+1}} \right\rceil } \in M. \end{aligned}$$

There exists $r \in \mathbb {N}$ such that $2^r > n$. Then for every $1\le t\le n$ we have $\lceil \frac{t}{2^{r}} \rceil =1$. Consequently, $s_1s_2s_3\ldots s_n,\; s_2s_3^2s_4^3\ldots s_n^{n-1}\in M$.

Step III. We prove (iii) by induction on n. For $n=1$ it is clear. Assume the assertion for n and consider $s_1, s_2, \ldots , s_n, s_{n+1}\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$, such that $s_1s_2^2s_3^3\ldots s_n^ns_{n+1}^{n+1}\in M$. By step II we have

$$\begin{aligned} s_1s_2s_3\ldots s_ns_{n+1}, s_2s_3^2s_4^3\ldots s_n^{n-1}s_{n+1}^n \in M. \end{aligned}$$

Then by the inductive assumption we have

$$\begin{aligned} s_{n+1}, s_ns_{n+1}, s_{n-1}s_ns_{n+1}, \ldots , s_2s_3\ldots s_ns_{n+1}\in M. \end{aligned}$$

$\mathrm{(iii)}\Rightarrow \mathrm{(ii)}$

Assume (iii). We prove (ii) by induction on n. For $n=0$ it is clear.

We assume the assertion for n, that is, if $s_0,s_1,{\ldots },s_n {\in } \mathcal{S}(H)$, then $s_0s_1^2s_2^{2^2}{\ldots } s_n^{2^n}{\in } M$ implies $s_{n-l}\prod \limits _{j=0}^{l-1} s_{n-l+j+1}^{2^{j}} \in M$ for every $l \in \{0, 1, \ldots , n\}$.

We prove the assertion for $n+1$. Let $a=s_0s_1^2s_2^{2^2}\ldots s_{n+1}^{2^{n+1}}\in M$, where $s_0,s_1,\ldots ,s_{n+1}\in \mathcal{S}(H)$. Then the element a can be presented in the form $a=t_1t_2^2t_3^3\ldots t_m^m$, where $m=2^{n+2}-1$ and $t_1,\ldots , t_m\in \mathcal{S}(H)$, $t_i{\mathrm{rpr}}_H t_j$, for $i\ne j$ (for details see the proof of $\mathrm{(ii)} \Rightarrow \mathrm{(vi)}$ in [16], Proposition 1(b). From (iii) we have $t_m, t_{m-1}t_m,\ldots , t_1t_2\ldots t_m \in M$. Note that m is odd. Multiplying the elements of the form $t_rt_{r+1}\ldots t_m$ for all odd r we obtain $t_1t_2t_3^2t_4^2\ldots t_m^{\lceil \frac{m}{2} \rceil }\in M$. Multiplying the elements of that form for all even r we obtain $t_2t_3t_4^2t_5^2\ldots t_m^{\lfloor \frac{m}{2} \rfloor }\in M$. Since $t_2t_3t_4^2t_5^2\ldots t_m^{\lfloor \frac{m}{2} \rfloor }\sim _H s_1s_2^2s_3^4\ldots s_{n+1}^{2^n}$, by the inductive assumption we have $s_{n+1-l}\prod \limits _{j=0}^{l-1} s_{(n+1)-l+j+1}^{2^{j}} \in M$ for $l \in \{0, 1, \ldots , n\}$. Moreover, $t_1t_2t_3^2t_4^2\ldots t_m^{\lceil \frac{m}{2} \rceil }\sim _H s_0s_1s_2^2s_3^4\ldots s_{n+1}^{2^n}$, which gives the assertion for $l=n+1$.

$\mathrm{(iii)} \Leftrightarrow \mathrm{(iv)}$ follows from the equivalence of presentations (ii) and (iii) in Proposition 3.4 (for details see [16], the proofs of $\mathrm{(iv)} \Rightarrow \mathrm{(vi)}$ in Proposition 1(a) and $\mathrm{(vi)} \Rightarrow \mathrm{(iv)}$ in Proposition 1(b).

$\mathrm{(iv)} \Rightarrow \mathrm{(v)}$

Assume (iv). Consider $a\in H$, $b\in \mathcal{S}(H)$ such that $a\mid b^n$ for some $n\ge 1$, and $ab\in M$. Let $a=s_1s_2\ldots s_m$, where $s_1,\ldots ,s_m\in \mathcal{S}(H)$, $s_i\mid s_{i+1}$ for $i=1,\ldots ,m-1$. Then $s_m\mid b^n$, hence $s_m\mid b$, because $s_m\in \mathcal{S}(H)$. We have $s_1s_2\ldots s_mb=ab\in M$. By (iv) we obtain $s_1, s_2,\ldots , s_m, b\in M$, so $a,b\in M$.

$\mathrm{(v)} \Rightarrow \mathrm{(iv)}$

Assume (v). Let $s_1s_2\ldots s_n\in M$, where $s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i\mid s_{i+1}$ for $i=1,\ldots ,n-1$. Put $a=s_1s_2\ldots s_{n-1}$, $b=s_n$. Then $a\mid b^{n-1}$. By (v) we have $s_1s_2\ldots s_{n-1}\in M$ and $s_n\in M$, and the assertion follows by induction. $\square$

5 Necessary and sufficient conditions for $\mathcal{S}(M)\subset \mathcal{S}(H)$

In this section we obtain a full characterization of submonoids of a factorial monoid for which all square-free elements of a submonoid are square-free in a monoid.

Let us note that the formulation and the proof of Proposition 4.1 from [15] involve only the multiplicative structure of a domain. Thus we have the equivalence of the conditions (vi)–(viii) of the following Theorem 5.1. For the same reason implication $\mathrm{(viii)}\Rightarrow \mathrm{(i)}$ of Theorem 5.1 follows from the proof of implication $\mathrm{(ii)}\Rightarrow \mathrm{(i)}$ of Theorem 3.4 from [14].

Theorem 5.1

Let H be a factorial monoid. Let $M\subset H$ be a submonoid such that $M^{\times }=H^{\times }$. The following conditions are equivalent:

(i) $\mathcal{S}(M)\subset \mathcal{S}(H)$,

(ii) $\mathcal{A}(M)\subset \mathcal{S}(H)$ and, for every $a,b\in M$,

$$\begin{aligned} a{\mathrm{rpr}}_M b\Rightarrow a{\mathrm{rpr}}_H b, \end{aligned}$$

(iii) $\mathcal{A}(M)\subset \mathcal{S}(H)$ and, for every $a,b\in \mathcal{A}(M)$,

$$\begin{aligned}a\not \sim _M b\Rightarrow a{\mathrm{rpr}}_H b,\end{aligned}$$

(iv) $M=H^{\times }\times {\textsf {F}}(B)$, where B is any set of pairwise relatively prime (in H), square-free non-units of H,

(v) for every $n\ge 1$ and $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$ such that $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$,

$$\begin{aligned} s_1s_2^2s_3^3\ldots s_n^n\in M\Rightarrow s_1,s_2,\ldots ,s_n\in M, \end{aligned}$$

(vi) for every $n\ge 1$, $k_1,\ldots ,k_n\ge 0$ and $q_1,\ldots ,q_n\in \mathcal{A}(H)$ such that $q_i\not \sim _H q_j$ for $i\ne j$,

$$\begin{aligned}q_1^{k_1}\dots q_n^{k_n}\in M\Rightarrow q_1^{c^{(1)}_i}\dots q_n^{c^{(n)}_i}\in M\; \text{ for } \text{ each }\; i,\end{aligned}$$

where $k_j=c^{(j)}_r2^r+\ldots +c^{(j)}_02^0$ for $j=1,\ldots ,n$, with $c^{(j)}_i\in \{0,1\}$ for $i=0,\ldots ,r$.

(vii) for every $n\ge 0$ and $s_0,\ldots ,s_n\in \mathcal{S}(H)$,

$$\begin{aligned} s_n^{2^n}\ldots s_1^2s_0\in M\Rightarrow s_0,\ldots , s_n\in M, \end{aligned}$$

(viii) for every $a\in H$ and $b\in \mathcal{S}(H)$,

$$\begin{aligned} a^2b\in M\Rightarrow a,b\in M. \end{aligned}$$

Proof

First, observe that H is a BF-monoid and the submonoid M satisfies $M^{\times }=H^{\times }\cap M$, so M is also a BF-monoid, by [11], Corollary 1.3.3, p. 17. In particular, M is atomic.

$\mathrm{(i)}\Rightarrow \mathrm{(iii)}$ Assume $\mathcal{S}(M)\subset \mathcal{S}(H)$. Since $\mathcal{A}(M)\subset \mathcal{S}(M)$, we have $\mathcal{A}(M)\subset \mathcal{S}(H)$.

Suppose that there exist $a,b\in \mathcal{A}(M)$ such that $a\not \sim _M b$ and a, b are not relatively prime in H. Then $t=\gcd _H(a,b)\in H\setminus H^{\times }$, so $a=tu$, $b=tv$ for some $u,v\in H$, $u{\mathrm{rpr}}_H v$. Since $a,b\in \mathcal{A}(M)$, we have $a,b\in \mathcal{S}(H)$, but $u\mid _H a$, $v\mid _H b$, so $u,v\in \mathcal{S}(H)$, and then $uv\in \mathcal{S}(H)$, because $u{\mathrm{rpr}}_H v$.

Now, we have $ab=t^2uv\not \in \mathcal{S}(H)$, so $ab\not \in \mathcal{S}(M)$. Consequently, $c^2\mid _H ab$ for some $c\in M\setminus M^{\times }$. We may assume that c is minimal (with respect to the natural length function in H). We have $c^2\mid _H t^2uv$, where $uv\in \mathcal{S}(H)$, so $c\mid _H t$, because H is factorial, and then $t=cw$ for some $w\in H$.

We obtain $a=tu=cwu$, so $wu\in \mathcal{S}(H)$, since $a\in \mathcal{S}(H)$. We have $ac=c^2wu\not \in \mathcal{S}(H)$, so $ac\not \in \mathcal{S}(M)$, hence $ac=e^2h$ for some $e\in M\setminus M^{\times }$, $h\in M$. Since $e^2h=c^2wu$, where $wu\in \mathcal{S}(H)$, we infer $e\mid _H c$. We have $ab=c^2w^2uv=e^2hwv$, and hence $e^2\mid _H ab$. Therefore, $e\sim _H c$ by the minimality of c. Then $e\sim _M c$, because $M^{\times }=H^{\times }$. But $ac=e^2h$, so $a\sim _M eh\sim _M ch$. Then $a\sim _M c$, since $a\in \mathcal{A}(M)$ and $c\in M\setminus M^{\times }$.

Analogously we show that $b\sim _M c$, so $a\sim _M b$, a contradiction.

$\mathrm{(ii)}\Rightarrow \mathrm{(iii)}$ It is enough to note that for every $a,b\in \mathcal{A}(M)$,

$$\begin{aligned} a\not \sim _M b\Rightarrow a{\mathrm{rpr}}_M b. \end{aligned}$$

Namely, if $a,b\in \mathcal{A}(M)$ are not relatively prime in M, then $a=cd$ and $b=ce$ for some $c\in M\setminus M^{\times }$, $d,e\in M$, so $d,e\in M^{\times }$ and $a\sim _M b$.

$\mathrm{(iii)}\Rightarrow \mathrm{(ii)}$ Assume (iii) and consider elements $a,b\in M$ such that $a{\mathrm{rpr}}_M b$. We already know that M is atomic. Let $a=a_1\dots a_m$ and $b=b_1\dots b_n$ be factorizations into atoms in M. Since $a{\mathrm{rpr}}_M b$, for all i, j we have $a_i\not \sim _M b_j$, so $a_i{\mathrm{rpr}}_H b_j$, but then $a{\mathrm{rpr}}_H b$.

$\mathrm{(iii)}\Rightarrow \mathrm{(iv)}$ Assume (iii). Let B be a maximal (with respect to inclusion) set of pairwise non-associated (in M) atoms of M. By (iii) the elements of B are pairwise relatively prime in H. H is a factorial monoid, so B generates a free submonoid. Since M is atomic and $M^{\times }=H^{\times }$, we obtain $M=H^{\times }\times {\textsf {F}}(B)$.

$\mathrm{(iv)}\Rightarrow \mathrm{(v)}$ Assume (iv). Let $a=s_1s_2^2s_3^3\ldots s_n^n\in M$, where $s_1,\ldots ,s_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$. By (iv), the element a can be presented in the form $a=ct_1t_2^2t_3^3\ldots t_m^m$ with $c\in H^{\times }$, $t_i=\prod _{j=1}^{r_i}b_j^{(i)}\in M$, $r_i\ge 0$, $m\ge n$, and pairwise different all $b_j^{(i)}\in B$. Since $b_j^{(i)}$ are square-free and pairwise relatively prime in H, then $t_1,\ldots ,t_m$ are also square-free and pairwise relatively prime in H. Finally, for $i=1,\ldots ,n$ we have $s_i\sim _H t_i$, so $s_i\in M$.

$\mathrm{(v)}\Rightarrow \mathrm{(vi)}$ Assume (v). Let $a=q_1^{k_1}\dots q_n^{k_n}\in M$, where $q_1,\ldots ,q_n\in \mathcal{A}(H)$, $q_i\not \sim _H q_j$ for $i\ne j$, and $k_1,\ldots ,k_n\ge 0$. Put $m=\max (k_1,\ldots ,k_n)$. For $l=1,\ldots ,m$ denote $s_l=\prod _{j:k_j=l}q_j$. Then $s_1,s_2,\ldots ,s_m\in \mathcal{S}(H)$ and $s_i{\mathrm{rpr}}_H s_j$ for $i\ne j$. We have $a=s_1s_2^2\ldots s_m^m$, so $s_1,s_2,\ldots ,s_m\in M$, by (v).

Now, let $k_j=c^{(j)}_r2^r+\cdots +c^{(j)}_02^0$ for $j=1,\ldots ,n$, with $c^{(j)}_i\in \{0,1\}$ for $i=0,\ldots ,r$. Note that if $k_{j_1}=k_{j_2}$, then $c^{(j_1)}_i=c^{(j_2)}_i$ for each i, so we may denote $d^{(l)}_i=c^{(j)}_i$ for each j such that $k_j=l$, where $l=1,\ldots ,m$. Then $q_1^{c^{(1)}_i}\ldots q_n^{c^{(n)}_i}= s_1^{d^{(1)}_i}\ldots s_m^{d^{(m)}_i}\in M$. $\square$

The only type of factorizations from Proposition 3.4 we haven’t considered in Theorem 4.3 nor Theorem 5.1 is (i). There is no surprise that in this case we obtain a divisor-closed submonoid [10].

Proposition 5.2

Let H be a monoid such that each element $a\in H$ can be presented in the form $a=s_1s_2\ldots s_n$, where $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$. Let $M\subset H$ be a submonoid. The following conditions are equivalent:

(i) for every $a,b\in H$,

$$\begin{aligned} ab\in M\Rightarrow a,b\in M. \end{aligned}$$

(ii) for every $n\ge 1$ and $s_1,s_2,\ldots ,s_n\in \mathcal{S}(H)$,

$$\begin{aligned} s_1s_2\ldots s_n\in M\Rightarrow s_1,s_2,\ldots ,s_n\in M. \end{aligned}$$

6 Radical elements and the uniqueness of factorizations

Let H be a monoid. Recall from [21] that an element $a\in H$ is called radical if the principal ideal aH is radical, equivalently, if for arbitrary $b\in H$ and $n\ge 1$,

$$\begin{aligned} a\mid b^n\Rightarrow a\mid b. \end{aligned}$$

Denote by $\mathcal{R}(H)$ the set of radical elements of H, and by $\mathcal{P}(H)$ the set of prime elements.

Clearly, every prime element is radical:

$$\begin{aligned} \mathcal{P}(H)\subset \mathcal{R}(H). \end{aligned}$$

This is an analog of the fact that every atom is square-free.

Note also that every radical element is square-free, (see [15], Lemma 3.2 b), what is an analog of the fact that a prime element is an atom.

Proposition 6.1

Let H be a monoid. Then

$$\begin{aligned}\mathcal{R}(H)\subset \mathcal{S}(H).\end{aligned}$$

The next lemma completes Lemma 3.1.

Lemma 6.2

Let H be a monoid and let $a\in \mathcal{R}(H)$ and $b\in H$. If $b\mid a$, then $b\in \mathcal{R}(H)$.

Proof

Let $a\in \mathcal{R}(H)$ and $b\mid a$. Let $c\in H$ and $b\mid c^n$ for some $n\ge 1$. By assumption we have $a=bd$, where $d\in H$. Then $a\mid c^nd^n$ and this implies $a\mid cd$, so $b\mid c$. $\square$

In Lemma 6.3 (a), (b) below we recall Lemma 2 (a), (d) from [16] in terms of monoids.

Lemma 6.3

Let H be a decomposition monoid.

(a) Let $a,b,c\in H$. If $a\mid bc$ and $a{\mathrm{rpr}}b$, then $a\mid c$.

(b) Let $a_1,\ldots ,a_n,b\in H$. If $a_i{\mathrm{rpr}}b$ for $i=1,\ldots ,n$, then $a_1\ldots a_n{\mathrm{rpr}}b$.

(c) Let $a,b_1,\ldots ,b_n\in H$. If $a\mid b_1\ldots b_n$, then there exist $a_1,\ldots ,a_n\in H$ such that $a=a_1\ldots a_n$ and $a_i\mid b_i$ for $i=1,\ldots ,n$.

(d) Let $a_1,\ldots ,a_n\in \mathcal{S}(H)$, $b\in H$. If $a_i{\mathrm{rpr}}a_j$ for $i\ne j$ and $a_i\mid b$ for $i=1,\ldots ,n$, then $a_1\ldots a_n\mid b$.

Proof

(c) Simple induction.

(d) Induction. Assume the assertion for n. Consider $a_1,\ldots ,a_n,a_{n+1}\in \mathcal{S}(H)$, $a_i{\mathrm{rpr}}a_j$ for $i\ne j$, and $b\in H$ such that $a_i\mid b$ for $i=1,\ldots ,n+1$. Put $a=a_1\ldots a_n$. Then, by the induction hypothesis, $a\mid b$, so $b=ac$ for some $c\in H$. Moreover, $a{\mathrm{rpr}}a_{n+1}$ by (b). Since $a_{n+1}\mid ac$, by (a) we obtain $a_{n+1}\mid c$, and then $aa_{n+1}\mid ac$. $\square$

Now we can prove that in a decomposition monoid every square-free element is radical. This is an analog of the fact that in a decomposition monoid atoms are primes.

Proposition 6.4

Let H be a decomposition monoid. Then

$$\begin{aligned} \mathcal{R}(H)=\mathcal{S}(H). \end{aligned}$$

Proof

Let $a\in \mathcal{S}(H)$. Assume that $a\mid b^n$ for some $b\in H$ and $n\ge 1$. Then, by Lemma 6.3 (c), there exist $a_1,\ldots ,a_n\in H$ such that $a=a_1\ldots a_n$ and $a_i\mid b$ for $i=1,\ldots ,n$. Observe that $a_1,\ldots ,a_n\in \mathcal{S}(H)$ and $a_i{\mathrm{rpr}}a_j$ for $i\ne j$, by Lemma 3.1, so $a_1\ldots a_n\mid b$ by Lemma 6.3 (d). $\square$

In the rest of this section we concern uniqueness properties of factorizations (ii)–(iv) and extractions (v), (vi) from Proposition 3.4. In an arbitrary monoid we have the uniqueness of factorization (ii) and extraction (v) for radical elements.

Proposition 6.5

Let H be a monoid.

(a) For every $r_1,\ldots ,r_n,t_1,\ldots ,t_n\in \mathcal{R}(H)$ such that $r_i\mid r_{i+1}$ and $t_i\mid t_{i+1}$, $i=1,\ldots ,n-1$, if

$$\begin{aligned} r_1r_2\dots r_n\sim t_1t_2\dots t_n, \end{aligned}$$

then $r_i\sim t_i$ for $i=1,\ldots ,n$.

(b) For every $a,c\in H$, $b,d\in \mathcal{R}(H)$ such that $a\mid b^m$ and $c\mid d^n$ for some $m,n\ge 1$, if

$$\begin{aligned}ab\sim cd,\end{aligned}$$

then $a\sim c$ and $b\sim d$.

Proof

(a) Assume that $r_1r_2\dots r_n\sim t_1t_2\dots t_n,$ where $r_1,\ldots ,r_n,t_1,\ldots ,t_n\in \mathcal{R}(H)$, $r_i\mid r_{i+1}$ and $t_i\mid t_{i+1}$ for $i=1, \ldots ,n-1$. We have $r_n\mid t_1 \ldots t_n$, so $r_n\mid t_n^n$. Since $r_n\in \mathcal{R}(H)$ we obtain $r_n\mid t_n$. Analogously, we get $t_n\mid r_n$. Hence $r_n\sim t_n$ and $r_1\dots r_{n-1}\sim t_1\dots t_{n-1}$. Then we repeat the above reasoning for $r_{n-1}$ and $t_{n-1}$, etc.

(b) Assume that $ab\sim cd$, where $a,c\in H$, $b,d\in \mathcal{R}(H)$, $a\mid b^m$ and $c\mid d^n$ for some $m, n\ge 1$. We see that $b\mid cd$, so $b\mid d^{n+1}$. Since $b\in \mathcal{R}(H)$ we obtain $b\mid d$. Analogously, we get $d\mid b$, so $b\sim d$, and then $a\sim c$. $\square$

In a decomposition monoid we have the uniqueness of factorization (iii) from Proposition 3.4.

Proposition 6.6

Let H be a decomposition monoid. For every $s_1,\ldots ,s_n$, $t_1$, $\ldots$, $t_n\in \mathcal{S}(H)$ such that $s_i{\mathrm{rpr}}s_j$ and $t_i{\mathrm{rpr}}t_j$ for $i\ne j$, if

$$\begin{aligned} s_1s_2^2s_3^3\ldots s_n^n\sim t_1t_2^2t_3^3\ldots t_n^n, \end{aligned}$$

then $s_i\sim t_i$ for $i=1,\ldots ,n$.

Proof

Assume that $s_1s_2^2s_3^3\ldots s_n^n\sim t_1t_2^2t_3^3\ldots t_n^n$, where $s_1,\dots ,s_n,t_1,\dots ,t_n\in \mathcal{S}(H)$, $s_i{\mathrm{rpr}}s_j$ and $t_i{\mathrm{rpr}}t_j$ for $i\ne j$. Put $s'_i=s_i\ldots s_n$, $t'_i=t_i\ldots t_n$ for $i=1,\ldots ,n$. Then

$$\begin{aligned} s'_1s'_2\ldots s'_n\sim t'_1t'_2\ldots t'_n. \end{aligned}$$

Note that $s'_i, t'_i\in \mathcal{S}(H)$ for $i=1,\ldots ,n$ by Lemma 3.2. Since $s'_{i+1}\mid s'_i$ and $t'_{i+1}\mid t'_i$ for $i=1,\ldots ,n-1$, from Proposition 6.5 (a) we obtain $s'_i\sim t'_i$ for $i=1,\ldots ,n$. Then $s_i\sim t_i$ for $i=1,\ldots ,n$. $\square$

Finally, recall from [16], Proposition 2 (i), (ii), the uniqueness of factorization (iv) and extraction (vi) for a GCD-monoid. It was formulated for a GCD-domain, but the proof is valid for a GCD-monoid.

Proposition 6.7

Let H be a GCD-monoid.

(a) For every $s_0,s_1,\ldots ,s_n,t_0,t_1,\ldots ,t_n\in \mathcal{S}(H)$, if

$$\begin{aligned} s_0s_1^2s_2^{2^2}\ldots s_n^{2^n}\sim t_0t_1^2t_2^{2^2}\ldots t_n^{2^n}, \end{aligned}$$

then $s_i\sim t_i$ for $i=0,\ldots ,n$.

(b) For every $a,c\in H$, $b,d\in \mathcal{S}(H)$, if

$$\begin{aligned} a^2b\sim c^2d, \end{aligned}$$

then $a\sim c$ and $b\sim d$.

7 Classifications of monoids with respect to square-free factorizations

In this section we show how to organize all the variety of cases when properties considered in Proposition 3.4 hold or do not. We would like to emphasize two advantages of this situations. First: it yields mostly non-trivial questions about existence of 7, 19, 22, or even 55 monoids, respectively. Second: it provides many ways of classifying monoids with respect to possessing or not different square-free factorizations or extractions, which may be more subtle than with respect to irreducible factorizations.

There are 7 possible combinations of logical values for properties (i)–(iv).

We would like to involve the following properties of monoids: ACCP, atomicity, GCD, decomposition. We introduce the value of “ACCP/atm” as follows.

Similarly, we introduce the value of “GCD/decomp”.

Now, we can collect all possibilities for conditions (i)–(vi) in Proposition 3.4, taking into account the properties mentioned above. By $1^{*}$ below we denote that 1 as the value of “ACCP/atm” is possible only when the value of “GCD/decomp” is 0, and also 1 as the value of “GCD/decomp” is possible only when the value of “ACCP/atm” is 0. In the leftmost column we indicate the number of cases for “ACCP/atm” and “GCD/decomp” with respect to given values of (i)–(iv). In the rightmost column we indicate the number of cases for extractions (v) and (vi) also with respect to (i)–(iv).

In the above table we take into account the following remark.

Reviewer’s remark

Since every square-free element of a decomposition monoid is radical, it follows from [20], Corollary 4.5, that every decomposition monoid that satisfies property (ii) has to be a GCD-monoid. Note that the notion of a GCD-monoid is equivalent to the notion of a t-Bézout monoid in [20]. Therefore, if H is a decomposition monoid that satisfies property (ii), then every principal ideal of H is a product of finitely many pairwise comparable radical principal ideals of H, and hence H is a t-Bézout monoid (i.e., a GCD-monoid) by [20], Corollary 4.5.

Let us extract possible combinations of (i)–(iv) for: atomic, ACCP, decomposition and GCD-monoids. We have:

• 6 possible combinations for atomic monoids,

  

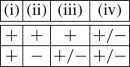
• 3 possible combinations for ACCP-monoids,

  

• 4 possible combinations for decomposition monoids,

  

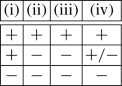
• 2 possible combinations for GCD-monoids.

  

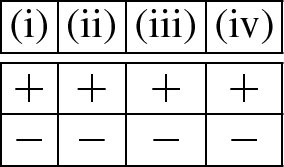
There are 22 classes of monoids with respect to properties:

$$\begin{aligned} \hbox {ACCP, atomicity, GCD, decomposition, (i)--(iv).} \end{aligned}$$

The question if all of them are non-empty is, in our opinion, of fundamental importance.

Extraction (vi) is a basic tool for exploring properties of subrings connected with square-free elements. This is why we think it is reasonable to consider the whole set of properties (i)–(vi). There arises a question if all combinations of logical values are possible, i.e., a question about 19 examples.

There are 55 classes of monoids with respect to all properties:

$$\begin{aligned} \hbox {ACCP, atomicity, GCD, decomposition, (i)--(vi).} \end{aligned}$$

We don’t think that all of them are non-empty. It may be true, e.g., that for ACCP-monoids there is $\mathrm{(ii)}\Leftrightarrow \mathrm{(v)}$. Hence, we state a question about 55 examples of monoids.

8 Some examples

Example 8.1

Put

$$\begin{aligned} B_{p,q}=\langle x_1,x_2,x_3,\ldots ,y_1,y_2,y_3,\ldots \mid y_i=x_{i+1}^py_{i+1}^q,i=1,2,3,\ldots \rangle , \end{aligned}$$

where p, q are positive integers.

Then $B_{p,q}$ is a non-factorial GCD-monoid for any p, q.

(a) $B_{1,1}$ satisfies all conditions (i)–(vi), in particular, it is a non-atomic monoid satisfying (ii), mentioned in Remark 3.5.6.

(b) if q is even, then $B_{p,q}$ satisfies (vi) and no one of (i)–(v), in particular, it is a non-factorial GCD-monoid satisfying $\mathrm{(vi)}\wedge \lnot \mathrm{(v)}$, mentioned in Remark 3.5.1.

(c) if q is odd and $(p,q)\ne (1,1)$, then $B_{p,q}$ satisfies no one of the conditions (i)–(vi).

Monoid $B_{1,1}$ gives an important argument in the discussion of how property (i) extends atomicity in the context of diagram (1.6):

Namely, we loose connection with the lower line of the diagram since $B_{1,1}$ satisfies the strongest one—GCD—and is not factorial, so in general the conjunction of (i) and GCD does not imply factoriality.

Example 8.2

Let ${\mathbb Q}_{\ge 0}$ denote the set of all non-negative rational numbers. $H=({\mathbb Q}_{\ge 0},+)$ is a GCD-monoid, because $\gcd (a,b)=\min \{a,b\}$ for all $a,b\in H$. It satisfies condition (vi), because for any $a\in H$ we have $a=\frac{a}{2}+\frac{a}{2}+0$ and $0\in \mathcal{S}(H)$. However it does not satisfy any of conditions (i)–(iv), because $\mathcal{S}(H)=\{0\}$ and $0+\ldots +0\ne a$ for $a\ne 0$. Neither condition (v), because if $c\in \mathcal{S}(H)$, then $c=0$ and $0+\ldots +0$ is not divisible in $({\mathbb Q}_{\ge 0},+)$ by a non-zero a (here $a\mid b$ iff $a\le b$). Clearly H is also non-factorial.

Example 8.3

For a non-negative integer k we denote by ${\mathbb N}_{\ge k}$ the set of integers greater or equal to k. Then $H=({\mathbb N}_{\ge 2}\cup \{0\},+)$ is not a decomposition monoid, since $\mathcal{A}(H)=\{2,3\}$ and $\mathcal{P}(H)=\emptyset$. See also Sect. 9.

Example 8.4

Let L and F be fields such that $L\subset F$. Consider $T=L+xF[x]$. Then the atoms of the ring T are known:

Theorem 8.5

([3], Theorems 2.9 and 5.3).

T is a half-factorial domain and $\mathcal{A}(T)=\{ax; a\in F\setminus \{0\}\}\cup \{a(1+xf(x)); a\in L\setminus \{0\}, f\in F[x], 1+xf(x)\in \mathcal{A}(F[x])\}.$

We can also determine all the square-free elements of T. Proposition 8.6, Corollary 8.7 and Example 8.8 have been proposed by the reviewer.

Proposition 8.6

Let L and F be fields such that $L\subset F$ and let $T = L + xF[x]$. Then $\mathcal{S}(T) = (\mathcal{S}(F[x])\cap T)\cup \{x^2h;h\in \mathcal{S}(F[x]),h(0)\not \in \{a^2b;a\in F,b\in L\}\}$.

Proof

Let $f\in \mathcal{S}(T)\setminus \mathcal{S}(F[x])$. There are some $g\in F[x]\setminus F[x]^{\times }$ and $k\in F[x]$ such that $f = g^2k$. Set $c = g(0)$. If $c\ne 0$, then since $c^{-1}g,c^2k\in T$ and $f = (c^{-1}g)^2c^2k$, we have $c^{-1}g\in T^{\times }$ and $g\in F[x]^{\times }$, a contradiction. Therefore, $c = 0$, and thus $f = x^2h$ for some $h\in F[x]$. Since $f\in S(T)$, we infer $h(0)\ne 0$. If $h(0) = a^2b$ for some $a\in F$ and $b\in L$, then $ax,a^{-2}h\in T$, and $f = (ax)^2a^{-2}h$, which contradicts the fact that $f\in \mathcal{S}(T)$. This implies that $h(0)\not \in \{a^2b; a\in F,b\in L\}$. Let $r,s\in F[x]$ be such that $h = r^2s$. Since $h(0)\ne 0$, we infer $r(0)\ne 0$. Set $d = r(0)$. Then $f = (d^{-1}r)^2d^2sx^2$ and $d^{-1}r,d^2sx^2\in T$. Consequently, $d^{-1}r\in T^{\times }$, and hence $r\in F[x]^{\times }$. This shows that $h\in \mathcal{S}(F[x])$.

Since $F[x]^{\times }\cap T = T^{\times }$, it follows that $\mathcal{S}(F[x])\cap T\subset \mathcal{S}(T)$. Now let $h\in \mathcal{S}(F[x])$ be such that $h(0)\not \in \{a^2b;a\in F,b\in L\}$. It remains to show that $x^2h\in \mathcal{S}(T)$. Clearly, $x^2h\in T$. Let $r,s\in T$ be such that $x^2h = r^2s$. Assume that $r\in xF[x]$. Then $r = xt$ for some $t\in F[x]$, so $h = t^2s$. Therefore, $h(0) = t(0)^2s(0)\in \{a^2b;a\in F,b\in L\}$, a contradiction. Consequently, $r\not \in xF[x]$, and thus $s = x^2w$ for some $w\in F[x]$. We infer $h = r^2w$, and hence $r\in F[x]^{\times } \cap T = T^{\times }$. $\square$

Corollary 8.7

Let L and F be fields such that $L\subset F$ and let $T = L + xF[x]$. Then $\mathcal{S}(T) = \mathcal{S}(F[x])\cap T$ iff $F = \{a^2b;a\in F,b\in L\}$. In particular, if F is algebraically closed, then $\mathcal{S}(T) = \mathcal{S}(F[x])\cap T$.

Proof

It follows from Proposition 8.6 that if $F = \{a^2b;a\in F,b\in L\}$, then $\mathcal{S}(T) = \mathcal{S}(F[x])\cap T$. Now let $F\ne \{a^2b;a\in F,b\in L\}$. There is some $c\in F \setminus \{a^2b;a\in F,b\in L\}$. By Proposition 8.6, we have $x^2c\in \mathcal{S}(T)$. Moreover, $x^2c\not \in \mathcal{S}(F[x])$, and thus $\mathcal{S}(T)\ne \mathcal{S}(F[x])\cap T$. Finally, if F is algebraically closed, then $F = \{a^2;a\in F\}$ and the statement follows. $\square$

Example 8.8

Let F be a field with ${{\,\mathrm{char}\,}}(F) = 2$ such that F is not perfect, let L be the prime subfield of F and let $T = L + xF[x]$. Then $\mathcal{S}(T)\ne \mathcal{S}(F[x])\cap T$.

Proof

Since ${{\,\mathrm{char}\,}}(F) = 2$ and F is not perfect, we have $F\ne \{a^2;a\in F\}$. Since $L = \{0,1\}$, this implies that $F\ne \{a^2b;a\in F,b\in L\}$. It is an immediate consequence of Corollary 8.7 that $\mathcal{S}(T)\ne \mathcal{S}(F[x])\cap T$. $\square$

In particular, if $T=\mathbb {R}+x\mathbb {C}[x]$, then $\mathcal{A}(T)=\{a+bx;\, a\in \mathbb {R}, b\in \mathbb {C}\setminus \{0\}\}$ and $\mathcal{S}(T)=\{a\prod _{b\in B}(1+bx);\, a\in \mathbb {R}\setminus \{0\}, B\subset \mathbb {C}, B\; {\text {is finite}}\}\cup \{ax\prod _{b\in B}(1+bx);\, a\in \mathbb {C}\setminus \{0\}, B\subset \mathbb {C}, B\; {\text {is finite}}\}$.

Using Corollary 8.7 we easily verify that if F is algebraically closed, then $L+xF[x]$ fulfills (i)–(vi).

If F and L are finite fields and it is a proper extension, then $L+xF[x]$ is a non-factorial ACCP domain (see [2, 9]).

9 The number of square-free elements of a reduced monoid

It is obvious that an arbitrary non-negative integer can be the number of atoms of a monoid. For example it can be the number of its free generators. In a group every element is square-free, since there is no non-invertible element. Hence, any positive integer can be the number of square-free elements of a monoid. It is not so obvious, but still true, that an arbitrary positive integer can be the number of square-free elements of a reduced monoid. It also remains valid if we assume that this reduced monoid is cancellative.

For integers a, b we define $[a,b]=\{c\in {\mathbb Z}; a\le c\le b\}$, that is, the set of all consecutive integers from a to b.

Theorem 9.1

Let n be a positive integer. Then there exists a reduced cancellative monoid H such that $\#\mathcal{S}(H)=n$.

Proof

Let m be an integer $\ge 2$. Consider a monoid

$$\begin{aligned} H={\mathbb N}_{\ge 2m}\cup \{0\}\cup \{m\} \end{aligned}$$

with the operation of addition.

Clearly $\mathcal{A}(H)=\{m\}\cup [2m+1,3m-1]$ and $\#\mathcal{A}(H)=m$. Then $\mathcal{S}(H)=\{0,m\} \cup [2m+1,3m-1]\cup [3m+1,4m-1]$ and consequently $\#\mathcal{S}(H)=2m$.

Now let m be an integer $\ge 3$ and consider a monoid

$$\begin{aligned} H={\mathbb N}_{\ge 2m-1}\cup \{0\}\cup \{m\}. \end{aligned}$$

In this case $\mathcal{A}(H)=\{m,2m-1\}\cup [2m+1,3m-2]$ and $\#\mathcal{A}(H)=m$. Then $\mathcal{S}(H)=\{0,m,2m-1\} \cup [2m+1,3m-1]\cup [3m+1,4m-3]$ and finally $\#\mathcal{S}(H)=2m-1$.

So far we have proved the assertion for $n\ge 4$. If $n=1$ we can take $H=\{0\}$. If $n=2$ we may consider $H={\mathbb N}_{\ge 0}$. If $n=3$ we can take the submonoid of ${\mathbb Q}_{\ge 0} \times {\mathbb Q}_{\ge 0}$ (with the operation of addition) generated by (1, 0), (0, 1) and elements of the form $(\frac{1}{2^n}, \frac{1}{2^n})$ for all positive integers n. Then the set of square-free elements of that submonoid is $\{(0,0),(1,0),(0,1)\}$. $\square$

Note that the proof could not be based solely on the monoids of the form $H_k={\mathbb N}_{\ge k}\cup \{0\}$, because $\#\mathcal{S}(H_k)$ grows faster than k.