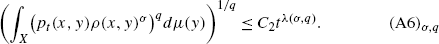1 Introduction

Let (X,ρ,μ) be a given metric measure space and let I be either a bounded interval [0,T] or the half line [0,∞). This article is concerned with the study of qualitative properties of the non-linear parabolic equation

$$\begin{aligned} \frac{\partial u}{\partial t}(t,x) = \varDelta u (t,x) + f\bigl(u(t,x)\bigr) \quad\text{in}\ I\times X \end{aligned}$$
(1)

with initial condition u(0,x)=ϕ(x) x∈X; see [4].

The study of (1) has been the focus of attention in several recent papers [3, 4, 7, 8, 11] due to its importance in many applications. These classes of equations are governed by a heat kernel p t (x,y) or a transition density. The heat kernels have been investigated in different type of spaces, such as Riemaniann manifolds, graphs, and in general metric measure spaces and encode many of the fundamental geometric properties of the underlying space on which are defined.

The approach we follow in this paper is to assume the existence of a heat kernel p t (x,y) on a metric measure space X. Then we show that under conditions on the kernel p t (x,y), such as time estimates and the Hölder uniform continuity on the space variable x yield properties of regularity and existence of solutions for (1).

For the non linear problem (1) we prove existence and uniqueness of continuous solutions in [0,T]. Moreover, for problem (1) we show that there exists a unique global solution u(t,⋅) which is continuous and bounded for all t∈[0,∞). We present the Hajłasz-Sobolev spaces introduced by [9, 10] to study the space regularity, these spaces play the role of the Sobolev spaces on metric spaces. Furthermore, we show the time regularity on the space of Hölder continuous functions on [0,T]. We notice that the hypothesis of Hölder uniform continuity on the heat kernel imply space regularity on the space of Hölder continuous functions on X.

Hereafter we assume that (X,ϱ,μ) is a metric measure space with a Borel measure μ and a metric ϱ. We assume throughout this paper that the measure of every open ball is positive and finite. A family {p t } t≥0 of measurable nonnegative functions on X×X is called a heat kernel on the metric measure space (X,ϱ,μ) if for all t>0 and all x,y∈X, the function p t (x,y) is differentiable in t and satisfy the following assumptions:

  1. (i)

    p t (x,y)=p t (y,x),

  2. (ii)

    ∫ X p t (x,y)dμ(y)=1,

  3. (iii)

    p t+s (x,y)=∫ X p t (x,z)p s (z,y)dμ(z),

  4. (iv)

    \(\lim_{t\rightarrow0+} \| \mathcal{T}(t) f - f\|_{L^{p}(X)} = 0\), for f∈L p(X) (any 1≤p<∞), in which

    $$ \mathcal{T}(t) f(x) = \int_X p_t(x,y) f(y) d \mu(y). $$
    (2)

We remark that the (i)–(iv) above and Lemma 1.1 below imply that \((\mathcal{T}(t))_{t\geq0}\) defines a strongly continuous semigroup of linear operators on L p(X), 1≤p<∞. Moreover \((\mathcal{T}(t))_{t\geq0} \) is Markovian, that is f≥0 implies that \(\mathcal{T}(t)f\geq0\) and if f≤1 implies \(\mathcal {T}(t)f\leq1\). Next, for p∈[1,∞] we define the operator Δ to be the infinitesimal generator of \((\mathcal{T}(t))_{t\geq0}\) on L p(X), that is,

$$D(\varDelta )= \biggl\{f\in L^p(X): \lim_{t\rightarrow0+} \frac{\mathcal {T}(t) f - f}{t}\ \mathrm{exists} \biggr\}. $$

Furthermore we shall assume the following two conditions on the heat kernel:

  1. (a)

    There exists a positive constant C and 0≤γ and δ∈(0,1] such that

    $$ \bigl|p_t(x_1,y)-p_t(x_2,y)\bigr| \leq C \frac{\rho(x_1, x_2)^{\delta }}{t^{\gamma}} $$
    (A5)

    for t>0 and x 1,x 2,y∈X. The Hölder continuity of the heat kernel will be needed for the regularity of the solutions with respect of the space variable.

  2. (b)

    For σ∈(0,1], and q≥1 there exists C 2 and λ(σ,q) such that for all x∈X

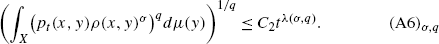
    figure a

Remark 1

We notice that if we assume that the measure is α-regular, then the above condition (A6) σ,q is satisfied under some hypothesis on the kernel (e.g., see [3]). Furthermore for the Gauss-Wierstrass kernel and the Cauchy-Poisson kernel, the corresponding exponents are,

$$\begin{aligned} \lambda_{GW}(\sigma, q)= \frac{1}{2} \biggl(\sigma+n \biggl( \frac {1}{q}-1 \biggr) \biggr), \qquad\lambda_{CP}(\sigma, q)= \sigma+n \biggl(\frac{1}{q}-1 \biggr). \end{aligned}$$

Next we recall some standard notations. Given a function g on I×X we set g(s)=g(s,⋅). Then for s∈I, and under the assumptions that g(s,⋅)∈L p(X), and for almost all x∈X the function s↦g(s,x) is locally integrable. We define the convolution \((\mathcal{T}*g)(t,x)=\int_{0}^{t} (\mathcal {T}(t-s)g(s,\cdot))(x) d s\), a.e. for x∈X. We set \((\mathcal{T}*g)(t)=(\mathcal{T}*g)(t,\cdot)\) and denote \((\mathcal {T}*g)(t)=\int_{0}^{t} \mathcal{T}(t-s)g(s) d s\).

A function u on I×X is a solution to problem (1) if

$$ u(t,x) = \bigl(\mathcal{T}(t)\phi\bigr) (x) + (\mathcal{T}*g) (t,x),\quad t \in I,\ \mbox{a.e.}\ x\in X. $$
(3)

Furthermore if we let u(t)=u(t,⋅), then

$$ u(t) =\mathcal{T}(t)\phi+ (\mathcal{T}*g)(t)\quad t\in I. $$
(4)

Lemma 1.1

The linear operators \(\{\mathcal{T}(t)\}_{t\geq0}\) defined by (2) are bounded on L p(X), for all p∈[1,∞]. Moreover, the following estimate

$$ \bigl\|\mathcal{T}(t)f\bigr\|_{L^p(X)} \leq \| f\|_{L^p(X)} $$
(5)

is satisfied.

Proof

First, we shall show that the inequality (5) is verified when p=1 and p=∞. Indeed, because of Fubini’s Theorem and the second property of the heat kernel we get

$$\begin{aligned} \bigl\|\mathcal{T}(t)f\bigr\|_{L^1(X)} =& \int_X \biggl|\int_X f(y) p_t(x,y) d \mu(y)\biggr| d \mu(x)\\\leq& \int_X \bigl|f(y)\bigr| \biggl(\int_X p_t(x,y) d \mu(x) \biggr)d \mu (y)=\| f\|_{L^1(X)}. \end{aligned}$$

Next for p=∞ we obtain that,

$$\begin{aligned} \bigl\|\mathcal{T}(t)f\bigr\|_{L^{\infty}(X)} =\mathit{ess} \sup_{x \in X} \biggl|\int_X f(y) p_t(x,y) d \mu(y)\biggr| \leq\|f\|_{L^{\infty}(X)}. \end{aligned}$$

Now, for arbitrary p≥1 the proof follows by an application of the Riesz-Thorin Interpolation Theorem; (see [2]). □

We notice that for p∈[1,∞) the solution u defined in (3) belongs to C([0,T];L p(X)), because of property (iv) of the heat kernel and Lemma (1.1); cf., [1].

2 The linear equation

In this section we study regularity properties of the linear equation,

$$ \begin{array}{@{}rcl@{\quad}l} \displaystyle\frac{\partial u}{\partial t}(t,x) &=& \varDelta u (t,x) + g(t,x) & \text{in}\ [0,T]\times X,\\ u(0,x) &=& \phi(x) & \text{in}\ X. \end{array} $$
(6)

For the problem (6) we will show time regularity for local solutions and space regularity on Hölder spaces and also on Sobolev spaces.

2.1 Estimates

To show regularity properties of equation (6) we first show the continuity of the solution, that is:

Theorem 2.1

Let p∈[1,∞), and g∈L 1([0,T];L p(X)). If ϕ∈L p(X), then the solution u to problem (6) belongs to C([0,T];L p(X)), and

$$\begin{aligned} \|u\|_{C([0,T]; L^p(X))} \leq\bigl(\|\phi\|_{L^p(X)} + \|g \|_{L_1([0,T]; L^p(X))}\bigr). \end{aligned}$$
(7)

Moreover, if p=∞, then u belong to the space L ∞([0,T];L p(X)) and

$$\begin{aligned} \|u\|_{L_{\infty}([0,T]; L^p(X))} \leq \bigl(\|\phi\|_{L^p(X)} + \|g\| _{L_1([0,T]; L^p(X))}\bigr). \end{aligned}$$
(8)

Proof

By a direct application of Lemma 1.1 we obtain that

$$\bigl\|(\mathcal{T}*g)(t)\bigr\|_{L^p(X)}\leq\int_0^t \bigl\| g(s) \bigr\|_{L^p(X)}d s. $$

Since the solution u to problem (6) is given by (4), that is, \(u(t) =\mathcal{T}(t)\phi+ (\mathcal {T}*g)(t)\). It then follows that

$$\begin{aligned} \bigl\|u(t)\bigr\|_{ L^p(X)} \leq\|\phi\|_{L^p(X)} +\int_0^t \bigl\| g(s) \bigr\|_{L^p(X)}d s. \end{aligned}$$

But then, taking supremum over the interval [0,T] we have

$$\begin{aligned} \|u\|_{L_{\infty}([0,T]; L^p(X))} \leq\|\phi\|_{L^p(X)} + \|g\| _{L_1([0,T]; L^p(X))}. \end{aligned}$$

This concludes with the proof. □

As a corollary of above theorem we get the following maximum principle.

Corollary 2.1

Let us assume g≤0 and ϕ∈L ∞(X). If u is the solution to problem (6), then

$$\begin{aligned} \sup_{X \times[0,T]}u \leq \mathit{ess}\sup_{X} |\phi|. \end{aligned}$$

Proof

Since g≤0 it then follows that \((\mathcal {T}*g)(t,x)\leq0\) by the positivity preserving of \((\mathcal {T}(t))_{t\geq0}\). Then the proof of the assertion is now clear. □

2.2 Time regularity

We will prove that if the force function g in (6) belongs to the space of α-Hölder continuous functions C α([0,T];L p(X)) then the solution of problem (6) also belongs to C α([0,T];L p(X)).

First we set

$$ u_a(t)=\mathcal{T}(t)\phi\quad\text{and}\quad u_b(t)=(\mathcal{T}*g)(t),\quad t\in[0,T]. $$
(9)

It then follows that u(t)=u a (t)+u b (t) by (4).

Theorem 2.2

Let α∈[0,1]. If g∈C α([0,T];L p(X)) and ϕ∈L p(X) such that

$$\begin{aligned} \limsup_{h\rightarrow0} \frac{\|\mathcal{T}(h) \phi-\phi\|}{h^{\alpha }} < \infty, \end{aligned}$$

then the solution u to problem (6) belongs to the space C α([0,T];L p(X)). Moreover, if

$$\overline{\lim_{h\rightarrow0}}\frac{\|\mathcal{T}(h) \phi-\phi\| }{h^{\alpha}}=\varDelta (\alpha), $$

then there exists δ>0 such that the following estimate holds

$$\begin{aligned} \sup_{0\leq h\leq T} \frac{\|u(t+h)-u(t)\| _{L^{p}(X)}}{h^{\alpha}} \leq&2 \varDelta (\alpha)+ \frac{6}{\delta^{\alpha}}\|\phi\|_{L^{p}(X)} + 4T\|g\|_{C^{\alpha }([0,T];L^{p}(X))}\\&{}+4T^{1-\alpha}\|g\|_{L^{\infty}([0,T];L^{p}(X))}. \end{aligned}$$

Proof

We notice by (9) that

$$u_a(t+h)-u_a(t)=\mathcal{T}(t)\bigl(\mathcal{T}(h) \phi- \phi\bigr). $$

Therefore,

$$\overline{\lim_{h\rightarrow0}}\biggl\|\frac{u_a(t+h)-u_a(t)}{h^{\alpha }}\biggr\|_{L^{p}(X)}\leq2 \overline{{\lim_{h\rightarrow0}}} \biggl\|\frac{\mathcal{T}(h) \phi- \phi}{h^{\alpha}}\biggr\|_{L^{p}(X)}, $$

because of (5). Thus by assumption, we have that

$$ \overline{\lim_{h\rightarrow0}}\biggl\|\frac{u_a(t+h)-u_a(t)}{h^{\alpha }}\biggr\|_{L^{p}(X)}\leq2\varDelta (\alpha), $$
(10)

On the other hand,

$$u_b(t+h)-u_b(t)=\frac{1}{h^{\alpha}}\int _0^t\mathcal {T}(s) \bigl(g(t+h-s)-g(t-s) \bigr)ds +J(h), $$

in which \(J(h)=T(h)(\frac{1}{h^{\alpha}} \int_{t}^{t+h}\mathcal{T}(t-s)g(s)ds)\). Moreover,

$$\begin{aligned} &\frac{1}{h^{\alpha}}\int_0^t\bigl\|\mathcal{T}(s) \bigl(g(t+h-s)-g(t-s) \bigr)\bigr\|_{L^{p}(X)}ds\\&\quad{}\leq\frac{2}{h^{\alpha}}\int _0^t\bigl\| \bigl(g(t+h-s)-g(t-s) \bigr) \bigr\|_{L^{p}(X)}ds. \end{aligned}$$

Because g∈C α([0,T];L p(X)) it follows that

$$\frac{1}{h^{\alpha}} \bigl\| \bigl(g(t+h-s)-g(t-s) \bigr)\bigr\|_{L^{p}(X)}\leq\| g \|_{C^{\alpha}([0,T];L^{p}(X))}. $$

Thus

$$ \frac{1}{h^{\alpha}}\int_0^t \bigl\|\mathcal{T}(s) \bigl(g(t+h-s)-g(t-s) \bigr)\bigr\|_{L^{p}(X)}ds\leq2T \|g \|_{C^{\alpha}([0,T];L^{p}(X))}. $$
(11)

To estimate J(h) we notice that

$$ \bigl\|J(h)\bigr\|\leq4 \biggl(\frac{1}{h^{\alpha}} \int_{t}^{t+h}\bigl\|g(s)\bigr\|_{L^{p}(X)}ds \biggr) \leq4h^{1-\alpha}\|g\| _{L^{\infty}([0,T];L^p(X))}. $$
(12)

Since 0<α<1 the right hand side of (12) approaches to 0 as h→0. Then by (10), (11), (12) it follows that

$$\overline{\lim_{h\rightarrow0}}\biggl\|\frac{u(t+h)-u(t)}{h^{\alpha }}\biggr\|_{L^{p}(X)}\leq2\varDelta (\alpha)+2T \|g\|_{C^{\alpha}([0,T];L^{p}(X))}. $$

But then, there is δ>0 such that

$$ \sup_{0\leq h\leq\delta}\biggl\|\frac{u(t+h)-u(t)}{h^{\alpha }}\biggr\|_{L^{p}(X)}\leq2\varDelta (\alpha)+2T \|g\|_{C^{\alpha}([0,T];L^{p}(X))}. $$
(13)

Furthermore by a direct computation we have that

$$\begin{aligned} \sup_{\delta\leq h\leq T} \biggl\|\frac{u(t+h)-u(t)}{h^{\alpha}}\biggr\|_{L^{p}(X)} \leq&\frac{6}{\delta ^{\alpha}}\|\phi\|+2T\|g\|_{C^{\alpha}([0,T];L^{p}(X))} \\&{}+4T^{1-\alpha}\| g\|_{L^{\infty}([0,T];L^{p}(X))}. \end{aligned}$$
(14)

Now the proof follows from (13) and (14). □

2.3 Space regularity

Let u(t) be a local solution of (6). Then under mild assumptions on g of and integrability assumptions on the initial data of (6) we show that the solution u(t)=u(t,⋅) belongs to the Hölder space C δ(X). The exponent γ from assumption (A5), will play a fundamental role in the study of space regularity.

Hölder regularity: the case γ<1

First we assume that the exponent γ form condition (A5) satisfies the inequality γ<1. We remark that this assumption is very natural in fractal geometry; see [3, 4].

Theorem 2.3

Let us assume that the heat kernel p t satisfies condition (A5) with γ<1. Let us consider ϕ∈L 1(X)∩L ∞(X), and g∈L p([0,T];L 1(X)∩L ∞(X)) in which \(p> \frac{1}{1-\gamma}\). If q∈[1,1/γ) then u∈L q([0,T];C δ(X)). Moreover, there exists a positive constant C T such that the following estimate holds

$$\begin{aligned} \|u\|_{L^q([0,T]; C^{\delta}(X))} \leq C_T \bigl(\|\phi\|_{L^1(X)\cap L^{\infty}(X)} + \|g \|_{L^p([0,T]; L^1(X)\cap L^{\infty}(X))}\bigr). \end{aligned}$$

Proof

We recall from (9) that \(u_{a}(t)=\mathcal{T}(t)\phi\) and we first show the estimate for u a . By definition of the Hölder norm we get that

$$\begin{aligned} \bigl\|u_a(t)\bigr\|_{C^{\delta}(X)} =& \sup_{x\in X} \bigl|u_a(t,x)\bigr| + \sup_{x,y\in X, x\neq y}\frac{|u_a(t,x)-u_a(t,y)|}{\rho(x,y)^{\delta}} \\\leq&\|\phi\|_{L^{\infty}(X)}+\frac{C}{t^{\gamma}}\|\phi\|_{L^{1}(X)}. \end{aligned}$$

Hence, we get

$$\begin{aligned} \|u_a\|_{L^q([0,T];C^{\delta}(X))}\leq T^{\frac{1}{q}} \|\phi\| _{L^{\infty}(X)} + C\biggl(\frac{T^{\frac{1-\gamma q}{q}}}{1-\gamma q}\biggr)\|\phi\|_{L^{1}(X)}. \end{aligned}$$

Now, we turn our attention to the u b term. First we recall that the norm on L 1(X)∩L ∞(X) is defined as

$$\bigl\|g(s)\bigr\|_{L^1(X)\cap L^{\infty}(X)}= \bigl\|g(s)\bigr\|_{L^1(X)}+\bigl\|g(s)\bigr\| _{L^{\infty}(X)}. $$

Thus \(|g(s,y)|\leq\|g(s)\|_{L^{1}(X)\cap L^{\infty}(X)}\) for almost all y∈X. Then by properties of the heat kernel and by Hölder inequality we get:

$$\begin{aligned} \bigl\|u_b(t)\bigr\|_{C^{\delta}(X)} \leq&\sup_{x\in X}\int _0^t\int_X \bigl\vert p_{t-s}(x,y)g(s,y)\bigr\vert d\mu(y)ds+C\int_0^t \int_X\frac {|g(s,z)|}{(t-s)^{\gamma}}d \mu(z)ds \\\leq& \int_0^t \bigl\|g(s)\bigr\|_{L^1(X)\cap L^{\infty}(X)}ds\\&{}+C \|g\|_{L^p([0,T];L^1(X)\cap L^{\infty}(X))} \biggl(\int_0^t \frac{1}{(t-s)^{\gamma p'}}ds \biggr)^{\frac{1}{p'}} \\\leq& T^{1/p'}\|g\|_{L^p([0,T];L^1(X)\cap L^{\infty}(X))}\\&{}+ C \biggl(\frac {T^{\frac{1-\gamma q}{q}}}{1-\gamma q} \biggr) \|g\|_{L^p([0,T];L^1(X)\cap L^{\infty}(X))} \end{aligned}$$

where \({\frac{1}{p'}}+{\frac{1}{p}}=1\). Finally, we obtain the estimate:

$$\begin{aligned} \|u_b\|_{L^q([0,T];C^{\delta}(X))}\leq C \|g\|_{L^p([0,T];L^{1}(X)\cap L^{\infty}(X))}, \end{aligned}$$

in which C is a generic constant. This finishes with the proof. □

Hölder regularity: the case γ≥1

Theorem 2.4

Let us assume that the heat kernel p t satisfies conditions ( A5 ), with γ≥1, (A6) \(_{\alpha_{1},1}\) and (A6) \(_{\alpha_{2},1}\). If \(\phi\in L^{1}(X)\cap C^{\alpha_{1}}(X)\) and \(g\in L^{\infty}([0,T]; L^{1}(X)\cap C^{\alpha_{2}}(X))\), then the solution u of (6) belongs to \(L^{\infty}([0,T]; C^{\min\{ \alpha_{1}',\alpha_{2}'\}}(X))\), in which

$$\begin{aligned} \alpha_1'= \min \biggl\{\alpha_1, \frac{\delta\lambda(\alpha_1, 1)}{\gamma+ \lambda(\alpha_1, 1)} \biggr\},\qquad \alpha_2'= \min \biggl \{\alpha_2, \frac{\delta}{\gamma} \biggr\}, \end{aligned}$$

and λ(α 1,1) is determined by (A6) \(_{\alpha_{1},1}\).

Proof

We need to show that the functions u a and u b are in appropriate Hölder spaces. Let us stress out that it is enough to consider x,y∈X such that ρ(x,y)≤1. Let us start with u a . We consider the following two cases: \(t \geq\rho(x,y)^{\frac{\delta }{\gamma+\lambda(\alpha_{1})}}\) and \(t < \rho(x,y)^{\frac{\delta}{\gamma +\lambda(\alpha_{1})}}\). In the first case we get

$$\begin{aligned} \bigl|u_a(t,x)-u_a(t,y)\bigr| =&\biggl\vert \int _X \bigl(p_t(x,z) - p_t(y,z) \bigr) \phi (z) d \mu(z)\biggr\vert \\\leq& C_1 \|\phi\|_{L^1(X)}\frac{\rho(x,y)^{\delta}}{t^{\gamma}} \leq C_1 \|\phi\|_{L^1(X)}\rho(x,y)^{\frac{\delta\lambda(\alpha_1)}{\gamma +\lambda(\alpha_1)}}. \end{aligned}$$
(15)

On the other hand, if \(t < \rho(x,y)^{\frac{\delta}{\gamma+\lambda (\alpha_{1})}}\) we obtain

$$\begin{aligned} \bigl|u_a(t,x)-u_a(t,y)\bigr| \leq&\int_X p_t(x,z)\bigl|\phi(z)-\phi(x)\bigr|d\mu(z)+ \bigl|\phi (x)-\phi(y)\bigr|\\&{} + \int _X p_t(y,z)\bigl|\phi(z)-\phi(y)\bigr|d\mu(z) \\\leq&\|\phi\|_{C^{\alpha_1}(X)} \biggl(\rho(x,y)^{\alpha_1} +\int _X p_t(x,z) \rho(x,z)^{\alpha_1} d \mu(z)\\&{} + \int_X p_t(y,z) \rho (y,z)^{\alpha_1} d \mu(z) \biggr) \\\leq&\|\phi\|_{C^{\alpha_1}(X)} \bigl(\rho(x,y)^{\alpha_1} +2C_2 t^{\lambda(\alpha_1)} \bigr)\\\leq&\|\phi\|_{C^{\alpha_1}(X)} (1+2C_2 ) \rho(x,y)^{\alpha_1'}. \end{aligned}$$

Combining the above estimate with (15) we get that

$$\begin{aligned} \bigl|u_a(t,x)-u_a(t,y)\bigr| \leq \bigl((1+2C_2)\| \phi\|_{C^{\alpha_1}(X)} + \| \phi\|_{L^1(X)} \bigr)\rho(x,y)^{\alpha_1'}. \end{aligned}$$

Now, we turn our attention to u b . First we consider \(t \leq \rho (x,y)^{\frac{\delta}{\gamma}}\)

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq&\int_t^{ \rho(x,y)^{\frac{\delta}{\gamma}}} \int_X \bigl|p_{t-s}(z,x)-p_{t-s}(z,y)\bigr|\bigl|g(s,z)\bigr|d\mu(z)ds \\&{}+ \int_{t-\rho(x,y)^{\frac{\delta}{\gamma}}}^t \int_X \bigl|p_{t-s}(z,x)-p_{t-s}(z,y)\bigr|\bigl|g(s,z)\bigr| d \mu(z) ds \\\leq& C_1\int_t^{ \rho(x,y)^{\frac{\delta}{\gamma}}} \frac{\rho (x,y)^{\delta}}{(t-s)^{\gamma}} \int_X \bigl|g(s,z)\bigr| d \mu(z)ds\\&{}+ 2 \|g\| _{L^{\infty}([0,T];C^{\alpha_2}(X))}\rho(x,y)^{\frac{\delta}{\gamma}} \\\leq&2C_1 \rho(x,y)^{\delta} \|g\|_{L^{\infty}([0,T]; L^1(X))} \rho (x,y)^{(1-\gamma)\frac{\delta}{\gamma}}\\&{}+ 2\|g\|_{L^{\infty }([0,T];C^{\alpha_2}(X))}\rho(x,y)^{\frac{\delta}{\gamma}} \\\leq&2(C_1+1)\|g\|_{L^{\infty}([0,T];L^1(X)\cap C^{\alpha_2}(X))}\rho (x,y)^{\frac{\delta}{\gamma}}. \end{aligned}$$

Thus we obtain

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq 2(C_1+1)\|g\|_{L^{\infty}([0,T];L^1(X)\cap C^{\alpha_2}(X))}\rho(x,y)^{\frac{\delta}{\gamma}}. \end{aligned}$$
(16)

Now when \(t > \rho(x,y)^{\frac{\delta}{\gamma}}\) we can write

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq& \int_0^t\int _X\bigl|p_{t-s}(z,x)\bigl(g(s,z)-g(s,x)\bigr)\bigr|d\mu(z)ds \\&{}+\int_0^t\bigl|g(s,x)-g(s,y)\bigr|ds \\&{}+ \int_0^t \int_X \bigl|p_{t-s}(z,y)\bigl(g(s,z)-g(s,y)\bigr)\bigr|d\mu(z)ds \\\leq&2C_2 \|g\|_{L^{\infty}([0,T];C^{\alpha_2}(X))}t^{\lambda(\alpha _2)+1} \\&{}+ t\|g\|_{L^{\infty}([0,T];C^{\alpha_2}(X))} \rho(x,y)^{\alpha _2} \\\leq& \|g\|_{L^{\infty}([0,T];C^{\alpha_2}(X))}\bigl(2C_2\rho (x,y)^{\frac{\delta}{\gamma}(\lambda(\alpha_2)+1)} +T\rho(x,y)^{\alpha_2}\bigr). \end{aligned}$$

Therefore, thanks to (16) we obtain the estimate

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq \bigl(2(C_1+C_2+1)+T \bigr)\|g\|_{L^{\infty }([0,T];L^1(X)\cap C^{\alpha_2}(X))}\rho(x,y)^{\alpha_2'}, \end{aligned}$$

and the proof is now complete. □

Remark 2

We conjecture that Hölder regularity of Theorem 2.4 can also be obtained by an application of the Campanato-type theorems of [6], but the price would be to add some extra assumptions on the measure μ; see also [5].

2.3.1 Sobolev regularity

We recall the definition of Hajłasz-Sobolev spaces. Let (X,ϱ) be a metric space and let μ be a Borel measure on X such that each ball has a finite measure. Given \(f: X \rightarrow\mathbb{R}\) a μ-measurable function. We denote by \(\mathcal{D}_{\alpha}(f)\) the class of all μ-measurable functions \(g :X \rightarrow\mathbb{R}_{+}\) such that

$$\begin{aligned} \bigl|f(x)-f(y)\bigr|\leq \varrho(x,y)^{\alpha} \bigl(g(x)+g(y)\bigr) \quad\text{a.e.} \end{aligned}$$

Then a function f∈L p(X), 1<p≤∞, belongs to Hajłasz-Sobolev space M α,p(X), if the intersection \(\mathcal {D}_{\alpha}(f)\cap L^{p}(X)\) is nonempty. This space is endowed with the norm

$$\begin{aligned} \Vert f\Vert _{M^{\alpha,p}} = \Bigl( \Vert f\Vert ^p_{L_p(X)} + \Bigl(\inf_{g\in\mathcal{D}_\alpha} \Vert g\Vert _{L_p(X)} \Bigr)^p \Bigr)^{\frac{1}{p}}. \end{aligned}$$
(17)

The space M α,p(X) with the norm (17) is a Banach space. We also need the local version of M α,p(X) space. The space \(M^{\alpha,p}_{\mathit{loc}}(X)\) consists of all those functions \(f\in L^{p}_{\mathit{loc}}(X)\) for which every point z∈X has a neighborhood U z such that f∈M α,p(U z ).

Theorem 2.5

Let us assume that the heat kernel p t satisfies the conditions ( A5 ), with γ≥1, and (A6) \(_{\alpha_{1},1}\), (A6) \(_{\alpha_{2},1}\), (A6) \(_{\alpha_{2},q}\). Suppose that \(\phi \in L^{1}(X)\cap M^{\alpha_{1}, p}(X)\) in which  \(\frac{1}{q} + \frac {1}{p}=1\) and \(g\in L^{\infty}([0,T]; L^{1}(X)\cap M^{\alpha_{2},p}(X))\). Then \(u \in L^{\infty}([0,T]; M^{\min\{\alpha_{1}',\alpha_{2}'\},p}_{\mathit{loc}}(X))\), where

$$\begin{aligned} \alpha_1' =& \min \biggl\{\alpha_1, \frac{\delta\min_{i=1,q} \{\lambda (\alpha_1), i\}}{\gamma+ \min_{i=1,q} \{\lambda(\alpha_1), i\}} \biggr\},\\\alpha_2' =& \min \biggl \{\alpha_2, \frac{\delta\min\{\lambda(\alpha _2),1\}}{\gamma-1 +\min\{\lambda(\alpha_2),1\}} \biggr\}. \end{aligned}$$

Proof

Let us fix z∈X. We shall show that \(u(t) \in M^{\alpha, p}(B(z,\frac{1}{2}))\). For this purpose we take \(x, y \in B(z,\frac{1}{2}) \setminus\mathcal{N}\), where \(\mathcal{N}\) is a nullset. We proceed in the same way like in the proof of the previous theorem. First of all we shall estimate u a . Let us denote the quantity min i=1,q {λ(α 1,i)} by \(\lambda_{1}'\). Then for \(t \geq \rho(x,y)^{\frac{\delta}{\gamma+\lambda_{1}'}}\) we obtain

$$\begin{aligned} \bigl|u_a(t,x)-u_a(t,y)\bigr|\leq C_1 \|\phi\|_{L^1(X)}\rho(x,y)^{\frac{\delta \lambda_1'}{\gamma+ \lambda_1'}}. \end{aligned}$$

If \(t < \rho(x,y)^{\frac{\delta}{\gamma+\lambda_{1}'}}\), we get

$$\begin{aligned} \bigl|u_a(t,x)-u_a(t,y)\bigr| \leq&\int_X p_t(x,z)\bigl|\phi(z)-\phi(x)\bigr|d\mu(z)+ \bigl|\phi (x)-\phi(y)\bigr| \\&{}+\int _X p_t(y,z)\bigl|\phi(z)-\phi(y)\bigr|d\mu(z) \\\leq&\rho(x,y)^{\alpha_1}\bigl(h(x)+h(y)\bigr) +h(x)\int _X p_t(x,z) \rho (x,z)^{\alpha_1} d \mu(z) \\&{}+h(y)\int_X p_t(y,z)\rho(y,z)^{\alpha_1}d \mu(z)\\&{}+\int_X\bigl(p_t(x,z)\rho (x,z)^{\alpha_1}+ p_t(y,z) \rho(y,z)^{\alpha_1}\bigr)h(z) d\mu(z) \\\leq& \bigl(\rho(x,y)^{\alpha_1}+ C_2 \rho(x,y)^{\frac{\lambda(\alpha _1, 1) \delta}{\gamma+\lambda_1'}} \bigr) \bigl(h(x)+h(y)\bigr)\\&{}+2C_2 \|h\| _{L^p} \rho(x,y)^{\frac{\lambda(\alpha_1, q)\delta}{\gamma+\lambda_1'}}, \end{aligned}$$

where \(h\in\mathcal{D}_{\alpha_{1}} (\phi)\cap L^{p}(X)\).

Now, we estimate u b . For this purpose we set \(\beta=\frac{\delta }{\gamma-1 +\min(\lambda(\alpha_{2}),1)}\). Then we consider two cases: t≥ρ(x,y)β and t<ρ(x,y)β. For the first case t≥ρ(x,y)β we have that

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq2(C_1+1)\|g\|_{L^{\infty}([0,T];L^1(X)\cap L^{\infty}(X))}\rho(x,y)^{\beta\min(\lambda(\alpha_2),1)}. \end{aligned}$$

For t<ρ(x,y)β we get

$$\begin{aligned} \bigl|u_b(t,x)-u_b(t,y)\bigr| \leq& \bigl(\rho(x,y)^{\alpha_2} + C_2 \rho (x,y)^{\beta\lambda(\alpha_2, 1)} \bigr) \int_0^t \bigl(h_g(s,x)+h_g(s,y) \bigr) ds \\&{}+ 2C_2 \rho(x,y)^{\beta\lambda(\alpha_2, q)} \|h_g \|_{L^{\infty }([0,T]; L^p(X))}. \end{aligned}$$

The proof is complete. □

3 Nonlinear equation

In this section we shall deal with the existence and uniqueness of solutions of the following nonlinear diffusion equation:

$$ \begin{array}{@{}rcl@{\quad}l} \displaystyle\frac{\partial u}{\partial t}(t,x) &=& \varDelta u (t,x) + g \bigl(u(t,x)\bigr) & \text{in}\ I\times X,\\ u(0,x) &=& \phi(x) & \text{in}\ X. \end{array} $$
(18)

We recall that u is a weak solution of (18) if it satisfies the equation

$$u(t,x)={\mathcal{T}}(t)\phi(x)+\int_0^t{\mathcal{T}}(t-s)g \bigl(u(s,x)\bigr)ds, \quad x\in X. $$

3.1 Local solutions

In this section we shall show the existence of solutions which are local in time.

Theorem 3.1

Let p∈[1,∞). Let us assume that for each ball B⊂L p(X) there exists L(B) a positive constant such that for each u,v∈B the following inequality holds

$$\begin{aligned} \bigl\|g(u) - g(v)\bigr\|_{L^p}\leq L(B) \|u-v\|_{L^p}. \end{aligned}$$

Moreover, if μ(X)=∞ we assume that g(0)=0. If ϕ∈L p(X), then there exists unique local in time solution u∈C([0,T];L p(X)) to problem (18).

Proof

The proof will be given only in the case μ(X)=∞. Simple modification we leave to the reader. Let us fix T>0 and define the set

$$\begin{aligned} B_T= \bigl\{u\in C\bigl([0,T];L^p\bigr): \|u \|_{C([0,T];L^p(X))}\leq4\|\phi\| _{L^p} \bigr\}. \end{aligned}$$

Next, we define the map \(\mathcal{F}\):

$$\begin{aligned} \mathcal{F}: B_T \rightarrow C\bigl([0,T];L^p(X)\bigr), \qquad\mathcal{F}(u) = \tilde{u}, \end{aligned}$$

where \(\tilde{u}\) is a solution to the problem

$$\begin{array}{@{}rcl@{\quad}l} \displaystyle\frac{\partial\tilde{u}}{\partial t}(t,x) &=& \varDelta \tilde{u} (t,x) + g\bigl(u(t,x)\bigr) & \text{in}\ [0,\infty)\times X,\\ \tilde{u}(0,x) &=& \phi(x) & \text{in}\ X. \end{array} $$

We shall show that, there exists T such that \(\mathcal{F}: B_{T} \rightarrow B_{T}\) and that the map \(\mathcal{F}\) is a contraction on B T . For this purpose we take u∈B T . Then, by Theorem 3.1 we obtain

$$\begin{aligned} \bigl\|\mathcal{F}(u)\bigr\|_{C([0,T];L^p)} \leq& 2 \|\phi\|_{L^p} + 2\bigl\|g(u)\bigr\|_{L^1(0,T;L^p)} \\\leq& 2 \|\phi\|_{L^p} + 2L \bigl(B\bigl(0, 4 \|\phi\|_{L^p}\bigr) \bigr) T\|u\| _{C(0,T;L^p)} \\\leq& 2 \|\phi\|_{L^p} \bigl(1 + 4T L \bigl(B \bigl(0, 4 \|\phi \|_{L^p}\bigr) \bigr) \bigr). \end{aligned}$$

Hence, for \(T= \frac{1}{4 L(B(0, 4 \|\phi\|_{L^{p}}))}\) we obtain that \(\mathcal{F}: B_{T} \rightarrow B_{T}\). Now, we show that the map \(\mathcal{F}\) is a contraction. Let us take u,v∈B T . Then, by Theorem 3.1 we have the estimate

$$\begin{aligned} \bigl\|\mathcal{F}(u)-\mathcal{F}(v)\bigr\|_{C([0,T];L^p)} \leq&2 \bigl\|g(u)-g(v)\bigr\| _{L^1(0,T;L^p)} \\\leq&2TL \bigl(B\bigl(0, 4 \|\phi\|_{L^p}\bigr) \bigr)\|u-v \|_{C(0,T;L^p)}. \end{aligned}$$

Thus, for \(T= \frac{1}{4 L(B(0, 4 \|\phi\|_{L^{p}}))}\) we get a contraction. Finally, thanks to the Banach fixed point theorem we obtain the existence of a unique solution. □

As a corollary we obtain the following global result.

Corollary 3.1

Let p∈[1,∞). Let us assume that there exists L such that for each u,v∈L p(X) the following inequality holds

$$\begin{aligned} \bigl\|g(u) - g(v)\bigr\|_{L^p}\leq L\|u-v\|_{L^p}. \end{aligned}$$

Moreover, if μ(X)=∞ we assume that g(0)=0. If ϕ∈L p, then there exists unique global in time solution u∈C([0,∞);L p(X)) to problem (18).

3.2 Global solution

Under some assumptions on the heat kernel and on the metric we construct global in time solutions to problem (18). Namely, in the next theorem we assume that there exist C and positive constants α and κ such that

$$\begin{aligned} \int_0^{\infty} p_t(x,y)dt \leq\frac{C}{\rho(x,y)^{\alpha-\kappa}}, \quad p_t(x,y)\leq\frac{C}{\rho(x,y)^{\alpha}}. \end{aligned}$$
(19)

In addition to (19) we assume that for each ξ>α there exists D such that

$$ \int_X \frac{1}{\rho(x,y)^{\alpha-\kappa}(1+\rho(y,\tilde{x})^{\xi})} d \mu(y) \leq\frac{D}{1+\rho(x,\tilde{x})^{\alpha-\kappa}}. $$
(20)

Theorem 3.2

Let us assume that the heat kernel p t satisfies the above condition (19) and that assumption (20) is satisfied. Moreover, we assume that the nonlinearity g satisfies the growth conditions:

$$\begin{aligned} \bigl|g(u)\bigr|\leq A|u|^p, \qquad\bigl|g'(u)\bigr|\leq B|u|^{p-1}, \end{aligned}$$

where (p−1)(α−κ)>α. Let ϕ∈L 1(X)∩L ∞(X), be such that \(\|\phi\|_{L^{1}\cap L^{\infty}}\) is small and suppose that there exists \(\tilde{x}\) such that \(\lim_{\rho(y,\tilde {x})\rightarrow\infty} \phi(y) \rho(y, \tilde{x})^{\beta}=0\) where β≥α. Then there exists a unique global in time solution u∈L ∞([0,∞);L ∞(X)) to problem (18).

Proof

First of all we claim that for each ϵ>0 there exists R ϵ >0 such that the inequality holds

$$\begin{aligned} \bigl|\mathcal{T}(t) \phi(x)\bigr|\leq \frac{(1+R_{\epsilon}^{\alpha-\kappa})\|\phi\|_{L^{\infty}(X)} +R_{\epsilon}2^{\alpha+1}C\|\phi\|_{L^1}+ 2^{\alpha- \kappa}\epsilon }{1+\rho(x,\tilde{x})^{\alpha-\kappa}}. \end{aligned}$$
(21)

Indeed, since \(\lim_{\rho(y,\tilde{x})\rightarrow\infty} \phi(y) \rho (y, \tilde{x})^{\beta}=0\), there exists R ϵ >1 such that for almost each \(y \in B^{c}(\tilde{x}, \frac{R_{\epsilon}}{2})\), the inequality holds \(|\phi(y)|\leq\frac{\epsilon}{1+\rho(y,\tilde{x})^{\alpha-\kappa}}\).

If \(\rho(x, \tilde{x})\geq R_{\epsilon}\) we obtain

$$\begin{aligned} \bigl|\mathcal{T}(t) \phi(x)\bigr| \leq&\int_X \bigl| \phi(y)\bigr|p_t(x,y)d\mu(y) \\=& \int_{B (\tilde{x},\frac{\rho(x,\tilde{x})}{2} )} \bigl|\phi (y)\bigr|p_t(x,y)d\mu(y)+\int _{B^c (\tilde{x}, \frac{\rho(x,\tilde {x})}{2} )} \bigl|\phi(y)\bigr|p_t(x,y)d\mu(y) \\\leq&\int_{B (\tilde{x}, \frac{\rho(x,\tilde{x})}{2} )} \bigl|\phi (y)\bigr|\frac{C}{\rho(x,y)^{\alpha}} d \mu(y)\\&{}+\int _{B^c (\tilde{x}, \frac{\rho(x,\tilde{x})}{2} )} \frac{\epsilon}{1+\rho(y,\tilde {x})^{\alpha-\kappa}}p_t(x,y)d\mu(y) \\\leq&\frac{R_{\epsilon}2^{\alpha+1}C\|\phi\|_{L^1}}{1+\rho(x,\tilde {x})^{\alpha}} + \frac{\epsilon2^{\alpha-\kappa}}{2^{\alpha-\kappa }+\rho(x,\tilde{x})^{\alpha-\kappa}}\leq\frac{R_{\epsilon}2^{\alpha +1}C\|\phi\|_{L^1}+ 2^{\alpha-\kappa}\epsilon}{1+\rho(x,\tilde {x})^{\alpha-\kappa}}. \end{aligned}$$

Hence, we obtain (21). Now, for each δ>0 we define the set

$$\begin{aligned} X^{\delta} = \biggl\{ u \in L^{\infty}\bigl([0,\infty); L^{\infty}(X)\bigr): \bigl|u(t,x)\bigr| \leq\frac{\delta}{1 + \rho(x,\tilde{x})^{\alpha- \kappa }} \biggr\}. \end{aligned}$$

Next, we define the map \(\mathcal{G}\):

$$\begin{aligned} \mathcal{G}: X^{\delta} \rightarrow L^{\infty}\bigl([0,\infty \bigr);L^{\infty }(X)), \qquad\mathcal{G}(u) = \tilde{u}, \end{aligned}$$

where \(\tilde{u}\) is a solution to the problem

$$\begin{array}{@{}rcl@{\quad}l} \displaystyle\frac{\partial\tilde{u}}{\partial t}(t,x) &=& \varDelta \tilde{u} (t,x) + g\bigl(u(t,x)\bigr) & \text{in}\ [0,\infty)\times X,\\ \tilde{u}(0,x) &=& \phi(x) & \text{in}\ X. \end{array} $$

We shall show that there exists δ such that \(\mathcal{G}: X^{\delta} \rightarrow X^{\delta}\) and the map \(\mathcal{G}\) is a contraction. Let us take u∈X δ, then we get

$$\begin{aligned} \bigl|\mathcal{G}(u) (x,t)\bigr| \leq& \bigl|\mathcal{T}(t) \phi(x)\bigr|+\int_0^t \int_X p_{t-s}(x,y)\bigl|g\bigl(u(y,s)\bigr)\bigr|d\mu(y)ds \\\leq&\bigl|\mathcal{T}(t) \phi(x)\bigr| + A\int_0^t \int_X p_{t-s}(x,y)\bigl|u(y,s)\bigr|^p dy ds \\\leq&\bigl|\mathcal{T}(t) \phi(x)\bigr| + A\delta^p\int_0^{\infty} \int_X p_{t-s}(x,y)\frac{1}{(1+\rho(y,\tilde{x})^{\alpha-\kappa})^p} d \mu(y) ds \\\leq&\bigl|\mathcal{T}(t) \phi(x)\bigr| + A\delta^p \int_X \frac{C}{\rho (x,y)^{\alpha-\kappa}}\frac{1}{1+\rho(y,\tilde{x})^{(\alpha-\kappa) p}} d \mu(y) \\\leq&\frac{(1+R_{\epsilon}^{\alpha-\kappa})\|\phi\|_{L^{\infty}(X)} +R_{\epsilon}2^{\alpha+1}C\|\phi\|_{L^1}+ 2^{\alpha- \kappa}\epsilon }{1+\rho(x,\tilde{x})^{\alpha-\kappa}}+\frac{A\delta^p D}{1+\rho (x,\tilde{x})^{\alpha-\kappa}} \\\leq&\frac{\delta}{1+\rho(x,\tilde{x})^{\alpha-\kappa}}, \end{aligned}$$

provided ϕ is small. Subsequently, we show that \(\mathcal{G}\) is a contraction map. Let us take u,v∈X δ. Then, thanks to the Mean Value theorem we obtain

$$\begin{aligned} &\bigl|\mathcal{G}(u) (x,t) -\mathcal{G}(v) (x,t)\bigr| \\&\quad{}\leq\int_0^t \int_X p_{t-s}(x,y)\bigl|g\bigl(u(y,s)\bigr)-g \bigl(v(y,s)\bigr)\bigr|d \mu(y) ds \\&\quad{}\leq\int_0^t\int_X p_{t-s}(x,y)2^pB\delta^{p-1}\frac{\|u-v\| _{L^{\infty}([0,\infty);L^{\infty}(X))}}{1+\rho(y,\tilde {x})^{(p-1)(\alpha-\kappa)}}d \mu(y)ds \\&\quad{}\leq 2^pB\delta^{p-1}CD\|u-v\|_{L^{\infty}([0,\infty);L^{\infty}(X))}. \end{aligned}$$

Hence, if δ is sufficiently small, we obtain that

$$\begin{aligned} \bigl\|\mathcal{G}(u) -\mathcal{G}(v)\bigr\|_{L^{\infty}([0,\infty);L^{\infty }(X))}\leq\frac{1}{2}\|u-v\|_{L^{\infty}([0,\infty);L^{\infty}(X))}. \end{aligned}$$

Finally, we need to show the uniqueness. For this purpose we take u,v∈L ∞([0,∞);L ∞(X)). Then

$$\begin{aligned} \bigl\|u(t)-v(t)\bigr\|_{L^{\infty}(X)} \leq& B2^{p-1}\mathit{ess}\sup _{X}\int_0^t\int _X p_{t-s}(x,y)\bigl\|u(s)-v(s)\bigr\|_{L^{\infty}(X)} \\ &{}\cdot\bigl(\|u\|_{L^{\infty}([0,\infty);L^{\infty}(X))}^p +\|v\| _{L^{\infty}([0,\infty);L^{\infty}(X))}^p \bigr) d\mu(y)ds \\ \leq& B2^{p-1}\bigl(\|u\|_{L^{\infty}([0,\infty);L^{\infty}(X))}^p\\&{}+\|v\| _{L^{\infty}([0,\infty); L^{\infty}(X))}^p\bigr) \int_0^t \bigl\|u(s)-v(s)\bigr\|_{L^{\infty}(X)}ds. \end{aligned}$$

Hence, by Gronwall lemma we obtain that u=v. □