Skip to main content
SpringerLink
Log in

Natural convection heat transfer from a vertical single cylinder with eccentric grid spacer in liquid sodium

  • Original Article
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

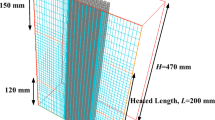
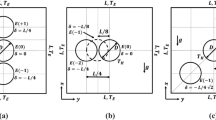
Natural convection heat transfer from a vertical single-cylinder with eccentric grid spacer in liquid sodium was numerically analyzed on the following seven effects, the influences of grid spacer, surface heat flux, the gap between grid spacer and heated cylinder surface, grid spacer thickness, height, eccentricity, and material on heat transfer. The unsteady laminar three-dimensional basic equations for natural convection heat transfer caused by a step heat flux were numerically solved until the numerical solution reaches a steady state. The PHOENICS code was used for the calculation considering the temperature dependence of thermo-physical properties concerned. The heated cylinder for diameter (D = 7.6 mm), heated length (L = 200 mm) and L/d (= 26.32), and the round cell type grid spacers for gaps (0.05 to 0.5 mm), inner diameters (di = 7.7 to 8.6 mm), thickness (w = 0.2, 0.3 and 0.5 mm), outer diameters (do = 8.1 to 9.2 mm), heights (h = 10, 30 and 50 mm), eccentricity (B = 0, 0.3333, 0.6667 and 0.8333: s = 0, 0.1, 0.2 and 0.25 mm) and materials (SUS304, SUS316, Hastelloy X and Adiabatic) were used in this work. The surface heat fluxes for each cylinder with eccentric grid spacer were equally given for a modified Rayleigh number, (Raf,L)g-s, ranging from 3.057 × 104 to 3.171 × 107 (q = 1 × 104 to 7 × 106 W/m2) in liquid temperature (TL = 673.15 K). The values of gap were given 0.05, 0.1, 0.2, 0.3, 0.4 and 0.5 mm at w = 0.2 mm, h = 30 mm, B = 0 and SUS316, those of thickness were given 0.2, 0.3 and 0.5 mm at a gap of 0.3 mm, h = 30 mm, B = 0 and SUS316, those of height were given 20, 30 and 50 mm at a gap of 0.3 mm, w = 0.2 mm, B = 0 and SUS316, those of eccentricity were given 0, 0.3333, 0.6667 and 0.8333 at a gap of 0.3 mm, w = 0.2 mm, h = 30 mm and SUS316, and those of material were given SUS304, SUS316, Hastelloy X and Adiabatic at a gap of 0.3 mm, w = 0.2 mm, h = 30 mm and B = 0 on each cylinder with eccentric grid spacer. The spatial distributions of local and average Nusselt numbers, (Nuθ,z)g-s and (Nuav)g-s, on vertical single-cylinder with eccentric grid spacer, were clarified. The values of average Nusselt number, (Nuav)g-s, for a vertical single-cylinder with eccentric grid spacer were calculated to examine the effects of grid spacer, (Raf,L)g-s, gap, thickness, height, eccentricity, and material on heat transfer. The correlation for (Nuav)g-s for a vertical single-cylinder with eccentric grid spacer above mentioned, including the effects of grid spacer, (Raf,L)g-s, gap, thickness, height, eccentricity, and the material was developed. The correlation can describe the theoretical values of (Nuav)g-s for a vertical single-cylinder with eccentric grid spacer within -1.897 to 1.432% differences.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35

Similar content being viewed by others

Abbreviations

B :

 = 2 s/(E-1)/D, Eccentricity

C :

Parameter in Eqs. (14), (19) and (33)

C 1 :

Constant in Eqs. (30), (31), (33) and (34)

c:

Specific heat, J/kg K

c p :

Specific heat at constant pressure, J/kg K

D :

Cylinder diameter and rod diameter, m

d :

Helical wire diameter, m

d i :

Inner diameter of grid spacer, m

d o :

Outer diameter of grid spacer, m

E :

 = di/D, Expansion rate

Gr L * :

 = g βl q L4/λl νl2, Grashof number for constant heat flux without eccentric grid spacer

( Gr L * ) g-s :

 = g βl q L4/λl νl2, Grashof number for constant heat flux with eccentric grid spacer

Gr z * :

 = g βl q z4/λl νl2, Local Grashof number for constant heat flux without eccentric grid spacer

( Gr z * ) g-s :

 = g βl q z4/λl νl2, Local Grashof number for constant heat flux with eccentric grid spacer

g :

Acceleration of gravity, m/s2

H :

Height, liquid head, m

h :

=(ρcλ)0.5, thermal activity factor, J/m2Ks0.5

h av :

Average heat transfer coefficient for a vertical single-cylinder without eccentric grid spacer, W/(m2K)

( h av ) g-s :

Average heat transfer coefficient for a vertical single-cylinder with eccentric grid spacer, W/(m2K)

h z :

Local heat transfer coefficient for a vertical single-cylinder without helical wire spacer, W/(m2K)

( h z ) g-s :

Local heat transfer coefficient for a vertical single-cylinder with eccentric grid spacer, W/(m2K)

L :

Heated length, m

N r :

Grid point for the r-component

N z :

Grid point for the z-component

N θ :

Grid point for the θ-component

n :

Exponent in Eqs. (30), (31), (33) and (35)

Nu :

Nusselt number

Nu av :

Average Nusselt number for a vertical single-cylinder without eccentric grid spacer

( Nu av ) g-s :

Average Nusselt number for a vertical single-cylinder with eccentric grid spacer

Nu z :

= q z/λl (TS-TL), Local Nusselt number for a vertical cylinder without eccentric grid spacer

Nu θ , z :

= q z/λl (TS-TL), Local Nusselt number for a vertical cylinder without eccentric grid spacer at a peripheral angle of the heated cylinder, θ

( Nu θ , z ) g-s :

= q z/λl (TS-TL), Local Nusselt number for a vertical cylinder at a peripheral angle of the heated cylinder, θ

Pr :

= cpl μl/λl, Prandtl number

q :

Heat flux, W/m2

Ra L * :

 = GrL*Pr, Rayleigh number for constant heat flux without eccentric grid spacer

( Ra L * ) g-s :

 = GrL*Pr, Rayleigh number for constant heat flux with eccentric grid spacer

Ra z * :

= Grz*Pr, Local Rayleigh number for constant heat flux without eccentric grid spacer

( Ra z * ) g-s :

= Grz*Pr, Local Rayleigh number for constant heat flux with eccentric grid spacer

R a f ,z :

= Grz*Pr2/(4 + 9Pr1/2 + 10Pr), Modified local Rayleigh number without eccentric grid spacer

{( R a f ) θ ,z } g-s :

= Grz*Pr2/(4 + 9Pr1/2 + 10Pr), Modified local Rayleigh number with eccentric grid spacer

R a f,L :

 = GrL*Pr2/(4 + 9Pr1/2 + 10Pr), Modified Rayleigh number without eccentric grid spacer

( R a f,L ) g-s :

 = GrL*Pr2/(4 + 9Pr1/2 + 10Pr), Modified Rayleigh number with eccentric grid spacer

r :

Radius of a cylinder, m

Δr :

First control volume width for r-component, m

s :

Distance between central axes, m

T :

Temperature, K and °C

TEM :

Analyzed liquid temperature of the first control volume, K

T f :

Liquid temperature, K

T L :

Bulk liquid temperature, K

T s :

Heater surface temperature, K

( T s ) av :

Average surface temperature without eccentric grid spacer, K

{( T s ) av } g-s :

Average surface temperature with eccentric grid spacer, K

( T s ) z :

Local surface temperature without eccentric grid spacer, K

{( T s ) θ ,z } g-s :

Local surface temperature with eccentric grid spacer, K

T ∞ :

Temperature of the fluid outside the thermal boundary layer, K

t :

Time, s

Δ t :

Time step, s

U ∞ :

Fictitious velocity, m/s

(v θ ) g -s :

Velocity component in θ-direction, m/s

(v r ) g -s :

Velocity component in r-direction, m/s

(v z ) g -s :

Velocity component in z-direction, m/s

w:

Thickness of grid spacer, m

z :

Cylinder height and the vertical distance from the leading edge of the heated section, m

β :

Volumetric expansion coefficient, K−1

δ :

Hydrodynamic boundary layer thickness, m

δ CSL :

Thickness of conductive sublayer, m

δ t :

Thermal boundary layer thickness, m

θ :

Peripheral angle from inside on the r-θ plane, degree

λ :

Thermal conductivity, W/(m K)

μ :

Viscosity, Ns/m2

ν :

Kinematic viscosity, m2/s

ρ :

Density, kg/m3

l :

Liquid

References

  1. Schultheiss GF (1977) Model for formation and growth of local blockages in grid spaced fast sodium cooled breeder fuel elements. Nucl Eng Des 43:329–341

    Article  Google Scholar 

  2. Möller R, Tschöke H (1980) Steady-state, local temperature fields with turbulent liquid sodium flow in nominal and disturbed bundle geometries with spacer grids. Nucl Eng Des 62:69–80

    Article  Google Scholar 

  3. Pacio J, Daubner M, Fellmoser F, Litfin K, Marocco L, Stieglitz R, Taufall S, Wetzel Th (2014) Heavy-liquid metal heat transfer experiment in a 19-rod bundle with grid spacers. Nucl Eng Des 273:33–46

    Article  Google Scholar 

  4. Batta A, Class AG (2017) CFD analysis of pressure drop across grid spacers in rod bundles compared to correlations and heavy liquid metal experimental data. Nucl Eng Des 312:121–127

    Article  Google Scholar 

  5. Mathur A, Uitslag-Doolaard H, Roelofs F (2020) Reduced-resolution RANS approach to grid spacer fuel assemblies. Nuclear Engineering and Design 356:110374 -1–13

  6. Hata K, Liu QS, Nakajima T (2019) Natural Convection Heat Transfer from a Vertical Single Cylinder with Helical Wire Spacer in Liquid Sodium. Nucl Eng Des 341:73–90

    Article  Google Scholar 

  7. Hata K, Takeuchi Y, Hama K, Shiotsu M, Shirai Y, Fukuda K (2014) Natural convection heat transfer from a vertical cylinder in liquid sodium. Mechanical Engineering Journal 1(1):1–12

    Article  Google Scholar 

  8. Hata K, Fukuda K, Mizuuchi T (2016) Natural Convection Heat Transfer from Vertical Rod Bundles in Liquid Sodium. Mech Eng J 3(3):1–16

    Article  Google Scholar 

  9. Hata K, Fukuda K, Mizuuchi T (2017) Natural Convection Heat Transfer from Vertical 5×5 Rod Bundles in Liquid Sodium. J Heat Transfer Trans ASME 139:032502–1–11

  10. Hata K, Fukuda K, Mizuuchi T (2019) Laminar Natural Convection Heat Transfer from Vertical 7×7 Rod Bundles in Liquid Sodium. Journal of Nuclear Engineering and Radiation Science Trans ASME 5:021002–1–15

  11. Hata K, Liu QS, Nakajima T (2021) Natural Convection Heat Transfer from Vertical 9×9 Rod Bundles in Liquid Sodium. Heat Mass Transf. https://doi.org/10.1007/s00231-020-02986-8,Vol.57,pp.807-828

    Article  Google Scholar 

  12. Hata K, Takeuchi Y, Shiotsu M, Sakurai A (1999) Natural convection heat transfer from a horizontal cylinder in liquid sodium (Part 1: Experimental results). Nucl Eng Des 193:105–118

    Article  Google Scholar 

  13. Hata K, Takeuchi Y, Shiotsu M, Sakurai A (1999) Natural convection heat transfer from a horizontal cylinder in liquid sodium (Part 2: Generalized correlation for laminar natural convection heat transfer). Nucl Eng Des 194:185–196

    Article  Google Scholar 

  14. Hata K, Takeuchi Y, Hama K, Shiotsu M (2015) Natural convection heat transfer from horizontal Rod bundles in liquid sodium Part 1: Correlations for two parallel horizontal cylinders based on experimental and theoretical results. J Nucl Sci Technol 52(2):214–227

    Article  Google Scholar 

  15. Hata K, Takeuchi Y, Hama K, Shiotsu M (2015) Natural convection heat transfer from horizontal Rod bundles in liquid sodium Part 2: Correlations for horizontal rod bundles based on theoretical results. J Nuclear Sci Technol. https://doi.org/10.1080/00223131.2014. 947347, 52(No.3):342–354.

  16. SolidWorks 2011–2012 Education Edition Media Kit (2011) SolidWorks Japan K.K., Tokyo, (in Japanese)

  17. Spalding DB (1991) The PHOENICS Beginner's Guide, CHAM Ltd., London, United Kingdom

  18. Patankar SV (1980) Numerical Heat Transfer and Fluid Flow (1991). Hemisphere Pub. Corp, New York

    MATH  Google Scholar 

  19. Favre-Marinet M, Tardu S, Convective Heat Transfer (2009) ISTE Ltd and John Wiley & Sons, Inc., Great Britain and United States

  20. Hanjalic K, Kenjeres ST, Tummers MJ, Jonker HJ (2009) Analysis and Modeling of Physical Transport Phenomena (2009), Published by VSSD

  21. Holman JP (2002) Heat Transfer, Ninth Edition (2002), McGraw-Hill, p. 317

  22. Le Fevre EJ, Ede AJ (1957) Laminar Free Convection from the Outer Surface of a Vertical Circular Cylinder. Proceedings of the 9th Int Congress Appl Mechanics Brussels 4:175–183

  23. Mabuchi I (1961) Laminar Free Convection from a Vertical Cylinder with Uniform Surface Heat Flux. Trans Jpn Soc Mech Eng 27(180):1306–1313 ((in Japanese))

    Article  Google Scholar 

  24. Burmeister LC (1983) Convective Heat Transfer. John Willy & Sons, p. 536

Download references

Acknowledgements

This work was supported by the “Joint Usage/Research Program on Zero-Emission Energy Research, Institute of Advanced Energy, Kyoto University, Japan, ZE30B-03, 2018 and ZE31B-05, 2019.”

Author information

Authors and Affiliations

  1. Graduate School of Maritime Sciences, Kobe University, 5-1-1, Fukae-minami, Kobe, Hyogo, 658-0022, Japan

    Koichi Hata & Makoto Shibahara

Authors
  1. Koichi Hata
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Makoto Shibahara
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Koichi Hata.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hata, K., Shibahara, M. Natural convection heat transfer from a vertical single cylinder with eccentric grid spacer in liquid sodium. Heat Mass Transfer 58, 1607–1636 (2022). https://doi.org/10.1007/s00231-022-03199-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-022-03199-x

Search

Navigation