Experimental investigation of heat transfer from elliptic tubes heat exchanger immersed in a fluidized bed

Abstract

In this work, heat transfer, wall-to-bed, characteristics from elliptic tubes heat exchangers, both inline and staggered tubes arrangements, were studied experimentally. Bundles of twenty tubes of the same total surface area of 0.015 m² and a length of 200 mm are immersed in a bed of granulated charcoal of different grain sizes, 2, 4 and 6 mm. Air was used as a fluidizing fluid. One of these tubes which was made of copper, instrumented, electrically heated and positioned in the middle of tube bundle, while the others are wooden dummy to be influenced only by the presence of the neighbouring tubes. Measurements are reported in the range of fluidization number within range of 1 to1.4. The results showed that, the local Nusselt number around the elliptic heated tube is about uniform with its maximum value at the tube sides and minimum at the stagnation and rear points of the tube. In addition, the average Nusselt number increases with the increase of the fluidization number and with the decrease in particle diameter. Heat transfer characteristics were found to improve in staggered tube bundle if compared with the inline tube arrangements. The present results of pressure drop and average Nusselt numbers were validated with a numerical model of the same conditions for the case of particle diameter of 2 mm. Good qualitative and quantitative agreements have been achieved between experimental and numerical data. Finally, correlation equations for the average heat transfer in terms of Nu, fluidization number and tube to particle diameter ratio are deduced.

1 Introduction

The implementation of Egypt's Vision 2030 in the field of energy requires that the energy sector be able to meet all the requirements of sustainable national development of energy resources and maximize the efficient utilization of its diverse sources. Fluidized bed reactors play an important role of in the “clean wastes technology” for power generation, because of their low emissions, high efficient and clean combustion of coal, biomass and other wastes [1]. Thermal energy addition/ extraction is required to control the temperature in fluidized bed applications. For this purpose, heat exchangers are equipped to reactors to remove generated heat or add required heat to the fluidized bed by cooling or heating coils. Heat transfer and flow patterns around immersed surfaces in fluidized beds have been studied numerically as well as experimentally. These studies aim to understand the heat transfer characteristics and fluid flow through heat exchanger tubes to enhance fluidization quality and reduce the drawbacks of the fluidization process. In order to achieve this, changing tube shape and configurations are used as most important solutions to reduce losses such as pressure drop, channelling, slugging, particles’ fluctuations and bed expansion, as well as to improve particles activity inside the bed region, which leads to good heat and mass transfer [2,3,4]. Changing the tube shape of tube banks in crossflow studied intensively by numerous researchers. Park et al. [5] studied experimentally and compared heat transfer characteristics around elliptic cylinder with that of circular cylinder in tube banks. Their results show that, the friction factor in case of the elliptic cylinder is lower than that of its corresponding circular cylinder. Also, the Nusselt number in case of elliptic cylinder showed to be only about 9.3% lower than that of circular one. The elliptic cylinder has smaller facial area compared to the circular cylinder, enabling more compact design of heat exchangers. El Gharbi et al. [6] investigated numerically the influence of tubes’ shapes arranged in a staggered style in crossflow pattern on heat transfer, the pressure drop and effectiveness characteristics. They concluded that circular tubes had higher-pressure drops compared to non-circular tubes of streamlined shapes i.e. elliptic shape. Berbish [7], Veerraju and Gopal [8] found that, the average Nusselt number of the downstream cylinder for both inline and staggered arrangements was higher than that of the single elliptic cylinder.

In case of tube banks in fluidized bed, lesser attention were found paid in the open literature to changing tube geometry. Kurochkin [9] studied the effect of the tube profile, circular, elliptical, and lenticular horizontal tubes, on the local heat transfer coefficient. Unfortunately, their experiments were carried out only with gravitational downward flows of particulate. Dong et al. [10] studied numerically the effects of two different shaped, square and circular, tubes on the flow characteristics and local surface-to-bed heat transfer coefficients. Their simulated results reveal that, a square heated tube show greater drag forces on the bed particles than the circular tube and this results in retarding the process of fluidization. Also, more flow obstruction caused by the flatter base of the tube results in larger build-up of air under the tube increasing the bed expansion. Natale et al. [11] studied experimentally the surface-to-bed heat exchange with different shaped surfaces (sphere, cone, frustum of cone, circular cylinders and parallelepiped) by the variation of bed fluidising gas velocity and material properties. The results showed that the surface geometry strongly affect the heat transfer coefficient by as much as 40 percent, while no dramatic effect was observed on the heat transfer due to particle thermal conductivity. Tan et al. [12] investigated numerically heat transfer performance of elliptic tubes in granular flow with different axis ratio and concluded that elliptic tubes have a narrow area of heat transfer deterioration which led to a higher effective heat transfer coefficient than of circular tube of the same long axis. Moreover, changing tube configurations (vertically and horizontally) were presented extensively by the majority of researchers in the fluidization literature. Furui et al. [13] studied the impact of vertical internals on the heat transfer and hydrodynamics in a gas–solid fluidized bed. They found that, the immersed vertical tubes improved the heat transfer performance, increased the heat transfer coefficient, reduced the pressure drop, affect the flow regimes and their transition velocities, as well as enhanced the performance of the gas–solid fluidization. Blaszczuk et al. [14] investigated the characteristics of heat transfer in a bubbling fluidized bed with a submerged super heater tube bundles under conditions of an integrated fluidized bed heat exchanger of a large-scale circulating fluidized bed boiler. They proposed an empirical packet-renewal model depending on the emulsion density and local bed hydrodynamics to estimate the heat transfer coefficient. They concluded that, the average heat transfer coefficient increased with decreasing bed particle size while it decreased with increasing emulsion contact time on the tube surface and with the reduction of the solids mixing. Yusuf et al. [15], Armstrong et al. [16], Bartsch & Zunft [17], Bartsch et al. [18], Sin & Lim [19] and Hou et al. [20] investigated numerically the coupled effects of local hydrodynamics on heat transfer from tube bundles immersed horizontally in a gas–solid fluidized bed. They further considered the effects of some other parameters as: material properties, fluidization and pulsation velocities, and tube array settings, on flow pattern and heat transfer characteristics in fluidized beds with tubes systems. Their results revealed, however the same trends as: (i) uniformity of particles velocity and temperature distribution are significantly influenced by material properties as well as gas velocity in a complicated manner, (ii) heat transfer rates from tubes to the bed are enhanced by the increase of the number of tubes, and (iii) the flow and heat transfer characteristics are affected by tube array settings.

On the other hand, Olsson and Almstedt [21] studied experimentally the effect of fluidization velocity and pressure on local instantaneous and average bed-to-tube heat transfer under a cold pressurized bed condition. Their study was carried out within three different tube bundle geometries immersed in a silica sand bed of 0.7 mean particle diameter. The heat transfer results showed a significant increase of the bed-to-tube heat transfer coefficient with higher fluidization velocity and bed pressure. Bordulya et al. [22] conducted experiments to find out the influence of fluidizing velocity and system pressure on heat transfer processes for horizontal square inline tube bundles immersed in glass beads fluidized beds of 1.25 and 3.1 mm particle size. They found that, heat transfer coefficient values increased with particle diameter, system pressure but were almost independent of the tube pitch. Catipovic [23] carried out experimental and theoretical investigations on heat transfer in a closely-spaced tube array immersed in a bed of a wide range of particle size. His theory assumed that, "heat exchange between a cold fluidized bed and a horizontal tube takes place through three parallel paths: by packets of particles, by gas layer in between neighbouring particles and the surface of heated tube, and by bubbles". Goshayeshi [24] obtained experimentally time-average local heat transfer coefficients for arrays of horizontal tubes immersed in a hot fluidized bed of particles having mean diameters of 2.14 and 3.23 mm. He concluded that, higher rates of heat transfer were obtained with higher superficial gas velocity, smaller particles and/or higher bed temperatures. Grewal [25, 26] proposed a generalized correlation for heat transfer coefficient between a horizontal staggered tube bundle and a gas–solid fluidized bed of small particles (< l mm). Bansal [27] conducted an experimental investigation of the fluid-flow and heat transfer mechanisms associated with the performance of an equilaterally pitched horizontal tube bundle in a gas fluidized bed. He found that, heat transfer coefficient increased with fluidization velocity for the range of particle sizes and types, pitch-to-diameter ratios, levelling off at a value of the ratio of about 1.7 used in the investigation. He modified an empirical correlation with an additional correction factor for the influence of the pitch-to-diameter ratio, CR, to account for the effect of P/D_t ratio of the tube bundles, = [1- 0.4(P/D_t)]^−2.5. Kim et al. [28] concluded that, the average heat transfer coefficient exhibited a maximum value with variation of gas velocity and the local heat transfer coefficient exhibited maximum values at the side of the tube while bubble frequency increased and the emulsion contacting time decreased with increasing gas velocity. Moawed et al. [29] found that, the heat transfer coefficient values were dependent on the particle size, fluidization velocity and longitudinal and transversal distances between neighbouring tubes in the bundle.

On reviewing the previous research, one can conclude that, most studies to date have focused on heat transfer from tube bundles of circular cross section. Although, elliptical geometries in crossflow outperform circular geometries as they offer less flow resistance and higher heat-transfer rates than circular cylinders. There are no available experimental data published about tube banks of elliptic geometries immersed in fluidized beds. Also, a little attention is paid to studying fluidized bed of large particles. So, the current study serves to fill this gap in the field of coupled effects between fluidization velocity and heat transfer in fluidized bed of large particles containing immersed elliptic tube bundles.

2 Experimental setup

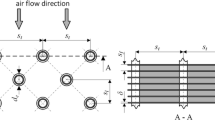
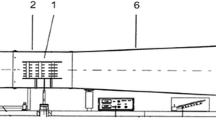
The experimental setup employed in the present investigation is the same of our previous work [30] as shown schematically in Fig. (1). It consists mainly of an air passage, fluidized bed reactor, measuring instruments and a power supply with the necessary associated controls. The reactor has a square cross section of 0.2 m × 0.2 m and height of 1.5 m. The reactor is made up of 1.5 mm thick steel sheet and is provided with a plexiglas front and back walls to enable visual observations. The reactor is designed to give air flow across horizontal cylinders immersed in a bed of pulverized coal. A centrifugal-type air blower is driven by a 2-HP electric motor is used to supply the required air flow, which is controlled by means of a ball valve. Air passes through the distributor plate to fluidize a pulverised coal bed 2, 4, 6 mm mean particle diameter, Geldart D, according to Geldart’s classification of powders [31]. The heat exchanger installed in the fluidized bed consists of five rows of horizontal elliptic tubes of the same total surface area of As ≈ 0.015 m² and a length of 200 mm. Inline and staggered tube bundles are used and the bottom row is being located about 10 mm above the distributor plate, as shown in Fig. (2). Semi cylinders of the same dimensions have been fixed to the side walls of the column against the horizontal rows of tubes in order to simulate the extension of the rows of tubes. The tubes are spaced with equal horizontal and vertical pitches of 50 mm. One of these tubes which made of copper is electrically heated and positioned in the middle of tube bundle while the others are wooden dummy to be influenced only by the presence of neighbouring tubes. A cartridge heater of 16 mm outer diameter is used to heat the copper heated tube with a constant heat flux. Both ends of the heated tube are well-insulated to minimize the axial heat losses. The static bed height, H_st, is chosen to be fixed at 250 mm to cover all tube bundles. The local heat transfer coefficient between the fluidized bed and the heated tube in the bundle is measured using eight thermocouples made of Copper-Constantan, T-type (0.2 mm wire diameter). These thermocouples are distributed circumferentially at 45° fixed intervals and embedded on the tested cylinder surface of the central section, as shown in Fig. (3). The junctions and wires of the thermocouples are fixed smoothly in their positions by means of plastic steel epoxy (devcon) avoiding any hindrance to the flow of air and particles over the tested cylinder. The free wire terminals are connected via 12-channel selector switch to the temperature recorder. Also, the mean bed temperature is measured by using four thermocouples of the same type located at the centre-line of the bed region.

A standard Pitot-tube anemometer was employed to measure the air flow velocity just before entering the reactor. The pressure drop in the bed is measured by using U-tube manometer, connected through holes on the side wall of the test section. A digital multimeter with a minimum reading of 0.1 °C is employed for all the temperature measurements. The power consumed in the heater is measured with digital multimeter through continuous recording of the electric current and voltage across the cartridge heater. All the experiments were carried out at room temperature and atmospheric pressure. Various fluidization numbers, U_sup/U_mf, based on the hydraulic diameter of the tested tube, were experimented with covering the range of 1 to 1.4. The experimental data are based on the equivalent hydraulic diameter, D_h, having a value of 25.3 mm for the tested cylinder and generally can be calculated as follows:

$${D}_{h}=4 {A}_{c}/P$$

(1)

The input electrical power, Q, is adjusted using a voltage regulator and is determined from the current and voltage of the cartridge heater as:

$$Q=VI$$

(2)

The steady state condition is normally reached in some 2.00 to 2:30 h, and the surface temperatures of the tested cylinder, T_s,θ, and the bed temperature, T_b, are measured using the calibrated thermocouples and a digital thermometer. Then average surface temperature of the tested cylinder, T_s, could be estimated, and the mean film temperature between the tested cylinder and the bed is hence calculated as:

$${T}_{mf}=({T}_{s}+{T}_{b})/2$$

(3)

The local heat transfer coefficients, h_θ and the corresponding local Nusselt numbers, Nu_θ, are calculated, respectively, as follows

$${h}_{\theta }=\frac{Q}{{A}_{s}\left({T}_{s,\theta }-{T}_{b}\right)}$$

(4)

$${Nu}_{\theta }=\frac{{h}_{\theta }{D}_{h}}{{K}_{a}}$$

(5)

The average Nusselt number, Nu, is calculated by integrating the local values of Nu_θ over the entire perimeter of the tested cylinder as:

$$Nu= {\int }_{-\pi }^{\pi }{Nu}_{\theta }{d}_{\theta }/2\pi$$

(6)

Moreover, the Reynolds number based on the hydraulic cylinder diameter, Re, is calculated from:

$$Re= \frac{{\rho }_{a}{U}_{\infty }{D}_{h}}{{\mu }_{a}}$$

(7)

Archimedes number

$$Ar= \frac{g {\rho }_{g}({\rho }_{s}-{\rho }_{g}){d}_{p}^{3} }{{\mu }_{g}^{2}}$$

(8)

The thermophysical properties of the air are obtained at the mean film temperature, T_mf, [32] whereas the solid phase properties are illustrated in Table (1).

2.1 Measurements’ uncertainties

The experimental error analysis indicates the implication of error of the measured parameters on the uncertainty of the results. A detailed analysis of the various experimental uncertainties is carried out using the differential approximation method for error analysis [33]. The maximum uncertainties occurred in measuring parameters involved are presented in Table (2) and their detailed calculations are listed in Appendix (6).

3 Results

3.1 Minimum fluidization velocity

The minimum fluidization velocity can be estimated from the pressure drop versus superficial velocity diagrams as shown in Figs. (4) and (5) for particle size, d_p = 6 mm for the inline and staggered bed geometries. In these figures, the minimum fluidization velocity, U_mf, is located at the point when the superficial velocity is increased, and pressure drop becomes constant. From these figures it is depicted that, the minimum fluidization velocity is independent of the bed configuration. With this method, the minimum fluidization velocity of the particles for different bed geometries are determined.

The experimental values of U_mf are compared with those calculated using well-known published correlations. It is found that, the present data agree with predictions from Shaul et al. [34] correlation within ± 10% as shown in Fig. (6).

$${U}_{mf}=\frac{{\mu }_{g}}{{d}_{p}{\rho }_{g}}\left[0.059{Ar}^{0.56}\right]$$

(9)

It has been also found that, the minimum fluidization velocity increased with the increase in particle sizes, and this agree with the previous results of Taofeeq et al. [35].

3.2 Local heat transfer

The variation of the local Nusselt numbers, with the angular position around the heated tube circumference, for various fluidization numbers N, is presented in this section. For both inline and staggered tube bundles immersed in a fluidized bed, variations of the local Nusselt number with N are shown in Figs. (7, 8, 9, 10, 11, 12) for particle mean diameters, dp, of 2, 4, and 6 mm, respectively. The values of Nu_θ at eight angular positions, from 0° to ± 180° with 45° increments, are all considered in these figures. Generally, these figures demonstrate that the local Nusselt number is increased with increasing the Reynolds number. It is also noticed that the local Nusselt number distribution on the right (positive θ) and left (negative θ) sides of the heated cylinders is satisfactorily symmetric for all the fluidization numbers. Figure (7) shows only moderate variations of Nu value around the surface of tube with the angular position of the elliptic tube bundles immersed in the fluidized bed. Insignificant variations of Nu values are also noticeable from Figures from (8, 9, 10, 11, 12). At minimum fluidization velocity, the Nu_θ reaches its maximum value at the sides of the heated tube and minimum at the stagnation, θ = 0°, and top, θ = 180°, of the tube. This may be attributed to the occurrence of a region of motionless solid particles due to gas “pockets” before the stagnation point and a stagnant "caps" of defluidized solid particles at the top. With the increase of fluidization velocity, a steady increase in Nuθ is also quite noticeable at all angular locations, with the maximum value shifting towards the top edge location where more dynamic flow conditions presented and particle residence time shortens due to the rising bubbles. With further increase in the air velocity to the level where the bed become highly agitated, the variation of Nu_θ around the circumference becomes relatively negligible, and the distribution of the local coefficients along the circumference of tube becomes generally more uniform [17, 18 and 26]. The Nu_θ reaches its maximum value at staggered bundle immersed in the bed of smallest particles size, d_p = 2 mm, at higher end of the fluidizing velocity investigated. This is likely due to minimizing the zone of the defluidized cap caused by the proximity of the tubes and zigzag flow pattern of the air stream, and it is subjected to rapid changes at higher fluidization velocities [27]. Moreover, the local heat transfer at a particular angular position, decreases with larger solid particle diameter. The decrease of local heat transfer with the increase of particle size is mostly due to the decrease of particle surface area per unit volume of the bed that lead to less efficiency in exchanging heat with the surface, [36, 37].

3.3 Average heat transfer results

The average Nusselt number for elliptic tube bundles immersed in a fluidized bed of pulverized coal of particle sizes of 2, 4, 6 mm, is calculated using the present experimental data. Nusselt numbers, Nu, have been obtained by integrating the local Nusselt numbers over the entire circumference of the heated tube. The present experiments covered ranges of fluidization velocities corresponding to the particle sizes experimented with. It is considered therefor, more logic to express the results in terms of the fluidization number, (N = U_sup/ U_mf) instead of Re, in order to compare the experimental results which are in the range of 1:1.4, which is limited by the bed expansion. The experimental results are presented in terms of fluidization velocity and particle size influence on the average Nusselt number of tube bundles with equilateral pitch. Figures (13) through (17) show that, the average Nusselt number, Nu, increases as fluidization velocity increases for both inline and staggered tube bundles. This increase could be interpreted a result of convection conditions caused by rapid particles motion and the associated bed voidage. Also, the results show that the average Nusselt number, Nu increased with decrease of particle size. This is most likely due to the relatively larger contact area between particles and the tube surface, in addition to the increase in particle motion/hydrodynamics that in turn increases the particle convection which would increase for smaller particles. When comparing Fig. (15) and Fig. (17) at the low fluidization velocities, the activity of the particles in staggered bundle is observed to be more efficient than in inline bundle. Also, the size of stagnation region and defluidized cap are found somewhat smaller for the staggered tube bundle than for the cases of inline tube bundle because of the zigzag-shaped air flow passage Figs. (14) and (16) [27].

3.4 Comparison with previous work

Chen et al. [38] compared several different correlations against a set of experimental data for heat transfer in a fluidized bed and concluded that there is only little agreement among the various correlations, or between the correlations and experimental data with almost about 100% deviations. Despite empirical correlations are easy to use and may be rather appropriate for specific scale-up applications, their generality is questionable. The present data are compared therefore, with the closest previous published work of circular cylinders. Two of the available heat transfer correlations for Nu, are found to be close to reproduce the present experimental data. These are due Gelperin et al. [39] and Ainshtein et al. [40] as shown in Figs. (18), (19) and (20). 

4 Comparison with previous work

Gelperin et al. [39] correlation:

$$Nu=4.38{\left[\frac{1}{6\left(1-\varepsilon \right)}\left(\frac{{\rho }_{g}{U}_{sup}{d}_{p}}{{\mu }_{g}}\right)\right]}^{0.32}\left(\frac{1-\varepsilon }{\varepsilon }\right)\left(\frac{{D}_{h}}{{d}_{p}}\right)$$

(10)

Ainshtein et al. [40] correlation:

$$Nu=5.76\left(1-\varepsilon \right){\left(\frac{{\rho }_{g}{U}_{sup}{d}_{p}}{{\mu }_{g}\varepsilon }\right)}^{0.34}{\left(\frac{{Cp}_{g}{\mu }_{g}}{{K}_{g}}\right)}^{0.33}{\left(\frac{{H}_{bed}}{{D}_{bed}}\right)}^{0.16}\left(\frac{{D}_{h}}{{d}_{p}}\right)$$

(11)

These figures show that, the substitution in the above correlations (for circular tube) by the present data gives under predicted values of Nu compared with experimental values of Nu. Table (3) illustrates the relative percentage improvement in values of Nu estimated from the examined correlations compared to the experimentally estimated Nu considering the two tube bundle configurations and three particle sizes considered in the present work. It is clear from the above evaluation that the predictions examined here are inadequate for predicting wall-to-bed heat transfer from elliptic tube immersed in a fluidized bed of pure cold pulverized coal of large particle fluidized bed systems. This may be attributed to the different tube geometry and material properties [11].

4.1 Proposed correlations of the experimental results

The present experimental data are utilized to get empirical correlations in the form of dimensionless variables for the two cases (inline and staggered tube bundles). Average Nusselt number, Nu, is therefore, correlated with the fluidization number, U_sup/U_mf, and tested cylinder hydraulic diameter to particle diameter ratio using the least square method for curve fitting, and could hence, be expressed by the following closed-form equations:

- In line tubes:

$$Nu=224\left[{\left(\frac{{U}_{sup}}{{U}_{mf}}\right)}^{0.497}{\left(\frac{{D}_{h}}{{d}_{p}}\right)}^{0.076}\right]$$

(12)

For 1 ≤ U_sup/U_mf ≤ 1.4 and 4.2 ≤ D_h/d_p ≤ 12.65, with maximum error of “ ± 2%” as illustrated in Fig. (21).

- Staggered tubes:

$$Nu=190\left[{\left(\frac{{U}_{sup}}{{U}_{mf}}\right)}^{0.745}{\left(\frac{{D}_{h}}{{d}_{p}}\right)}^{0.17}\right]$$

(13)

For 1 ≤ U_sup/U_mf ≤ 1.4 and 4.2 ≤ D_h/d_p ≤ 12.65, with maximum error of “ ± 5%” as illustrated in Fig. (22).

4.2 Validation of the present work

The present experimental results are checked and validated through comparison with the approximate CFD model simulations [41]. Pressure drop across the fluidized bed and the average Nusselt Number obtained from simulation of the same case of d_p = 2 mm are compared to those of the present experimental measurements as illustrated in Figs. 23 through 26. The simulations were found to predict pressure drop values for all fluidization numbers, with deviations of about 3 to 4 percent from the measured corresponding values, for both inline and staggered tube bundle arrangements, as depicted in Figs. 23 and 24. Also, the experimental and analytically-predicted average Nusselt Numbers are presented versus fluidization numbers as seen in Figs. 25 and 26. These figures exhibit good qualitative as well as quantitative agreements between numerical predictions of the average Nusselt numbers with the experimental ones within an experimental scatter limit of less than 5% throughout.

Fig. 1

The experimental set-up

Fig. 2

Tube bundle configurations

Fig. 3

Details of the elliptical cylinder

Fig. 4

Bed pressure drop versus superficial velocity for the inline arrangement tube immersed in pulverized coal particles of d_p = 6 mm

Fig. 5

Bed pressure drop versus superficial velocity for the staggered arrangement tubes immersed in pulverized coal particles of d_p = 6 mm

Fig. 6

Comparison between measured minimum fluidization velocity with correlations in the literature for different particle sizes and bed geometries

Fig. 7

Variation of Nu_θ versus θ from stagnation point for an inline tube bundle immersed in a bed of d_p = 2 mm

Fig. 8

Variation of Nu_θ versus θ from stagnation point for an inline tube bundle immersed in a bed of d_p = 4 mm

Fig. 9

Variation of Nu_θversus θ from stagnation point for an inline tube bundle immersed in a bed of d_p = 6 mm

Fig. 10

Variation of Nu_θ versus θ from stagnation point for a staggered tube bundle immersed in a bed of d_p = 2 mm

Fig. 11

Variation of the Nu_θ versus θ from stagnation point for a staggered tube bundle immersed in a bed of d_p = 4 mm

Fig. 12

Variation of the Nu_θ versus θ from stagnation point for a staggered tube bundle immersed in a bed of d_p = 6 mm

Fig. 13

Effect of fluidization velocity and particle size on average Nu (Inline tube bundle)

Fig. 14

Effect of fluidization velocity and particle size on average Nu

Fig. 15

Effect of fluidization velocity on average Nu (Particle size of 2 mm)

Fig. 16

Effect of fluidization velocity on average Nu (Particle size of 4 mm)

Fig. 17

Effect of fluidization velocity on average Nu (Particle size of 6 mm)

Fig. 18

Comparison between present data for average Nusselt number, Nu, of inline and staggered tube bundles immersed in a bed of d_p = 2 mm with that of Gelperin [39] and Ainshtein [40] correlations for circular tubes

Fig. 19

Comparison between present data for average Nusselt number, Nu, of inline and staggered tube bundles immersed in a bed of d_p = 4 mm with that of Gelperin [39] and Ainshtein [40] correlations for circular tubes

Fig. 20

Comparison between present data for average Nusselt number, Nu, of inline and staggered tube bundles immersed in a bed of d_p = 6 mm with that of Gelperin [39] and Ainshtein [40] correlations for circular tubes

Fig. 21

Comparison between the experimental and predicted values of the Nusselt number for inline tube bundle

Fig. 22

Comparison between the experimental and predicted values of the Nusselt number for staggered tube bundle

Fig. 23

Comparison between simulation and experimental data of pressure drop for inline tubes bundle with bed size, d_p = 2 mm

Fig. 24

Comparison between simulation and experimental data of pressure drop for staggered tubes bundle with bed size, d_p = 2 mm

Fig. 25

Comparison between predicted and experimental average Nusselt values for inline tube bundle, with bed particles size, d_p = 2 mm

Fig. 26

Comparison between predicted and experimental average Nusselt values for staggered tube bundle, with particles size, d_p = 2 mm

Fig. 27

Effect of fluidization number and particle size, d_p on the bed expansion ratio for inline tubes bundle using Llop definition [43]

Fig. 28

Effect of fluidization number and particle size, d_p on the bed expansion ratio for staggered tube bundle using Llop definition [43]

Fig. 29

Effect of fluidization number and tubes configurations on the bed expansion ratio for bed particle size, d_p = 2 mm, Llop [43]

Fig. 30

Effect of fluidization number and tubes configurations on the bed expansion ratio for bed particle size, d_p = 4 mm, Llop [43]

Fig. 31

Effect of fluidization number and tubes configurations on the bed expansion ratio for bed particle size, d_p = 6 mm, Llop [43]

4.2.1 Bed expansion

Staub [42] proposes a definition for the expansion ratio as a relationship between the percentage of expansion and some effective linear dimensions, or heights which are independent of the superficial velocity. Llop et al. [43] used the minimum fluidization bed height, H_mf, as a reference height such that:

$$R\%=\frac{{H}_{f}-{H}_{mf}}{{H}_{mf}}$$

(14)

Figures (27) and (28) show that bed expansion is noticeably increased with increasing fluidization number. It can also, be observed that the bed expansion ratio for the smaller particle-size bed, d_p = 2 mm is relatively larger than that for the 4 and 6-mm sized particle ones, that is, finer particles provide higher degree of bed expansion ratios for both inline and staggered tube bundle configurations. Figures (29, 30 and 31) show that for all particle sizes used, the bed expansion ratio is a bit greater for inline bundle than the staggered one. This could be interpreted as for staggered-tube arrangement, the volume of air passing through the bundle may have become somewhat diminished because of the proximity of the tubes and due to the zigzag passage of air flow [27].

5 Conclusions

The afore-mentioned results and discussions of the present study led to the following concluding remarks:

• 1- The minimum fluidization velocity increases with the increase of the bed particle size.

• 2- The local Nusselt number around elliptic tubes is quasi-uniform and having a maximum value at the sides of the heated tube and minimum at the stagnation point, θ = 0°, and top, θ = 180°, of the tube.

• 3- The local and average Nusselt numbers increase with the increase of the fluidization velocity and decrease in particles’ diameter.

• 4- The percentage differential increase of the average Nusselt number between staggered and inline arrangements of the tube bundles is 26%, 11% and 8.6% for the particle diameters of 2, 4 and 6 mm respectively.

• 5- The average Nusselt number for the elliptic tube is higher than that of the circular tube bundle in inline arrangement by 123%, 87.5% and 32% for particle diameters of 6, 4 and 2 mm, respectively.

• 6- For the staggered tube bundle arrangement, the average Nusselt number is found to be 128%, 88% and 58% higher for the elliptic tube over the corresponding circular tube bundles for particle diameters of 6, 4 and 2 mm, respectively.

• 7- The average bed expansion is greater for the inline tube bundle if compared with that evaluated for the case of the staggered tube bundle because of the relative particle obstruction caused by the tubes.

• 8- Two empirical formulae have been deduced for the average Nu in terms of fluidization number and hydraulic to particle diameter ratio.

• 9- The elliptic tubes show, in general, a relatively better performance than the circular ones.

Table 1 Properties of solid phase used in the present study

Table 2 Uncertainties of the measured and derived quantities

Table 3 Relative improvement in % for values of Nu estimated from the previous correlations

Appendix (A) Uncertainty analysis

The average heat transfer coefficient is calculated by:

$$\mathrm{h}={q}_{conv}\,/ \,({T}_{s}-{T}_{b})$$

(15)

$$={Q}_{con}\, /\, {A}_{s}({T}_{s}-{T}_{b})W{m}^{2\circ }C$$

(16)

The maximum relative error of Nusselt number is determined by.

$$\begin{array}{c}|\mathrm{\delta Nu}{|}_{m}\hspace{0.17em}=|\mathrm{\delta h}{|}_{m}\hspace{0.17em}+|\updelta {\mathrm{D}}_{h}{|}_{m}\hspace{0.17em}+|\mathrm{\delta k}{|}_{m}\\ \mathrm{\delta h}{|}_{m}\hspace{0.17em}=|\updelta {\mathrm{Q }}_{conv}{|}_{m}\hspace{0.17em}+|\updelta {\mathrm{A}}_{s}{|}_{m}\hspace{0.17em}+|\updelta ({\mathrm{T}}_{s}-{\mathrm{T}}_{b}){|}_{m}\end{array}$$

(17)

where:

|δ Dh|m is the maximum relative error in hydraulic diameter of the heated tube.

|δk|m is the maximum relative error in air thermal conductivity.

|δ Qconv|m is the maximum relative error in heat transfer.

|δ As|m is the maximum relative error in the heated tube surface area

|δ(Ts-Tb)|m is the maximum relative error in temperature difference

Evaluation of this maximum relative error will be as follows:

1.1 Error in measuring the hydraulic diameter, D_h

$$|\updelta {\mathrm{D}}_{h} {|}_{m}\hspace{0.17em}=|\Delta {\mathrm{D}}_{h} {|}_{m} /| {\mathrm{D}}_{h} |$$

(18)

$$|\updelta {\mathrm{D}}_{h} {|}_{m}\hspace{0.17em}=\hspace{0.17em}(\mathrm{0.1/25.3})\hspace{0.17em}\times \hspace{0.17em}100=0.40\%$$

(19)

1.2 Error in measuring surface area, A_s

$$\begin{array}{c}|\updelta {\mathrm{A}}_{s}{|}_{m}\hspace{0.17em}=|{|}_{m}\hspace{0.17em}+|\Delta {\mathrm{D}}_{h}/{D}_{h}{|}_{m}\\ =\left(\frac{1}{200}+\frac{0.1}{25.3}\right)\times 100\\ =0.90\%\end{array}$$

(20)

1.3 Error in measuring temperature difference, ∆T

$$\begin{array}{c}|\updelta ({\mathrm{T}}_{s}-{\mathrm{T}}_{b})|\mathrm{m}\frac{|\Delta {T}_{s}{|}_{m}+|\Delta {T}_{b}{|}_{m}}{|{T}_{s}-{T}_{b}|}\\ \left|\Delta {T}_{s}\right|=0.1\\ \begin{array}{c}|\updelta \left({T}_{s}-{T}_{b}\right){|}_{m}=(0.1+0.1)/40]\times 100\\ =0.50\%\end{array}\end{array}$$

(21)

1.4 Error in measuring heat transferred, Q

The maximum relative error in measuring the heat transferred is given by:

$$|\updelta (\mathrm{Q}){|}_{m}\hspace{0.17em}=|\frac{\Delta I}{I}{|}_{m}\hspace{0.17em}+|\frac{\Delta V}{V}{|}_{m}$$

(22)

$$=(\frac{0.1}{5}+\frac{0.5}{40})\times 100$$

$$=3.25\mathrm{\%}$$

|δ h|_m =|δ Q|_m +|δ A_s|_m +|δ (T_s-T_b)|_m

|δ h|_m = 3.25% + 0.9% + 0.50% = 4.65%

Finally, the maximum relative error in calculating Nusselt number will be equal to:

$$|\mathrm{\delta Nu}{|}_{m}\hspace{0.17em}=|\mathrm{\delta h}{|}_{m}\hspace{0.17em}+|\updelta {\mathrm{D}}_{h}{|}_{m}$$

(23)

$$|\mathrm{\delta Nu}{|}_{m}=4.65\mathrm{\%}+0.4\mathrm{\%}$$

$$=5.05\mathrm{\%}$$

1.5 Error in measuring Reynolds number, Re

The maximum error in the estimation of Reynolds number is:

$$|\mathrm{\delta Re}{|}_{m}\hspace{0.17em}=|\updelta {\mathrm{U}}_{sup}{|}_{m}\hspace{0.17em}+|\updelta {\mathrm{D}}_{h}{|}_{m}$$

(24)

$$|\mathrm{\delta Re}{|}_{m}={0.5}^{*}|\updelta \Delta \mathrm{h}{|}_{m}+|\updelta {\mathrm{D}}_{h}{|}_{m}$$

$$|\mathrm{\delta Re}{|}_{m}={0.5}^{*}(0.58)\times 100+0.4\mathrm{\%}=3.53\mathrm{\%}$$

1.6 Error in measuring pressure drop

The difference in pressure between the unknown pressure P and the atmosphere is determined as a function of the differential height Δh of the U-tube manometer. So, the uncertainty of the column height measurement is calculated as follow:

$$\begin{array}{c}|\delta P{|}_{m}=|\delta \cdot \Delta {|}_{m}\\ =(0.5/23{)}^{*}100=2.17\mathrm{\%}\end{array}$$

(25)