1 Introduction

Wood is a strongly anisotropic material with moisture- and temperature-dependent properties. Comprehensive descriptions on the physical characteristics of wood can be found in e.g. [1] and [2]. To predict the performance, damage, durability or bearing capacity of wooden structures, models are needed, which are capable to describe the multiphysical transport processes as well as the elastic, plastic, viscous and fracture behaviour. Beside other application fields, especially wooden artwork shall be protected from even small cracks and damage. Damage of wooden artwork is often caused by large changes of climatic conditions, e.g. inappropriately conditioned exhibition or storage locations and during transport. The climatic conditions of the environment have large impact on the mechanical features. Environmental moisture and temperature changes affect the state of moisture and temperature in the material and lead to transport processes in the wood continuum. Moisture is found in wood at three states of aggregation: fluid water and water vapour in the lumens as well as bound water in the cell walls. The phases exhibit different diffusion properties. In most cases, wood is not exposed to fluid water, therefore, many descriptions of water transport do not consider this phase. Inside wood, exchange processes take place between these phases of water. Bound water is the phase that directly influences the structural deformation and mechanical behaviour. Adsorption and desorption of moisture cause swelling and shrinking. Furthermore, moisture affects the mechanical behaviour, e.g. by moisture-dependent elasticity and strength characteristics. In addition, mechano-sorptive creep takes place. For complex structures, transient moisture transport yields extensive deformations and stresses due to moisture gradients and, thereby, different degrees of swelling and shrinking and moisture-dependent mechanical properties in the same sample. Additionally, temperature influences the mechanical behaviour of wood, but mostly indirectly by affecting moisture transport. During sorption, heat is absorbed or emitted. The saturation vapour pressure as well as the equilibrium of bound water and water vapour pressure are temperature-dependent. Also moisture diffusion is influenced by temperature. Beside the indirect influence of temperature on the mechanical behaviour, deformation due to thermal expansion and temperature-dependent elasticity and strength properties is observed, but the influence is relatively small. In complex structures, transient heat transport processes yield temperature gradients, different degrees of thermal expansion in a structure and, thus, stresses and deformations. To simulate the coupling of mechanical behaviour, moisture and heat transport, thermo-hygro-mechanical modelling is required.

For the non-linear numerical analysis of complex structures, the Finite Element Method (FEM) evolved in the last decades. By the spatial discretisation of a structure with an assemblage of elements with simple geometries, approximate solutions can be achieved for the whole complex structure. This method can be applied with respect to the mechanical behaviour as well as to transport processes. It also can be used for coupled analyses, computing the multiphysical solution simultaneously. This is reasonable, since the different physical processes depend on each other.

Up to now, modelling of the mechanical behaviour and transport processes in wood and the simulation by the FEM have been subject of intensive research. Approaches are available considering the coupling of mechanical behaviour and moisture transport of wood, e. g. [ 3, 4, 5, 6]. Many of them include moisture as one single-phase, but [7] shows the inadequacy of single-phase moisture description whenever no instant equilibrium of water vapour and bound water is present. Therefore, a two-phase moisture transport model is discussed by Frandsen et al. in [11] including approaches for phase transition and sorption hysteresis. Based on the model presented by Frandsen et al. a coupled two-phase hygro-mechanical formulation is presented in [11] and applied to the analysis of a panel painting in [12]. In the publications [13] and [13], hygro-thermally coupled moisture and heat transport are described by two moisture phases and temperature as third physical field. In the publication at hand, a new thermo-hygro-mechanically coupled three-dimensional model with degrees of freedom for displacements, two moisture phases, i.e. bound water and water vapour, and temperature is presented as well as the implementation into a monolithic solution algorithm within the FEM. It combines the advantages of the hygro-mechanical descriptions in [14] and the multi-physical moisture- and heat-transport formulations in [14] and [8,9,10]. For the mechanical part, elastic behaviour without time-dependent mechanical effects is considered. By coupling of models for two moisture phases and temperature to the mechanical formulation, the presented description is expected to improve the numerical analysis of wood at transient changes of moisture and temperature significantly. Moisture and heat transport are expected to influence the stress- and strain-state significantly so that a thermo-hygro-mechanical simulation is necessary for the damage analysis of climatically loaded wood.

In the present article, modelling of the mechanical behaviour and moisture- and heat-transport is described. At first, the physical background and the mathematical description are introduced and the required model parameters are identified. Subsequently, the algorithmic implementation into the in-house FE-software WoodFEM is introduced. The model is verified and validated by comparing simulation results to several experimental data. Furthermore, the material model is applied to analyse the structure of a panel painting by L. Cranach the Elder.

2 Constitutive thermo-hygro-mechanical model for wood

2.1 Balance equations

The 3D mechanical sub-model includes three degrees of freedom, i.e. the displacement vector \(u=\left[ u_x,u_y,u_z\right] ^{T}\). For moisture transport, as mentioned before, two phases are considered, which are represented in the model by the concentration of bound water \(c_b\) and the water vapour pressure \(p_v\). Water vapour pressure correlates with the concentration of water vapour \(c_v=M_{H_2O}/(R\cdot T)\cdot \varphi \cdot p_v\), where \(M_{H_2O}\) is the molar mass of water, R the gaseous constant, T the temperature and \(\varphi\) the porosity, i.e. the fraction of pore volume filled with air. To analyse the mechanical state, moisture and heat flux, the balance equations of momentum Eq. (1), mass (Eqs. (2) and (3)) and energy Eq. (4)

$$\begin{aligned} 0=\rho \, b+ \frac{\partial }{\partial {\varvec{x}}}\cdot {{\underline{\varvec{\sigma }}}}, \end{aligned}$$
(1)
$$\begin{aligned} 0=\frac{\mathrm {d}c_b}{\mathrm {d}t}+\frac{\partial }{\partial {\varvec{x}}}\cdot {\varvec{J}}_b-\dot{c}, \end{aligned}$$
(2)
$$\begin{aligned} 0=\frac{\mathrm {d}}{\mathrm {d}t}\frac{M_{H_2O}}{R\, T}\,\varphi \, p_v+\frac{\partial }{\partial {\varvec{x}}}\cdot {\varvec{J}}_v+\dot{c}, \end{aligned}$$
(3)
$$\begin{aligned} 0=\frac{\mathrm {d}\rho e}{\mathrm {d}t}+\frac{\partial }{\partial {\varvec{x}}}\cdot {\varvec{J}}_{\vartheta }-\rho b +\frac{\partial }{\partial {\varvec{x}}}\cdot {\varvec{J}}_b\bar{h}_b+\frac{\partial }{\partial {\varvec{x}}}\cdot {\varvec{J}}_v h_v+\dot{c}(h_b-h_v) \end{aligned}$$
(4)

have to be evaluated with

\(\dot{c}\)

sorption rate,

e

specific internal energy,

b

external energy source per mass unit,

\({\varvec{J}}_{\vartheta }\)

heat flux,

\(h_b\), \(h_v\)

specific enthalpy of bound water and water vapour,

\((h_v-h_b)\)

specific enthalpy of the phase transition,

\(\bar{h}_b\)

average enthalpy of bound water.

It has to be noted, that Eqs. (1) to (4) do not consider any inertia phenomena and strain rate dependencies, which is reasonable for the analysis of climatically loaded wood.

2.2 Constitutive equations

2.2.1 Elasticity

The total strain tensor \({{\underline{\varvec{\varepsilon }}}}=\partial {\varvec{u}}/\partial {\varvec{x}}\) is in case of wood typically split additively into

$$\begin{aligned} {{\underline{\varvec{\varepsilon }}}}={{\underline{\varvec{\varepsilon }}}}^{mech}+{{\underline{\varvec{\varepsilon }}}}^{m}+{{\underline{\varvec{\varepsilon }}}}^{\vartheta } \end{aligned}$$
(5)

with the components of mechanical strain \({{\underline{\varvec{\varepsilon }}}}^{mech}\), swelling and shrinking \({{\underline{\varvec{\varepsilon }}}}^{m}\) and thermal expansion \({{\underline{\varvec{\varepsilon }}}}^{\vartheta }\). The elastic stress-strain-relation is described by Hooke’s law

$$\begin{aligned} {{\underline{\varvec{\sigma }}}}={{\underline{\underline{\varvec{C}}}}}:{{\underline{\varvec{\varepsilon }}}}^{el} \end{aligned}$$
(6)

with the material tensor \({{\underline{\underline{\varvec{C}}}}}\). In the paper at hand, only elastic material features are considered for simplicity. In this case, \({{\underline{\varvec{\varepsilon }}}}^{mech}\) equals the elastic strain \({{\underline{\varvec{\varepsilon }}}}^{el}\). The approach can easily be expanded to plastic and viscous behaviour. The consideration of plastic strain is described in [15], viscous and mechano-sorptive creep are accounted for in [6].

Swelling and shrinking are calculated by

$$\begin{aligned} {{\underline{\varvec{\varepsilon }}}}^{m}={{\underline{\varvec{\beta }}}}\cdot \Delta m_b \end{aligned}$$
(7)

with the shrinking tensor \({{\underline{\varvec{\beta }}}}\) and the moisture increment \(\Delta m_b\). Thermal expansion is calculated by

$$\begin{aligned} {{\underline{\varvec{\varepsilon }}}}^{\vartheta }={{\underline{\varvec{\alpha }}}}\cdot \Delta T \end{aligned}$$
(8)

with the thermal expansion tensor \({{\underline{\varvec{\alpha }}}}\) and the temperature increment \(\Delta T\).

2.2.2 Moisture

Based on Fick’s first law, moisture flux is given as

$$\begin{aligned} {\varvec{J}}_b=-{{\underline{\varvec{D}}}}_b\cdot \frac{\partial c_b}{\partial \varvec{x}}-{{\underline{\varvec{D}}}}_{bT}\cdot \frac{\partial T}{\partial \varvec{x}} \end{aligned}$$
(9)

for bound water diffusion and

$$\begin{aligned} {\varvec{J}}_v=-{{\underline{\varvec{D}}}}_v\frac{M_{H_2O}}{R\,T}\cdot \left( \frac{\partial p_v}{\partial {\varvec{x}}}\,\varphi -\frac{p_v}{T}\,\frac{\partial T}{\partial {\varvec{x}}}\,\varphi +p_v\,\frac{\partial \varphi }{\partial c_b}\,\frac{\partial c_b}{\partial {\varvec{x}}}\right) -{{\underline{\varvec{D}}}}_{vT}\cdot \frac{\partial T}{\partial {\varvec{x}}} \end{aligned}$$
(10)

for water vapour diffusion. In Eqs. (9) and (10), the first term describes the diffusion driven by the gradient of concentration according to Fick’s first law. The second term describes the Soret-effect, i.e. moisture diffusion driven by the gradient of temperature. This formulation is derived in [10].

2.2.3 Heat

Heat flux is described by Fourier’s law as

$$\begin{aligned} {\varvec{J}}_{\vartheta }=-{{\underline{\varvec{K}}}}\cdot \frac{\partial T}{\partial \varvec{x}}. \end{aligned}$$
(11)

The conduction process with the conduction tensor \({{\underline{\varvec{K}}}}\) is driven by the gradient of the temperature.

2.3 Boundary conditions

At the faces of a specimen, boundary conditions allow for moisture and heat exchange. For a realistic simulation of the exchange process, the boundary layer theory (BLT) is used considering the flow properties of the ambient air. A model for mass- and heat-flux is given in [16]. Moisture flux

$$\begin{aligned} \phi _v=-k_v\,(c_v^s-c_v^{\infty })=-k_v\,(p_v^s-p_v^{\infty })\,\frac{M_{H_2O}}{R\,T} \end{aligned}$$
(12)

and heat flux

$$\begin{aligned} \phi _{\vartheta }=-k_\vartheta \,(T^s-T^{\infty }) \end{aligned}$$
(13)

through the surface are driven by the difference of water vapour concentration or temperature between the surface and the ambient air. The emission parameters

$$\begin{aligned} \bar{k}_v=\frac{0.66\,D_a\,Re^{0.5}\,Sc^{0.33}}{L}, \end{aligned}$$
(14)
$$\begin{aligned} \bar{k}_\vartheta =\frac{0.66\,K_a\,Re^{0.5}\,Pr^{0.33}}{L} \end{aligned}$$
(15)

consider the properties of the air by use of the diffusion and conduction in air, \(D_a\) and \(K_a\), the Reynold-number Re, the Schmidt-number Sc and the Prandtl-number Pr, as well as the stream properties of the boundary layer by use of Re.

2.4 Algorithmic implementation

To solve the non-linear partial differential balance equations numerically, weak forms of these equations are required. Employing the principle of virtual displacements, applying the divergence theorem and spatial and time discretization leads in combination with the constitutive equations to

$$\begin{aligned} {\varvec{F^{nr}}}&=\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\underline{\varvec{C}}}}}:\left( \frac{\partial {\varvec{u}}}{\partial {\varvec{x}}}-{{\underline{\varvec{\varepsilon }}}}^{m}-{{\underline{\varvec{\varepsilon }}}}^{\vartheta }\right) \,\mathrm {d}V-\int _{V}N\,\rho {\varvec{b}}\,\mathrm {d}V-\int _{S}N\,{\varvec{t}}\,\mathrm {d}S, \end{aligned}$$
(16)
$$\begin{aligned} \begin{aligned} F_{c_b}=\;&\frac{1}{\Delta t}\int _{V}N\left( c_{b,t}-c_{b,t-\Delta t}\right) \,\mathrm {d}V + \int _{V}\frac{\partial N}{\partial {\varvec{x}}} \cdot {{\underline{\varvec{D}}}}_b\cdot \frac{\partial c_b}{\partial {\varvec{x}}}\,\mathrm {d}V \\&+ \int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{D}}}}_{bT}\cdot \frac{\partial T}{\partial {\varvec{x}}}\,\mathrm {d}V - \int _{V}N\,\dot{c}\,dV-\int _{S}N\,\phi _b\,\mathrm {d}S, \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned} \begin{aligned} F_{p_v}=&\frac{1}{\Delta t}\int _{V}N\left( \left( \frac{p_v\,\varphi }{T}\right) _{t}- \left( \frac{p_v\,\varphi }{T}\right) _{t-\Delta t}\right) T\,\mathrm {d}V + \int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{D}}}}_{vT}\cdot \frac{\partial T}{\partial {\varvec{x}}}\,\frac{R\,T}{M_{H_2O}}\,\mathrm {d}V \\&+\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{D}}}}_v\cdot \left( \frac{\partial p_v}{\partial {\varvec{x}}}\,\varphi -\frac{1}{T}\,\frac{\partial T}{\partial {\varvec{x}}}\,p_v\,\varphi +\frac{\partial \varphi }{\partial c_b}\frac{\partial c_b}{\partial {\varvec{x}}}\,p_v\right) \mathrm {d}V\\&+\int _{V}N\,\dot{c}\,\frac{RT}{M_{H_2O}}\,\mathrm {d}V-\int _{S}N\,\phi _v\,\frac{RT}{M_{H_2O}}\,\mathrm {d}S, \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned} \begin{aligned} F_T=&\frac{1}{\Delta t}\int _{V}N\,\left( h_b\,c_b+h_v\,p_v\,\varphi \,\frac{M_{H_2O}}{R\,T}+\rho _0\,h_0\right) \mathrm {d}V+\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{K}}}}\cdot \frac{\partial T}{\partial {\varvec{x}}}\,\mathrm {d}V \\&+\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot \left( {{\underline{\varvec{D}}}}_b\cdot \frac{\partial c_b}{\partial {\varvec{x}}}+{{\underline{\varvec{D}}}}_{bT}\cdot \frac{\partial T}{\partial {\varvec{x}}}\right) \left( \frac{\partial h_b}{\partial T}\,T+\frac{\partial h_b}{\partial c_b}\,c_b\right) \,\mathrm {d}V\\&+\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{D}}}}_v\cdot \left( \frac{\partial p_v}{\partial {\varvec{x}}}\,\varphi -\frac{1}{T}\,\frac{\partial T}{\partial {\varvec{x}}}\,p_v\,\varphi +\frac{\partial \varphi }{\partial c_b}\frac{\partial c_b}{\partial {\varvec{x}}}\,p_v\right) \frac{M_{H_2O}}{RT}\frac{\partial h_v}{\partial T}\,T\,\mathrm {d}V\\&+\int _{V}\frac{\partial N}{\partial {\varvec{x}}}\cdot {{\underline{\varvec{D}}}}_{vT}\cdot \frac{\partial T}{\partial {\varvec{x}}}\frac{\partial h_v}{\partial T}\,T\,\mathrm {d}V \\&+\int _{V}N\,\dot{c}(h_b-h_v)\,\mathrm {d}V-\int _{S}N\,\phi _{\vartheta }\,\mathrm {d}S-\int _{S}N\,\phi _v\, h_v\, \mathrm {d}S. \end{aligned} \end{aligned}$$
(19)

In contrast to previous approaches, in the publication at hand, the solution is computed by the monolithic solution of a fully coupled system of all six equations, i.e. three mechanical Eq. 16, two mass balance Eqs. 17 and 18, and one heat balance Eq. 19. For the solution of the non-linear equations, the Newton-Raphson-Method is used. Therefore, the derivatives of Eqs. (16) to (19) with respect to the degrees of freedom have to be computed. Linearization yields the overall equation system

$$\begin{aligned} \begin{bmatrix} {\varvec{K}}_{{\varvec{u}},{\varvec{u}}} &{}{\varvec{K}}_{{\varvec{u}},c_b} &{}{\varvec{0}}&{}{\varvec{K}}_{{\varvec{u}},T}\\ {\varvec{0}} &{}K_{c_b,c_b} &{}K_{c_b,p_v}&{}K_{c_b,T}\\ {\varvec{0}} &{}K_{p_v,c_b} &{}K_{p_v,p_v}&{}K_{p_v,T}\\ {\varvec{0}} &{}K_{T,c_b} &{}K_{T,p_v} &{}K_{T,T}\\ \end{bmatrix} \begin{bmatrix} {\varvec{u}}\\ c_b\\ p_v\\ T\\ \end{bmatrix} = \begin{bmatrix} {\varvec{F}}^{apl}\\ 0\\ 0\\ 0\\ \end{bmatrix} - \begin{bmatrix} {\varvec{F}}^{nr}\\ F_{c_b}\\ F_{p_v}\\ F_T\\ \end{bmatrix}, \end{aligned}$$
(20)

where the entries of the tangential matrix on the left hand side are given as \(K_{i,j}=\partial F_i/\partial j\) for \(i,j \in [{\varvec{u}},c_b,p_v,T]\). The term \({\varvec{F}}^{apl}\) on the right-hand side marks the external mechanical loads. For time integration, a generalised trapezoidal method

$$\begin{aligned} u_n = u _{n-1} + \left( 1-\vartheta \right) \Delta t \cdot \dot{u}_{n-1}+\vartheta \Delta t \cdot \dot{u}_n \end{aligned}$$
(21)

is used. The index n indicates the values of the current time-step. The index \(n-1\) stands for the last time-step. By the parameter \(\vartheta\), the influence of the current and the last time-step on the computation of the increment is described.

For the modelling of wood samples, solid elements with 20 nodes and, for the surface modelling, surface elements with 8 nodes, both based on quadratic shape-functions, are used. By Gaußian quadrature, the equations are integrated numerically over the volume using 27 Gauss points or 9 in the case of surface elements.

2.5 Dependencies of physical properties

The coupling of the degrees of freedom, represented in Eq. 20 by the terms \(K_{i,j}\) with \(i\ne j\), arises on the one hand from the coupling terms of the Soret-effect, heat convection by moisture transport and the sorption rate in the heat balance equation, and, on the other hand, from material properties, which depend on the bound water concentration, water vapour pressure and temperature. An overview of material parameters and dependencies is given in Table 1.

Table 1 Parameters of the thermo-hygro-mechanical model and their dependencies on the state variables
Full size table

For the temperature- and history-dependency of the moisture equilibrium and different modelling approaches, see Fig. 1.

Fig. 1
figure 1

Sorption curves for a sequence of moistening and drying (0% RH \(\rightarrow\) 95% RH \(\rightarrow\) 40% RH \(\rightarrow\) 80% RH), comparison of the sorption models of (a) Hailwood-Horrobin [14, 21], (b) Avramidis [6, 22], (c) Patera [23], (d) Frandsen [9, 10, 14]

Full size image

3 Validation of the model

3.1 Validation of moisture transport

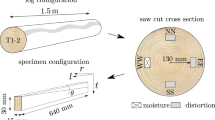
For the validation of moisture transport, an experiment of Wadsö [24], see also [8], is simulated. Figure 2 shows the specimen with material directions, dimensions and boundary conditions.

Fig. 2
figure 2

Test specimen of Wadsö [24] with (a) material directions, (b) dimensions and boundary conditions

Full size image

Four sides are coated to yield one-dimensional moisture flow. Moisture and heat transfer are possible at the two opposite faces at \(x=0\) mm and \(x=16.2\) mm. The transfer is described by surface elements or by prescribing water vapour pressure and temperature at the surface nodes directly. In Table 2, dry density as well as thermal and hygrical expansion coefficients are given.

Table 2 Material parameters for the simulation of the experiment of Wadsö [24]
Full size table

In the original experiment in [24], the fractional weight increase due to moisture uptake is measured.

Three different moisture steps are conducted in [24]. Since the first step is just done for initial conditioning, only the second step, step B, from 54% RH to 75% RH, and the third step, step C, from 75% RH to 84% RH, are evaluated. Table 3 shows the experimental conditions.

Table 3 Boundary conditions for the experiment of Wadsö [24]
Full size table

For the simulations, the Hailwood-Horrobin-Isotherm [21] is used with the parameters taken from [8].

Fig. 3
figure 3

Validation of moisture transport, fractional weight increase of the specimen, comparison of experimental results by Wadsö [24] and simulation results of the presented model as well as of a single-phase model: (a) step B (54% to 75% RH), (b) step C (75% to 84% RH)

Full size image

In the experiment in [24], the fractional weight increase due to moisture uptake is measured. Figure 3 compares the experimental results to the simulation results of the presented model. A good agreement can be seen for both steps, step B and step C. As described in [24], a single phase moisture transport model shows larger discrepancies in step c.

In [8], a moisture diffusion model is validated by comparing the simulation results for the weight increase to the experimental results of [24]. With this model, the moisture distribution in the direction of diffusion is calculated and given for different time steps. Figure 4 compares the simulation results of the moisture distribution [8] and the model used in the publication at hand. In contrast to [8], the climatic conditions are considered by a boundary layer at air velocity \(v=3\,\mathrm {m\,s^{-1}}\) (see [8]) and are not prescribed directly for the boundary nodes. The porosity \(\varphi\) is supposed to be constant in [8], but dependent on the moisture content in here.

Fig. 4
figure 4

Comparison of the simulation results to simulations in [8] (-\(\cdot\)-\(\cdot\)): (a) moisture content \(m_b\), (b) temperature T and (c) relative humidity RH

Full size image

As supposed in [11], the slower wetting might result from a decreasing porosity with increasing moisture content. The results at the surfaces are close to the results in [8]. The compared results show differences in the middle of the specimen, which are a consequence of the faster diffusion in [8]. Figure 4b shows the temperature distribution of the experiment. At the beginning, the temperature is rising due to enthalpy gain induced by wetting. When sorption slows down, temperature returns to the temperature of ambient air.

3.2 Validation of heat transport

For the validation of heat transport, an experiment described in [25] is simulated. A beech wood specimen is heated and dried by increasing the temperature and decreasing the relative humidity in the ambient air. The specimen with the material directions and boundary conditions is shown in Fig. 5. Dry density as well as thermal and hygric expansion coefficients are given in Table 4.

Fig. 5
figure 5

Specimen for the experiment of [25] with (a) material directions, (b) dimensions and boundary conditions

Full size image
Table 4 Material parameters for the simulation of the experiment of Fleischhauer et al. [25]
Full size table

Solid-elements are used to represent the beech wood specimen and surface-elements to represent the boundary layer. In this simulation, the sorption isotherms of Avramidis are used, because the temperature dependency of the sorption is considered. The beech specimen is heated from \(20\,^\circ \text {C}\) to \(120\,^\circ \text {C}\) within 60 seconds. Then, this temperature is kept for 45 minutes. The initial moisture content is measured as 8 %, the final relative humidity is 0.1 %. This procedure results in a final moisture content of 0.01 % and an initial relative humidity of 75 %. The climatic conditions are also given in Table 5. For the ambient air, the flow characteristics are not given, but the convection parameters \(k_m=1\cdot 10^{-10} \mathrm {kg\,mm^{-2}s^{-1}}\) and \(k_{\vartheta }=15 \mathrm {kg\,s^{-3}K^{-1}}\) are documented in [25]. The parameter \(k_v\) is calculated as

$$\begin{aligned} k_v=\frac{R\cdot T}{M_{H_2O}\cdot p_v^{sat}}\cdot k_m. \end{aligned}$$
(22)
Table 5 Parameters for the simulation of the experiment of Fleischhauer et al. [25]
Full size table
Fig. 6
figure 6

Position of the evaluation points for the experiment of Fleischhauer et al. [25]

Full size image

During the experiment, the temperature is measured at five locations. The positions of the measuring points can be seen in Fig. 6. To compare the simulation results to the experimental results, the simulation is also evaluated at the five measuring points.

In Fig. 7, the simulations are compared to the experimental results of the temperature at the five indicated measuring points.

Fig. 7
figure 7

Heating experiment, temperature versus time at five measuring points, comparison of the experimental results in [25]: (a) MP1, (b) MP2, (c) MP3, (d) MP4, (e) MP5

Full size image

Since the simulation yields underestimated temperature using the calculation of the conduction tensor as in [18] and the convection parameters given in [25], these parameters are varied. It should be noted that the coefficients for the conductivity presented in [18] are valid for spruce, which is a softwood, while beech is a hardwood. Additionally, the regression polynomial is valid for temperatures just up to 80 %. In [20], the thermal conductivities

$$\begin{aligned} \lambda _R&=0.19958\,\mathrm {\frac{W}{m\cdot K}}+0.3321\cdot 10^{-3}\,\mathrm {\frac{W}{m\cdot K^2}}\cdot (T-273.15\,\mathrm {K}), \end{aligned}$$
(23)
$$\begin{aligned} \lambda _T&=0.19933\,\mathrm {\frac{W}{m\cdot K}}+0.18888\cdot 10^{-3}\,\mathrm {\frac{W}{m\cdot K^2}}\cdot (T-273.15\,\mathrm {K}),\end{aligned}$$
(24)
$$\begin{aligned} \lambda _L&=0.29937\,\mathrm {\frac{W}{m\cdot K}}+0.70147\cdot 10^{-3}\,\mathrm {\frac{W}{m\cdot K^2}}\cdot (T-273.15\,\mathrm {K}) \end{aligned}$$
(25)

are given for beech wood as functions of temperature. With this conductivity parameters, the simulation results are fitting well for point M01 and M03 at the surfaces in longitudinal direction. In the middle of the specimen, the temperature is underestimated. Therefore, another simulation with the same conduction parameters in every material direction is carried out. Here, the simulation results are in good agreement for the middle part of the specimen, but the temperatures for M01 and M03 are overestimated. For the surfaces with maximal and minimal y-coordinate, lower temperature is calculated than measured. Due to this fact, it is supposed, that realistic convection parameters have to be larger than given in [25]. In a third simulation, the thermal conductivities from [20] are used, and the convection parameters are fitted. This parameter set yields acceptable results, which are in the range of the results of the previous two simulations. Since the conduction parameter in longitudinal direction affects mainly points M01 and M03, but rarely the points in the middle, it seems reasonable to assume a smaller conduction parameter in longitudinal direction and a larger convection parameter in radial and tangential direction.

It can be seen, that the model is able to predict the temperature distribution versus time well for transient climatic conditions. It is evident, that the identification of material parameters and climatic conditions is important and has large impact on the prediction accuracy. In case of material parameters and boundary conditions, that cannot be clearly identified, data uncertainty has to be taken into account.

4 Discussion

For a full validation of the presented model, validation experiments would be necessary accounting for changes in moisture and temperature measuring moisture-distribution, temperature-distribution, stress and strain. Up to now, adequate experimental data are missing in the literature. However, a brief example is presented to show the necessity of considering heat transport in the hygro-mechanical model.

Fig. 8
figure 8

Specimen for comparison of hygro-mechanical and thermo-hygro-mechanical modelling, material directions, dimensions and boundary conditions

Full size image

Figure 8 shows the specimen of the simulated experiment, in Tables 6 and 7 material parameters and boundary conditions of the simulation are given.

Table 6 Parameters for the comparison simulation of hygro-mechanical and thermo-hygro-mechanical modelling
Full size table
Table 7 Boundary conditions for the comparison simulation of hygro-mechanical and thermo-hygro-mechanical modelling
Full size table

A 200 mm long piece of wood is loaded climatically by changes of relative humidity and temperature in the environment. Moisture and heat exchange take place at two faces, so that transport processes are one-dimensional in longitudinal direction. A drop of relative humidity from 85% RH to 20% RH and a temperature increase from 10°C to 40°C are simulated. Simulation results of the presented model and a two-phase hygro-mechanical model are depicted in Fig. 9. In the hygro-mechanical simulation, the temperature change is also considered, but at constant temperature distribution in the specimen.

Fig. 9
figure 9

Comparison of simulation results with hygro-mechanical (–) and thermo-hygro-mechanical (-\(\cdot\)-\(\cdot\)) modelling: (a) moisture distribution in longitudinal direction at several time steps, (b) maximum of normal stress in longitudinal direction

Full size image

It can be seen, that different moisture distributions result from the two approaches. The hygro-mechanical model predicts faster transport, the thermo-hygro-mechanical model results in higher moisture gradients. As result of the climatic loading, also mechanical stresses occur, see Fig. 9b. The maximum stresses in longitudinal direction along the x-axis are presented. As can be seen, the discrepancy of both approaches is at some points about 70%. It must be noted, that the discrepancy might be higher in more complex structures consisting of several parts with different material properties and grain orientations, since moisture gradients exhibit a larger effect.

5 Investigation of a panel painting at climate changes

A panel painting of L. Cranach the Elder is simulated employing the presented models. The transient thermo-hygro-mechanically coupled analysis enables to evaluate the influence of climatic loads on complex structures. The chosen panel is the inner side of the left wing of the Katharinenaltar from 1506 (see [12]), shown in Fig. 10.

Fig. 10
figure 10

Katharinenaltar, left wing, inner side: (a) varnished front face, (b) back face with supporting framework (photograph by Hans Peter Kluth/Elke Estel, Staatliche Kunstsammlungen Dresden)

Full size image

The panel painting consists of nine bonded basswood (Tilia) panels, coated with a primer, several oil paints and a varnish layer. The on both sides originally coated altar wing has been sawn in an inner and an outer part, so that the thickness is now about 2.6 to 4 mm and the back side is uncoated. On the back, a support construction made of pine has been installed to stabilize the panel and minimise bending deformations. Due to constraining forces, caused by the massive supporting framework, different used wood types and fibre directions, the relatively rigid support construction led to damage of the panel and the paint layers. Therefore, the supporting framework has been removed in 2015 during restoration measures.

For the simulation, solid-elements with 20 nodes and a linear-elastic orthotropic material formulation are used. Since only few properties for basswood are published in literature, the properties of cherrywood, which can be found in [6], are used instead. For the support frame, the properties of spruce are taken instead of pine. This modification is appropriate, because the dry densities are similar and the properties are mainly dependent on the dry density. The coating is included in the front surface layer, modelled by surface-elements with 8 nodes. The finite element model is shown in Fig. 11, where the panel is depicted in grey and the support construction is shown in red and blue.

Fig. 11
figure 11

FEM model of the panel painting: (a) front face, (b) back face with the support construction in red and blue

Full size image

For the thermal convection parameter, the boundary layer theory is used. The properties of shellac are assumed for the hygric surface resistance at the front surface. The thickness-dependent permeability is given as \(P_t=3.08989\cdot 10^{-15}\mathrm {kg \,m^{-1}\,s^{-1}\,Pa^{-1}}\) (see [6]), the supposed thickness of \(t=50\,\mathrm {\mu m}\) leads to a permeability of \(P_p=6.1798\cdot 10^{-11}\mathrm {kg\,m^{-2}\,s^{-1}\,Pa^{-1}}\). The hygric convection parameter is calculated using the ideal gas equation as

$$\begin{aligned} k_v=P_p\cdot \frac{R\cdot T}{M_{H_2O}}. \end{aligned}$$
(26)

This characterisation is just taken for the coated front of the panel. For the other sides, a boundary layer is assumed with an air velocity of \(v=0.1\mathrm {m\,s^{-1}}\).

The climatic boundary conditions are shown in Fig. 12. Three climatic scenarios have been simulated, one cyclic humidity and temperature change and two single humidity changes at cyclic temperature change. For climate 1, the relative humidity, beginning at \(RH=65\,\%,\) changes alternating between 50 % and 80 %, simulating day night fluctuation. Temperature starts at 20 % and alternates with an amplitude of 4 %, while the temperature is overall increasing by 1 K per day. Climate 2 is a single change from \(RH=65\,\%\) to \(RH=80\,\%\). In climate 3, relative humidity also starts at \(RH=65\,\%\) and changes to \(RH=50\,\%\).

Fig. 12
figure 12

Simulation of the panel painting (10) at daily changing climatic conditions: (a) relative humidity and (b) temperature of ambient air versus time, (c) average moisture content, (d) displacement of the middle of the panel in z-direction

Full size image

Figure 12c and d show the results for the average concentration of bound water and the deflection of the middle of the panel painting. The change of the bound water concentration and the deflection follow the changes of the climatic conditions. It can be seen, that the moisture content does not reach equilibrium within 12 hours. The graph of the moisture just flattens when approaching equilibrium. Due to the overall increase of temperature, moisture is decreasing overall. The deflection results from the different material directions of the panel and the support construction. The x-direction equals to the tangential direction in the panel, but to the longitudinal direction in the support construction. Due to the different hygro-expansion coefficients of the material directions, much larger swelling and shrinking arises in the panel compared to the support beams in x-direction. Figure 12 shows also the deflection due to the single humidity changes of climate 2 and climate 3. It reveals, that also with constant relative humidity in the ambient air, oscillations result from the temperature changes, due to the temperature-dependent sorption equilibrium. Furthermore, constant relative humidity together with changing temperature yield changing water vapour pressure.

Figure 13 shows the deformed panel painting as well as temperature and moisture distribution after 118 h (dashed line in Fig. 12a and b), when a change from dry, warm to wet, cool climate takes place It can be seen, that the dependency of the temperature and moisture in the structure on the overall thickness of the panel is represented by the introduced approach. At the areas, where no support frame is connected to the panel, the cross-section is the thinnest, therefore, cooling is fastest. Most heat is buffered at the thickest parts of the panel. The back of the panel cools down faster than the front, due to the larger surface. Also, the moisture distribution depends on the thickness. Here, the overall drying shows the effect, that the points at the thickest cross-sections of the panel painting on the coated side are the wettest, due to the small permeability of the surface and the long diffusion distance through the material. The overall drying has to be considered instead of local change, because diffusion takes time and equilibrium is not reached at any of the moisture stages.

Fig. 13
figure 13

Simulation of the panel painting Eq. (10) at daily changing climatic conditions, evaluation at time \(t=118\,\mathrm {h}\) (dashed line in Fig. 12a and b), ten times scaled deformations, bound water concentration at the (a) front and (c) back of the panel and temperature at the (b) front and (d) back, displayed by colours

Full size image

In conclusion, it can be stated, that temperature influences moisture transport significantly and, thus, also the mechanical response of the panel painting. Sorption and diffusion are temperature-dependent processes. Simultaneously, moisture exchange affects temperature. Therefore, thermo-hygro-mechanical modelling seems to be reasonable and relevant.

6 Summary and conclusion

A new thermo-hygro-mechanically coupled monolithic FEM algorithm with multi-Fickian moisture transport is presented, which links models for two phase moisture transport, heat transport and mechanical behaviour of wood. The specific approaches are introduced and combined by an overall equation system for the monolithic computation of mechanical, thermal and hygrical states. The model is validated by one moisture transport experiment and one heat transport experiment. Both simulations show a good agreement with the experimental results. Therefore, it can be stated, that the model is able to well predict the transport processes individually. For the validation of coupling of transport processes and the mechanical response, experimental data are missing. But it can be seen, that results of thermo-hygro-mechanical simulations differ from results of hygro-mechanical simulations at combined moisture- and temperature load. Heat transport affects the moisture distribution and by this results in higher climate-induced stresses. Since the thermo-hygro-mechanical model considers in reality appearing heat transport, it is supposed to yield more realistic results than the hygro-mechanical model.

To illustrate a possible application of the introduced model, a panel painting of L. Cranach the Elder is simulated. Daily cycles of relative humidity and temperature are computed as climatic load. Moisture and temperature distribution as well as the deformation response of the panel painting are presented. The application of the model shows, that it is able to analyse also relatively complex structures at changing climatic conditions. The simulation results are reasonable. It is possible to estimate critical climatic conditions by evaluation of the mechanical response.

A huge need for experimental investigation of material properties can be seen due to large scattering of wood properties depending on the wood species, location and conditions of growth, moisture state, temperature, age and history. Furthermore, the uncertainty of wood properties (see e.g. [26]) has to be taken into account numerically as well. Moreover, the formulation can be extended by more phases, e.g. fluid water as in [27]. Finally, the application of further mechanical descriptions, like thermo-hygro-mechanically coupled fracture, plasticity (e.g. [15]), viscous creep and mechano-sorption (e.g. [28]) approaches has to be investigated.