An experimental test of the Mocikat-Herwig theory of local turbulent heat transfer measurements on cold objects

Abstract

Experimental results are presented of a test of the theory of local turbulent heat transfer measurements proposed by Mocikat and Herwig in 2007. A miniaturized multi-layer heat transfer sensor was developed and employed in this study. The new heat transfer sensor was designed to work in air and liquids, and this capability enabled the simultaneous investigation of different Prandtl numbers. Two basic configurations, namely the flow past a blunt plate and the flow past an inclined square cylinder, were investigated in test sections of wind and water tunnels. Convective heat transfer coefficients were obtained through conventional testing (i.e., employing thoroughly heated test objects) and using the new miniaturized sensor approach (i.e., utilizing cold test objects without heating). The main prediction of the Mocikat-Herwig theory that a specific thermal adjustment coefficient of the employed actual miniaturized heat transfer sensor should exist in the fully turbulent flow regime was proven for developed two-dimensional flow. The observed effect of the Prandtl number on this coefficient was in good agreement with the prediction of the asymptotic expansion method. The square cylinder results indicated the inherent limits of the local turbulent heat transfer measurement approach, as suggested by Mocikat and Herwig.

1 Introduction

Substantial efforts are required for determining experimentally convective heat transfer coefficients from fully heated test objects in high Reynolds and Prandtl number flows. Very high heating power levels are necessary for such a conventional approach, especially in liquids like water. Hence, it would be of great practical interest to avoid fully heated test objects and use only local heating to obtain the desired heat transfer coefficients. Although it is always possible to measure heat transfer rates from locally heated objects, it is believed that such locally determined heat transfer coefficients are not the same as values obtained for fully heated test objects. However, Mocikat and Herwig [1, 2] proposed in this journal in 2007 a unique approach using the results of an asymptotic study of turbulent heat transfer. Following their theory [1,2,3], it should be possible to obtain experimentally turbulent heat transfer coefficients through miniaturized heat transfer sensors placed on unheated objects using only local marginal heating. These heat transfer coefficients would be related to the desired values for fully heated test objects through a simple thermal adjustment coefficient, called TAC.

This approach was tested by Mocikat and Herwig [1, 2], employing a small foil sensor placed on a circular cylinder subjected to a stream of air. As known to the authors, no other independent test has been conducted so far. Mocikat and Herwig considered only a single configuration (circular cylinder), and the universality of their approach was not checked. Furthermore, the Mocikat-Herwig method would be desirable in the case of liquids, but they did not consider the impact of the Prandtl number on their approach in detail.

One additional remark might be helpful for some readers to avoid confusion. Although the present study is largely concerned with local heat transfer coefficients, the main objective was to answer the question if it is possible to obtain experimentally the heat transfer coefficients which are rigorously defined only for a fully heated object by measuring local heat transfer coefficients utilizing an unheated object. This is the vital item of the Mocikat-Herwig theory because it would avoid the need to apply substantial heating powers for test objects. In the case of small test objects or in several convective heat transfer experiments using air as working fluid, it is still feasible to apply the heating power necessary for achieving useful driving temperature differences for heat transfer measurements. However, especially for configurations using water as working fluid or at relatively high Reynolds numbers, it might by very hard – if not impossible – to apply sufficiently high heating power levels in the usual laboratory environments. Then, the possibility to conduct heat transfer experiments with cold objects would represent a major opportunity.

The present contribution presents the outcome of an independent test of the Mocikat-Herwig theory. The objective of this study was to assess the applicability of their idea for heat transfer measurements in air and water, and it was intended to identify potential practical limitations of their approach. Before the presentation of the results of this experimental study, the theoretical background of the asymptotic analysis and its consequence for heat transfer measurements in turbulent flows are briefly summarized. It will be shown that some limitations of this heat transfer measurement method exist in practical applications, which are directly related to mathematical details of the flow analysis.

2 Theory

The Mocikat-Herwig theory of local heat transfer measurements for turbulent flows rests on the asymptotic study of turbulent flows. The most important example of an asymptotic study is certainly given by the classical boundary layer theory [4,5,6]. In boundary layer theory, it is assumed that a thin boundary layer exists if the flow Reynolds number Re = u_m L ρ/µ is large, i. e. the asymptotic expansion Re → ∞ is considered [7]. The asymptotic analysis does not only provide a better understanding of flow phenomena, but it is often the starting point of relatively efficient numerical methods as well.

While asymptotic methods are frequently applied to laminar flows, much less is available regarding the asymptotic expansion of the Navier–Stokes equations and the thermal energy equation for turbulent flow in the high Reynolds number regime. In this section, some fundamentals about the asymptotic analysis are reviewed concerning the Mocikat-Herwig theory of local heat transfer measurements for turbulent flows.

2.1 Asymptotic structure of the flow field

A classical configuration for asymptotic studies is the entrance flow into a channel or a pipe. Laminar entrance flow in the high Reynolds number limit was studied by van Dyke in 1970 [8]. An asymptotic study (Re → ∞) of flow and convective heat transfer in the entrance regions of turbulent channel and pipe flows was performed by Voigt and Herwig in 1995 [9, 10]. Following their analysis, the basic equations for two-dimensional turbulent flow can be deduced from an asymptotic expansion of the Navier–Stokes equations. The solutions of these asymptotic equations are independent of the specific thermal boundary conditions. The effect of thermal boundary conditions is asymptotically a second-order effect in turbulent flows, in contrast to laminar flows.

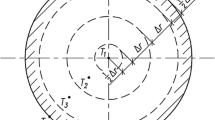
The turbulent entrance flow in channels and pipes is illustrated in Fig. 1. The mean inflow velocity in stream-wise direction x is denoted by u_m. The normal coordinate is n, and the local wall-normal coordinate is denoted by y. The characteristic length scale of the configuration is given by L. In the case of a plane channel, L is half of the total channel width. In the case of a pipe, L is the pipe radius. The developed turbulent flow is characterized by a viscous sub-layer and a turbulent core region [6, 7]. The separation of the flow domain into two different regions corresponds to a singular perturbation problem in terms of mathematics [7]. The mathematical formalism requires the introduction of a suitable perturbation parameter ε. The perturbation parameter has to be determined in the way that its value yields exactly the structure of the flow field as illustrated in Fig. 1, and the limit case Re → ∞ corresponds to ε → 0.

Fig. 1

Illustration of turbulent entrance flow

The singular structure of the flow field results from an expansion of the two-dimensional Reynolds-averaged Navier–Stokes equations concerning the perturbation parameter

$$\varepsilon =\frac{{u}_{\tau }}{{u}_{m}}=O\left(\frac{1}{\mathrm{lnRe}}\right)$$

(1)

with the local skin friction velocity, u_τ = (τ_w/ρ)^1/2, serving as scaling quantity [9, 11]. In the asymptotic analysis, the local skin friction τ_w is the given quantity, and the corresponding mean velocity u_m is the derived quantity. Then, the viscous sub-layer is that part of the flow field which is described by the primary expansion, and the turbulent core region is matched to the viscous sub-layer by a secondary expansion.

Without any specific turbulence modeling, the behavior of the viscous sub-layer u⁺  = y⁺ is universal for all wall-bounded flows (with non-zero shear stress), and the well-known logarithmic law

$${u}^{+}=\frac{1}{\kappa }\mathrm{ln}{y}^{+}+{C}^{+}$$

(2)

follows for y⁺  → ∞ [5, 6, 9, 10]. To get a solution that is independent of Re (as required for the limit case Re → ∞), the asymptotic expansion of the core region yields equations analogous to slender channel theory. The new coordinates of the slender channel type equations are

$${x}^{=}=\frac{x}{L}\varepsilon\quad and\quad {y}^{=}=\frac{n}{L}.$$

(3)

The momentum equation reduces in lowest order to

$$\frac{\partial {u}^{=}}{\partial {x}^{=}}=\frac{\partial {\tau }_{t}{}^{+}}{\partial \left(n/L\right)}-{\left.\frac{\partial {\tau }_{t}{}^{+}}{\partial \left(n/L\right)}\right|}_{c}+O({\varepsilon }^{2})$$

(4)

with a slender channel type velocity

$${u}^{=}=\frac{{u}_{c}-u}{{u}_{\tau }}+\frac{1}{\kappa }\mathrm{ln}\left(1-n/L\right),$$

(5)

and turbulent shear stress, which is normalized through the wall shear stress [9, 10]. Interestingly, the slender channel type equation is formally equivalent to a boundary layer equation after multiplying it with the perturbation parameter ε. Equation (4) covers the entire stream-wise coordinate range, i.e., from the entrance region up to the fully developed turbulent flow region. In the limit case Re → ∞, no extra expansion is necessary for the turbulent entrance flow. This is in strong contrast to laminar flow, where the entrance region is strictly different from the fully developed flow region.

2.2 Convective heat transfer

The above treatment can be extended to include the temperature field in a Newtonian incompressible flow with constant material properties. A characteristic temperature is the local skin friction temperature

$${T}_{\tau }=-\frac{{q}_{w}}{\rho {c}_{p}{u}_{\tau }}$$

(6)

defined by the skin friction velocity u_τ> and the wall heat flux q_w. Introducing the normalized temperature

$$\theta =\frac{T-{T}_{w}}{{T}_{\tau }}$$

(7)

leads to the universal turbulent temperature distributions

$$\begin{array}{cc}{y}^{+}=0:& \theta ={\mathrm{Pr}\;}{y}^{+}\\ {y}^{+}\to \infty :& \theta =\frac{1}{{\kappa }_{\theta }}{\mathrm{ln}\;}{y}^{+}+{C}_{\theta }^{+}\end{array}$$

(8)

with Prandtl number Pr. The value of the thermal von Karman constant might be assumed to be κ_θ = 0.47 [10].

An asymptotic expansion for the temperature field can be performed analogously to the velocity field. As a result, the local Nusselt number Nu can be expanded in the lowest order in the series

$$\frac{\mathrm{Nu}}{\mathrm{Nu}_{fd}}=1+\frac{\varepsilon }{\kappa }\gamma ({x}^{=})+\frac{{\varepsilon }_{\theta }}{{\kappa }_{\theta }}{\gamma }_{\theta }({x}^{=})+O({\varepsilon }^{2})$$

(9)

with universal expansion functions γ and γ_θ [10]. Remarkably, the above solution does not depend on thermal boundary conditions directly. The exact thermal boundary conditions affect the formal behavior of the solution only as a secondary effect. The actual thermal boundary conditions are only of primary relevance for the transformation of the universal solution to the actual temperature distribution. As an important consequence, the same heat transfer correlation results for both isothermal (T_w = constant) and isoflux (q_w = constant) boundary conditions in the case of fully turbulent pipe or channel flow [6, 10]. This contrasts with laminar flow [6], where Nusselt number expressions depend significantly on the applied thermal boundary conditions.

The asymptotic study indicates that – in contrast to laminar flow – a somewhat universal behavior results regarding turbulent entrance flow and heat transfer. For a given location x > 0 within the fully developed turbulent flow region, the actual entrance flow phenomena or the nature of the thermal boundary conditions are not primarily relevant for the asymptotic behavior of the Nusselt number. This might be interpreted in a sense “that two-dimensional turbulent flow does not have a memory regarding up-stream events.” If only local phenomena are considered, such a behavior might be assumed for any two-dimensional wall-bounded fully turbulent flow at sufficiently high Reynolds numbers. This assumption is of significant importance for the Mocikat-Herwig method, as demonstrated in the following section. However, it should be emphasized that this assumption is only asymptotically accurate for wall-bounded two-dimensional turbulent flow. In the case of turbulent wakes behind bluff bodies, significant deviations from the asymptotic solution have to be expected.

2.3 Heat transfer sensor concept

The goal that “it would be highly desirable to get some information about the heat transfer behavior of a part without subjecting it to the full thermal load” was firstly mentioned in 2007 by Mocikat and Herwig [1]. To achieve it, they presented a small heat transfer sensor concept. They also noticed that their approach would permit short measurement times due to the miniaturization of the device.

The fundamental difference between convective heat transfer measurements in the case of a fully thermal loaded (heated) test object and a test object equipped with only a local heating zone is schematically illustrated in Fig. 2. In Fig. 2, case (a) corresponds to a configuration typically desired in technical applications. The test object is equipped with a large heating zone. Then, a thermal boundary layer with increasing thickness δ_θ results downstream of the leading thermal edge. Typically, heat transfer coefficients, h, for fully heated objects are involved in technical applications. Accordingly to boundary layer theory, the convective heat transfer coefficient, h, is a decreasing function of the coordinate x as illustrated in Fig. 2a. At position x = x₀, a sensor would measure the “true” value h(x₀). A suitable heat transfer measurement approach might be given by recording the ambient fluid temperature, T_∞, the wall temperature, T_w, and the wall heat flux, q_w. Then the heat transfer coefficient is obtained by the simple relationship h = q_w/(T_w–T_∞). In case (b), only a local heating zone is applied, and a local sensor would formally measure a heat transfer coefficient h*. That is not the “true” value due to a completely different thermal boundary layer thickness occurring for the cold test object with only local heating. Although the value of the local heat transfer coefficient h* might be roughly affected by the forced flow in the usual manner (i.e., increase of h* with increasing free-stream velocity u_m), it certainly differs substantially from the “true” value h as illustrated through Fig. 2. However, under certain conditions, the local value, h*, can be used for calculating the “true” value, h, as discussed by Mocikat and Herwig [1,2,3]. Following their analysis, local heat transfer sensors placed on cold objects can be used to determine heat transfer coefficients for fully heated objects if the following conditions are satisfied:

Fig. 2

Measurement of the heat transfer coefficient h at position x₀ for a fully thermal loaded test object (a) and in the case of a local measurement (b)

Forced convection flows

In forced convection flows, the heat transfer coefficient h is independent of the local temperature difference, ∆T = T_w–T_∞. Hence, the value of h can be obtained for marginal heating, i.e., ∆T → 0. This assumption excludes any case with noticeable mixed or natural convection effects.

Fully turbulent flows

In fully turbulent flows, the heat transfer is local, and upstream and downstream thermal events do not affect the local value of h at position x₀. Hence, local heating is in principle sufficient, and a simple relation

$$h=A\cdot h*$$

(10)

with a so-called “thermal adjustment coefficient” (TAC), A, connects the local value, h*, with the “true” value, h. The local value, h*, can be obtained by the small sensor area A* that is equipped with a small heating device releasing a heating power P* and the capability to measure the local wall temperature T*. Then, the “true” heat transfer coefficient corresponding to the fully thermal loaded test object is given by

$$h=A\cdot \frac{P^*{/}{A}^*}{T^*-{T}_{\infty }}.$$

(11)

Reynolds number independence of thermal adjustments effects

Then, TAC A in Eqs. (10) and (11) becomes a sensor-specific constant. Its value might be obtained through a single laboratory experiment, for which the “true” value h is known, and h* is measured. After calibrating, A = h/h*, the sensor should apply to other flow configurations. This condition requires a comment. Initially, Mocikat and Herwig [1] assumed that this condition would be satisfied in the case that a “universal” behavior of the heat transfer coefficient would exist, and they argued that TAC A would be a simple sensor-specific constant. In a later paper [2], they introduced a slightly more complex relation, but they came back in reference [3] to the simple relation (11).

A close inspection of the asymptotic study indicates that the universal behavior of TAC assumed by Mocikat and Herwig can be expected in the case of two-dimensional wall-bounded turbulent flows at sufficiently high Reynolds numbers. In the case of three-dimensional boundary layers, this concept is not rigorously justified. There is also a strong indication that in three-dimensional flows a much more complex situation might be present. For instance, the local Nusselt number correlations for convective heat transfer from a fully turbulent flow over a rotating disk depend on the applied thermal boundary conditions [12]. However, in many technical applications, the turbulent flow past an object is essentially two-dimensional, and hence the above approach still covers a large range of interesting applications.

Regarding the asymptotic study of turbulent flow, the quantity A should not depend on Re in the high Reynolds number limit. It should only be a function of the Prandtl number Pr (i. e., A = A(Pr)). The asymptotic study [10], leads to a turbulent heat transfer correlation.

$$\mathrm{Nu}\hspace{0.17em}=\hspace{0.17em}C\; \mathrm{Re}^m$$

(12)

with

$$C=\varepsilon {\varepsilon }_{\theta }{\mathrm{PrRe}}^{1-m}\quad and\quad m=1-\frac{\varepsilon }{\kappa }-\frac{{\varepsilon }_{\theta }}{{\kappa }_{\theta }}.$$

(13)

It follows that the ratio between two TAC values obtained at different Prandtl numbers Pr should be identical with the ratio between two values for the heat transfer constant C given by Eq. (13). Since Mocikat and Herwig did investigate only a single configuration in airflow (Pr = 0.7), this vital prediction concerning the impact of the Prandtl number was not assessed so far.

3 Experimental set-up and procedure

In this section, the miniaturized heat transfer sensor employed for the experimental assessment of the asymptotic study of two-dimensional turbulent flows is described, and the considered test configurations are presented. To check the TAC concept, conventional heat transfer measurements with full thermal loads and measurements using cold test objects equipped with the new sensors were conducted in water and air, and their results will be presented in Sect. 4.

3.1 Miniaturized heat transfer sensor device

The first generation of small heat transfer sensors for technical applications in air and water flows has been designed and manufactured at Ulm University. Details can be found elsewhere [13]; the following subsection presents key elements of the prototype. It should be remarked that this first sensor generation does not exhaust the full potential of modern microelectronics and device technology; instead, the first sensors should be interpreted as the first step into a new field of heat transfer measurements.

The multi-layer design of the new heat transfer sensor is shown schematically in Fig. 3. The corresponding temperature profile in normal direction y is schematically plotted in Fig. 4. The sensor device, shown in Fig. 5, was embedded in a small thermal insulation box. The chemical insulation to the fluid was established by a thin glass plate. The complete sensor device was mounted on the test objects. The first active layer was an electrical heating layer (denoted by A in Fig. 4) followed by an electrical insulation layer (denoted by E in Fig. 4). Both temperatures T₁ and T₂ were measured by two electrical resistance layers (B and D in Fig. 4). These layers had well-defined electrical resistance curves R₁(T) and R₂(T), respectively. Due to heating, a heat flux, q, occurred. Between both electrical layers, a thermal insulation layer (C in Fig. 4) was placed.

Fig. 3

Multi-layer design of the new heat transfer sensor (schematically, not to scale)

Fig. 4

Sensor temperature profile in the normal direction (schematically, not to scale)

Fig. 5

Design of the first generation of miniaturized heat transfer sensors: final sensor including wires, lithography layout, and design of the resistance layers for temperature measurements (from top to bottom, all dimensions in µm)

Because the sensor should be operated in water or aggressive fluids, a thin glass layer (F in Fig. 4) was mounted at the top. Due to its finite thickness, a temperature drop between T₂ and the unknown T₃ occurred. In the thermal boundary layer, a finite temperature difference T₃ – T_∞ existed, too. If the heat flux q was in steady-state operation, the one-dimensional heat conduction analysis yielded

$$h^*=\frac{{\lambda }_{1}}{{l}_{1}}\cdot \frac{{T}_{1}-{T}_{2}}{{T}_{2}-{T}_{\infty }-\frac{{\lambda }_{1}}{{l}_{1}}\frac{{l}_{2}}{{\lambda }_{2}}\left({T}_{1}-{T}_{2}\right)},$$

(14)

and the sensor-based heat transfer coefficient h* was obtained using temperature measurements T₁ and T₂. The temperatures were measured utilizing the temperature-dependency of the electrical resistance of the sensor layer materials.

The material selection, the design of the miniaturized sensor, and the results of thermal simulations are reported in detail in reference [13]. In Fig. 5, the final sensor prototype device and some layout details are shown. The electrical resistance layers were designed as curved wires. This enabled an excellent resistance–temperature behavior due to its significant resistance length. The temperature sensor core zone was of order 330 µm, and the wire contact zones required most of the total system area. Of course, smaller and even more miniaturized sensor designs would be possible, but for the first experimental test campaign, it was decided to use a robust device to ensure easy handling.

The main differences of the new miniaturized heat transfer sensors to conventional ones as described in [14,15,16] might be summarized as follows: The miniaturization, feasible by modern microsystem technology, enables extremely fast thermal response times compared to conventional, medium-sized sensors. Hence, it was unnecessary to utilize a control loop to achieve steady temperature levels during operation, as done by Mocikat and Herwig [1,2,3]. In this context, it is interesting that this fundamental advantage of microsystems was already seen in [2]. A further advantage of miniaturized sensors would be the parallelization in operation. It would be possible to resolve spatial heat transfer coefficients distributions through an array of miniaturized sensors. However, such an approach was out of the scope of the present study since a fundamental test of the Mocikat-Herwig method was the objective of the present investigation. The new sensor worked with a miniaturized heating element, and hence the thermal load into the environment was essentially negligible. This means an advantage in comparison to larger active sensors since thermal pollution was practically avoided. Finally, the new sensor was equipped with thin glass protection. This chemically inert protection enabled operation in a large variety of fluids, including water and also aggressive fluids (in preliminary tests, the sensors were successfully faced with gasoline and acid liquids).

However, the miniaturization of devices for measuring local heat transfer coefficients leads to an interesting theoretical question. The definition of a local heat transfer coefficient is not free from a formal difficulty, as discussed in length by Zudin [17]. In some cases, it is important to consider a conjugate heat transfer problem. In the case of significant spatio-temporal fluctuations or changes, there would be a systematic deviation between the experimentally measured and the “true” heat transfer coefficient. In terms of mathematics, that can be covered by utilizing a factor of conjugation, which is the result of solving a conjugate heat transfer problem, and which is explained in detail by Zudin in [17]. In the present experiments, the length scale for spatial changes of the heat transfer coefficients was much larger than the effective size of the sensors. Furthermore, the measurements were performed with steady flows, and hence the temporal fluctuations were of minor relevance. An estimation of the factor of conjugation for the present sensors and experiments led to the conclusion that the present heat transfer coefficient fluctuations were not high enough to create substantial deviations between the measured and the true heat transfer coefficients due to the conjugate heat transfer phenomenon. However, a careful data reduction procedure including conjugate heat transfer effects might be necessary for further miniaturization and applications with strong fluctuating flows and heat transfer coefficients.

3.2 Experimental approach

The new miniaturized sensors were tested, and the concept was validated through laboratory tests. The laboratory tests were conducted in wind and water tunnels at Muenster University of Applied Sciences. Heat transfer experiments in the wind and water tunnels were carried out employing a conventional method (hot test object under full thermal load and with conventional resistance thermometer instrumentation) and a cold object equipped with the new heat transfer sensors. The main purpose of the laboratory tests was to check the validity of the TAC concept proposed by Mocikat and Herwig [1,2,3], which is a consequence of the predictions of the asymptotic study of two-dimensional turbulent flows.

In the present laboratory tests, identical test objects were placed in test sections of the wind and water tunnels at nearly identical Reynolds numbers. This procedure enabled a statement about the influence of the Prandtl number. The direct comparison of conventionally obtained heat transfer data and heat transfer data obtained by the new sensor approach permitted identification of the TAC values and their behavior as a function of flow regime and Prandtl number.

The following parameters were explicitly varied during the experimental program:

• Ambient fluid (i.e., Prandtl number Pr): Air at atmospheric conditions and pure water at room temperature level were chosen. Since their Prandtl numbers differed nearly by one magnitude, the impact of the Prandtl number of the new local heat transfer measurement approach could be assessed.

• Reynolds number Re: In order to assess the impact of the inflow Reynolds number on the convective heat transfer, different levels of the Reynolds numbers were considered for the two working fluids.

• Inclination angle α (also known as angle of attack) of the square cylinder: Since the inclination angle governs the flow and the convective heat transfer regimes in the case of a square cylinder, this quantity was also varied. In the case of a blunt plate, only the parallel configuration was considered due to the availability of reliable literature data.

The test section dimensions of the utilized wind and the water tunnels were 450 mm × 150 mm and 160 mm × 160 mm, respectively. These dimensions led to blockage ratios of 4.9% and 13.8% for the blunt plate and 11.1% and 31.3% for the square cylinder plate in the wind and the water tunnel test sections, respectively. Regarding these significant blockage ratios, the present test configurations should not be directly compared with literature results obtained for objects placed in essentially infinite streams. It might be more appropriate to consider the current test configurations as channels with obstacles. However, for the purpose of the present study, that fact is not of further relevance.

3.3 Blunt-plate configuration

Regarding the conditions listed in Sect. 3, the new miniaturized sensor method is, in theory, (only) applicable in fully two-dimensional turbulent flows in the high Reynolds number limit. A suitable first test case was given by a blunt plate subjected to a stream of air or water. This case has been well treated in the scientific literature [18,19,20] at least for air flows with a Prandtl number close to unity (i.e., Pr = 0.7). Concerning water (with a Prandtl number largely different from unity), much less is known. The flow is characterized by a separation bubble at the leading edge and a reattached turbulent boundary layer further downstream.

Flow and schematics of the test set-up are illustrated in Fig. 6. One side of the blunt plate (plastic, thickness 2H = 22 mm, length a = 370 mm) was equipped with a conventional heating foil (steel, thickness 25 µm) covering one surface. Directly under the heating foil, several resistance thermometers (PT100, 2 × 2 mm) were placed. The opposite side was equipped with two of the new sensors placed in holes at one half on the plate, see Fig. 6a. By inverting the plate in the test section, four different sensor locations were investigated, namely two in the turbulent boundary layer zone and two in the separation bubble and reattachment zone. This test set-up was placed in the closed test sections of wind and water tunnels, see Fig. 6b. The inflow velocity, u_m, of the water and the wind tunnels was adjusted to ensure comparable Reynolds number levels (water tunnel: u_m = 0.08 m/s up to 0.5 m/s; wind tunnel: u_m = 1.8 m/s up to 19 m/s).

Fig. 6

Blunt plate test case: schematics of the test set-up (a) and test object in the test section of the water tunnel (b)

3.4 Square cylinder configuration

As a second test configuration, the sensors were also applied for measuring the convective heat transfer from a square cylinder placed in a crossflow (at a different orientation angle α). This test case enabled valuable insights into the sensor performance under different flow regimes because the square cylinder in crossflow exhibits a variety of flow and heat transfer regimes [21]. In the case of a square cylinder oriented normally to the flow, a laminar stagnation flow at the front side (angle of attack α = 0°) exists, and at the rear side (α = 180°) a turbulent wake flow due to flow separation at the edges occurs.

The square cylinder device employed for the present study is shown in Fig. 7. Whereas the upper part of the square cylinder device was designed and instrumented for conventional heat transfer measurements, the lower part of the square cylinder was designed as a passive plastic body in which the new heat transfer sensors could be placed, see Fig. 7. As the base, a solid rectangular plastic body (polyvinyl chloride with sidewall length 5 cm) was chosen for the cylinder.

Fig. 7

Square cylinder device: (1) heat transfer sensor, (2) insulation box, (3) hole

In the upper part of the part, a heating foil (25 µm 1.4301 steel) with a passivation layer (adhesive tape from 3 M) and nine resistance thermometers (PT1000 with dimensions 1.75 mm × 1.25 mm supplied by Heraeus) for measuring the wall temperature were placed. Five serpentines, 11.2 ± 0.1 mm wide, were cut out with 0.8 mm spacing to increase the electrical resistance of the heating foil, R, up to 3.02 Ω. The redirections at the backside had an equal area resistance as the stripes. Prior to the cutting process, the nine temperatures sensors were glued under the foil with two-component polyurethane with a spacing of 5 mm. The heat losses were reduced by a 4 mm wide air slot beneath the sensors. No leakage issues were detected for the square cylinder device during the experiments with water. The square cylinders' sidewalls were finished to prepare a hydraulically smooth surface, particularly in a stream-wise direction for both air and water flows.

In the lower part of the cylinder, the new heat transfer sensors (denoted by 1 in Fig. 7) were placed in a thermal insulation box (denoted by 2 in Fig. 3), and this sensor arrangement was mounted on the cylinder using a corresponding hole (3 in Fig. 7) to establish a smooth square cylinder surface. The entire square cylinder device was placed in the test sections of laboratory water and wind tunnels. It was possible to rotate the square cylinder within the test section permitting the measurement of local heat transfer coefficients at different orientation angles α. The flow Reynolds numbers were of order Re = 4,000 up to 20,000.

3.5 Data reduction and experimental uncertainty analysis

The data reduction procedure and the experimental uncertainty level were essentially identical to the ones reported in a prior (conventional) heat transfer study [21], considering the square cylinder configuration. The relative uncertainties regarding the relevant parameters are listed in Table 1. Due to the strong temperature-dependency of the material properties for water, a slightly higher uncertainty level resulted in that liquid compared to air. Special care required the temperature-dependency of the fluid material properties, especially during the water tunnel experiments. Here, the data reduction method recommended by Gersten and Herwig [22, 23] was employed.

Table 1 Experimental uncertainty level

The surfaces of the two test objects were smooth in terms of hydraulics. The wind and water tunnel inflow turbulence levels were of order 0.3 up to 0.5% that was verified employing hot-wire anemometry. In the case of the wind tunnel experiments, the inflow velocity was obtained by means of a Prandtl probe, whereas in the case of the water tunnel, the inflow velocity was obtained by means of PIV. This method worked well since the velocity level of the water flows was relatively low. The uncertainty levels regarding the velocity were of order 1%.

All heat transfer data were collected with a sampling rate of 1 Hz (1 NPLC) with the DAQ 34972A/34902A from Keysight. The heating foils were electrically heated through two power supply units, HMP4040 from R&S, for the conventional heat transfer measurements of the blunt plate and the square cylinder. The electrical heating power P and hence the heat flux, q, was kept constant during each inflow velocity test run. In the case of the square cylinder tests, no power adjustments during the inclination of the square cylinder were carried out.

The uncertainty level of the heat flux was below 5%, caused by uncertainties regarding the determination of the effective heating foil area, the applied voltage, and the electrical current. An additional uncertainty resulted in the experiments in water from the electric conductivity of water, which decreased the electrical resistance R of the thin steel foil serpentine slightly. However, this effect was less than 2%, and its impact on the heat transfer measurements was treated indirectly by the effective uncertainty levels of voltage and current. Further, minor uncertainty sources regarding the Nusselt numbers were given by the uncertainties due to radiation and natural convective heat losses. In the case of experiments with air flows, the radiation heat transfer was estimated to be less than 3% for the low Reynolds number flows, and less than 0.9% for the high Reynolds number flows. During the water experiments, the radiation contribution was much smaller and was hence neglected for all flow regimes. Regarding natural convection heat transfer effects, it was found based on the procedure described by the VDI Wärmeatlas (see also [24] for further details) that at high Reynolds number levels, the additional natural convection contribution remained small. It was less than 0.3% for air and negligible for water because the volumetric expansion coefficient was relatively low.

The temperature dependency of the kinematic viscosity v=μ/ρ, has to be carefully considered regarding the data reduction. Water has a steeper, negative dependency ∆ν/∆T, whereas air shows a more moderate, positive dependency ∆ν/∆T in the range of the present experiments. Moderate driving temperature differences, ∆T = T_w – T_∞, were chosen to prevent a large difference between the Prandtl and Reynolds numbers evaluated at bulk (∞)and wall (w) conditions. The typical values of the driving temperature difference, ∆T = T_w – T_∞, were 5 K for water and 16 K for air. The thermophysical properties for calculating the Nusselt numbers were obtained from the VDI Heat Atlas [24] evaluated at film temperature, (T_∞ + T_w)/2. The uncertainty of the thermophysical properties was less than 1%. The free stream or bulk temperature, T_∞, was measured with a PT100 1/10 DIN Kl. B sensor. The temperature coefficient of platinum (0.0039 1/K) was used to determine the surface or wall temperatures T_w. The uncertainty of the temperature difference, ∆(∆T), was in the range between 0.15 and 0.3 K, whereas the higher values resulted from turbulent temperature fluctuations and finite measurement time.

The blunt plate and the square cylinder devices were designed to be capable of measuring heat transfer coefficients up to 10³ – 10⁴ W/(m²K) occurring typically in water flows. However, many low values in the range of order 10 – 100 W/(m²K) were achieved in air flows during the lowest Reynolds number level in the wind tunnel experiments. This means that the relative uncertainty level was higher in the case of air as fluid because the test apparatus was mainly optimized for operation in water. Internal heat conduction within the PVC block led to a slight decrease in the temperature gradient along with the foil. In the case of water with its much higher convective heat transfer coefficients, this parasitic heat loss due to conduction was negligible.

The maximum uncertainty levels for calculating the mean and side-averaged quantities are listed in Table 1. Due to the temperature-dependency and the temperature measurement uncertainty, an uncertainty about few percent regarding the Prandtl number occurred. The resulting Reynolds number uncertainty was a little bit higher due to the additional velocity measurement uncertainty.

4 Results and discussion

In this section, the outcome of a sensor functionality test and the heat transfer measurements for the two configurations and fluids are presented and discussed regarding the TAC concept.

4.1 Sensor test

Before functionality tests were conducted, the sensor layers were calibrated, i.e., the temperature-resistance-line was obtained. The results of this calibration are shown in Fig. 8a. An essentially linear relationship was found for the temperature sensor layers within the desired temperature range. The quadratic term in the calibration function was nearly negligible in comparison with the linear contribution. The reproducibility was excellent for all sensor layers.

Fig. 8

Sensor check: in-situ result for layer resistor calibration (a) and assessment of linearity (b)

After calibrating the temperature sensor layers, the heat transfer sensors were placed in the water tunnel test section, and their heating input, P*, was varied at fixed water velocity values. With decreasing heating power (or heat flux q*), the driving temperature difference, ∆T, decreased as expected. A linear behavior q* = h* ∆T was found for the sensors: Fig. 8b shows representative data points obtained at different fluid velocities. All curves can be extrapolated to the origin. The gradient of the curves corresponds to the sensor heat transfer coefficient value h*. This value depended – as expected – on the ambient fluid velocity u_m: Higher values for h* resulted in increasing velocity. The miniaturized sensor was considered to rest on a reliable heat transfer measurement mechanism based on this test.

4.2 Blunt plate configuration

In the first set of experiments, the local Nusselt number Nu_x = h_x x/ as a function of the local Reynolds number Re_x = u_∞ xρ /µ were obtained for water and air through conventional measurements for a fully heated bunt plate test object employing the heating foil. The results are shown in Fig. 9. To compare the different fluids, the Nusselt numbers were divided by the factor Pr^1/3 [6]. As known from the literature [18,19,20], the fully turbulent blunt plate heat transfer results can be correlated with high accuracy by a simple power law, see Eq. (12), with a Reynolds number exponent of order m = 0.8 at sufficiently high Reynolds numbers. This reflects the existence of a fully developed turbulent flow regime far downstream of the leading edge and the separation bubble. At lower local Reynolds numbers, the heat transfer is no longer a unique function of the local Reynolds number Re_x. In this case, the local Nusselt number data points did not collapse to a single line in Fig. 9 (for Re_x < 80,000). The conventional measurements were in reasonable agreement with literature data [6, 18,19,20].

Fig. 9

Results of the conventional heat transfer measurements for the blunt plate: water (a) and air (b)

In the second set of experiments, the sensor heat transfer coefficient h* was obtained utilizing an unheated blunt plate equipped with miniaturized sensors. For the sensor Nusselt number definition, the sensor heat transfer coefficient h* was used (Nu_H,S = h* H/λ). This quantity was compared with the conventional Nusselt number Nu_H = h H/λ defined by the true (i.e., conventionally measured) heat transfer coefficient h. The TAC concept predicted a simple relationship Nu_H = A Nu_H,S in the fully turbulent flow region. Assuming the validity of the TAC concept in this region enabled a determination of A using relation A = h/h* = Nu_H/Nu_H,S. The outcome of the blunt plate experiments for air and water is shown in Fig. 10. The simple linear relation Nu_H = A Nu_H,S was fulfilled for sufficiently large normalized distances x/H ≥ 20.2 where a fully developed turbulent flow can be assumed (see also Fig. 9). The validity of the Mocikat-Herwig theory is reflected by the fact that the corresponding data points of Fig. 10 are located on a straight line through the origin (but with a different gradient or TAC value A for the two fluids). As expected, the TAC concept was certainly not applicable in the separation bubble up to the reattachment zone (corresponding to the data points obtained at x/H = 6.7). For that data points, no correlation with a straight line through the origin was obtained. Noticeable deviations from the linear relationships were also observed at a position x/H = 13.4 in Fig. 10.

Fig. 10

Conventional Nusselt numbers Nu_H against sensor Nusselt Numbers Nu_H,S for the blunt plate configuration obtained at different locations x/H for air (left) and water (right)

Figure 11 shows the calculated TAC values against the local Reynolds number for air (Pr = 0.7) for different inflow velocities and sensor locations x/H. Both sensor devices led asymptotically (Re_x → ∞) to the same TAC value A = 0.72, see Table 2. Remarkably, the TAC values diverged rapidly with decreasing Reynolds numbers corresponding to flow regimes not fulfilling the conditions formulated in Sect. 2. In Table 2, the asymptotic results for the blunt plate in air and water streams are summarized. In addition to the TAC values, the ratio A(Pr = 4.5)/A(Pr = 0.7) was compared with the theoretical ratio (i. e., the ratio of the asymptotic heat transfer constants C, see Eq. (13)) in Table 2. A good agreement was found, supporting the prediction of the asymptotic study regarding the Prandtl number effect.

Fig. 11

Calculated TAC values against local Reynolds number for the blunt plate in a stream of air

Table 2 Values of TAC A in case of the blunt plate for the actual miniaturized sensor (Re = 146,000)

4.3 Square cylinder configuration

As the second test configuration, a square cylinder at different orientation angles α was investigated. In the first set of experiments, local heat transfer coefficients, h, were obtained conventionally. Although the blockage effect was significant due to the comparable large square cylinder in the water tunnel test section, the obtained results were in qualitative agreement with literature data [21] obtained under conditions of virtually vanishing blockage. The behavior of the “true” heat transfer coefficient h against the orientation angle α is shown in the top picture of Fig. 12. The different orientations of the square cylinder are illustrated by the bottom picture line in Fig. 12. The instrumented surface is marked as a red line on the bottom cylinder symbol line in Fig. 12. At the front side (or slight angle of attack), the heat transfer was governed by a laminar stagnation flow. At the rear side (or large orientation angle), the heat transfer was substantially higher due to the turbulent wake flow. Between, there was a local increase caused by flow regime transition and corresponding vortex flow (at α ≈ 75°). In general, the convective heat transfer level increased with increasing free-stream velocity (or Reynolds number level).

Fig. 12

Conventionally obtained heat transfer coefficients h (top) and TAC values (bottom)

In the second set of experiments, sensor-based heat transfer coefficients h* were obtained by the small sensor mounted on the cold square cylinder and finally compared with the “true” values h. Using the simple relation A = h/h*, the corresponding TAC value A was calculated, and the results for A are shown in the bottom picture of Fig. 12. For the turbulent water flow regime (α > 120°), the TAC value was nearly constant, and its value was of order A = 0.55 ± 0.1 (see curves on the right in the bottom plot of Fig. 12). This agreed well with the findings of the blunt plate water tunnel experiments, see Table 2. In other words: If one would assume a TAC value A as obtained through the blunt plate experiment, one could predict the true heat transfer coefficient h using relation h = A h* with good accuracy in the case of fully turbulent flows for which the conditions of Sect. 2 are satisfied. Interestingly, A = h/h* would lead to completely different values in the laminar flow regimes (see small orientation angles α) or in the transitional flow regimes (α about 75°). This indicates that the heat transfer measurement approach proposed by Mocikat and Herwig [1] is indeed restricted to a certain class of turbulent flows in the asymptotic limit and must not be employed for laminar flows.

Despite the good TAC value agreement for water tunnel experiments, the following critical remark is important. The turbulent wake flow of a square cylinder is far away from being comparable with two-dimensional wall-bounded flows, and it is hence not rigorously ensured that the predictions of the asymptotic study of Sect. 2 would still be applicable in that case. And indeed, a similar square cylinder test in a wind tunnel at the same Reynolds number levels led to noticeable deviations and scattering of the TAC values. The calculated TAC values for air were found to be within a substantial range of 0.8 < A < 1.2. That is not a satisfying result if one compares that substantial scattering with the well-defined value obtained at the blunt plate (A = 0.72, see Sect. 4.2). This observation is a strong indication that the Mocikat-Herwig theory is only rigorously valid for two-dimensional wall-bounded turbulent flow at sufficiently high Reynolds numbers. Hence the important class of separated flows is excluded from the miniaturized heat transfer sensor approach.

5 Conclusions

An experimental test of the asymptotic expansion of the two-dimensional turbulent boundary layer flow was conducted employing miniaturized multi-layer heat transfer sensors. This new heat transfer sensor was designed to work in air and liquids, and this enabled the investigation of the different Prandtl numbers. Two basic test configurations, namely the flow past a blunt plate and the flow past an inclined square cylinder, were investigated in the test sections of wind and water tunnels. Convective heat transfer coefficients were obtained through conventional testing (i.e., employing fully heated test objects) and through the new miniaturized sensor approach (i.e., employing passive test objects without further heating).

The main prediction of the Mocikat-Herwig theory that a sensor-specific thermal adjustment coefficient (TAC) of the employed actual miniaturized heat transfer sensor should exist in the developed two-dimensional turbulent flow regime was proven. The observed effect of the Prandtl number on this coefficient was in good agreement with the prediction of the asymptotic expansion method in the case of a blunt plate configuration.

The new experiments indicated that the TAC concept seems to be only applicable if certain conditions are satisfied. A necessary condition is the presence of a two-dimensional turbulent boundary layer flows at higher Reynolds numbers. This condition should be fulfilled the case for measurements on streamlined bodies or airfoils for which essentially two-dimensional turbulent boundary layer flows occur.

Inconsistent results were found in the case of separated flows past cylinders. Whereas the TAC concept was still successful in our square cylinder test case using water (i.e., a higher Prandtl number flow), it failed in the case of an airflow past an square cylinder. Based on that observation, the good agreement reported by Mocikat and Herwig [1,2,3] for the flow of air past a circular cylinder might be to a somewhat extend arbitrary, and future tests are necessary.

However, the outcome of the present study is promising because it opens the door to relatively fast and efficient convective heat transfer coefficient measurements in the high Reynolds number range at least for streamlined bodies. This approach would be of particular interest for heat transfer measurements in water, for which conventionally very high heating power levels would be required to heat the test object to a certain temperature level.