Heating of a water droplet on inclined transparent polydimethylsiloxane (PDMS) surface

Abstract

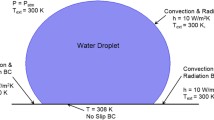
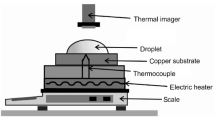
Heat transfer from replicated hydrophobic and transparent PDMS surface to a water droplet is considered. The laser texturing of alumina surface is carried out to obtain hydrophobic surface and later the textured surface is replicated by polydimethylsiloxane (PDMS) via a solvent casting method. An experiment is carried out to assess the water droplet pinning on the replicated inclined PDMS surface while keeping the replicated surface at uniform temperature (308 K). The flow and temperature fields inside the inclined water droplet are simulated in line with the experimental conditions. The flow velocities inside the droplet are validated through the data obtained from the particle imaging velocimetry (PIV). It is found that the velocity predictions agree well with the PIV data. The droplet heating results in a circulation cell inside the droplet due to the Marangoni and the buoyancy currents. Increasing inclination angle of the PDMS replicated surface enhances the maximum velocity inside the droplet, which is more pronounced for the large size droplets. The Nusselt and the Bond numbers increase with the inclination angle of the PDMS surface.

Appendix 1: Evaporation of water from liquid droplet

Evaporation of liquid from the droplet was presented previously [18] and the formulation of rate of evaporation is introduced briefly herein. Evaporation of water from a water droplet depends on water temperature, air temperature, air humidity and air velocity above the water surface.

The amount of evaporated water (kg/s) can be expressed as:

$$ {m}_{eva}=\phi A\left({x}_s-x\right)/3600 $$

(20)

where ϕis the evaporation coefficient ((ϕ = 25 − 19v), v velocity of air above the water surface (m/s)), A is droplet free surface area (m²), x_s is the maximum humidity ratio of saturated air at the same temperature as the water surface (kg H₂O in kg Dry Air), and x is the humidity ratio air (kg/kg) (kg H₂O in kg Dry Air).

1.1 Appendix 2: Formulation of thermal contact resistance

Consider the interface condition as shown in Fig. 16 The thermal contact resistance between the textured surface and the droplet meniscus at the interface can be formulated while assuming the air gaps in the textured surface act like porous structures. In addition, temperature equilibrium is assumed between the air inside the air gap and the texture of the solid surface. The overall effective thermal resistance (R) in accordance Fig. 16 can be written as:

$$ \frac{1}{R}=\frac{1}{\frac{\varepsilon L}{k_aA}+\frac{\left(1-\varepsilon \right)L}{k_sA}}+\frac{1}{\frac{L}{k_sA}} $$

(21)

where R is the overall thermal contact resistance, L is the total PDMS layer thickness including the air-gap due to surface texture, ε is the void fraction, which corresponds to the fraction of air gap volume in the overall texture volume including solid pillars and the air gap volume. In 2-dimensional analogy, the void fraction can be simplified as the ratio of area occupied by air pockets in the pillars gap over the total projected area including the air gap and the solid pillars. Eq. 21 can be simplified as:

$$ \frac{1}{R}=\frac{A\left({k}_a{k}_s+{k}_s\left[\varepsilon {k}_s+\left(1-\varepsilon \right){k}_a\right]\right)}{L\left[\varepsilon {k}_s+\left(1-\varepsilon \right){k}_a\right]} $$

(22)

Fig. 16

A Schematic view textures surface and droplet meniscus: a) air gap and PDMS on the textured surface, b) an approximate illustration of air gap and PDMS surface, and c) thermal resistance at interface

However, the overall effective contact resistance is:

$$ {k}_{eff}=\frac{L}{AR} $$

(23)

Hence, the combination of equations Eqs. 22 and 23 yieds:

$$ {k}_{eff}=\frac{k_a{k}_s+{k}_s\left[\varepsilon {k}_s+\left(1-\varepsilon \right){k}_a\right]}{\varepsilon {k}_s+\left(1-\varepsilon \right){k}_a} $$

(24)

The overall effective thermal conductivity yields:

$$ {k}_{eff}={k}_s+\frac{k_a{k}_s}{\varepsilon {k}_s+\left(1-\varepsilon \right){k}_a} $$

(25)