Theoretical and experimental research on interfacial shear stress and interfacial friction factor of gas-liquid two-phase wavy stratified flow in horizontal pipe

Abstract

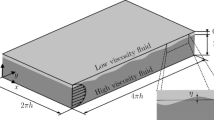
The external flow field over wave interface is reached by the aid of conformal transformation thought, and velocity boundary layer of inner flow field is deduced also, which gives fundamental description of shear stress over wave interface. The viscous drag coefficient is induced with considering the characteristics of interface wave, such as wave height, wave length and ratio between wave lengths of both ascending and descending semi periods, which significantly impact the velocity gradient over the wave interface that accounts for the differences in distribution of local shear stress. The influence of fluid flow is studied also, which gives support that the earlier separating point of the fluid flow over wave interface the stronger depression to the turbulent perturbation is made, and a reduced drag force arrived. There are otherness and commonness between fluid flow over wave interface and interface appearing in air-water wave stratified flow, and a new model is proposed to intrinsically construct the interfacial friction factor encountered in wave stratified flow. The models for viscous drag coefficient and interfacial friction factor are tested, different models are studied, predicted values are compared with experimental data and that computed by solving there-dimension unsteady Navier-Stokes equations, which gives proof that the values predicted by newly proposed models well fit the real values.

Appendices

Appendix 1

There is no simple trigonometric function to describe the interface profile appearing in the gas-liquid two-phase wave stratified flow, instead, a more complicated one is needed. Considering the complicated interface profile, complicated formulations are assumed as follows.

$$ {x}_0={\lambda}_0{\theta}_0/2\pi, y= acos{\theta}_1 $$

(A.1)

The variables ×0 and y is function of phase angles θ₀ and θ₁ respectively that referred in equation (A.1), the variable wavelength λ₀ varies periodically with phase angle θ₀. To some extent, the fluid flow over wave interface can be treated as fluid flow around a cylinder, which takes simple functions to describe the flow field out of the cylinder. There are two steps needs to be done to conduct the transform.

• Step.1

The phase angles θ₀ and θ₁ should be correlated, a same phase angle should be defined to describe the variables x₀ and y. In the synthesis the analysis above, the relationship between the phase angles is defined as follows, and new x₁ coordinate axis is correspondingly defined.

$$ {\theta}_0={\theta_1}^p=2\pi \frac{x_0}{\lambda_0} $$

(A.2)

$$ {x}_1={\lambda}_0\frac{\theta_1}{2\pi } $$

(A.3)

• Step.2

The variable wavelength should be uniform, and the interface wave can be described by new functions in x₂-y coordinate system.

$$ {x}_2=\lambda \frac{\theta_1}{2\pi },y= acos{\theta}_1 $$

(A.4)

The interface profile of cylinder is actually circle arc, its horizontal and vertical coordinates value are functions of the same radius. As a result, a new coordinate transform is made and the wave interface is transformed into a circle arc.

$$ {x}_3=a\sin \left({\theta}_1\right),y= acos{\theta}_1 $$

(A.5)

Appendix 2

Viscous drag coefficient is function of fluid flow parameters, and can be deduced basing equation (13).

$$ {c}_{f,D}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0)/\sqrt{\mathit{\operatorname{Re}}} cos\theta dx}{\rho_f{U}^2x} $$

(B.1)

It is difficult to define characteristic length to solve the equation (B.1). However, it can be eliminated by using of Reynolds number Re_D, where the characteristic length is substituted by equivalent diameter D. Considering the flow area is constant, the equivalent diameter D calculated with flow area is constant also. Consequently, the calculation of viscous drag coefficient can be deduced as follows.

$$ \genfrac{}{}{0pt}{}{c_{f,D}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0)/\sqrt{{\mathit{\operatorname{Re}}}_x} cos\theta dx}{\rho_f{U}^2x}}{\begin{array}{c}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0) cos\theta dx}{\rho_f{U}^2x\sqrt{{\mathit{\operatorname{Re}}}_D}}\\ {}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0) cos\theta dx}{\mu U\frac{\rho_f Ux}{\mu}\sqrt{{\mathit{\operatorname{Re}}}_D}}\\ {}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0) cos\theta dx}{\mu U{\mathit{\operatorname{Re}}}_x\sqrt{{\mathit{\operatorname{Re}}}_D}}\\ {}=\frac{2\int {\rho}_f{U}^2{f}^{\prime \prime }(0) cos\theta dx}{\mu U{{\mathit{\operatorname{Re}}}_D}^{1.5}}\end{array}} $$

(B.2)

The second order derivative f^′′(0) is calculated by solving the equation (12.a), and the other parameters are functions of interface profile.

Appendix 3

For the flow field with interface length of x, the mean value of shear stress over the interface can be deduced as follows.

$$ \overline{\tau_i}=\frac{F_{D, visc}}{x}=\frac{1}{2}{c}_{f,D}{\rho}_f{U}^2 $$

(C.1)

The interfacial shear stress is influenced by the two fluids, and it is correlated as function of the fluids properties and fluids velocities to solve the Double Fluids Model. A large number of experiments data has proved that the liquid velocity is much smaller than that of gas phase for stratified flow. As a result, the equation (21) can be simplified as follows.

$$ {\tau}_i=\frac{1}{2}{\rho}_G{f}_i{U_G}^2 $$

(C.2)

The mechanisms of the mean value of shear stress over the interface $\overline{\tau_i}$ and interfacial shear stress τ_i are the same. It is reasonable to acknowledge that the interfacial shear stresses calculated by equation (C.1) and equation (C.1) should be identical while expanding the equation (C.1) to calculate that working on the interface in gas-liquid two-phase wave stratified flow. Substituting the equation (C.2) into equation (C.1), interfacial friction factor could be related with viscous drag coefficient, and the relationship is written as follows.

$$ {c}_{f,D}=C{f}_i $$

(C.3)

The viscous drag coefficients are computed by the newly proposed model, and it is compared with experimental values of interfacial friction factors. Finally, the validity of equation (C.3) was verified, and the constant number C = 1.0.