1 Introduction

Volume changes of concrete, induced by temperature variations, increase the risk of cracks in massive structures, particularly at the early age of concrete, when its strength is low. The problem is well known and there are models of thermal stresses generated in early age massive concrete structures which can induce cracks development [1]. The temperature variations in massive concrete structure are associated with an exothermic reaction of cement hydration. Therefore the low-heat cements are chosen for such applications. A well-known solution to reduce the amount of generated heat is a partial replacement of Portland cement with a supplementary cementitious materials. Obviously, such modification of the binder composition changes not only strength development of concrete [2] or its heat release characteristics but also the thermal properties of hardening cement paste. Their values and the character of their changes in early age concrete could be a good starting point to refine models of young concrete like the one used by Zhou [3]. So there is a need to identify them.

Usually, the hydration heat is determined by means of calorimetric measurements using the semi-adiabatic method (BSEN 196–9 [4]) or the solution method (BSEN 196–8 [5]). The thermal conductivity and the heat capacity of concrete can be determined using guarded hot plate apparatus and several transient dynamic techniques intended mostly for homogeneous solid materials. These are hardly useful for characterization of very early age concrete. However, De Schutter and Taerwe [6] were able to propose the adequate test method to study the evolution of thermal properties of hardening cement paste. It was concluded that the specific heat and the thermal diffusivity decreased linearly with increasing degree of cement hydration. Experimental results show, however, that the four major clinker phases of cement, viz. C3S, C2S, C3A and C4AF have different rates of reaction with water. Because of different reaction rates of the clinker phases and their interactions, it is generally accepted that the so-called degree of hydration of cement is just an overall and approximate measure [7]. Due to the difficulty of identifying and simulating the complicated interactions, the overall degree of hydration is still used in modelling the early age behaviour of concrete [8]. It becomes much less justified in the case of blended cements containing supplementary cementitious materials exhibiting complex hydraulic and pozzolanic characteristics. This is a case of calcareous fly ash conforming to class C of ASTM C618, not used at industrial scale in Europe yet in spite of rather abundant resources [9]. It was shown that, in the case of partial cement replacement with European calcareous fly ash, beneficial effects on the strength of concrete [10, 11] and its durability [12, 13] were observed. However, the early age thermal properties of concrete were not extensively studied. Therefore, an investigation aimed to develop a method for determination of thermal properties of hardening concrete, not limited to fly ash containing concrete, was performed. The proposed method consists of an experimental procedure and a numerical model based on the inverse heat transfer problem (IHTP) solution.

The literature review reveals several papers, which deal with the estimation of thermal properties of hydrating cement pastes by means of the inverse problem. Ukrainczyk [14] determined thermal conductivity and separately thermal diffusivity. Chirdon [15] determined transient thermal diffusivity for hydrating Portland cement mortars using an oscillating boundary temperature. Czél and Gróf [16] proposed a method for identification of the thermal conductivity without the heat source by means of genetic algorithms and the BICOND measurement technique. The authors in their next paper [17] solved a similar problem to determine simultaneously the specific heat capacity and the thermal conductivity. The inverse analysis along with genetic algorithms were used by Koči [18] to analyse heat release of hydrating cement. Also a widely used hot wire method is based on a solution of an inverse problem [19]. To the best of authors’ knowledge only two papers [20, 21] deal with problem similar to the one presented in this paper. The authors of [20] determined time-dependent thermal properties of concrete only for synthetic data. Moreover, they did not take into account the dependence of these parameters on the history of the process as it is in the real object, where the values of thermal parameters vary with the maturity of concrete and not explicitly with time. For the numerical tests they used a hypothetical one-dimensional measurement mould of height 2 m and two-dimensional mould. The inverse heat transfer problem was solved by means of genetic algorithms. Based on the simulation results this method was found adequate. The authors of [21] presented a similar method, called a prism method, because of the shape of the measurement moulds, used in the experiment. The temperature was recorded along the axis of the four concrete prisms. To describe the heat transport in four prismatic moulds authors used one-dimensional numerical model. To determine the unknown thermal parameters the least squares method was used. A form of heat source as a piecewise linear function of normalised total generated heat was assumed. The conductivity and the activation energy were defined as piecewise constant functions but the specific heat was assumed as a constant and it wasn’t numerically determined.

An original method proposed in this paper is based on a point temperature measurement in a relatively slim concrete cylinder and the numerical solution of the inverse heat transfer problem by means of a direct search optimization algorithm. The experimental details, mathematical foundations and the validation of this method are discussed in the next sections.

2 Experimental programme

2.1 Test set-up and measurements

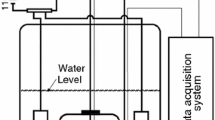
One dimensional temperature distribution in time was measured in thermally isolated cylindrical moulds on hardening concrete specimens to determine their thermal properties as a function of the equivalent time. Figure 1 shows the schema of the moulds with the positions of temperature sensors. The thermal insulation of the mould is made of polyethylene foam and polystyrene foam, in order to minimize the heat loss through the walls. The temperature was measured by LM 35 sensors embedded in fresh concrete at intended positions along the longitudinal axis of cylindrical concrete specimen. The temperature measurement system was fully automated and the data acquisition was performed in a continuous manner at 2 s intervals. To improve the accuracy of determination of parameters a tested concrete mixture can be examined simultaneously in two moulds with different boundary conditions - so called procedure A and B. In the procedure A the top of the mould is covered by the cap made of extruded polystyrene foam to hinder the heat exchange with the environment. In the procedure B the mould isn’t covered (only a very thin plastic cover is placed on the top to avoid moisture evaporation) to allow a free heat exchange between hardening concrete specimen and ambient air.

Fig. 1
figure 1

The cross-section of one dimensional moulds (A and B) and the position of temperature sensors

Full size image

Large 3D moulds were also designed and the temperature measurements of hardening concrete were performed. This was to allow the experimental validation of the temperature distribution calculations using IHTP with the input from one dimensional mould data. Two rectangular blocks of size 900 mm × 800 mm × 700 mm and 1000 mm × 800 mm × 700 mm of concrete were cast in thermally isolated moulds. In the first configuration all side faces of the block and its bottom were lined with 10 mm of polystyrene. In the second configuration only three out of four side faces were thermally isolated. Seven temperature sensors were placed in the cross section of each block.

2.2 Materials and mix design

Experimental tests were performed on hardening concrete made using Portland cement CEM I 42.5R and Portland-slag cement CEM II/B-S 32.5 N manufactured in Górażdze cement plant in Poland. The content of ground blast-furnace slag was about 30%. Local natural sand 0–2 mm, crushed amphibolite aggregate 2–8 mm and crushed granodiorite aggregate 8–16 mm were used as aggregates. Calcareous fly ash from Bełchatów power plant in Poland was used for partial replacement of cement in certain mixes. After long-term monitoring of composition and properties of calcareous fly ash a representative lot was selected for use as addition to concrete mix. As shown in Table 1 the content of MgO, SO3, CaOfree is moderate and the loss on ignition is low.

Table 1 Chemical composition of calcareous fly ash
Full size table

The fineness of calcareous fly ash (Table 2) is rather coarse in comparison to these used in North America. Considering that the content of reactive CaO and SiO2 are greater than 15 and 25% respectively, this type of fly ash is expected to exhibit both pozzolanic and self-hardening properties [22]. Concrete mixes were designed at a constant w/c ratio of 0.50 and a constant volume fraction of aggregates.

Table 2 Physical properties of calcareous fly ash
Full size table

The composition of concrete mixes is shown in Table 3. Concrete mixes were cast into the instrumented, thermally isolated one-dimensional moulds and large 3D moulds.

Table 3 Composition of concrete mixtures
Full size table

3 Mathematical formulation

3.1 Heat conduction equation

The problem of heat transfer in a concrete structure in its full detail is very complex. In general a coupled heat and moisture transfer equations should be considered, taking into account Fourier’s law, Dufour and Soret effects and Fick’s law. However the effects linked with the moisture field have been recognized as playing a negligible role at near room temperatures and very often are disregarded, because the moisture content in mass concrete does not change significantly during early ages [23]. So the heat transfer problem in concrete structures can be approximately described by means of relationship between the conduction rate in a material and the temperature gradient in the direction of heat flow (Fourier’s Law) and the law of conservation of energy. It leads to the heat conduction equation, which in Cartesian coordinate system is written as follows:

$$ \rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+q $$
(1)

where k is the thermal conductivity [W/m K], q – the internal heat source [W/m3] (i.e. the time rate of heat evolution by the hydrating cement at point (x, y, z) in the structure), ρ - the concrete density [kg/m3] and c – the specific heat capacity [J/kg K]. In developing a numerical model of the evolution of temperature in concrete structures one should take into account also the concrete hardening rate. Temperature field develops in each point of the structure in a different way and therefore time-dependent concrete properties are changing unevenly. For this purpose so called maturity index βT is commonly used, which is based on a temperature history. By means of that index a conventional time is replaced by the equivalent age of concrete. The most commonly used formula was proposed by Freiesleben Hansen and Pederesen [24] and was used in evaluation of early age mechanical properties of concrete by Wang and Yan [25]. Based upon the experimental relation between temperature and compressive strength the authors proposed the following expression:

$$ {\beta}_T=\mathit{\exp}\left(\frac{E}{R}\left(\frac{1}{293.15}-\frac{1}{T+273.15}\right)\right) $$
(2)

where R is the gas constant 8.314 J/(mol K), E is the activation energy [J/mol] and temperature of concrete T is expressed in Celsius degrees. However, in the literature there is no consensus on the value of the activation energy [26,27,28,29]. The most widely used formula for the activation energy recommended by RILEM [28] has the following form:

$$ \frac{E}{R}=\left\{\begin{array}{c}4000\ \left[K\right]\kern8.1em for\ T>{20}^{{}^{\circ}}C\ \\ {}4000+175\left(20-T\right)\ \left[K\right]\kern1.7em for\ T\le {20}^{{}^{\circ}}C\end{array}\right. $$
(3)

And it is used in this paper despite the fact that according to some researchers it is incompatible with the Arrhenius’s law [26] and the value should be constant for full temperature range. However, based on the data available in the literature [26] one can conclude that obtained values are inconsistent with each other and discrepancies between the results are greater than 20 kJ. Mentioned difficulties and differences between models can be overcome using the proposed method of determination of thermophysical properties by means of the IHTP solution. The influence of the binder type on the activation energy is included implicitly, namely the determined parameters k and c as well as heat source function S, are in fact the effective ones, it means that calculated values improve the accuracy of estimated value of activation energy. Based on Eq. (2) and Eq. (3) the equivalent age te is calculated as:

$$ {t}_e={\int}_0^t{\beta}_T\left({t}^{\prime}\right){dt}^{\prime } $$
(4)

where t denotes time and t’ is variable of integration with dimension of time. According to the Eq. (2) in case of isothermal process in the reference temperature 20 °C, equivalent age is equal to the conventional time. The equivalent time te is included in the heat transfer equation by coupling Eqs. (1) and (4):

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+q\\ {}\frac{d{t}_e}{dt}=\mathit{\exp}\left(\frac{E}{R}\left(\frac{1}{293.15}-\frac{1}{T+273.15}\right)\right)\kern5.5em \end{array}\\ {} where:c=c\left({t}_e\right);k=k\left({t}_e\right);q=q\left({t}_e\right)\kern2em \end{array}} $$
(5)

Wherein Eq. (4) was written in the differential form. Determination of the temperature field using the set of Eq. (5) is possible, provided that both initial and boundary conditions are known. The condition describing initial temperature distribution is written as:

$$ T\left(t=0,x,y,z\right)={T}_0\left(x,y,z\right) $$
(6)

And by analogy for the equivalent time:

$$ {t}_e\left(t=0,x,y,z\right)=0 $$
(7)

The boundary condition in the general form can be written as a function ϕ, which include Dirichlet and Neumann conditions:

$$ \phi \left(x,y,z,t,T,\nabla T,{T}_a\right)=0 $$
(8)

where Ta denotes the ambient temperature. A model proposed by Cesaraccio [30] is used to predict Ta.

The method of lines [31] was used to solve the one dimensional heat transfer equation. The solution of 3D problem was obtained by means of finite element method.

3.2 Heat conduction equation

The identification task is solved as an optimization problem. For this purpose an objective function is formulated in form of Euclidean norm from the difference between experimentally measured temperature Tm and calculated numerically Tc:

$$ E={\left\Vert {\boldsymbol{T}}^{\boldsymbol{m}}-{\boldsymbol{T}}^{\boldsymbol{c}}\right\Vert}^2 $$
(9)

Where both Tm and Tc are the vectors which contain temperature values in particular point in time and space in analysed cylindrical moulds. Moreover values Tc, which are calculated by means of one dimensional version of set of equations Eq. (5), are dependent on set of unknown (searched) parameters α which define heat of hydration q, specific heat c and thermal conductivity k. It can be symbolically expressed as:

$$ E\left(\boldsymbol{\alpha} \right)={\sum}_{i=1}^{N_s}{\sum}_{j=1}^{N_m}{\left({T}_{ij}^m-{T}_{ij}^c\left(\boldsymbol{\alpha} \right)\right)}^2 $$
(10)

where Ns is the number of sensors and Nm is the number of time intervals. In the discussed case the measurements from four sensors are used (Ns = 4) (Fig. 1), which were recorded in one minute intervals during 72 h after mixing of concrete (Nm = 4320). The unknown functions q, c and k can be defined in many ways. The simplest case from optimization point of view is when an analytical form of sought functions is known. In the literature several proposition of such formulation can be found, e.g. [32,33,34]. In many cases it allows to limit the number of unknown parameters to the minimum, what simplifies the optimization process. Unfortunately in a general case it leads to very complicated mathematical formulation, which depends on a huge number of parameters. Especially, our own experimental results it was noticed, that a partial replacement of cement with fly ashes has a big influence on temperature evolution [35]. For example in a case of concrete with calcareous fly ash the time of maximum temperature occurrence is shifted and also the peak value decreases. In Fig. 2 the temperature evolution in cylindrical mould for two different concrete mixture is shown. Temperature was measured 50 mm above the bottom of the mould in configuration B. The solid line denotes the temperature evolution for a reference mixture containing cement CEM I. It is a common unimodal shape which is obtained from 1D measurements. In contrast the dashed line denotes the temperature evolution in case of mixture of calcareous fly ash with water. The character of curve has changed dramatically: maximum temperature decreased and two peaks were recorded. Bearing in mind these observations, instead of analytical form of heat of hydration a piecewise linear functions are used. The heat of hydration is parametrized in the equivalent time space in the following way:

Fig. 2
figure 2

Temperature evolution in time of early hardening of cement-water mixture (solid line) and calcareous fly ash-water mixture (dashed line) in one dimensional thermally isolated mould

Full size image
$$ q\left({t}_e\right)={\sum}_{i=1}^L{q}_l{N}_l\left({t}_e\right) $$
(11)

where interpolation functions Nl are defined as:

$$ {N}_l(t)=\left\{\begin{array}{c}\frac{t-{\tau}_{l-1}}{\tau_l-{\tau}_{l-1}}\kern4.5em {\tau}_{l-1}\le t<{\tau}_l\kern0.75em \\ {}1-\frac{t-{\tau}_l}{\tau_{l+1}-{\tau}_l}\kern3em {\tau}_l\le t<{\tau}_{l+1}\kern1em \\ {}0\kern7.5em t\notin \left[{\tau}_{l-1}\right.,\left.{\tau}_{l+1}\right)\ \end{array}\right. $$
(12)

and τ is the vector which contains L interpolation nodes.

The length of the vector τ depends on the accuracy of required estimation of the heat source function. Too big number of parameters in the optimization problem hinders its solution, because the problem becomes ill-conditioned [36]. To estimate the development of specific heat and thermal conductivity in time a bilinear relation between these parameters and the equivalent age is assumed:

  • specific heat c:

$$ c\left({t}_e\right)=\left\{\begin{array}{c}\kern-2em {a}_c{t}_e+{b}_c\kern1.25em 0\le {t}_e\le 72\ h\ \\ {}{c}_{\infty}\kern4.5em {t}_e>72\ h\kern2.25em \end{array}\right. $$
(13)

  • thermal conductivity k:

$$ k\left({t}_e\right)=\left\{\begin{array}{c}\kern-2em {a}_k{t}_e+{b}_k\kern1.25em 0\le {t}_e\le 72\ h\ \\ {}{k}_{\infty}\kern4.5em {t}_e>72\ h\kern2.25em \end{array}\right. $$
(14)

where ac, bc, ak and bk are unknown parameters and values c∞ and k∞ can be determined based on the condition of continuity of functions k and c:

$$ {\displaystyle \begin{array}{c}{c}_{\infty }=72{a}_c+{b}_c\\ {}{k}_{\infty }=72{a}_k+{b}_k\end{array}} $$
(15)

The unknown parameters from Eqs. (11), (13) and (14) constitute the vector which was introduced in the Eq. (10):

$$ \boldsymbol{\alpha} =\left[{q}_1,{q}_2,\dots {q}_L,{a}_c,{b}_c,{a}_k,{b}_k\right] $$
(16)

The idea of parametrization of specific heat and thermal conductivity is based mainly on experimental observations presented in paper [37]. Obtained by the authors of cited paper results show the nonlinear relationship with respect to conventional time, what suggest that approach based on the equivalent time can more adequately imitate real situations. Moreover, in the literature very often these material properties are described as the function of hydration rate [38,39,40] which in some way is similar to the equivalent time. The thermal conductivity and the specific heat of concrete do not vary significantly with temperature in the standard temperature range [41]. Returning to the possible ill-posedness of the IHTP, a regularization techniques can be applied to overcome this kind of situations. In case of identification of nonlinear models very often Tikhonov regularization is used [42]. In a general case the regularization involves replacement of an original problem by approximate task, solution of which is more stable numerically and less noise-sensitive. After Tikhonov regularization of order one the objective function given by Eq. (10) becomes:

$$ E\left(\boldsymbol{\alpha} \right)={\sum}_{i=1}^{N_s}{\sum}_{j=1}^{N_m}{\left({T}_{ij}^m-{T}_{ij}^c\left(\boldsymbol{\alpha} \right)\right)}^2+\lambda \underset{0}{\overset{t_{max}}{\int }}\left({\left(\frac{dq}{dt}\right)}^2+{\left(\frac{dk}{dt}\right)}^2+{\left(\frac{dc}{dt}\right)}^2\right) dt $$
(17)

where λ denotes a regularization parameter. Selection of the proper value of λ is a nontrivial task: a too small value might result in a too noisy underregularized solution, while a too large value leads to an overly smooth overregularized solution. In general, a number of methods can be used to select λ; a comprehensive practical review can be found in [43] and a specific method that leads to optimal convergence rates is described in [44]. One may also pursue analogies to robust MART algorithms known in tomography [45]. Here, the approach used in [46] is followed, where first the direct simulation was performed by assuming a typical, analytical form of the heat of hydration (as well as the specific heat and the thermal conductivity) and then the inverse problem defined by Eq. (17) was repeatedly solved using various values of λ to obtain a good fit between the assumed and identified heat of hydration. It was found that in the considered case λ = 0.1 gives satisfactory results, and this value is used with the actual measurement data. One should also mention, that the position of interpolation nodes does not have to be uniform. Moreover the appropriate selection of their position facilitate the whole process of estimation of unknown parameters. Therefore, in the proposed technique, on the basis on the temperature profile the interpolation nodes are distributed more densely in a region of expected peak values. The uniqueness of the problem solution is guaranteed by taking into account the information about the heat loss through the walls, which is estimated by means of temperature measurements of cooling of sand (this issue is discussed later in the paper).

3.3 Direct search algorithm

To solve the optimization problem defined by Eq. (17) the direct search algorithm [47,48,49] is used. It is a method of solving optimization problems without calculating the gradient of the objective function. The solution is based only on the goal function evaluation. It allows in contrast to conventional methods to determine the minimum of the objective function, which is non differentiable or discontinuous. Of course, other optimization routines such as classical gradient based methods, genetic algorithms [50], swarm algorithms [51] or simulated annealing [52] can be used.

The choice of the algorithm was dictated by properties of the objective function. The gradient based method are used in case where the objective function is smooth (continuous) and well defined in a search area. Moreover, in that case its evaluation time should not be numerically costly due to a huge number of function evaluation. In case of considered optimization process a single function call takes a relatively long time, because during its evaluation, in fact, the heat conduction equation is solved. Also the objective function value depends on experimental data, which are affected by random errors which makes the function noisy. Additionally the result of gradient based methods is very often a local minimum, but in case of considered problem the goal is to find the global minimum. It is argued that simulated annealing algorithm converges to global minimum [53] but in general time of solution is unacceptably long. For this reason it was decided to use mentioned direct search algorithm, which does not guarantee convergence to the global minimum, but it is less sensitive on local minima than gradient based algorithms.

Direct search algorithm is implemented in MATLAB software as a function patternsearch. There are also available non-commercial implementation such as NOMAD [54]. The idea of used algorithm is based on a term pattern – the set of vectors in multidimensional space, where the dimension of the space is linked with the number of unknown parameters. The search for the optimal values in presented method is done by sift through values of the objective function on the set of points so called mesh. In each step a new mesh is created in two stages: firstly a set of vectors di is created by multiplying each pattern wi by current mesh size, next the set of vectors di is added to the current optimal point which was determined in the previous iteration. Depending on the success of the particular iteration, the mesh size increases when smaller function value was found or decreases in other case. The mesh size changes by multiplying it by scaling factor, which by default is equal to 2 or 0.5 depending on the success of current iteration. The algorithm stops when any of the following conditions occurs: the mesh size is less than the set tolerance; the distance between the point found in two consecutive iterations is less than set tolerance; the change in the objective function in two consecutive iterations is less than set tolerance; the number of iterations reaches the set value; the total number of objective function evaluations reaches the set value. To improve efficiency of the algorithm in each iteration there is a possibility to perform a run of auxiliary searching algorithm such as genetic algorithm or Nelder-Mead algorithm [55].

Like most procedures used algorithm needs the initial values. In case of heat source a constant values in the range of time 0–72 h are used most often. After 72 h a linear vanishing is assumed. The starting points for the estimation of specific heat and thermal conductivity are usually chosen randomly according to the following rules:

  • specific heat: c0 = 100 · rand() + 1000

  • thermal conductivity: k0 = rand() + 1.5

where rand() denotes pseudorandom number from uniform distribution on the interval [0–1]. Also the initial mesh size is generated randomly. For that reason the optimization problem is solved at least twenty times and the final result is the average of all runs. As it was mentioned earlier each objective function call forces a solution of one dimensional heat conduction equation to calculate the temperature of concrete in the cylindrical mould. To solve this problem a Dirichlet boundary conditions are used. It means that experimentally measured temperature by means of peripheral sensors is used as the information during solving the problem. As a consequence, the unknown parameters are estimated by fitting the temperature distribution to two middle sensors.

It should be noted that in case of the inverse problem solution one has to deal with the determination of parameters in different scales, e.g. value of thermal conductivity expressed in W/(m K) is the order of 100 and heat capacity expressed in J/(kg K) is the order of 103. It imposes the need for scaling to improve numerical condition of the task. Also a constraints are applied on these parameters, which eliminate nonphysical values (e.g. negative heat of hardening). As a result, restrictions lead to new objective function formulation. Detailed procedure in such case is presented in the following papers [49, 56, 57].

4 Results and discussion

4.1 Numerical test

First the numerical test of the proposed procedure is presented. One dimensional IHTP was solved for synthetic data. The temperature distribution in cylindrical mould was calculated for the following parameters:

  • the specific heat:

$$ c=\left\{\begin{array}{c}\kern-2em \left(\frac{50}{72}{t}_e+950\right)\left[\frac{J}{kg\ K}\right]\kern1.5em 0\le {t}_e\le 72\ h\ \\ {}1000\ \left[\frac{J}{kg\ K}\right]\kern5em {t}_e>72\ h\kern2.25em \end{array}\right. $$
(18)

  • the thermal conductivity:

$$ k=\left\{\begin{array}{c}\kern-2em \left(1.7-\frac{0.4}{72}{t}_e\right)\ \left[\frac{W}{m\ K}\right]\kern1.5em 0\le {t}_e\le 72\ h\ \\ {}1.3\ \left[\frac{W}{m\ K}\right]\kern5.75em {t}_e>72\ h\kern2.25em \end{array}\right. $$
(19)

  • the heat source:

$$ q={10}^5\mathit{\sin}{\left(\frac{\pi {t}_e}{100}\right)}^{1.4}{e}^{-0.2{t}_e}-{q}_{-}\ \left[\frac{W}{m^3}\right] $$
(20)

Coefficients in the Eqs. (18)–(20) were chosen in such way that the functions values were similar to the real values. The term q− in Eq. (20) simulates heat loss through the walls and its form will be discussed in the next section. Additionally to simulate a measurement errors a Gaussian noise with mean value 0 °C and standard deviation 0.1 °C was added to the calculated temperature. For estimation of heat source 19 parameters were used (distribution of the interpolation nodes was non-uniform) and two parameters to estimate both specific heat and thermal conductivity. Sensors arrangement corresponds to the configuration B in Fig. 1. The result of the inverse problem solution for source term are compared in Fig. 3 with the target function described by Eq. (20) (without term q− which was given in advance). As can be seen the agreement between analytical form and estimated values is satisfactory. Error bars represents the variability (standard deviation) of obtained solution, which is the consequence of random noise added and the multidimensional “flatness” of the target function. As a consequence the algorithm leads to a little different solution in each iteration, but all the solutions are placed in a confined space. Estimated values of parameters describing specific heat and thermal conductivity with a standard deviation are shown in Table 4.

Fig. 3
figure 3

Comparison of the heat source given by formula 20 (without term q−) with the values obtained by means of the inverse problem solution

Full size image
Table 4 Comparison of selected coefficients describing the specific heat and thermal conductivity with the values determined by the inverse problem solution
Full size table

The maximum value of total relative error, which is defined as:

$$ \left|{\delta}_x\right|=\left|\frac{x-{x}_0}{x_0}\right|\bullet 100\% $$
(21)

where x - measured/estimated value, x0 - target value, in case of thermal conduction coefficient is δk ≈ 11% (average relative error < δk > = 5.5%), and for specific heat δc is not greater than 1%. Based on achieved accuracy between direct and inverse problem it can be conclude that proposed method can be used in real-life examples. One has to bear in mind that chart presented in Fig. 3 shows the solution of the inverse problem not as a function of conventional time (as in the case of temperature evolution), but as a function of equivalent time te. From Eq. (4) and Eq. (2) which describe parameter te one can easy observe, that for constant temperature T = 20 °C equivalent time te is equal to conventional time t. So this chart could be read as a heat source obtained in isothermal test.

4.2 Experimental results

First the experimental test of assumption about one dimensional heat transfer in cylindrical mould is examined. For this purpose measurement in case of three different concrete mixtures were prepared and the temperature was measured in two points on the height of 30 cm in the axis of the cylinder and 3 cm next to the axis of symmetry. The mean difference of temperature was equal in each case 0.23 °C, 0.33 °C and 0.09 °C and standard deviation 0.09 °C, 0.19 °C and 0.08 °C respectively. Mean differences are on the level of accuracy of used sensor, so based on that fact one can conclude that proposed one dimensional model is sufficient for mathematical description of such types of experiments. But it should be noticed that the difference between measured temperature in the axis and next to the wall is always non-negative. This is a result of imperfect thermal isolation. From mathematical point of view it is not possible to include a boundary conditions (Neumann type), which describe this situation, in 1D model, so additional source term with negative values is added. In order to estimate the amount of heat lost through the wall of cylindrical mould the temperature during cooling of heated sand was measured. The sand was dried and the four sensors were located in the axis of the mould in positions 10 cm, 20 cm, 30 cm and 40 cm from the bottom of the mould. As a result a heat loss coefficient αloss was determined. Coefficient αloss is analogous to heat loss of the calorimeter according to European standard BSEN-196-9 [4]. Based on measured data the negative source term can be written as follows:

$$ {q}_{-}=\left(51.5898+0.2394\bullet \delta T\right)\delta T $$
(22)

And in such form is included into the model of temperature of self-heated concrete in one dimensional measurement moulds. Experimental results of 1D and 3D measurements are presented in the next sections together with numerical solutions.

4.3 Inverse problem results

The temperature evolution in time during hardening of concrete mixture P50 0 in 1D mould is presented in Fig. 4. Compositions of examined in this section mixtures are listed in Table 3. As was previously mentioned, this kind of data is the input to the inverse calculation procedure. The calculated heat of hardening is shown also in Fig. 4.

Fig. 4
figure 4

Temperature evolution in time during hardening of concrete in 1D mould and determined heat of hardening – the mixture P50 0

Full size image

In this case for parametrization of heat source a 19 interpolation nodes were used. The amount of released heat during the hardening is shown as the cumulative graph, which looks similar to the results obtained in a standard semi-adiabatic tests on heat of cement hydration. Results for four concrete mixtures DP 0, DP 30, DZ 0 and DZ 30, are presented in Fig. 5. From the Tab. 3 it can be derived that the clinker content in these four mixtures is as follows: 380, 285, 266 and 200 kg/m3 for DP0, DZ0, DP30 and DZ30 respectively.

Fig. 5
figure 5

Determined heat of hardening for the four concrete mixtures: DP 0, DP 30, DZ 0 and DZ 30

Full size image

It can be observed that the arrangement of concrete mixtures according to the total released heat corresponds to the clinker content in the binder.

The following formulas were obtained for the heat capacity and the thermal conductivity of hardening concrete mixtures:

  • mixture DP 0:

$$ {\displaystyle \begin{array}{c}c=\Big\{\begin{array}{c}\kern-1.8em 0.458{t}_e+1079\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ \ 0\le {t}_e\le 72\ h\ \\ {}1112\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\\ {}k=\Big\{\begin{array}{c}\kern-2em 1.354-0.0067{t}_e\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.50em \ 0\le {t}_e\le 72\ h\ \\ {}0.869\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\end{array}} $$

  • mixture DP 30:

$$ {\displaystyle \begin{array}{c}c=\Big\{\begin{array}{c}\kern-1.8em 0.375{t}_e+1103\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ 0\le {t}_e\le 72\ h\ \\ {}1130\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\\ {}k=\Big\{\begin{array}{c}\kern-2.5em 1.226-0.0055{t}_e\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.50em \ 0\le {t}_e\le 72\ h\ \\ {}0.8267\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.75em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\end{array}} $$

  • mixture DZ 0:

$$ {\displaystyle \begin{array}{c}c=\Big\{\begin{array}{c}\kern-1.8em 0.514{t}_e+1067\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ 0\le {t}_e\le 72\ h\ \\ {}1104\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\\ {}k=\Big\{\begin{array}{c}\kern-3em 1.688-0.0048{t}_e\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.50em \ 0\le {t}_e\le 72\ h\ \\ {}1.339\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern1.5em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\end{array}} $$

  • mixture DZ 30:

$$ {\displaystyle \begin{array}{l}c=\Big\{\begin{array}{c}\kern-1.8em 0.403{t}_e+1087\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ 0\le {t}_e\le 72\ h\ \\ {}1116\ \left[\frac{\mathrm{J}}{\mathrm{kg}\ \mathrm{K}}\right]\kern0.50em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\\ {}k=\Big\{\begin{array}{c}\kern-2.5em 2.079-0.0073{t}_e\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern0.50em \ 0\le {t}_e\le 72\ h\ \\ {}1.552\ \left[\frac{\mathrm{W}}{\mathrm{m}\ \mathrm{K}}\right]\kern1.5em \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \kern-1em {t}_e>72\ h\ \ \ \ \ \ \ \ \ \end{array}\end{array}} $$

Based on obtained results the temperature fields in concrete elements with more complex geometries are calculated and compared with the empirical data.

4.4 Numerical model results - the three dimensional case

In Figs. 6 and 7 the comparisons of numerical results with experimental results in case of 3D measurements for the concrete mixture DP 0 are shown. Calculations were performed for the cross section using 2D FEM. The agreement between the model (solid lines in Figs. 6 and 7) and experiment (circles in Figs. 6 and 7) is satisfactory taking into account the applied simplifications. In case of experimental configuration with thermal isolation on each side wall (Fig. 6) the temperature was measured with three sensors on central axis of the block and one at the centre of the side surface. The mean temperature differences for each sensor are equal: 2.5 °C, 2.8 °C, 1.8 °C, 2.9 °C which gives a mean error of 4% with respect to the maximum temperature.

Fig. 6
figure 6

Comparison of temperature distributions in 3D concrete block: measured temperature (circles) and the temperature calculated by means of 2D model (solid lines). Mixture DP 0, configuration with the thermal insulation on all walls

Full size image
Fig. 7
figure 7

Comparison of temperature distributions in 3D concrete block: measured temperature (circles) and the temperature calculated by means of 2D model (solid lines). Mixture DP 0, configuration with one wall without thermal insulation

Full size image

Similar calculations concerning the results presented in Fig. 7 give the temperature difference between numerical and experimental evaluation for block with one wall without thermal insulation. In this case the localization of sensors is presented in Fig. 8. Mean temperature differences for each sensor are equal: 2.4 °C, 1.2 °C, 1.6 °C, 1.3 °C, 2.7 °C, 3.4 °C, 4.1 °C, which is respectively: 4.3%, 2.2%, 2.9%, 2.4%, 4.9%, 5.9 and 7.3% with respect to the maximum temperature. Obtained in both cases the average accuracy of 4% confirms that the implemented 2D model is a good approximation of numerical simulation of temperature in three-dimensional objects. The source of inconsistency besides the geometric simplifications may be the omission of the influence of heat exchange by radiation. The so-called radiative cooling can cause the object’s surface temperature drop below ambient temperature. Therefore, this factor should be taken into account when the self-heating of concrete objects in the field condition is modelled.

Fig. 8
figure 8

Localization of the temperature sensors for concrete block (configuration with one wall without thermal insulation): a) side view, b) top view

Full size image

5 Further discussion

Provided examples support the observation that the identification problem is appropriately formulated and solved in an efficient way. However, the significance of several simplifications requires further discussion. Physical properties of maturing concrete are known to depend also on moisture content [58]. It has been omitted assuming the material is almost fully saturated with water during considered hardening time. The same hydration degree (equivalent time of hydration) can be reached for example by concrete at lower temperature and higher humidity, and the one at higher temperature and lower humidity, resulting in visibly different physical properties. Therefore the proposed model is not adequate for concrete elements exhibiting large moisture differences during hardening. The assumption that the effect of temperature on the hydration rate can be described by means of a common activation energy for all the components of concrete mixture including calcareous fly ash is an effective simplification [59, 60]. At higher temperatures one can observe differences in the shape of heat source function for concrete containing Portland cement and fly ashes. The assumed simplification turned out to be effective but further improvement of the accuracy of temperature prediction would require more sophisticated approach. This could be achieved using experimental data not available at present. Direct measurements of evolution of heat of hydration by e.g. the isothermal calorimetry, could be useful for this purpose and also for validation of calculated heat source function. Also direct measurements of thermal conductivity and thermal capacity of concrete, at least at the final stage of hydration, could be used for validation of the predicted values [61]. In such a way the accuracy of the obtained solutions would be verified by independent experimental methods.

6 Summary and conclusions

The presented method of determination of thermophysical parameters and modelling of time-dependent temperature profiles of concrete at early ages was based on the solution of the IHTP. For this purpose the algorithm for solving the heat conduction equation using the finite element method and the algorithm for solving the inverse problem was developed considering the equivalent time as a fundamental parameter. Thermal properties of hardening concrete were effectively determined using an unconventional approach: the inverse heat transfer problem solution achieved using 1D temperature measurements and optimization by non-gradient direct search algorithm. The main advantages of proposed method is the fact that moulds do not have to be stored in a strictly controlled thermal environment and also the ability to determine the heat of hardening for any concrete mixture without knowing its exact composition.

It was found that the thermophysical parameters obtained on the basis of the analysis of the measured data are qualitatively correct. Their validation was made by comparing the calculated and the measured temperature in the objects of more complex geometry. The obtained results of the simulations are consistent with experimental data. Furthermore, for examined concrete mixtures it was observed that the specific heat is a monotonically increasing function of the equivalent time. Conversely, the heat conduction coefficient is a monotonically decreasing function of te.

The influence of addition of calcareous fly ash on the identified thermal properties of examined concrete mixtures can be summarized as follows: fly ash reduces the total heat of hardening and as a consequence lowers the peak temperature; no clear relationship between amount of fly ash addition and the thermal conductivity was found; in case of the specific heat obtained result suggest that its value increases about 1–2% when ash is added.