1 Introduction

Salt is one of the factors, which affect the durability of the porous building materials (corrosion of steel bars inside reinforced concrete elements induced by chlorides, efflorescence on the surface, crystallization pressure). Generally salt may exist in two phases: dissolved salt and precipitated salt. One of the most adverse phenomenon, which is related to the salt and moisture presence in the pore system of building materials, is salt crystallization [1, 2]. Salt efflorescence causes the optical and chemical damage of painting and surface layers of structures often of great historical value. Additionally, the pressure which is released during crystallization is responsible for splitting off the surface layers. Salt also affects the moisture and energy transport in pore system. Hence, the correct recognition and prediction of phenomena related to salt crystallization are of great importance while considering the durability of structures and conservation of the cultural heritage. Therefore, a lot of theoretical and experimental research was devoted to the subject. The works of Scherer [3], Flatt [4], Coussy [5] focused on the investigation of the crystallization pressure, which was exerted on the solid skeleton. The crystallization pressure depended on the supersaturation ratio, which was usually given as a fraction: salt concentration/solution solubility. NaCl crystallization in bricks was investigated using NMR [6]. The salt crystallization could not be avoided when the element is exposed to the external environment. The heat produced during the salt crystallization induced by drying and decrease of temperature was analyzed using calorimeter [7, 8].

The paper consists of two parts: the experimental and theoretical investigation of mass and energy transport considering salt phase change. In the experimental part the results concerning thermal effects of salt crystallization were analyzed. Heat, which was released during crystallization or consumed during salt dissolution, was measured. The enthalpy of sodium sulphate crystallization and dissolution as a function of temperature was experimentally determined [9]. The experimental setup was constructed. It consisted of two brick samples, one saturated with pure water and the later with sodium sulphate solution, whose saturation strongly depended on the temperature. The samples were put into the climatic chamber. They were cooled and then warmed. The temperature was measured in the same places in both samples. The difference of temperature between two samples resulted from the additional heat source/sink, which is related to the crystallization/dissolution process. In the theoretical part the mathematical model describing heat, moisture and salt transport and its numerical solution was shortly described. In order to calculate the supersaturation ratio the kinetics of salt phase change was taken into account. In such a model one did not know the explicit relation between the dissolved salt concentration and the amount of the precipitated salt. The relation, which might be derived from the experiment, describes the increment of salt crystals volume as a function of solution supersaturation ratio. Using the developed software the above described experiment was simulated. In such an experiment one could observe the salt crystallization due to cooling and the dissolution of salt crystals due to warming. The computer simulations were carried out by means of the HMTRA_SALT software [10], which was appropriately extended. In order to take into account the kinetics of salt phase change the additional state variable describing the amount of precipitated salt had to be introduced. Comparing the experimental data with the computer simulation results, which take into account the crystallization/dissolution enthalpy, the material parameters appearing in the rate law for brick saturated with the sodium sulphate solution were determined.

2 Experimental research

To perform the experiment the bricks saturated with pure water and with 25 % sodium sulphate in water solution were prepared. The brick properties used in this study were: n = 0.20, intrinsic permeability k = 3.0 × 10−16 m2, specific heat C p  = 880 J/(kg K), thermal conductivity λ dry  = 0.77 W/(m K), density ρs = 1,700 kg/m3. Sodium sulphate solubility strongly varies with the temperature and the composition of crystals. When the solution was supersaturated in the temperature lower than 32.4 °C the mirabilite Na2SO4·10H2O was formed. In such temperature range the solution saturation depended on the temperature according to the equation:

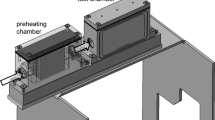
$$ \omega_{\hbox{max} } = 0.0448\exp (0.0625\theta ) $$
(1)

where θ is temperature (°C). The Eq. (1) is valid for θ ∈ [5 °C, 32.4 °C]. Above this temperature the thenardite Na2SO4 would have arisen from the supersaturated solution, whose solubility became almost independent on the temperature. By cooling the brick containing the sodium sulphate solution, whose initial temperature equals 30 °C, the mirabilite growth was induced. Then by warming up the mirabilite dissolution was caused. The crystallization/dissolution process was accompanied with the thermal effects. Two bricks were prepared: the first one containing pure water, the second one containing sodium sulphate solution. By comparing the resulted obtained in both samples, one is able to measure the thermal effects of salt crystallization/dissolution. The bricks were placed in the polystyrene thermal insulation of 10 cm thick—Fig. 1a, b.

Fig. 1
figure 1

a, b Cross-section of the experimental setup. Location of the sensor inside the sample: 1—temperature sensor; 2—brick; 3—moisture barrier; 4—expanded polystyrene

Full size image

Sensor was placed into each brick to measure the temperature. Eight-channel thermometer LB-711 was designed for temperature measurement. The LB-711 was connected with 4 temperature sensors containing thermometric resistors Pt1000. In a standard version TL-2 each sensor was made of stainless steel. Concentrator LB-476 was designed to ensure the cooperation between LB-711 and sensors. Data sent by the sensors were collected in the concentrator’s operational memory (over 20,000 records for each sensor in a typical configuration). The temperature was measured every 1 min with an accuracy of 0.1 °C. The bricks covered with hygral and thermal insulation were placed in the climatic chamber. The climatic chamber (Weiss-Voetsch Environmental Testing Instruments Co. Ltd. Type: C 1,000) allowed to control both the temperature and the relative humidity in the following range: −40 °C up to 180 °C and 5 % up to 98 % appropriately. The heat flux was possible only in one direction—along the longest edge of the brick—Fig. 1b. It was induced by the temperature variation inside the climatic chamber. Before the test cycles were started the samples had been stored for 24 h at 30 °C.

The temperature inside the climatic chamber changed according to the testing cycle (Fig. 2—chamber):

Fig. 2
figure 2

Temperature measured by sensor inside samples and in the climatic chamber

Full size image

  • cooling from temperature 30 °C down to 11 °C–16 h,

  • constant temperature of 11 °C–16 h,

  • heating temperature from 11 °C up to 30 °C–16 h,

  • constant temperature of 30 °C–16 h.

Two such cycles were investigated. A periodically changing temperature was shown in Fig. 2. In the first period of cooling there was no change between the temperature measured inside the brick saturated with pure water and with sodium sulphate solution. Even when the supersaturation ratio was greater than one there was no additional heat source due to crystallization yet. Only when the supersaturation ratio approached ap. 1.7 crystals growed spontaneously. It was manifested by the temperature peak comparing with the temperature measured in the brick saturated with pure water. When the temperature raised the crystals dissolute, what might have been observed after 48th hour. The temperature measured in the brick saturated with the sodium sulphate solution became lower than the temperature recorded inside the brick saturated with pure water. The crystals dissolution consumed energy. At the beginning of the second temperature loop, about 76th hour, whole crystals were dissolved, hence the temperature measured in both bricks was the same. The secondary crystallization started at higher temperature when supersaturation ratio was close to 1.0. Secondary crystals dissolution (after 115 h) proceeded at the same temperature as the primary one. The results obtained in the experiment might serve as a benchmark problem, used for validation of the theoretical and numerical models concerning the salt crystallization in porous building materials.

3 Mathematical model

There exist computer codes, which can be used to simulate the energy, moisture and salt transport in porous building materials [11, 12]. They assume the equilibrium between the precipitated and dissolved salt, therefore they could not be used to calculate the solution supersaturation and the additional stress which was released during salt crystallization.

The proposed mathematical model is the extension of the formulation developed by Lewis and Schrefler [13] and then modified by Gawin and Schrefler [14], describing heat and moisture transport in porous building materials, with salt transport and its influence on thermal and hygral processes. A porous material consists of the following phases: solid skeleton, liquid water (salt solution), water vapour plus dry air and precipitated (crystallized) salt. It is assumed that only one salt is dissolved in the solution. The voids in the skeleton are partly filled with a liquid phase consisting of water and dissolved salt, partly with a gaseous phase consisting of dry air and water vapour, and partly with the precipitated salt. The liquid phase consists of bound water, which is present in the whole range of water content, and capillary water, which appears when water content exceeds the upper limit of hygroscopic region—S ssp . The liquid content is described by the water saturation degree—S w . Salt appears in two phases: the former is the salt dissolved in the liquid phase, described by the mass concentration—ω, the later is the precipitated salt, which is described by the degree of pore saturation with the precipitated salt—S p . The degrees of saturation with all phases of the material follow the formula: S g  + S w  + S p  = 1. It is assumed that the solution is ideal and the gas is the perfect one. The chosen primary variables of the model are: p g(x, t), p c(x, t), T(x, t), (x, t) and S p (x, t) is internal variable of the model. The mathematical model consists of four governing equations: moisture mass conservation, dry air mass conservation, salt mass conservation and energy conservation as well as evolution equation describing salt precipitation-dissolution kinetics.

Using Volume Averaging Theory formulated by Gray and Hassanizadeh [15–17] four macroscopic balance equations were derived. At the macroscopic scale one could measure all necessary coefficients and materials properties (density of materials, water dynamic viscosity, permeability, diffusivity factors, characteristic lengths of dispersion) experimentally.

3.1 Governing equations

The mass conservation equation of dry air included both diffusive (the second term on the left hand side) and advective (the last term on the left hand side) components of the mass flow, an influence of the precipitated salt on the gas saturation degree was also considered:

$$ \phi \frac{\partial }{{\partial {\kern 1pt} t}}\left( {S_{g} \rho^{a} } \right) + {\text{div}}\left( {{\mathbf{J}}_{g}^{a} } \right) + {\text{div}}\left( {\phi S_{g} \rho^{a} {\mathbf{v}}^{gs} } \right) = 0 $$
(2)

The mass conservation of moisture was obtained by summing together liquid water mass balance and water vapour mass balance equations. Evaporation of water determined the sink term for liquid water, on the other hand it constituted the source term in water vapour mass balance equation. After summing up the liquid and vapour water mass balance equations the following moisture mass conservation equation was obtained:

$$ \phi \frac{\partial }{\partial t}\left( {S_{w} \rho^{w} + S_{g} \rho^{v} } \right) + {\text{div}}\left( {{\mathbf{J}}_{g}^{v} } \right) + {\text{div}}\left( {\phi S_{w} \rho^{w} {\mathbf{v}}^{ws} } \right) + {\text{div}}\left( {\phi S_{g} \rho^{v} {\mathbf{v}}^{gs} } \right) = 0 $$
(3)

The first term in Eq. (3) describes the accumulation of moisture in the porous material. The third and the fourth term define the capillary flow of water and advective flow of water vapour. Both of these flows were described by the modified Darcy’s law given in paragraph 3.3.

It was assumed that salt influences the water density, dynamic viscosity and water retention characteristics [18]. The sources or sinks of dissolved salt influenced the saturation degrees of water and gas due to the physical constraint, S g  + S w  + S p  = 1. The mass conservation of the salt dissolved in the fluid phase and precipitated (crystallized) salt was expressed as:

$$ \phi \frac{\partial }{{\partial {\kern 1pt} t}}\left( {\rho^{w} \omega {\kern 1pt} S_{w} } \right) + \phi {\kern 1pt} \rho^{p} \frac{{\partial S_{p} }}{{\partial {\kern 1pt} t}} + {\text{div}}\left( {\phi S_{w} \omega {\kern 1pt} \rho^{w} {\mathbf{v}}^{ws} } \right) + {\text{div}}\left( {{\mathbf{J}}^{dysp} } \right) = 0 $$
(4)

The first term in Eq. (4) describes the accumulation of dissolved salt. The second one defines the accumulation of salt crystals created during the salt phase change, it is described in detail in Sect. 3.2. The third term describes the salt transport together with the capillary flow of water.

The enthalpy conservation equation of the multiphase medium, obtained by summing the appropriate balance equations of the constituents, including the heat effects due to phase change of water and the heat released during the salt crystal grow (the terms on the right hand side), as well as the heat convection and conduction, were expressed by the equation:

$$ \left( {\rho C_{p} } \right)_{ef} \frac{\partial T}{\partial t} + \left( {\rho^{{_{w} }} C_{p}^{w} {\mathbf{v}}^{ws} + \rho^{{_{g} }} C_{p}^{g} \, {\mathbf{v}}^{gs} } \right) \cdot {\text{grad }}T + {\text{div(}}{\mathbf{q}} )= - \dot{m}_{vap} \, \Updelta H_{vap} - \dot{m}_{prec} \Updelta H_{prec} $$
(5)

where ∆H prec is enthalpy of crystallization per unit mass. The latent heat transport was considered in the above equation by adding the product of water sink-source term due to evaporation–condensation, \( \dot{m}_{vap} \), and the water phase change enthalpy, ∆H vap . The precipitated salt mass source, \( \dot{m}_{prec} = \dot{S}_{p} \phi \rho^{p} \), was obtained from the evolution Eq. (6) describing the salt precipitation-dissolution process.

3.2 The kinetics of salt crystallization-dissolution

In the presented paper the kinetic model of salt phase change was applied. It was assumed that there were no salt crystals in pores until the solution saturation limit ω sat (i.e. the salt mass concentration of the saturated solution at a current temperature) was exceeded. After exceeding the maximum salt concentration the solution was supersaturated. The supersaturation ratio (i.e. current concentration/concentration at saturation), S, was the driving force of the salt crystallization, which started when solution supersaturation ratio was greater than one. The first crystals were formed on the crystallization nuclei, which were usually built by dust or other contaminations. There existed no equilibrium between dissolved salt and salt crystals, therefore the relation between the increment of salt crystals mass and solution supersaturation was often called non-equilibrium isotherm [19]. An increase of solid salt mass was calculated on the basis of the supersaturation ratio, according to the following equation [19]:

$$ \dot{S}_{p} = \left\{ {\begin{array}{*{20}c} {S_{w} K(\omega - A'\omega_{sat} )^{p} ,} \hfill & {\omega \ge A'\omega_{sat} \wedge S_{p} < 1} \hfill \\ { - S_{w} K|\omega - A'\omega_{sat} |^{p} ,} \hfill & {\omega < A'\omega_{sat} \wedge 0 < S_{p} < 1} \hfill \\ \end{array} } \right. $$
(6)

The process order, p, and coefficient K depended on the properties of a porous body and the kind of the salt [7]. For primary crystallization the supersaturation parameter A′ = 1. The secondary crystallization proceeds at A′ = 1. The proposed rate law [20], was also valid for the dissolution of crystals—second line Eq. (6). In this case there existed salt crystals in the pore system and solution supersaturation was lower than one. Therefore, the right hand side term in the Eq. (6) was negative and the left hand side was likewise. The increase of the solid salt mass was also negative—which physically means the dissolution of salt crystals. Assuming the kinetic (non-equilibrium) model of salt phase change it was not possible to calculate directly the saturation degree with the precipitated salt but only its increment. The solution saturation depends on the temperature for some kinds of salts, e.g. Na2SO4. Hence during cooling the crystallization process could be observed. An additional heat was released or consumed during the phase change of salt. The heat of sodium sulphate solution depends on salt concentration and temperature, according to Eq. (9):

$$ \Updelta H_{prec} = - \left( {\frac{{m_{w}^{'} H_{IS} \left( {\omega ',T} \right) - m_{w} H_{IS} \left( {\omega ,T} \right)}}{{\Updelta n_{cryst} }} - \Updelta H_{hyd} \left( T \right)} \right) $$
(7)

3.3 Constitutive relations

As a constitutive equation for the capillary water flow (2) and advective gas flow (3), the modified Darcy’s law was applied [22]:

$$ \phi S_{w} {\mathbf{v}}^{ws} = - \frac{{{\mathbf{k}}k^{rw} }}{{\mu^{w} }}\left[ {{\text{grad}}\left( {p^{g} } \right) - {\text{grad}}\left( {p^{c} } \right) + \rho^{w} {\mathbf{g}}} \right] $$
(8)
$$ \phi S_{g} {\mathbf{v}}^{gs} = - \frac{{{\mathbf{k}}k^{rg} }}{{\mu^{g} }}\left[ {{\text{grad}}\left( {p^{g} } \right) + \rho^{g} {\mathbf{g}}} \right] $$
(9)

Darcy’s law may be derived for fully saturated porous media from the macroscopic balance equation for fluid momentum [13]. When several phases occupy the pores the permeability for the fully saturated state should be modified accounting the presence of the other fluids. This change was defined by the relative permeability and depended on the fraction of other phases, capillary effects [23, 24]. For the isotropic media, which were analysed using the model, the intrinsic permeability tensor equals: k = Ik, where k was intrinsic permeability, which was the scalar. In porous material, the intrinsic permeability depended on the effective porosity; usually for the same material, e.g. concrete, the lower effective porosity the lower intrinsic permeability. When salt crystals grow, they fill part of pores, hence the effective porosity was reduced. Due to the lack of the experimental results concerning the influence of salt crystals on the intrinsic permeability, the simplified model presented in [10] was applied in the paper, where:

$$ k = k_{0} \exp \left( {A_{k} n_{ef} } \right) $$
(10)

where k 0 is the intrinsic permeability of the material without salt crystals, n ef is the actual value of porosity (including salt crystals), A k is the material parameter. There exist a lot of methods to determine the permeability coefficient. One of them is the direct measurement of the amount of water, which passes through the sample under the water pressure using Darcy’s law. There exist numerous variants of the method adopted for cracked materials or materials under load [25, 26]. The Cembureau method [27–29] is intended to be suitable for concretes of 250–400 kg/m3 cement content giving a specific permeability coefficient to oxygen within the range 10−14–10−19 m2. The underlying principle is the Hagen-Poiseuille relationship for laminar flow of a compressible fluid through the porous body under steady-state conditions. Another type of permeability test, very often used by civil engineers, is the Rapid Chloride Permeability Test (RCPT) [30]. The permeability is assessed based on the electric current measurement, which passes through the sample surrounded by two reservoirs on both sides of the specimen: one side filled with the NaOH and from the other side by NaCl. The above mentioned methods are suitable for different materials and may be used to compare the permeability of different materials or to monitor the change of permeability due to the loading or the degradation process.

The salt dispersive flux resulted from both mechanical dispersion and molecular diffusion [19, 22]. Mechanical dispersion expressed the effect of the microscopic variation of velocity (direction and value) in the vicinity of the considered point. Molecular diffusion was caused by the random motion of molecules in the fluid from regions of higher tracer concentration to regions with a lower one. The hydrodynamic dispersion was modelled using extended linear Fick’s law expressed as [19, 22]:

$$ {\mathbf{J}}^{dysp} = - \rho^{w} {\mathbf{D}}^{d} {\text{grad(}}\omega ) $$
(11)
$$ D_{ij}^{d} = \left( {\alpha_{T} \left| {\,{\mathbf{j}}\,^{ws} } \right| + \phi S_{w} D^{mol} )\delta_{ij} + (\alpha_{L} - \alpha_{T} } \right)\frac{{j_{i}^{ws} j_{j}^{ws} }}{{\left| {\,{\mathbf{j}}^{ws} \,} \right|}} $$
(12)

The diffusion process in the binary gas mixture consisting of the dry air and water vapour was described by Fick’s law [13]:

$$ {\mathbf{J}}_{g}^{a} = - {\mathbf{J}}_{g}^{v} = \rho^{g} \frac{{M_{a} M_{w} }}{{M_{g}^{2} }}{\mathbf{D}}_{v}^{g} {\text{grad}}\left( {\frac{{p^{v} }}{{p^{g} }}} \right) $$
(13)

Generally D g v is a function of porosity and tortuosity. As it could have been noticed the water vapour and dry air diffusive fluxes were the same according to their value but opposite in the direction. Gas diffusion could take place in the absence of the gas pressure gradient due to the concentration gradient of a particular constituent only. For the isotropic media the effective value of diffusion coefficient depends on the effective porosity according to the equation [31]:

$$ D^{i} = D_{0}^{i} \frac{{n_{ef} }}{{n_{0} }}\left( {\frac{{n_{ef} - A_{D} }}{{n_{0} - A_{D} }}} \right)^{2} $$
(14)

where D i0 and n 0 are the diffusion coefficient and porosity of material without salt crystals, n ef is the porosity of material containing salt crystals, A D is material parameter.

Heat conduction was described by the Fourier’s law:

$$ {\mathbf{q}} = - \lambda_{ef} grad(T) $$
(15)

Effective thermal conductivity depends on the temperature and moisture content. This effective value was measured experimentally and taken into account several phenomena inside pores, like radiation and convection. The thermal conductivity depends on the moisture content, solution concentration and the amount of the salt crystals. It was noticed during the experiment that the temperature in the first 24 h (before primary crystallization peak)—Fig. 2, was almost the same in the brick saturated with pure water and with sodium sulphate solution. Based on that observation we concluded that the effective thermal conductivity very slightly depended on the salt concentration. Therefore for the calculation the, characteristic value for the wet brick was taken [32] and λ ef  = 0.91 W/mK. Unfortunately there was no available data in the literature concerning the influence of precipitated and dissolved salt on the effective thermal conductivity of porous materials.

The other material parameters and properties, which were needed to complete the mathematical model (densities, dynamic viscosity, sorption isotherms etc.), depend on the primary variables. They were described in detail in the appropriate literature [10, 21]. The model was strongly nonlinear and the proper numerical methods had been applied in order to solve the set of governing equations.

3.4 Numerical solution

The mathematical model consisted of the set of partial parabolic differential equations:

$$ {\mathbf{C}}\frac{{\partial {\mathbf{x}}}}{\partial t} + {\mathbf{Kx}} = {\mathbf{f}} $$
(16)

In order to solve them both initial and boundary conditions were needed. Initial conditions constituted the values of the primary variables assigned to all points of the analysed domain at the beginning of the process t = 0. The boundary conditions might have been of three types: Dirichlet (the values of primary variables), Neumann (fluxes related to the primary variables), Robin (linear combination of two previous types). They had to be assigned to the boundary of the domain during the whole time, \( t \in \left( {0,t_{\hbox{max} } } \right]. \)

The spacial and time derivatives were calculated by means of the finite element method and finite difference method (implicit Euler method) appropriately. After this procedure Eq. (16) might have been written as:

$$ \Uppsi^{i} \left( {{\mathbf{x}}_{n + 1} } \right) = {\mathbf{C}}_{ij} \left( {{\mathbf{x}}_{n + 1} } \right)\frac{{{\mathbf{x}}_{n + 1} - {\mathbf{x}}_{n} }}{{\Updelta {\kern 1pt} t}} + {\mathbf{K}}_{ij} \left( {{\mathbf{x}}_{n + 1} } \right)\,{\mathbf{x}}_{n + 1} - {\mathbf{f}}_{i} \left( {{\mathbf{x}}_{n + 1} } \right) = 0 $$
(17)

The Green’s theorem was employed in order to weaken the requirements for shape functions and to consider the boundary condition in the explicit form. The Newton scheme was applied for the linearization of the problem [33]:

$$ \Uppsi^{i} \left( {{\mathbf{x}}_{n + 1}^{l} } \right) = - \frac{{\partial \,\Uppsi^{i} }}{{\partial \,{\mathbf{x}}}}\left| {_{{{\mathbf{x}}_{n + 1}^{l} }} } \right.\Updelta \,{\mathbf{x}}_{n + 1}^{l} ;\quad {\mathbf{x}}_{n + 1}^{l + 1} = {\mathbf{x}}_{n + 1}^{l} + \Updelta \,{\mathbf{x}}_{n + 1}^{l} $$
(18)

where l is iteration index.

The developed computer code allowed to calculate 2D problems. It was verified against some experimental data for fully and partly saturated state in non-isothermal conditions assuming the equilibrium between dissolved and precipitated salt [10].

4 Numerical simulations

Two problems concerning sodium sulphate crystallization were investigated, using the software developed basing on the mathematical model. First, the experiment described in chapter 2 was simulated. Sodium sulphate solubility in water strongly depended on temperature, Eq. (1). The salt crystallization was induced by the rapid cooling of the material. During warming up of the sample, the salt crystals dissolved.

Crystallization/dissolution was accompanied with the thermal effects, which were measured in the experiment. Based on that the material parameters appearing in the kinetic equation were determined. The second problem considered the drying of a brick sample containing sodium sulphate solution. The crystallization pressure for three rate laws were analysed. The software allowed to model 2D domains. The governing Eqs. (2–5) written in the matrix form (16) were valid in all points of the domain. Hence, they could be integrated over the whole domain. The integration was performed using the Gauss method. The isoparametric eight-nodded finite elements were used. The brick was modelled as a 2D domain. It was divided into 100 of equal size elements—Fig. 3. The boundary conditions were listed in Table 1.

Fig. 3
figure 3

Geometry and boundary conditions for numerical simulations

Full size image
Table 1 Boundary conditions for both analyzed experiments
Full size table

As shown in Fig. 1a, b the temperature changes in the climatic chamber were transmitted into the brick only by surfaces A. Side B was insulated using 10 cm of polystyrene therefore no thermal flux appeared on this side. Such an experiment could have been modelled as one dimensional problem.

4.1 Cooling-warming simulation

Two cases of the same experiments were modelled. Firstly the brick was saturated with pure water (case 1), secondly with sodium sulphate solution (case 2). The initial conditions were as follows: p g o  = 101,325 Pa, S wo  = 1.0, T o  = 303.15 K (30 °C), ω o  = 0.0 kg/kg 1st case ω o  = 0.25 kg/kg 2nd case. For the second case the initial dissolved salt concentration was lower than the solution saturation and no solid salt was initially present in the pores system, S p,0  = 0. The ambient temperature changed from 30 to 11 °C, then it remained constant at 11 °C, then rose up to 30 °C and lastly it remained constant at 30 °C. Each stage lasted 16 h. The whole temperature loop took 64 h. Two temperature loops were investigated. During the numerical simulations three different rate orders were tested: p = 1.5, p = 2.5, p = 3.5. Figure 4 presented the comparison of experimental data and numerical simulations results. The temperature difference between the calculated results (assuming various rate orders) and experimental data measured inside brick saturated with sodium sulphate solution were determined relative to the experimental data obtained inside the brick filled only with pure water (no crystallization effects).

Fig. 4
figure 4

The temperature difference between the calculated (p = 1.5, p = 2.5, p = 3.5) and the measured data obtained for bricks saturated with sodium sulphate solutions relative to the results measured in brick saturated with pure water

Full size image

In such a comparison the temperature difference was the consequences of the additional heat sinks/sources due to salt crystallization/dissolution. Parameter A’ influenced the point and the height of the first peak in the temperature difference graph—Fig. 4. One could notice a sudden peak of temperature difference after 20 h, when the salt crystallization started and the crystallization heat was released. The second peak was observed about 80th hour but this one was smoother. The temperature difference was related with the primary (after 20 h) and the secondary (about 80 h) crystallization. The best agreement between the experimental data and calculated results was obtained for, p = 1.5 and A = 1.7, see Fig. 4.

Assuming such values of material parameters the further analysis of transport processes in a brick considering salt crystallization was presented. Figure 5a, b showed the temperature change inside the sample. The comparison of numerical results obtained for case 1 and case 2 was presented in Fig. 5a. One could have noticed a sudden peak of temperature after 20th hour, which corresponded to primary crystallization (supersaturation ratio equals 1.7). The secondary crystallization, which started after 80th hour was not accompanied with such effects. Figure 5b showed the temperature profiles for case 2. The temperature changed very slowly according to the boundary conditions. Figure 6a, b presented the dissolved salt concentration variation obtained in the cooling-warming experiment simulation. During cooling the solution solubility decreased—Eq. (1).

Fig. 5
figure 5

a Temperature changes in the place of sensor, b temperature profiles in the sample

Full size image
Fig. 6
figure 6

a Dissolved salt concentration profiles, b dissolved salt concentration inside the sample and on the surface

Full size image

The solution became supersaturated and the salt crystals grew. Therefore the dissolved salt concentration rapidly decreased, Fig. 6a, starting from the surface. Figure 6b presented the comparison of dissolved salt concentration on the sample’s surface and in the centre of the sample. Dissolved salt concentration changed in the centre of the sample but the changes were delayed compared to the value calculated on the surface. It was the result of both the brick thermal capacity and the kinetics of salt phase change. Crystal growth started from the surface, where the temperature decreased firstly and the solution became supersaturated—Fig. 7a. Salt crystals occupied 4 % of pores. During crystallization the additional crystallization pressure was released—Eq. (19). During the increase of temperature one could have observed the dissolution of salt crystals due to the fact that the solution solubility increased (Eq. 1)—Fig. 7b. The whole volume of crystals, which appeared during cooling, was dissolved during warming up the sample. Salt crystallization took place firstly on the brick’s surface then inside the sample, see Fig. 7a.

Fig. 7
figure 7

a The degree of precipitated salt profiles, b the degree of precipitated salt inside the sample and on the surface

Full size image

4.2 Drying experiment

Another experiment, which was analysed, was the drying of concrete containing sodium sulphate. Initially the sample was saturated with the 10 % solution, the degree of saturation with the liquid phase S w  = 68.7 %, p g o  = 101,325 Pa, T o  = 293.15 K (20 °C), the initial dissolved salt concentration was lower than the solution saturation, so no solid salt was initially present in the pores system, S p,0  = 0. The drying was caused by the rapid decrease of the ambient air relative humidity RH = 20 %. The porosity of the analyzed concrete was equal to φ = 0.12, the intrinsic permeability k = 3.0 × 10−21, and the sorption isotherms as given in Baroghel-Bouny et al. [23]. It was assumed that the primary crystallization had already passed, therefore A′ = 1. Three different rate orders were analysed p = 1.5, p = 2.5, p = 3.5. The boundary conditions were the same on both sides of the sample therefore only half of the material thickness was analysed for this problem. Concrete was a material with very fine structure and low intrinsic permeability. Therefore it had a very typical profile of drying: rapid decrease of liquid saturation close to the surface, almost no changes inside the sample. The profiles of moisture content and Darcy’s velocity were very similar for all analysed rate orders, hence the results were presented only for case 2 (p = 2.5): steep front of drying moving inward the sample—Fig. 8a.

Fig. 8
figure 8

a The profile of saturation degree with the liquid phase assuming the rate order p = 2.5, b the profile of Darcy’s velocity of the liquid phase assuming the rate order p = 2.5

Full size image

The Darcy’s velocity of the liquid phase was analysed in Fig. 8b. One can notice that the velocity of the liquid phase was significant close to the surface. In the middle of the sample its value almost vanished. The fastest the liquid velocity was at the beginning of the drying and its value diminished in the course of time. The liquid lying in the interior of the material became mobile while the drying advanced.

The fast evaporation caused the rapid increase of dissolved salt concentration in the vicinity of the surface—Fig. 9a, b, c. It could have been noticed, that the higher rate law order the higher value of dissolved salt concentration was reached (ω = 0.155, ω = 0.183 and ω = 0.225). When the salt concentration exceeded the solution solubility, it became supersaturated. Then the crystals started to grow. The rate of crystal formation depended on the rate law power—Fig. 10a, b, c. The saturation degree with the salt crystal was the highest for the problem assuming p = 1.5, and reached 25 %, the smallest was for the highest rate law p = 3.5. The distance occupied by precipitated salt was longer for higher rate law order. During the salt crystallization the additional crystallization pressure was released. The equation describing crystallization pressure was firstly derived by Correns and Steinborn [34]:

$$ p^{cryst} = \frac{RT}{{V_{m} }}\ln S $$
(19)

where p cryst is the crystallization pressure, R is the gas constant, T is the absolute temperature, V m is molar volume of salt and S is the solution supersaturation ratio. The pressure, which was exerted on the solid skeleton, was summed over the phases occupying the pores: gas pressure, capillary pressure defined by the Kelvin equation [34], and additional term defining the crystallization pressure [35]:

$$ p^{s} = p^{g} - \left( {\chi_{s}^{ws} p^{c} - \chi_{s}^{cs} p^{cryst} } \right) $$
(20)

where p s is the pressure exerted by the solid skeleton, χ ws s describes the fraction of the pore structure, which is in direct contact with the liquid phase, χ cs s the fraction of the pore structure, which is in direct contact with the growing crystal. The detailed derivation of parameter χ cs s can be found in [31]. It were estimated by the saturation degree with the precipitated salt. Therefore the pressure which was exerted on the pore structure was reduced. Figure 11a, b showed the graphs of the crystallization pressure and the pressure which was exerted on the solid skeleton in the vicinity of the element surface.

Fig. 9
figure 9

Dissolved salt concentration profiles a for case one (p = 1.5), b for case two (p = 2.5), c for case three (p = 3.5)

Full size image
Fig. 10
figure 10

Degree of precipitated salt profiles a for case one (p = 1.5), b for case two (p = 2.5), c for case three (p = 3.5), d degree of precipitated salt-comparison of values for all cases on the surface

Full size image
Fig. 11
figure 11

a Pressure induced during salt crystallization (Eq. 19) b pressure exerted by the growing crystal on the solid skeleton in the surface layer assuming rate order p = 1.5, p = 2.5, p = 3.5

Full size image

The highest pressure was observed in the first period of drying, when the fastest evaporation took place. The crystallization pressure varied from 1.8 MPa (p = 1.5) to 5.5 MPa (p = 3.5). The pressure exerted on the solid skeleton was reduced proportionally to the saturation degree with the precipitated salt, according to Eq. (20). The pressure exerted on the solid skeleton rose during the whole analysed time for case two and three. It might be explained by the fact that the degree of pores saturation with salt crystals increased during the whole analysed time.

5 Conclusions

The paper presents the experimental and the numerical analysis of sodium sulphate crystallization and its influence on the energy and mass transport in the porous building materials. The heat which was produced during the crystals growth and consumed during the crystals dissolution was analysed. Based on it one could have estimated the material parameters appearing in the equation defining the salt crystallization kinetics.

The experimental setup, which could be used to measure the kinetics of salt crystallization and dissolution, was constructed. It was based on the temperature measurement, therefore only the salt, whose solubility depends on the temperature could be analyzed. Using such an equipment, the salt crystallization and salt dissolution in the brick was investigated. The thermal effects of both crystallization and dissolution were measured. The primary crystallization was strongly manifested by a sudden peak of temperature. The secondary crystallization was not accompanied with such evident effects. Only the gradual increase of temperature could have been observed. Salt dissolution consumed energy. Therefore it was manifested with the temperature reduction. The results obtained in the performed experiment may serve as a benchmark problem, which can be used for validation of the theoretical and numerical models concerning the salt crystallization in non-isothermal conditions in porous building materials.

The mathematical model of salt, moisture and energy transport considering the salt phase change kinetics was proposed. The crystallization heat was taken into account, while considering the energy transport. Based on it, the computer code was developed and verified against the obtained experimental data. The results calculated using the developed software were in the good agreement with the data obtained in the experiment. Solving the appropriate inverse problem the material parameters defining salt phase change kinetics equation were estimated. Salt crystallization produced additional pressure, which affected the durability of the building materials and elements. It can be analysed only using the mathematical models considering the salt phase change kinetics, which allows for the calculation the solution supersaturation ratio. The calculated results indicated that, the lower power in the rate law was, the faster salt crystals growth and the smaller crystallization pressure was produced. It was the consequence of the fact that the faster crystals growth the lower solution supersaturation ratio, which was, on the other hand, the driving force of the crystallization pressure.