Temperature distributions in a periodically stratified layer with a vertical dug well

Abstract

The stationary problems of heat conduction in a periodically stratified layer with a vertical cylindrical hole is considered. The lateral surface of the hole is kept at a given piece-wise constant temperature. The boundary planes at zero temperature are taken into account, and the ideal thermal contact between the composite constituents is assumed. The problem within the homogenized model with microlocal parameters is solved.

1 Introduction

The knowledge of temperature distributions in layered bodies with periodic structures play an important role in many technological applications. Periodically stratified materials can be found in nature (varved clays, sandstone–sandstone-slates, sandstone-shales, thin-layered limenstones) or are made by man. The thermal behavior of systems, which are made of a large number of repeated laminae, is described within the framework of the classical heat conduction approach by a partial differential equation with discontinuous, oscillating coefficients. Thus formulated problems are too complicated for an analytical and numerical analysis. For this reason, applications of some approximate models seem to be useful. Some effective approaches to the modeling of heat conduction problem in periodic composites are presented in papers of Aurialt [3], Bufler [4], Bufler and Meier [5]. One of the models is the homogenized model with microlocal parameters devised by Woźniak [2] and developed for microperiodic layered composites by Matysiak and Woźniak [1]. It is important that this model satisfies continuity conditions for temperature and heat fluxes on interfaces (the conditions of perfect thermal contact). The homogenized model with microlocal parameters was applied to solve many problems, which were partially reassumed in papers of Matysiak [6], Woźniak and Woźniak [7]. The problems of heat conduction in a periodically stratified layer with a vertical, cylindrical hole was considered by Matysiak and Perkowski [8]. In this paper, zero temperature or zero radial heat flux on the lateral surface of hole is assumed and the body is heated by given temperature on the upper boundary plane. The problem has been solved within the framework of the homogenized model with microlocal parameters.

In the present paper the stationary problem of heat conduction in a periodically stratified layer with vertical, cylindrical hole is considered. The upper and lower boundary planes with circular cut-out are assumed to be kept at zero temperature. The later surface of hole is heated by a given constant temperature on some part of the surface (lower), the remaining part is kept at zero temperature. Moreover, the ideal thermal contact between the laminae is assumed. The considered problem can be determined some approximated model of heat conduction in a periodically layered stratum with a vertical cylindrical dug well, partically filled by fluid (for instance water). This a reason to entitle of the presented contribution.

The problems connected with various approaches heat conduction in a stratum were considered in many papers, see for instance Rudraiah and Nagaraj [9], Jha [10], Lu and Ge [11], Nahhi and Kalla [12], Kou and Lu [13], Povstenko [14].

2 Formulation and solution of the problem

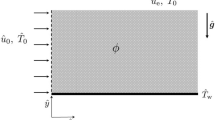
Consider a rigid, periodically stratified layer (stratum) with a cylindrical hole (dug well) normal to the layering. The constituents of the nonhomogeneous body are assumed to be isotropic and homogeneous heat conductors, and denoted by 1 and 2; here and in the sequel, all quantities (e.g. thermal constants, heat fluxes) pertaining to these sublayers will be associated with the index α taking the values 1 and 2, respectively. The problem is investigated by using the cylindrical coordinate system (r, φ, z) with the axis z being the symmetry axis of the hole, see Fig. 1. Let a be the radius of hole and l ₁, l ₂ be the thicknesses of the subsequent layers, l = l ₁ + l ₂ be thickness of the fundamental lamina (the repeated unit). Let K ₁, K ₂ denote the coefficients of heat conductivities of the subsequent layers. Let the parts of planes z = h ₁, r ≥ a, and z = −h ₂, r ≥ a, where h ₁, h ₂ are positive constants, be the boundaries of the nonhomogeneous body, and h = h ₁ + h ₂ be thickness of the layer, see Fig. 1. Moreover it is assumed that h ₁ = n ₁ l, h ₂ = n ₂ l, n ₁, n ₂ ∈ N and n = n ₁ + n ₂ is a sufficiently large natural number. The upper and lower boundary planes with circular cut-outs are assumed to be kept at zero temperature (zero temperature is taken as a surroundings temperature). Let the upper part of lateral surface of the hole r = a, −h ₂ < z < 0, (see, Fig. 1) be kept at zero temperature, the reaming part of the lateral surface 0 < z < h ₁, r = a is heated by constant temperature ϑ₀. The presented above problem is stationary and axially symmetric. The ideal contact between the layers being constituents of the periodically stratified stratum is taken into account. The continuity conditions on the interfaces lead to some difficulty in analytical and numerical approaches. For small thickness of the fundamental lamina l with a comparison to the thickness of the nonhomogeneous layer h, l ≪ h it is suitable to use the homogenized model with microlocal parameters (see Woźniak [2], Matysiak and Perkowski [8]) to the approximated formulation of the considered problem. This model has been derived by using the non-standarard analysis combined with some a priori postulated assumptions. An application of the homogenization procedure leads to equations given in terms of unknown macro-temperature and thermal microlocal parameters. The model permits to evaluate not only mean but also local values of heat fluxes in every material component of the composite. Moreover, the model satisfies the continuity conditions for temperature and heat flux vector on interfaces. Making reference to the microlocal modeling method given in (Matysiak and Woźniak [1], Woźniak [2], Matysiak and Perkowski [8] we recall a brief outline of governing relations of the model. Following (Matysiak, Woźniak [1], Woźniak [2], Matysiak and Perkowski [8] the temperature T (r, z) is postulated in the form

$$ T(r,z) = \theta (r,z) + \underline{h(z)\gamma (r,z)} , $$

(1)

where θ(r, z) is an unknown function (called the macro-temperature and being the averaged temperature), γ(r, z) stands for the unknown thermal microlocal parameter, and h(z) is a given l periodic function (called the shape function):

$$ \begin{aligned} h(z) & = \left\{ {\begin{array}{*{20}c} {z - 0.5l_{1} ,} \hfill & {{\text{for}}\quad 0 \, \le \, z \, \le \, l_{1} ,} \hfill \\ {\frac{{ - \eta z}}{{1 - \eta }} - 0.5l_{1} + \frac{{l_{1} }}{{1 - \eta }},} \hfill & {{\text{for}}\quad l_{1} \, \le \, z \, \le \, l,} \hfill \\ \end{array} } \right. \\ h(z + l) & = h\left( z \right) \\ \end{aligned} $$

(2)

where

$$ \eta = \frac{{l_{1} }}{l}. $$

(3)

The shape function h (·) satisfies the following conditions

$$ h(z) \in 0(l),\quad h^{\prime } (z) \in 0(1),\quad \langle h \rangle \equiv \frac{1}{l}\int\limits_{0}^{l} {h(z){\text{dz}} = 0} . $$

(4)

Bearing in mind the relations (2), (4), the underlined term in (1) is small for small l and will be neglected, and the following approximate relations can be written

$$ \begin{gathered} T(r,z) \approx \theta (r,z), \hfill \\ {\text{grad}}\;T(r,z) \approx \left[ {\frac{\partial \theta (r,z)}{{\partial {\text{r}}}},\frac{\partial \theta (r,z)}{{\partial {\text{z}}}} + h^{\prime } (z)\gamma (r,z)} \right], \hfill \\ \end{gathered} $$

(5)

where h′(z) is the derivative of function h(z) taking the value 1 if α = 1 and −η/(1 − η) if α = 2.

Fig. 1

The scheme of the periodically stratified layer

The governing equations of the homogenized model with microlocal parameters in the stationary axisymmetric case take the form (Matysiak and Perkowski [8]):

$$ \begin{gathered} \tilde{K}\left( {\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{\partial r} + \frac{{\partial^{2} \theta }}{\partial z}} \right) + [K]\frac{\partial \gamma }{\partial z} = 0, \hfill \\ \hat{K}\gamma = - [K]\frac{\partial \theta }{\partial z}, \hfill \\ \end{gathered} $$

(6)

where

$$ \tilde{K} = \eta K_{1} + (1 - \eta )K_{2} ,\quad [K] = \eta (K_{1} - K_{2} ),\quad \hat{K} = \eta K_{1} + \frac{{\eta^{2} }}{{1 - \eta}}K_{2} . $$

(7)

From Eq. (6) it follows that the macro-temperature $\theta$ satisfies the following equation

$$ \frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \theta }{\partial r} + \hat{K}^{ - 1} K^{ * } \frac{{\partial^{2} \theta }}{{\partial z^{2} }} = 0, $$

(8)

with

$$ K^{ * } = \tilde{K} - \frac{{[K]^{2} }}{{\hat{K}}} = \frac{{K_{1} K_{2} }}{{(1 - \eta )K_{1} + \eta K_{2} }}. $$

(9)

The heat flux vector q ^(j)(r, z), j = 1, 2 in the layer of j-th kind is given by

$$ {\mathbf{q}}^{(j)} (r,z) = [q_{r}^{(j)} (r,z),q_{z}^{(j)} (r,z)],\quad q_{r}^{(j)} (r,z) = K_{j} \frac{\partial \theta }{\partial r},\quad q_{z}^{(j)} (r,z) = - K^{ * } \frac{\partial \theta }{\partial z}. $$

(10)

From Eqs. (8) and (10) it is seen that the continuity conditions on interfaces are satisfied by the homogenized model.

The considered problem is determined by the following boundary conditions.

$$ \theta (r, - h_{2} ) = 0,\quad r > a, $$

(11)

$$ \theta (r,h_{1} ) = 0,\quad r > a, $$

(12)

$$ \theta (a,z) = \left\{ {\begin{array}{*{20}c} {\theta_{0} ,} & {0 < {\text{z}} < {\text{h}}_{1} } \\ {0,} & { - h_{2} < z < 0,} \\ \end{array} } \right. $$

(13)

and

$$ \mathop {\lim }\limits_{r \to \infty } \theta (r,z) = 0,\quad - h_{2} < z < h{}_{1}. $$

(14)

From the mathematical reason caused by boundary condition (13) we divide the investigated layer on the two sublayers S _I  = {(r, z); r > a, −h ₂ < z < 0} and S _II  = {(r, z); r > a, 0 < z < h ₁}. It leads to the continuous boundary conditions on the lateral holes in S _I and S _II Let θ _I and θ _II denote the macro-temperature in the sublayers S _I and S _II , respectively. The unknowns θ _I and θ _II satisfy Eq. (8) together with the following boundary conditions

$$ \theta_{I} (r, - h_{2} ) = 0,\quad r > a, $$

(15)

$$ \theta_{I} (a,z) = 0 ,\quad - h_{2} \, < \, z \, < \, 0, $$

(16)

and

$$ \theta_{II} (r,h_{1} ) = 0,\quad r > a, $$

(17)

$$ \theta_{II} (a,z) = \theta_{ 0} ,\quad 0 \, < \, z \, < \, h_{1} , $$

(18)

as well as the continuity conditions

$$ \theta_{I} (r,0^{ - } ) = \theta_{II} (r,0^{ + } ),\quad r > a, $$

(19)

$$ \frac{{\partial \theta_{I} (r,0^{ - } )}}{\partial z} = \frac{{\partial \theta_{II} (r,0^{ + } )}}{\partial z},\quad r > a. $$

(20)

To solve the boundary value problems in sublayers S _I and S _II the Weber-Orr integral transforms will be applied (Titchmarsh [15], Krajewski and Olesiak [16], Olesiak [17]). Introduce the following notations

$$ \left( {\bar{\theta }_{I} (\xi ,z),\,\,\bar{\theta }_{II} \,(\xi ,z)} \right) = W_{00} \left[ {\left( {\theta_{I} (r,z),\theta_{II} (r,z);r \to \xi } \right)} \right] = \int\limits_{a}^{\infty } {rC_{00} (\xi r,\xi a ) (\theta_{I} (r,z),\theta_{II} (r,z) )} {\text{dr}}, $$

(21)

where

$$ C_{\mu \nu } (\xi r,\xi a) = J_{\mu } (\xi ,r)Y_{\nu } (\xi ,a) - J_{\nu } (\xi ,a)Y_{\mu } (\xi ,r), \quad \mu ; \nu = 0 $$

(22)

and J _μ(·), Y _ν(·) are Bessel’s and Neumann’s functions, respectively. The transformation W ₀₀ acting on the differential operator

$$ B_{0} \equiv \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{1}{{r^{2} }}\frac{\partial \theta }{\partial r}, $$

(23)

leads to the following relation (Olesiak [17]):

$$ W_{00} [B_{0} (\theta_{I} (r,z),\theta_{II} (r,z)),r \to \xi ] = - \frac{2}{{{\uppi}}}(\theta_{I} (a,z),\theta_{II} (a,z)) - \xi^{2} \left( {\bar{\theta }_{I} \left( {\xi ,z} \right),\bar{\theta }_{II} \left( {\xi ,z} \right)} \right). $$

(24)

The inverse transforms take the form

$$ (\theta_{I} (r,z),\theta_{II} (r,z)) = \int\limits_{0}^{\infty } {\xi \frac{{C_{00} \left( {\xi r,\xi a} \right)}}{{J_{0}^{2} \left( {\xi a} \right) + Y_{0}^{2} \left( {\xi a} \right)}}\left( {\bar{\theta }_{I} (\xi ,z),\bar{\theta }_{II} (\xi ,z)} \right)} d\xi . $$

(25)

Transforming the Eq. (8) for θ _I and θ _II in S _I and S _II , respectively and using boundary conditions (16) and (18), we obtain the following ordinary differential equations

$$ \left( {\tilde{K}^{ - 1} K^{ * } \frac{{\partial^{2} }}{{\partial z^{2} }} - \xi^{2} } \right)\bar{\theta }_{I} (\xi ,z) = 0,\quad - h_{2} \, < \, z < \, 0, $$

(26)

$$ \left( {\tilde{K}^{ - 1} K^{ * } \frac{{\partial^{2} }}{{\partial z^{2} }} - \xi^{2} } \right)\bar{\theta }_{II} (\xi ,z) = \frac{2}{{{\uppi}}}\theta_{0} ,\quad 0 \, < \, z \, < \, h_{1} . $$

(27)

From Eqs. (26), (27) it follows that

$$ \bar{\theta }_{I} (\xi ,z) = A\exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) + B\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right), $$

(28)

$$ \bar{\theta }_{II} (\xi ,z) = C\exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) + D\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) - \frac{2}{\pi }\theta_{0} \frac{1}{{\xi^{2} }}, $$

(29)

where A, B, C, D are unknowns, which should be determined from boundary conditions (15), (17), (19) and (20). Satisfying these boundary conditions by $\bar{\theta }_{I} (\xi ,z)$ given in (28) and $\bar{\theta }_{II} (\xi ,z)$ given in (29) we obtain four linear algebraic equations for unknowns A, B, C, D and the solution takes the form

$$ \begin{aligned} \bar{\theta }_{I} (\xi ,z) & = \frac{{2\theta_{0} }}{{W\pi \xi^{2} }}\left\{ {\left[ {\cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{1} } \right) - \exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)} \right]} \right. \\ & \quad \times \exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) + \left[ {\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right) - \exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{1} } \right)\cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)} \right] \\ & \quad \times \left. {\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) - W\cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right)} \right\}, \\ \end{aligned} $$

(30)

and

$$ \begin{aligned} \bar{\theta }_{II} (\xi ,z) & = \frac{{2\theta_{0} }}{{W\pi \xi^{2} }}\left\{ {\left[ {\cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{1} } \right) - \exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)} \right]} \right. \\ & \quad \times \exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) + \left[ {\exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right) - \exp \left( { - \sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{1} } \right)\cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)} \right] \\ & \quad \left. { \times \exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right) - W} \right\}, \\ \end{aligned} $$

(31)

where

$$ W = \exp \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} + h_{2} )} \right) - \exp \left( { - \sqrt { \frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} + h_{2} )} \right) = 2\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right). $$

(32)

To obtain the distribution of temperature θ _I (r, z) in S _I , and θ _II (r, z) in S _II in the integral forms we will substitute Eqs. (30), (31) and (32) into (25). Thus, we have

$$ \begin{aligned} \bar{\theta }_{I} (r,z) & = \frac{{2\theta_{0} }}{\pi }\int\limits_{0}^{\infty } {\frac{{C_{00} \left( {\xi r,\xi a} \right)}}{{\xi \left[ {J_{0}^{2} \left( {\xi a} \right) + Y_{0}^{2} \left( {\xi a} \right)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. \\ & \quad + \sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] - \cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right)\left. {\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)} \right\}{\text{d}}\xi \quad {\text{for}}\quad - h_{2} \, < \, z \, \le \, 0 \, , \\ \end{aligned} $$

(33)

and

$$ \begin{aligned} \bar{\theta }_{II} (r,z) & = \frac{{2\theta_{0} }}{\pi }\int\limits_{0}^{\infty } {\frac{{C_{00} (\xi r,\xi a)}}{{\xi \left[ {J_{0}^{2} (\xi a) + Y_{0}^{2} (\xi a)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. \\ & \quad + \sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] - \left. {\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)} \right\}{\text{d}}\xi ,\quad {\text{for}}\quad 0 \le z < h_{1} \, . \\ \end{aligned} $$

(34)

The obtained integrals will be calculated numerically, and the results will be presented in the form of graphs. Moreover, knowing the temperature we will determine the distributions of heat flux. By using the relation (Olesiak [17], Olesiak and Krajewski [16]):

$$ \frac{d}{{{\text{d}}x}}\left[ {x^{\mu } C_{\mu \nu } (\xi x,\xi a)} \right] = \xi x^{\mu } C_{\mu + 1,\nu } (\xi x,\xi a), $$

(35)

and Eqs. (10), (25), (30), (31) we obtain the components of heat flux vector in the layers S _I and S _II in the form:

$$ \begin{gathered} q_{zI}^{(j)} (\xi ,z) = \frac{{2\theta_{0} }}{\pi }\sqrt {K^{ * } \tilde{K}} \int\limits_{0}^{\infty } {\frac{{C_{00} (\xi r,\xi a)}}{{\left[ {J_{0}^{2} (\xi a) + Y_{0}^{2} (\xi a)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \hfill \\ \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\cosh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. - \cosh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] \hfill \\ + \sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right]\left. {\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)} \right\}{\text{d}}\xi \quad {\text{for}}\quad - h_{2} \, < \, z \, \le \, 0, \hfill \\ \end{gathered} $$

(36)

$$ \begin{gathered} q_{zII}^{(j)} (\xi ,z) = \frac{{2\theta_{0} \sqrt {K^{ * } \tilde{K}} }}{\pi }\int\limits_{0}^{\infty } {\frac{{C_{00} (\xi r,\xi a)}}{{\left[ {J_{0}^{2} (\xi a) + Y_{0}^{2} (\xi a)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \hfill \\ \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\cosh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. - \cosh \left. \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] \right\}{\text{d}}\xi ,\quad {\text{for}}\quad 0 \, \le \, z \, < \, h_{1} \hfill \\ \end{gathered} $$

(37)

and

$$ \begin{aligned} q_{rI}^{(j)} (\xi ,z) & = K_{j} \frac{{2\theta_{0} }}{\pi }\int\limits_{0}^{\infty } {\frac{{C_{10} (\xi r,\xi a)}}{{\left[ {J_{0}^{2} (\xi a) + Y_{0}^{2} (\xi a)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. \\ & \quad + \sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] - \cos h\left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi z} \right)\left. {\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)} \right\}{\text{d}}\xi \quad {\text{for}}\quad - h_{2} \, < \, z \, \le \, 0, \\ \end{aligned} $$

(38)

$$ \begin{aligned} q_{rII}^{(j)} (\xi ,z) & = K_{j} \frac{{2\theta_{0} }}{\pi }\int\limits_{0}^{\infty } {\frac{{C_{10} (\xi r,\xi a)}}{{\left[ {J_{0}^{2} (\xi a) + Y_{0}^{2} (\xi a)} \right]\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)}}} \left\{ {\cosh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h_{2} } \right)\sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{1} - z)} \right]} \right. \\ & \quad + \sinh \left[ {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi (h_{2} + z)} \right] - \left. {\sinh \left( {\sqrt {\frac{{\tilde{K}}}{{K^{ * } }}} \xi h} \right)} \right\}{\text{d}}\xi ,\quad {\text{for}}\quad 0 \, \le \, z \, < \, h_{1} . \\ \end{aligned} $$

(39)

3 Numerical results

The obtained results given by Eqs. (33), (34), (36)–(39) determine the temperature and heat flux distributions in the periodically stratified layer with the vertical cylindrical hole in the form of integrals, which will be calculated numerically. For this aim, the following dimensionless variables and parameters are introduced

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} = r/a,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = z/a,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = h_{1} /a,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = h_{2} /a,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} = h/a. $$

(40)

Figure 2 shows the curves of constant values of dimensionless temperature θ/θ₀. Figure 2a–c present isotherms for the thickness $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1}$ of lower layer two times greater than the thickness $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2}$ of upper layer for three case of the ratio K ₁/K ₂ = 1.0; 4.0; 8.0 and η = 0.5. The first case (K ₁/K ₂ = 1.0) represents the results for a homogeneous body. The dimensional isothermal lines for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = 1.0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = 1.0,\eta = 0.5$ and three case of ratio K ₁/K ₂ = 1.0; 4.0; 8.0 are presented in Fig. 2d–f. It is seen, that the greater values of dimensional temperature θ/θ₀ are achieved in the case of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = 2.0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = 1.0$ (when the part of layer with heated on the lateral surface of hole is thicker than the remained part).

Fig. 2

The isothermal lines in the periodically stratified layer

The dimensional radial component of heat flux vector $q_{r} /(\theta_{0} K^{*} )$ as a function of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}$ near the lateral surface is showed in Fig. 3a, b. The radial component is discontinuous on the interfaces. For the better visibility the curves of $q_{r}^{\left( j \right)} /\left( {\theta_{0} K^{*} } \right),\,\,j = 1,2$, are extended ($q_{r}^{(1)}$ in the layers of the second kind and $q_{r}^{(2)}$ in the layers of the first kind, respectively). The greatest jumps of the heat flux $q_{r}^{\left( j \right)}$ are achieved on the interfaces near upper boundary plane of the layer $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = 1.0$ and the plane $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = 0$. The values of the jumps are dependent on the ratio K ₁/K ₂.

Fig. 3

The dimensional radial component of heat flux as a function of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}$

Figure 4a, b present in the same manner as in Fig. 3 radial flux component $q_{r}^{(j)} /(\theta_{0} K^{*} )$ as a function of η, η = l ₁/l for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = 1.0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} = 1.05$ and K ₁/K ₂ = 4.0; 8.0. Figure 4a shows $q_{r}^{(j)} /(\theta_{0} K^{*} )$ for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} /2$ and Fig. 4b for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} /2$ (symmetrically with respect the plane $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = 0$).

Fig. 4

The dimensional radial component of heat flux as a function of parameter η

The dimensional component of heat flux $q_{z}^{(j)} /(\theta_{0} K^{*} )$ normal to the layering as a function of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r}$ for two cases of depths $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} /2$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} /2$, and two cases of ratio K ₁/K ₂ = 4.0; 8.0 is presented in Fig. 5a, b. This component is continuous on the interfaces. The black curves represent the case of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = 1.0$ the grey curves are suitable for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} = 2.0, \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} = 1.0$.

Fig. 5

The dimensional component of heat flux normal to the layering as a function of radius $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r}$

Figure 6a, b show the dimensional heat flux $q_{z}^{(j)} /(\theta_{0} K^{*} )$ as a function of parameter η for two cases of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{2} /2\;{\text{and}}\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h}_{1} /2$, and K ₁/K ₂ = 4.0; 8.0, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} = 1.05$. The results for η = 0 and η = 1 are adequate for a homogeneous layer.

Fig. 6

The dimensional component of heat flux normal to the layering as a function of parameter η

4 Final remarks

The temperature and heat flux distributions in the periodically stratified layer with cylindrical vertical hole is obtained within the framework of the homogenized model with microlocal parameters. The obtained results stand for some approximated solution to the considered problem. The boundary conditions are satisfied exactly, the equation of heat conduction with the periodically pice-wice constant coefficients is replaced by the equation with constant coefficients. The analysis of accuracy of the model were investigated in papers (Kulchytsky-Zhyhailo and Matysiak [18, 19], Matysiak and Perkowski [20]), where the satisfactory consistency of the results obtained within the framework of homogenized model with microlocal parameters and within the classical heat conduction are confirmed.