Heat flux determination for nucleate boiling in subsurface tunnel structures

Abstract

The paper focuses on theoretical analysis of boiling heat transfer on surfaces with tunnel structures formed by fins with microfins and covered with perforated foil. The investigations were conducted for water, ethanol and R-123. The theoretical heat flux, based on modified Chien and Webb model, when compared to the experiments, showed satisfying agreement in low and medium ranges for water and ethanol, and in all heat flux ranges for R-123.

1 Introduction

The paper deals with the theoretical analysis of pool boiling heat transfer on finned surfaces with microfins and perforated foil. The proposed new model for boiling heat transfer in tunnel structures was based on Nakayama et al. model [9], later improved by Chien and Webb [4] for surfaces investigated in [2, 3].

The quoted model was developed through experimental studies of pool boiling on cylindrical surfaces with subsurface tunnels, formed by placing foil with small holes on a finned tube. The authors assumed that the tunnels are almost entirely filled with vapor except for menisci in the corners. The basic quantity determined in the model is the instantaneous evaporation rate inside the tunnel, obtained through the analysis of meniscus sizes, the bubble growth, the bubble departure diameter, and transient convection outside the tunnels. One of the significant parameters is the number of menisci in the tunnel.

Pastuszko and Poniewski [11] proposed their own model for extended surfaces with connected horizontal and vertical tunnels. Extended surface nonisothermality and the characteristic process of vapor bubble formation and departure were also considered. Regarding the calculated bubble parameters (diameter, nucleation sites density, generation frequency), the heat fluxes for evaporation within the tunnels and convection on the tunnel external surfaces were determined.

Similarly to the assumptions adopted in previous models [4, 6, 8, 9], the authors assumed the total heat flux to be a sum of the heat flux in the tunnel q_tun and external heat flux q_ext. Evaporation from the menisci surfaces determines the heat flux q_tun, whereas q_ext depends on a transient conductivity and convection caused by departing vapor bubbles.

Nakayama et al. [10] distinguished three possible types of boiling in tunnels:

• Flooding—for the lowest heat fluxes and superheats. The tunnels are filled with liquid and the openings/holes act as single nucleation sites.

• Suction-evaporation—for higher heat fluxes. Departing active bubbles remove the vapor from the tunnels, and evoke sucking the liquid inside. The liquid spreads along the tunnels, and the menisci in the corners become evaporation sites.

• Drying—tunnels are fully filled with vapor (for the highest heat fluxes).

The proposed model, alike Nakayama’s concept, refers to one boiling type only—suction-evaporation, and assumes sucking the liquid into the tunnels through inactive pores (holes) using the pumping function of bubbles departing in the active pores. The liquid diffuses inside the tunnels and evaporates from the menisci in the corners.

2 Object of research

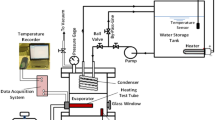
The experiments were conducted on copper finned surfaces with microfins and perforated foil; water, ethanol and refrigerant R-123 were used as working liquids. Figures 1, 2 and 3 present a finned sample with microfins.

Fig. 1

A finned sample with microfins: a before perforated foil placement, b with the sintered layer of perforated foil

Fig. 2

Magnification of fin tip

Fig. 3

Dimensions of the finned sample with microfins before being covered with perforated foil

Parameters of the studied samples were as follows: microfin thickness: 0.7, 0.95, 1.2 mm; diameter of the holes in foil—0.3, 0.4, 0.5 mm and pitch of the holes: 0.6, 0.8, 1.0 mm. The constant parameters were as follows, Figs. 1, 2 and 3: fin number: 3, fin height (h_f): 5 mm, fin thickness (δ_f): 5 mm, fin interspace width (w_f-f): 5 mm, fin array width (a): 27 mm, micro-fin height (h_mf): 1.6 mm, tunnel width (w_tun): 1.3 mm.

Foil hole (pore) pitch for one direction is equal to the pitch of microfins; for the other direction it is constant as an algorithm—in each case it is two times the diameter.

3 Main model assumptions

Similarly to the model [4] the bubble growth cycle was divided into three periods: standby period Δt_stb, bubble development period Δt_dvp and liquid intake period Δt_itk, Fig. 4.

Fig. 4

The process of bubble development and evaporation in subsurface tunnels

Standby period—Δt_stb. The liquid in the tunnel evaporates. The meniscus radius decreases from its initial value R_ms,stb to R_ms,dvp. In this period the tunnel is filled with vapor except for the liquid menisci in the corners.

Bubble development period—Δt_dvp. Vapor permeates through the surface pores into the bubble whose radius increases. Due to the liquid evaporation, the radius of the meniscus changes from R_ms,dvp to R_ms,itk.

Liquid intake period—Δt_itk. After bubble departure the liquid is sucked into the tunnel and retained in the corners. In a very short time after the bubble departure, the pressure in the tunnel is lower than that of the liquid pool and as a result, the liquid flows into the tunnel.

According to the observations already quoted in the literature [4, 10], this period is a lot shorter than the two previous ones so it was skipped in the calculations of bubble departure frequency.

The discussed model was chosen because it can be modified, and due to the presence of only two experimental constants and high accuracy of experimental data mapping. The authors determined theoretical heat flux with accuracy of ±33% [4].

The surfaces studied in the quoted works had horizontal internal tunnels, while these ones studied here have both horizontal (in the space between main fins) and vertical tunnels, Fig. 5. It was assumed that evaporation takes place in the same way in both tunnels. The holes in the foil act as elements through which the liquid is supplied to the tunnel. The liquid flows along the tunnel, and the evaporation takes place from menisci in four corners of the tunnel.

Fig. 5

Evaporation in horizontal and vertical tunnels inside the tunnel structure

4 Calculations

4.1 Overall heat flux

According to the former approach [4], complemented with our own modifications, overall heat flux consists of external heat flux—q_ext, heat flux in the tunnel—q_tun, and heat flux transferred from the fin surface—q_f.

$$ {\text{q}}_{\text{ov}} = {\text{q}}_{\text{tun}} + {\text{q}}_{\text{ext}} + {\text{q}}_{\text{f}} $$

(1)

Overall heat flux was supplemented with a term referring to heat transfer on the fin face surface, assuming that on its face surface heat transfer takes place through convection. This modification was chosen because surfaces used by Chien and Webb [4] consisted of microfins and perforated foil, whereas our tunnel surfaces are composed of fins, microfins and foil with holes.

4.2 Tunnel heat flux

After Chien and Webb [4, 5] it has been assumed that liquid evaporation occurs in the tunnel corners, Fig. 6. The overall latent heat of evaporation while one bubble is being formed can be represented as an integral:

$$ {\text{Q}}_{\text{tun}} = \int\limits_{0}^{1/\omega } {\Updelta {\text{T}}_{\text{w,sat}} \left[ {2{\text{Ln}}\int\limits_{0}^{\pi /4} {\frac{{\lambda_{1} {\text{R}}_{\text{ms}} ({\text{t}}){\text{d}}\varphi }}{{\left[ {{\text{R}}_{\text{ms}} ({\text{t}}) + \delta_{\text{n - ev}} } \right]\left( {\cos \,\varphi } \right)^{ - 1} - {\text{R}}_{\text{ms}} ({\text{t}})}}} } \right]{\text{dt}}} $$

(2)

Fig. 6

Vapor-liquid meniscus in the tunnel corner of the capillary-porous structure, by Chien and Webb [4]

The heat flux in the tunnel is determined from:

$$ {\text{q}}_{\text{tun}} = \frac{{{\text{Q}}_{\text{tun}} \omega }}{{{\text{F}}_{\text{tun}} }} $$

(3)

In order to calculate bubble departure frequency ω = (Δt_stb + Δt_dvp)⁻¹ proposed by Chien and Webb, dependences for standby period Δt_stb and bubble development period Δt_dvp were used. In calculations it was also assumed that liquid suction period Δt_itk, being much shorter than the preceding periods, was negligible.

Q_tun was calculated with appropriate procedure in Mathematica, where integration was done by changing the value of the meniscus radius in each time step, according to the equation:

$$ {\text{R}}_{{{\text{ms}},{\text{t}} + \Updelta {\text{t}}}} = \left[ {{\text{R}}_{{{\text{ms}},{\text{t}}}}^{2} + \frac{{\Updelta {\text{V}}_{\text{l}} }}{{{\text{Ln}}\left( {1 - \pi /4} \right)}}} \right]^{1/2} $$

(4)

where: ΔV_l—change in the liquid volume in one time step.

From the mass and energy balance it follows that:

$$ \Updelta {\text{V}}_{\text{l}} = \Updelta {\text{Q}}_{\text{ms}} \rho_{\text{l}}/\hbox{h}_{\text{lv}} $$

(5)

On the basis of Eqs. 2 and 5, the liquid volume change in one time step is as follows:

$$ \Updelta {\text{V}}_{\text{l}} = \Updelta {\text{t}}\frac{{2{\text{Ln}}\Updelta {\text{T}}_{\text{w,sat}} }}{{{\text{h}}_{\text{lv}} {{\uprho}}_{\text{l}} }}\int\limits_{0}^{\pi /4} {\frac{{{{\uplambda}}_{\text{l}} {\text{R}}_{\text{ms}} \left( {\text{t}} \right){\text{d}}\varphi }}{{\left[ {{\text{R}}_{\text{ms}} \left( {\text{t}} \right) + \delta_{\text{n - ev}} } \right]\left( {\cos \varphi } \right)^{ - 1} - {\text{R}}_{\text{ms}} \left( {\text{t}} \right)}}} $$

(6)

The integration (2–6) starts with the initial value of meniscus radius R_ms = R_ms,init, characteristic of the onset of vapor bubble forming cycle. The meniscus radius decreases in succeeding time steps until R_ms = R_ms,itk. The initial meniscus radius R_ms,init depends on the quantity of liquid which flows into the tunnel during the cycle of vapor bubble forming.

From the geometric analysis R_ms,init is given by:

$$ {\text{R}}_{\text{ms,init}} = \left[ {{\text{R}}_{\text{ms,itk}}^{ 2} + \frac{{\Updelta {\text{f}}_{\text{l,cl}} }}{{{\text{n}}\left( {1 - \pi /4} \right)}}} \right]^{1/2} $$

(7)

where Δf_l,cl is the change of the meniscus cross-sectional area for one bubble forming cycle. It is proportional to the quantity of liquid flowing into the tunnel during this cycle.

For calculating R_mk,init and Δf_l,cl Chien and Webb [4] proposed the procedure based on the results of their own experimental studies.

4.3 External heat flux

The external heat flux was assumed to be between two asymptotes. One of them results from the assumption that the heat transfer depends on the unsteady conduction and according to the solution by Mikic and Rohsenow [8] q_ext,MR is expressed by the following equation:

$$ {\text{q}}_{\text{ext,MR}} = 2\sqrt {\pi {{\uplambda}}_{\text{l}} {{\uprho}}_{\text{l}} {\text{c}}_{\text{p,l}} \omega } {\;\text{d}}_{\text{d}}^{ 2}\, {\text{N}}\left( {{\text{T}}_{\text{w}} - {\text{T}}_{\text{sat}} } \right) $$

(8)

The other asymptote corresponds to the steady convection induced by the departing vapor bubbles. It was obtained by modifying the expression of Haider and Webb [6] who investigated this problem referring to a flat surface:

$$ {\text{q}}_{\text{ext}} = {\text{q}}_{{{\text{ext}},{\text{MR}}}} \left[ {1 + \left( {\frac{0.66\pi C}{{\Pr^{1/6} }}} \right)^{2} } \right]^{1/2} $$

(9)

In expression Eq. 9 for external heat flux the value of constant C was chosen according to the authors’ experimental data. In their further modifications constant C was replaced with approximation polynomial that contained four experimental constants. In this work the constant was replaced by our own similarity number that characterizes the studied tunnel structure (taking into consideration the microfin thickness and diameters of foil holes) and liquid and vapor properties [7]. Number M was selected under the trial-and-error method, through testing various combinations of quantities describing the properties of boiling liquid and studied tunnel structure:

$$ {\text{M}} = \frac{{\delta_{\text{mf}} }}{{{\text{d}}_{\text{p}} }}\frac{{\rho_{\text{v}} }}{{\rho_{\text{l}} }} $$

(10)

Number M characterizes liquid and vapor properties in relation to geometrical parameters of the structure. It was chosen from among several tested simplexes.

Finally, the heat flux received from the external surface is given by the dependence:

$$ {\text{q}}_{\text{ext}} = 2\sqrt {\pi \lambda_{\text{l}} \rho_{\text{l}} {\text{c}}_{{{\text{p}},{\text{l}}}} \omega } {\;\text{d}}_{\text{d}}^{2} {\;\text{N}}({\text{T}}_{\text{w}} - {\text{T}}_{\text{sat}} )\left[ {1 + \left( {\frac{{0,66\pi {\text{M}}}}{{\hbox{Pr}^{1/6} }}} \right)^{2} } \right]^{1/2} $$

(11)

Figure 7 compares the value of q_ext(ΔT_w,sat) for own dependence (11) with the values which result from the mathematical models discussed briefly at the beginning of the paper:

Fig. 7

Comparison of q_ext(ΔT_w,sat) values by own dependence, Eq. 11, and dependences for the models of Ayub and Bergles [1], Chien and Webb [4], Mikic and Rohsenow [8] and Nakayama et al. [9]

• own dependence, Eq. 11;

• Mikic and Rohsenow [8], Webb and Haider [12], Eq. 8;

• Nakayama et al. [9], ${\text{q}}_{\text{ext}} = \left( {\frac{{\Updelta {\text{T}}}}{\text{C}}} \right)^{\text{a}} {\text{N}}^{\text{b}} ,$ where C, a and b are experimentally determined constants (C = 0.05 K m^4/5W^−3/5, a = 5/3, b = 1/3);

• Ayub and Bergles [1], ${\text{q}}_{\text{ext}} = \left( {\frac{{\Updelta {\text{T}}}}{\text{C}}} \right)^{\text{a}} {\text{N}}^{\text{b}} ,$ where C, a and b are experimentally determined constants (C = 0.075 K m^4/5W^−3/5, a = 5/3, b = 1/3);

• Chien and Webb [4], Haider and Webb [6], Eq. 9, constant C = 6.42.

Points in Fig. 7 were computed on the basis of dependences named above, and the solid lines denote their power approximation on a double logarithmic scale. The computed values of q_ext(ΔT_w,sat) are in fixed proportions to each other, which results from the use of various experimental constants in the discussed mathematical models of the boiling process inside the tunnels.

Calculations were performed for those values of fin base superheat ΔT_w,sat = T_w−T_sat, for which the experimental values of heat flux q_exp, presented in Fig. 10 [7] were measured in own studies.

The broad scatter of q_ext values, as seen in Fig. 7, results in part from the adoption of nucleation site densities calculated from the own model (modified [4], model). In their models, Nakayama et al. [9] and Ayub and Bergles [1] applied their own dependences for determining nucleation site density. Despite the fact that the own dependence, Eq. 11, includes an analogical multiplier, as in dependences presented in Chien and Webb [4], Haider and Webb [6], the introduction of number M makes values q_ext comparable with dependence of Mikic and Rohsenow [8].

4.4 Heat flux transferred from the fin

The heat flux transferred from the main fin surface q_f is given by:

$$ {\text{q}}_{\text{f}} = \lambda_{\text{m}} {\text{m}}({\text{T}}_{\text{w}} - {\text{T}}_{\text{sat}} )\frac{{\frac{\alpha }{{{\text{m}}\lambda_{\text{m}} }} + {\text{tgh}}({\text{mh}}_{\text{f}} )}}{{1 + \frac{\alpha }{{{\text{m}}\lambda_{\text{m}} }}{\text{tgh}}({\text{mh}}_{\text{f}} )}} $$

(12)

where: m² = α Π/(λ_m δ_f a).

With the assumption that the tunnel is fully filled with vapor, Pastuszko and Poniewski [11] obtained the dependence for the average thermal conductivity:

$$ \lambda_{\text{m}} = \frac{{\lambda_{\text{v}} {\text{h}}_{\text{mf}} {\text{w}}_{\text{tun}} + \lambda_{\text{Cu}} \left( {\left( {\delta_{\text{mf}} + w_{\text{tun}} } \right){{\delta_{\text{f}} } \mathord{\left/ {\vphantom {{\delta_{\text{f}} } {2 - {\text{h}}_{\text{mf}} {\text{w}}_{\text{tun}} }}} \right. \kern-\nulldelimiterspace} {2 - {\text{h}}_{\text{mf}} {\text{w}}_{\text{tun}} }}} \right)}}{{\left( {\delta_{\text{mf}} + {\text{w}}_{\text{tun}} } \right){{\delta_{\text{f}} } \mathord{\left/ {\vphantom {{\delta_{\text{f}} } 2}} \right. \kern-\nulldelimiterspace} 2}}} $$

(13)

4.5 Calculation algorithm

The following calculation algorithm was used:

• 1. calculating the diameter of the vapor bubble departure for the set pore diameter and known heat properties of the boiling liquid, according to [4],

• 2. determining the bubble growth time Δt_dvp for the set ΔT_w,sat and the diameter computed in step 1,

• 3. determining the initial value of the meniscus radius,

• 4. calculating the latent heat of evaporation during the formation of one bubble,

• 5. calculating the standby period Δt_stb and the radius of the meniscus value R_ms,dvp at the beginning of the growth period,

• 6. determining heat flux Q_tun for Δt_stb < t < Δt_dvp and decreasing radius of the meniscus R_ms,

• 7. determining the bubble departure frequency ω = (Δt_stb + Δt_dvp)⁻¹ and heat flux in the tunnel q_tun,

• 8. calculating the density of nucleation sites,

• 9. calculating heat flux q_ext,

• 10. determining heat flux on the fin surface,

• 11. determining overall heat flux.

The integration starts from the initial value of the meniscus radius R_ms = R_ms,init, the right value for the beginning of the vapor bubble formation. The radius decreases with the subsequent time steps until it reaches the value of R_ms = R_ms,itk.

5 Calculation results

Figures 8, 9 and 10 present:

Fig. 8

The shares of heat flux, which result from: a evaporation from liquid menisci q_tun, b external heat flux q_ext; c heat transfer on the fin q_f—in the total heat flux q_ov in own theoretical model for R-123

Fig. 9

The shares of heat flux, which result from: a evaporation from liquid menisci q_tun, b external heat flux q_ext, c heat transfer on the fin q_f—in the total heat flux q_ov in own theoretical model for ethanol

Fig. 10

The shares of heat flux, which result from: a evaporation from liquid menisci q_tun, b external heat flux q_ext; c heat transfer on the fin q_f—in the total heat flux q_ov in own theoretical model for water

• (a) the share of external heat flux q_ext/q_ov, which is determined by the unsteady heat conduction and convection caused by departing vapor bubbles;

• (b) the share of heat flux resulting from evaporation from liquid menisci—q_tun/q_ov;

• (c) the share of heat flux which is the effect of heat transfer on the fin in the total heat flux—q_f/q_ov for R-123, ethanol and the distilled water.

It can be seen that particular portions in the overall heat flux change with the heat flux increase for the three boiling liquids: R-123, ethanol and the distilled water.

For R-123, Fig. 8, q_tun has the largest share of the heat flux in the heat flux range 7–11 kW m⁻². Its share of the total heat flux decreases with the heat flux increase.

The external heat flux for q_ext > 11 kW m⁻² has the largest share in q_ov that is q_ext/q_ov increases with the heat flux increase.

Figure 8 shows that the heat flux for R-123 resulting from the heat transfer on the fin has the smallest share of q_ov. The share of q_f/q_ov decreases with the heat flux increase. Particular shares in q_ov are as follows:

• q_tun is 8–67% of q_ov;

• q_ext is 21–87% of q_ov;

• q_f is 4–22% of q_ov.

In the Nakayama et al. [9] model (for R-11) the share of q_tun increases when the heat flux decreases.

In the model by Chien and Webb [4] q_tun rates approximately 15–30% of the total heat flux and increases for low heat fluxes. They also noticed that q_ext/q_ov is smaller than q_tun/q_ov and compared the tunnel heat flux share in the total heat flux for R-134a, R-22 and R-123.

The ratio q_tun/q_ov was larger for R-134a and R-22 than for R-123 at the same heat flux. Such a result was expected due to significantly different values of vapor density of the investigated boiling liquids [5]. Their second conclusion was that according to Eq. 11, the external heat flux q_ext was proportional to ω ^0.5d ²_d N. From this it follows that q_ext may be the effect of smaller mixing of bubbles on the external surface.

For the ethanol, Fig. 9, and heat fluxes from 5 to 200 kW m⁻², q_tun has the highest share in q_ov. Its share decreases with the increase of q_ov. The external heat flux increases with increasing q_ov and for q = 5–10 kW m⁻² it has the smallest share of q_ov, whereas for q_ov > 200 kW m⁻² it has the largest share of q_ov. The heat flux coming from the heat transfer on the fin q_f for q_ov > 11 kW m⁻² has the smallest part of the total heat flux value and decreases with increasing q_ov.

Particular shares in q_ov are as follows:

• q_tun is 24–81% of q_ov;

• q_ext is 7–71% of q_ov;

• q_f is 3–18% of q_ov.

For the distilled water, Fig. 10, for heat fluxes from 11 to 300 kW m⁻², q_tun has the largest share in q_ov and decreases with the heat flux increase. For q_ov > 400 kW m⁻², q_ext is the largest part of q_ov; the external heat flux increases with increasing q_ov.

The heat flux connected with the heat transfer through the fin decreases with increasing q_ov and for q_ov > 30 kW m⁻² has the smallest share in overall heat flux.

Particular shares of q_ov are as follows:

• q_tun is 22–78% of q_ov;

• q_ext is 13–72% of q_ov;

• q_f is 3–29% of q_ov.

On the basis of the former studies [4, 5] and Figs. 8, 9, 10 it has been concluded that the type of boiling liquid influences the shares of particular heat fluxes in q_ov. For ethanol and distilled water, similar tendencies occur in the changes of particular heat flux shares. On the basis of the Chien and Webb model, supplemented by our own modifications we were able to calculate the theoretical heat flux for R-123, ethanol and water for finned surfaces with microfins and perforated foil.

Figure 11 compares theoretical and experimental value of the overall heat flux.

Fig. 11

A comparison of the theoretical and experimental heat flux [7]

The model-based theoretical heat flux for R-123, ethanol and water reflects the experimental data with accuracy equal to ±40% (87% of the results fit the given accuracy range). Large discrepancies between theoretical and experimental data for the heat flux over 200 kW m⁻² especially, for the boiling of water or, to a lesser degree, for ethanol result from vapor bubble coalescence. Similar tendency occurs in the model described in Pastuszko and Poniewski [11].

6 Conclusions

The analysis of several models for boiling on technically smooth and/or finned surfaces with various porous coatings led to the choice of the Chien and Webb model [4] as suitable for our theoretical considerations.

The authors proposed the generalization of the former model over finned structures with microfins and perforated foil (tunnel structures) through the introduction of their own similarity number that characterizes the porous structure and vapor and liquid properties, and by the addition of term q_f, describing heat transfer on the fin, to the overall heat flux.

The Haider and Webb [6] model was used to determine the external heat flux. The experimental constants given by the Chien and Webb model [4] were employed for determining the theoretical heat flux.

The use of finned surfaces with microfins and perforated foil (tunnel structures) induced the increase in heat flux and heat transfer coefficients along the whole nucleate boiling range for water, ethanol and R-123, with regard to finned surfaces with microfins without foil, smooth fins and technically smooth surface.

The presented model makes it possible to calculate the theoretical heat flux for water, ethanol and R-123 refrigerant. The obtained agreement of the results is satisfactory for small and medium heat fluxes with regard to water and ethanol and for the full range of the used heat fluxes for the boiling of R-123.