Skip to main content
SpringerLink
Log in

Multiple Steady State Solutions Resulting From Coupling Between Mixed Convection And Radiation In An Inclined Channel

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

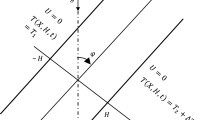
In this work, we present a numerical study of mixed convection coupled with radiation in an inclined channel with an aspect ratio B = L′/H′=10, and locally heated from one side. Convective, radiative and total Nusselt numbers, evaluated on the cold surface and at the exit of the channel, are presented for different combinations of the governing parameters namely, the surface emissivity (0 ≤ ε ≤ 1), the Reynolds number (10 ≤ Re ≤ 50), the inclination of the channel with respect to the horizontal surface (0° ≤ θ ≤ 90°) and the Rayleigh number (Ra = 105). The ratio, R = QC/QE, of the heat quantities, leaving the channel through the cold wall, QC, and through the exit, QE, is presented to identify the most favorable issue to the heat transfer in the studied configuration. The results obtained show that the flow structure is significantly altered by radiation which contributes to reduce or to enhance the number of the solutions obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

B:

aspect ratio of the channel, B = L′/H′

cv:

convection

Fij:

view factor between Si and Sj elements

g:

acceleration due to the gravity, m/s2

H′:

height of the channel, m

Ii:

dimensionless irradiation, \(I_{\text{i}} = {{I{\prime}_{\text{i}} } \mathord{\left/ {\vphantom {{I{\prime}_{\text{i}} } {\sigma T{\prime}_{\text{C}}^4 }}} \right. \kern-\nulldelimiterspace} {\sigma T{\prime}_{\text{C}}^4 }}\)

Ji:

dimensionless radiosity, \(J_{\text{i}} = {{J{\prime}_{\text{i}} } \mathord{\left/ {\vphantom {{J{\prime}_{\text{i}} } {\sigma T{\prime}_{\text{C}}^4 }}} \right. \kern-\nulldelimiterspace} {\sigma T{\prime}_{\text{C}}^4 }}\)

L′:

length of the channel, m

Nr:

convection-radiation interaction parameter, \(N_{\text{r}} = {{\sigma T{\prime}_{\text{C}}^4 H{\prime}} \mathord{\left/ {\vphantom {{\sigma T{\prime}_{\text{C}}^4 H{\prime}} {\lambda \left( {T{\prime}_{\text{H}} - T{\prime}_{\text{C}} } \right)}}} \right. \kern-\nulldelimiterspace} {\lambda \left( {T'_{\text{H}} - T'_{\text{C}} } \right)}}\)

Nu:

average Nusselt number

Pr:

Prandtl number, Pr = ν /α

Qr:

dimensionless radiative heat flux, \(Q_{\text{r}} = {{Q{\prime}_{{\text{ r}}} } \mathord{\left/ {\vphantom {{Q{\prime}_{{\text{ r}}} } {\sigma T{\prime}_{\text{C}}^4 }}} \right. \kern-\nulldelimiterspace} {\sigma T{\prime}_{\text{C}}^4 }}\)

R:

ratio of the heat quantities evacuated through the cold wall and the exit, R = QC/QE

Ra:

Rayleigh number, Ra = g β (T′H − T′C) H′3/α ν

rd:

radiation

Re:

Reynolds number, Re = u′o H′/ν

t:

dimensionless time, t = t′ u′o/H′

T:

dimensionless fluid temperature, T = (T′ − T′C)/(T′H − T′C)

T′C:

temperature of the cold plate, K

T′H:

temperature of the heated elements, K

To:

dimentionless reference temperature, To = T′C/(T′H − T′C)

u′o:

velocity of the imposed flow, m/s

(u, v):

dimensionless horizontal and vertical velocities, (u, v) = (u′, v′)/u′o

(x, y):

dimensionless coordinates, (x, y) = (x′, y′)/H′

α:

thermal diffusivity of fluid, m2/s

β:

thermal expansion coefficient of fluid, 1/K

ε:

emissivity of the walls

λ:

thermal conductivity of fluid, W/(K m)

ν:

kinematic viscosity of fluid, m2/s

Ω:

dimensionless vorticity, Ω = Ω′ H′/u′o

Ψ:

dimensionless stream function, Ψ = Ψ′/u′o H′

σ:

Stéfan-Boltzman constant, σ = 5669×10−8 W/(m2 K4)

θ:

inclination of the channel, (in degree)

C:

cold surface

CR:

critical parameter

E:

exit of the channel

H:

heated surface

I:

inlet of the channel

′:

dimensional variable

References

  1. Tomimura T, Fujii M (1988) Laminar mixed convection heat transfer between parallel plates with localized heat sources. In: Aung W (ed) Proceedings of the International symposium on cooling technology for electronic equipement, Honolulu, pp 233–247

  2. Yücel C, Hasnaoui M, Robillard L, Bilgen E (1993) Mixed convection heat transfer in open ended inclined channels with discrete isothermal heating. Num. Heat Transfer 24: 109–126

    Google Scholar 

  3. Raji A, Hasnaoui M, Zrikem Z (1995) Convection mixte dans un canal incliné de longueur finie contenant des obstacles et chauffé de manière isotherme et discrète. Revue Générale de Thermique, no. 399: 202–209

    Google Scholar 

  4. Hsu TH, Hsu PH, How SP (1997) Mixed convection in partially divided rectangular enclosure. Numerical Heat Transfer Part A, 31: 655–683

    Google Scholar 

  5. Raji A, Hasnaoui M (1998) Mixed convection heat transfer in a rectangular cavity ventilated and heated from the side. Numerical Heat Transfer Part A, 33: 533–548

    Google Scholar 

  6. Raji A, Hasnaoui M (1998) Corrélations en convection mixte dans des cavitées ventilées. Revue Générale de Thermique 37: 874–884

    Article  CAS  Google Scholar 

  7. Raji A, Hasnaoui M (2000) Mixed convection heat transfer in ventilated cavities with opposing and assisting flows. Engineering Computations. Int J Comput Aided Eng Softw 17(5): 556–572

    Article  Google Scholar 

  8. Larson DW, Viskanta R (1976) Transient combined laminar free convection and radiation in a rectangular enclosure. J Fluid Mech Part 1 78: 65–85

    Google Scholar 

  9. Kim DM, Viskanta R (1984) Effect of wall conduction and radiation on natural convection in a rectangular cavity. Numerical Heat Transfer 7:449–470

    Google Scholar 

  10. Balaji C, Venkateshan SP (1993) Interaction of surface radiation with free convection in a square cavity. Int J Heat Fluid Flow 14(3): 260–267

    Article  CAS  Google Scholar 

  11. Akiyama M, Chong QP (1997) Numerical analysis of natural convection with surface radiation in a square enclosure. Numerical Heat Transfer Part A 31: 419–433

    Google Scholar 

  12. Balaji C, Venkateshan SP (1994) Interaction of radiation with free convection in an open cavity. Int J Heat Fluid Flow 15(4): 317–324

    Article  Google Scholar 

  13. Dehghan, AA, Behnia M (1996) Combined natural convection-conduction and radiation heat transfer in a discretely heated open cavity. ASME Trans 118: 56–64

    Google Scholar 

  14. Buller L, McNelis B (1988) Effects of radiation on enhanced electronic cooling. IEEE Trans Components Hybrids Manufacturing Technol 11(4): 538–544

    Google Scholar 

  15. Raji A, Hasnaoui M (2001) Combined mixed convection and radiation in ventilated cavities. Engineering Computations, Int J Comput Aided Eng Softw 18(7): 922–949

    Google Scholar 

  16. Gururaja Rao C, Balaji C, Venkateshan, SP (2002) Effect of surface radiation on conjugate mixed convection in a vertical channel with discrete heat sources in both the walls. Int J Heat Mass Transfer 45: 3331–3347

    Article  CAS  Google Scholar 

  17. Gururaja Rao C, Balaji C, Venkateshan SP (2003) Conjugate mixed convection with surface radiation from a vertical channel with symmetric and uniform wall heat generation. Int J Transport Phenomena 5(2): 75–101

    Google Scholar 

  18. Woods LC (1954) A note on the numerical solution of fourth order differential equations. Aero Quart 5: 176–184

    Google Scholar 

  19. Roache PJ (1982) Computational fluid dynamics. Hermosa Publishers, Albuquerque

Download references

Author information

Authors and Affiliations

  1. Département de Physique, Faculté des Sciences et Techniques, Université Cadi Ayyad, UFR de Chimie Appliquée et Sciences de l’Environnement, Equipe de Modélisation des Ecoulements et des Transferts (EMET), B.P. 523, Béni-Mellal, Maroc

    A. Bahlaoui & A. Raji

  2. Département e Physique, Faculté des Sciences Semlalia, Université Cadi Ayyad, UFR de Thermique et Mécanique des Fluides, Laboratoire de Mécanique des Fluides et d’Energétique, B.P. 2390, Marrakech, Maroc

    M. Hasnaoui

Authors
  1. A. Bahlaoui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Raji
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Hasnaoui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Raji.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bahlaoui, A., Raji, A. & Hasnaoui, M. Multiple Steady State Solutions Resulting From Coupling Between Mixed Convection And Radiation In An Inclined Channel. Heat Mass Transfer 41, 899–908 (2005). https://doi.org/10.1007/s00231-004-0590-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-004-0590-9

Keywords

Search

Navigation