Analysis of ammonia vapor absorption into ammonia water mixtures: mass diffusion flux

Abstract

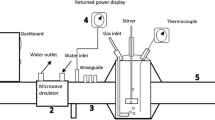
Ammonia absorption phenomenon is investigated experimentally by allowing superheated ammonia vapor to flow into a test cell to be absorbed into a stagnant pool of ammonia water mixtures of several ammonia mass fractions, C_i. Two main objectives are sought in this paper. The first one is to find out the dependency of the total mass absorption, which is estimated by two different methods; interface heat flux and vapor pressure drop, upon C_i. An equation is developed which allows calculating ammonia total mass absorption per unit area for the whole range of C_i. The second objective is to visualize the diffusion process in the liquid mixture. The visualized fringes show two layers with different speeds of fringes propagation. The layer with fast propagation represents pure thermal diffusion while the slow propagation layer is characterized by a superposition of mass and heat diffusions where heat effect is big at short time from starting the absorption and this effect decreases with the elapse of time. Mass diffusion flux is obtained by the developed equation and the visualized fringes and the predicted values from both methods are found to agree well. Mass diffusion flux shows a strong dependency on C_i in a way that it decreases dramatically with increasing C_i.

Appendices

Appendix 1

Heat of solution

The released heat during ammonia vapor absorption depends upon the final concentration of the formed mixture, C_f. When one mole of ammonia vapor is absorbed into huge amount of water liquid, the mixture C_f is almost 0.0 mol fraction, and the reaction can be written as

$$ {\text{NH}}_3 ({\text{g}}) + \infty {\text{H}}_2 {\text{O}}({\text{l}}) \to {\text{NH}}_3 ({\text{aq}}) + Q_1 , $$

(31)

where, Q₁=34.18 kJ/mol is the heat of solution, the same of the standard solution enthalpy $\Delta H_{{\text{sol}}}^0$ at 298 K and 1 atm. The molar heat Q₁ consists of two parts, latent heat of condensation −ΔH_cond with the value of 23.35 kJ/mol at 1 atm, and solution enthalpy −ΔH_sol,0.0. When one mole of ammonia vapor is absorbed into 1 mole of water liquid, the mixture C_f is 0.5 mole fraction and the reaction is written as

$$ {\text{NH}}_3 ({\text{g}}) + {\text{H}}_2 {\text{O}}({\text{l}}) = {\text{NH}}_3 ({\text{H}}_2 {\text{O}}) + Q_2 . $$

(32)

In this case, the heat of solution Q₂ is less than Q₁ of reaction (3131), Q₂=−ΔH_sol,0.5=32.87 kJ/mol. However, because there is no data about the molar heat reactions that cover the whole range of ammonia mass fraction, we consider reaction 31 as a representative of the absorption reaction and, consequently, its molar heat is used in the related calculations.

It is worth mentioning that inside the liquid mixture a chemical reaction takes place to dissociate the ammonium hydroxide into ions:

$$ {\text{NH}}({\text{aq}}) + \infty {\text{H}}_2 {\text{O}} = {\text{NH}}_4^ + + {\text{OH}}^ - + Q_3 $$

(33)

The equilibrium constant of this reaction is very small, of the order 10⁻⁵, which indicates that the concentrations of the ionic products are very small compared to that of the reactants, ammonia and water molecules. This leads us to conclude that the released heat Q₃ inside the liquid mixture is too small to cause an effect.

Appendix 2

Refractive index dependency on amonia mass fraction

Fig. 17

Refractive index of ammonia solution at 297 K [15]

Appendix 3

Concentration distribution by Eq. 20

The initial and boundary conditions of Eq. 20 are

$$ {\text{I}}{\text{.C}}.:t = 0,\quad C = C_{\text{i}} = {\text{const}}{\text{.}} $$

$$ {\text{B}}{\text{.C}}{\text{.}}z = 0,\quad C = C_{\operatorname{int} } = r_0 + r_1 t^{0.5} + r_2 t $$

$$ z = \infty ,\quad C = C_{\text{i}} = {\text{const}}{\text{.}} $$

The solution of Eq. 20 is

$$ \begin{aligned} C(z,t) = \left( {r_0 - C_i } \right){\text{erfc}}\left[ {\frac{z} {{2\sqrt {Dt} }}} \right] + r_1 \Gamma \left( {1.5} \right)\left[ {\frac{{2\sqrt t }} {{\sqrt \pi }}{\text{e}}^{^{ - \frac{{z^2 }} {{4Dt}}} } - \frac{z} {{\sqrt D }}{\text{erfc}}\left( {\frac{z} {{2\sqrt {Dt} }}} \right)} \right] & \\ \quad \quad \quad \;\; + r_2 t\left\{ {\left( {1 + \frac{{z^2 }} {{2Dt}}} \right){\text{erfc}}\left( {\frac{z} {{2\sqrt {Dt} }}} \right) - \frac{z} {{\sqrt {\pi Dt} }}{\text{e}}^{^{ - \frac{{z^2 }} {{4Dt}}} } } \right\} + C_i & \\ \end{aligned} $$

(34)

where, Γ is the gamma function.

Table 4 Coefficients r _j of Eq. 21 for the two cases C_i=0.17 and 0.59 kg/kg