Abstract
We prove a finiteness theorem and a comparison theorem in the theory of étale cohomology of rigid analytic varieties. By a result of Huber, for a quasi-compact separated morphism of rigid analytic varieties with target being of dimension \(\le 1\), the compactly supported higher direct image preserves quasi-constructibility. Though the analogous statement for morphisms with higher dimensional target fails in general, we prove that, in the algebraizable case, it holds after replacing the target with a modification. We deduce it from a known finiteness result in the theory of nearby cycles over general bases and a new comparison result, which gives an identification of the compactly supported higher direct image sheaves, up to modification of the target, in terms of nearby cycles over general bases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We prove a new finiteness theorem and a new comparison theorem on étale cohomology of rigid analytic varieties, more specifically, on the compactly supported higher direct image sheaves for algebraizable morphisms of algebraizable rigid analytic varieties.
1.1 Finiteness and modification
Let k be a non-archimedean field and \(k^\circ \) denote the subring of power pounded elements of k, i.e, the ring of integers. Let \(\mathsf f:\mathsf X\rightarrow \mathsf Y\) be a quasi-compact separated morphism of adic spaces locally of finite type over \(\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) and \(\mathsf F\) be a quasi-constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on \(\mathsf X_\mathrm{\acute{e}t}\), with n an integer invertible in \(k^\circ \). A finiteness theorem of Huber ([11, Theorem 2.1]) states that, if the characteristic of k is zero and if \(\dim \mathsf Y\le 1\), then the compactly supported higher direct image sheaves \(R^i\mathsf f_!\mathsf F\) are again quasi-constructible. Here, roughly speaking, a quasi-constructible sheaf is a sheaf which étale locally admits a stratification by intersections of constructible locally closed subsets and Zariski locally closed subsets such that the restriction to each stratum is locally constant. (See [10, 12] for variants of this finiteness result.)
We note that the analogous statement for \(\mathsf f\) with \(\dim \mathsf Y\ge 2\) fails as pointed out in [11, Example 2.2]. Nonetheless, the author expects that there exists a modification \(\pi :\mathsf Y'\rightarrow \mathsf Y\) such that the pullback \(\pi ^*R^i\mathsf f_!\mathsf F\) is quasi-constructible, and we prove this expectation in the case where \(\mathsf f:\mathsf X\rightarrow \mathsf Y\) and \(\mathsf F\) are algebraizable.
To be precise, let us introduce some notations. For a scheme X locally of finite type over \(k^\circ \), let \(X^\textrm{rig}\) denote the Raynaud generic fiber of the \(\varpi \)-adic completion of X for some pseudo-uniformizor \(\varpi \in k^\circ \), viewed as an adic space. For a morphism \(f:X\rightarrow Y\) of schemes locally of finite type over \(k^\circ \), let \(f^\textrm{rig}\) denote the associated morphism \(X^\textrm{rig}\rightarrow Y^\textrm{rig}\). Finally, for a sheaf \(\mathcal F\) on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\) of a scheme X locally of finite type over \(k^\circ \), let \(\mathcal F^\textrm{rig}\) denote the sheaf on \(X^\textrm{rig}_\mathrm{\acute{e}t}\) obtained by pulling back \(\mathcal F\).
Now we can state our finiteness result:
Theorem 1.1
(Theorem 5.5) Let k be a non-archimedean field and n be an integer invertible in \(k^\circ \). Let \(f:X\rightarrow Y\) be a morphism of schemes of finite type over \(k^\circ \) which is separated and of finite presentation. Let \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\). Then there exists a modification \(\pi :Y'\rightarrow Y\) such that the sheaves \(\pi ^{\textrm{rig}*}R^if^\textrm{rig}_!\mathcal F^\textrm{rig}\) are quasi-constructible.
Our proof is totally different from Huber’s and reproves his finiteness result in the algebraizable case. Contrary to Huber’s case, we do not need any assumption on the characteristic of k. In fact, we will not make any reference to the base field in the proof and will work with much more general setting (see §5 for details).
Further, our approach gives a remarkable simplification of the proof. We do not need any of complicated reduction arguments that Huber made in [11]. We do not rely on deep results used in his proof, namely, the preservation of constructibility by smooth compactly supported pushforward [9, Theorem 6.2.2], and the p-adic Riemann’s existence theorem due to Lütkebohmert [17, Theorem 2.2], which requires the assumption on the characteristic of k. We prove Theorem 1.1 as a direct consequence of the following two results: One is a known finiteness result in the theory of nearby cycles over general bases due to Orgogozo [20], and the other is a new comparison result, which gives an identification of the compactly supported higher direct image sheaves, up to modification of the target, in terms of nearby cycles over general bases. This comparison result is the heart of this paper and will be briefly explained in the next subsection.
The idea of our approach comes from a recent work of K. Ito [16], in which the theory of nearby cycles over general bases is used to study étale cohomology of rigid analytic varieties. Though his aim is different from proving a finiteness result, his work includes a new proof of a special case of Huber’s finiteness result; namely the special case of Theorem 1.1 where \(\dim Y^\textrm{rig}=1\) and \(\mathcal F\) is constant ([16, Theorem 6.10]). Let us mention that his proof does not rely on the p-adic Riemann existence theorem, but still relies on the preservation of constructibility by smooth compactly supported pushforward.
It is natural to ask if one can also apply our argument to higher direct image sheaves without support. The author expects that a similar statement with “quasi-constructible” replaced by “oc-quasi-constructible” (see [10] for the definition and the case where \(\dim \mathsf Y=1\)) holds. However, it seems much more difficult and he does not know how to address it even in the algebraizable case (see Remark 5.6).
One of typical applications of a finiteness result of higher direct image is the existence of a tubular neighborhood that does not change the cohomology. For instance, in [11], the following is proved as a consequence of his finiteness result: Under the assumption that k is of characteristic zero, every hypersurface in an affinoid adic space of finite type over \(\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) admits a tubular (closed) neighborhood that does not change the compactly supported cohomology (see [10, 11, 16] for variants). In a celebrated paper of Scholze [22], such a existence result is used in the proof of the weight monodromy conjecture for varieties of complete intersection.
Similarly, as an application of Theorem 1.1, we give a variant for families of rigid analytic varieties. For instance, we prove the following. We consider an algebraizable family of hypersurfaces parametrized by the unit disk, i.e,  with A topologically of finite type over \(k\langle T\rangle \) and \(\mathsf X\) a hypersurface defined by some \(f\in A\). We show that there exist a small neighborhood \({\mathbb {B}}^1_k(\delta )=\{x\in {\mathbb {B}}^1_k\mid |T(x)|\le \delta \}\) of the origin of \({\mathbb {B}}^1_k\) with \(\delta \in |k^\times |\) and a tubular (closed) neighborhood \(\mathsf X\) defined over the punctured disk \({\mathbb {B}}^1_k(\delta )^*=\{x\in {\mathbb {B}}^1_k\mid 0<|T(x)|\le \delta \}\) which has the same compactly supported higher direct image sheaves on \({\mathbb {B}}^1_k(\delta )^*\). For the precise statement, see Proposition 6.1. This result might lead us to a relative version of Scholze’s approach to the weight monodromy conjecture for varieties of complete intersection.
with A topologically of finite type over \(k\langle T\rangle \) and \(\mathsf X\) a hypersurface defined by some \(f\in A\). We show that there exist a small neighborhood \({\mathbb {B}}^1_k(\delta )=\{x\in {\mathbb {B}}^1_k\mid |T(x)|\le \delta \}\) of the origin of \({\mathbb {B}}^1_k\) with \(\delta \in |k^\times |\) and a tubular (closed) neighborhood \(\mathsf X\) defined over the punctured disk \({\mathbb {B}}^1_k(\delta )^*=\{x\in {\mathbb {B}}^1_k\mid 0<|T(x)|\le \delta \}\) which has the same compactly supported higher direct image sheaves on \({\mathbb {B}}^1_k(\delta )^*\). For the precise statement, see Proposition 6.1. This result might lead us to a relative version of Scholze’s approach to the weight monodromy conjecture for varieties of complete intersection.
1.2 Comparison result
One of the most fundamental results in the theory of étale cohomology of rigid analytic varieties is the comparison theorem between the étale cohomology of an algebraizable rigid analytic variety and the nearby cycle cohomology, due to Fujiwara and Huber ( [5, Corollary 6.6.2], [9, Theorem 5.7.6]). More generally, the results in Huber’s book [9] show the following description of the stalks of the compactly supported higher direct image sheaves. Let k be a non-archimedean field. Let \(f:X\rightarrow Y\) be a separated morphism of schemes of finite type over \(k^\circ \) and \(\mathcal F\) a sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\), for an integer n. We consider the higher direct image \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) by the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) between the Raynaud generic fibers. For every geometric point \(\xi \) (possibly of higher rank) of \(Y^\textrm{rig}\), the stalk \((Rf^\textrm{rig}_!\mathcal F^\textrm{rig})_\xi \) is canonically isomorphic to the cohomology of the nearby cycle taken over the valuation ring \(\kappa (\xi )^+\) corresponding to \(\xi \).
Thus, we know that there is a comparison isomorphism at each geometric point between the stalk of \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) and a suitable nearby cycle cohomology. The main discovery of this article is a uniform construction of those separately constructed isomorphisms. More precisely, we construct a relative variant of nearby cycle cohomology as a complex on \(Y^\textrm{rig}_\mathrm{\acute{e}t}\) and a canonical morphism to \(Rf^\textrm{rig}_!\mathcal F\). Then we prove that the canonical morphism becomes an isomorphism after a modification of Y, under the assumption that n is invertible in \(k^\circ \) and that \(\mathcal F\) is constructible.
For the construction, we use the theory of nearby cycles over general bases as in [14]. We first construct a relative variant of nearby cycle cohomology as a complex \(\Xi _f\mathcal F\) on the topos \(Y\overleftarrow{\times }_YY\) called the vanishing topos of Y (see §2.3 for details). Roughly speaking, the vanishing topos \(Y\overleftarrow{\times }_YY\) is a topos whose points correspond to specializations \(y\leftarrow z\) of two geometric points of Y, and the complex \(\Xi _f\mathcal F\) is a complex whose stalk at \(y\leftarrow z\) is canonically isomorphic to the cohomology of the nearby cycle taken with respect to the specialization \(y\leftarrow z\) over the strict henselization \(Y_{(y)}\). Here, as mentioned in Illusie’s survey article [13, 6.4], the vanishing topos \(Y\overleftarrow{\times }_YY\) receives a canonical morphism of topoi \(\widetilde{\lambda }_Y:(Y^\textrm{rig}_\mathrm{\acute{e}t})^\sim \rightarrow Y\overleftarrow{\times }_YY\) from the étale topos of \(Y^\textrm{rig}\) which sends a geometric point \(\xi \) of \(Y^\textrm{rig}\) to the specialization defined by the closed point and the generic point of the spectrum of the valuation ring \(\kappa (\xi )^+\). Then the desired complex on \(Y^\textrm{rig}_\mathrm{\acute{e}t}\) is defined to be the pullback \(\widetilde{\lambda }^*_Y\Xi _f\mathcal F\).
Theorem 1.2
Let \(f:X\rightarrow Y\) be a compactifiable morphism of schemes of finite type over \(k^\circ \) and \(\mathcal F\) be a sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\), for an integer n. Then there exists a canonical morphism
satisfying the following: Assume that n is invertible in \(k^\circ \), that f is of finite presentation, and that \(\mathcal F\) is constructible. Then, after replacing Y by a modification and f by the base change, the morphism \(\theta _f\) becomes an isomorphism.
We note that the nearby cycle appearing in the description of \((Rf^\textrm{rig}_!\mathcal F^\textrm{rig})_\xi \) is taken over the valuation ring \(\kappa (\xi )^+\), while that appearing in \((\widetilde{\lambda }_Y^*\Xi _f\mathcal F)_\xi \) is taken over the strict henselization \(Y_{(y_\xi )}\), where \(y_\xi \) is the image of the closed geometric point of \(\mathop {\textrm{Spec}}\nolimits \kappa (\xi )^+\) by the natural map \(\mathop {\textrm{Spec}}\nolimits \kappa (\xi )^+\rightarrow Y\). In general, the formation of nearby cycle does not commute with base change, and in particular, the above two nearby cycles are different (and \(\theta _f\) can be non-isomorphic as seen in Example 4.13). But, as proved by Orgogozo in [20], it commutes with base change after a modification, i.e, after replacing Y by a modification and f by the base change, the formation of the nearby cycle commutes with base change. In particular, the above two nearby cycles agree after this replacement.
Once we have proved Theorem 1.2, we can easily deduce Theorem 1.1 from the constructibility of the complex \(\Xi _f\mathcal F\) on the vanishing topos \(Y\overleftarrow{\times }_YY\), which is a consequence of finiteness results on nearby cycles over general bases due to Orgogozo [20].
The canonical morphism \(\theta _f\) in Theorem 1.2 is constructed as a certain base change morphism with respect to a certain square diagram involving the vanishing topoi of X and Y (see Construction 4.7). To check that \(\theta _f\) becomes isomorphic after modification, we show that, using results of Orgogozo in [20], after replacing Y by a modification and f by the base change, the formation of \(\Xi _f\mathcal F\) commutes with base change. After this replacement, the morphism \((\theta _f)_\xi \) induced on the stalks at each geometric point \(\xi \) of \(Y^\textrm{rig}\) is identified with the comparison morphism constructed by Huber.
1.3 Organization of the article
We recall basic definitions and some results on the theory of nearby cycles over general bases in §2. After a preliminary section §3 concerning on adic spaces, we give in §4 the key constructions and prove Theorem 1.2. We deduce Theorem 1.1 from Theorem 1.2 in §5. Finally we deduce the existence of a good tubular neighborhood for families in §6.
Convention For a scheme, or a pseudo-adic space X, we denote the associated étale site by \(X_\mathrm{\acute{e}t}\). We use the same letter X for the associated étale topos by abuse of notation.
A morphism \(f:X\rightarrow Y\) of schemes is called compactifiable if there exist a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) and an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\). Note that, by Nagata’s compactification theorem ([4, Chapter II, Theorem F.1.1]), if f is separated and of finite type and if Y is quasi-compact and quasi-separated, then f is compactifiable.
2 Vanishing topos and Nearby cycles over general bases
2.1 Review of definition
Let \(f:X\rightarrow S\) and \(g:Y\rightarrow S\) be morphisms of topoi. For the definition of the oriented product \(X\overleftarrow{\times }_SY\), we refer to [14]. It comes with morphisms \(p_1:X\overleftarrow{\times }_SY\rightarrow X\) and \(p_2:X\overleftarrow{\times }_SY\rightarrow Y\) and a 2-morphism \(\tau :gp_2\rightarrow fp_1\), and is universal for these data. Recall that giving a 2-morphism \(a\rightarrow b\) between two morphisms \(a,b:X\rightarrow Y\) of topoi is equivalent to giving a morphism \(a_*\rightarrow b_*\) of functors ( [7, 3.2]).
If \(f:X\rightarrow S\) and \(g:Y\rightarrow S\) are morphisms of schemes, then a point of the topos \(X\overleftarrow{\times }_SY\), i.e., a morphism from the punctual topos, is described by a triple (x, y, c) consisting of a geometric point x of X, a geometric point y of Y, and a specialization \(c:g(y)\rightarrow f(x)\) of geometric points, i.e, a morphism \(g(y)\rightarrow S_{(f(x))}\) of schemes. We use the notation \(x\leftarrow y\) for the triple (x, y, c).
For a morphism \(f:X\rightarrow S\) of schemes, the topos \(X\overleftarrow{\times }_SS\) is called the vanishing topos and we have the natural morphism \(\Psi _f:X\rightarrow X\overleftarrow{\times }_SS\) induced from \(\textrm{id}_X:X\rightarrow X\), \(f:X\rightarrow S\), and the 2-morphism \(\textrm{id}:f\rightarrow f\) by the universal property of \(X\overleftarrow{\times }_SS\). For a ring \(\Lambda \), the nearby cycle functor \(R\Psi _f:D^+(X,\Lambda )\rightarrow D^+(X\overleftarrow{\times }_YY,\Lambda )\) is defined to be the derived functor \(R(\Psi _f)_*\).
Remark 2.1
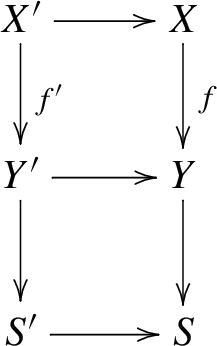
Let X be a scheme and \(\Lambda \) be a ring. We consider the 2-commutative diagram
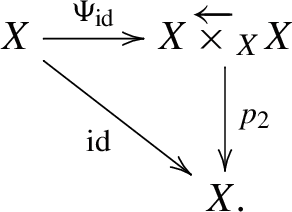
Recall that the morphism \(p_2^*\rightarrow R\Psi _\textrm{id}\) of functors \(D^+(X,\Lambda )\rightarrow D^+(X\overleftarrow{\times }_XX,\Lambda )\) induced by \(p_2\Psi _\textrm{id}\cong \textrm{id}\) is an isomorphism [14, Proposition 4.7].
For a morphism \(f:X\rightarrow S\) of schemes, we have the 2-commutative diagram
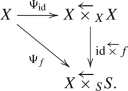
Thus, we have canonical isomorphisms
Notation 2.2
(Sliced nearby cycles) Let \(f:X\rightarrow S\) be a morphism of schemes and \(s\leftarrow t\) be a point of \(S\overleftarrow{\times }_SS\). We consider the diagram
of schemes, where the first map is induced by the specialization map \(S_{(t)}\rightarrow S_{(s)}\) corresponding to \(s\leftarrow t\). The functor \(i_s^*Rj_{(t)*}:D^+(X\times _SS_{(t)},\Lambda )\rightarrow D^+(X_s,\Lambda )\) (or \(D^+(X,\Lambda )\rightarrow D^+(X_s,\Lambda )\)) is denoted by \(R\psi _f^{s\leftarrow t}\). We call it the sliced nearby cycle functor over \(s\leftarrow t\) for f. As in [15, 1.3], denoting the composite \(X_s\cong X_s\overleftarrow{\times }_St\rightarrow X\overleftarrow{\times }_SS\) by \(\iota _{s\leftarrow t}\), we have a canonical isomorphism
of functors \(D^+(X,\Lambda )\rightarrow D^+(X_s,\Lambda )\).
2.2 Base change morphisms
We recall the base change morphism for \(R\Psi \). For a morphism \(f:X\rightarrow Y\) of schemes, we consider base change by a morphism \(Y^\prime \rightarrow Y\). Consider the Cartesian diagram
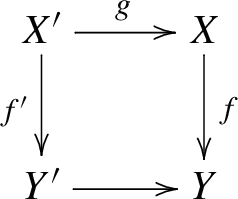
of schemes, which induces the diagram of topoi
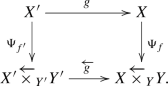
We consider the base change morphism
Definition 2.3
Let \(f:X\rightarrow Y\) be a morphism of schemes, \(\Lambda \) a ring, and \(\mathcal F\) an object of \(D^+(X,\Lambda )\). We say that the formation of \(R\Psi _f\mathcal F\) commutes with base change if, for every morphism \(Y'\rightarrow Y\) of schemes, the base change morphism
defined above is an isomorphism.
The following analogue of the proper base change theorem is indispensable in our construction.
Lemma 2.4
Let
be a commutative diagram of schemes with the upper square being Cartesian. We assume that f is proper. We consider the diagram of topoi

Let \(\Lambda \) be a torsion ring. Then the base change morphism
is an isomorphism of functors \(D^+(X\overleftarrow{\times }_SS,\Lambda )\rightarrow D^+(Y'\overleftarrow{\times }_{S'}S',\Lambda )\).
Though this is essentially proved in [20, Lemme 10.1], we include a proof for completeness.
Recall that, if \(X\rightarrow S\) and \(Y\rightarrow S\) are coherent morphisms of coherent topoi, then the oriented product \(X\overleftarrow{\times }_SY\) is also coherent [14, Lemma 2.5]. Thus, by [6, Proposition 9.0], it has enough points, that is, a morphism \(\mathcal F\rightarrow \mathcal G\) of objects of \(X\overleftarrow{\times }_SY\) is an isomorphism if and only if the morphism \(\mathcal F_{x\leftarrow y}\rightarrow \mathcal G_{x\leftarrow y}\) is bijective for any point \(x\leftarrow y\) of \(X\overleftarrow{\times }_SY\) [6, Définition IV.6.4.1]. This implies that for any diagram \(X\rightarrow S\leftarrow Y\) of schemes, the oriented product \(X\overleftarrow{\times }_SY\) has enough points.
Proof (Proof of Lemma 2.4)
[Proof of Lemma 2.4] For each object \(\mathcal F\) of \(D^+(X\overleftarrow{\times }_SS,\Lambda )\) and for each point \(y'\leftarrow t'\) of \(Y'\overleftarrow{\times }_{S'}S'\), we check that the morphism induced on the stalks is an isomorphism. For this, we may assume that \(Y'=Y'_{(y')}\) and \(Y=Y_{(y)}\), where y is the image of \(y'\). Further, by [14, 1.12 and 1.13], we may assume that \(S'=S'_{(s')}\) and \(S=S_{(s)}\) are strictly local, where \(s'\) and s are the images of \(y'\) in \(S'\) and S respectively. We denote the image of \(t'\) in S by t. Then the morphism \((R(f\overleftarrow{\times }\textrm{id})_*\mathcal F)_{y\leftarrow t}\rightarrow (R(f'\overleftarrow{\times }\textrm{id})_*{\varphi '}^*\mathcal F)_{y'\leftarrow t'}\) induced on the stalks is identified with the morphism
induced by the adjunction morphism \(\textrm{id}\rightarrow R\varphi '_*{\varphi '}^*\). We consider the diagram
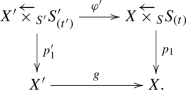
The morphism in question is identified with
Then, by the (usual) proper base change theorem, it suffices to show that the base change morphism \(g^*Rp_{1*}\mathcal F\rightarrow Rp'_{1*}{\varphi '}^*\mathcal F\) is an isomorphism. We check that, for each geometric point \(x'\) of \(X'\), the morphism \((Rp_{1*}\mathcal F)_x\rightarrow (Rp'_{1*}{\varphi '}^*\mathcal F)_{x'}\) induced on the stalks is an isomorphism, where x is the image of \(x'\). But it is identified with the natural morphism \(R\Gamma (X_{(x)}\overleftarrow{\times }_SS_{(t)},\mathcal F)\rightarrow R\Gamma (X'_{(x')}\overleftarrow{\times }_{S'}S'_{(t')},{\varphi '}^*\mathcal F)\), which is an isomorphism since \(\varphi ':X'_{(x')}\overleftarrow{\times }_{S'}S'_{(t')}\rightarrow X_{(x)}\overleftarrow{\times }_SS_{(t)}\) is a local morphism of local topoi [14, Corollaire 2.3.2]. Thus, the assertion follows. \(\square \)
2.3 Higher direct image with compact support for vanishing topoi
Let S be a scheme and \(f:X\rightarrow Y\) be a morphism of S-schemes. We consider the natural morphism
We assume that \(f:X\rightarrow Y\) is compactifiable and choose a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \({{\bar{f}}}j=f\). Note that the topos \(X\overleftarrow{\times }_SS\) is an open subtopos of \({{\bar{X}}}\overleftarrow{\times }_SS\) (in the sense of [7, 9.2.1]), and hence, the functor \((j\overleftarrow{\times }\textrm{id})^*\) admits a left adjoint \((j\overleftarrow{\times }\textrm{id})_!\) by [7, Proposition 9.2.4]. For a torsion ring \(\Lambda \), we define a functor
to be the composite \(R({{\bar{f}}}\overleftarrow{\times }\textrm{id})_*\circ (j\overleftarrow{\times }\textrm{id})_!\) (cf. [18, Construction 1.8]). Lemma 2.4 (together with [3, 3.3]) implies that the composite \(R({{\bar{f}}}\overleftarrow{\times }\textrm{id})_*\circ (j\overleftarrow{\times }\textrm{id})_!\) is independent of the choice of a compactification up to a canonical isomorphism. Lemma 2.4 also implies the following:
Lemma 2.5
Let notation be as in Lemma 2.4. We assume that f is compactifiable. Then we have a canonical isomorphism
of functors \(D^+(X\overleftarrow{\times }_SS,\Lambda )\rightarrow D^+(Y'\overleftarrow{\times }_{S'}S',\Lambda )\).
We consider a pair \((X,L_X)\) of a scheme X and a constructible closed subset \(L_X\) of X. We call such a pair a scheme with support. A morphism \(f:(X,L_X)\rightarrow (Y,L_Y)\) of schemes with support is a morphism \(f:X\rightarrow Y\) of schemes such that \(L_X\subset f^{-1}(L_Y)\). We often regard \(L_X\) as a subscheme of X with the reduced scheme structure.
Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) be an object of \(D^+(X,\Lambda )\). We are interested in the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) on \(L_Y\overleftarrow{\times }_YY\), where \(f\overleftarrow{\times }\textrm{id}\) denotes the natural morphism \(L_X\overleftarrow{\times }_YY\rightarrow L_Y\overleftarrow{\times }_YY\), and where the restriction of \(R\Psi _f\mathcal F\) to \(L_X\overleftarrow{\times }_YY\) is also denoted by \(R\Psi _f\mathcal F\). This complex plays a role of a family of nearby cycle cohomology, which was denoted by \(\Xi _f\mathcal F\) in the introduction: more precisely, with Notation 2.2, for a point \(y\leftarrow z\) of the topos \(L_Y\overleftarrow{\times }_YY\), the stalk of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) at \(y\leftarrow z\) is identified with the compactly supported cohomology of the sliced nearby cycle complex over \(y\leftarrow z\) for f, i.e., we have a canonical isomorphism
Construction 2.6
Let \(\mathcal F\) be an object of \(D^+(X,\Lambda )\). We study a base change morphism for the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\). Let
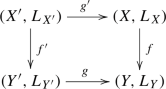
be a Cartesian diagram of schemes with support (being Cartesian means that the underlying diagram of schemes is Cartesian and \({f'}^{-1}(L_{Y'})\cap {g'}^{-1}(L_X)=L_{X'}\)). Recall that we have the base change morphism
where \(\overleftarrow{g'}\) is the natural morphism \(L_{X'}\overleftarrow{\times }_{Y'}Y'\rightarrow L_{X}\overleftarrow{\times }_YY\) (see the beginning of §2.2). Combining this with the base change isomorphism in Lemma 2.5, we obtain
where \(\overleftarrow{g}\) denotes the natural morphism \(L_{Y'}\overleftarrow{\times }_{Y'}Y'\rightarrow L_Y\overleftarrow{\times }_YY\).
Remark 2.7
-
1.
The morphism \(\alpha \) is not an isomorphism in general (see §2.5).
-
2.
By Lemma 2.5, if the formation of \(R\Psi _f\mathcal F\) commutes with base change, then so does that of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\).
-
3.
The morphism \(\alpha \) is an isomorphism if f is proper and if \(\Lambda \) is killed by an integer invertible on Y (even when the formation of \(R\Psi _f\mathcal F\) does not commute). In fact, for each point \(y'\leftarrow z'\) of \(Y'\overleftarrow{\times }_{Y'}Y'\), by the proper base change theorem, the morphism induced by \(\alpha \) on the stalks is identified with the canonical morphism \(R\Gamma (X_z,\mathcal F)\rightarrow R\Gamma (X'_{z'},\mathcal F)\), which is an isomorphism by the invariance of the étale cohomology under change of base separably closed field ([2, Corollaire 1.6]).
It will be convenient to prepare the following notation.
Definition 2.8
For a morphism \(f:(X,L_X)\rightarrow (Y,L_Y)\) of schemes with support with \(f:X\rightarrow Y\) being compactifiable, we consider the natural morphism \(\overleftarrow{f}:L_X\overleftarrow{\times }_XX\rightarrow L_Y\overleftarrow{\times }_YY\) of topoi. We define a functor
by \(R\overleftarrow{f}_!=R(f\overleftarrow{\times }\textrm{id})_!R(\textrm{id}\overleftarrow{\times }f)_*\).
Lemma 2.9
Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. We take morphisms \((X,L_X)\overset{j}{\rightarrow }({{\bar{X}}},L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow } (Y,L_Y)\) of schemes with support such that \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) is a proper morphism, \(j:X\rightarrow {{\bar{X}}}\) and \(L_X\rightarrow L_{{{\bar{X}}}}\) are open immersions, and \({{\bar{f}}}j=f\). Then we have a canonical isomorphism
where \(\overleftarrow{{{\bar{f}}}}\) denotes the natural morphism \(L_{{{\bar{X}}}}\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\rightarrow L_Y\overleftarrow{\times }_YY\) and \(\overleftarrow{j}\) denotes the natural open immersion \(L_X\overleftarrow{\times }_XX=L_X\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\rightarrow L_{{{\bar{X}}}}\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\).
Proof
Consider the diagram of topoi
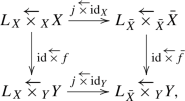
which induces a natural isomorphism
Its inverse induces a morphism
By adjunction, we obtain
Now let i denote the closed immersion \(Z=L_{{{\bar{X}}}}{\setminus } L_X\rightarrow L_{{{\bar{X}}}}\). Then the base change morphism
is an isomorphism by the proof of [18, Corollary 1.2]. Thus, the morphism (2.1) is an isomorphism, and hence, we obtain a canonical isomorphism \(R\overleftarrow{f}_!\cong R\overleftarrow{{{\bar{f}}}}_*\overleftarrow{j}_!\).
\(\square \)
Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. We consider the following morphisms of topoi:
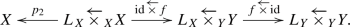
We note that, by Remark 2.1, we have a canonical isomorphism \(R\overleftarrow{f}_!p_2^*\cong R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\).
The following will be used (only) in the proof of Lemma 4.9.
Construction 2.10
Again we consider a Cartesian diagram
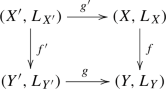
of schemes with support. We consider the diagram
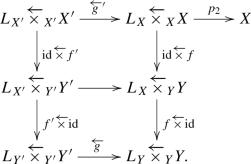
This induces a base change morphism
of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+(L_{Y'}\overleftarrow{\times }_{Y'}Y',\Lambda )\). For an object \(\mathcal F\) of \(D^+(X,\Lambda )\), we have the following commutative diagram
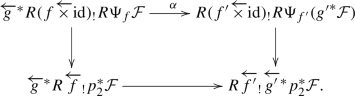
in \(D^+(L_{Y'}\overleftarrow{\times }_{Y'}Y',\Lambda )\).
2.4 Constructibility
For a scheme or a morphism of schemes, being coherent means being quasi-compact and quasi-separated.
Definition 2.11
([20, §§8–9]) Let \(X\rightarrow S\) and \(Y\rightarrow S\) be coherent morphisms of coherent schemes. Let \(\Lambda \) be a noetherian ring. We say that a sheaf \(\mathcal F\) of \(\Lambda \)-modules on \(X\overleftarrow{\times }_SY\) is constructible if there exist partitions \(X=\coprod _{i\in I}X_i\) and \(Y=\coprod _{j\in J}Y_i\) by finitely many locally closed constructible subsets \(X_i\subset X\) and \(Y_j\subset Y\) such that the restriction of \(\mathcal F\) to the subtopos \(X_i\overleftarrow{\times }_SY_j\) is locally constant of finite type for every \((i,j)\in I\times J\).
The full subcategory of the category of sheaves of \(\Lambda \)-modules on \(X\overleftarrow{\times }_SY\) consisting of constructible sheaves is a thick subcategory, i.e., closed under extensions. Thus, complexes \(\mathcal K\) such that the cohomology sheaves \(\mathcal H^i(\mathcal K)\) are constructible for all i form a triagulated subcategory of \(D^b(X\overleftarrow{\times }_SY,\Lambda )\), which is denoted by \(D^b_c(X\overleftarrow{\times }_SY,\Lambda )\).
Remark 2.12
Let \(f:X\rightarrow Y\) be a morphism of finite presentation of coherent schemes with Y having only finitely many irreducible components. Let \(\mathcal F\) be an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\), for an integer n invertible on Y. Then, by [20, Théorème 8.1, Lemme 10.5], if the formation of \(R\Psi _f\mathcal F\) commutes with base change, then \(R\Psi _f\mathcal F\) is an object of \(D_c^b(X\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\).
Lemma 2.13
Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support (§2.3) such that Y is a coherent scheme having only finitely many irreducible components and \(f:X\rightarrow Y\) is a separated morphism of finite presentation. Let n be an integer invertible on Y and \(\mathcal F\) an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\). We assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) is an object of \(D^b_c(L_Y\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\), where \(f\overleftarrow{\times }\textrm{id}\) denotes the natural morphism \(L_X\overleftarrow{\times }_YY\rightarrow L_Y\overleftarrow{\times }_YY\) and \(R\Psi _f\mathcal F\) also denotes its restriction to \(L_X\overleftarrow{\times }_YY\).
Proof
By Remark 2.12, the complex \(R\Psi _f\mathcal F\) is an object of \(D^b_c(X\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\). Then the assertion follows from [20, Proposition 10.2] together with a standard limit argument. \(\square \)
Remark 2.14
We only need to assume that the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) (instead of \(R\Psi _f\mathcal F\)) commutes with base change (which holds when f is proper as mentioned in Remark 2.7.3). In fact, by [20, Lemme 10.5], we may replace f with the base change along a modification \(Y'\rightarrow Y\). Then, by [20, Théorème 2.1], we may assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change.
2.5 An example
Recall that the formation of \(R\Psi _f\mathcal F\) does not commute with base change in general (see [20, §11] for an example). In this subsection, we give an example where the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) does not commute with base change, and provide an explicit modification that makes the formation commute with base change.
Let A be a strictly henselian regular local ring and \(s,t\in A\) be a part of a system of regular parameters. Let \(\pi :\widetilde{Y}\rightarrow Y=\mathop {\textrm{Spec}}\nolimits A\) be the blowup along the ideal (s, t) and \(Z\subset \widetilde{Y}\) be the proper transform of the closed subscheme \(\mathop {\textrm{Spec}}\nolimits A/(t)\) of Y (so \(Z\cong \mathop {\textrm{Spec}}\nolimits A/(t)\)). Let \(f:X=\widetilde{Y}{\setminus } Z\rightarrow Y\) denote the restriction of \(\pi \). Let \(\Lambda \) be a noetherian torsion ring. Then the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\Lambda \) does not commute with base change.
To see this, we consider a strictly henselian discrete valuation ring \(A'\) together with a local homomorphism \(A/(t)\rightarrow A'\) such that the image of s is non-zero, and the induced morphism \(g:Y'\rightarrow Y\) (e.g., \(A'=\mathop {\textrm{Spec}}\nolimits A/(t,t_1,\ldots ,t_n)\) for a system of regular parameters \((s,t,t_1,\ldots ,t_n)\) of A). Then, letting \(f'\) denote the base change \(X'=X\times _YY'\rightarrow Y'\) of f, we claim that the canonical morphism
from Construction 2.6 is not an isomorphism. In fact, as we show in the following claim, it is not an isomorphism at the point \(y\leftarrow \xi \) of the topos \(Y'\overleftarrow{\times }_{Y'}Y'\), where y (resp. \(\xi \)) denotes a closed (resp. generic) geometric point of \(Y'\).
Claim 2.15
With Notation 2.2, the complex of sliced nearby cycle cohomology over \(y\leftarrow \xi \) for f is nonzero, while that for \(f'\) is zero, i.e., we have
Proof
Since \(X'\times _{Y'}Y'_{(\xi )}=X\times _Y\xi =\emptyset \), the second equality holds. We consider the distinguished triangle
By the proper base change theorem, the middle term is isomorphic to \(R\Gamma (\widetilde{Y}_\xi ,\Lambda )=R\Gamma (\xi ,\Lambda )= \Lambda \). We claim that the 0-th cohomology group of the third term is not finitely generated, which we show by following the argument given in [20, §11].
First of all, since \(Z_y\) consists of a single geometric point z, the third term is identified with \(R\Gamma (\widetilde{Y}_{(z)}\times _{Y}Y_{(\xi )},\Lambda )\). Denoting the field of fractions of Y (resp. \(\widetilde{Y}_{(z)}\), resp. \(Y_{(\xi )}\)) by K (resp. \(K_{(z)}\), resp. \(K_{(\xi )}\)), the 0-th cohomology group of the latter complex is identified with \(\Gamma (\mathop {\textrm{Spec}}\nolimits (K_{(z)}\otimes _KK_{(\xi )}),\Lambda )\). To show that this group is not finitely generated, we take an element \(f\in K\) which does not have zeros or poles at z (e.g., \(f=\frac{s+t}{s}\)). Then, the \(\widetilde{Y}\)-scheme \(\widetilde{Y}[f^{\pm 1},f^{1/m}]\) is an étale neighborhood of z for any integer m that is prime to the characteristic of the residue field of A, and hence, the both \(K_{(z)}\) and \(K_{(\xi )}\) contain \(L=\bigcup _mK(f^{1/m})\), which is an infinite algebraic extension of K. Since the natural map \(\Gamma (\mathop {\textrm{Spec}}\nolimits (L\otimes _KL),\Lambda )\rightarrow \Gamma (\mathop {\textrm{Spec}}\nolimits (K_{(z)}\otimes _KK_{(\xi )}),\Lambda )\) is injective, and since the source is not finitely generated, the assertion follows. \(\square \)
Let n be an integer that is invertible on Y (and take \(\Lambda \) to be \({\mathbb {Z}}/n{\mathbb {Z}}\)). Similarly to [20, §11], base changing along the blowup \(\widetilde{Y}\rightarrow Y\) makes the formation of \(R\Psi _f{\mathbb {Z}}/n{\mathbb {Z}}\) commute with base change.
Claim 2.16
We consider the second projection \(\textrm{pr}_2:\widetilde{Y}\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) and let \(\widetilde{f}:X\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) be the base change of f. Then the following hold.
-
1.
The formation of \(R\Psi _{\textrm{pr}_2}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change. In particular, so does that of \(R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\).
-
2.
The formation of \(R(\widetilde{f}\overleftarrow{\times }\textrm{id})_!R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change.
In the case where Y is the strict henselization of k[s, t] at the maximal ideal (s, t) for a separably closed field k, assertion 1 is explained in [20, §11]. In general, it is proven by a “global-to-local” argument as in the proof of [20, Proposition 6.1] (explained in the proof of Lemma 2.17).
Proof
As the formation of \(R(\widetilde{f}\overleftarrow{\times }\textrm{id})_!\) commutes with base change by Lemma 2.5, assertion 2 follows from assertion 1. Since assertion 1 is a local problem, it suffices to show the claim about \(\textrm{pr}_2\).
At each geometric point y of \(\widetilde{Y}\), the base change \(X\times _Y\widetilde{Y}_{(y)}\) to \(\widetilde{Y}_{(y)}=\mathop {\textrm{Spec}}\nolimits B\) can be locally identified (over \(\widetilde{Y}_{(y)}\)) with \(\mathop {\textrm{Spec}}\nolimits B[T]/(uT)\) for a nonzero element u of B. Since the problem is local, the assertion follows from Lemma 2.17 below. \(\square \)
Lemma 2.17
Let \(S=\mathop {\textrm{Spec}}\nolimits B\) be an affine scheme, \(u\in B\) be a (non-zero) element, X be the S-scheme \(\mathop {\textrm{Proj}}\nolimits B[T_0,T_1]/(uT_1)\), and \(f:X\rightarrow S\) denote the structural morphism. Then, for an integer n invertible in B, the formation of \(R\Psi _f{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change.
Proof
We have to show that for any morphism \(S'\rightarrow S\) of schemes and any point \(x'\leftarrow t'\) of \(X'\overleftarrow{\times }_{S'}S'\), where \(X'=X\times _SS'\), the canonical morphism
is an isomorphism, where x, s, and \(s'\) (resp. t) denote the geometric points induced by \(x'\) (resp. \(t'\)).
When x maps into the open subset defined by \(u\ne 0\), this holds as f is isomorphic on that locus. We note that, away from the locus where \(T_1=0\), X maps smoothly onto \(Z=\mathop {\textrm{Spec}}\nolimits B/(u)\) and that the Milnor tube \(X_{(x)}\times _SS_{(t)}\) is identified with \(X_{(x)}\times _{Z}Z_{(t)}\). Thus, by the local acyclicity of smooth morphisms ([1, Théorème 2.1]), morphism (2.2) is an isomorphism when x maps into the open subset define by \(T_1\ne 0\).
We now assume that x maps into the closed subset of X defined by \(u=T=0\) and show that the canonical morphism
is an isomorphism, where g denotes the natural morphism \(X'_{s'}\rightarrow X_s\). Let C denotes the cone of this morphism. Then, by what we have observed above, it is supported on the closed subset defined by \(u=T=0\) of \(X'_{s'}\), which consists of a single point, so that we have \(R\Gamma (X'_{s'},C)\cong C_{x'}\). But, by the proper base change theorem, \(R\Gamma (X'_{s'},C)\) is identified with the cone of \(R\Gamma (X_t,{\mathbb {Z}}/n{\mathbb {Z}})\rightarrow R\Gamma (X'_{t'},{\mathbb {Z}}/n{\mathbb {Z}})\). This last morphism is an isomorphism by the invariance of the étale cohomology group under change of separably closed base field ( [2, Corollaire 1.6]). Thus, the assertion follows. \(\square \)
3 Preliminaries on analytic adic spaces
We refer to [8, 9] for details on adic spaces.
3.1 Analytic adic spaces
We first recall from [9, 1.9] the analytic adic space associated to a formal scheme. We consider a formal scheme \(\mathfrak X\) satisfying the following condition from [9, 1.9]:
-
(*)
Any point of \(\mathfrak X\) admits an affine neighborhood \(\mathop {\textrm{Spf}}\nolimits A\subset \mathfrak X\) such that the topology of A is \(\varpi \)-adic for some element \(\varpi \in A\) and the ring \(A[1/\varpi ]\) equipped with the topology induced from A is a strongly noetherian Tate ring (see [8, §2] or [9, 1.1] for the definition of being strongly noetherian).
Then we can consider the analytic adic space \(d(\mathfrak X)\) associated to \(\mathfrak X\) defined in [9, Proposition 1.9.1]: if \(\mathfrak X=\mathop {\textrm{Spf}}\nolimits A\) is affine with the topology of A being \(\varpi \)-adic for some \(\varpi \in A\) and if \(A[1/\varpi ]\) is strongly noetherian, then \(d(\mathfrak X)=\mathop {\textrm{Spa}}\nolimits (A[1/\varpi ],A^+)\), where \(A^+\) is the integral closure of A in \(A[1/\varpi ]\). The adic space \(d(\mathfrak X)\) comes with a natural morphism \(\lambda _{\mathfrak X}:d(\mathfrak X)\rightarrow \mathfrak X\) of topologically ringed spaces. It induces a natural morphism \(d(\mathfrak X)_\mathrm{\acute{e}t}\rightarrow \mathfrak X_\mathrm{\acute{e}t}\) of sites as in [9, Lemma 3.5.1], which we denote again by \(\lambda _{\mathfrak X}\) and call the specialization morphism. In this article we focus on formal schemes coming from schemes.
Definition 3.1
Let X be a scheme and \(X_0\) the closed subset defined by vanishing of a locally finitely generated ideal sheaf. Consider the formal completion \(\widehat{X}\) of X along a locally finitely generated ideal sheaf defining \(X_0\) (note that \(\widehat{X}\) is independent of the choice of a locally finitely generated ideal sheaf). The pair \((X,X_0)\) is called an admissible pair if \(\widehat{X}\) satisfies the condition (*). A morphism \((X,X_0)\rightarrow (Y,Y_0)\) of admissible pairs is a morphism \(f:X\rightarrow Y\) of schemes such that \(X_0=f^{-1}(Y_0)\).
For an admissible pair \((X,X_0)\), let \(\widehat{X}\) denote the formal completion of X along a locally finitely generated ideal sheaf defining \(X_0\) and let \((X,X_0)^a\) be the associated analytic adic space \(d(\widehat{X})\). The assignment \((X,X_0)\mapsto (X,X_0)^a\) defines a functor from the category of admissible pairs to that of analytic adic spaces. If there is no risk of confusion, we simply write \(X^a\) for \((X,X_0)^a\).
Let U denote the complementary open \(X\setminus X_0\). The adic space \(X^a\) comes with the following two natural morphisms of sites;
-
\(\lambda _X:X^a_\mathrm{\acute{e}t}\rightarrow X_{0,\mathrm{\acute{e}t}}\) defined to be the composite of the specialization morphism \(\lambda _{\widehat{X}}:X^a_\mathrm{\acute{e}t}\rightarrow \widehat{X}_\mathrm{\acute{e}t}\) and the natural equivalence \(\widehat{X}_\mathrm{\acute{e}t}\cong X_{0,\mathrm{\acute{e}t}}\),
-
\(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\) defined in [9, 3.5.12], which we call the analytification morphism.
Example 3.2
Let k be a non-archimedean field and X a scheme locally of finite type over \(k^\circ \). Then we can form an admissible pair \((X,X_0)\) by letting \(X_0\) be the closed fiber of X. Then the analytic adic space \((X,X_0)^a\) is nothing but the Raynaud generic fiber ([21, 8, Remark 4.6.ii], [9, Example 1.9.2.ii]) viewed as an adic space, which is denoted by \(X^\textrm{rig}\). Similarly, for a morphism \(f:X\rightarrow Y\), we denote the associated morphism \(X^\textrm{rig}\rightarrow Y^\textrm{rig}\) by \(f^\textrm{rig}\). For a sheaf \(\mathcal F\) on \(X_\mathrm{\acute{e}t}\), we denote the pullback \(\varphi _X^*\mathcal F\) by \(\mathcal F^\textrm{rig}\).
3.2 Analytic pseudo-adic spaces
In the proof of Theorem 1.2, we will need to consider geometric points of adic spaces, for which we need to work with the framework of pseudo-adic spaces. We refer to [9, 1.10] for details on pseudo-adic spaces. Let us just recall that a pseudo-adic space is a pair \(X=({\underline{X}},|X|)\) of an adic space \({\underline{X}}\) and a subset |X| of \({\underline{X}}\) satisfying certain conditions. A morphism \(f:({\underline{X}},|X|)\rightarrow ({\underline{Y}},|Y|)\) of pseudo-adic spaces is a morphism \(f:{\underline{X}}\rightarrow {\underline{Y}}\) of adic spaces such that \(f(|X|)\subset |Y|\). We often regard an adic space X as a pseudo-adic space via the fully faithful functor \(X\mapsto (X,X)\) from the category of adic spaces to that of pseudo-adic spaces.
As in [9, 3.5.3], to a pair \((\mathfrak X,L)\) of a formal scheme \(\mathfrak X\) satisfying (*) and a locally closed subset L of \(\mathfrak X\), we can associate an analytic pseudo-adic space \((d(\mathfrak X),\lambda _{\mathfrak X}^{-1}(L))\), which is denoted by \(d(\mathfrak X,L)\). It comes with a natural morphism \(\lambda _{(\mathfrak X,L)}:d(\mathfrak X,L)_\mathrm{\acute{e}t}\rightarrow L_\mathrm{\acute{e}t}\) of sites [9, 3.5.3, 3.5.5], where L is regarded as a subscheme of \(\mathfrak X\) with reduced scheme structure. We call \(\lambda _{(\mathfrak X,L)}\) the specialization morphism.
We define an algebro-geometric datum which gives an analytic pseudo-adic space.
Definition 3.3
An admissible triple is a triple \((X,X_0,L)\) with \((X,X_0)\) being an admissible pair (Definition 3.1) and L being a constructible closed subset of \(X_0\). A morphism \((X,X_0,L)\rightarrow (Y,Y_0,M)\) of admissible triples is a morphism \(f:(X,X_0)\rightarrow (Y,Y_0)\) of admissible pairs such that \(f(L)\subset M\).
For an admissible triple \((X,X_0,L)\), we can consider the pseudo-adic space \(d(\widehat{X},L)\) associated to the pair \((\widehat{X},L)\), which we denote by \((X,X_0,L)^a\), or simply by \(X^a\). The assignment \((X,X_0,L)\mapsto (X,X_0,L)^a\) defines a functor from the category of admissible triples to that of analytic pseudo-adic spaces. We often regard L as a closed subscheme with reduced scheme structure. By taking L to be \(X_0\), we recover the adic space associated to the admissible pair \((X,X_0)\), that is, we have \((X,X_0,X_0)^a=(X,X_0)^a\).
Let \((X,X_0,L)\) be an admissible triple and U denote the open subscheme \(X\setminus X_0\). Similarly to the case of admissible pairs, the associated analytic pseudo-adic space \(X^a\) comes with the two natural morphisms of sites;
-
the specialization morphism \(\lambda _X=\lambda _{(\widehat{X},L)}:X^a_\mathrm{\acute{e}t}\rightarrow L_\mathrm{\acute{e}t}\),
-
\(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\) defined to be the composite \(X^a_\mathrm{\acute{e}t}=(X,X_0,L)^a_\mathrm{\acute{e}t}\rightarrow (X,X_0)^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\).
Important examples of admissible triples are those coming from schemes of finite type over a microbial valuation ring. Recall that a valuation ring B is called microbial if B has a prime ideal of height one ([9, Definition 1.1.4]). For instance, any finitely dimensional valuation ring is microbial.
Definition 3.4
[cf. [9, Example 1.9.2.i]] Let B be a microbial valuation ring. The admissible triple \((S,S_0,L_S)\) associated to B is defined as follows. Put \(S=\mathop {\textrm{Spec}}\nolimits B\), let \(S_0\) be the closed set defined by vanishing of the unique height one prime ideal \({\mathfrak {p}}\) of B, and \(L_S\) the singleton consisting of the closed point of S. Note that, as a finitely generated ideal defining \(S_0\), we can take the ideal generated by a nonzero element of \({\mathfrak {p}}\).
Remark 3.5
-
1.
Let a be a nonzero element of \({\mathfrak {p}}\). Note that the a-adic topology on B coincides with the valuation topology, and hence the formal completion of S along the ideal generated by a is isomorphic to the formal spectrum \(\mathop {\textrm{Spf}}\nolimits B\) with B being equipped with the valuation topology.
-
2.
Let K denote the field of fractions of B and \(S^a\) the pseudo-adic space associated to \((S,S_0,L_S)\). Then the analytification morphism \(\varphi _S:S^a\rightarrow \mathop {\textrm{Spec}}\nolimits K\) gives an equivalence of topoi [9, Proposition 2.3.10]. In particular, if K is separably closed, then the topos \(S^a\) is equivalent to the punctual topos.
Example 3.6
Let \((Y,Y_0,L_Y)\) be an admissible triple and \(Y^a\) denote the associated pseudo-adic space. Let \(\xi =(\mathop {\textrm{Spa}}\nolimits (\kappa (\xi ),\kappa (\xi )^+),\{*\})\rightarrow Y^a\) be a geometric point, i.e, \(\kappa (\xi )^+\) is a microbial valuation ring with separably closed field of fractions \(\kappa (\xi )\) and \(*\) is the closed point of \(\mathop {\textrm{Spa}}\nolimits (\kappa (\xi ),\kappa (\xi )^+)\) ( [9, Definition 2.5.1]). Let \((S,S_0,L)\) denote the pseudo-adic space associated to the microbial valuation ring \(\kappa (\xi )^+\). Then \(\xi \) is identified with the pseudo-adic space \(S^a\) associated to the admissible triple \((S,S_0,L)\). Note that we have a natural morphism \((S,S_0,L_S)\rightarrow (Y,Y_0,L_S)\) of admissible triples. The associated morphism \(S^a\rightarrow Y^a\) is canonically identified with the geometric point \(\xi \rightarrow Y^a\).
3.3 Adic spaces and vanishing topoi
For an admissible triple \((X,X_0,L)\), we construct a canonical morphism \(\widetilde{\lambda }_X:X^a\rightarrow L\overleftarrow{\times }_XX\) of topoi (cf. [13, 6.4]). We denote the complement of \(X_0\) by U. Then we have a natural diagram of topoi
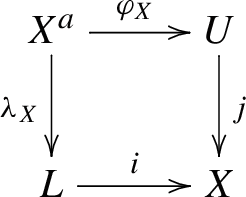
with a natural 2-map \(\tau :j\varphi _X\rightarrow i\lambda _X\) defined as follows (cf. the proof of [9, Theorem 3.5.13]): For an object V of \(X_\mathrm{\acute{e}t}\), we have a natural morphism
from [9, 1.9.5], which induces, for a sheaf \(\mathcal F\) on \((X^a)_\mathrm{\acute{e}t}\), a morphism
Thus, by the universal property of the vanishing topos \(L\overleftarrow{\times }_XU\), the above diagram induces a canonical morphism of topoi
We denote the composite \(X^a\rightarrow L\overleftarrow{\times }_XU\rightarrow L\overleftarrow{\times }_XX\) also by \(\widetilde{\lambda }_X\) when there is no risk of confusion.
4 Compactly supported direct image for rigid analytic varieties
Our main interest in this section is the compactly supported direct image \(Rf^a_!\) for a morphism \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) of admissible triples (Definition 3.3) with \(f:X\rightarrow Y\) compactifiable, where \(f^a\) denotes the induced morphism \(X^a\rightarrow Y^a\) of analytic pseudo-adic spaces.
We note that a compactification of \(f:X\rightarrow Y\) induces a compactification of \(f^a:X^a\rightarrow Y^a\). More precisely, we make the following construction.
Construction 4.1
Let \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) be a proper morphism with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\). Let \({{\bar{X}}}_0\) be the pullback \({{\bar{f}}}^{-1}(Y_0)\) and \(L_{{{\bar{X}}}}\) be the closure of \(L_X\) in \({{\bar{X}}}_0\), so that we have morphisms \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(Y,Y_0,L_Y)\) of admissible triples whose composite is f. Let \({{\bar{X}}}^a\) denote the pseudo-adic space associated to \(({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\). Then \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion and \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow Y^a\) is a proper morphism (this can be checked using [9, Corollary 1.3.9, Lemma 1.3.10], see also [19, Lemma 3.5]). Thus, by the definition of the compactly supported direct image [9, Definition 5.4.4], we have an identification \(Rf^a_!=R{{\bar{f}}}^a_*\circ j^a_!\) of functors \(D^+(X^a,\Lambda )\rightarrow D^+(Y^a,\Lambda )\), for a torsion ring \(\Lambda \).
4.1 Cohomology of fibers via nearby cycle
Let \((X,X_0,L)\) be an admissible triple (Definition 3.3) and U the complement of \(X_0\). For a torsion ring \(\Lambda \) and an object \(\mathcal F\) of \(D^+(U,\Lambda )\), we put \(\mathcal F^a=\varphi _X^*\mathcal F\). The diagram (3.1) induces a canonical morphism
which is an isomorphism by the proof of [9, Corollary 3.5.15] (cf. [5, Theorem 6.5.4]).
Here, we give an interpretation of the canonical morphism (4.1) via vanishing topos. We consider the diagram of topoi
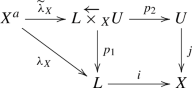
with canonical 2-morphisms \(jp_2\rightarrow ip_1\) and \(p_1\widetilde{\lambda }_{X}\cong \lambda _X\). This diagram induces the morphisms
whose composite is identified with the morphism (4.1).
Lemma 4.2
The two morphisms in (4.3) are isomorphisms.
Proof
The first one is an isomorphism by [14, Théorème 2.4], and so is the second, since the composite is an isomorphism as mentioned above. \(\square \)
Construction 4.3
Let \((S,S_0,L_S)\) be the admissible triple associated to a microbial valuation ring with separably closed field of fractions (Definition 3.4). Let \(f:(X,X_0,L_X)\rightarrow (S,S_0,L_S)\) be a morphism of admissible triples with \(f:X\rightarrow S\) being locally of finite type. Then we have the associated morphism \(f^a:X^a\rightarrow S^a\) of pseudo-adic spaces, which is locally of finite type.
We denote the generic point (resp. closed point) of S by \(\eta \) (resp. s). For a torsion ring \(\Lambda \) and a sheaf \(\mathcal F\) of \(\Lambda \)-modules on \(X_{\eta ,\mathrm{\acute{e}t}}\), we consider the nearby cycle complex \(R\psi _S\mathcal F=i^*Rj_*\mathcal F\) over S, where j is the natural open immersion \(X_\eta \rightarrow X\) and i is the natural closed immersion \(X_s\rightarrow X\). We denote by \(\mathcal F^a\) the pullback of \(\mathcal F\) by the analytification morphism \(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow X_{\eta ,\mathrm{\acute{e}t}}\). Then the canonical isomorphism \(R\psi _S\mathcal F\cong R\lambda _{X*}\mathcal F^a\) induces a canonical isomorphism
Construction 4.4
In the situation of Construction 4.3, we assume that the morphism \(f:X\rightarrow S\) is compactifiable. We recall the construction of a canonical isomorphism from [9, Theorem 5.7.8]
We take a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow S\) with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\). Let \({{\bar{X}}}_0\) be the pullback \({{\bar{f}}}^{-1}(S_0)\) and \(L_{{{\bar{X}}}}\) be the closure of \(L_X\) in \({{\bar{X}}}_0\), so that we have morphisms \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(S,S_0,L_S)\) of admissible triples whose composite is f. The induced morphism \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow S^a\) is proper, and \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion, as recalled in the beginning of this section. We consider the diagram of topoi
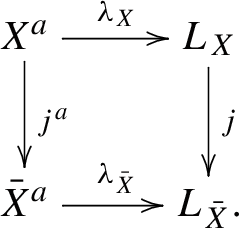
The isomorphism \(R\psi _S\mathcal F\cong R\lambda _{X*}\mathcal F^a\) and the canonical isomorphism \(j_!R\lambda _{X*}\cong R\lambda _{{{\bar{X}}}*}j^a_!\) from [9, Corollary 3.5.11] induce
4.2 Compactly supported direct image via nearby cycles over general bases
We globalize Huber’s construction of the isomorphism between the étale cohomology of an algebraizable rigid analytic variety and the nearby cycle cohomology.
We frequently use the fact that the étale topos of any pseudo-adic space has enough points ([9, Proposition 2.5.5], see also [9, Proposition 2.5.17]).
Construction 4.5
Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3) and let \(f^a:X^a\rightarrow Y^a\) denote the induced morphism of analytic pseudo-adic spaces. We consider the natural diagram of topoi
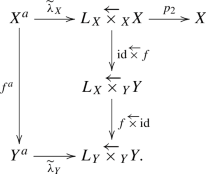
Here \(\widetilde{\lambda }_X\) and \(\widetilde{\lambda }_Y\) denote the morphisms defined in §3.3. We denote the natural morphism \(L_X\overleftarrow{\times }_XX\rightarrow L_Y\overleftarrow{\times }_YY\) by \(\overleftarrow{f}\). The diagram above induces the base change morphism \(\widetilde{\lambda }_Y^*R\overleftarrow{f}_*\rightarrow Rf^{a}_*\widetilde{\lambda }_X^*\).
Let \(\Lambda \) be a ring and \(\mathcal F\) be an object of \(D^+(X,\Lambda )\). Note that we have canonical isomorphisms \(R\Psi _f\mathcal F\cong R(\textrm{id}\overleftarrow{\times }f)_*R\Psi _\textrm{id}\mathcal F\cong R(\textrm{id}\overleftarrow{\times }f)_*p_2^*\mathcal F\) from Remark 2.1. Thus, the base change morphism \(\widetilde{\lambda }_Y^*R\overleftarrow{f}_*\rightarrow Rf^{a}_*\widetilde{\lambda }_X^*\) induces
We also give a variant for higher direct image with compact support. For the construction, we use the following lemma.
Lemma 4.6
Let \(j:(X,X_0,L_X)\rightarrow ({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\) be a morphism of admissible triples such that \(j:X\rightarrow {{\bar{X}}}\) is an open immersion and that the image of \(L_X\) is open in \(L_{{{\bar{X}}}}\). Let \(j^a:X^a\rightarrow {{\bar{X}}}^a\) denote the induced open immersion of analytic pseudo-adic spaces. We consider the diagram of topoi
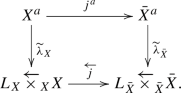
Let \(\Lambda \) be a ring. Then the natural morphism
of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+({{\bar{X}}}^a,\Lambda )\) is an isomorphism.
Proof
Let \(\mathcal F\) be an object of \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\). We show that, for each geometric point \(\xi \) of \({{\bar{X}}}^a\), the morphism \((j^a_!\widetilde{\lambda }_X^*\mathcal F)_\xi \rightarrow (\widetilde{\lambda }_{{{\bar{X}}}}^*\overleftarrow{j}_!\mathcal F)_\xi \) induced on the stalks is an isomorphism. For this, it suffices to show that \(\xi \) lies over \(X^a\) if \(x\leftarrow \xi \) lies over \(L_X\overleftarrow{\times }_XX\), where \(x\leftarrow \xi \) denotes, by abuse of notation, the image of \(\xi \) by \(\widetilde{\lambda }_{{{\bar{X}}}}\). Since \(x\leftarrow \xi \) lies over \(L_X\overleftarrow{\times }_XX\) if and only if x lies over \(L_X\), the assertion follows from the fact that \(\lambda _{{{\bar{X}}}}^{-1}(L_X)=X^a\) as a subset of \({{\bar{X}}}^a\). \(\square \)
Construction 4.7
Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3) and let \(f^a:X^a\rightarrow Y^a\) denote the induced morphism. We now assume that \(f:X\rightarrow Y\) is compactifiable and let \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(Y,Y_0,L_Y)\) be a decomposition as in Construction 4.1.
Let \({{\bar{X}}}^a\) denote the pseudo-adic space associated to \(({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\). Then \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion and \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow Y^a\) is a proper morphism, as recalled in the beginning of this section.
Let \(\Lambda \) be a torsion ring. Then we have the following sequence of canonical morphisms of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+(Y^a,\Lambda )\);
where the first isomorphism comes from Lemma 2.9, the second is the base change morphism induced by the diagram (4.5) for \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\), and the third one comes from Lemma 4.6.
Let \(\mathcal F\) be an object of \(D^+(X,\Lambda )\). By considering \(p_2^*\mathcal F\), we obtain a canonical morphism
To state the compatibility of the canonical morphism \(\theta _f\) with base change, we make the following construction.
Construction 4.8
Let

be a commutative diagram of admissible triples. We assume that \(f:X\rightarrow Y\) is compactifiable and that the diagram is Cartesian, i.e, the diagram

is a Cartesian diagram of schemes and \({f'}^{-1}(L_{Y'})\cap {g'}^{-1}(L_{X})=L_{X'}\).
Then, for a torsion ring \(\Lambda \) and an object \(\mathcal F\) of \(D^+(X,\Lambda )\), we have the base change morphism
defined in Construction 2.6. On the other hand, we have a Cartesian diagram
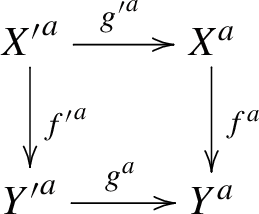
of pseudo-adic spaces, which induces the base change morphism
Thus, we have the diagram
in \(D^+({Y'}^a,\Lambda )\).
Lemma 4.9
-
1.
The diagram (4.6) is commutative.
-
2.
If the formation of \(R\Psi _f\mathcal F\) commutes with base change, then the morphism \(\alpha \) is an isomorphism.
-
3.
The morphism \(\beta \) is an isomorphism if one of the following conditions is satisfied:
-
(a)
\(\Lambda \) is killed by an integer invertible in Y,
-
(b)
\((Y',Y'_0,L_{Y'})\) is the admissible triple associated to a geometric point \(\xi \) of \(Y^a\) (Example 3.6) and \(g:(Y',Y'_0,L_{Y'})\rightarrow (Y,Y_0,L_Y)\) is the natural morphism.
-
(a)
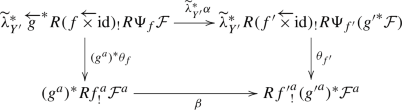
Proof
1. By Construction 2.10, the morphism \(\alpha \) is identified with the base change morphism
induced by the diagram
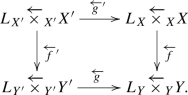
Thus, both of \(\theta _{f'}\circ \widetilde{\lambda }_{Y'}^*\alpha \) and \(\beta \circ ({g^a})^*\theta _{f}\) are identified with the base change morphism induced by the diagram
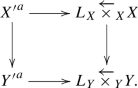
2. This is clear from the definition of \(\alpha \).
3. This follows from [9, Theorem 5.3.9, Corollary 5.3.10]. \(\square \)
Lemma 4.10
Let \((S,S_0,L_S)\) be the admissible triple associated to a microbial valuation ring with separably closed field of fractions (Definition 3.4). Let \(f:(X,X_0,L_X)\rightarrow (S,S_0,L_S)\) be a morphism of admissible triples with \(f:X\rightarrow S\) being compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) an object of \(D^+(X,\Lambda )\). Then the morphism
in \(D^+(S^a,\Lambda )\) is identified with the morphism (4.4) in Construction 4.4 via the equivalence \(R\Gamma (S^a,-):D^+(S^a,\Lambda )\cong D^+(\Lambda )\) (Remark 3.5.2), and hence is an isomorphism.
Proof
Since \(S^a\) and \(L_S\overleftarrow{\times }_S\eta \), where \(\eta \) is the generic point of S, are equivalent to the punctual topos, the morphism (4.7) is identified with the morphism
induced by the adjunction morphism \(\theta :p_2^*\mathcal F\rightarrow R\widetilde{\lambda }_{X*}\widetilde{\lambda }_X^*p_2^*\mathcal F=R\widetilde{\lambda }_{X*}\mathcal F^a\). We consider the diagram of topoi
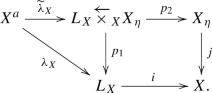
The morphism (4.8) is identified with the morphism
induced from the above diagram. Then the assertion follows from Lemma 4.2. \(\square \)
Theorem 4.11
Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3) with \(f:X\rightarrow Y\) being compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) an object of \(D^+(X,\Lambda )\). We assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then the morphism
from Construction 4.7 is an isomorphism.
Proof
We prove that \(\theta _f\) induces an isomorphism of the stalks at each geometric point \(\xi \) of \(Y^a\). Example 3.6 shows that we have the natural morphism \((S,S_0,L_S)\rightarrow (Y,Y_0,L_Y)\) of admissible triples such that the associated morphism \(S^a\rightarrow Y^a\) of pseudo-adic spaces is canonically identified with the geometric point \(\xi \rightarrow Y^a\). By forming a Cartesian diagram

of admissible triples and applying Lemma 4.9 to it, the problem is reduced to the case where \((Y,Y_0,L_Y)=(S,S_0,L_S)\). Then the assertion follows from Lemma 4.10. \(\square \)
Proof (Proof of Theorem 1.2)
[Proof of Theorem 1.2] Follows from Theorem 4.11 and [20, Théorème 2.1].
\(\square \)
Remark 4.12
-
1.
In Theorem 4.11, it is strictly necessary to assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change as seen in Example 4.13 below. See also Remark 5.6.1.
-
2.
It seems impossible to give a similar comparison isomorphism for \(Rf^a_*\) (see Remark 5.6.2).
We now explicitly see that \(\theta _f\) can be non-isomorphic.
Example 4.13
We let k be a strictly henselian discrete valuation field and use the notation established in Example 3.2. We fix a uniformizor \(\varpi \in k^\circ \). Let A be a regular ring that is flat and of finite type over \(k^\circ \) and \(Y=\mathop {\textrm{Spec}}\nolimits A\). We take a regular sequence \(s,t\in A\) satisfying the following three conditions (we assume that there exists such a regular sequence: see below for explicit choices).
-
(a)
\(Z=\mathop {\textrm{Spec}}\nolimits A/(t)\) is regular and flat over \(k^\circ \),
-
(b)
A/(s, t) is regular,
-
(c)
\(A/(\varpi ,s,t)\ne 0\).
Let \(\pi :\widetilde{Y}\rightarrow Y\) be the blowup along the ideal (s, t). We consider the complement X of the proper transform of Z and let \(f:X\rightarrow Y\) denote the restriction of \(\pi \). Then the canonical morphism
from Construction 4.7 is not an isomorphism.
To see this, we take a maximal ideal \(\mathfrak m\) of A that contains \((\varpi ,s,t)\), which exists by c), and then take a prime ideal \(\mathfrak p\subset \mathfrak m\) that is maximal among those satisfying \(t\in \mathfrak p\) and \(s\varpi \notin \mathfrak p\), which exists as \(s\varpi \ne 0\) in A/(t) by a). Then, we consider the normalization \(A'\) of the integral local domain \(A/\mathfrak p\), which is a finite extension of \(k^\circ \). Setting \(Y'=\mathop {\textrm{Spec}}\nolimits A'\), we obtain a morphism \((Y')^\textrm{rig}\rightarrow Y^\textrm{rig}\). Let \(\nu \) be a geometric point of \((Y')^\textrm{rig}\). Then the stalk of the right hand side at \(\nu \) is zero since \(X^\textrm{rig}\times _{Y^\textrm{rig}}(Y')^\textrm{rig}=\emptyset \).
On the other hand, the stalk of the left hand side is described as follows. Let \(\nu _s\) (resp. \(\nu _\eta \)) be the closed (resp. generic) geometric point of \(Y'\). Then, by construction (see §2.3 and §3.3), we have a canonical isomorphism
The latter complex is non-zero by Claim 2.15. Thus, the morphism \(\theta _f\) is not an isomorphism.
Let n be an integer invertible in \(k^\circ \) and take \(\Lambda \) to be \({\mathbb {Z}}/n{\mathbb {Z}}\). Then the morphism \(\theta _f\) becomes an isomorphism after base changing along \(\pi :\widetilde{Y}\rightarrow Y\). More precisely, let \(\widetilde{f}:X\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) be the base change of f. Then, by Claim 2.16, the formation of \(R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change. Thus, the morphism \(\theta _{\widetilde{f}}\) is an isomorphism by Theorem 4.11.
The above example includes the following two suggestive cases.
-
1.
When \(A=k^\circ [T]\), \(s=\varpi \), \(t=T\), the blowup \(\pi :\widetilde{Y}\rightarrow Y\) is an admissible blowup and the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) is identified with the natural open immersion from the annuli defined by \(|\varpi |\le |T|\le 1\) to the unit disk. In this case, we can take \(\nu \) to be a geometric point over the origin of the unit disk \(Y^\textrm{rig}\).
-
2.
When \(A=\mathop {\textrm{Spec}}\nolimits k^\circ [S,T]\), \(s=S\), \(t=T\), the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) is identified with the morphism f in [11, Example 2.2], or equivalently with the morphism \(\mathop {\textrm{Spa}}\nolimits (k\langle S,T\rangle ,k^\circ \langle S,T\rangle )\rightarrow \mathop {\textrm{Spa}}\nolimits (k\langle S,T\rangle ,k^\circ \langle S,T\rangle )\) given by \((S,T)\mapsto (ST,T)\). In this case, we can take \(\nu \) to be a geometric point over the point \((\varpi ,0)\in (k^\circ )^2=Y^\textrm{rig}(k)\).
5 Quasi-constructibility
In §5.1, we state and deduce from Theorem 4.11 our finiteness result (Theorem 5.5). In §5.2, we focus on the case where the target is the 2-dimensional disk to give a concrete consequence (Corollary 5.11) of Theorem 5.5.
5.1 Modification and finiteness
Definition 5.1
Let \(\mathsf X\) be an analytic pseudo-adic space which is quasi-compact and quasi-separated. Let \(\Lambda \) be a noetherian ring.
-
1.
Let \(\mathsf F\) be a sheaf of \(\Lambda \)-modules on \(\mathsf X\). We say that \(\mathsf F\) is strictly quasi-constructible if there exist a finite partition \(\mathsf X=\coprod _{i\in I}\mathsf L_i\) by locally closed constructible subsets \(\mathsf L_i\) and a finite partition \(\mathsf X=\coprod _{j\in J} \mathsf Z_j\) by Zariski locally closed subsets \(\mathsf Z_j\) such that the restriction of \(\mathsf F\) to \(\mathsf L_i\cap \mathsf Z_j\) is locally constant of finite type for every \((i,j)\in I\times J\).
-
2.
Let \(\mathsf F\) be an object of \(D^b(\mathsf X,\Lambda )\). We say that \(\mathsf F\) is strictly quasi-constructible if the all cohomology sheaves \(\mathcal H^i(\mathsf F)\) are strictly quasi-constructible.
Remark 5.2
If \(\mathsf F\) is strictly quasi-constructible, then \(\mathsf F\) is quasi-constructible in the sense of [11, Definition 1.1].
Lemma 5.3
Let \((X,X_0,L_X)\) be an admissible triple (Definition 3.3) with X being quasi-compact and quasi-separated and let \(X^a\) denote the associated analytic pseudo-adic space (§3.2). We consider the natural morphism \(\widetilde{\lambda }_X:X^a\rightarrow L_X\overleftarrow{\times }_XU\) defined in §3.3, where U is the complement of \(X_0\). Let \(\Lambda \) be a noetherian ring and \(\mathcal K\) an object of \(D_c^b(L_X\overleftarrow{\times }_XU,\Lambda )\). Then \(\widetilde{\lambda }_X^*\mathcal K\) is strictly quasi-constructible.
Proof
We may assume that \(L_X=X_0\). We take finite partitions \(X_0=\coprod _{i\in I}L_i\) and \(U=\coprod _{j\in J}Z_j\) by locally closed subsets \(L_i\subset X_0\) and \(Z_j\subset U\) such that \(\mathcal K\) is locally constant on \(L_i\overleftarrow{\times }_XZ_j\). Let \(\mathsf L_i\) be the pullback of \(L_i\) by the map \(\lambda _X:X^a\rightarrow X_0\) and \(\mathsf Z_i\) the pullback of \(Z_i\) by the map \(\varphi _X:X^a\rightarrow U\). Then each \(\mathsf L_i\) is a constructible locally closed subset, and each \(\mathsf Z_j\) is a Zariski locally closed subset. Further, the restriction of \(\widetilde{\lambda }_X^*\mathcal K\) to \(\mathsf L_i\cap \mathsf Z_j\) is locally constant. Thus, \(\widetilde{\lambda }_X^*\mathcal K\) is quasi-constructible.
\(\square \)
Definition 5.4
A morphism \(X'\rightarrow X\) of schemes is called a modification if it is proper and surjective, if there exists a dense open subscheme U of X such that the restriction \(X'\times _XU\rightarrow U\) is an isomorphism, and if every generic point (i.e, maximal point) of \(X'\) is sent to a generic point of X.
Theorem 5.5
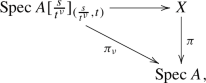
Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3). We assume that Y is a coherent scheme having only finitely many irreducible components and that \(f:X\rightarrow Y\) is separated and of finite presentation. Let n be an integer invertible on Y and \(\mathcal F\) be an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\). Then there exists a modification \(\pi :Y'\rightarrow Y\) such that the complex \({\pi ^a}^*Rf^a_!\mathcal F^a\) is strictly quasi-constructible. Here \(\pi ^a\) is the morphism \((Y')^a\rightarrow Y^a\) of pseudo-adic spaces induced by the morphism \(\pi :(Y',\pi ^{-1}(Y_0),\pi ^{-1}(L_Y))\rightarrow (Y,Y_0,L_Y)\) of admissible triples.
Proof
Recall that the formation of \(Rf^a_!\) commutes with base change ( [9, Theorem 5.3.9]). Hence, we can freely replace Y by a modification. By [20, Théorème 2.1], there exists a modification \(Y'\rightarrow Y\) such that the formation of \(R\Psi _{f'}\mathcal F'\) commutes with base change, where \(f'\) is the base change \(X'=X\times _YY'\rightarrow Y'\) and \(\mathcal F'\) is the pullback of \(\mathcal F\) by the projection \(X'\rightarrow X\). Thus, we may assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then, by Theorem 4.11, we have \(\widetilde{\lambda }_Y^*R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\cong Rf^a_!\mathcal F^a\). On the other hand, by Lemma 2.13, \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) is constructible. Thus, by Lemma 5.3, \(Rf^a_!\mathcal F^a\) is strictly quasi-constructible. \(\square \)
In particular, Theorem 1.1 follows.
Remark 5.6
-
1.
As mentioned in the introduction, the modification is strictly necessary in Theorem 1.1. In fact, if \(f:X\rightarrow Y\) is as in Example 4.13.2, the complex \(Rf^\textrm{rig}_!{\mathbb {Z}}/n{\mathbb {Z}}\) is not quasi-constructible as shown in [11, Example 2.2].
-
2.
The above theorem does not hold for the direct image without support. In general, the complex \(Rf^a_*\mathcal F^a\) is not quasi-constructible even after any modification as seen in [10, Example 1.1].
5.2 Quasi-constructible sheaves on the 2-dimensional disk
In this subsection, we fix a non-archimedean field k and use the notations in Example 3.2.
Proposition 5.7
Let \(\pi :S'\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a modification and \(\mathsf F\) a sheaf of \(\Lambda \)-modules on \(S^\textrm{rig}\cong \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\), for a noetherian ring \(\Lambda \). We assume that \({\pi ^\textrm{rig}}^{*}\mathsf F\) is strictly quasi-constructible. Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that \(\mathsf F\) is locally constant on the open subset \(\{x\in S^\textrm{rig}\mid 0<|s(x)|\le |t^\nu (x)| \text { and }|t(x)|\le \delta \}\).
The aim of this subsection is to prove this propositioin and use it to obtain a concrete consequence (Corollary 5.11) of Theorem 5.5. To this end, we prepare some lemmas (Lemmas 5.8 and 5.10).
Lemma 5.8
Let \(\pi :S'\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a modification. For an integer \(\nu \ge 0\), we consider the S-scheme \(S_\nu =\mathop {\textrm{Spec}}\nolimits k^\circ [\frac{s}{t^\nu },t]\), that is, the scheme \(\mathop {\textrm{Spec}}\nolimits k^\circ [s',t]\) with S-scheme structure given by the \(k^\circ [t]\)-algebra homomorphism \(k^\circ [s,t]\rightarrow k^\circ [s',t]\) sending s to \(s't^\nu \). Then there exist an integer \(\nu \ge 0\), an open neighborhood \(\mathsf U\subset (S_\nu )^\textrm{rig}\) of the origin, and a commutative diagram
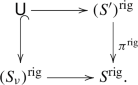
Proof
Applying Lemma 5.9 below to the regular local ring \(k[s,t]_{(s,t)}\), we can find a commutative diagram
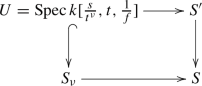
for some \(\nu \ge 1\) and \(f\in k[\frac{s}{t^\nu },t]\) which does not belong to the maximal ideal \((\frac{s}{t^\nu },t)\). We take \(\mathsf U\) to be the fiber product \(U\times _SS^\textrm{rig}\) ([8, Proposition 3.8]). Since we have a natural isomorphism \((S')^\textrm{rig}\cong S'\times _SS^\textrm{rig}\) ([9, Proposition 1.9.6]), we obtain a desired commutative diagram by applying \(\times _SS^\textrm{rig}\) to the above commutative diagram. \(\square \)
The following elementary lemma is used in the above proof.
Lemma 5.9
Let A be a regular local ring of dimension 2 with regular parameters s, t. Let \(\pi :X\rightarrow \mathop {\textrm{Spec}}\nolimits A\) be a modification. Then there exist an integer \(\nu \ge 0\) and a commutative diagram
where \(\pi _\nu \) is the natural morphism.
Proof
By the valuative criterion of proper morphisms, it suffices to show that the ring \({\widetilde{A}}=\varinjlim _\nu A[\frac{s}{t^\nu }]_{(\frac{s}{t^\nu },t)}\) is a valuation ring.
To see this, we claim that any nonzero element \(f\in A\) can be written as \(f=s^nt^m(g+\frac{s}{t^m}h)\) for some integers \(n,m\ge 0\) and some elements \(g\in A^\times \) and \(h\in A\). This can be checked as follows: take the maximum \(n\in {\mathbb {Z}}\) with \(f\in s^nA\) so that \(f=s^nf_1\) for some \(f_1\in A\setminus sA\); take the maximum \(m\in {\mathbb {Z}}\) with \(f\mod s\in t^m(A/sA)\) so that \(f_1\mod s=t^m{{\bar{g}}}\) for some \({{\bar{g}}}\in (A/sA){\setminus } t(A/sA)\); then \(f_1=t^mg+sh\) for some \(g\in A{\setminus }(s,t)=A^\times \) and \(h\in A\). Thus, any \(f\in A\) can be written in the claimed way.
We consider the map \(v:A\setminus \{0\}\rightarrow {\mathbb {Z}}^2\) sending f to (n, m) taken as above. This defines a valuation with respect to the lexicographic order on \({\mathbb {Z}}^2\) and canonically extends to a valuation on the field of fractions of A. Let V be the corresponding valuation ring. Then we have \(\widetilde{A}\subset V\), as we have \(v(\frac{s}{t^\nu })=(1,-\nu )\ge 0\) and \(v(u)=0\) for any \(u\in A[\frac{s}{t^\nu }]{\setminus }(\frac{s}{t^\nu },t)\). On the other hand, since the factor \(g+\frac{s}{t^m}h\) is a unit in \(A[\frac{s}{t^m}]_{(\frac{s}{t^m},t)}\), any nonzero element of V can be written as \(s^nt^mu\) for some \((n,m)\ge 0\) and some unit u of \({\widetilde{A}}\). Thus, we have \(\widetilde{A}=V\). \(\square \)
Lemma 5.10
Let \(\mathsf U\subset \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) be an open neighborhood of the origin and \(\mathsf Z\subsetneq \mathsf U\) be a proper Zariski closed subset. Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that \(\mathsf U\setminus \mathsf Z\) contains the open subset
Proof
We may assume that \(\mathsf U=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\). We take a nonzero function \(f\in k\langle s,t\rangle \) such that the zero of f contains \(\mathsf Z\), i.e, a nonzero element in an ideal defining \(\mathsf Z\). We may assume that \(\mathsf Z\) is the Zariski closed subset defined by f. Since we do not care about points x with \(|s(x)|=0\), we may assume that f is not divided by s. Then, by replacing f by cf for some \(c\in k^\times \) if needed, we can write
with \(a\in k^\times \), \(g\in k^\circ \langle t\rangle \), and \(h\in k^\circ \langle s,t\rangle \). Take \(\delta \in |k^\times |\) such that \(\delta <|a|\). Let \(x\in \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) be a point which satisfies \(0<|s(x)|\le |t^{\nu +1}(x)|\) and \(|t(x)|\le \delta \). Then we have
and hence, \(|f(x)|\ne 0\). This proves the assertion. \(\square \)
Proof (Proof of Proposition 5.7)
[Proof of Proposition 5.7] By Lemma 5.8, the problem is reduced to the case where \(\mathcal F\) is strictly quasi-constructible. Then there exists a constructible subset \(\mathsf L\) which contains the origin of \({\mathbb {B}}^2_k=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) and a Zariski closed subset \(\mathsf Z\subset {\mathbb {B}}^2_k\) such that \(\mathcal F\) is locally constant on \(\mathsf L\setminus (\mathsf L\cap \mathsf Z)\). Note that, since the origin is a maximal point, \(\mathsf L\) contains an open neighborhood of the origin. Then the assertion follows from Lemma 5.10. \(\square \)
Corollary 5.11
Let \(f:X\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a morphism separated of finite presentation and \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on X, for an integer n invertible in \(k^\circ \). Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that the cohomology sheaves of \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) are locally constant on the open subset \(S^\textrm{rig}=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) defined by \(0<|s|\le |t^\nu |\) and \(|t|\le \delta \).
Proof
By Theorem 5.5, there exists a modification \(\pi :S'\rightarrow S\) such that \(\pi ^{\textrm{rig}*}Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) is strictly quasi-constructible. As \(Rf^\textrm{rig}_!\) has finite cohomological dimension ([9, Corollary 0.5.8]), the assertion follows from Proposition 5.7. \(\square \)
6 Tubular neighborhoods
In this section, we fix a non-archimedean field k and assume that k is of characteristic zero. We also fix an integer n invertible in \(k^\circ \). We introduce some notations. The rigid affine line \(\mathop {\textrm{Spec}}\nolimits k[t]\times _{\mathop {\textrm{Spec}}\nolimits k}\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) ([8, Proposition 3.8]) is denoted by \({\mathbb {A}}\). For \(r\in |k^\times |\), the disk (resp. punctured disk) of radius r, i.e, the open subset \(\{x\in {\mathbb {A}}\mid |t(x)|\le r\}\) (resp. \(\{x\in {\mathbb {A}}\mid 0<|t(x)|\le r\}\)) is denoted by \({\mathbb {B}}(r)\) (resp. \({\mathbb {B}}^*(r)\)). We put \({\mathbb {B}}={\mathbb {B}}(1)\) and \({\mathbb {B}}^*={\mathbb {B}}^*(1)\).
Let \(p:P\rightarrow \mathop {\textrm{Spec}}\nolimits k^\circ [t]\) be a morphism of schemes separated of finite type and X a closed subscheme of P defined by a global function \(g\in \mathcal O_P(P)\). We denote the natural morphism \(X\rightarrow \mathop {\textrm{Spec}}\nolimits k^\circ [t]\) by f. For an integer \(\nu \ge 0\) and an element \(\varepsilon \in |k^\times |\), we consider the closed subset \(X^\textrm{rig}_{\nu ,\varepsilon }=\{x\in P^\textrm{rig}\times _{{\mathbb {B}}}{\mathbb {B}}^*\mid |g(x)|<\varepsilon \cdot |t^\nu (x)|\}\) and denote the natural morphism \(X^\textrm{rig}_{\nu ,\varepsilon }\rightarrow {\mathbb {B}}^*\) of pseudo-adic spaces by \(f^\textrm{rig}_{\nu ,\varepsilon }\).
Proposition 6.1
Let \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on P. There exist an integer \(\nu \ge 0\) and an element \(\varepsilon _0\in |k^\times |\) satisfying the following property. For every \(\varepsilon \in |k^\times |\) with \(\varepsilon \le \varepsilon _0\), there exists an element \(\delta \in |k^\times |\) such that the natural morphism
is an isomorphism on \({\mathbb {B}}^*(\delta )\).
We prove this proposition at the end of this section. To this end, we recall a structure theorem of finite étale coverings of annuli due to Lütkebohmert. For this, we introduce a terminology:
Definition 6.2
Assume that k is algebraically closed. Let \(r,R\in |k^\times |\) be elements with \(r\le R\) and \(X\rightarrow {\mathbb {B}}(r,R)=\{x\in {\mathbb {A}}\mid r\le |t(x)|\le R\}\) be a finite étale covering. We say \(X\rightarrow {\mathbb {B}}(r,R)\) is of Kummer type if it is isomorphic to the cover
Then Lütkebohmert’s structure theorem states the following.
Theorem 6.3
( [17, Theorem 2.2]) Let \(d\ge 1\) be an integer and k be an algebraically closed complete non-archimedean field extension of \({\mathbb {Q}}_p\). Then there exists an element \(\beta \in |k^\times |\) with \(\beta \le 1 \) such that every finite étale covering \(X\rightarrow {\mathbb {B}}(r,R)\) of degree d, for every \(r\le R\in |k^\times |\) with \(\beta ^{-1}r\le \beta R\), is of Kummer type over \({\mathbb {B}}(\beta ^{-1}r,\beta R)\).
For \(r\in |k^\times |\), the closed disk (resp. punctured closed disk) of radius r, i.e, the subset \(\{x\in {\mathbb {A}}\mid |t(x)|< r\}\) (resp. \(\{x\in {\mathbb {A}}\mid 0<|t(x)|< r\}\)) is denoted by \({\mathbb {D}}(r)\) (resp. \({\mathbb {D}}^*(r)\)). We put \({\mathbb {D}}={\mathbb {D}}(1)\) and \({\mathbb {D}}^*={\mathbb {D}}^*(1)\). We regard \({\mathbb {D}}(r)\) and \({\mathbb {D}}^*(r)\) as pseudo-adic spaces.
Lemma 6.4
[c.f. (II) in the proof of [11, Theorem 2.5]] Assume that k is algebraically closed and let \(d\ge 1\) be an integer. There exists an element \(\varepsilon _0(d)\in |k^\times |\) satisfying the following condition. Let \(\mathcal M\) be a locally constant constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on \({\mathbb {B}}^*\) that is trivialized by a finite étale cover \(X\rightarrow {\mathbb {B}}^*\) of degree d. Then for every \(\varepsilon \le \varepsilon _0(d)\), we have \(R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M)=0\).
We follow the proof of [16, Lemma 6.12].
Proof
Take \(\varepsilon _0\) to be an element \(\beta \) as in Theorem 6.3. Since \(H^i_c({\mathbb {D}}^*(\beta ),\mathcal M)\cong \varinjlim _{r\in |k^\times |}H^i_c({\mathbb {D}}(\beta ){\setminus }{\mathbb {D}}(r),\mathcal M)\), it suffices to prove that \(R\Gamma _c({\mathbb {D}}(\beta )\setminus {\mathbb {D}}(r),\mathcal M)=0\). By Theorem 6.3, we may assume that \(\mathcal M\) is a constant sheaf. Then the explicit description \(R\Gamma _c({\mathbb {D}}(r),{\mathbb {Z}}/n{\mathbb {Z}})\cong {\mathbb {Z}}/n{\mathbb {Z}}\) as in [9, Example 0.2.5] shows the assertion. \(\square \)
Lemma 6.5
Let \({\mathbb {B}}^2_k=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) and \(\nu \ge 0\) an integer. For an element \(\varepsilon \in |k^\times |\), we consider the subsets \(\mathsf U_\varepsilon =\{x\in {\mathbb {B}}^2_k\mid 0<|s(x)|\le \varepsilon \cdot |t^\nu (x)|\}\) and \(\mathsf U_\varepsilon '=\{x\in {\mathbb {B}}^2_k\mid 0<|s(x)|<\varepsilon \cdot |t^\nu (x)|\}\), which we regard as pseudo-adic spaces. We denote the second projection \(\mathsf U'_\varepsilon \rightarrow {\mathbb {B}}=\mathop {\textrm{Spa}}\nolimits (k\langle t\rangle ,k^\circ \langle t\rangle )\) by \(\textrm{pr}'_{\varepsilon ,2}\). Let \(\mathcal M\) be a locally constant constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\)-modules on \(\mathsf U_1\). Then there exists an element \(\varepsilon _0\in |k^\times |\) satisfying the following condition. For every element \(\varepsilon \in |k^\times |\) with \(\varepsilon \le \varepsilon _0\), there exists an element \(\delta \in |k^\times |\) such that the restriction of \(R\textrm{pr}'_{\varepsilon ,2!}(\mathcal M|_{\mathsf U'_\varepsilon })\) to \({\mathbb {B}}^*(\delta )\) vanishes.
Proof
We may assume that k is algebraically closed. Considering the isomorphism \(\varphi _\nu :\mathsf U_1\cong {\mathbb {B}}^*\times {\mathbb {B}}^*;(s,t)\mapsto (s/t^\nu ,t)\) of adic spaces, we may assume that \(\nu =0\). We denote the natural immersion \(\mathsf U'_\varepsilon \rightarrow {\mathbb {B}}^2_k\) by u. Then the sheaf \(u_!\mathcal M\) is strictly quasi-constructible (in particular, quasi-constructible). Thus, by [11, Theorem 2.1] and [11, 1.2.iv)], there exists an element \(\delta \in |k^\times |\) such that the restriction of \(R\textrm{pr}'_{\varepsilon ,2!}\mathcal M\) to \({\mathbb {B}}^*(\delta )\) is locally constant of finite type. Note that, for a classical point x of \({\mathbb {B}}^*(\delta )\), we have \((R\textrm{pr}'_{\varepsilon ,2!}\mathcal M)_x\cong R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M|_{{\mathbb {D}}^*(\varepsilon )\times x})\) by [9, Theorem 5.3.9]. We take a finite étale cover of that trivializes \(\mathcal M\) and let d denote its degree. Take \(\varepsilon _0=\varepsilon _0(d)\) to be an element as in Lemma 6.4. Then, if \(\varepsilon \le \varepsilon _0\), then the stalk \((R\textrm{pr}'_{\varepsilon ,2!}\mathcal M)_x\cong R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M|_{{\mathbb {D}}^*(\varepsilon )\times x})\), and hence \(R\textrm{pr}'_{\varepsilon ,2!}\mathcal M\) vanishes. \(\square \)
Proof (Proof of Proposition 6.1)
[Proof of Proposition 6.1] We consider the morphism \(g:P\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) over \(\mathop {\textrm{Spec}}\nolimits k^\circ [t]\) defined by \(s\mapsto g\in \mathcal O_{P}(P)\). By Corollary 5.11, we can apply Lemma 6.5 to the restriction of \(R^ig^\textrm{rig}_!\mathcal F^\textrm{rig}\) to the subset \(\{x\in S^\textrm{rig}\mid 0<|s(x)|\le |t^\nu (x)|\}\), which proves the assertion. \(\square \)
Remark 6.6
It would be straightforward to extend Proposition 6.1 to the case where the closed subscheme X is not necessarily defined by one global equation, i.e, the case of general closed subschemes X.
It might be also possible to remove the assumption on the characteristic of the base field k by an argument similar to the proof of [16, Lemma 7.1].
References
Artin, M.: Morphismes acycliques, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XV, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)
Artin, M.: Théoréme de changement de base par un morphisme lisse, et applications, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XVI, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)
Deligne, P.: Cohomologie á support propre, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XVII, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)
Fujiwara, K., Kato, F.: Foundations of Rigid Geometry. I, EMS Monographs in Mathematics. European Mathematical Society (EMS), Zürich (2018). MR3752648
Fujiwara, K.: Theory of tubular neighborhood in étale topology. Duke Math. J. 80(1), 15–57 (1995)
Grothendieck, A., Verdier, J.-L. Conditions de finitude. topos et sites fibrés. Applications aux questions de passage à la limite., Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 II), exposé VI, Lecture Notes in Mathematics, vol. 270. Springer-Verlag (1972)
Grothendieck, A., Verdier, J.-L.: Topos, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 I), exposé IV, Lecture Notes in Mathematics, vol. 269. Springer-Verlag (1972)
Huber, R.: A generalization of formal schemes and rigid analytic varieties. Math. Z. 217(4), 513–551 (1994)
Huber, R.: Étale cohomology of rigid analytic varieties and Adic spaces. In: Aspects of Mathematics. Vieweg, Braunschweig (1996)
Huber, R.: A finiteness result for direct image sheaves on the étale site of rigid analytic varieties. J. Algebr. Geom. 7(2), 359–403 (1998)
Huber, R.: A finiteness result for the compactly supported cohomology of rigid analytic varieties. J. Algebr. Geom. 7(2), 313–357 (1998)
Huber, R.: A finiteness result for the compactly supported cohomology of rigid analytic varieties. II. Ann. Inst. Fourier (Grenoble) 57(3), 973–1017 (2007)
Illusie, L.: Vanishing cycles over general bases after P. Deligne, O. Gabber, G. Laumon and F. Orgogozo, https://www.imo.universite-paris-saclay.fr/~illusie/vanishing1b.pdf (2006)
Illusie, L.: Exposé XI. Produits orientés, no. 363–364, 2014, Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, pp. 213–234. MR3329780
Illusie, L.: Around the Thom-Sebastiani theorem, with an appendix by Weizhe Zheng. Manuscr. Math. 152(1–2), 61–125 (2017)
Ito, K.: Uniform local constancy of étale cohomology of rigid analytic varieties. J. Inst. Math. Jussieu 23, no.2, 839–896 (2024)
Lütkebohmert, W.: Riemann’s existence problem for AP-ADIC field. Invent. Math. 111(1), 309–330 (1993)
Lu, Q., Zheng, W.: Compatible systems and ramification. Compos. Math. 155(12), 2334–2353 (2019)
Mieda, Yoichi: On the action of the Weil group on the \(\ell \)-adic cohomology of rigid spaces over local fields. Int. Math. Res. Not. 2006(9), 16429–16429 (2006)
Orgogozo, F.: Modifications et cycles proches sur une base générale. Int. Math. Res. Not. 25315, 38. MR2249998 (2006)
Raynaud, M.: Géométrie analytique rigide d’aprés Tate, Kiehl,.... Table Ronde d’Analyse Non Archimédienne (Paris, 1972), pp. 319–327. Supplément au Bull. Soc. Math. France, vol. Tome 102, Soc. Math. France, Paris, (1974). MR470254
Scholze, P.: Perfectoid spaces. Publ. Math. Inst. Hautes Études Sci. 116, 245–313 (2012)
Acknowledgements
The author would like to thank Teruhisa Koshikawa for pointing out mistakes in an earlier attempt of the author to directly generalize the proof in [11] and for suggesting to use nearby cycles over general bases. He is grateful to Kazuhiro Ito for explaining his work [16] to the author, especially how to apply nearby cycles over general bases to the theory of étale cohomology of rigid analytic varieties. He would also like to thank Daichi Takeuchi for various helpful discussions, especially for pointing out a mistake in Remark 3.5 of the earlier draft and suggesting to fix Definition 3.1 and Definition 3.4. He would like to express his gratitude to Takeshi Saito for various helpful discussion and for constant encouragement. Finally, the author thanks the referee for reading the manuscript carefully and giving numerous amount of advice. This project has received funding from Iwanami Fujukai Foundation and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 851146), and funding through the Max Planck Institute for Mathematics in Bonn, Germany (report number MPIM-Bonn-2023).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Data availability statement
This manuscript has no associated data.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kato, H. Étale cohomology of algebraizable rigid analytic varieties via nearby cycles over general bases. manuscripta math. (2024). https://doi.org/10.1007/s00229-024-01564-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00229-024-01564-0




