Abstract
We construct a general framework for tropical differential equations based on idempotent semirings and an idempotent version of differential algebra. Over a differential ring equipped with a non-archimedean norm enhanced with additional differential information, we define tropicalization of differential equations and tropicalization of their solution sets. This framework includes rings of interest in the theory of p-adic differential equations: rings of convergent power series over a non-archimedean normed field. The tropicalization records the norms of the coefficients. This gives a significant refinement of Grigoriev’s framework for tropical differential equations. We then prove a differential analogue of Payne’s inverse limit theorem: the limit of all tropicalizations of a system of differential equations is isomorphic to a differential variant of the Berkovich analytification.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Algebraic ODEs are systems of differential equations formed from polynomial expressions in an indeterminate function f and its derivatives. The algebraic theory was first developed by Ritt [24] and collaborators. Many important classes of models from the natural sciences, such as chemical reaction networks, are algebraic ODEs, and in pure mathematics algebraic ODEs appear in many parts of geometry, including periods and monodromy. Understanding their solutions and singularities has many important consequences in pure and applied mathematics.
In this paper we pursue the further development of the tropical mathematics tool set for studying differential equations. Tropical geometry is a field at the interface between combinatorics, computational algebra/geometry, and algebraic geometry. One of the foci of tropical geometry is the study of non-archimedean amoebae of affine varieties over non-archimedean normed fields, which can be viewed as combinatorial shadows of varieties. Tropical geometry has provided important computational and theoretical tools for algebraic geometry, and we hope to open the door to similar applications in differential algebra.
In [11] Grigoriev first introduced a theory of tropical differential equations and defined a framework for tropicalizing algebraic ODEs over a ring of formal power series R[[t]]. In this framework, one tropicalizes a differential equation by recording the leading power of t in each coefficient, and one tropicalizes a power series solution simply recording the powers of t that are present.
Solutions to a differential equation tropicalize to solutions to its tropicalization, and Grigoriev asked if all solutions to the tropicalization of an equation arise as tropicalizations of classical solutions; i.e., is the map from classical solutions to tropical solutions surjective? This is the differential equation analogue of the Fundamental Theorem of Tropical Geometry [22, Theorem 3.2.3], and this question was answered positively by Aroca et al. in [1] (assuming R is an uncountable algebraically closed field of characteristic 0). These ideas have also been extended to the case of algebraic partial differential equations in [6].
Paralleling the role of Gröbner theory in defining tropical varieties in the non-differential setting, [7] and [12] define initial forms and develop a Gröbner-theoretic approach to Grigoriev’s tropical differential equations. A similar approach is also presented in [4], which also gives an illuminating account of tropical ordinary and partial differential equations (in part based on a preliminary report of the algebraic perspective presented here).
A limitation present in all of the above work is that the tropicalization construction studied there records only the powers of t present in a power series solution; it does not record any information about the norms of the coefficients. Thus any information about convergence of power series solutions is lost when using Grigoriev’s tropicalization. In the theory of p-adic differential equations, one of the central problems is to understand the radii of convergence of formal power series solutions, which are controlled by the norms of the coefficients.
1.1 Results
The main purpose of this work is to build a refinement of Grigoriev’s framework that records and incorporates the norms of the coefficients in a power series solution so that convergence information is encoded in tropical solutions. This requires developing a theory of differentials on idempotent semirings in which the usual Leibniz rule is weakened to a tropical Leibniz rule, and this development includes constructing free tropical differential algebras (a tropical analogue of Ritt algebras).
We give a brief explanation of our framework here. A tropical pair \(\textbf{S}=(S_1 \rightarrow S_0)\) is a tropical differential semiring \(S_1\) and a homomorphism to a semiring \(S_0\). The coefficients of tropical differential equations live in \(S_0\). Solutions live in \(S_1\) (where they can be differentiated), but the condition that tests if something is a solution takes place in \(S_0\). We think of \(S_0\) as recording the leading behavior of elements of \(S_1\). The primary example of a tropical pair has \(S_1 = {\mathbb {T}}[[t]]\) (the semiring of formal power series with tropical real number coefficients), \(S_0 = \mathbb {R}^2_ lex \cup \{\infty \}\) is a rank 2 version of the tropical semiring, and the map \(S_1 \rightarrow S_0\) sends \(at^n + \cdots \) to (n, a).
We now state out main results informally.
Theorem A
We construct a category of \(\textbf{S}\)-algebras, and to a set E of tropical differential equations over \(\textbf{S}\) we associate an object of this category such that morphisms to an \(\textbf{S}\)-algebra \(\textbf{T}\) are in natural bijection with solutions to E with values in \(\textbf{T}\).
A system of algebraic differential equations over a field k is represented in coordinate-free form by a differential k-algebra A. To tropicalize A, we need two pieces of additional data:
-
(1)
A non-archimedean norm on k taking values in an idempotent semiring \(S_0\), and a differential enhancement of the norm, which is a lifting to a map \(A \rightarrow S_1\) that commutes with the differential. (These notions are defined in Sects. 2.3 and 4.7.)
-
(2)
A system of generators \(x_i \in A\) so that A is presented as a quotient of a Ritt algebra \(k\{x_1, \ldots , x_n\} \twoheadrightarrow A\).
Any differential algebra A admits a universal presentation \(k\{x_a \, | \, a\in A\} \rightarrow A\). Tropicalizing this presentation, we find:
Theorem B
The tropicalization of A with respect to its universal presentation is the colimit of its tropicalizations with respect to finite presentations.
Finally, we provide evidence for the appropriateness of our definitions and framework by proving a differential analogue of Payne’s inverse limit theorem [23]. Recall that, given an algebra A over a non-archimedean field k, the underlying set of the Berkovich analytification of \(\textrm{Spec}\,A\) is the set of all multiplicative seminorms on A that are compatible with the norm on k. Now suppose that k is a differential ring, the norm v on k has a differential enhancement \(\widetilde{v}\) taking values in a pair \(\textbf{S}\), and A is a differential algebra over k. In this setting, given an \(\textbf{S}\)-algebra \(\textbf{T}=(T_1 \rightarrow T_0)\), we can consider the set of all pairs \((w,\widetilde{w})\) where \(w: A\rightarrow T_0\) is a multiplicative seminorm on A compatible with v and \(\widetilde{w}: A \rightarrow T_1\) is a differential enhancement of w compatible with \(\widetilde{v}\). We call this the \(\textbf{T}\)-valued differential Berkovich space of A, denoted \( Berk _{\textbf{T}}(A)\).
Theorem C
There is a universal multiplicative seminorm with differential enhancement on A, compatible with the norm on k and it takes values in the tropicalization of the universal presentation of A. Hence the tropicalization of the universal presentation corepresents the functor \(\textbf{T} \mapsto Berk _{\textbf{T}}(A)\).
Combining this with Theorem B, we immediately obtain our differential analogue of Payne’s inverse limit theorem.
Corollary D
Let k be a differential ring equipped with a non-archimedean seminorm and differential enhancement taking values in \(\textbf{S}\), let A be a differential algebra over k, and let \(\textbf{T}\) be an \(\textbf{S}\)-algebra. The set \( Berk _{\textbf{T}}(A)\) is isomorphic to the inverse limit of the \(\textbf{T}\)-valued solution sets of the tropicalizations of all finite presentations of A.
2 Semirings and non-archimedean seminorms
Several algebraic foundations for tropical geometry have been developed, including hyperfields [2, 15, 18, 25] Lorscheid’s blueprints [16, 17], and idempotent semirings [3, 5, 8,9,10, 13, 14, 19,20,21, 26]. For the present work, we find that idempotent semirings provide the most convenient language for the development of our theory.
2.1 Idempotent semirings
An idempotent semiring is a semiring \((S, \oplus , \otimes )\) in which addition is an idempotent operation: \(a \oplus a = a\). An idempotent semiring carries a canonical partial order defined by \(a \le b\) if \(a\oplus b = b\). The additive unit \(0_S\) is the unique minimal element. In a semiring, we will often write the product \(a\otimes b\) simply as ab.
Example 2.1
-
(1)
Let \({\mathbb {T}}=\mathbb {R}_{\ge 0}\) with the operations \(a\otimes b = ab\) (ordinary multiplication), and \(a \oplus b = \textrm{max}(a,b)\). Note that the map \(a\mapsto -\textrm{log}(a)\) gives an isomorphism to the usual tropical semiring \((\mathbb {R}\cup \{\infty \}, \textrm{min},+)\).
-
(2)
Let \({\mathbb {T}}_n\) denote \((\mathbb {R}_{> 0})^n \cup \{(0,\ldots , 0)\}\). We define \(a\oplus b = \textrm{max}(a,b)\), where the maximum is taken with respect to the lexicographic ordering on the positive orthant, and we define \(a \otimes b\) to be component-wise multiplication.
-
(3)
The boolean semiring \(\mathbb {B}\) is the sub-semiring \(\{0,1\} \subset {\mathbb {T}}\). Note that \(\mathbb {B}\) is the initial object in idempotent semirings.
2.2 Congruences and bend relations
A quotient of a ring R is defined by an equivalence relation on R such that the ring structure descends to the set of equivalence classes. Such equivalence relations are of course in bijection with ideals via the correspondence
This correspondence does not hold for semirings in general, and so we must work with the equivalence relations themselves when defining quotients.
Recall that a congruence on a semiring S is an equivalence relation \(K \subset S\times S\) that is also a subsemiring. If K is a congruence on S, then the semiring structure on S descends to a well-defined semiring structure on S/K. Moreover, if \(f: S \twoheadrightarrow S'\) is a surjective homomorphism of semirings then its kernel congruence \(\textrm{ker}\,f= \{(a,b) \,\, | \,\, f(a) = f(b)\}\) is indeed a congruence and \(S/\textrm{ker}\, f \cong S'\).
Given a set of binary relations \(X \subset S\times S\), the congruence it generates can be described concretely. First take the subsemiring of \(S\times S\) generated by X, and then take the transitive and symmetric closure of this. See [9, Lemma 2.4.5].
We now come to a class of congruences on idempotent semirings that are essential in tropical geometry. Given an expression \(a_1 \oplus a_2 \oplus \cdots \oplus a_n\) in an idempotent semiring S, the bend relations of this expression, written  , is the congruence on S generated by the relations
, is the congruence on S generated by the relations
for each \(j = 1 \ldots n\). As special cases, when \(n=2\),  is generated by the single relation \(a \sim b\). When \(n=3\),
is generated by the single relation \(a \sim b\). When \(n=3\),  is generated by the relations
is generated by the relations
The motivation for the bend relations stems from the following fact. Recall that the tropical hypersurface of a tropical polynomial \(f \in {\mathbb {T}}[x_1, \ldots , x_n]\) can be described away from the boundary of \({\mathbb {T}}^n\) as the locus where the graph of f is non-linear (with respect to the \(\mathbb {R} \cup \{\infty \}\) parametrization of \({\mathbb {T}}\)).
Proposition 2.2
(Prop. 5.1.6 of [9]) Given a tropical polynomial \(f \in {\mathbb {T}}[x_1, \ldots , x_n]\), the tropical hypersurface of f is precisely the set of homomorphisms  .
.
2.3 Non-archimedean seminorms
A non-archimedean multiplicative seminorm on a ring R is a map v from R to the tropical semiring \({\mathbb {T}}=(\mathbb {R}_{\ge 0}, \oplus = \textrm{max}, \times )\) that is a homomorphism of multiplicative monoids, has \(v(0)=0\), and satisfies the ultrametric triangle inequality,
The map \(-\textrm{log}: \mathbb {R}_{\ge 0} \rightarrow \mathbb {R} \cup \{\infty \}\) identifies non-archimedean seminorms (always assumed to be multiplicative) with valuations, and so we will use the terms interchangeably as we adopt the following generalization.
Definition 2.3
A non-archimedean seminorm on a ring R is an idempotent semiring T and a map \(v: R \rightarrow T\) satisfying
-
(1)
\(v(0) = 0_T\),
-
(2)
\(v(1) = v(-1) = 1_T\),
-
(3)
\(v(ab) = v(a) v(b)\),
-
(4)
\(v(a+b) \oplus v(a) \oplus v(b) = v(a) \oplus v(b)\).
Remark 2.4
Condition (4) generalizes the ultrametric triangle inequality, as it says that \(v(a+b) \le v(a) \oplus v(b)\) in the canonical partial order on T. This definition thus becomes equivalent to the usual definition of a Krull valuation when the partial order is a total order, such as when \(T = {\mathbb {T}}_n\). This condition can also be written more symmetrically as \(v(a)\oplus v(b) \oplus v(c) = v(a) \oplus v(b)\) whenever \(a+b+c=0\) in A, since \(v(c)=v(a+b)\).
For use later on, we record the following simple observation. A rank 1 valuation \(v: R \rightarrow {\mathbb {T}}\) can be extended to a rank 2 valuation on the the ring \(R\{\!\{t\}\!\}\) of Puiseux series (or the subrings of formal Laurent series or polynomials) by the formula
2.4 Tropical differential semirings
Recall that a differential ring is a ring R equipped with an additive map \(d: R \rightarrow R\) that satisfies the Leibniz relations \(d(ab) = (da)b + a(db)\). This relation for 2-fold products easily implies that d also satisfies an analogous relation for n-fold products. We will call these relations the strict Leibniz relations, and a map d satisfying them will be called a strict differential.
In this work we propose that differentials on idempotent semirings should be required to satisfy a somewhat weaker condition than the strict Leibniz relations. Given an idempotent semiring S, an additive map \(d: S \rightarrow S\) is said to be a tropical differential if it satisfies the tropical Leibniz relations: for any pairs of elements \(x,y \in S\) the bend relations of the expression
hold. Note that we can view the tropical Leibniz relations as the tropicalization of the strict Leibniz relations.
Definition 2.5
A tropical differential semiring is an idempotent semiring equipped with a tropical differential. A morphism of tropical differential semirings
is a morphism of semirings such that \(f(d_S(x)) = d_T(f(x))\) for all \(x \in S\).
Remark 2.6
Just as the strict Leibniz relations for 2-fold products imply the strict Leibniz relations for n-fold products, such as
it is possible to derive n-fold tropical Leibniz relations from the 2-fold tropical Leibniz relations. I.e., in a tropical differential semiring the bend relations of any expression
hold. However, the tropical Leibniz relations are distinct from the strict Leibniz relations in two important ways. (1) A strict differential d automatically satisfies the tropical Leibniz relations, but there are many tropical differentials that are not strict. (2) The differential of a product xy is constrained by the tropical Leibniz relations and the differentials of x and y, but it is not uniquely determined by them.
Example 2.7
-
(1)
Let S be an idempotent semiring and let d be either the zero map or the identity; these are each strict differentials on S.
-
(2)
Consider the idempotent semiring \(\mathbb {B}[[t]]\) of formal power series with coefficients in \(\mathbb {B}\). This can be identified with the power set of \(\mathbb {N}\) by sending a power series to the set of exponents appearing in it; sum corresponds to union, and the product corresponds to Minkowski sum. The map defined by \(t^n \mapsto t^{n-1}\) (for any \(n \ge 1\) ) is a strict differential. If p is a prime, the map defined by
$$\begin{aligned} t^n \mapsto \left\{ \begin{array}{ll} t^{n-1} &{} n \ge 1 \text { and } p \not \mid n \\ 0 &{} n=0 \text { or } p \mid n \end{array}\right. \end{aligned}$$is a tropical differential that is not strict.
-
(3)
Consider the idempotent semiring of formal tropical power series \({\mathbb {T}}[[t]]\). It can be endowed with a strict differential, \(d_0\), defined by
$$\begin{aligned} d_0(t^n) = \left\{ \begin{array}{ll} t^{n-1} &{} n \ge 1\\ 0 &{} n=0. \end{array}\right. \end{aligned}$$ -
(4)
More generally, if \(v: \mathbb {N} \rightarrow {\mathbb {T}}\) is a non-archimedean seminorm, then there is a non-strict tropical differential \(d_v\) defined by,
$$\begin{aligned} d_v(t^n) = \left\{ \begin{array}{ll} v(n)t^{n-1} &{} n \ge 1\\ 0 &{} n=0. \end{array}\right. \end{aligned}$$(2.2)Indeed, this satisfies the tropical Leibniz relations since
$$\begin{aligned} d_v(t^n t^m) \oplus d_v(t^n)t^m \oplus t^n d_v(t^m) = (v(n+m) \oplus v(n) \oplus v(m))t^{n+m-1}, \end{aligned}$$and the coefficient \(v(n+m) \oplus v(n) \oplus v(m)\) on the right satisfies the bend relations (the argument is essentially the same for k-fold products with \(k>2\)). Note that v could be either a p-adic norm, or a degenerate p-adic norm where \(v(n) = 0\) if p divides n, and 1 otherwise.
Remark 2.8
While \(\mathbb {B}\) is the initial objects in the category of idempotent semirings, tropical differential semirings do not admit an initial object because the tropical Leibniz rule does not determine d(1).
2.5 Differential congruences
Let (S, d) be a semiring equipped with an additive map \(d: S \rightarrow S\). A differential congruence on S is a congruence \(K \subset S\times S\) that is closed under d; i.e., if \((a,b) \in K\) then \((da, db) \in K\). When K is a differential congruence, the map d descends to an additive map \(\overline{d}: S/K \rightarrow S/K\), and if d is a tropical differential then \(\overline{d}\) is as well.
Proposition 2.9
If \(\{I_\lambda \subset S\times S\}\) is a set of differential congruences, then the congruence generated by them is a differential congruence.
Proof
Let K denote the congruence generated by the \(I_\lambda \). It is the transitive and symmetric closure of the subsemiring \(K_0\) generated by the \(I_\lambda \).
We will first show that \(d(K_0) \subset K\). Suppose that \((a_1,a_2)\) is a relation in some \(I_i\) and \((b_1, b_2)\) is a relation in some \(I_j\). Since d is additive, it certainly sends the sum \((a_1 + b_1, a_2 + b_2)\) to a relation in K. For the product, we proceed as follows. In \(I_i\) we have \((a_1 b_1, a_2 b_1)\) and hence \((d(a_1 b_1), d(a_2 b_1))\) since \(I_i\) is a differential congruence. Likewise, in \(I_j\) we have the relations \((b_1 a_2, b_2 a_2)\) and hence \((d(b_1 a_2), d(b_2 a_2))\). Hence the relation \((d(a_1 b_1), d(a_2 b_2))\) is indeed contained in the transitive closure K. Since any element of \(K_0\) is produced by a finite sequence of sums and products of elements in the \(I_\lambda \), it follows that \(d(K_0) \subset K\), as desired.
Now, any relation in K can be decomposed as a finite transitive chain of relations in \(K_0\). Thus is follows that \(d(K) \subset K\).
3 Differential polynomials
The objective of this section is to construct a variant of the Ritt algebra of differential polynomials \(R\{x_1, \ldots , x_n\}\), where the coefficient ring R is replaced by a tropical differential semiring S.
3.1 Classical Ritt algebras and their universal property
Recall that, when R is a differential ring, the Ritt algebra of differential polynomials \(R\{x_1, \ldots , x_n\}\) is the commutative R-algebra freely generated by the variables \(x_i\) and their formal derivatives \(x_i^{(j)} = d^jx_i\). It carries a differential that sends \(x_i^{(j)}\) to \(x_i^{(j+1)}\) and extends as an additive derivation to arbitrary elements in \(R\{x_1, \ldots , x_n\}\).
Ritt algebras are characterized by a universal property: a homomorphism of differential rings \(\varphi : R\{x_1, \ldots , x_n\} \rightarrow R'\) is uniquely determined by the images of the generators \(\varphi (x_i) \in R'\), and there are no restrictions on these elements. It is this universal property that we wish to extend to the idempotent setting.
3.2 The failure of the naive definition of tropical Ritt algebra
While one can trivially replace the coefficient ring R with a differential idempotent semiring S in the above Ritt algebra construction, we shall now see that it impossible to endow this with a differential (either strict or tropical) for which the analogous universal property holds. In fact, we will show that there is no longer a unique choice of differential, and for any choice of differential the universal property fails.
Suppose that S is a differential idempotent semiring with tropical differential \(d_S\). The naive definition of differential polynomials over S suggested in the preceding paragraph will nevertheless be useful later on, so we give it a name:
Definition 3.1
Given a tropical differential semiring S, the algebra of basic differential polynomials over S, denoted
is the polynomial S-algebra on variables \(x_i\) and their formal derivatives \(x_i^{(j)}\).
Let us now attempt to extend the differential of S to this algebra. Obviously we would like to send \(x_i^{(j)}\) to \(x_i^{(j+1)}\), and we would like the map to be additive. The difficulty is in choosing how to extend it to arbitrary products. In contrast to the case of coefficients in a differential ring, the tropical Leibniz relations allow more freedom in extending a partially-defined differential to all products; there is not a uniquely determined extension of \(d_S\) to a map d on all of \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) satisfying the tropical Leibniz relations. In fact, \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) admits many distinct differentials.
Example 3.2
Suppose \(w: \mathbb {N} \rightarrow S\) is a non-archimedean seminorm. Then we can define a differential \(d_w\) on \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) by the following rule. First, for a pure power \((x^{(j)}_i)^k\), we define
Then, we extend this to monomials \(c (x^{(j_1)}_{i_1})^{k_1} \cdots (x^{(j_m)}_{i_m})^{k_m}\) as a strict derivation. E.g.,
It is straightforward to check that this map \(d_w\) does indeed satisfy the tropical Leibniz relations.
One can generalize this example by choosing a distinct non-archimedean seminorm \(w_{ij}\) for each generator \(x_i^{(j)}\), defining the differential on pure powers by the rule
and then extending to arbitrary monomials using the strict Leibniz rule.
The above example shows that there is at least one differential on \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) for each n-tuple of non-archimedean seminorms \(\mathbb {Q} \rightarrow S\).
Proposition 3.3
There is no tropical differential on \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) that extends the tropical differential on S and makes this the free object on n generators.
Proof
We use proof by contradiction. Suppose d is such a differential, so for any non-archimedean seminorm \(w: \mathbb {N} \rightarrow S\) the identity map must be a morphism of differential idempotent semirings
This implies that \(d=d_w\) on pure powers. But this is a contradiction since \(d_w \ne d_{w'}\) if w and \(w'\) are distinct seminorms.
We will show below that the idempotent semiring \(S\{x_1, \ldots , x_n\}_{basic}\) can be enlarged to a tropical differential semiring \(S\{x_1, \ldots , x_n\}\) enjoying the universal property that justifies calling it the tropical Ritt algebra.
3.3 Differential polynomials over a ring
As a warm-up to constructing tropical Ritt algebras, we first give an alternative construction of the classical Ritt algebras in terms of trees.
To avoid ambiguity, let us be precise about our graph theory definitions and conventions.
Definition 3.4
A forest is a finite set V (the vertices) together with a parent map \(P: V \rightarrow V\) such for n large enough \(P^n\) sends each vertex to a fixed point of P. The fixed points of P are the roots. A tree is a forest with a single root. The valence of a vertex \(v \in V\) is the cardinality of \(P^{-1}(v) \smallsetminus \{v\}\), and the vertices of valence 0 are the leaves.
Consider the set of isomorphism classes of forests with leaves labelled by elements of \(R \cup \{x_1, \ldots , x_n\}\). This set becomes an abelian monoid under the operation of disjoint union. Now let \(\textrm{Forest}(R,n)\) denote the quotient monoid obtained by imposing the following relations:
-
(1)
A tree with a leaf labelled by \(0\in R\) is identified with the empty forest.
-
(2)
Any leaf labelled by 1 can be deleted.

-
(3)
If there are two leaves with labels \(a, b \in R\) having the same parent in a tree, then we may replace these two leaves with a single leaf labelled ab.

-
(4)
If a leaf with label \(r\in R\) has a univalent non-root parent then we may replace the leaf and its parent by a single leaf with label dr.

-
(5)
Given elements \(r_1, r_2 \in R\) and a tree t, we may form trees \(r_1 \cdot t, r_2\cdot t\), and \((r_1 + r_2)\cdot t\) by grafting a leaf with label \(r_1, r_2\), and \((r_1 + r_2)\), respectively, at the root. We then identify the pair of trees \((r_1 \cdot t) \cup (r_2 \cdot t)\) with the single tree \((r_1 + r_2)\cdot t\).

We think of the set of leaves with a given parent as representing the monomial formed by multiplying their labels, and we think of internal node edges as representing the differential d. Thus a tree represents a differential monomial, i.e., an expression formed from the elements of R and the variable \(x_1, \ldots , x_n\) by taking products and applying the differential d.
Example 3.5
The expression \(r_1 x_1 d^2(x_2)d(r_2 x_1 d(x_2))\) corresponds to the tree:

Proposition 3.6
The monoid \(\textrm{Forest}(R,n)\) is a commutative R-algebra.
Proof
The addition operation is disjoint union (the original monoid operation). The product of two trees is defined by gluing their roots together, and we extend this operation to products of forests by the distributive rule. The elements \(r\in R\) sit inside \(\textrm{Forest}(R,n)\) as the trees consisting of just a root and a single leaf with label r. It is straightforward to verify that this is an R-algebra.
There is a map
that inserts an edge at each root in a forest:

This map is clearly not a derivation, so let
and let \(\langle L \rangle \) denote the differential ideal generated by L, i.e., the smallest ideal in \(\textrm{Forest}(R,n)\) that is closed under applying d. By construction, the differential d descends to a derivation on the quotient.
Proposition 3.7
There is a natural isomorphism of differential R-algebras,
Proof
It is straightforward to check that \(\textrm{Forest}(R,n)/\langle L \rangle \) has exactly the same universal property as the Ritt algebra.
3.4 Differential polynomials over a semiring
We now give a variation on the above construction of the Ritt algebra via trees, where we replace R with a differential idempotent semiring S, and we replace the classical Leibniz relations with the tropical Leibniz relations.
First consider the S-algebra \(\textrm{Forest}(S,n)\) defined exactly as above, and then consider the subset
Let \(\langle L_{\textrm{trop}} \rangle \) denote the smallest ideal containing \(L_{\textrm{trop}}\) and closed under applying d.
Definition 3.8
Given a differential idempotent semiring S, we define the tropical Ritt algebra

where  is the congruence of bend relations generated by \(\langle L_{trop} \rangle \).
is the congruence of bend relations generated by \(\langle L_{trop} \rangle \).
The tropical Ritt algebra enjoys a universal property in the category of differential idempotent semirings that is entirely analogous to the universal property of the classical Ritt algebra in the category of differential rings.
Proposition 3.9
Given a differential S-algebra \(S'\), there is a bijection
implemented by sending a homomorphism \(\varphi \) to the n-tuple \((\varphi (x_1), \ldots , \varphi (x_n))\).
Proof
By the construction of \(\textrm{Forest}(S,n)\), any n-tuple \((a_1, \ldots , a_n) \in (S')^n\) determines a homomorphism of semirings
that commutes with d, and since the tropical Leibniz relations hold in \(S'\), this homomorphism descends to the quotient by  . Conversely, a homomorphism provides an n-tuple of elements of \(S'\).
. Conversely, a homomorphism provides an n-tuple of elements of \(S'\).
The algebra \(S\{x_1, \ldots , x_n\}_{\textrm{basic}}\) of basic differential polynomials that was introduced earlier sits inside \(S\{x_1, \ldots , x_n\}\) as the set of forests where only the root vertices have valence larger than 1; as the notation suggests. Obviously the basic subalgebra is not closed under taking differentials.
4 Algebraic structures for tropical differential equations
In the classical world, a differential equation over a differential ring R is an element \(f \in R\{x_1, \ldots , x_n\}\), and a solution to f in an R-algebra A is an element \(p \in A^n\) such that \(f(p)=0\). Equivalently, p is a solution if the corresponding homomorphism \(p: R\{x_1, \ldots , x_n\} \rightarrow A\) factors through the quotient \(R\{x_1, \ldots , x_n\}/(f)\).
In the tropical world, we have introduced differential idempotent semirings, but these objects on their own are not sufficient to describe solutions to tropical differential equations. A tropical differential equation over a differential idempotent semiring S is an element \(f \in S\{x_1, \ldots , x_n\}\) (where this is the tropical Ritt algebra defined above). Solutions to this differential equation will live in \(S^n\), but asking that f vanish or tropically vanish at \(p\in S^n\) turns out to be too restrictive. Following the idea of Grigoriev’s framework, p should be considered a solution to f if f tropically vanishes at p to leading order (rather than to all orders). This suggests that we must equip our differential idempotent semirings with something like a non-archimedean seminorm that provides a way of measuring the leading order of elements. To this end, we will now define and study the category of tropical pairs.
4.1 The category of tropical pairs
A tropical pair \(\textbf{S}\) consists of a tropical differential semiring \(S_1\), an idempotent semiring \(S_0\), and a homomorphism of idempotent semirings \(\pi : S_1\rightarrow S_0\).
Remark 4.1
We think of \(S_1\) as a space of functions, and we think of \(S_0\) as a space of leading exponents of the series expansions of these functions. The map \(\pi \), like the usual norm on Puiseux series, sends a function to its leading exponent.
In category theoretic terms, if
is the forgetful functor from differential idempotent semirings to idempotent semirings, then the category of pairs is the simply the comma category \((F\downarrow \textrm{Semirings})\). Explicitly, a morphism of pairs \(\varphi \) from \((S_1\rightarrow S_0)\) to \((T_1 \rightarrow T_0)\) is a commutative diagram of idempotent semirings

in which the upper horizontal arrow \(\varphi _1\) is a morphism of differential idempotent semirings. Given a pair \(\textbf{S}\), the category of \(\textbf{S}\)-algebras is the category of pairs \(\textbf{T}\) under \(\textbf{S}\).
A pair \((S_1 {\mathop {\rightarrow }\limits ^{\pi }} S_0)\) is said to be reduced if \(S_1\) admits no nontrivial quotient differential idempotent semiring over \(S_0\); i.e., it is reduced if there is no nontrivial differential congruence contained in the congruence \(\textrm{ker}(\pi )\).
Example 4.2
-
(1)
For any morphism of idempotent semirings \(\nu : S \rightarrow T\) we have a pair
$$\begin{aligned} (S,d=0) \rightarrow T, \end{aligned}$$and it is reduced if and only if \(\nu \) is injective. If \(\nu \) is not injective, then we can replace S with \(\textrm{im}(\nu )\) to obtain a reduced pair.
-
(2)
Consider the homomorphism
$$\begin{aligned} \pi : \mathbb {B}[[t]] \rightarrow {\mathbb {T}} \end{aligned}$$defined by \(t^n \mapsto e^{-n}\), and endow \(\mathbb {B}[[t]\) with the differential \(t^n \mapsto t^{n-1}\). This is a pair, and it is reduced by the following argument. Suppose \(a \ne b \in \mathbb {B}[[t]]\). If \(a = \bigoplus a_i t^i\) and \(b = \bigoplus b_i t^i\), then there exists a minimal n such that \(a_n \ne b_n\). It then follows that \(\pi (d^n a) \ne \pi (d^n b)\), and so \((d^n (a),d^n(b)) \notin \textrm{ker}(\pi )\). Hence any differential congruence containing (a, b) is not contained in \(\textrm{ker}(\pi )\).
-
(3)
Consider
$$\begin{aligned} \pi : {\mathbb {T}}[[t]]\rightarrow {\mathbb {T}}_2, \end{aligned}$$where the source has any of the differentials from Example 2.7 and the morphism \(\pi \) is given by
$$\begin{aligned} (a_{n_0} t^{n_0} \oplus a_{n_1} t^{n_1} \oplus \cdots ) \mapsto (e^{-n_0}, a_{n_0}). \end{aligned}$$This is a pair, and a modification of the argument above shows that it is also reduced.
We let \(\mathbf {\textrm{Pairs}}_\textrm{red}\) denote the full subcategory of reduced pairs. We will show below in Sect. 4.3 that \(\mathbf {\textrm{Pairs}}_\textrm{red}\) is a reflective subcategory, and so any pair \(\textbf{S}=(S_1 \rightarrow S_0)\) has a functorial reduction \(\textbf{S}^\textrm{red}=(S_1^\textrm{red} \rightarrow S_0)\).
Finally we are ready to define the category that will describe tropical differential equations and their solutions.
Definition 4.3
Given a reduced pair \(\textbf{S}\), an \(\textbf{S}\)-algebra is a reduced pair under \(\textbf{S}\), and we let \(\textbf{S} \mathrm {-Alg}\) denote the category of \(\textbf{S}\)-algebras.
An important example of an \(\textbf{S}\)-algebras comes from the tropical Ritt algebra. Given a pair \(\textbf{S}=(S_1\rightarrow S_0)\), we first define an idempotent semiring \((S_0 | S_1)\{x_1, \ldots , x_n\}\) by taking the pushout:

This pushout can be described explicitly as the algebra of trees \(S_1\{x_1, \ldots , x_n\}\) modulo the congruence generated by the relations that identify \(a,b\in S_1 \subset S_1\{x_1, \ldots , x_n\}\) if they have the same image in \(S_0\); i.e. leaves incident at the root have labels in \(S_0\) rather than \(S_1\). Note that \((S_0 | S_1)\{x_1, \ldots , x_n\}\) contains the polynomial \(S_0\)-algebra \(S_0\{x_1, \ldots , x_n\}_\textrm{basic}\).
The right vertical arrow in the above diagram gives an \(\textbf{S}\)-algebra that we will denote by \(\textbf{S}\{x_1, \ldots , x_n\}\); these pairs will play the role of tropical Ritt algebras in the category of \(\textbf{S}\)-algebras.
Proposition 4.4
Let \(\textbf{S}=(S_1\rightarrow S_0)\) be a pair and \(\textbf{Y}=(Y_1 \rightarrow Y_0)\) an \(\textbf{S}\)-algebra. Morphisms of \(\textbf{S}\)-algebras \(\varphi : \textbf{S}\{x_1, \ldots , x_n\} \rightarrow \textbf{Y}\) are in bijection with \(Y_1^n\). The bijection is implemented by sending a morphism \(\varphi =(\varphi _1, \varphi _0)\) to \((\varphi _1(x_1),\ldots \varphi _1(x_n) )\).
Proof
Given \(y\in Y_1^n\), it follows from the universal property of the tropical Ritt algebra (Prop. 3.9) that there is a unique morphism of \(S_1\)-algebras
sending \(x_i\) to \(y_i\). By the universal property of pushouts, this induces an arrow
such that \((\varphi _1, \varphi _0)\) is a morphism of \(\textbf{S}\)-algebras, and this is unique since \(\varphi _1\) is unique.
4.2 Tropical differential equations and their solutions
We start with a reduced pair \(\textbf{S} = (S_1 {\mathop {\rightarrow }\limits ^{\pi }} S_0)\). A tropical differential equation is simply a differential polynomial \(f \in S_0\{x_1, \ldots , x_n\}_\textrm{basic}\). Let us write \(f = \sum _\alpha f_\alpha x^\alpha \), where \(x^\alpha \) runs over the differential monomials in f. If \(x^\alpha \) has any factors of the form \(d^n x_i\) for \(n>0\) then it does not make sense to evaluate \(x^\alpha \) at an element \(c\in S_0^n\) because \(S_0\) is not a differential semiring. However, we can evaluate \(x^\alpha \) at an element \(C \in S_1^n\) and then push down to \(S_0\) via \(\pi \). Thus we can evaluate \(f\in S_0\{x_1, \ldots , x_n\}_\textrm{basic}\) at \(C\in S_1^n\) by the expression
Definition 4.5
The solution set of a differential polynomial \(f=\bigoplus _\alpha f_\alpha x^\alpha \in S_0\{x_1, \ldots , x_n\}_\textrm{basic}\), denoted \(\textrm{Sol}(f)\), is the subset of \(S_1^n\) consisting of all elements \(C= (C_1, \ldots , C_n)\) such that the sum
tropically vanishes.
When the pair \(S_1 \rightarrow S_0\) is \(\mathbb {B}[[ t ]] {\mathop {\rightarrow }\limits ^{\pi }} {\mathbb {T}}\), the above definition recovers Grigoriev’s framework. A subset \(W \subset \mathbb {N}\) corresponds to the boolean formal power series \(\bigoplus _{i \in W} t^i\), and Grigoriev’s map \(\textrm{Val}_W(j)\) is precisely \(\pi (d^j W)\).
Example 4.6
Consider the pair \(\textbf{S} = {\mathbb {T}}[[t]] {\mathop {\rightarrow }\limits ^{\pi }} {\mathbb {T}}_2\), where \({\mathbb {T}}[[t]]\) has the differential from Example 2.7 part (4) corresponding to the 2-adic norm, \(d(t^n) = |n|_2t^{n-1}\). Over this pair we consider solutions to the differential equation
Let us look for solutions of the form
We have
If \(\alpha \ne 0\) then
and so evaluating f at x gives the expression
The maximum occurs only in the middle term, so there is no solution with \(\alpha \ne 0.\)
Assuming next that \(\alpha =0\) and \(\beta \ne 0\), we have
and
The second and third terms are equal and maximal, so this is a solution for any nonzero value of \(\beta \).
If \(\alpha =\beta =0\) and \(\gamma \ne 0\), then
and \(f(x) = (e^{-4},1) \oplus (e^{-2},8\gamma ) \oplus (e^{-2},4\gamma )\). The middle term is the sole maximal term, so this is not a solution.
If \(\alpha =\beta =\gamma =0\) and \(\delta \ne 0\) then
and \(f(x) = (e^{-4},1) \oplus (e^{-2},2\delta ) \oplus (e^{-2},2\delta ),\) so we have a solution since the second and third terms are jointly maximal.
The last case we will look at is \(\alpha =\beta =\gamma =\delta =0\) and \(\epsilon \ne 0\). Now
and \(f(x) = (e^{-4},1) \oplus (e^{-4},8\epsilon ) \oplus (e^{-4},2\epsilon ).\) If \(\epsilon = 1/8\), then the first two terms are jointly maximal and we have a solution but when \(\epsilon \ne 1/8\) either the first or second term is the sole maximum. In this case we see for the first time that the tropical framework here provides additional information about solutions beyond the information contained in Grigoriev’s framework.
4.3 The reduction functor
Given a pair \(\textbf{S}= (S_1{\mathop {\rightarrow }\limits ^{\pi }} S_0)\), it follows from Proposition 2.9 that the set of differential congruences contained in \(\textrm{ker} \, \pi \) has a unique maximal element \(R(\pi )\), and hence the pair \(\textbf{S}^\textrm{red} :=(S_1/R(\pi ) \rightarrow S_0)\) is reduced.
Proposition 4.7
The morphism \({\textbf {S}} \rightarrow {\textbf {S}}^{\textrm{red}}\) given by the projection onto the quotient \(S_1 \twoheadrightarrow S_1/R(\pi )\) is initial among morphisms from \(\textbf{S}\) to reduced pairs.
Proof
Suppose \(\textbf{T}=(T_1 {\mathop {\rightarrow }\limits ^{\psi }} T_0)\) is a reduced pair and

is a morphism of pairs. There are inclusions
The map \(\varphi _1\) sends \(\textrm{ker}\, \varphi _0 \circ \pi \) into \(\textrm{ker}\, \psi \), and the image of a differential congruence by a homomorphism of tropical differential semirings is again a differential congruence, so \(\varphi _1\) must send \(R(\pi )\) to a differential congruence contained in \(\textrm{ker}\, \psi \). Since \(\textbf{T}\) is reduced, the only such differential congruence on \(T_1\) is the diagonal, and so \(\varphi _1\) factors uniquely through the quotient map \(S_1 \rightarrow S_1 / R(\pi )\).
We now show that the above reduction construction exhibits \(\mathbf {\textrm{Pairs}}_\textrm{red}\) as a reflective subcategory of \(\mathbf {\textrm{Pairs}}\).
Proposition 4.8
Sending \(\textbf{S}\) to \(\textbf{S}^{\textrm{red}}\) defines a functor \(\mathscr {R}: \mathbf {\textrm{Pairs}}\rightarrow \mathbf {\textrm{Pairs}}_\textrm{red}\), and the quotient map \({\textbf {S}} \rightarrow {\textbf {S}}^\textrm{red}\) is a natural transformation \(\textrm{Id} \rightarrow \mathscr {R}\). Moreover \(\mathscr {R}\) is left adjoint to the inclusion \(\iota : \mathbf {\textrm{Pairs}}\hookrightarrow \mathbf {\textrm{Pairs}}_\textrm{red}\).
Proof
Suppose \(f: \textbf{S} \rightarrow \textbf{T}\) is a morphism of pairs and consider the composition \(\textbf{S} \rightarrow \textbf{T} \rightarrow \textbf{T}^\textrm{red}\). By Proposition 4.7, there is a unique factorization \({\textbf {S}} \rightarrow {\textbf {S}}^\textrm{red} \rightarrow {\textbf {T}}^\textrm{red}\), and hence we obtain a morphism \(\mathscr {R}(f): {\textbf {S}}^\textrm{red} \rightarrow {\textbf {T}}^\textrm{red}\). It is straightforward the check that this respects compositions: \(\mathscr {R}(f\circ g) = \mathscr {R}(f) \circ \mathscr {R}(g)\). Hence \(\mathscr {R}\) is a functor.
It is a straightforward verification that the quotient map \(\textbf{S} \rightarrow {\textbf {S}}^\textrm{red}\) defines a natural transformation from the identity on \(\mathbf {\textrm{Pairs}}\) to \(\iota \circ \mathscr {R}\). Clearly if \(\textbf{S}\) is reduced, then \({\textbf {S}}^\textrm{red} = {\textbf {S}}\), and there is trivially a natural transformation from \(\mathscr {R}\circ \iota \) to the identity on \(\mathbf {\textrm{Pairs}}_\textrm{red}\). It is now elementary to check that these two natural transformations give the claimed adjunction.
As a consequence of reduction being a left adjoint functor, it commutes with colimits.
4.4 Quotients of pairs
Let \(\textbf{S}=(S_1 \rightarrow S_0)\) be a pair. A quotient of \(\textbf{S}\) is a morphism of pairs

such that both \(f_1\) and \(f_0\) are surjective. The kernel of \(f_1\) is a differential congruence \(\ker f_1\) on \(S_1\), the kernel of \(f_0\) is a congruence \(\ker f_0\) on \(S_0\), and \(\pi \) sends \(\ker f_1\) into \(\ker f_0\). Conversely, a pair of congruences \((K_1 \subset S_1 \times S_1, K_0 \subset S_0 \times S_0)\) satisfying \(\pi (K_1) \subset K_0\) defines a quotient of \(\textbf{S}\).
We now describe an important class of quotients. Suppose we are given a pair \(\textbf{S}=(S_1 \rightarrow S_0)\) and a congruence K on the polynomial semiring \(S_0\{x_1, \ldots , x_n\}_{\textrm{basic}}\). By a slight abuse of notation, let \((S_0|S_1)\{x_1, \ldots , x_n\}/K\) denote the induced quotient, and then let
denote the reduction of the pair \(S_1\{x_1, \ldots , x_n\} \rightarrow (S_0|S_1)\{x_1, \ldots , x_n\}/K\). Quotients of this form will be used when we define the tropicalization of a system of differential equations in Sect. 5.
Proposition 4.9
Let \(\textbf{T} = (T_1 {\mathop {\rightarrow }\limits ^{\pi }} T_0)\) be a reduced \(\textbf{S}\)-algebra and K a congruence on \(S_0\{x_1, \ldots , x_n\}_\textrm{basic}\). Morphisms of \(\textbf{S}\)-algebras
correspond bijectively with n-tuples \(y_1, \ldots , y_n \in T_1\) such that the elements \(\pi (d^jy_i) \in T_0\) define an \(S_0\)-algebra homomorphism \(S_0\{x_1, \ldots , x_n\}_\textrm{basic} / K \rightarrow T_0\).
Proof
A morphism \((f_1, f_0): \textbf{S}\{x_1, \ldots , x_n\} \mathbin {/\hspace{-3.33328pt}/}K \rightarrow \textbf{T}\) determines elements \(y_i = f_1(x_i)\) that are immediately seen to satisfy the stated condition.
Going in the other direction, suppose \(y_i \in T_1\) are elements satisfying the above condition. By Proposition 4.4, there is a uniquely determined morphism \((f_1, f_0): \textbf{S}\{x_1, \ldots , x_n\} \rightarrow \textbf{T}\) with \(f_1(x_i) = y_i\). The images \(\pi (d^jy_i)\in T_0\) are equal to the elements \(f_0(d^jx_i)\) coming from \(S_0\{x_1, \ldots , x_n\}_\textrm{basic}\) (recall that this is the polynomial algebra on the symbols \(d^jx_i\)), and these define a semiring homomorphism
that descends to the quotient by K, and since \(\textbf{T}\) is reduced, this descends to the reduction by Proposition 4.8.
4.5 Solutions as morphisms
It follows directly from Proposition 4.9 and the definition of solutions to tropical differential equations that \(\textbf{S}\)-algebra morphisms

are in bijection with the solution set \(\textrm{Sol}(E)\). In fact, we have
Proposition 4.10
The functor \(\textbf{S}- \textrm{Alg} \rightarrow \textrm{Sets}\) sending an \(\textbf{S}\)-algebra \(\textbf{S} {\mathop {\rightarrow }\limits ^{u}} \textbf{T}\) to \(\textrm{Sol}(u_* E)\) is corepresented by  .
.
4.6 Colimits of pairs
In this section we show that colimits in the category of pairs can be computed by computing the colimits of the top and bottom individually. In order for this to be useful, it is helpful to note the following.
Proposition 4.11
The categories of idempotent semirings and differential idempotent semirings are cocomplete.
Proof
The category of idempotent semirings is cocomplete for the same reason as the category of rings; one can easily check that arbitrary coproducts and coequalizers exist. For differential idempotent semirings, one must only verify that tropical differentials \(d_i\) on \(S_i\) induce a tropical differential on the coproduct \(\bigoplus _i S_i\), and likewise for coequalizers. Both of these verifications are elementary and straightforward.
Proposition 4.12
The forgetful functors

commute with colimits, and \(\pi _t\) also commutes with limits.
Proof
It suffices to show that \(\pi _b\) admits a right adjoint and \(\pi _t\) admits both a left and a right adjoint.
We start with \(\pi _t\). Let
be the functor sending a differential idempotent semiring S to the pair \(S{\mathop {\rightarrow }\limits ^{id}} S\), and let \(R_t\) be the functor sending S to the pair \(S\rightarrow *\), where \(*\) denotes the trivial idempotent semiring consisting of a single element. Given a pair \(A {\mathop {\rightarrow }\limits ^{p}} B\), a morphism of differential idempotent semirings \(f: S \rightarrow A\) uniquely determines, and is uniquely determined by, a morphism of pairs

that is evidently natural in the semiring S and the pair \(A \rightarrow B\). Thus \(L_t\) is left adjoint to \(\pi _t\). For \(R_t\), observe that a morphism of differential semirings \(f: A\rightarrow S\) is equivalent to a morphism of pairs:

For \(\pi _b\), we will construct a right adjoint \(R_b\). Consider the subcategory
of pairs \(S \rightarrow T\), where a morphism is a morphism of pairs that is the identity on T. The colimit \(\mathop {\textrm{colim}}\limits _{\mathbf {\textrm{Pairs}}/ T} \pi _t\) comes with a natural semiring homomorphism to T, and this defines a pair \(R_b(T)\). It is straightforward to verify that \(R_b(T)\) is functorial in T. A morphism of pairs

clearly provides a semiring homomorphism \(B \rightarrow T\). Conversely, given a semiring homomorphism \(B \rightarrow T\), the composition \(A\rightarrow B \rightarrow T\) is an object of \(\mathbf {\textrm{Pairs}}/T\) and hence it has a canonical map to \(R_b(T)\).
Finally, note that since the reduction functor is idempotent and has a left adjoint (Proposition 4.8), the colimit of a diagram of reduced pairs is reduced.
4.7 Differential enhancements of seminorms
Given a seminorm v on R as in Definition 2.3, v(x) does not in general determine the seminorm of derivatives of x. In order to define tropical differential equations, we must enhance the seminorm with some additional information in order to determine the seminorms of sequences \(a, da, d^2a, \ldots \). To this end, we now introduce differential enhancements of seminorms.
Definition 4.13
Given a differential ring R and a non-archimedean seminorm \(v: R \rightarrow S_0\), a differential enhancement of v is a reduced pair \(\textbf{S} = (S_1\rightarrow S_0)\) and a map of sets \(\widetilde{v}: R \rightarrow S_1\) such that
-
(1)
\(\widetilde{v}(0) = 0\in S_1\) and \(\widetilde{v}(1) = 1\in S_1\);
-
(2)
it commutes with the differentials: \(d_{S_1} \widetilde{v}(x) = \widetilde{v}(d_R x)\) for any \(x\in R\);
-
(3)
the following diagram commutes:

We will use the term differentially enhanced seminorm \(\textbf{v}=(v,\widetilde{v}): A \rightarrow \textbf{S}\) to mean a seminorm v together with a differential enhancement \(\widetilde{v}\).
Note that if \((v,\widetilde{v}): A \rightarrow \textbf{S}\) is a differentially enhanced seminorm and \((f_0, f_1): \textbf{S} \rightarrow \textbf{T}\) is a morphism of pairs, then the composition

is also a differentially enhanced seminorm.
Example 4.14
Let k be a field and consider the differential ring of formal power series k[[t]] with differential d/dt. The t-adic norm \(k[[t]] \rightarrow {\mathbb {T}}\) admits a differential enhancement

in which the map \(\mathbb {B}[[t]] \rightarrow {\mathbb {T}}\) sends a boolean power series \(t^n \oplus \cdots \) to \(\textrm{exp}(-n)\). Note that while v is multiplicative, its differential enhancement \(\widetilde{v}\) is not. For instance,
This is the differentially enhanced seminorm used by Grigoriev [11] in his framework and subsequent works [1, 4, 6, 7].
Example 4.15
Consider the p-adic seminorm \(v_p: \mathbb {Q} \rightarrow {\mathbb {T}}\) and extend this to a seminorm \(\mathbb {Q}[[t]] \rightarrow {\mathbb {T}}_2\) as in (2.1). This admits a differential enhancement

where the differential on \({\mathbb {T}}[[t]]\) is by (2.2), and the vertical arrow sends \(a_0 t^{n_0} \oplus \cdots \) to \((\textrm{exp}(-n_0), a_0)\). Let \(\textbf{u} =(u,\widetilde{u})\). There is a morphism of pairs

given on the top by the sending all non-zero coefficients to 1, and on the bottom by projection onto the first component. This morphism of pairs sends the differentially enhanced seminorm \(\textbf{u}\) to the \(\textbf{v}\) of Example 4.14. Thus \(\textbf{u}\) provides a refinement of the structure considered by Grigoriev.
While a seminorm \(u: R \rightarrow S_0\) may admit multiple distinct differential enhancements \(\widetilde{u}\), as illustrated in the examples above, it turns out that there is at most one for any given reduced pair \(\textbf{S}\) over \(S_0\).
Proposition 4.16
Let \(u: R \rightarrow S_0\) be a seminorm and \(S_1 {\mathop {\rightarrow }\limits ^{\pi }} S_0\) a reduced pair. If \(\widetilde{u},\widetilde{u}': R \rightarrow S_1\) are two differential enhancements of u, then \(\widetilde{u} = \widetilde{u}'\).
Proof
Consider the congruence K on \(S_1\) generated by the relations \(\widetilde{u}(x) \sim \widetilde{u}'(x)\) for \(x\in R\). Since \(\widetilde{u}\) and \(\widetilde{u}'\) both commute with the differentials, K is a differential congruence, and since \(\pi \circ \widetilde{u} = \pi \circ \widetilde{u}'\), it follows that \(K \subset \ker \pi \). Now, since \(S_1 \rightarrow S_0\) is reduced, K must be trivial.
In a differential ring R, an element \(a\in R\) is said to be a constant if \(d(a)=0\). The constants form a subring of R.
Proposition 4.17
Given a differentially enhanced seminorm \(\textbf{v}=(\widetilde{v}: R \rightarrow S_1, v: R \rightarrow S_0)\) on R, \(\widetilde{v}\) restricts to a seminorm on the subring of constants in R.
Proof
Suppose a, b are constants and consider the semiring congruence K on \(S_1\) generated by the relations
Since v is a non-archimedean seminorm, the relations \(v(a+b) \oplus v(a) \oplus v(b) = v(a) \oplus v(b)\) and \(v(ab) = v(a)v(b)\) hold in \(S_0\), and hence the semiring homomorphism \(S_1 \rightarrow S_0\) factors through the quotient semiring \(S_1/K\) because each of the generators of K (as a semiring congruence) is a relation that holds in \(S_0\). Since \(\widetilde{v}\) commutes with the differentials, \(\widetilde{v}(1)\), \(\widetilde{v}(-1)\), \(\widetilde{v}(a)\), \(\widetilde{v}(b)\), \(\widetilde{v}(a+b)\) and \(\widetilde{v}(ab)\) are each constants in \(S_1\). From this we see that K is in fact a congruence of differential semirings. If K were nontrivial then the factorization \(S_1\rightarrow S_1/K \rightarrow S_0\) would contradict the fact that \(S_1\rightarrow S_0\) is reduced. Thus the equalities
must hold in \(S_1\).
4.8 The differential Berkovich space
Let k be a ring with a non-archimedean seminorm \(v: k \rightarrow {\mathbb {T}}\). Given a k-algebra A, recall that the Berkovich analytification of \(\textrm{Spec}\,A\) is the set of seminorms \(w: A \rightarrow {\mathbb {T}}\) that are compatible with v in the sense that the composition \(k \rightarrow A {\mathop {\rightarrow }\limits ^{w}} {\mathbb {T}}\) is equal to v. The analytification is denoted \((\textrm{Spec}\,A)^{ an }\). It is equipped with a topology that we will not discuss here.
We now propose a generalization to the differential setting. Suppose k is a differential ring equipped with a differentially enhanced seminorm \(\mathbb {v}\) to \(\textbf{S}= (S_1 \rightarrow S_0)\), and let A be a differential k-algebra. Given an \(\textbf{S}\)-algebra \(\textbf{T}\), a differentially enhanced seminorm \(\textbf{w}=(\widetilde{w}, w)\) is said to be compatible with \(\textbf{v}\) if the diagram

commutes.
Definition 4.18
Given an \(\textbf{S}\)-algebra \(\textbf{T}\), the differential Berkovich space of A, denoted \( Berk _{\textbf{T}}(A)\), is the set of differentially enhanced seminorms \(\textbf{w}: A \rightarrow \textbf{T}\) that are compatible with \(\textbf{v}\).
Note that there is a natural map \( Berk _{\textbf{T}}(A) \rightarrow (\textrm{Spec}\,A)^ an \) induced by sending a differentially enhanced seminorm \(\textbf{w}=(\widetilde{w},w)\) to its underlying ordinary seminorm w. This map is injective thanks to Proposition 4.16.
5 Tropicalization
5.1 Review of the non-differential case
In the familiar non-differential setting, one starts with a field k with a non-archimedean seminorm \(v: k \rightarrow {\mathbb {T}}\), and one then defines three tropicalization maps:
-
(1)
Tropicalization of points is the map
 given by applying the seminorm coordinate-wise.
given by applying the seminorm coordinate-wise. -
(2)
Tropicalization of equations is the map
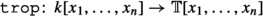 given by applying the seminorm coefficient-wise. This extends to a map sending ideals in \(k[x_1,\ldots , x_n]\) to ideals in \({\mathbb {T}}[x_1,\ldots , x_n]\).
given by applying the seminorm coefficient-wise. This extends to a map sending ideals in \(k[x_1,\ldots , x_n]\) to ideals in \({\mathbb {T}}[x_1,\ldots , x_n]\). -
(3)
Tropicalization of varieties sends V(I) to the subset of \({\mathbb {T}}^n\) defined by the intersection of the tropical hypersurfaces of all

An ideal \(I\subset k[x_1, \ldots , x_n]\) is of course a system of polynomial equations, and a solution to this system is the same as a homomorphism \(k[x_1,\ldots , x_n] /I \rightarrow k\) (or a homomorphism to some k-algebra A). Since the tropical hypersurface of a tropical polynomial f is exactly the solution set of the bend relations of  , it follows that the tropicalization of a variety is the set of solutions to the bend relations of the tropicalization of its defining ideal. Moreover, solutions to these bend relations are precisely homomorphisms of semirings
, it follows that the tropicalization of a variety is the set of solutions to the bend relations of the tropicalization of its defining ideal. Moreover, solutions to these bend relations are precisely homomorphisms of semirings  . One can thus think of the semiring
. One can thus think of the semiring  as the coordinate algebra of the tropical variety, and hence tropicalization of varieties has an incarnation at the level of algebras given by
as the coordinate algebra of the tropical variety, and hence tropicalization of varieties has an incarnation at the level of algebras given by

Note that this is a construction carried out when the seminorm v takes values in an idempotent semiring, not just \({\mathbb {T}}\); see [9] for further details.
5.2 Differential tropicalization
We now turn to the differential setting. Let k be a differential ring equipped with a differentially enhanced seminorm \(\textbf{v}=(\widetilde{v},v): k \rightarrow \textbf{S}=(S_1 {\mathop {\rightarrow }\limits ^{\pi }} S_0)\)
-
(1)
We tropicalize points \(p\in k^n\) via the map
 defined by applying \(\widetilde{v}\) component-wise.
defined by applying \(\widetilde{v}\) component-wise. -
(2)
We tropicalize differential equations by applying v coefficient-wise to define a map

We write
 for the ideal generated by the image of I, and so there is an induced a map sending ideals in \(k\{x_1, \ldots , x_n\}\) to ideals in \(S_0\{x_1, \ldots , x_n\}_\textrm{basic}\).
for the ideal generated by the image of I, and so there is an induced a map sending ideals in \(k\{x_1, \ldots , x_n\}\) to ideals in \(S_0\{x_1, \ldots , x_n\}_\textrm{basic}\). -
(3)
We use the tropicalization of equations map to define a construction sending quotients \(\alpha : k\{x_1, \ldots , x_n\} \twoheadrightarrow k\{x_1, \ldots , x_n\}/I\) to quotients \(\textbf{trop}(\alpha )\) of the pair \(\textbf{S}\{x_1, \ldots , x_n\}\). Define

where
 is the congruence on \((S_0 | S_1)\{x_1, \ldots , x_n\}\) generated by the bend relations of
is the congruence on \((S_0 | S_1)\{x_1, \ldots , x_n\}\) generated by the bend relations of 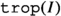 and we use the quotient construction at the end of Sect. 4.4.
and we use the quotient construction at the end of Sect. 4.4.
Remark 5.1
Since \((S_0 | S_1)\{x_1, \ldots , x_n\}\) is not a polynomial algebra, we cannot form the bend relations of an arbitrary element in it. The above construction uses the fact that applying v coefficient-wise lands in \(S_0\{x_1, \ldots , x_n\}_\textrm{basic} \subset (S_0 | S_1)\{x_1, \ldots , x_n\}\), and this algebra is a polynomial algebra so we can form bend relations in it.
Proposition 5.2
Given a differential ideal \(I \subset k\{x_1, \ldots , x_n\}\), tropicalization of points

sends  .
.
Proof
It suffices to show that if \(p\in k^n\) is a solution to \(f \in k\{x_1, \ldots , x_n\}\), then  is a solution to
is a solution to  . Write \(f= \sum _{\epsilon \in \textrm{supp} f} f_\epsilon x^\epsilon \), where \(x^\epsilon \) denotes a differential monomial in the variables \(x_i\). We have \(f(p) = 0\), so \(v(\sum _\epsilon f_\epsilon p^\epsilon ) = 0\) in \(S_0\). Since \(v: k \rightarrow S_0\) is a non-archimedean seminorm, this happens if and only if the sum
. Write \(f= \sum _{\epsilon \in \textrm{supp} f} f_\epsilon x^\epsilon \), where \(x^\epsilon \) denotes a differential monomial in the variables \(x_i\). We have \(f(p) = 0\), so \(v(\sum _\epsilon f_\epsilon p^\epsilon ) = 0\) in \(S_0\). Since \(v: k \rightarrow S_0\) is a non-archimedean seminorm, this happens if and only if the sum
tropically vanishes. Since the differential enhancement map \(\widetilde{v}\) commutes with the differentials, we have that \(v(f_\epsilon p^\epsilon )\) is equal to \(v(f_\epsilon ) \pi (\widetilde{v}(p)^\epsilon )\), which is equal to the evaluation of the differential monomial \(v(f_\epsilon )x^\epsilon \) at the point  . Thus
. Thus  tropically vanishes at
tropically vanishes at  .
.
5.3 Functoriality of tropicalization
Tropicalization of differential equations sends a presentation of a differential algebra to a tropical pair. Here we show that this defines a functor from a category of presentations to the category of tropical pairs.
A homomorphism of differential algebras
is said to be monomial if each variable \(x_i\) is sent to a monomial (with coefficient 1) in the variables \(y_i\) and their derivatives (it need not send monomials to monomials in general), and it is said to be linearly monomial if each \(x_i\) is sent to some \(y_j\), a derivative of \(y_j\), or to 0.
Example 5.3
The map \(f: k\{x\} \rightarrow k\{y\}\) given by \(f(x) = y dy\) is monomial even though it sends the monomial dx to \((dy)^2 + yd^2y\). However, it is not linearly monomial.
We now define the category of presentations \(\textrm{Pres}(A)\). Objects of this category are presentations of A; i.e., an object is a Ritt algebra \(k\{x_i \, | i \in \Lambda \}\) together with a surjective homomorphism \(k\{x_i \, | i \in \Lambda \} \rightarrow A\), and whose morphisms are commutative triangles

where f is a monomial morphism. We allow the set \(\Lambda \) of variables to be infinite, and let \(\text {Pres}^\textrm{fin}(A)\) denote the subcategory of finite presentations. Let \(\text {Pres}_\textrm{lin}(A) \subset \text {Pres}(A)\) denote the subcategory of presentations and linearly monomial morphisms.
Proposition 5.4
The tropicalization construction \((k\{x_i \, | \, i \in \Lambda \} {\mathop {\rightarrow }\limits ^{\alpha }} A) \mapsto \textbf{trop}(\alpha )\) yields a functor \(\textrm{Pres}(A) \rightarrow \textrm{S}\mathrm {-Alg}\).
Proof
Given a morphism of presentations

each monomial in \(k\{x_i \, | \, i \in \Lambda _1\}\) corresponds to a monomial in the tropical Ritt algebra \(\textbf{S}\{x_i \, | \, i \in \Lambda _1\}\), and so it follows from Proposition 3.9 that there is a functorially induced morphism of \(\textbf{S}\)-algebras
and this restricts to a morphism of the basic subalgebras on the bottom. Moreover, the congruence  on \(S_0\{x_i \,|\, i \in \Lambda _1\}_\textrm{basic}\) is sent into the congruence
on \(S_0\{x_i \,|\, i \in \Lambda _1\}_\textrm{basic}\) is sent into the congruence  by [9, Prop. 6.4.1]. Hence \(f_*\) descends to a morphism of quotient pairs:
by [9, Prop. 6.4.1]. Hence \(f_*\) descends to a morphism of quotient pairs:

and by Proposition 4.8 this induces a morphism of their reductions, which is precisely the desired morphism
5.4 The universal presentation
Given a differential k-algebra A, consider the presentation
defined by sending \(x_a\) to a. It takes a formal differential polynomial in the elements of A and evaluates it to an element of A using the differential algebra structure of A. A similar morphism was studied in the non-differential setting in [8]. In light of the following fact, we call this the universal presentation of A.
Proposition 5.5
The presentation \(k\{x_a \,| \, a \in A\} {\mathop {\twoheadrightarrow }\limits ^{ Univ }} A\) is
-
(1)
The final object in \(\textrm{Pres}_ lin (A)\), and
-
(2)
The colimit of the inclusion functor \(\iota : \textrm{Pres}^\textrm{fin}_\textrm{lin}(A) \hookrightarrow \textrm{Pres}_\textrm{lin}(A)\).
Proof
Part (1): Let \(\alpha : k\{y_i \, | \, i\in \Lambda \} \twoheadrightarrow A\) be a presentation. We will show that the set of morphisms \(\textrm{Hom}_{\textrm{Pres}(A)}(\alpha , Univ )\) contains exactly one element that is linearly monomial. Any morphism of presentations f from \(\alpha \) to \( Univ \) must send each variable \(y_i\) to a monomial in \(k\{x_a \, | \, a\in A\}\) that is mapped to \(\alpha (y_i)\) by \( Univ \). One option is \(f(y_i) = x_{\alpha (y_i)}\), and this is evidently the unique choice that defines a linearly monomial morphism.
Part (2): By (1), any finite presentation \(\alpha \) admits a unique linearly monomial morphism \(\alpha \rightarrow Univ \), and hence there is a canonical morphism \(u: \mathop {\textrm{colim}}\limits \iota \rightarrow Univ \). Given a finite presentation \(\alpha : k\{y_1, \ldots , y_n\} \rightarrow A\) and an element \(a \in A\), we extend to a new finite presentation \(\alpha ' : k\{y_1, \ldots , y_n, y_a\} \rightarrow A\) by \(y_a \mapsto a\). The morphism \(\alpha ' \rightarrow Univ \) sends \(y_a\) to \(x_a\), and thus any element \(x_a\) in the universal presentation is in the image of some finite presentation, so u is surjective.
We turn now to injectivity of u. If
are two finite presentations with \(\alpha (y_1) = \beta (z_1)\), then they each map to the presentation \(k\{w, y_2\ldots , y_n, z_2, \ldots , z_m\}\) by \(y_1, z_1 \mapsto w\) and identity of all of the other generators. Hence u is injective as well.
Example 5.6
Consider the presentation \(\alpha : k\{y_1,y_2\} \rightarrow k\{z\} = A\) given by \(\alpha (y_1) = z\) and \(\alpha (y_2)=zdz\). In addition to the linearly monomial morphism from \(\alpha \) to \( Univ \), there are also the monomial morphisms given by sending \(y_2\) to \(x_z x_{dz}\) or \(x_z dx_z\).
5.5 The universal tropicalization
We define the universal tropicalization of A to simply be the tropicalization of the universal presentation, \(\textbf{trop}( Univ )\).
Theorem 5.7
For any differential k-algebra A, there is a canonical isomorphism of pairs
and if A admits a finite presentation \(k\{x_1, \ldots , x_n\} \rightarrow A\) then the colimit can be taken over the subcategory \(\textrm{Pres}^\textrm{fin}_\textrm{lin}(A)\) of finite presentations.
Proof
The first statement is an immediate consequence of Proposition 5.5. For the second statement, consider the canonical morphism
Given any element \(a \in A\), any finite presentation \(\alpha : k\{x_1, \ldots , x_n\} \rightarrow A\) maps to a finite presentation \(\alpha ': k\{x_1, \ldots , x_n, x_a\} \rightarrow A\), with \(\alpha '(x_a) = a\). Hence it follows from Proposition 4.12 that \(j_1\) and \(j_0\) are both surjective. We turn to injectivity. Observe that the congruence  on \(S_0\{x_a \, | \, a \in A\}\) is the transitive closure of the symmetric semiring generated by the bend relations of elements in
on \(S_0\{x_a \, | \, a \in A\}\) is the transitive closure of the symmetric semiring generated by the bend relations of elements in  , and so for any relation
, and so for any relation  there exists a finite subset \(\Lambda \subset A\) containing all variables appearing in either f or g and such that, for the restriction \( Univ |_\Lambda : k\{x_a \, | \, a \in \Lambda \} \rightarrow A\), we have
there exists a finite subset \(\Lambda \subset A\) containing all variables appearing in either f or g and such that, for the restriction \( Univ |_\Lambda : k\{x_a \, | \, a \in \Lambda \} \rightarrow A\), we have

If \(\Lambda \) does not generate A as a differential algebra then we may add finitely many elements so that it does. We thus have a finite presentation \(\beta \) such that \((f \sim g)\) is in the image of the canonical map

Therefore the map

is an isomorphism. The claim now follows from Proposition 4.12.
We now come to our main result, which says that a differential algebra A admits a universal differentially enhanced seminorm which is valued in the tropicalization of the universal presentation of A, (c.f. [8, Theorem A]).
Theorem 5.8
Given a differential k-algebra A, there is a differentially enhanced seminorm
defined by sending \(a\mapsto x_a\), and this is initial among differentially enhanced seminorms on A compatible with the differentially enhanced seminorm \(\textbf{v}\) on k.
As an immediate corollary, we have:
Corollary 5.9
Let \(\textbf{T}\) be an \(\textbf{S}\)-algebra. There is a bijection
that is natural in \(\textbf{T}\). I.e., \(\textbf{trop}( Univ )\) co-represents the functor sending \(\textbf{T}\) to the set of differentially enhanced seminorms on A taking values in \(\textbf{T}\) and compatible with \(\textbf{v}\).
The proof of the theorem requires an explicit description of the congruence  , which we provide below.
, which we provide below.
Proposition 5.10
The differential ideal \(\ker Univ \subset k\{x_a \; | \; a\in A\}\) is generated as an ideal by the following family of elements:
-
(1)
\(x_1 - 1\);
-
(2)
\(x_{\lambda a} - \lambda x_a\) for \(a\in A\) and \(\lambda \in k\);
-
(3)
\(x_{da} - dx_a\) for \(a\in A\);
-
(4)
\(x_a x_b - x_{ab}\) for \(a,b \in A\);
-
(5)
\(x_a + x_b + x_c\) for \(a,b,c \in A\) satisfying \(a+b+c = 0\).
Proof
It is clear that all of these relations are in the kernel. Let f be an arbitrary element in the kernel. Using relations (2), (3) and (4) we move all coefficients and differentials into the subscripts and reduce each monomial to a single variable, so f is transformed into a degree 1 non-differential polynomial \(f' = \sum _{a\in \Lambda } x_a\), for some finite subset \(\Lambda \subset A\). We can then use relation (5) (and (2) with \(\lambda = -1\)) repeatedly to reduce the number of terms by replacing \(x_{a_1} + x_{a_2}\) with \(x_{a_1 + a_2}\), and thus we transform \(f'\) to a trinomial, which is in the kernel if and only if it is an expression of type (5).
Tropicalizing the above family of elements, we have:
Lemma 5.11
The congruence  on \(S_0\{x_a \; | \; a\in A\}_\textrm{basic}\) is generated by the bend relations of the polynomials:
on \(S_0\{x_a \; | \; a\in A\}_\textrm{basic}\) is generated by the bend relations of the polynomials:
-
(1)
\(x_1 \oplus 1_{S_0}\)
-
(2)
\(x_{\lambda a} \oplus v(\lambda ) x_a\) for \(a\in A\) and \(\lambda \in k\);
-
(3)
\(x_{da} \oplus dx_a\) for \(a\in A\);
-
(4)
\(x_a x_b \oplus x_{ab}\) for \(a,b \in A\);
-
(5)
\(x_a \oplus x_b \oplus x_c\) for \(a,b,c \in A\) satisfying \(a+b+c = 0\).
Proof
It suffices to show that the bend relations of listed expressions imply the the bend relations of any element  . As in the proof of Proposition 5.10 above, using the bend relations of (1)–(4) allows us reduce g to an expression of the form
. As in the proof of Proposition 5.10 above, using the bend relations of (1)–(4) allows us reduce g to an expression of the form
Let us call a finite set \(\Lambda \subset A\) a null set if \(\sum _\Lambda a = 0.\) It remains to show that the bend relations of sums over null sets of size 3 (i.e., relation (5) from the list) imply the bend relations for sums as above over null sets of arbitrary size.
We prove this by induction on the cardinality n of the null set \(\Lambda \). The base case \(n=3\) is simply relation (5). Assume the bend relations hold for all sums over null sets of size \(\le n\), and consider a null set \(\Lambda = \{a_1, \ldots , a_{n+1}\}\). Let
so we have null sets \(\Lambda _1 = \{a_1, a_2, -b\}\) and \(\Lambda _2 = \{b, a_3, \ldots , a_{n+1}\}\) of size 3 and n. Then

Since \(a_1\) was chosen arbitrarily, this shows that the bend relations of sums over null sets of size \(n+1\) hold.
Note that relations (1), (2), (4) and (5) correspond to the four conditions defining a non-archimedean seminorm in Definition 2.3.
Let us write \(U_1 {\mathop {\rightarrow }\limits ^{\pi }} U_0\) for the pair \(\textbf{trop}( Univ )\), which is the reduction of the pair

Lemma 5.12
The relation \(d(x_a) = x_{da}\) holds in \(U_1\).
Proof
Observe that for any \(a\in A\) and any \(n\in \mathbb {N}\) the elements \(d^nx_a\) and \(x_{d^na}\) in \(U_1\) are mapped to the elements in \(U_0\) that are equivalent modulo the congruence  by Lemma 5.11 relation (3). Hence the relation \(d(x_a) \sim x_{da}\) is in the reduction congruence and so it holds in \(U_1\).
by Lemma 5.11 relation (3). Hence the relation \(d(x_a) \sim x_{da}\) is in the reduction congruence and so it holds in \(U_1\).
Proof of Theorem 5.8
It is clear from the definition that \(\pi \circ \widetilde{u} = u\). By Lemma 5.12, the map \(\widetilde{u}: A \rightarrow U_1\) commutes with the differential, and by relations (1), (4), and (5) of Lemma 5.11, the map \(u: A \rightarrow U_0\) is a non-archimedean seminorm. Thus \(\textbf{u}\) is a differentially enhanced seminorm. Moreover, relation (2) implies that u is compatible with the seminorm \(v: A \rightarrow S_0\).
It remains to show that there is a unique morphism from \(\textbf{u}\) to any other differentially enhanced seminorm \(\textbf{w}=(w,\widetilde{w}): A \rightarrow \textbf{T}\) compatible with \(\textbf{v}: A \rightarrow \textbf{S}\). Let \(\widetilde{y}_a = \widetilde{w}(a) \in T_1\). Mapping these elements and their derivatives down to \(T_0\) gives a list of elements \(y^{(j)}_a=w(d^j a) \in T_0\) for \(a\in A\) and \(j\in \mathbb {N}\). Since w is a non-archimedean seminorm, it follows from Lemma 5.11 that the semiring homomorphism
sending \(d^j x_a \mapsto y^{(j)}_a\) descends to the quotient by the congruence  . Hence, by Proposition 4.9, there is a unique morphism of \(\textbf{S}\)-algebras \(f_\textbf{w}: \textbf{trop}( Univ ) \rightarrow \textbf{T}\) sending \(x_a\) to \(\widetilde{y}_a\) on top, and to \(y_a\) on the bottom. By construction, composition with \(f_\textbf{w}\) sends \(\textbf{u}\) to \(\textbf{w}\), and this completes the proof.
. Hence, by Proposition 4.9, there is a unique morphism of \(\textbf{S}\)-algebras \(f_\textbf{w}: \textbf{trop}( Univ ) \rightarrow \textbf{T}\) sending \(x_a\) to \(\widetilde{y}_a\) on top, and to \(y_a\) on the bottom. By construction, composition with \(f_\textbf{w}\) sends \(\textbf{u}\) to \(\textbf{w}\), and this completes the proof.
References
Aroca, F., Garay, C., Toghani, Z.: The fundamental theorem of tropical differential algebraic geometry. Pac. J. Math. 283(2), 257–270 (2016)
Baker, M., Bowler, N.: Matroids over partial hyperstructures. Adv. Math. 343, 821–863 (2019)
Bertram, A., Easton, R.: The tropical Nullstellensatz for congruences. Adv. Math. 308, 36–82 (2017)
Cotterill, E., Cristhian G., and Johana L.: Exploring tropical differential equations. arXiv:2012.14067 (2020)
Crowley, C., Giansiracusa, N., Mundinger, J.: A module-theoretic approach to matroids. J. Pure Appl. Algebra 224(2), 894–916 (2020)
Falkensteiner, S., Cristhian G.L., Mercedes, H., Marc Paul N., Zeinab, T., François, B.: The fundamental theorem of tropical partial differential algebraic geometry. In: Proceedings of the 45th international symposium on symbolic and algebraic computation, ISSAC ’20, Kalamata, Greece, July 20–23, 2020, pp. 178–185 (2020)
Fink, A., Zeinab, T.: Initial forms and a notion of basis for tropical differential equations. Pac. J. Math 318(2) 453–468 (2022)
Giansiracusa, J., Noah, G.: The universal tropicalization and the Berkovich analytification. Kybernetika 58(5), 790–815 (2022)
Giansiracusa, J., Giansiracusa, N.: Equations of tropical varieties. Duke Math. J. 165(18), 3379–3433 (2016)
Giansiracusa, J., Giansiracusa, N.: A Grassmann algebra for matroids. Manuscr. Math. 156(1–2), 187–213 (2018)
Grigoriev, D.: Tropical differential equations. Adv. Appl. Math. 82, 120–128 (2017)
Hu, Y., Gao, X.S.: Tropical differential gröbner bases. Math. Comput. Sci. 15, 255–269 (2021)
Joó, Dániel., Mincheva, Kalina: On the dimension of polynomial semirings. J. Algebra 507, 103–119 (2018)
Joó, D., Mincheva, K.: Prime congruences of additively idempotent semirings and a Nullstellensatz for tropical polynomials. Sel. Math. New Ser. 24(3), 2207–2233 (2018)
Jun, J.: Geometry of hyperfields. J. Algebra 569, 220–257 (2021)
Lorscheid, O.: The geometry of blueprints: part I: algebraic background and scheme theory. Adv. Math. 229(3), 1804–1846 (2012)
Lorscheid, O.: Scheme-theoretic tropicalization. arXiv:1508.07949 (2015)
Lorscheid, O.: Tropical geometry over the tropical hyperfield. Rocky Mt. J. Math, 52(1), 189–222 (2022)
Maclagan, D., Rincón, F.: Tropical ideals. Compos. Math. 154(3), 640–670 (2018)
Maclagan, D., Rincón, F.: Tropical schemes, tropical cycles, and valuated matroids. J. Eur. Math. Soc. (JEMS) 22(3), 777–796 (2020)
Maclagan, D., Rincón, F.: Varieties of tropical ideals are balanced. Adv. Math. 410, 108713 (2022)
Maclagan, D., Sturmfels, B.: Introduction to tropical geometry, Graduate Studies in Mathematics, vol. 161. American Mathematical Society, Providence, RI (2015)
Payne, S.: Analytification is the limit of all tropicalizations. Math. Res. Lett. 16(3), 543–556 (2009)
Ritt, J.F.: Differential algebra. Dover Publications, New York (1955)
Viro, O.: On basic concepts of tropical geometry. Proc. Steklov Inst. Math. 273, 252–282 (2011)
Yaghmayi, K.: Geometry over the tropical dual numbers. arXiv:1611.05508
Acknowledgements
We thank Alex Fink and Zeinab Toghani for many useful discussions and for organizing an influential workshop at QMUL in December 2019 in which the tropical differential equations community came together and shared many ideas. We also thank Andrea Pulita for his encouragement to do this. S.M. gratefully acknowledges the support of a Swansea University Strategic Partnerships Scholarship and funding from Université Grenoble Alpes IDEX.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest. This article does not contain any studies involving human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giansiracusa, J., Mereta, S. A general framework for tropical differential equations. manuscripta math. 173, 1273–1304 (2024). https://doi.org/10.1007/s00229-023-01492-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-023-01492-5










 given by applying the seminorm coordinate-wise.
given by applying the seminorm coordinate-wise.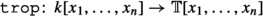 given by applying the seminorm coefficient-wise. This extends to a map sending ideals in
given by applying the seminorm coefficient-wise. This extends to a map sending ideals in 
 defined by applying
defined by applying 
 for the ideal generated by the image of I, and so there is an induced a map sending ideals in
for the ideal generated by the image of I, and so there is an induced a map sending ideals in 
 is the congruence on
is the congruence on 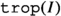 and we use the quotient construction at the end of Sect.
and we use the quotient construction at the end of Sect.