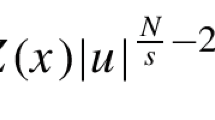Abstract
In this paper, we consider the Schrödinger equation involving the fractional \((p,p_1,\dots ,p_m)\)-Laplacian as follows
where \(\varepsilon \) is a positive parameter, \(N=ps, s\in (0,1), 2\le p<p_1< \dots< p_m<+\infty , m\ge 1\). The nonlinear function f has the exponential growth and potential function V is continuous function satisfying some suitable conditions. Using the penalization method and Ljusternik–Schnirelmann theory, we study the existence, multiplicity and concentration of nontrivial nonnegative solutions for small values of the parameter. In our best knowledge, it is the first time that the above problem is studied.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
Let \(\Omega \) be a bounded, open domain of \({\mathbb {R}}^N\;(N\ge 2).\) The standard Sobolev space \(W_0^{k,p}(\Omega )\) is defined by the completion of \(C_0^{\infty }(\Omega )\) equipped with the norm
The well-known Sobolev embedding theorem states that \(W_0^{k,p}(\Omega )\) embeds continuously into \(L^{Np/(N-kp)}(\Omega )\) for a positive integer \(k<N\) and \(1\le p<\dfrac{N}{k}.\) When \(p=\dfrac{N}{k},\) the embedding \(W_0^{k,N/k}(\Omega )\subset L^{\infty }(\Omega )\) fails. To overcome this difficulty, Trudinger [55] proved that functions in \(W_0^{1,N}(\Omega )\) has property
Furthermore, the function \(E_{\beta }\) is continuous on \(W_0^{1,N}(\Omega ).\) In 1970, Moser [41] gave the optimal \(\beta \) and proved that \(\beta \le \alpha _N=N\omega _{N-1}^{1/(N-1)},\) where \(\omega _{N-1}\) is the area of the surface of the unit ball. From this work, many works are done and made the research direction about Trudinger–Moser type inequality and applications. Special, In 2007, Adimurthi-Sandeep [2] extended the work of Trudinger–Moser for singular case on bounded domain. When \(\Omega \) is unbounded, Adachi and Tanach [1] and do Ó [23] gave a subcritical Trudinger–Moser-type inequality as follows: For \(0<\alpha <\alpha _N,\) there exists a positive constant \(C_N\) such that
where \(\Phi (t)=e^t-\sum _{i=0}^{N-2}\dfrac{t^i}{i!}.\) Moreover, the constant \(\alpha _N\) is sharp in the sense that if \(\alpha \ge \alpha _N,\) the supremum will become infinite. In 2010, Adimurthi-Yang [3] extended the result of Adachi and Tanach [1] and do Ó [23] for singular case. In 2019, Parini and Ruf [43] extended the result of Trudinger–Moser to fractional Sobolev-Slobodeckij spaces and obtained the following result: Let \(\Omega \) be a bounded open domain of \({\mathbb {R}}^N,\; (N\ge 2)\) with Lipschitz boundary, and let \(s\in (0,1),\) \(N=ps.\) Then there exists an exponent \(\alpha \) of the fractional Trudinger–Moser inequality such that
Set
Moreover, \(\alpha _{*}\le \alpha _{s,N}^{*},\) where
By replacing the norm \([u]_{W^{s,p}({\mathbb {R}}^N)}\) by \(||u||_{W^{s,p}({\mathbb {R}}^N)},\) Iula [33] proved that the result of Parini and Ruf is still true in \({\mathbb {R}}.\) In 2019, Zhang [61] has been extended the that result of Parini and Ruf, and Iula to \({\mathbb {R}}^N\) and get a fractional Trudinger–Moser type imequality. Using that result, Zhang studied the existence of weak solution to Schrödinger equation involving the fractional p-Laplacian. For some more results and the applications of Trudinger–Moser inequality and fractional Trudinger–Moser type inequality, we refer the readers to [4, 24,25,26,27, 31, 36, 37, 39, 45, 59] and the references therein for more details. On singular Trudinger–Moser type inequality in fractional Sobolev space and its application, we recommend the readers to [52] for more details.
Using the fractional Trudinger–Moser type inequality, in this paper, we study the existence and concentration of nontrivial nonnegative solution for the following Schrödinger equation involving fractional \((p,p_1,\dots ,p_m)\)-Laplacian:
where \(\varepsilon \) is small positive parameter, \(0<s<1, 2\le p<p_1<\dots<p_m<+\infty , m\ge 1, N=ps,\) the potential V is bounded below by \(V_0>0\), the nonlinearity f has exponential critical growth, and \((-\Delta )_{t}^{s}\; (t\in \{p,p_1,\dots ,p_m\})\) is the fractional t-Laplace operator which may be defined along a function \(\varphi \in C_{0}^{\infty }({\mathbb {R}}^{N})\) (up to a normalization constant) as
for \(x\in {\mathbb {R}}^{N},\) where \(B_{\varepsilon }(x)\) is a ball with center x and radius \(\varepsilon .\)
Assume that the continuous function V verifies the following conditions:
\((V_1)\) There exists \(V_0>0\) such that \(V(x)\ge V_0\) for all \(x\in {\mathbb {R}}^N;\)
\((V_2)\) There exists a bounded set \(\Lambda \subset {\mathbb {R}}^N\) such that
Observe that
Moreover, we assume that the nonlinear function f satisfying the following conditions:
\((f_1)\) The nonlinearity \(f\in C^1({\mathbb {R}})\) such that \(f(t)=0\) for all \(t\in (-\infty ,0],\) \(f(t)>0\) for all \(t>0\) and there exist constants \(\alpha _0\in (0,\alpha _{*}),\) \(b_1,b_2>0\) such that for any \(t\in {\mathbb {R}},\)
where \(\Phi _{N,s}(y)=e^{y}-\sum _{i=0}^{j_p-2}\dfrac{y^{j}}{j!}, j_p=\min \{j\in {\mathbb {N}}: j\ge p\}\) and \(\alpha _{*}\le \alpha _{s,N}^{*}\) (see Lemma 1).
\((f_2)\) There exists \(\mu >p_m\) such that
for all \(t\in {\mathbb {R}},\) where \(F(t)=\int \limits _{0}^{t}f(\tau )d\tau .\)
\((f_3)\)
\((f_4)\) There exists \(\gamma _1>0\) large enough such that \(F(t)\ge \gamma _1 |t|^{\mu }\) for all \(t\ge 0.\)
\((f_5)\) \(\dfrac{f(t)}{t^{p_m-1}}\) is a strictly increasing function in \({\mathbb {R}}^{+}.\)
Recently, Alves–Ambrosio–Isernia [7], Ambrosio–Radulescu [8] studied the fractional (p, q)-Laplacian as follows:
where \(\varepsilon >0\) is a parameter, \(s\in (0,1),1<p<q<\dfrac{N}{s}\) and f has the subcritical growth and satisfies some suitable conditions. For more results on fractional (p, q)-Laplace or (p, q)-Laplace, we refer the readers to [9,10,11]. When \(s\rightarrow 1^{-1},\) the Eq. (1.2) becomes the following equation
where \(\Delta _ru=\text {div}(|\nabla u|^{r-2}\nabla u), r\in \{p,q\}.\) The study of Eq. (1.3) is connected to more general reaction-diffusion equation
which has many applications in biophysics, physics of plasmas and chemical reaction design [13, 21]. In that equation, c(x, u) is related to source and loss process. The multiple phases quation is motivated from the following Born–Infeld equation [18,19,20] that appears in electromagnetism, electrostatics and electrodynamics as a model based on a modification of Maxwell’s Lagrangian density
We refer the readers to the work of Zhang–Tang–Radulescu [62] for more information and motivation as well as application of double-phases equation.
In 2021, Ambrosio–Repovs [12] have been studied the problem (1.3) when \(1<p<q<N,\) \(V:{\mathbb {R}}^N\rightarrow {\mathbb {R}}\) is a continuous function satisfying the global Rabinowitz condition, and \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) is a continuous function with subcritical growth. Using suitable variational arguments and Ljusternik–Schnirelmann category theory, they study the relation between the number of positive solutions and the topology of the set where V attains its minimum for small \(\varepsilon .\)
When \(p=q\) and \(\varepsilon =1,\) the Eq. (1.2) becomes
where V and f satisfy some suitable assumptions. Many works were achieved on that equation such as [14,15,16, 25, 28, 29]. In particular, when \(p=2,\) the Eq. (1.5) becomes
which has been proposed by Laskin [34, 35] as a result of expanding the Feynman path integral, from the Brownian like to the Lévy quantum mechanical paths. We refer the readers to [5, 6, 30, 49,50,51] for more results about Eq. (1.6). Recently, many authors studied the existence of multiple solution to (1.5) in subcritical growth, exponential growth and Kirchhoff type problem involving fractional p-Laplace such as Xiang, Zhang and [58], Zhang, Fiscella and Liang [60], Wang and Xiang [63]. In that works, they use Krasnoselskii’s genus theory to study their problems. Motivate by above works, we study the problem (1.1) with exponential growth. We point out that as far as we know, in the literature appears only few papers on fractional (p, q)-Laplace problems, and there are no results on the multiplicity and concentration of solutions to the problem (1.1). So the aim of this work is to give the first result in this direction. We use the Ljusternik–Schnirelmann category theory instead of Krasnoselskii’s genus theory as in some previous works.
Before starting our results, we recall some useful notations. Suppose that \(N=ps\) or \(N>ps.\) The fractional Sobolev space \(W^{s, p}({\mathbb {R}}^N)\) is defined by
where \([u]_{s, p}\) denotes by the seminorm Gagliardo, that is
\(W^{s, p}({\mathbb {R}}^N)\) is a uniformly convex Banach space (similar to [46]) with norm
Set \(\eta >0,\) we denote another norm on \(W^{s, p}({\mathbb {R}}^N)\) as follows
Then ||.|| and \(||.||_{\eta ,W^{s, p}({\mathbb {R}}^N)}\) are two norms equivalent on \(W^{s, p}({\mathbb {R}}^N).\) For each \(\varepsilon >0,\) let \(W_{\varepsilon }\) denote by the completion of \(C_0^{\infty }(\mathbb R^N),\) with respect to the norm
Then \(W_{V,\varepsilon }^{s,p}({\mathbb {R}}^N)\) is uniformly convex Banach space (similar to [46], Lemma 10), and then \(W_{V,\varepsilon }^{s,p}({\mathbb {R}}^N)\) is a reflexive space. By the condition (V) and Theorem 6.9 [42], we have the embedding from \(W_{V,\varepsilon }^{s,p}({\mathbb {R}}^N)\) into \(L^{\nu }({\mathbb {R}}^N)\) is continuous for any \(\nu \in [\dfrac{N}{s},+\infty ).\) Similarly, we can define the space \(W_{V,\varepsilon }^{s,p_i}({\mathbb {R}}^N), i=1,\dots ,m.\) We denote \(W_{\varepsilon }=W_{V,\varepsilon }^{s,p}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W_{V,\varepsilon }^{s,p_i}({\mathbb {R}}^N)\) endowed with the norm
Then \(W_{\varepsilon }\) is uniformly convex Banach space (similar to [46], Lemma 10) and we have the embeddings
are continuous for any \(\nu \in [\dfrac{N}{s},+\infty ).\) Hence, there exists a best constant \(S_{\nu ,\varepsilon }>0\) for all \(\nu \in [\dfrac{N}{s}, +\infty )\) as follows:
This implies
Definition 1
We say that \(u\in W_{\varepsilon }\) is a weak solution of problem (1.1) if
for any \(\varphi \in W_{\varepsilon }.\)
We denote \(\text {cat}_B(A)\) by the category of A with respect to B, namely the least integer k such that \(A\subset A_1\cup \dots \cup A_k,\) where \(A_i\; (i=1,\dots ,k)\) is closed and contractible in B. We set \(\text {cat}_{B}(\emptyset )=0\) and \(\text {cat}_B(A)=+\infty \) if there is no integer with above property. We refer the reader to [57] for more details on Ljusternik–Schnirelmann theory. Now, we state the main result in this paper.
Theorem 2
Let \((V_1),\) \((V_2)\) and \((f_1)-(f_5)\) hold. Then for any \(\delta >0\) such that
there exists \(\varepsilon _{\delta }>0\) such that problem \((P_{\varepsilon })\) has at least \(\text {cat}_{M_{\delta }}(M)\) nontrivial nonnegative weak solutions for any \(0<\varepsilon <\varepsilon _{\delta }.\) Moreover, if \(u_{\varepsilon }\) denotes one of these solutions and \(\eta _{\varepsilon }\) is its global maximum, then
Remark 3
We use the Nehari manifold, penalization method, concentration compactness principle and Ljusternik–Schnirelmann theory to prove the main result. There are some difficulties in proving our theorem. The first difficulty is that the nonlinearity f has exponential critical growth. The second is that the fractional Sobolev embedding is the lack of compactness. Furthermore, our problem cannot transfer to local problem via to Caffarelli–Silvestre’s method. Compare with subcritical case due to Ambrosio–Radulescu [8] as \(m=1\), we need estimate the Mountain pass level due to the Trudinger–Moser nonlinearity and all our steps need focus it. Then our duties are complex and they are not the same in the work of Ambrosio–Radulescu. We emphase that the work Ambrosio–Radulescu studied the Eq. (1.1) when \(m=1\) and \(0<N<ps.\) In this case we have the continuous embedding from \(W^{s,p}(\Omega )\) into \(L^{Np/(N-sp)}(\Omega ).\) In our work, \(N=ps,\) then we do not have the previous embedding. Hence, our work is independent with work of Ambrosio–Radulescu [8]. Furthermore, our problem is more complicated than the problem in [8] due to many phases, not only double phases.
The paper is organized as follows. In Sect. 2, we study the autonomous problem associated. In Sect. 3, we study the modified problem. We prove the Palais-Smale condition for the energy functional and provide some tools which are useful to establish a multiplicity result. This allows us to show that the modified problem has multiple solutions. In Sect. 4, we prove the existence of ground state solution to modified problem. In the final part of this paper, we complete the paper with the proof of Theorem 2.
2 Autonomous problem
In this section, we study the autonomous problem associated to (1.1) as following
where \(\eta >0\) is a constant. Set \(W=W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N).\) We denote \(J_{\eta }: W\rightarrow {\mathbb {R}}\) by the corresponding energy functional for problem (2.1)
From the condition \((f_3),\) there exist \(\tau >0\) and \(\delta >0\) such that for all \(|t|\le \delta ,\) we have
Moreover from the condition \((f_1)\) and f is a continuous function, for each \(q\ge \dfrac{N}{s},\) we can find a constant \(C=C(q,\delta )>0\) such that
for all \(|t|\ge \delta .\) Combine (2.2) and (2.3), we get
for all \(t\ge 0\) and
for all \(t\ge 0.\)
Definition 4
We said that \(u\in W\) is a weak solution of (2.1) if
for any \(\varphi \in W.\)
In order to prove the result in this paper, we need the following result:
Lemma 1
([61]) Let \(s\in (0,1)\) and \(sp=N.\) Then for every \(0\le \alpha <\alpha _{*}\le \alpha _{s,N}^{*},\) the following inequality holds:
where \(\Phi _{N,s}(t)=e^{t}-\sum _{i=0}^{j_p-2}\dfrac{t^j}{j!}, \; j_p=\min \{j\in {\mathbb {N}}: j\ge p\}.\) Moreover, for \(\alpha >\alpha _{s,N}^{*},\)
Remark 5
From Lemma 1, if we use the norm \(||.||_{\eta }\) on \(W^{s,N/s}({\mathbb {R}}^N),\) then we have
then we get
for all \(0\le \alpha <\alpha _{*}\le \alpha _{s,N}^{*}.\)
Using Lemma 1 and note that \(C_0^{\infty }({\mathbb {R}}^N)\) is a density subspace of \(W^{s,p}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N),\) we see that \(J_{\eta }\) is well defined on \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N).\) Furthermore, we have
We know that W is uniformly convex with norm
Another norm is
By Theorem 6.9 [42], we have the embedding from \(W^{s,N/s}({\mathbb {R}}^N)\) into \(L^{\nu }({\mathbb {R}}^N)\) is continuous for any \(\nu \in [\dfrac{N}{s},+\infty )\) and \(W=W^{s,p}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\) is continuously embedded into \(W^{s,p}({\mathbb {R}}^N).\) Hence, W is continuously embedded into \(L^{\nu }({\mathbb {R}}^N)\) is continuous for any \(\nu \in [\dfrac{N}{s},+\infty ).\) Then there exists a best constant \(A_{\nu ,\eta }>0\) for all \(\nu \in [\dfrac{N}{s}, +\infty )\) as follows:
This implies
We can check that \(J_{\eta }\) satisfies the geometry condition of Mountain Pass Theorem. Indeed, we have the following result:
Lemma 2
Suppose that \((f_1)\) and \((f_3)\) hold. Then there exist constants positive \(t_0, \rho _0\) such that \(J_{\eta }(u)\ge \rho _0\) for all \(u\in W,\) with \(||u||_{\eta ,W}=t_0.\)
Proof
From (2.4), for some \(q>p_m,\) we have
for all \(t\in {\mathbb {R}}.\) Then we get
Using Hölder inequality, we have
where \(t>1, t'>1\) such that \(\dfrac{1}{t}+\dfrac{1}{t'}=1.\) By Lemma 2.3 [38], for any \({\mathfrak {b}}>t,\) there exist a constant \(C({\mathfrak {b}})>0\) such that
on \({\mathbb {R}}^N.\) Denote by \({\mathfrak {d}}=\min \{1,\eta \},\) we get
We know that \(||u||_{\eta ,W^{s,p}({\mathbb {R}}^N)}\le ||u||_{\eta ,W},\) then \(||u||_{\eta ,W}\) is small enough implies that \(||u||_{\eta ,W^{s,p}({\mathbb {R}}^N)}\) is also small enough. Therefore, when \({\mathfrak {b}}\) near t, we have
by Remark 5, (2.10) and (2.11), there exists a constant \(D>0\) such that
Since the embedding from \(W\rightarrow L^{qt'}({\mathbb {R}}^N)\) is continuous, we get
From (2.6), we have
Note that the function \(f(t)=t^{p_m}\) is convex, then
for all \(a_i\ge 0,i=1,\dots ,m+1.\) Hence apply above inequality, combine (2.7), (2.12) and (2.13), when \(||u||_{\eta ,W}\) is small enough, we obtain
We see \(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau A_{p_m,\eta }^{-p_m}>0\) for \(\tau \) small enough. Let
We now prove there exists \(t_0>0\) small satisfying \(h(t_0)\ge \dfrac{1}{2}(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau A_{p_m,\eta }^{-p_m}).\) We see that h is continuous function on \([0, +\infty )\) and \(\lim _{t\rightarrow 0^{+}}h(t)=\dfrac{(m+1)^{1-p_m}}{p_m}-\tau A_{p_m,\eta }^{-p_m},\) then there exists \(t_0\) such that \(h(t)\ge \dfrac{(m+1)^{1-p_m}}{p_m}-\tau A_{p_m,\eta }^{-p_m}-\varepsilon _1\) for all \(0\le t\le t_0,\) \(t_0\) is small enough such that \(||u||_{\eta ,W}=t_0\) satisfies (2.11). If we choose \(\varepsilon _1= \dfrac{1}{2}(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau A_{p_m,\eta }^{-p_m}),\) we have
for all \(0\le t\le t_0.\) Especialy,
From (2.14) and (2.15), for \(||u||_{\eta ,W}=t_0,\) we have
\(\square \)
Lemma 3
Suppose that \((f_4)\) holds. Then there exists a function \(v\in C_0^{\infty }({\mathbb {R}}^N)\) with \(||v||_{\eta ,W}>t_0,\) such that \(J_{\eta }(v)<0,\) where \(t_0>0\) is the number given in Lemma 3.
Proof
For all \(u\in C_0^{\infty }({\mathbb {R}}^N)\) with \(||u||_{\eta ,W}=1,\) from the condition \((f_4)\) and all \(t>0,\) we obtain
By (2.6), for all \(\nu \ge \dfrac{N}{s},\) we have
where \(\varepsilon >0.\) Since \(\mu >p_m,\) we have \(J_{\eta }(tu)\rightarrow -\infty \) as \(t \rightarrow +\infty .\) Taking \(v=\rho _1u, \rho _1>t_0>0\) large enough, we have \(J_{\eta }(v)<0, ||v||_{\eta ,W}>t_0.\) \(\square \)
Using the version of Mountain Pass Theorem without the Palais-Smale condition, we get a sequence \(\{u_n\}\subset W\) such that
where the level \(c_{\eta }\) is characterized by
and \(\Gamma =\{\gamma \in C([0,1], W): \gamma (0)=0, J_{\eta }(\gamma (1))<0\}.\)
Lemma 4
Let \(\{u_n\}\) be \((PS)_{c_{\eta }}\) sequence for \(J_{\eta }.\) Then there exists a constant \(C_{\gamma _1}\) such that \(\rho _0\le c_{\eta }\le C_{\gamma _1}.\)
Proof
We choose a function \(w\in W{\setminus } \{0\}\) such that \(||w||_{L^{\mu }({\mathbb {R}}^N)}=1\) and \(||w||_{\eta ,W}\le A_{\mu ,\eta }+\varepsilon \) for some \(\varepsilon >0\) small enough. We see that
Set \(g(t)=\sum _{i=1}^{m}\dfrac{(A_{\mu ,\eta }+\varepsilon )^{p_i}t^{p_i}}{p_i}+\dfrac{s(A_{\mu ,\eta } +\varepsilon )^{N/s}t^{N/s}}{N}-\gamma _1t^{\mu }\) on \([0,+\infty ).\) We have
When \(t\in [0,1],\) we get
We denote \(a=\dfrac{s(A_{\mu ,\eta }+\varepsilon )^{N/s}}{N}+\sum _{i=1}^{m}\dfrac{(A_{\mu ,\eta }+\varepsilon )^{p_i}}{p_i},b=\gamma _1.\) Compute directly, we have
where
as \(\gamma _1\ge \dfrac{a N}{s\mu }=\gamma ^{*}.\) Compute directly, we get
We see that \(\lim _{\gamma _1\rightarrow +\infty }\theta _{\gamma _1}=0,\) then \(\lim _{\gamma _1\rightarrow +\infty }h(\theta _{\gamma _1})=0.\) By arguments as above, for all \(t\ge 1,\) we get
and \(h_{*}\) has uniqueness local maximum point at \(\beta _{\gamma _1}=\left( \dfrac{a p_m}{\gamma _1\mu }\right) ^{1/(\mu -p_m)}\) on \((0,+\infty ).\) Note that if we choose \(\gamma _1\ge \gamma _{*},\) where \(\gamma _{*}\) satisfies
we deduce
Set \(\gamma _{**}=\sum _{i=1}^{m}\dfrac{(A_{\mu ,\eta }+\varepsilon )^{p_i}}{p_i} +\dfrac{s(A_{\mu ,\eta }+\varepsilon )^{N/s}}{N}.\) We have
Combine (2.17), (2.18), (2.19) and (2.20), we obtain
for \(\gamma _1\ge \max \{\gamma ^{*}, \gamma _{*},\gamma _{**}\}.\) Therefore, the Mountain Pass level c is small enough when \(\gamma _1\) is large enough, which will be used later. Combine Lemma 2, (2.16) and (2.21), we get \(\rho _0\le c_{\eta }\le C_{\gamma _1}.\) \(\square \)
The following result is a version of Lions’s result:
Lemma 5
([54]) If \(\{u_n\}\) is a bounded sequence in \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\) and
for some \(R>0, t\ge \dfrac{N}{s},\) then \(u_n\rightarrow 0\) strongly in \(L^q({\mathbb {R}}^N)\) for all \(q\in (t,+\infty ).\)
Lemma 6
Let \(\{u_n\}\) be a sequence in W converging weakly to 0 verifying
where \({\mathfrak {c}}>1\) is a suitable constant and assume that \((f_1)\) holds and \(\lim _{t\rightarrow 0^{+}}\dfrac{f(t)}{t^{p_m-1}}=0.\) If there exists \(R>0\) such that \(\liminf _{n\rightarrow \infty }\sup _{y\in {\mathbb {R}}^N}\int \limits _{B_R(y)}|u_n|^{p_m}dx=0,\) it follows that
Proof
Since \(\liminf _{n\rightarrow \infty }\sup _{y\in {\mathbb {R}}^N}\int \limits _{B_R(y)}|u_n|^{p_m}dx=0,\) by Lemma 5, we get \(u_n\rightarrow 0\) strongly in \(L^{t}({\mathbb {R}}^N)\) for all \(t\in (p_m,+\infty ).\) From the condition \((f_1)\) and
then for any \(\varepsilon >0\) and \(q>p_m,\) there exists \(C(q,\varepsilon )>0\) such that
For \(t>1,t'>1\) and \(t'\) near 1 such that \(\dfrac{1}{t}+\dfrac{1}{t'}=1,\) using Hölder inequality, we get
Then by Lemma 2.3 [38], for any \({\mathfrak {c}}>t'\) and near \(t',\) there exist a constant \(C({\mathfrak {c}})>0\) such that
on \({\mathbb {R}}^N\) and all n. We have
Since \(||u_n||_{\eta ,W^{s,p}({\mathbb {R}}^N)}\le ||u||_{\eta ,W},\) from Remark 5, we get
Combine (2.23)-(2.26) and the fact that \(u_n\rightarrow 0\) in \(L^{qt}({\mathbb {R}}^N),\) we obtain
as \(n\rightarrow \infty \) since \(\{u_n\}\) is a bounded sequence in \(L^{p_1}({\mathbb {R}}^N).\) Similarly as (2.27), we also get \(\int \limits _{{\mathbb {R}}^N}|F(u_n)|dx\rightarrow 0\) as \(n\rightarrow \infty .\) \(\square \)
Proposition 1
Assume that the conditions \((f_1)-(f_5)\) satisfies. Then problem (2.1) admits a nontrivial nonnegative weak solution.
Proof
From Lemma 2, Lemma 3 and a version of Mountain Pass Theorem without the Palais–Smale condition [47, 57], we get a sequence \(\{u_n\}\subset W\) such that
where the level \(c_{\eta }\) is characterized by
By the assumption \((f_5),\) using the idea in [43] and Lemma 3.2 [7], we can get
where \({\mathcal {N}}_{\eta }\) is Nehari manifold for \(J_{\eta }.\)
Note that \(\{u_n\}\) is a (PS) sequence with level \(c_{\eta }\in {\mathbb {R}}\) in W. This means
as \(n\rightarrow \infty .\) We show that the sequence \(\{u_n\}\) is bounded in W. From (2.28), we have
when n large enough. It implies
where \(\mu \) is a parameter in the condition \((f_2).\) We have
Therefore, we have
Combine (2.29) and (2.30), we get
Note that
where \({\mathfrak {a}}>0\), \({\mathfrak {b}}_1>0,\dots ,{\mathfrak {b}}_m>0.\) Then from (2.31), we conclude that the sequence \(\{u_n\}\) is bounded in W. Since
as \(n\rightarrow \infty ,\) then
and
for all \(i=1,\dots ,m.\) Hence, we deduce
Moreover, we claim that there exists \(R>0, \delta >0\) and a sequence \(\{y_n\}\subset {\mathbb {R}}^N\) such that
If the above inequality doesnot hold, it means that
for some \(R>0,\) then from (2.21) and (2.34), when \(\gamma _1\) large enough, we get
Using Lemma 6, we have \(\lim _{n\rightarrow \infty }\int \limits _{{\mathbb {R}}^N}f(u_n)u_n dx\rightarrow 0\) as \(n\rightarrow \infty .\) Then
as \(n\rightarrow \infty .\) Hence \(u_n\rightarrow 0\) strongly in W. It implies that
as \(n\rightarrow \infty .\) It contradicts with \(c_{\eta }>0.\) Therefore (2.35) holds. We denote \(v_n(x)=u_n(x+y_n),\) then from (2.35) we get
Because \(J_{\eta }\) and \(J'_{\eta }\) are both invariant by the translation, it implies that
Because \(||v_n||_{\eta ,W}=||u_n||_{\eta ,W},\) then \(\{v_n\}\) is also bounded in W, then exists \(v\in W\) such that \(v_n\rightarrow v\) weak in W, \(v_n\rightarrow v\) in \(L_{loc}^{q}({\mathbb {R}}^N)\; (q\in (p_m,+\infty ))\) and \(v_n(x)\rightarrow v(x)\) almost everywhere in \({\mathbb {R}}^N.\) From (2.36), we get \(\int \limits _{B_R(0)}|v|^{p_m}dx\ge \delta /2>0,\) then \(v\not \equiv 0.\) By arguments as in [53, 54], we get \(J_{\eta }'(v)=0.\) Furthermore, from the condition \(f(t)=0\) for all \(t\in (-\infty ,0],\) we can get \(v\ge 0.\)
By Fatou’s lemma, we have
Hence v is a ground state solution to the problem (2.1). \(\square \)
3 The modified problem
Now, we introduce a penalized function in the spirit of [44] which will be fundamental to get our main result. First of all, without loss of generality, we may assume that
Let us choose \(k>\dfrac{\mu }{\mu -p_m}>1\) and \(a>0\) such that
We define
and
We show that if \(u_{\varepsilon }\) is a solution in W to
with \(u_{\varepsilon }(x)\le a\) for all \(x\in \Lambda _{\varepsilon }^{c}={\mathbb {R}}^N{\setminus } \Lambda _{\varepsilon },\) where \(\Lambda _{\varepsilon }:=\{{\mathbb {R}}^N: \varepsilon x\in \Lambda \},\) then \(g(\varepsilon x,u_{\varepsilon })=f(u_{\varepsilon }).\) Hence \(u_{\varepsilon }\) is a solution of (1.1).
Definition 6
We say that \(u\in W_{\varepsilon }\) is a weak solution of problem (2.37) if
for any \(\varphi \in W_{\varepsilon }.\)
We have that g satisfies the following properties [40]:
\((g_1)\) \(g(x,t)=0\) for all \(t\le 0\) and \(g(x,t)>0\) for all \(t>0\) and \(x\in {\mathbb {R}}^N;\)
\((g_2)\) \(\lim _{t\rightarrow 0^{+}}\dfrac{g(x,t)}{t^{p_m-1}}=0\) uniformly with respect to \(x\in {\mathbb {R}}^N;\)
\((g_3)\) \(g(x,t)\le f(t)\) for all \(t\ge 0\) and \(x\in {\mathbb {R}}^N;\)
\((g_4)\) \(0<\mu G(x,t)\le g(x,t)t\) for all \(x\in \Lambda \) and \(t>0,\) where \(G(x,t)=\int \limits _{0}^{t}g(x,\tau )d\tau ;\)
\((g_5)\) \(0<p_mG(x,t)\le g(x,t)t\le \dfrac{V_0}{k}t^{p_m}\) for all \(x\in \Lambda ^{c}\) and \(t>0.\)
\((g_6)\) for each \(x\in \Lambda ,\) the function \(\dfrac{g(x,t)}{t^{p_m-1}}\) is a strictly increasing of t in \((0,+\infty );\)
\((g_7)\) for each \(x\in \Lambda ^{c},\) the function \(\dfrac{g(x,t)}{t^{p_m-1}}\) is a strictly increasing of t in (0, a). Further, if \(t\ge a,\) we have \(\dfrac{g(x,t)}{t^{p_m-1}}=\dfrac{V_0}{k}.\)
In order to study the Eq. (2.37), we consider the energy functional \(I_{\varepsilon }: W_{\varepsilon }\rightarrow {\mathbb {R}}\) given by
By the condition \((f_1)\) and \((g_3),\) \(I_{\varepsilon }\) is well defined on \(W_{\varepsilon }\), \(I_{\varepsilon }\in C^{2}(W_{\varepsilon },{\mathbb {R}})\) and its critical points are weak solution of problem (2.37). Associated to \(I_{\varepsilon },\) we consider the Nehari manifold \({\mathcal {N}}_{\varepsilon }\) given by
where
for any \(u,\varphi \in W_{\varepsilon }.\)
Proposition 2
There exists \(r_{*}>0\) such that
Proof
We are easy to get the inequality
Then from Lemma 1 and (2.38), we have
and
for all \(0\le \alpha <\alpha _{*}.\) From the condition \((f_1)\), \((f_3)\) and \((g_3),\) for any \(\varepsilon _{*}>0\) and \(q>p_m,\) there exists \(C_{q,\varepsilon _{*}}>0\) such that
for all \(t\ge 0.\) Combining (2.39) and (2.41), by arguments as Proposition 2 in [54], we can get the result of Proposition 2. We omit the details at here. \(\square \)
Lemma 7
The functional \(I_{\varepsilon }\) satisfies the following conditions:
(i) There exists \(\alpha>0,\rho >0\) such that \(I_{\varepsilon }(u)\ge \alpha \) for all \(u\in W_{\varepsilon }\) with \(||u||_{W_{\varepsilon }}=\rho .\)
(ii) There exists \(e\in W_{\varepsilon }\) with \(||e||_{W_{\varepsilon }}>\rho \) such that \(I_{\varepsilon }(e)<0.\)
Proof
First we prove the statement (i). From (2.41), for any \(\tau >0\) and some \(q>p_m,\) there exists \(C>0\) such that
for all \(t\in {\mathbb {R}}.\) Then for all \(u\in W_{\varepsilon }\) such that \(||u||_{W_{\varepsilon }}\in (0,1),\) we have
Using Hölder inequality, we have
where \(t>1, t'>1\) such that \(\dfrac{1}{t}+\dfrac{1}{t'}=1.\) By Lemma 2.3 [38], for any \({\mathfrak {b}}>t,\) there exist a constant \(C({\mathfrak {b}})>0\) such that
on \({\mathbb {R}}^N.\) We get
When \(||u||_{W_{\varepsilon }}\) is small enough and \({\mathfrak {b}}\) near t, we have
From (2.45) and (2.46), there exists a constant \(D>0\) such that
Since the embedding from \(W_{\varepsilon }\rightarrow L^{qt'}({\mathbb {R}}^N)\) is continuous, we get
From (1.7), we have
Hence, combine (2.42), (2.47) and (2.48), we obtain
We see \(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau S_{p_m,\varepsilon }^{-p_m}>0\) for \(\tau \) small enough. Let
We now prove there exists \(t_0>0\) small satisfying \(h(t_0)\ge \dfrac{1}{2}(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau S_{p_m,\varepsilon }^{-p_m}).\) We see that h is continuous function on \([0, +\infty )\) and \(\lim _{t\rightarrow 0^{+}}h(t)=\dfrac{(m+1)^{1-p_m}}{p_m}-\tau S_{p_m,\varepsilon }^{-p_m},\) then there exists \(t_0\) such that \(h(t)\ge \dfrac{(m+1)^{1-p_m}}{p_m}-\tau S_{p_m,\varepsilon }^{-p_m}-\varepsilon _1\) for all \(0\le t\le t_0,\) \(t_0\) is small enough such that \(||u||_{W_{\varepsilon }}=t_0\) satisfies (2.46). If we choose \(\varepsilon _1= \dfrac{1}{2}(\dfrac{(m+1)^{1-p_m}}{p_m}-\tau S_{p_m,\varepsilon }^{-p_m}),\) we have
for all \(0\le t\le t_0.\) Especialy,
From (2.49) and (2.50), for \(||u||_{W_{\varepsilon }}=t_0,\) we have
Second, we prove the statement (ii). Set \(u\in C_0^{\infty }({\mathbb {R}}^N){\setminus } \{0\}\) such that \(\text {supp}(u)\subset \Lambda _{\varepsilon }.\) From the condition \((f_4)\) and all \(t>0,\) we obtain
Since \(\mu>p_m>\dfrac{N}{s},\) we have \(I_{\varepsilon }(tu)\rightarrow -\infty \) as \(t \rightarrow +\infty .\) Taking \(v=\rho _1u, \rho _1>t_0>0\) large enough, we have \(I_{\varepsilon }(v)<0, ||v||_{\eta }>t_0.\) \(\square \)
From Lemma 7 and the version of Mountain Pass Theorem, there exists a \((PS)_{c_{\varepsilon }}\) sequence \(\{u_n\}\subset W_{\varepsilon },\) that is,
where
and \(\Gamma =\{\gamma \in C([0,1], W_{\varepsilon }): \gamma (0)=0, I_{\varepsilon }(\gamma (1))<0\}.\)
The following result is the characteristic of Mountain Pass level which the original idea comes from [43]:
Proposition 3
We have \(c_{\varepsilon }=\inf _{u\in W_{\varepsilon }{\setminus } \{0\}}\sup _{t\ge 0}I_{\varepsilon }(tu) =\inf _{u\in {\mathcal {N}}_{\varepsilon }}I_{\varepsilon }(u).\)
Proof
We denote \(c_{\varepsilon }^{*}=\inf _{u\in W_{\varepsilon }{\setminus } \{0\}}\sup _{t\ge 0}I_{\varepsilon }(tu)\) and \(c_{\varepsilon }^{**} =\inf _{u\in {\mathcal {N}}_{\varepsilon }}I_{\varepsilon }(u).\) For each \(u\in {\mathcal {N}}_{\varepsilon }{\setminus } \{0\},\) there exists a unique \(t(u)>0\) such that \(t(u)u\in {\mathcal {N}}_{\varepsilon }\) and the maximum of \(I_{\varepsilon }(tu)\) for all \(t\ge 0\) is achieved at \(t=t(u).\) Indeed, by Lemma 7, \(h_u(t)=I_{\varepsilon }(tu)>0\) when \(t>0\) is small enough and \(h_u(t)=I_{\varepsilon }(tu)<0\) when \(t>0\) is large enough. Then there exists \(t(u)>0\) such that \(h_u(t(u))=I_{\varepsilon }(t(u)u)=max_{t\ge 0}I_{\varepsilon }(tu).\) By Fermat’s Theorem, we have \(h'_u(t(u))=0\) iff \(t(u)u\in {\mathcal {N}}_{\varepsilon }.\) From \(g(\varepsilon x, t)=0\) for all \(t\le 0,\) it follows that
We conisder the case \(m\ge 2,\) the case \(m=1\) is proved similarly. Arguing by a contradiction, there exists two positive numbers \(t_1>t_2>0\) such that \(t_1u, t_2u \in {\mathcal {N}}_{\varepsilon },\) from \((g_6),\) we get
We have
By the definition of g, we have \(I=0.\) Since \(g(\varepsilon x, t)={\tilde{f}}(t)=\dfrac{V_0}{k}t^{p_m-1}\) for all \(x\in \Lambda _{\varepsilon }^{c}\) and \(t>a,\) we get
We have \(\dfrac{g(\varepsilon x, t_2u^{+})}{(t_2u^{+})^{p_m-1}} =\dfrac{f(t_2u^{+})}{(t_2u^{+})^{p_m-1}}\le \dfrac{f(a)}{a^{p_m-1}}=\dfrac{V_0}{k}\) since \(\dfrac{f(t)}{t^{p_m-1}}\) is an increasing function. Therefore \(II\ge 0.\) By the condition \((g_7)\) and \(t_1u^{+}>t_2u^{+},\) we have \(III>0.\) Since \(t_1>t_2,\) then we have \(\dfrac{1}{t_1^{p_m-p}}-\dfrac{1}{t_2^{p_m-p}}<0\) and \(\dfrac{1}{t_1^{p_m-p_i}}-\dfrac{1}{t_2^{p_m-p_i}}<0\) for all \(i=1,\dots ,m-1.\) Combine that property, (2.51) and \(I+II+III>0,\) we get a contradiction. Thus t(u) is uniqueness. Therefore, we see that
and \(t(u)u\in {\mathcal {N}}_{\varepsilon }.\) It implies that \(c_{\varepsilon }^{*}=c_{\varepsilon }^{**}.\) On the other hand, for fixed \(u\in W_{\varepsilon }{\setminus } \{0\},\) we have \(I_{\varepsilon }(tu)<0\) when t large enough. Then there exist \(t_0>>0\) such that \(I_{\varepsilon }(tu)<0\) for all \(t\ge t_0.\) We consider the curve \(g_u: [0,1]\rightarrow W_{\varepsilon }\) such that \(g_u(t)=tt_0 u\) for all \(t\in [0,1]\) and \(g_u\in \Gamma .\) Hence, we obtain \(\max _{t\ge 0} I_{\varepsilon }(tu)=\max _{t\in [0,1]}I(g_u(t))\) and it implies that
Next we prove that \(c_{\varepsilon }\ge c_{\varepsilon }^{**}.\) Indeed, we only need show that every path \(\gamma \in \Gamma \) has to cross \({\mathcal {N}}_{\varepsilon }.\) Conversly, if \(\gamma \cap {\mathcal {N}}_{\varepsilon }=\emptyset ,\) then \(<I'_{\varepsilon }(\gamma (t)),\gamma (t)>>0\) or \(<I'(\varepsilon )(\gamma (t)),\gamma (t)> <0\) for all \(t\in [0,1].\) We have
Using Trudinger–Moser inequality we get
when \(||\gamma (t)||_{W_{\varepsilon }}\) is small enough. Then the case \(<I'(\varepsilon )(\gamma (t)),\gamma (t)> <0\) for all \(t\in [0,1]\) is not true. Next, we prove that \(<I'_{\varepsilon }(\gamma (t)),\gamma (t)>>0\) for all \(t\in [0,1]\) can not occur.
From the assumptions \((g_4)\) and \((g_5),\) we have
Then, we get
for all \(t\in [0,1].\) By the definition of \(\gamma ,\) when t near 1, we have \(I_{\varepsilon }(\gamma (t))<0\) due to the continuous of \(I_{\varepsilon }\) on \(W_{\varepsilon }.\) Then we get
It is a contradiction. Hence \(\gamma \cap {\mathcal {N}}_{\varepsilon }\ne \emptyset \) and then \(c_{\varepsilon }\ge c_{\varepsilon }^{**}.\) \(\square \)
Lemma 8
Assume that \(\{u_ n\}\subset W_{\varepsilon }\) is a \((PS)_d\) sequence for the functional \(I_{\varepsilon }\) and \(k>\dfrac{\mu }{\mu -p_m}.\) If \(0<d\) and d satisfies the condition
if \(m\ge 2\) and
if \(m=1,\) then \(\{u_n\}\) is a bounded sequence in \(W_{\varepsilon }\) and
where \({\mathfrak {c}}>1\) is a suitable constant and \({\mathfrak {d}}_{*}=\min \{1,V_0\}.\)
Proof
We only consider the case \(m\ge 2.\) The case \(m=1\) is proved similarly as \(m\ge 2.\) We omit the details. First, we see that
Therefore, we get
Since \(k>\dfrac{\mu }{\mu -p_m},\) using the property
where \(a>0,a_1>0,\dots ,a_m>0,\) we have \(\{u_n\}\) is a bounded sequence in \(W_{\varepsilon }.\) Then, we deduce
for all \(i=1,\dots ,m-1\) and
From the assumption of d, we get
\(\square \)
Lemma 9
Let \(d>0\) and d satisfies the condition
if \(m\ge 2\) and
if \(m=1,\) and \(\{u_n\}\subset W_{\varepsilon }\) be a \((PS)_d\) sequence for \(I_{\varepsilon }\) such that \(u_n\rightarrow 0\) weak in \(W_{\varepsilon }.\) Then we have either:
(i) \(u_n\rightarrow 0\) in \(W_{\varepsilon }\) or
(ii) there exists a sequence \(\{y_n\}\subset {\mathbb {R}}^N\) and constants \(R>0,\beta >0\) such that
Proof
Suppose that (ii) doesnot occur. By Lemma 8, we have
Since the embeddings \(W_{\varepsilon }\rightarrow W_{V,\varepsilon }^{s,N/s}({\mathbb {R}}^N)\rightarrow W^{s,p}({\mathbb {R}}^N)\) are continuous, then we can apply Lemma 5 and get \(u_n\rightarrow 0\) in \(L^q({\mathbb {R}}^N)\) for \(q\in (p_m,+\infty ).\) By arguments as Lemma 6, from the conditions \((g_2)\) and \((g_3),\) using the inequality (2.40), we have \(\lim _{n\rightarrow \infty }\int \limits _{{\mathbb {R}}^N}f(u_n)u_ndx=0.\) Recalling that \(<I_{\varepsilon }'(u_n),u_n>\rightarrow 0\) as \(n\rightarrow \infty ,\) then we deduce \(u_n\rightarrow 0\) strongly in \(W_{\varepsilon }.\) The proof of Lemma 9 is completed. \(\square \)
Lemma 10
The number \(c_{\varepsilon }\) and \(c_{V_0}\) satisfy the following inequality
for all \(\gamma _1\ge a,\)
for some \(\varepsilon _*>0.\)
Proof
First, we consider the case \(m\ge 2.\) Let \(\phi \in C_{0}^{\infty }({\mathbb {R}}^N,[0,1])\) be such that \(\phi \equiv 1\) on \(B_{\delta /2}(0),\) \(\text {supp}(\phi )\subset B_{\delta }(0)\subset \Lambda \) for some \(\delta >0\) and \(\phi \equiv 0\) on \({\mathbb {R}}^N{\setminus } B_{\delta }(0).\) For each \(\varepsilon >0,\) let us define \(v_{\varepsilon }(x)=\phi (\varepsilon x)w(x),\) where w is a ground state solution of the problem \((P_{V_0})\) given in Proposition 1. Then \(v_{\varepsilon }\rightarrow w\) strong in \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\) (see Lemma 2.4 [14]). We see that support of \(v_{\varepsilon }\) is contained in \(\Lambda _{\varepsilon }=\{x\in {\mathbb {R}}^N: \varepsilon x\in \Lambda \}.\) For each \(v_{\varepsilon },\) there exists \(t_{\varepsilon }>0\) such that \(t_{\varepsilon }v_{\varepsilon }\in {\mathcal {N}}_{\varepsilon },\) and we have
Since \(t_{\varepsilon }v_{\varepsilon }\in {\mathcal {N}}_{\varepsilon },\) we have
Then we get
From (2.53), we see that the sequence \(\{t_{\varepsilon }\}\) must be bounded as \(\varepsilon \rightarrow 0^{+}.\) Indeed, if \(t_{\varepsilon }\rightarrow +\infty \) as \(\varepsilon \rightarrow 0^{+},\) then using the condition \((f_4),\) we have
which is a contradiction with (2.53). Thus, we can assume that \(t_{\varepsilon }\rightarrow t_0\) as \(\varepsilon \rightarrow 0^{+}.\) Then we get
via to Vitali’s theorem. If \(t_0=0,\) by the condition \((f_1)\) and \((f_3),\) we have
for all \(t\ge 0\) and some constants \(q>p_m.\) Then from (2.52), we get
Choose \(\varepsilon _{*}>0\) is small enough, using Trudinger–Moser inequality and note that \(v_{\varepsilon }\rightarrow w\) strong \(W^{s,t}({\mathbb {R}}^N)\; (t\ge \dfrac{N}{s})\) from (2.54), we get a contradiction since the left side tends to \(\infty \) and the right side tends to zero. Hence \(t_0>0.\) Using Vitali’s theorem and take limit of (2.52) as \(\varepsilon \rightarrow 0^{+},\) we deduce
Note that \(w\in {\mathcal {N}}_{V_0}\) and using the condition \((f_5)\), we obtain \(t_0=1.\) Therefore
By Lemma 4, we get \( c_{V_0}\le C_{\gamma _1}=a(1-\dfrac{N}{s\mu })(\dfrac{aN}{\gamma _1 s \mu })^{N/(\mu s-N)}\) for all \(\gamma _1\ge a.\) In the case \(m=1,\) we can proved similarly as above. We omit the details. \(\square \)
Lemma 11
The functional \(I_{\varepsilon }\) satisfies the \((PS)_d\) condition at any level \(d>0\) and d satisfies the condition
if \(m\ge 2\) and
if \(m=1,\) where \({\mathfrak {c}}>1\) is a suitable constant and near 1.
Proof
Let \(\{u_n\}\) be a \((PS)_d\) sequence of \(I_{\varepsilon },\) then by Lemma 8, \(\{u_n\}\) is a bounded sequence in \(W_{\varepsilon }\) and
where \({\mathfrak {c}}>1\) is a suitable constant and \({\mathfrak {c}}\) near 1. Therefore, up to a subsequence, we can assume that \(u_n\rightarrow u\) weak in \(W_{\varepsilon },\) \(u_n\rightarrow u\) in \(L_{loc}^{q}({\mathbb {R}}^N)\) for all \(q\in [\dfrac{N}{s},+\infty )\) and \(u_n(x)\rightarrow u(x)\) almost everywhere on \({\mathbb {R}}^N.\) By arguments as Lemma 2.5 [8], for any \(\varepsilon _{*}>0,\) there exists \(R=R(\varepsilon _{*})>0\) such that \(\Lambda _{\varepsilon }\subset B_R(0)\) and
Then, we obtain
for all n large enough. From the condition \((f_1),\) \((f_3)\) and \((g_3),\) we get
for all \(t\in {\mathbb {R}}, x\in {\mathbb {R}}^N\) and some \(\delta>0, q>p_m.\) Using (2.55), (2.57) and Trudinger–Moser inequality, Hölder inequality, there exists \(D>0\) such that
for some constant \(t>1.\)
For any \(\nu \in (\dfrac{N}{s},+\infty ),\) choose \({\mathfrak {a}}>\dfrac{N}{s}\) such that \(\nu \in (\dfrac{N}{s},{\mathfrak {a}}),\) there exists \(\sigma _1\in (0,1)\) such that \(\dfrac{1}{\nu }=\dfrac{s\sigma _1}{N}+\dfrac{1-\sigma _1}{{\mathfrak {a}}}.\) Apply the Hölder inequality to estimate \(\int \limits _{{\mathbb {R}}^N{\setminus } B_R(0)}|u_n(x)|^{\nu }dx,\) and we get
From (2.48), we have
On combining that inequality with (2.59), we deduce
From (2.55), (2.56) and (2.60), there exists constant \({\mathcal {D}}>0\) such that
Join (2.56), (2.58) and apply (2.61) to \(\nu =qt,\) we get
for all n large enough and \(\kappa ^{*}>0\) is a suitable constant. Hence, we deduce
Note that \(\Lambda _{\varepsilon }\subset B_R(0),\) and the embedding from \(W_{\varepsilon }\) into \(L^{{\mathfrak {q}}}(B_R(0))\) is compact for any \({\mathfrak {q}}\in [\dfrac{N}{s},+\infty ),\) we have
by the Lebesgue Dominated convergence theorem or Vitali’s theorem. Using Trudinger–Moser inequality, we get \(g(\varepsilon x,u)u\in L^1({\mathbb {R}}^N),\) then can choose R large enough such that
From (2.62), (2.63) and (2.64), we obtain
By arguments as in [54], we get \(<I_{\varepsilon }^{'}(u),\varphi >=0\) for all \(\varphi \in W_{\varepsilon }.\) Consequently, we get \(<I_{\varepsilon }^{'}(u),u>=0,\) or equivalently
Since \(\{u_n\}\) is (PS) sequence, then \(<I_{\varepsilon }^{'}(u_n),u_n>=o_n(1)\) as \(n\rightarrow \infty .\)
Apply Brezis–Lieb lemma, (2.66) and (2.67), we obtain \(u_n\rightarrow u\) strong in \(W_{\varepsilon }.\) We finish the proof of Lemma 11. \(\square \)
Lemma 12
The functional \(I_{\varepsilon }\) restricted to \({\mathcal {N}}_{\varepsilon }\) satisfies the \((PS)_d\) condition at any level \(d>0\) and d verifies
if \(m\ge 2\) and
if \(m=1,\) where \({\mathfrak {c}}>1\) is a suitable constant and near 1.
Proof
Let \(\{u_n\}\subset {\mathcal {N}}_{\varepsilon }\) be such that \(I_{\varepsilon }(u_n)\rightarrow d\) and \(||I_{\varepsilon }^{'}(u_n)|_{{\mathcal {N}}_{\varepsilon }}||_{W_{\varepsilon }^{*}}=o_n(1)\) as \(n\rightarrow \infty ,\) where \(W_{\varepsilon }^{*}\) is the dual space of \(W_{\varepsilon }.\) Then there exists \(\{\lambda _n\}\subset {\mathbb {R}}\) such that
where
Taking into account \(<I_{\varepsilon }^{'}(u_n),u_n>=0,\) we have
When \(x\in \Lambda _{\varepsilon }^{s}\) and \(t>a,\) we have \(g(\varepsilon x, t)=\dfrac{V_0}{k}t^{p_m-1}.\) It implies that
Therefore, we get
via to the conditions \((g_6)\) and \((g_7).\) By arguments as Lemma 8, for \(\gamma _1\) large enough, we have \(\{u_n\}\) is a bounded sequence in \(W_{\varepsilon }\) and
where \({\mathfrak {c}}>1\) is a suitable constant and \({\mathfrak {c}}\) near 1. Therefore, up to a subsequence, we can assume that \(u_n\rightarrow u\) weak in \(W_{\varepsilon },\) \(u_n\rightarrow u\) in \(L_{loc}^{q}({\mathbb {R}}^N)\) for all \(q\in [\dfrac{N}{s},+\infty )\) and \(u_n(x)\rightarrow u(x)\) almost everywhere on \({\mathbb {R}}^N.\) We prove that \(\text {sup}_{n\in {\mathbb {N}}}<T_{\varepsilon }^{'}(u_n),u_n> <0.\) Conversly, if \(\text {sup}_{n\in {\mathbb {N}}}<T_{\varepsilon }^{'}(u_n),u_n>=0,\) then up to a subsequence, we can assume that \(\lim _{n\rightarrow \infty } <T_{\varepsilon }^{'}(u_n),u_n>=0.\) Using Fatou’s lemma and (2.69), we have
due to the condition \((g_7).\) Hence \(u\equiv 0\) in \(\Lambda _{\varepsilon }.\) Then \(u_n\rightarrow 0\) in \(L^{q}(\Lambda _{\varepsilon }).\) Using Trudinger–Moser inequality and (2.70), we get
Hence, we obtain
thanks to the condition \((g_5).\) Then, we deduce
as \(n\rightarrow \infty ,\) it is a contradiction with the fact that \(||u_n||_{W_{\varepsilon }}\ge r_{*}>0\) for all n. In conclusion, we get \(\text {sup}_{n\in {\mathbb {N}}}<T_{\varepsilon }^{'}(u_n),u_n> <0,\) and (2.68) implies \(\lambda _n=o_n(1)\) as \(n\rightarrow \infty .\) Therefore, \(\{u_n\}\) is a \((PS)_c\) sequence of \(I_{\varepsilon }\) and Lemma 12 is obtained from Lemma 11. \(\square \)
Corollary 1
The critical points of \(I_{\varepsilon }\) on \({\mathcal {N}}_{\varepsilon }\) are critical points of \(I_{\varepsilon }\) in \(W_{\varepsilon }.\)
Now, we prove the existence of a ground state solution for problem \((P_{\varepsilon }^{*}).\) That is a critical point \(u_{\varepsilon }\) of \(I_{\varepsilon }\) satisfying \(I_{\varepsilon }(u_{\varepsilon })=c_{\varepsilon }.\)
Theorem 7
Assume that \((f_1)-(f_5)\) and (V) hold. Then there exists \({\overline{\varepsilon }}>0\) such that \((P_{\varepsilon }^{*})\) has a ground state solution for all \(0<\varepsilon <{\overline{\varepsilon }}.\)
Proof
By Lemma 10 and Lemma 11, there exists \({\overline{\varepsilon }}>0\) such that \(c_{\varepsilon }\le c_{V_0}\) for all \(\varepsilon \in (0,{\overline{\varepsilon }}).\) We can choose \(d=c_{V_0}\le a(1-\dfrac{N}{s\mu })(\dfrac{aN}{\gamma _1 s \mu })^{N/(\mu s-N)}\) and \(\gamma _1\ge \max \{a,\gamma _3\}\) where \(\gamma _3\) satisfies the condition
in which \({\mathfrak {b}}=a(1-\dfrac{N}{s\mu })(\dfrac{aN}{\gamma _3 s \mu })^{N/(\mu s-N)}\) and \(m=1.\) When \(m\ge 2,\) \(\gamma _3\) satisfies the condition
Lemma 11 implies that \(I_{\varepsilon }\) satisfies the \((PS)_{c_{\varepsilon }}\) condition. Combine that result with Lemma 7, \(I_{\varepsilon }\) has a critical point at level \(c_{\varepsilon }.\) \(\square \)
4 Multiplicity of solutions to \((P_{\varepsilon }^{*})\)
In this section, we show that the existence of multiple weak solutions and study the behavior of its maximum points related with the set M. The main result of this section is equivalent to Theorem 2 and it is stated as follows:
Theorem 8
Assume that \((f_1)-(f_5)\) and (V) hold. Then for any \(\delta >0,\) there exists \(\varepsilon _{\delta }>0\) such that \((P_{\varepsilon }^{*})\) has at least \(cat_{M_{\delta }}(M)\) nontrival nonnegative solutions, for any \(0<\varepsilon <\varepsilon _{\delta }.\) Moreover, if \(u_{\varepsilon }\) denotes one of these solutions and \(z_{\varepsilon }\) is its global maximum, then
Proof
We consider the energy function
of problem \((P_{V_0}).\) We recall that \(c_{V_0}\) is the minimax level related to \(J_{V_0}\) and \({\mathcal {N}}_{V_0}\) is the Nehari manifold related to \(J_{V_0}\) is given by
Let \(\delta >0\) be a fixed and w be a ground state solution of problem \((P_{V_0}).\) It means that \(J_{V_0}(w)=c_{V_0}\) and \(J_{V_0}^{'}(w)=0.\) Let \(\eta \) be a smooth nonincreasing cut-off function in \([0,+\infty )\) such that \(\eta (s)=1\) if \(0\le s\le \dfrac{\delta }{2}\) and \(\eta (s)=0\) if \(s\ge \delta .\) For any \(y\in M,\) we denote
and \(\Phi _{\varepsilon }: M \rightarrow {\mathcal {N}}_{\varepsilon }\) which is defined by \(\Phi _{\varepsilon }(y)=t_{\varepsilon }\psi _{\varepsilon ,y},\) where \(t_{\varepsilon }>0\) satisfies
From the construction, \(\Phi _{\varepsilon }(y)\) has compact support for any \(y\in M.\) \(\square \)
Lemma 13
The function \(\Phi _{\varepsilon }\) satisfies the following limit
Proof
Suppose that the statement of Lemma 13 doesnot hold, then there exists \(\delta _0>0,\) \(\{y_n\}\subset M\) and \(\varepsilon _n\rightarrow 0\) such that
By Lemma 2.2 [14], we have
and
for all \(i=1,\dots ,m.\) Since \(<I_{\varepsilon _n}^{'}(t_{\varepsilon _n}\psi _{\varepsilon _n,y_n}),t_{\varepsilon _n}\psi _{\varepsilon _n,y_n}>=0,\) using the change of variable \(z=\dfrac{\varepsilon _nx-y_n}{\varepsilon _n},\) then we get
We observe that if \(z\in B_{\delta /{\varepsilon _n}}(0),\) then \(\varepsilon _n z+y_n\in B_{\delta }(y_n)\subset M_{\delta }\subset \Lambda .\) Then
Now we prove that \(t_{\varepsilon _n}\rightarrow 1.\) First we show that \(t_{\varepsilon _n}\rightarrow t_0<+\infty .\) Conversly if \(t_{\varepsilon _n}\rightarrow +\infty ,\) from (4.4) we have
if \(m=1,\) and
if \(m\ge 2.\) From the condition \((f_2)\) and \((f_4),\) we have \(f(t)\ge \gamma _1\mu |t|^{\mu -1}\) for all \(t\ge 0.\) If \(m=1,\) combine that property and (4.4), we deduce
as \(n\rightarrow \infty .\) It is a contradiction with (4.2) and (4.3). Similarly, we get a contradiction in the case \(m=2.\) Therefore, up to a subsequence, we may assume that \(t_{\varepsilon _n}\rightarrow t_0\ge 0\) as \(n\rightarrow \infty .\) We consider the case that \(t_0=0.\) From (2.41), we have
due to \(\Phi _{N,s}(t)\) is an increasing function on \([0,+\infty ),\) where \(\tau >0\) is small enough and \(q>p_m.\) Combine (4.6) and (4.8), we get
Since \(||t_{\varepsilon _n}\psi _{\varepsilon _n,y_n}||_{W_{V,\varepsilon _n}^{s,p}({\mathbb {R}}^N)}\rightarrow 0\) and \(||t_{\varepsilon _n}\psi _{\varepsilon _n,y_n}||_{W_{V,\varepsilon _n}^{s,p_i}({\mathbb {R}}^N)}\rightarrow 0\) as \(n\rightarrow \infty \) for all \(i=1,\dots , m,\) then
Using Trudinger–Moser inequality and note that \(t_{\varepsilon _n}\rightarrow 0\) as \(n\rightarrow \infty ,\) take \(\tau >0\) is small enough such that \((m+1)^{1-p_m}-\tau A_{p_m,V_0}^{-p_m}>0,\) from (4.9) and (4.10), we obtain \(((m+1)^{1-p_m}-\tau A_{p_m,V_0}^{-p_m})||w||_{V_0,W}^{p_m}\le o_n(1)\) as \(n\rightarrow \infty \) due to
as \(n\rightarrow \infty .\) It is a contradiction. Hence, \(t_0>0.\) Now we prove that \(t_0=1.\) From (4.6), using Lebesgue Dominated convergence theorem, we have
and
if \(m\ge 2.\) Note that \(w\in {\mathcal {N}}_{V_0},\) then the condition \((f_5)\) implies \(t_0=1.\) Still using Lebesgue Dominated convergence theorem or Vitali’s theorem, we get
Hence, we obtain
which contradicts with (4.1). \(\square \)
For any \(\delta >0,\) let \(\rho =\rho (\delta )>0\) be such that \(M_{\delta }\subset B_{\rho }(0).\) Let \(\chi :{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N\) be define as
Next, we define the barycenter map \(\beta _{\varepsilon }: {\mathcal {N}}_{\varepsilon }\rightarrow {\mathbb {R}}^N\) given by
Lemma 14
([54]) The functional \(\Phi _{\varepsilon }\) satisfies the following limit
Proof
For the convenience to the readers, we present a proof to above lemma. Suppose by a contradiction that there exists \(\delta _0>0,\) \(\{y_n\}\subset M\) and \(\varepsilon _n\rightarrow 0\) such that
for all n large enough. Using the definitions of \(\Phi _{\varepsilon _n}(y_n),\beta _{\varepsilon _n},\eta \) and the change of variable \(z=\dfrac{\varepsilon _n x-y_n}{\varepsilon _n},\) we have
From the assumptions \(\{y_n\}\subset M\subset B_{\rho }(0)\) and \(|\chi (x)|\le \rho \) for all \(x\in {\mathbb {R}}^N,\) use the Dominated convergence theorem by taking \(n\rightarrow \infty \) in (4.13), we get
which contradicts with (4.12). \(\square \)
Lemma 15
Let \(\varepsilon _n\rightarrow 0^{+}\) and \(\{u_n\}\subset {\mathcal {N}}_{\varepsilon _n}\) be such that \(I_{\varepsilon _n}(u_n)\rightarrow c_{V_0}.\) Then there exists \(\{{\tilde{y}}_n\}\subset {\mathbb {R}}^N\) such that the translation sequence \(v_n(x)=u_n(x+{\tilde{y}}_n)\) has a subsequence which converges in \(W^{s,N/s}({\mathbb {R}}^N) \cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N).\) Moreover, up to a subsequence, \(\{y_n\}: y_n=\varepsilon {\tilde{y}}_n\rightarrow y\in M.\)
Proof
Since \(<I_{\varepsilon _n}^{'}(u_n),u_n>=0\) and \(I_{\varepsilon _n}(u_n)\rightarrow c_{V_0},\) by arguments Lemma 8 and Lemma 10, \(\{||u_n||_{W_{\varepsilon _n}}\}\) is a bounded sequence and when \(\gamma _1\) is choosen such that \(\gamma _1\ge \max \{a,\gamma _{3}\}\) and
for some \(\varepsilon _*>0\) and \(\gamma _3\) satisfies
if \(m=1\) and
if \(m\ge 2.\) Then, we deduce
and
if \(m=1\) and
\(i=1,\dots ,m-1\) if \(m\ge 2.\) Hence, we obtain
We also get
due to the continuous embedding from \(W_{\varepsilon }\) into W. Now, we show that there exist a sequence \(\{{\tilde{y}}_n\}\subset {\mathbb {R}}^N\) and constants \(r>0,\beta >0\) such that
Indeed, if (4.15) is false, then for any \(r>0,\) we have
By Lemma 5, we have \(u_n\rightarrow 0\) strongly in \(L^{q}({\mathbb {R}}^N)\) for any \(q\in (p_m,+\infty ).\) Using Trudinger–Moser inequality and (4.14), we deduce
Combine that result and \(u_n\in {\mathcal {N}}_{\varepsilon _n},\) we obtain \(||u_n||_{W_{\varepsilon _n}}\rightarrow 0\) as \(n\rightarrow \infty .\) It is a contradiction with \(I_{\varepsilon _n}(u_n)\rightarrow c_{V_0}>0.\) Therefore, (4.15) holds. Let us define \(v_n:=u_n(x+{\tilde{y}}_n).\) Since the \(||.||_{V_0}\) is invariant with the translation, then \(\{v_n\}\) is a bounded sequence in W, thus up to a subsequence, we can assume that there exists \(v\in W\) such that \(v_n\rightarrow v\) weak in W and \(v_n(x)\rightarrow v(x)\) a.e. in \({\mathbb {R}}^N\) and \(v_n\rightarrow v\) in \(L^{q}_{loc}({\mathbb {R}}^N)\) for any \(q\in [\dfrac{N}{s},+\infty ).\) From that result and (4.15), we get \(v\not \equiv 0.\) Let \(t_n>0\) such that \(w_n=t_nv_n\in {\mathcal {N}}_{V_0}\) and we set \(y_n:=\varepsilon _n {\tilde{y}}_n.\) Thus, using the change of the variable \(z=x+{\tilde{y}}_n,\) \(V(\varepsilon _n(x+{\tilde{y}}_n))\ge V_0\) and the invariance by translation, we can see that
due to the condition \((g_3).\) Then we get \(J_{V_0}(w_n)\rightarrow c_{V_0}.\) Since \(\{w_n\}\subset {\mathcal {N}}_{V_0},\) using the condition \((f_2),\) there exists a constant \(K>0\) such that \(||w_n||_{W,V_0}\le K\) for all n. We have \(v_n\not \rightarrow 0\) strongly in W. Indeed, if \(v_n\rightarrow 0\) in W, then \(v_n\rightarrow v\) weak in W, it contradicts with \(v_n\rightarrow v\not \equiv 0\) in W. Hence, there exists \(\alpha >0\) such that \(||v_n||_{V_0,W}\ge \alpha >0\) for all n. Consequently, we have
which yields \(t_n\le \dfrac{K}{\alpha }\) for all \(n\in {\mathbb {N}}.\) Therefore, up to a subsequence, we can assume that \(t_n\rightarrow t_0\ge 0.\) We prove that \(t_0>0.\) If \(t_0=0,\) then \(||w_n||_{V_0,W}\rightarrow 0,\) it is a contradiction with \(w_n\in {\mathcal {N}}_{V_0}.\) Up to a subsequence, we suppose that \(w_n\rightarrow w:=t_0v\not \equiv 0\) weak in W and \(w_n(x)\rightarrow w(x)\) a.e. on \({\mathbb {R}}^N.\) By arguments as in Proposition 1 (also see [54]), we can get \(J_{V_0}^{'}(w)=0.\) Now we prove that
and
Using Brezis–Lieb’s lemma, (4.16) and (4.17), we obtain \(w_n\rightarrow w\) strong in W. By Fatou’s lemma, we have
and
Assume that by contradiction that
or
for some \(i\in \{1,\dots , m\}.\) We see that
Using the condition \((f_2),\) and Fatou’s lemma, we get
which is a contradiction. Then
and
Combine (4.18) and (4.20), (4.19) and (4.21), we get (4.16). Since \(t_n\rightarrow t_0\) as \(n\rightarrow \infty ,\) then \(v_n\rightarrow v\) in \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\) as \(n\rightarrow \infty .\) Now we prove that \(\{y_n\}\) has a subsequence such that \(y_n\rightarrow y\in M.\) Indeed, if \(\{y_n\}\) is not bounded, that is there exists a subsequence, still denoted by \(\{y_n\},\) such that \(|y_n|\rightarrow +\infty .\) Choose \(R>0\) such that \(\Lambda \subset B_R(0).\) Then for all n large enough, we have \(|y_n|>2R,\) and for any \(x\in B_{R/{\varepsilon _n}}(0),\) we have
From the condition \((V_1),\) \(u_n\in {\mathcal {N}}_{\varepsilon _n}\) and the definition of g we have
Using the change of variable \(z=x+{\tilde{y}}_n,\) from (4.22), we get
Note that \({\tilde{f}}(t)\le \dfrac{V_0}{k}|t|^{p_m-1}.\) Then (4.23) implies
Since \(v_n\rightarrow v\) strong in W, then \(v_n\rightarrow v\) strong \(L^{q}({\mathbb {R}}^N)\) for all \(q\ge \dfrac{N}{s},\) then for any \(\varepsilon _{*}>0,\) we can choose R as above large enough such that
for some \(q>p_m.\) Using the condition \((g_3)\) and Trudinger–Moser inequality, we get
where \(\kappa _{*}>0\) is a suitable constant and n large enough. Combine (4.24) and (4.25), we have
if \(m\ge 2\) and
if \(m=1.\) That is \(v_n\rightarrow 0\) strong in \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\) which contradicts with \(v_n\rightarrow v\not \equiv 0.\) Therefore, we may assume that \(y_n\rightarrow y_0.\) If \(y_0\not \in {\overline{\Lambda }}.\) Then there exists \(r>0\) such that for every n large enough, we have \(|y_n-y_0|<r\) and \(B_{2r}(y_0)\subset \overline{\Lambda }^{c}.\) Thus if \(x\in B_{r/{\varepsilon _n}}(0),\) we have that \(|\varepsilon _n x+y_n-y_0|<2r\) so that \(\varepsilon _nx+y_n\in \overline{\Lambda }^{c}.\) By arguments as above, we get a contradiction. Hence, \(y_0\in {\overline{\Lambda }}.\) We now prove \(V(y_0)=V_0.\) Indeed, if \(V(y_0)>V_0,\) using the Fatou’s lemma and the change of variable \(z=x+{\tilde{y}}_n,\) then we have
From above inequality, we deduce
which is an absurd. \(\square \)
Let \({\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) be a positive function such that \(h(\varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0^{+}\) and let
By Lemma 14, we have \(h(\varepsilon )=|I_{\varepsilon }(\Phi _{\varepsilon }(y))-c_{V_0}|\rightarrow 0\) as \(\varepsilon \rightarrow 0^{+}.\) Hence \(\Phi _{\varepsilon }(y)\in {\mathcal {N}}_{\varepsilon }\) and \(\tilde{{\mathcal {N}}}_{\varepsilon }\ne \emptyset \) for any \(\varepsilon >0.\) Moreover, we have the following result:
Lemma 16
([7]) For any \(\delta >0,\) it holds that
Lemma 17
Assume that (V) and \((f_1)-(f_5)\) hold and let \(v_n\) be a nontrivial nonnegative solution of the following problem
where \(V_n(x)=V(\varepsilon _n x+\varepsilon _n {\tilde{y}}_n)\) and \(\varepsilon _n{\tilde{y}}_n\rightarrow y\in M.\) If \(\{v_n\}\) is a bounded sequence in W verifying
where \({\mathfrak {c}}>1\) is a suitable constant and \(v_n\rightarrow v\) strong in W, then \(v_n\in L^{\infty }({\mathbb {R}}^N)\) and there exists \(C>0\) such that \(||v_n||_{L^{\infty }({\mathbb {R}}^N)}\le C\) for all \(n\in {\mathbb {N}}.\) Furthermore
Proof
For any \(L>0\) and \(\beta >1,\) let us to consider the function \(\gamma (t)=t(\min \{t,L\})^{p(\beta -1)}\) and
Set
Then we have [14]
From (4.28), we get
Therefore, taking \(\gamma (v_n)=v_nv_{L,n}^{p(\beta -1)}\) as a test function in (4.27), we have
From the condition \((f_1),\) \((f_3)\) and \((g_3)\), for any \(\varepsilon >0,\) there exist \(C(\varepsilon )>0\) such that
for all \(x\in {\mathbb {R}}^N\) and \(t\in {\mathbb {R}}.\) By arguments as [7], we have
for all \(i=1,\dots ,m.\) Combine that inequality with (4.29), we have
Since \(\Gamma (v_n)\ge \dfrac{1}{\beta }v_n v_{L,n}^{\beta -1},\) \(v_nv_{L,n}^{\beta -1}\ge \Gamma (v_n)\) and the embedding from \(W^{s,N/s}({\mathbb {R}}^N)\rightarrow L^{N^{*}}({\mathbb {R}}^N)\) \((N^{*}>\dfrac{N}{s})\) is continuous, then there exists a suitable constant \(S_{*}>0\) such that
We know that the embedding from \(W^{s,N/s}({\mathbb {R}}^N)\cap \cap _{i=1}^{m}W^{s,p_i}({\mathbb {R}}^N)\rightarrow W^{s,N/s}({\mathbb {R}}^N)\rightarrow L^{\nu }({\mathbb {R}}^N)\; (\nu \ge \dfrac{N}{s})\) is continuous, then there exists a best constant
This implies
Then we obtain
Choose \(0<\varepsilon <\beta ^{-p}{\mathcal {S}}_p^{p},\) then (4.32) implies
Using Trudinger–Moser inequality in \(W^{s,N/s}({\mathbb {R}}^N)\) with \(q>>\dfrac{N}{s}\) such that \(N^{**}=qp<N^{*},\) \(q'>1\) and \(q'\) near 1, then there exists a constant \(D>0\) such that
Let \(L\rightarrow +\infty \) in above inequality, we deduce
Now, we set \(\beta =\dfrac{N^{*}}{N^{**}}>1.\) Then \(\beta ^2N^{**}=\beta N^{*}\) and (4.33) holds with \(\beta \) replaced by \(\beta ^2.\) Therefore, we obtain
Iterating this process as in (4.34), we can infer that for any positive integer m,
Taking the limit in (4.35) as \(m\rightarrow \infty ,\) we get
for all n, where \(C=D^{\sum _{j=1}^{\infty }\dfrac{1}{p\beta ^{j}}}\beta ^{\sum _{j=1}^{\infty }j\beta ^{-j}}\sup _{n}||v_n||_{L^{N^{**}\beta }({\mathbb {R}}^N)}<+\infty .\) Since \(v_n\rightarrow v\) strong in W, then \( \lim _{|x|\rightarrow +\infty }v_n(x)=0\; \text {uniformly in}\; n.\) \(\square \)
Let \(\delta >0\) be small enough such that \(M_{\delta }\subset \Lambda \). By Lemma 14 and Lemma 16, there exists \({\overline{\varepsilon }}={\overline{\varepsilon }}_{\delta }>0\) such that the following diagram
is well-defined for any \(\varepsilon \in (0,{\overline{\varepsilon }})\). Thanks to Lemma 14 and by decreasing \({\overline{\varepsilon }}\) if necessary, we obtain that
for all \(y\in M\), for some function \(\theta =\theta (\varepsilon ,y)\) satisfying \(|\theta (\varepsilon ,y)|<\frac{\delta }{2}\) uniformly in \(y\in M\), and for all \(\varepsilon \in (0,{\overline{\varepsilon }})\). Therefore, \(H(t,y):=y+(1-t)\theta (\varepsilon ,y)\), with \((t,y)\in [0,1]\times M\), is a homotopy between \(\beta _{\varepsilon }\circ \Phi _{\varepsilon }\) and the inclusion map \(\text {id}: M\rightarrow M_{\delta }\). By [17, Lemma 4.3] (see also Lemma [22, Lemma 2.2]), we get
Since the functional \(I_{\varepsilon }\) satisfies the \((PS)_{c_\varepsilon }\) condition on \({\mathcal {N}}_{\varepsilon }\) with \(0<c_{\varepsilon }\le c_{V_0}+h(\varepsilon ))\), then by Lusternik-Schnirelmann’s theory of critical points (see [57, Theorem 5.20]), \(I_{\varepsilon }\) has at least \(\text {cat}_{\widetilde{{\mathcal {N}}_{\varepsilon }}}(\widetilde{{\mathcal {N}}_{\varepsilon }})\ge \text {cat}_{M_{\delta }}(M)\) critical points on \(\widetilde{{\mathcal {N}}_{\varepsilon }}\subset {\mathcal {N}}_{\varepsilon }\). By Corollary 1, \(I_{\varepsilon }\) has at least \(\text {cat}_{M_{\delta }}(M)\) critical points restricted to \(\widetilde{{\mathcal {N}}_{\varepsilon }}\) which are critical points of \(I_{\varepsilon }\) in \(W_{\varepsilon }\). This means that \((P_{\varepsilon })^{*}\) has at least \(\text {cat}_{M_{\delta }}(M)\) solutions.
Now, we show that there exists \({\hat{\varepsilon }}={\hat{\varepsilon }}_{\delta }\) such that, for any \(\varepsilon \in (0,{\hat{\varepsilon }}_{\delta })\) and any solution \(u_{\varepsilon }\in \widetilde{{\mathcal {N}}_{\varepsilon }}\) of (2.37), it holds
Assuming (4.36) to be false, then there exists a sequence \(\varepsilon _n\rightarrow 0\) and a sequence \(\{u_{\varepsilon _n}\}\subseteq \widetilde{{\mathcal {N}}}_{\varepsilon _n}\) such that \(I'_{\varepsilon _n}(u_{\varepsilon _n})=0\) and
Since \(V(\varepsilon _nx)\ge V_0\) for all \(x\in {\mathbb {R}}^N\) and \(n\in \mathbb {N}\), then
and \(h(\varepsilon _n)\rightarrow 0\). It implies that \(I_{\varepsilon _n}(u_{\varepsilon _n})\rightarrow c_{V_0}\). By Lemmas 15 and 17, we can find a sequence \(\{{\tilde{y}}_n\}\subset \mathbb {R}^N\) such that \(v_n(\cdot )=u_{\varepsilon _n}(\cdot +{\tilde{y}}_n)\rightarrow v\) in W and \(y_n=\varepsilon _n{\tilde{y}}_n\rightarrow y\in M\). Then, we can find \(r>0\) such that \(B_r(y)\subset B_{2r}(y) \subset \Lambda \) and so \(B_{r/{\varepsilon _n}}(y/{\varepsilon _n})\subset \Lambda _{\varepsilon _n}\), for all n large enough. In particular, for any \(y\in B_{r/{\varepsilon _n}}({\tilde{y}}_n)\), we have
and \(\Lambda _{\varepsilon _n}^{c}\subset B_{r/{\varepsilon _n}}^{c}({\tilde{y}}_n) \) for n large enough. Since \(v_n\rightarrow v\) in W, we deduce that \(v_n(x)\rightarrow 0\) as \(|x|\rightarrow +\infty \) uniformly in \(n\in {\mathbb {N}}\), and hence there exist \(R,n_0>0\) such that \(v_n(x)<a\) for all \(|x|\ge R\) and \(n\ge n_0\). Consequently,
Increasing \(n_0\) if necessary, we can assume that \(\frac{r}{\varepsilon _n}>R\), and we get \(\Lambda _{\varepsilon _n}^{c}\subset B_{r/{\varepsilon _n}}^{c}({\tilde{y}}_n)\subset B_{R}^{c}({\tilde{y}}_n)\). So,
which contradicts (4.37). Hence (4.36) holds.
Setting \(\varepsilon _{\delta }=\min \{{\overline{\varepsilon }}_{\delta },{\hat{\varepsilon }}_{\delta }\}\), we can then guarantee that problem (2.37) admits at least \(\text {cat}_{M_{\delta }}(M)\) non-trivial solutions. If \(u_{\varepsilon }\in {\mathcal {N}}_{\varepsilon }\) is one of these solutions, in the light of (4.36) and the definition of g, \(u_{\varepsilon }\) is a solution of (2.37) and \({\hat{u}}_{\varepsilon }(x)=u_{\varepsilon }(x/{\varepsilon })\) is a solution of problem (1.1).
Final we consider the behavior of maximum points of \({\hat{u}}_{\varepsilon }(x)\) as \(\varepsilon \rightarrow 0\). Take \(\varepsilon _n\rightarrow 0^{+}\) and the sequence \(\{u_{\varepsilon _n}\}\) of solutions of (2.37) for \(\varepsilon =\varepsilon _n\). By \((g_1)\) we can find \(\gamma >0\) small enough such that
Arguing as before, we can take \(R>0\) such that, for n large enough,
Up to a subsequence, we may assume that, for n large enough,
otherwise we would get \(\left\| u_n\right\| _{L^{\infty }({\mathbb {R}}^N)}<\gamma \). Since \(I'_{\varepsilon _n}(u_n)(u_n)=0\), we obtain
and hence \(\left\| u_{\varepsilon _n}\right\| _{W_{\varepsilon _n}}\rightarrow 0\) as \(n\rightarrow \infty \), in contrast with \(I_{\varepsilon _n}(u_{\varepsilon _n})\rightarrow c_{V_0}>0.\) From (4.41) and (4.42), we deduce that the global maximum points \(p_{\varepsilon _n}\) of \(u_{\varepsilon _n}\) belong to \(B_R({\tilde{y}}_n)\), that is \(p_{\varepsilon _n}=q_n+{\tilde{y}}_n\) for some \(q_n\in B_R(0)\). Recalling that \({\hat{u}}_n(x)=u_n(x/{\varepsilon _n})\) solves (1.1), then the maximum points \(\eta _{\varepsilon _n}\) of \({\hat{u}}_n\) are \(\eta _{\varepsilon _n}=\varepsilon _n{\tilde{y}}_n+\varepsilon _n q_n\). Noting that \(q_n\in B_R(0)\), \(\varepsilon _n {\tilde{y}}_n\rightarrow y\in M\), we get \(V(y)=V_0=\lim _{n\rightarrow \infty }V(\eta _{\varepsilon _n})\). Then, we deduce
and the proof is concluded. \(\square \)
References
Adachi, S., Tanaka, K.: Trudinger type inequalities in \({\mathbb{R} }^N\) and their best exponents. Proc. Am. Math. Soc. 128, 2051–2057 (2000)
Adimurthi, A., Sandeep, K.: A singular Moser–Trudinger embedding and its applications. Nonlinear Differ. Equ. Appl. 13, 585–603 (2010). Int. Math. Res. Not. IMRN 13, 2394–2426 (2007)
Adimurthi, A., Yang, Y.: Interpolation of Hardy inequality and Trudinger–Moser inequality in \({\mathbb{R} }^N\) and its applications. Int. Math. Res. Not. IMRN 13, 2394–2426 (2010)
Alves, C.O., Figueiredo, G.M.: Multiplicity and concentration of positive solutions for a class of quasilinear problems with critical exponential growth in \({\mathbb{R} }^N,\). J. Differ. Equ. 246, 1288–1311 (2009)
Alves, C.O., do Ó, J.M., Miyagaki, O.H.: Concentration phenomena for fractional elliptic equations involving exponential critical growth. Adv. Nonlinear Stud. 16(4), 843–861 (2016)
Alves, C.O., Miyagaki, O.H.: Existence and concentration of solution for a class of fractional elliptic equation in \({\mathbb{R} }^N\) via penalization method. Calc. Var. PDE 55(3), 47 (2016)
Alves, C.O., Ambrosio, V., Isernia, T.: Existence, multiplicity and concentration for a class of fractional \((p, q)\)-Laplacian problems in \({\mathbb{R} }^N\). Commun. Pure Appl. Anal. 18(4), 2009–2045 (2019)
Ambrosio, V., Radulescu, V.D.: Fractional double-phase patterns: concentration and multiplicity of solutions. J. Math. Pures Appl. 142, 101–145 (2020)
Fiscella, A., Pucci, P.: Degenerate Kirchhoff \((p, q)\)-fractional systems with critical nonlinearities. Fract. Calc. Appl. Anal. 23(3), 723–752 (2020)
Isernia, T.: Fractional \((p, q)\)-Laplacian problems with potentials vanishing at infinity. Opusc. Math. 40(1), 93–110 (2020)
Isernia, T., Repovs, D.: Nodal solutions for double phase Kirchhoff problems with vanishing potentials. Asymptot. Anal. 124(3–4), 371–396 (2021)
Ambrosio, V., Repovs, D.: Multiplicity and concentration results for a \((p, q)\)-Laplacian problem in \({\mathbb{R} }^N\). Z. Angew. Math. Phys. 72, 1–33 (2021)
Antontsev, S.N., Shmarev, S.I.: Elliptic equations and systems with nonstandard growth conditions: existence, uniqueness and localization properties of solutions. Nonlinear Anal. 65, 722–755 (2006)
Ambrosio, V., Isernia, T.: Multiplicity and concentration results for some nonlinear Schrödinger equations with the fractional \(p\)-Laplace. Discret. Contin. Dyn. Syst. A 38(11), 5835–5881 (2018)
Ambrosio, V.: On a fractional magnetic Schrödinger equation in \({\mathbb{R} }\) with exponential critical growth. Nonlinear Anal. 183, 117–148 (2019)
Ambrosio, V., Isernia, T., Radulescu, V.D.: Concentration of positive solutions for a class of fractional p-Kirchhoff type equations. Proc. R. Soc. Edinb. Sect. A Math. 151(2), 601–651 (2021)
Benci, V., Cerami, G.: Multiple positive solutions of some elliptic problems via Morse theory and the domain topology. Calc. Var. Partial Differ. Equ. 2, 29–48 (1994)
Bonheure, D., d’Avenia, P., Pomponio, A.: On the electrostatic Born–Infeld equation with extended charges. Commun. Math. Phys. 346, 877–906 (2016)
Born, M., Infeld, L.: Foundations of the new field theory. Nature 132, 1004 (1933)
Brezis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88, 486–490 (1983)
Cherfils, L., Il’yasov, V.: On the stationary solutions of generalized reaction diffusion equations with p &q-Laplacian. Commun. Pure Appl. Anal. 1(4), 1–14 (2004)
Cingolani, S., Lazzo, M.: Multiple positive solutions to nonlinear Schrödinger equation with competing potential. J. Differ. Equ. 160, 118–138 (2000)
do Ó, J.A.M.B.: N-Laplacian equations in \({\mathbb{R}}^N\) with critical growth. Abstr. Appl. Anal. 2, 301–315 (1997)
do Ó, J.M., Souto, M.A.S.: On a class of nonlinear Schrödinger equations in \({\mathbb{R}}^2\) involving critical growth. J. Differ. Equ. 174, 289–311 (2001)
do Ó, J.A.M., Miyagaki, O.H., Squassina, M.: Nonautonomous fractional problems with exponential growth. NoDEA Nonlinear Differ. Equ. Appl. 22, 1395–1410 (2015)
do Ó, J.A.M., Miyagaki, O.H., Squassina, M.: Ground states of nonlocal scalar field equations with Trudinger–Moser critical nonlinearity. Topol. Methods Nonlinear Anal. 48, 477–492 (2016)
de Figueiredo, D.G., Miyagaki, O.H., Ruf, B.: Elliptic equations in \({\mathbb{R} }^2\) with nonlinearities in the critical growth range. Calc. Var. PDE 3, 139–153 (1995)
Figueiredo, G.M., Siciliano, G.: A multiplicity result via Ljusternick–Schnirelmann category and Morse theory for a fractional Schrödinger equation in \({\mathbb{R} }^N\). NoDEA Nonlinear Differ. Equ. Appl. 23(2), 12 (2016)
Figueiredo, G.M., Molica Bisci, G., Servadei, R.: The effect of the domain topology on the number of solutions of fractional Laplace problems. Calc. Var. 57, 103 (2018)
He, X., Zou, W.: Existence and concentration result for the fractional Schrödinger equations with critical nonlinearity. Calc. Var. PDE 55, 91 (2016)
Iannizzotto, A., Squassina, M.: \(\dfrac{1}{2}\)-Laplacian problems with exponential nonlinearity. J. Math. Anal. Appl. 414, 372–385 (2014)
Iula, S., Maalaoui, A., Martinazzi, L.: A fractional Moser–Trudinger type inequality in one dimension and its critical points. Differ. Integral Equ. 29, 455–492 (2016)
Iula, S.: A note on the Moser–Trudinger inequality in Sobolev–Slobodeckij spaces in dimension one. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 28, 871–884 (2017)
Laskin, N.: Fractional quantum mechanics and Levy path integrals. Phys. Lett. A 268, 298–305 (2000)
Laskin, N.: Fractional Schrödinger equation. Phys. Rev. E 66, 056108–056114 (2002)
Lam, N., Lu, G.: Existence and multiplicity of solutions to equations of \(N\)-Laplace type with critical exponential growth in \({\mathbb{R} }^N\). J. Funct. Anal. 262, 1132–1165 (2012)
Lam, N., Lu, G.: A new approach to sharp Moser–Trudinger and Adams type inequalities: a rearrangement-free argument. J. Differ. Equ. 255, 298–325 (2013)
Lia, Q., Yang, Z.: Multiple solutions for a class of fractional quasi-linear equations with critical exponential growth in \({\mathbb{R} }^N\). Complex Var. Elliptic Equ. 61, 969–983 (2016)
Martinazzi, L.: Fractional Adams–Moser–Trudinger type inequalities. Nonlinear Anal. 127, 263–278 (2015)
Molica Bisci, G., Thin, N.V., Vilasi, L.: On a class of nonlocal Schrödinger equations with exponential growth. Adv. Differ. Equ. 27, 571–610 (2022)
Moser, J.: A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20, 1077–1092 (1971)
Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2012)
Parini, E., Ruf, B.: On the Moser–Trudinger inequality in fractional Sobolev–Slobodeckij spaces. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 29, 315–319 (2018)
Pino, M.D., Felmer, P.L.: Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial. Differ. Equ. 4, 121–137 (1996)
Perera, K., Squassina, M.: Bifurcation results for problems with fractional Trudinger–Moser nonlinearity. Discret. Contin. Dyn. Syst. Ser. S 11, 561–576 (2018)
Pucci, P., Xiang, M., Zhang, B.: Multiple solutions for nonhomogeneous Schrödinger–Kirchhoff type equations involving the fractional \(p\)-Laplacian in \({\mathbb{R} }^N\). Calc. Var. PDE 54, 2785–2806 (2015)
Rabinowitz, P.: Minimax Methods in Critical Point Theory with Applications to Differential Equations. CBMS Regional Conference Series in Mathematics. American Mathematical Society, Providence (1986)
Rabinowitz, P.: On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43(2), 270–291 (1992)
Secchi, S.: Ground state solutions for nonlinear fractional Schrödinger equations in \({\mathbb{R} }^N\). J. Math. Phys. 54, 031501 (2013)
Shang, X., Zhang, J., Yang, Y.: On fractional Schrödinger equations with critical growth. J. Math. Phys. 54(12), 121502 (2013)
Shang, X., Zhang, J.: Ground states for fractional Schrödinger equations with critical growth. Nonlinearity 27(2), 187–208 (2014)
Thin, N.V.: Singular Trudinger–Moser inequality and fractional \(p\)-Laplace equation in \({\mathbb{R} }^N\). Nonlinear Anal. 196, 111756 (2020)
Thin, N.V.: Existence of solution to singular Schrödinger systems involving the fractional \(p\)-Laplacian with Trudinger–Moser nonlinearity in \({\mathbb{R} }^N\). Math. Methods Appl. Sci. 44(8), 6540–6570 (2021)
Thin, N.V.: Multiplicity and concentration of solutions to a fractional \((p, p_1)\)-Laplace problem with exponential growth. J. Math. Anal. Appl. 506(2), 125667 (2022)
Trudinger, N.S.: On imbeddings into Orlicz spaces and some applications. J. Math. Mech. 17, 473–483 (1967)
Wang, X.: On concentration of positive bound states of nonlinear Schrödinger equations. Commun. Math. Phys. 53, 229–244 (1993)
Willem, M.: Minimax Theorems. Basel, Birkhäuser (1996)
Xiang, M., Zhang, B., Repovs, D.: Existence and multiplicity of solutions for fractional Schrödinger-Kirchhoff equations with Trudinger–Moser nonlinearity. Nonlinear Anal. 186, 74–98 (2019)
Xiang, M., Radulescu, V.D., Zhang, B.: Fractional Kirchhoff problems with critical Trudinger–Moser nonlinearity. Calc. Var. PDE 58, 57 (2019)
Zhang, B., Fiscella, A., Liang, S.: Infinitely many solutions for critical degenerate Kirchhoff type equations involving the fractional \(p\)-Laplacian. Appl. Math. Optim. 80, 63–80 (2019)
Zhang, C.: Trudinger–Moser inequalities in fractional Sobolev–Slobodeckij spaces and multiplicity of weak solutions to the fractional-Laplacian equation. Adv. Nonlinear Stud. 19, 197–217 (2019)
Zhang, Y., Tang, X., Radulescu, V.D.: Concentration of solutions for fractional double-phase problems: critical and supercritical cases. J. Differ. Equ. 302, 139–184 (2021)
Wang, F., Xiang, M.: Multiplicity of solutions for a class of fractional Choquard–Kirchhoff equations involving critical nonlinearity. Anal. Math. Phys. 9, 1–16 (2019)
Acknowledgements
Thin Van Nguyen is supported by Ministry of Education and Training of Vietnam under project with the name “Some properties about solutions to differential equations, fractional partial differential equations” and grant number B2023-TNA-14. The research of Vicenţiu D. Rǎdulescu was supported by a grant of the Romanian Ministry of Research, Innovation and Digitization, CNCS/CCCDI-UEFISCDI, project number PCE 137/2021, within PNCDI III.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Conflict of interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen, T.V., Rădulescu, V.D. Multiplicity and concentration of solutions to fractional anisotropic Schrödinger equations with exponential growth. manuscripta math. 173, 499–554 (2024). https://doi.org/10.1007/s00229-022-01450-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-022-01450-7