Costello’s pushforward formula: errata and generalization

Abstract

Costello’s pushforward formula relates virtual fundamental classes of virtually birational algebraic stacks. Its original formulation omits a necessary hypothesis, whose addition is not sufficient to correct the proof. We supply a substitute for Costello’s notion of pure degree and prove the pushforward formula with this definition. We also show the hypotheses of the corrected pushforward formula are satisfied in a variety of its applications. Some adjustments to the original proofs are required in several cases, including the original one.

Appendix A. Degree of a Generically Finite Morphism

The stacks project offers two definitions of generic finiteness. We assume our stacks are locally noetherian and elaborate on definition (1) of [10, 073A].

Definition A.1

Let $f : X \rightarrow Y$ be locally of finite type and $\eta \in Y$ be a maximal point. We say f is generically finite at $\eta$ if the preimage $X \times _Y \eta$ is a finite, nonempty set. Equivalently, there’s an affine open $V \subseteq Y$ and finitely many $U_1, \dots , U_n$ such that $U_i \rightarrow V$ is finite and $\eta \in V$ and $X \times _Y \eta \subseteq \bigcup _n U_i$ [10, 02NW].

Given that $f : X \rightarrow Y$ is generically finite at some maximal $\eta$, we say it is of degree d at $\eta$ if [10, 02NY]

$$\begin{aligned} d = \sum _{\xi \in f^{-1}(\eta )} \dim _{R(\eta )} {\mathcal {O}}_{X, \xi }. \end{aligned}$$

A morphism $f : X \rightarrow Y$ locally of finite type is said to be generically finite or of degree d if it is so at every maximal point $\eta \in Y$.

A representable morphism $X \rightarrow Y$ locally of finite type between algebraic stacks is said to be generically finite or of degree d (at a specific maximal point $\eta \in Y$ or for all) if the same is true for pulling back along some smooth cover $V \rightarrow Y$ by a scheme (with $\xi \in V$ mapping to $\eta$).

Remark A.2

Generically finite and degree d both pull back along flat, quasicompact morphisms $Y' \rightarrow Y$ and may be checked after some (equivalently any) flat, quasicompact cover. This is because generalizations lift along flat, quasicompact morphisms, ensuring that maximal points map to each maximal point.

Lemma A.3

Let $X \rightarrow {\text {Spec}}k$ be a finite morphism from a DM stack to a field. Then X admits a finite étale cover from a scheme.

Proof

Pick a finite type étale cover $P \rightarrow X$. Then $P \rightarrow X$ is locally quasifinite [10, 03WS] and hence quasifinite [10, 01TD]. The composite $P \rightarrow {\text {Spec}}k$ is quasifinite, hence finite [10, 02NH]. The map $P \rightarrow X$ is then finite. $\square$

Definition A.4

A finite DM-type morphism $X \rightarrow {\text {Spec}}k$ is of pure degree d if, for some (equiv. any) finite étale cover $P \rightarrow X$ by a scheme,

$$\begin{aligned} \dfrac{\deg (P/{\text {Spec}}k)}{\deg (P/X)} = d. \end{aligned}$$

A DM-type morphism $X \rightarrow Y$ of locally noetherian artin stacks is generically finite if, for all maximal points $\eta \rightarrow Y$, the pullback

$$\begin{aligned} X \times _Y \eta \rightarrow \eta \end{aligned}$$

is finite.

Remark A.5

The definition of degree d for generically finite morphisms is determined by its properties:

• A composite $X \overset{f}{\rightarrow } Y \overset{g}{\rightarrow } Z$ for which $\deg f$, $\deg g$, $\deg g \circ f$ are well defined satisfies

  $$\begin{aligned} \deg (g \circ f) = \deg f \cdot \deg g.\end{aligned}$$

• Given a pullback square

  

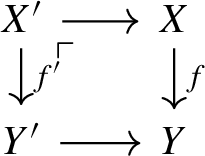
  with $Y' \rightarrow Y$ flat and quasicompact, f is generically finite (of degree d) if and only if $f'$ is.

• Agreement with the notion for representable morphisms in Definition A.1.

We conclude with two folklore observations that we use in the body of the text.

Remark A.6

(“Stability is an open condition”) Suppose $f : X \rightarrow Y$ is locally finite type and X, Y are algebraic stacks. There is a substack $U \subseteq X$ representing morphisms $T \rightarrow X$ such that $f|_T$ is DM type, and this substack is open. A map is DM type when the diagonal is unramified, which is an open condition by The Stacks Project Authors [10, 0475].

This shows that the locus where a family of prestable maps is stable is open in the base.

Remark A.7

If X is an algebraic stack locally of finite type, then its normalization $X^\nu \rightarrow X$ is finite. This is because normalizations are integral [10, 035Q] and the map is locally of finite type [10, 01WJ].