Abstract
We study the behavior of connections and curvature under the HK/QK correspondence, proving simple formulae expressing the Levi-Civita connection and Riemann curvature tensor on the quaternionic Kähler side in terms of the initial hyper-Kähler data. Our curvature formula refines a well-known decomposition theorem due to Alekseevsky. As an application, we compute the norm of the curvature tensor for a series of complete quaternionic Kähler manifolds arising from flat hyper-Kähler manifolds. We use this to deduce that these manifolds are of cohomogeneity one.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper concerns itself with the hyper-Kähler/quaternionic Kähler (HK/QK) correspondence, which is a duality between hyper-Kähler and quaternionic Kähler manifolds with (infinitesimal) circle symmetries. It was discovered by Haydys [10], and has since attracted the attention of physicists and mathematicians alike [1, 2, 4, 12, 13].
One of the most important applications of the HK/QK correspondence is to the study of a construction of quaternionic Kähler manifolds known as the (supergravity) c-map [9, 11]. This construction, first discovered by theoretical physicists, was extended to produce one-parameter families of quaternionic Kähler metrics [14], known as one-loop deformed Ferrara–Sabharwal metrics (reflecting their physical origins).
The starting point for the c-map construction is not a hyper-Kähler manifold, but rather a projective special Kähler (PSK) manifold \({\bar{M}}\), which is by definition the Kähler quotient of a corresponding conical affine special Kähler (CASK) manifold M with respect to a preferred circle action. The c-map and its one-loop deformation are most conveniently described by first passing to M, then to its cotangent bundle \(N=T^*M\), which comes with a natural (pseudo-)hyper-Kähler structure. The circle action on M moreover lifts to a natural circle symmetry of N, making it possible to apply the HK/QK correspondence to N to produce a quaternionic Kähler manifold \({\bar{N}}\) of the same dimension as N (see [1, 2, 4] for details). The resulting quaternionic Kähler metric admits a (non-zero) Killing field, and in fact any quaternionic Kähler manifold with a Killing field can be locally obtained in this fashion.
An important feature of the HK/QK correspondence is that, in its applications to the c-map, the one-parameter family of one-loop deformed Ferrara–Sabharwal metrics \(g_\text {FS}^c\) can be studied in uniform fashion. This is due to the fact that, on the hyper-Kähler side, the deformation parameter c corresponds to the additive freedom in choosing a Hamiltonian for the circle action, which is easy to handle.
In this paper, we study the behavior of curvature tensors under the HK/QK correspondence. We make use of the point of view put forward by Macia and Swann [13], which builds on Swann’s twist construction [15], casting the HK/QK correspondence as a variation on this general method. The main advantage of this approach is that the twist construction gives explicit relations between certain tensor fields on both sides of the HK/QK correspondence.
In Sect. 2, we briefly recall the general twist formalism and its application to the HK/QK correspondence. Using these methods, we investigate how connections and curvature tensors change under the HK/QK correspondence in Sect. 3. This culminates in elegant expressions for the Levi-Civita connection and curvature of the quaternionic Kähler metric in terms of the hyper-Kähler data on the other side of the correspondence. Our formulas apply in particular to the quaternionic Kähler manifolds that arise from the c-map, whose curvature tensors have previously been studied in the physics literature [8] (see also [5] for curvature formulas in the special case of the so-called q-map).
In Sect. 4, we apply our results to a series of examples considered in [7]. There, we showed that, under the (one-loop deformed) c-map, automorphisms of the initial PSK manifold yield isometries of the resulting quaternionic Kähler metric. This leads to lower bounds on the degree of symmetry of one-loop deformed c-map spaces. In particular, applying the one-loop deformed c-map to a homogeneous PSK manifold results in a quaternionic Kähler metric of cohomogeneity at most one. By contrast, our curvature formula can be used to give upper bounds on the degree of symmetry. To demonstrate this, we consider a one-parameter deformation of the symmetric spaces \(SU(n+1,2)/S(U(n+1)\times U(2))\), which arise by applying the c-map to complex hyperbolic spaces, regarded as homogeneous PSK manifolds. Our curvature formula enables us to compute the norm of the curvature endomorphisms of these quaternionic Kähler metrics, which the HK/QK correspondence relates to a series of flat hyper-Kähler manifolds. This leads to a proof that these quaternionic Kähler manifolds are not locally homogeneous. In fact, combining this with our results in [7], we establish that the isometry group acts with cohomogeneity precisely one in this family of examples.
2 Twist construction and HK/QK correspondence
In this section, we describe the HK/QK correspondence as a variation on the twist construction [15], following Macia and Swann [13]. For a more detailed review, we refer the reader to [7].
2.1 Twists
The twist construction is a general method to produce new manifolds with (infinitesimal) torus actions out of others. In the following, we will restrict to free circle actions, since this is the case of interest for the HK/QK correspondence. Let N be a manifold endowed with a free circle action, generated by a vector field Z. Our goal is to construct another manifold, which carries a “twisted” circle action.
To this end, we first pick a closed, integral two-form \(\omega \) on N and construct a circle bundle \(\pi _N{:}\,P\rightarrow N\) equipped with a connection \(\eta \) with curvature \(\omega \). Now we ask for a lift of Z to P which preserves \(\eta \) and commutes with \(X_P\), the generator of the principal circle action on P. Such a lift exists if and only if Z is \(\omega \)-Hamiltonian, i.e. there exists a function \(f\in C^\infty (N)\) such that \(\iota _Z\omega =-{\mathrm {d}}f\). In this case, it is given by \(Z_P={\tilde{Z}}+ \pi _N^* f X_P\), where \({\tilde{Z}}\) denotes the \(\eta \)-horizontal lift of Z. We will always assume that f is nowhere-vanishing, so that \(Z_P\) is transversal to the horizontal distribution \(\mathcal {H}\,{:}{=}\,\ker \eta \subset TP\). Now we define the twist of N with respect to the twist data \((Z,\omega ,f)\) as \({\bar{N}}\,{:}{=}\,X/\langle Z_P\rangle \). Then P has the structure of a double fibration:

and the action of \(X_P\) pushes down to a vector field \(Z_{{\bar{N}}}\) on \({\bar{N}}\) which plays a dual role to Z.
Since both \(X_P\) and \(Z_P\) are transversal to \(\mathcal {H}\), we have pointwise identifications of the tangent spaces of both N and \({\bar{N}}\) with the horizontal subspaces of TP. This sets up a correspondence between tensor fields. On each space, we have a notion of horizontal lift to P for arbitrary tensor fields, induced by the usual horizontal lift on vector fields and the composition of pullback and restriction to \(\mathcal {H}\) for one-forms. We then say that tensor fields T on N and \(T'\) on \({\bar{N}}\) are \(\mathcal {H}\)-related, denoted \(T\sim _{\mathcal {H}}T'\), if their horizontal lifts agree. We may also call \(T'\) the twist of T—the twist data implicitly understood. Note, however, that the existence of a well-defined twist implicitly presumes Z-invariance of T (and, dually, \(Z_{{\bar{N}}}\)-invariance of \(T'\)), so the correspondence only makes sense for Z-invariant tensor fields.
This method of carrying invariant tensor fields from N over to \({\bar{N}}\), and vice versa, is compatible with tensor products and contractions and respects algebraic relations. However, it typically does not preserve differential conditions, introducing correction terms dependent on the twist data. For example, if \(\alpha \sim _{\mathcal {H}}\alpha '\) are differential forms, then \({\mathrm {d}}\alpha -f^{-1}\omega \wedge \iota _Z\alpha \sim _{\mathcal {H}}{\mathrm {d}}\alpha '\).
2.2 Elementary deformations and HK/QK correspondence
Let us now consider the case where \((N,g,\omega _1,\omega _2,\omega _3)\) is a (pseudo-)hyper-Kähler manifold and comes equipped with a rotating (circle) symmetry, that is, the generating vector field Z of the circle action satisfies \(L_Z g=L_Z \omega _1=0\), while \(L_Z\omega _2=\omega _3\) and \(L_Z\omega _3=-\omega _2\). We also assume that Z is \(\omega _1\)-Hamiltonian, i.e. \(\iota _Z\omega _1=-{\mathrm {d}}f_Z\), and that \(\omega _1\) is integral, so that \((Z,\omega _1,f_Z)\) can be used as twist data.
The resulting twist manifold will inherit an almost quaternion-Hermitian structure from N. However, the fundamental four-form, which is the twist of the Z-invariant parallel four-form \(\Omega =\sum _{j=1}^3\omega _j\wedge \omega _j\) on N, will fail to be parallel because of the general failure of the twist construction to preserve differential relations. This means that the twist manifold is not quaternionic Kähler.
Macia and Swann investigated how to deform the hyper-Kähler structure in order to produce a quaternionic Kähler manifold out of a hyper-Kähler manifold. To this end, they defined the notion of elementary deformations of such manifolds. An elementary deformation \(g_{\mathrm {H}}\) of the hyper-Kähler metric g with respect to a rotating symmetry Z (with \(\omega _1\)-Hamiltonian \(f_Z\)) is a new metric of the form
for smooth, nowhere-vanishing functions a, b on N. Note that the second term is equal to \(b\cdot g(Z,Z)g|_{{\mathbb {H}}Z}\), so we think of \(g_{\mathrm {H}}\) as resulting from a conformal scaling composed with an independent scaling along the quaternionic span of Z. In [13], Macia and Swann study the twists of elementary deformations and prove the following result:
Theorem 2.1
[13] Let \((N,g,\omega _j)\), \(j=1,2,3\), be a (pseudo-)hyper-Kähler manifold endowed with a rotating circle symmetry with \(\iota _Z\omega _1=-{\mathrm {d}}f_Z\). Then an elementary deformation \(g_{\mathrm {H}}\) of g with respect to Z twists to a (pseudo-)quaternionic Kähler metric on the twist manifold \({\bar{N}}\) if and only if the twist data are given by \((Z,\omega _{\mathrm {H}}\,{:}{=}\,k(\omega _1+{\mathrm {d}}\iota _Z g),f_{\mathrm {H}}\,{:}{=}\,k(f_Z+g(Z,Z)))\) and the elementary deformation is
where \(k,B\in {\mathbb {R}}{\setminus }\{0\}\) are constants.
In the following, we will only consider the elementary deformation given in the theorem, and will refer to it as the elementary deformation of g.
Remark 2.2
-
(i)
The constants k and B simply scale the curvature of P and the metric, respectively. In the following, we will set them to 1, and assume that \(\omega _1\) is integral. Nevertheless, there is a one-parameter freedom in the construction, which arises because we may add a constant to \(f_Z\). Thus, one actually obtains a one-parameter family of quaternionic Kähler metrics.
-
(ii)
In the case of interest for the c-map and its one-loop deformation, the resulting quaternionic Kähler metric is positive-definite [1].
2.3 Notation and some useful identities
In this section, we introduce some notation and derive a number of identities that will be useful to us in the following computations.
In the following, it will often be convenient to discuss the metric and its Kähler forms in uniform manner. Therefore, we introduce \(I_0\,{:}{=}\,{{\,\mathrm{id}\,}}\) and \(\omega _0\,{:}{=}\,g\), so that \(\omega _\mu (\cdot ,\cdot )=g(I_\mu \cdot ,\cdot )\), \(\mu =0,1,2,3\). We also set \(\alpha _\mu \,{:}{=}\,\iota _Z\omega _\mu \). In what follows, Greek indices will be understood to run from 0 to 3, while Latin indices run from 1 to 3.
We briefly discuss the relation between \(g_{\mathrm {H}}\) and g.
Definition 2.3
Define the endomorphism field \(\mathcal {K}:TN\rightarrow TN\) by \(g_{\mathrm {H}}(\mathcal {K} X,Y)=g(X,Y)\). Equivalently, regarding both \(g_{\mathrm {H}}\) and g as maps \(TN\rightarrow T^*N\), we have \(\mathcal {K}=g_{\mathrm {H}}^{-1}\circ g\).
Since \(\sum _\mu \alpha _\mu ^2=g(Z,Z)g|_{{\mathbb {H}}Z}\), we can rewrite the elementary deformation as follows:
This shows that \(\mathcal {K}|_{({\mathbb {H}}Z)^\perp }=f_Z\) and \(\mathcal {K}|_{{\mathbb {H}}Z}=\frac{f_Z^2}{f_{\mathrm {H}}}\).
Lemma 2.4
\(\mathcal {K}\) is self-adjoint with respect to g and commutes with each \(I_\mu \).
Proof
The above description of \(\mathcal {K}\) implies that
Indeed, the right-hand side restricts to the appropriate multiples of the identity on \({\mathbb {H}}Z\) and its orthogonal complement. Self-adjointness is easy to check. Now we compute
In passing to the second line, we made the substitution \(I_\lambda \mapsto I_\mu I_\lambda \) in the sum. We can do this without introducing any additional signs, because \(I_\lambda \) appears twice in the expression. \(\square \)
Now we study how g relates to the twisting form \(\omega _{\mathrm {H}}\).
Lemma 2.5
Denoting the Levi-Civita connection of g by D, the one-forms \(\alpha _\mu \,{:}{=}\,\iota _Z \omega _\mu \) satisfy
Proof
The first identity follows from Cartan’s formula and the Killing equation, while the second follows by applying Cartan’s formula and the fact that \(L_Z=D_Z-DZ\) on differential forms, remembering that each \(\omega _k\) is parallel. \(\square \)
Definition 2.6
We define the skew-symmetric (with respect to g) endomorphism field \(I_{\mathrm {H}}\,{:}{=}\,I_1+2DZ\).
By definition of \(\omega _{\mathrm {H}}\) and the first part of the above Lemma, we have \(\omega _{\mathrm {H}}(\cdot ,\cdot )=g(I_{\mathrm {H}}\cdot ,\cdot )\).
Using \(I_{\mathrm {H}}\) and the action of Z on \(\omega _k\), we deduce the following consequence of (2):
where \(\delta \) is the Kronecker delta symbol. Now we may sum over \(\mu \) to obtain the following identity:
To obtain the right-hand side, we substituted \(I_\mu \) for \(I_\mu I_1\) in the first terms (the same trick as in the proof of Lemma 2.4).
Lemma 2.7
\(I_{\mathrm {H}}\) commutes with each \(I_\mu \).
Proof
From \(L_Z\omega _1=0\), \(L_Z\omega _2=\omega _3\) and \(L_Z\omega _3=-\omega _2\) and the second line of (2), one obtains
Rearranging each line and using our definition of \(I_{\mathrm {H}}\), we can write this compactly as \(g(I_k I_{\mathrm {H}}A,B)=g(I_k I_{\mathrm {H}}B,A)\) for \(k=1,2,3\). We also have \(g(I_0 I_{\mathrm {H}}A,B)=-g(I_0 I_{\mathrm {H}}B, A)\), and in summary find
Now, we conclude with a short computation:
which implies the claim. \(\square \)
Remark 2.8
In fact, this line of reasoning shows that, given an arbitrary vector field Z on a hyper-Kähler manifold, the condition that \(I_1+2DZ\) defines a skew-symmetric endomorphism field which commutes with every \(I_\mu \) is equivalent to requiring that Z is an infinitesimal rotating symmetry.
2.4 General twisting formulae for connections and curvature
Before we can study the behavior of the Riemann curvature tensor under the HK/QK correspondence, we must understand how the Levi-Civita connection changes under elementary deformations and twists.
Lemma 2.9
Let \((N,g,\omega _k)\), \(k=1,2,3\) be a hyper-Kähler manifold endowed with a rotating circle action, and let \(g_{\mathrm {H}}\) be the elementary deformation of g (cf. Theorem 2.1). If D and \(D^{\mathrm {H}}\) denote the Levi-Civita connections of g and \(g_{\mathrm {H}}\), respectively, we have \(D^{\mathrm {H}}=D+S^{\mathrm {H}}\), where
for all vector fields A, B, C on N.
Proof
This follows from cyclically permuting the vector fields A, B, C in the identity
and taking the appropriate signed sum. \(\square \)
Definition 2.10
Let N be a manifold endowed with twist data, and let \(\nabla \) be a Z-invariant connection on N. We say that \(\nabla \) is \(\mathcal {H}\)-related to a connection \(\nabla '\) on the twist manifold if, for all Z-invariant vector fields \(A\sim _{\mathcal {H}}A'\), \(B\sim _{\mathcal {H}}B'\), we have \(\nabla '_{A'}B'\sim _{\mathcal {H}}\nabla _AB\).
Lemma 2.11
Let \((N,g_{\mathrm {H}})\) be a Riemannian manifold endowed with the twist data \((Z,\omega _{\mathrm {H}},f_{\mathrm {H}})\). Assume that \(g_{\mathrm {H}}\) is Z-invariant, and let \(g_{\mathrm {Q}}\) be the \(\mathcal {H}\)-related metric on the twist manifold \({\bar{N}}\). Denote the corresponding Levi-Civita connections by \(D^{\mathrm {H}}\) and \(D^{\mathrm {Q}}\). Then \(D^{\mathrm {Q}}\sim _{\mathcal {H}}D^{\mathrm {H}}+ S^{\mathrm {Q}}\), where
for arbitrary Z-invariant vector fields A, B, C.
Proof
We use the Koszul formula for \(D^{\mathrm {Q}}\) using vector fields \(A',B',C'\), \(\mathcal {H}\)-related to A, B, C:
We pull this function back to P and look for the function on N which pulls back to the same expression.
The first three terms are easily handled, using the compatibility of the twist construction with tensor products and contractions. However, for the remaining terms we must use the formula for twists of commutators of vector fields [15]:
We work out one of the terms explicitly, using tildes to denote horizontal lifts of vector fields on N and hats for horizontal lifts from \({\bar{N}}\):
This shows that
as claimed. \(\square \)
Combining the two lemmata, we see that, under the HK/QK correspondence, the Levi-Civita connection \(D^{\mathrm {Q}}\) of the quaternionic Kähler metric \(g_{\mathrm {Q}}\) is \(\mathcal {H}\)-related (in the sense of the previous lemma) to the connection \(\nabla ^S\,{:}{=}\,D+S^{\mathrm {H}}+S^{\mathrm {Q}}\), where D is the Levi-Civita connection of the hyper-Kähler metric g. Now we turn to the curvature:
Lemma 2.12
Let (N, g) be a manifold with twist data \((Z,\omega _{\mathrm {H}},f_{\mathrm {H}})\) such that g is invariant, and D the Levi-Civita connection, with curvature tensor R. Let \(\nabla =D+S\) be a Z-invariant connection on N and \(\nabla '\) the \(\mathcal {H}\)-related connection on the twist manifold, with curvature \(R^{\nabla '}\). Then, for Z-invariant vector fields \(A,B,C\sim _{\mathcal {H}}A',B',C'\), we have:
where T is the \({{\,\mathrm{End}\,}}(TM)\)-valued two-form given by
Proof
Using the curvature formula \(R(A,B)C =[\nabla _A,\nabla _B]C-\nabla _{[A,B]}C\), our definition of \(\mathcal {H}\)-relatedness for connections means that \([\nabla '_{A'},\nabla '_{B'}]C'\sim _{\mathcal {H}}[\nabla _A,\nabla _B]C\), while \(\nabla '_{[A',B']}C'\sim _{\mathcal {H}} \nabla _{[A,B]}C+\frac{1}{f_{\mathrm {H}}}\omega _{\mathrm {H}}(A,B)\nabla _Z C\). Since C is Z-invariant and D is torsion-free, we may rewrite \(\nabla _Z C=D_CZ+S_ZC\). \(\square \)
In the setting of the HK/QK correspondence, we use \(S=S^{\mathrm {H}}+S^{\mathrm {Q}}\), and will denote the curvature tensor of \(\nabla ^S\) by \(R^S\).
3 Main theorems
The formulae deduced in the previous section determine, in principle, the curvature of the quaternionic Kähler metric in terms of hyper-Kähler data. In their current form, however, they are not particularly useful because they are too complicated to allow for effective computations. The main complication arises from the repeated appearance of the tensor field S. Our goal in the following is to rewrite these expressions in a more usable form.
3.1 Formula for the Levi-Civita connection
We first study the Levi-Civita connection under the HK/QK correspondence, aiming to simplify the expression for \(S=S^{\mathrm {H}}+S^{\mathrm {Q}}\) given by (5) and (6).
Theorem 3.1
Let \((N,g,I_k)\) be a (pseudo-)hyper-Kähler manifold with Levi-Civita connection D, and rotating circle action generated by the vector field Z. Denote its image under the HK/QK correspondence by \(({\bar{N}},g_{\mathrm {Q}})\). Then the Levi-Civita connection \(D^{\mathrm {Q}}\) of \(g_{\mathrm {Q}}\) is \(\mathcal {H}\)-related to \(\nabla ^S=D+S\), where, in the notation of Sect. 2, we have
Proof
This is a long computation involving the identities derived in Sect. 2.3. Regarding both \(\iota _Zg_{\mathrm {H}}\otimes \omega _{\mathrm {H}}\) and \(D g_{\mathrm {H}}\) as linear maps \(\Gamma (TN^{\otimes 3})\rightarrow C^\infty (N)\), we may write
Recalling from Sect. 2.3 that \(\frac{f_Z^2}{f_{\mathrm {H}}}g_{\mathrm {H}}|_{{\mathbb {H}}Z}=g|_{{\mathbb {H}}Z}\) and making use of the shorthand \(g_\alpha =\sum _{\mu =0}^3(\alpha _\mu )^2\), we may rewrite the (0, 3)-tensor in the first parenthesis as
where the final step uses (2). Our next step is to rework the final two terms, which feature derivatives of Z. We have
and thus, using (2) and the fact that Z generates a rotating circle symmetry, we find
With this, we arrive at
We rewrite this as
Now, applying the endomorphism \(\mathcal {K}\) to the first argument will bring this to the form \(2f_Z^2g_{\mathrm {H}}(S^{\mathrm {H}}_AB+S^{\mathrm {Q}}_AB,C)\), from which we can read off \(S^{\mathrm {H}}_AB+S^{\mathrm {Q}}_AB\). Using the formula (1) for \(\mathcal {K}\), we find
Dividing by \(2f_Z^2\) and exchanging \(\mu \) and \(\lambda \) in the double summation, we obtain
Let us study the last line in detail. We use the fact that we can replace \(I_\lambda \) by \(I_\lambda I_1\) in the summation over \(\lambda \); this introduces no additional signs because \(I_\lambda \) appears twice in the expression. Therefore we can rewrite it as
where in the last step we used the fact that \(I^{-1}_k=-I_k\) for \(k\in \{1,2,3\}\), while \(I_0^{-1}=I_0\). The second line cancels out immediately in the expression for \(S^{\mathrm {H}}_AB+S^{\mathrm {Q}}_AB\), leaving us with
Once again, we focus on the last line. First, we replace \(I_\mu \) by \(I_\mu I_1\) (as before, no additional signs appear), and consider the expression \(\sum _\lambda g(I_\lambda I_1 Z,A)g(I_\lambda I_\mu I_1 Z,B)\), for fixed \(\mu \). When \(\mu =0\), this is manifestly symmetric in (A, B). If \(\mu \ne 0\), however, the substitution \(I_\lambda \mapsto I_\lambda I_\mu \) yields
which shows that the expression is antisymmetric in (A, B). Therefore, all terms from the last line except those corresponding to \(\mu =0\) vanish, but for \(\mu =0\) they cancel in the expression for \(S^{\mathrm {H}}_AB +S^{\mathrm {Q}}_AB\). In summary, we have shown:
This completes the proof. \(\square \)
Remark 3.2
Note that, in order to arrive at this expression, we have thoroughly mixed the contributions of \(S^{\mathrm {H}}\) and \(S^{\mathrm {Q}}\). Thus, it seems that treating both the elementary deformation and the twist simultaneously is crucial.
3.2 Curvature formula
As explained in Sect. 2.4, the curvature tensor \(R^{\mathrm {Q}}\) of the quaternionic Kähler metric \(g_{\mathrm {Q}}\) on \({\bar{N}}\) is \(\mathcal {H}\)-related to \({\tilde{R}}\,{:}{=}\,R^S-\frac{1}{f_{\mathrm {H}}}\omega _{\mathrm {H}}\otimes (DZ+S_Z)\), where S is given by Theorem 3.1, and \(R^S\) is the curvature of \(\nabla ^S=D+S\), where D is the Levi-Civita connection of the hyper-Kähler metric g on N.
To state the final result, it is convenient to introduce the following pieces of notation:
Definition 3.3
-
(i)
We define the Kulkarni–Nomizu map

by setting

for arbitrary vector fields A, B, C, X.
-
(ii)
We define a second map

by setting

For (0, 2)-tensors \(\alpha \) and \(\beta \), we set  and analogously define
and analogously define  . Note that our first definition then reduces to the usual Kulkarni–Nomizu product.
. Note that our first definition then reduces to the usual Kulkarni–Nomizu product.
It is well-known that the Kulkarni–Nomizu product of two symmetric bilinear forms is an algebraic curvature tensor, i.e. possesses the algebraic symmetries of a (lowered) Riemann curvature tensor. When applied to two-forms, however, the resulting (0, 4)-tensor generally fails to satisfy the Bianchi identity. This is remedied by  , which constructs an algebraic curvature tensor out of two-forms.
, which constructs an algebraic curvature tensor out of two-forms.
Our main result is the following formula, which completely determines the curvature of the quaternionic Kähler metric:
Theorem 3.4
The Riemann curvature of the quaternionic Kähler metric \(g_{\mathrm {Q}}\) on \({\bar{N}}\) is \(\mathcal {H}\)-related to \({\tilde{R}}\), which is given by the expression

where R is the curvature tensor of the initial (pseudo-)hyper-Kähler metric on N, and A, B, C, X are arbitrary vector fields.
Remark 3.5
Each \(I_k\), \(k=1,2,3\), is skew with respect to \(g_{\mathrm {H}}\), and the properties of \(I_{\mathrm {H}}\) imply that \(\omega _{\mathrm {H}}(I_k\cdot ,\cdot )\) is a symmetric bilinear form. Thus, each individual term in the expression for \({\tilde{R}}\) is an algebraic curvature tensor.
We divide the proof up into two steps. First, we give expressions for the various terms that make up \({\tilde{R}}\) [cf. (7)]. We do this in the form of three lemmata. Then we sum them all up and further simplify to obtain the final curvature formula.
Lemma 3.6
With S as in Theorem 3.1 and D the Levi-Civita connection of g, we have
for arbitrary vector fields A, B, C on N.
Proof
We first compute the covariant derivative of S, and anti-symmetrize later:
where, in the second step, we used the definitions of \(f_Z\) and \(f_{\mathrm {H}}\) as Hamiltonians, replaced \(I_\mu \) by \(I_\mu I_1\) in some of the terms, and used \(DZ=\frac{1}{2}(I_{\mathrm {H}}-I_1)\) on the final term. We then grouped the terms according to their prefactors.
After anti-symmetrizing in (A, B), some of the terms involving covariant derivatives of Z can be simplified considerably. Firstly,
Secondly, we may apply the identity (3) to the first term on the last line.
Taking these two points into account, the claimed expression appears directly upon anti-symmetrization. \(\square \)
Lemma 3.7
In the same notation as the previous lemma we have
Proof
Before getting started, we rewrite the formula for S by replacing \(I_\mu \) by \(I_\mu I_1\) in the second part, so that we have
Now we apply this formula, replacing B by \(S_BC\):
We can rewrite all terms of the form \(g(I_\mu X,I_\lambda Y)I_\mu W\) by replacing \(I_\mu \) by \(I_\lambda I_\mu \) as follows:
Doing this several times, and also exchanging the labels \(\mu \) and \(\lambda \) in some terms, we obtain
We note that, among the terms multiplied by \(f_Z^{-2}\), the second and third combine into an expression symmetric in (A, B). The same is true for the first and third terms which come with a factor \((f_Z f_{\mathrm {H}})^{-1}\), Antisymmetrizing, these cancel out and we find
The final two lines can be further simplified: Since \(I_{\mathrm {H}}\) is skew, \(g(I_\mu I_{\mathrm {H}}A,B)\) is symmetric in (A, B) unless \(\mu =0\), in which case it is anti-symmetric. Therefore, only this terms survives. Furthermore, \(g(I_\mu I_1 Z,Z)\) vanishes unless \(\mu =1\). We are now left with
which is the expression we were after. \(\square \)
This determines \(R^S\). Now, there is one more term to compute, namely \(-\frac{1}{f_{\mathrm {H}}}\omega _{\mathrm {H}}\otimes (DZ+S_Z)\). Since we understand \(\omega _{\mathrm {H}}\) well, we only need to study the second part:
Lemma 3.8
The (1, 1)-tensor field \(DZ+S_Z\) is given by the following expression:
Proof
This is the result of a relatively short computation:
In the second step, we once again used that \(g(I_\mu I_1 Z,Z)\) vanishes unless \(\mu =1\), while the final step used \(f_{\mathrm {H}}=f_Z+g(Z,Z)\). \(\square \)
Proof of Theorem 3.4
Now that we have computed all the individual pieces that make up \({\tilde{R}}\), we put them all together. We group terms according to their prefactors, and obtain the following expression:
Note that the final terms of the expressions computed in Lemmas 3.6 and 3.8 canceled each other out.
Now consider the terms proportional to \((f_Zf_{\mathrm {H}})^{-1}\). The first two terms cancel, and we are left with
where, to get the last equality, we used \(I_{\mathrm {H}}=I_1+2DZ\) and substituted \(I_\mu I_1\) for \(I_\mu \) in the last line. Now we compare to other terms from the expression for \({\tilde{R}}\). Observe that the entire second line is canceled out, as are the terms featuring DZ on the first line.
This leaves us with
Now we turn to the first group of terms, those multiplied by \(f_{\mathrm {H}}^{-2}\). After splitting off the case \(\lambda =0\) in the double summation, we can simplify:
The \(f_Z^{-2}\)-terms may be simplified analogously. This yields:
Now, making the substitutions \(I_\lambda \mapsto I_\lambda ^{-1}\) and \(I_\mu \mapsto I_\mu I_\lambda \), we obtain
where the last step consists of replacing \(I_\lambda \) by \(I_\lambda I_1\) and recalling \(g_\alpha \,{:}{=}\,\sum \alpha _\mu ^2\).
With these simplifications, we have arrived at
where we used that R(A, B) and \(I_{\mathrm {H}}\) both commute with each \(I_\mu \) in the last step.
Recalling (1), we have
Applying this to the vector fields R(A, B)C, \(I_{\mathrm {H}}A\) and \(I_{\mathrm {H}}B\) and using that \(I_\mu \) and \(\mathcal {K}\) commute (cf. Lemma 2.4), we find
To obtain the expression given in the statement of the theorem, we contract with an auxiliary vector field X, and split off the case \(\mu =0\) in the summations:

In the final step, we grouped terms into algebraic curvature tensors. This finishes the proof. \(\square \)
A well-known theorem of Alekseevsky [3] asserts that the curvature tensor of any quaternionic Kähler manifold \({\bar{N}}\) is of the form \(R^{\mathrm {Q}}=\nu R_0+R_1\), where \(\nu =\frac{{{\,\mathrm{scal}\,}}}{4n(n+2)}\) is the reduced scalar curvature (n being the quaternionic dimension), \(R_0\) is the curvature tensor of quaternionic projective space \({\mathbb {H}}{\mathrm {P}}^n\) and \(R_1\) (or rather its lowered version) is an algebraic curvature tensor of hyper-Kähler type. The latter condition means that, for any two vector fields X and Y, the endomorphism \(R_1(X,Y)\) commutes with any section of the rank three bundle \(Q\subset {{\,\mathrm{End}\,}}T{\bar{N}}\) defining the quaternionic Kähler structure. The tensor \(R_1\) is sometimes called the quaternionic Weyl curvature.
With respect to its symmetric metric \(g_0\) of reduced scalar curvature 1, the curvature of \({\mathbb {H}}{\mathrm {P}}^n\) is locally given by the expression

where \(\{J_1,J_2,J_3\}\) is a local orthonormal frame for Q. Comparing to Theorem 3.4, this clearly corresponds to the second line of our curvature formula (note that \(\nu =-1\)). We can check explicitly that the remaining terms are of hyper-Kähler type.
Lemma 3.9
The algebraic curvature tensor \(R_1\) on \({\bar{N}}\), determined by the relation

is of hyper-Kähler type.
Proof
We need to check that \(R_1\) commutes with any section of Q. Since this is a pointwise condition, it suffices to check the assertion on a frame, which we may transfer to the hyper-Kähler side. There, we can work with respect to the convenient frame provided by \(\{I_1,I_2,I_3\}\). Thus, it suffices to prove that the \(\mathcal {H}\)-related tensor field on N commutes with each \(I_k\). This is obviously the case for the first term, which is just the hyper-Kähler curvature tensor of g (up to a pointwise scaling). For the remaining terms, we have:

where, in the final step, we replaced each instance of \(I_\mu \) by \(I_j^{-1}I_\mu \) in the summation. This suffices to prove the claim, since for any endomorphism E and vector fields \(X,I_kY\), we have \(g([E,I_k]X,I_kY)=g(E I_k X,I_k Y)-g(EX,Y)\). \(\square \)
Thus, our results refine Alekseevsky’s decomposition by providing a precise expression for the quaternionic Weyl curvature.
4 Application: curvature norm
The main use of the curvature formula is to enable us to compute curvature quantities for quaternionic Kähler manifold that arise via the HK/QK correspondence. This approach is most effective if the curvature of the corresponding hyper-Kähler manifold is as simple as possible. Here, we study the extreme case where its curvature tensor vanishes identically.
For any non-negative integer n, we consider the manifold
where \(c\ge 0\) is a real constant, and equip it with the standard flat (pseudo-)hyper-Kähler structure induced by
The (inverse of the) standard action of \({\mathbb {C}}^*\) induces a rotating circle symmetry, generated by the vector field
It preserves \(\omega _1\), with Hamiltonian function
which is everywhere positive for \(c\ge 0\).
To apply the HK/QK correspondence, we consider the elementary deformation \(g_{\mathrm {H}}\) of the metric and the twist data \((Z,\omega _{\mathrm {H}},f_{\mathrm {H}})\), where
and
Lemma 4.1
On every \(N_n\), the endomorphism fields \(\mathcal {K}\), \(I_\mu \), \(\mu =0,1,2,3\), and \(I_{\mathrm {H}}\) all commute, and \(I_{\mathrm {H}}^2=-{{\,\mathrm{id}\,}}\).
Proof
We already know that \(\mathcal {K}\) and \(I_{\mathrm {H}}\) each commute with every \(I_\mu \), so all that remains is to prove that \(I_{\mathrm {H}}\) commutes with \(\mathcal {K}\). This will follow once we prove that \(I_{\mathrm {H}}\) preserves the subbundle \({\mathbb {H}}Z\) of TN, as well as its orthogonal complement \(({\mathbb {H}}Z)^\perp \), since \(\mathcal {K}\) restricts to multiples of the identity on these complementary subbundles.
In fact, it is enough to check that \(g(I_{\mathrm {H}}Z,X)=0\) for any \(X\in \Gamma (({\mathbb {H}}Z)^\perp )\subset {\mathfrak {X}}(N)\). This follows from the fact that \(I_{\mathrm {H}}\) is skew with respect to g and commutes with each \(I_\mu \), and that each \(I_\mu \) acts g-orthogonally. We find
where we used the fact that Z is a Killing field. Using the explicit coordinate expressions given for g and Z, we find \(g(Z,Z)=-\Big (|z_0 |^2-\sum _{j=1}^n|z_j |^2\Big )\) and consequently
This shows that \(X(g(Z,Z))=0\), proving our claim. Thus, \(\mathcal {K}\), \(I_{\mathrm {H}}\) and \(I_k\) all commute in this case. The fact that \(I_{\mathrm {H}}^2=-{{\,\mathrm{id}\,}}\) can be seen by comparing the coordinate expressions (10) and (11) for \(\omega _1\) and \(\omega _{\mathrm {H}}\). \(\square \)
It is known that, for \(c=0\), the HK/QK correspondence maps this flat hyper-Kähler manifold to the non-compact symmetric space \({\bar{N}}_n=\frac{SU(n+1,2)}{S(U(n+1)\times U(2))}\). For \(c>0\), the resulting quaternionic Kähler metric is known to be complete [6], but its isometry group is not well-understood. In [7], we use general arguments to prove that it acts by cohomogeneity at most one. In the following, we will show that this result is sharp, i.e. that the metric is of cohomogeneity exactly one.
Concretely, we will use our curvature formula to compute the norm of the curvature, regarded as a self-adjoint endormorphism \(\mathcal {R}^{\mathrm {Q}}:\bigwedge ^2 T{\bar{N}}_n\rightarrow \bigwedge ^2 T{\bar{N}}_n\) (up to a factor of four, this is the same as the so-called Kretschmann scalar). With respect to an orthonormal frame \(\{e_a\}\) of \(T{\bar{N}}_n\), this curvature invariant can be expressed as follows:
where the summation runs over the corresponding orthonormal basis of \(\bigwedge ^2T{\bar{N}}_n\).
Due the compatibility of the twist construction with respect to tensor products and contractions, we can compute this quantity on the hyper-Kähler side of the correspondence:
where \(\{e'_a\}\) is now an orthonormal frame with respect to \(g_{\mathrm {H}}\). Our first step is to write this function invariantly. Using the metric \(g_{\mathrm {H}}\), we can extend the definition of the Kulkarni–Nomizu product  to endomorphisms of \(TN_n\). Indeed, for \(E,F\in {{\,\mathrm{End}\,}}TN_n\) and vector fields A, B, C, X, we may define
to endomorphisms of \(TN_n\). Indeed, for \(E,F\in {{\,\mathrm{End}\,}}TN_n\) and vector fields A, B, C, X, we may define  via
via

Of course, we are mostly interested in the case where E and F are self-adjoint with respect to \(g_{\mathrm {H}}\) (so that we obtain an algebraic curvature tensor). For skew-adjoint endomorphisms E, F, we may analogously define  . This notation allows us to succinctly express the operator \(\tilde{\mathcal {R}}{:}\,\bigwedge ^2TN_n\rightarrow \bigwedge ^2TN_n\) associated to \({\tilde{R}}\):
. This notation allows us to succinctly express the operator \(\tilde{\mathcal {R}}{:}\,\bigwedge ^2TN_n\rightarrow \bigwedge ^2TN_n\) associated to \({\tilde{R}}\):

Theorem 4.2
Let \(\mathcal {R}^{\mathrm {Q}}\) denote the curvature endomorphism of the quaternionic Kähler manifold \(({\bar{N}}_{n-1},g_{\mathrm {Q}})\), \(n\ge 1\), obtained by twisting \((N_{n-1},g_{\mathrm {H}})\) with respect to the twist data \((Z,\omega _{\mathrm {H}},f_{\mathrm {H}})\). Then
Proof
In this family of examples, the curvature \(\mathcal {R}\) of the hyper-Kähler metric vanishes. We can therefore express the norm of \(\mathcal {R}^{\mathrm {Q}}\) as follows:

Thus, we have to compute three types of terms. The following lemma reduces this to the computation of traces of various compositions of the endomorphisms involved.
Lemma 4.3
Let h be a (pseudo-)Riemannian metric on a manifold N, let E, F be self-adjoint endomorphisms of TN and let K, L be skew-adjoint endomorphisms of TN, with respect to h. Then
-
(i)
 .
. -
(ii)
 .
. -
(iii)
 .
.
Proof
Let \(\{e_a\}\) be an orthonormal basis for h with \(h(e_a,e_a)=\epsilon _a\in \{\pm 1\}\).
-
(i)
Directly from the definition of
 , we have
, we have 
Note that this part of the lemma does not use any properties of E and F.
-
(ii)
The proof proceeds analogously, but there are several extra terms:

Note that we used the fact that K and L are skew in arriving at the penultimate expression.
-
(iii)
Again, this is a straightforward computation:

where we used both self-adjointness of E and skew-adjointness of K.
\(\square \)
Now we must compute the relevant traces:
Lemma 4.4
On \(N_{n-1}\), the following trace identities hold for any non-negative integer m and any \(k\in \{1,2,3\}\):
-
(i)
\({{\,\mathrm{tr}\,}}(\mathcal {K}^m)=4\Big ((n-1)f_Z^m+ \frac{f_Z^{2m}}{f_{\mathrm {H}}^m}\Big )\).
-
(ii)
\({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_k)=0\).
-
(iii)
\({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_{\mathrm {H}})=0\).
-
(iv)
\({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_{\mathrm {H}}I_k)=0\).
Proof
Firstly, since \(\mathcal {K}\) restricts to multiples of the identity on \({\mathbb {H}}Z\) and its orthogonal complement, it is easy to compute the traces of its powers:
In order to see that both \({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_k)\) vanishes, we recall that \(\mathcal {K}\) is self-adjoint with respect to g, while \(I_k\) is skew, and that \(\mathcal {K}\) and \(I_k\) commute. This means that \(\mathcal {K}^m I_k\) is skew, and has vanishing trace. The same argument applies to \({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_{\mathrm {H}})\). Finally, we consider \({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_{\mathrm {H}}I_j)\). We know that \(I_j=I_k I_l\), where (j, k, l) is a cyclic permutation of (1, 2, 3). This, combined with the fact that the endomorphisms all commute, yields
whence \({{\,\mathrm{tr}\,}}(\mathcal {K}^m I_{\mathrm {H}}I_j)=0\). \(\square \)
Since, in this class of examples, \(\mathcal {K}\), \(I_{\mathrm {H}}\) and \(I_k\) all commute and \(I_{\mathrm {H}}^2=I_k^2=-{{\,\mathrm{id}\,}}\), any trace of a composition of these endomorphisms can be reduced to one of the four traces computed in the above lemma. That means that we are now in a position to compute the curvature norm.
This was precisely the claim. \(\square \)
Through the HK/QK correspondence, the function \(2f_Z\) corresponds to a global coordinate function on \({\bar{N}}_{n-1}\), conventionally denoted by \(\rho \) (and \(2f_{\mathrm {H}}=-(\rho +2c)\)). We have therefore just proven that \(\Vert \mathcal {R}^{\mathrm {Q}} \Vert ^2\) is a function only of \(\rho \). This was to be expected in light of our results in [7], where we showed that the isometry group of \(({\bar{N}}_{n-1},g^c_\text {FS})\) acts transitively on the level sets of \(\rho \).
It follows from a short computation that \(\Vert \mathcal {R}^{\mathrm {Q}} \Vert ^2\) is an injective function of \(\rho \) for any \(c>0\), proving that the isometry group must preserve its level sets (for more details, see section 4 of [7]). All this is summarized in the following theorem, which is also stated in the above-mentioned paper.
Theorem 4.5
The metrics \(g_\text {FS}^{c>0}\) on \({\bar{N}}_n\) are of cohomogeneity one. In particular, for every non-negative integer n, the quaternionic Kähler manifold \(({\bar{N}}_n,g^{c>0}_\text {FS})\) is not a locally homogeneous space. \(\square \)
References
Alekseevsky, D.V., Cortés, V., Dyckmanns, M., Mohaupt, T.: Quaternionic Kähler metrics associated with special Kähler manifolds. J. Geom. Phys. 92, 271–87 (2015)
Alekseevsky, D.V., Cortés, V., Mohaupt, T.: Conification of Kähler and hyper-Kähler manifolds. Commun. Math. Phys. 324, 637–55 (2013)
Alekseevsky, D.V.: Riemannian spaces with unusual holonomy groups. Funkt. Anal. Priloz. 2, 1–10 (1968)
Alexandrov, S., Persson, D., Pioline, B.: Wall-crossing, Rogers Dilogarithm, and the QK/HK correspondence. J. High Energy Phys. 1112, 027 (2011)
Cortés, V., Dyckmanns, M., Jüngling, M., Lindemann, D.: A class of cubic hypersurfaces and quaternionic Kähler manifolds of co-homogeneity one. arXiv:1701.07882 [math.DG]. To appear in Asian J. Math. Accepted (March 13, 2020)
Cortés, V., Dyckmanns, M., Suhr, S.: Completeness of projective special Kähler and quaternionic Kähler manifolds. In: Special Metrics and Group Actions in Geometry, pp. 81–106. Springer, Cham (2017)
Cortés, V., Saha, A., Thung, D.: Symmetries of Quaternionic Kähler Manifolds with \(S^1\)-symmetry. arXiv:2001.10026 [math.DG]. To appear in Trans. Lond. Math. Soc. Accepted (December 21, 2020)
de Wit, B., Vanderseypen, F., van Proeyen, A.: Symmetry structure of special geometries. Nucl. Phys. B 400, 463–521 (1993)
Ferrara, S., Sabharwal, S.: Quaternionic manifolds for type II superstring vacua of Calabi–Yau spaces. Nucl. Phys. B 332, 317–332 (1990)
Haydys, A.: HyperKähler and quaternionic Kähler manifolds with \(S^1\)-symmetries. J. Geom. Phys. 58, 293–306 (2008)
Hitchin, N.: Quaternionic Kähler moduli spaces. In: Riemannian Topology and Geometric Structures on Manifolds, pp. 49–61. Birkhäuser, Boston (2009)
Hitchin, N.: On the hyperkähler/Quaternion Kähler correspondence. Commun. Math. Phys. 324, 77–106 (2013)
Macia, O., Swann, A.: Twist geometry of the c-map. Commun. Math. Phys. 336, 1329–57 (2015)
Robles Llana, D., Saueressig, F., Vandoren, S.: String loop corrected hypermultiplet moduli spaces. J. High Energy Phys. 0603, 081 (2006)
Swann, A.: Twisting Hermitian and hypercomplex geometries. Duke Math. J. 155, 403–31 (2010)
Acknowledgements
This work was supported by the German Science Foundation (DFG) under the Research Training Group 1670, and under Germany’s Excellence Strategy—EXC 2121 “Quantum Universe”—390833306.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cortés, V., Saha, A. & Thung, D. Curvature of quaternionic Kähler manifolds with \(S^1\)-symmetry. manuscripta math. 168, 35–64 (2022). https://doi.org/10.1007/s00229-021-01294-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-021-01294-7


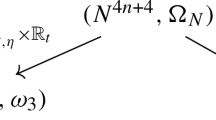





 .
. .
. .
. , we have
, we have 

