Abstract
Differential systems of pure Gaussian type are examples of D-modules on the complex projective line with an irregular singularity at infinity, and as such are subject to the Stokes phenomenon. We employ the theory of enhanced ind-sheaves and the Riemann–Hilbert correspondence for holonomic D-modules of D’Agnolo and Kashiwara to describe the Stokes phenomenon topologically. Using this description, we perform a topological computation of the Fourier–Laplace transform of a D-module of pure Gaussian type in this framework, recovering and generalizing a result of Sabbah.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of D-modules with irregular singularities has recently experienced new impulses by a remarkable result of D’Agnolo and Kashiwara, the Riemann–Hilbert correspondence for holonomic D-modules (see [5]). It states that on a complex manifold X there is a fully faithful functor
associating to any holonomic D-module an object in the category of enhanced ind-sheaves from which one can reconstruct the D-module. The construction of the target category is technical, but it is related to sheaf theory of vector spaces and hence of a topological nature. The theory has since been applied to the study of Stokes phenomena and Fourier–Laplace transforms (see e.g. [4, 6, 13, 21]). Other recent approaches to the study of Fourier transforms of Stokes data have been developed in [24, 27].
In their original article [5, Sect. 9.8], the authors give an outlook on a topological study of the Stokes phenomenon of a D-module. In this paper, we develop rigorously these ideas in the case of D-modules of pure Gaussian type \({\mathcal {M}}\), meromorphic connections on \({\mathbb {P}}={\mathbb {P}}^1({\mathbb {C}})\) with a unique (and irregular) singularity at \(\infty \) and exponential factors \(-\frac{c}{2z'}\) in the corresponding Levelt–Turrittin decomposition (for \(z'\) a local coordinate at \(\infty \)). In this precise form they were studied by Sabbah in [30] using Deligne’s approach of Stokes-filtered local systems (see [8, 23, 29]) in order to find a transformation rule for the Stokes data attached to such a module. Similar (and more general) systems of differential equations with exponents of pole order 2 have already been introduced by Boalch in [2, 3] (where they are called “type 3” connections) with a different motivation. In the latter article, the author shows that a large class of certain quiver varieties arises as moduli spaces (wild character varieties) of such systems and uses this result to construct symplectic isomorphisms between these moduli. From the perspective of the Fourier–Laplace transform, the Gaussian case is especially interesting since this class is invariant: The Fourier–Laplace transform of this kind of system has again a formal type with exponential factors of pole order 2. Moreover, studying these connections is a natural step further, given that the theory of enhanced ind-sheaves has already proved to be useful in the case of exponents of pole order 1 (cf. e.g. [4]), which play a prominent role in mirror symmetry.
It is the main purpose of the present article to reconstruct the results of [30] about the Fourier–Laplace transform of Stokes data with the new methods and to show how these computations can without much effort be adapted to more general cases. This research is based upon the dissertation [11].
Let us briefly outline the main ideas and the structure of the article:
In the second section, we recall the basic notation and results from the theories of D-modules and enhanced ind-sheaves.
The third section then collects well-known results about Stokes phenomena: Classically, the Stokes phenomenon manifests itself in the fact that a formal solution of a differential equation has different convergent asymptotic lifts in different sectors around an irregular singularity. In the language of D-modules, this is expressed by the statement that the formal Levelt–Turrittin decomposition can locally (on sufficiently small sectors) be lifted to an analytic decomposition. By the Riemann–Hilbert correspondence, this induces a decomposition of the associated topological object \({\mathcal {S}}ol_{X}^\mathrm {E}({\mathcal {M}})\) (Proposition 3.1).
In Sects. 4–7, we introduce the notion of D-modules of pure Gaussian type in the language of D-modules and describe step-by-step the topological object of enhanced solutions \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) of such a D-module \({\mathcal {M}}\): Starting from the Stokes phenomenon, which yields a direct sum decomposition on small sectors, we discuss how large the radius and angular width of these sectors may be, introducing notions like Stokes multipliers in this framework. It will finally turn out (Theorem 7.2) that \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) is described by an ordinary sheaf on \({\mathbb {C}}\times {\mathbb {R}}\), which in turn is determined by a small set of linear algebra data, the Stokes data. In the spirit of [30], we present Stokes data and a Riemann–Hilbert correspondence for D-modules of pure Gaussian type in Sect. 8.
We will then use this description to compute the Fourier–Laplace transform of a D-module of pure Gaussian type and describe its Stokes data in terms of the Stokes data of the original system. This computation, too, will involve (constructible) sheaves rather than enhanced ind-sheaves in the end and will therefore reduce to calculations in algebraic topology (cohomology groups with compact support). For this purpose, we recall the notions of Fourier–Laplace transform for D-modules and enhanced ind-sheaves in Sect. 9 before we carry out our computations in the two final sections.
Compared to the approach via Stokes-filtered local systems, our considerations have various advantages: Although the theory is a priori more involved, it turns out that the actual computations to be made are computations in the theory of sheaves of vector spaces and algebraic topology. In particular, one does not need to deal with filtrations, which are often more intricate to handle. A particularly nice feature of this new approach in dealing with integral transforms is the fact that the functor \({\mathcal {S}}ol_{X}^\mathrm {E}\), which we use for translating between D-modules and topology, is compatible with proper direct images. In the context of Stokes filtrations, the Riemann–Hilbert functor does not have this property. Instead, it was necessary to deal with sequences of blow-ups to compute direct images (cf. [10, 30]), using a result of Mochizuki [25]. Finally, our method of computation needs less input in the following sense: By results like the stationary phase formula (see [6, 28]), we could know a priori that the Fourier–Laplace transform of a D-module of pure Gaussian type is again of pure Gaussian type, and we can explicitly write down the exponential factors of the Fourier–Laplace transform. However, this a-priori-knowledge does not enter our arguments, but is rather obtained as a by-product of our computations automatically.
Our main results are the following: We first recover a theorem of Sabbah [30, Theorem 4.2], who proved an explicit transformation rule for Stokes data in the case where all the parameters c appearing in the exponential factors share the same argument. In Theorem 10.1, we prove such a transformation rule for enhanced sheaves of pure Gaussian type, which as a corollary (Corollary 10.2) yields the result from loc. cit. We then show how such a result can be generalized to situations with weaker assumptions on the parameters. Therefore, we treat a more general case (Theorem 11.2), illustrating how the methods of the above theorem are naturally adapted to other situations.
2 Enhanced ind-sheaves and D-modules
Let X be a complex manifold. We denote the field of complex numbers by \({\mathbf {k}}={\mathbb {C}}\). We mainly use the notation of [5, 17].
Denote by \({\mathcal {D}}_X\) the sheaf of rings of differential operators on X, by \(\mathrm {Mod}({\mathcal {D}}_{X})\) the category of (left) \({\mathcal {D}}_X\)-modules and by \(\mathrm {D}^\mathrm {b}({\mathcal {D}}_{X})\) its bounded derived category. Let \(\mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{X})\) (resp. \(\mathrm {D}^\mathrm {b}_\mathrm {hol}({\mathcal {D}}_{X})\)) be the full subcategory of objects which are holonomic (resp. have holonomic cohomologies). (We refer to [1, 12, 15] for details on D-modules).
In [5], the authors introduced the triangulated category \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{X})\) of enhanced ind-sheaves on X as a quotient of the derived category of ind-sheaves on \(X\times ({\mathbb {R}}\sqcup \{\pm \infty \})\). Together with the convolution product \(\mathbin {\overset{+}{\otimes }}\) it is a tensor category, and an important object is

They proved the following result, which is a generalization of the classical Riemann–Hilbert correspondence (see [14]) to not necessarily regular holonomic D-modules.
Theorem 2.1
(cf. [5, Theorem 9.5.3]]) The functor of enhanced solutions
is fully faithful.
By this result, the object \({\mathcal {S}}ol_{X}^\mathrm {E}({\mathcal {M}})\) is the topological counterpart of a D-module \({\mathcal {M}}\), containing all the information about \({\mathcal {M}}\). In particular, it must encode the Stokes phenomenon.
We refer to [5] for further details on enhanced ind-sheaves (see also [7, 16, 20]). Let us only recall the bifunctor (cf. [5, Definition 4.5.2])
where \(\pi :X\times {\mathbb {R}}\rightarrow X\) is the projection. This functor enables us to consider the “restriction” \(\pi ^{-1}{\mathbf {k}}_Z\otimes K\) of an enhanced ind-sheaf \(K\in \mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{X})\) to a locally closed subset \(Z\subseteq X\). (One considers this object rather than the inverse image along the embedding since it keeps track of the behaviour at the boundary of Z). In this way, one can use gluing techniques similar to sheaf theory in \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{X})\) by carrying over sequences of sheaves like
for two closed subsets \(Z_1,Z_2\subseteq X\). Thus, given a description of an enhanced ind-sheaf on two sets, one can obtain a description on their union. In fact, although the third object of a distinguished triangle is generally unique up to (non-unique) isomorphism only, uniqueness will always be guaranteed in our constructions (by [19, Proposition 10.1.17] or [9, Corollary IV.1.5]).
2.1 Enhanced sheaves
There is a natural functor \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{X\times {\mathbb {R}}})\rightarrow \mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{X})\), and we consider sheaves on \(X\times {\mathbb {R}}\) as enhanced ind-sheaves through this functor. Objects of \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{X\times {\mathbb {R}}})\) will be called enhanced sheaves on X. (Note that other authors usually define the category of enhanced sheaves as a certain subcategory of \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{X\times {\mathbb {R}}})\), cf. [4, 6]. We will not introduce it here, although we actually work in this subcategory).
There is a convolution product on \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{X\times {\mathbb {R}}})\) defined by

where the maps \(\mu ,q_1,q_2:X\times {\mathbb {R}}^2\rightarrow X\times {\mathbb {R}}\) are given by \(\mu (x,t_1,t_2)=(x,t_1+t_2)\), \(q_1(x,t_1,t_2)=(x,t_1)\) and \(q_2(x,t_1,t_2)=(x,t_2)\). Via the natural functor above it corresponds to the convolution functor \(\mathbin {\overset{+}{\otimes }}\) for enhanced ind-sheaves.
For a locally closed subset \(Z\subseteq X\), we will write  .
.
2.2 Exponential enhanced (ind-)sheaves
We recall here the definition of enhanced exponentials as introduced in [6].
Let \(U\subseteq X\) be an open subset and let \(\varphi ,\varphi ^-,\varphi ^+:U\rightarrow {\mathbb {R}}\) be continuous functions. Let moreover \(Z\subseteq U\) be locally closed with \(\varphi ^-(x)\le \varphi ^+(x)\) for any \(x\in Z\).
We consider the enhanced sheaves

where we write for short  , and similarly
, and similarly  .
.
Furthermore, we consider the enhanced ind-sheaves

The following lemma is an easy observation.
Lemma 2.2
If \(U\subseteq X\) is open, \(\varphi ,\psi :U\rightarrow {\mathbb {R}}\) are continuous functions, and \(Z\subseteq U\) is locally closed such that \(\varphi -\psi \) is bounded on Z, then there is a canonical isomorphism
It is a fundamental observation (cf. [5, Corollary 9.4.12]) that \({\mathcal {S}}ol_{X}^\mathrm {E}({\mathcal {E}}^{\varphi }_{U|X})\simeq {\mathbb {E}}^{{\text {Re}}\varphi }_{U|X}\), where \({\mathcal {E}}^{\varphi }_{U|X}\) is the exponential D-module for some meromorphic function \(\varphi \in {\mathcal {O}}_X(*D)\) with poles on a closed hypersurface \(D\subset X\) and \(U=X\smallsetminus D\).
3 Stokes phenomena for enhanced solutions
In dimension one, the Stokes phenomenon describes the fact that around an irregular singularity formal solutions are not necessarily convergent, but admit asymptotic expansions on sufficiently small sectors. In the language of D-modules, this is known as the theorem of Hukuhara–Turrittin, stating that the formal Levelt–Turrittin decomposition lifts to a local analytic decomposition on the real blow-up space (cf. [23]). We now explain how this is expressed in terms of enhanced ind-sheaves.
Let \(X={\mathbb {C}}\) and let \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{X})\) be a meromorphic connection with pole at 0, i.e. \({\mathcal {M}}(*0)\simeq {\mathcal {M}}\) and \(\mathrm {SingSupp}({\mathcal {M}})=\{0\}\). Assume \({\mathcal {M}}\) has an (unramified) Levelt–Turrittin decomposition at 0, i.e.
for some finite index set I, meromorphic functions \(\varphi _i\in {\mathcal {O}}_X(*0)\) and regular holonomic \({\mathcal {D}}_X\)-modules \({\mathcal {R}}_i\). Here,  is the formal completion of the stalk.
is the formal completion of the stalk.
The following result has been stated in [5, Sect. 9.8]. It is also given as a corollary of a more general result in [13, Corollary 3.7]. We give a direct proof in the unramified case.
Proposition 3.1
If \({\mathcal {M}}\) has a Levelt–Turrittin decomposition at 0, then for any direction \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\) there exist constants \(\varepsilon , R\in {\mathbb {R}}_{>0}\), determining an open sector \(S_\theta =\{ z\in X \mid 0<|z|<R,\; \arg z \in (\theta -\varepsilon ,\theta +\varepsilon )\}\), such that we have an isomorphism in \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{X})\)
We first establish the following lemma, which is the crucial step in proving the proposition. We denote by \(\varpi :{\widetilde{X}}\rightarrow X\) the real blow-up of X at 0 and refer to [5, Sects. 7.3 and 9.2] for details and notation regarding D-modules and enhanced De Rham functors on blow-up spaces.
Lemma 3.2
Let \(V\subseteq {\widetilde{X}}\) be open and \({\mathcal {N}}\in \mathrm {D}^\mathrm {b}({\mathcal {D}}_{{\widetilde{X}}}^{\mathcal {A}})\). Then there is an isomorphism in \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{{\widetilde{X}}})\)
Proof
We will use the notation from [18] here to emphasize the difference between the two functors \(\iota _{{\widetilde{X}}}\) and \(\beta _{{\widetilde{X}}}\) from sheaves to ind-sheaves. (Note that \(\beta _{{\widetilde{X}}}\) is often suppressed in the notational conventions of [5]).
By [18, Lemma 3.3.3] and [18, Proposition 4.2.14], respectively, we have
and therefore
since \(U\cap U'\) ranges through the family of all relatively compact open subsets of \({\widetilde{X}}\) as U and \(U'\) do. This now enables us to use [18, Theorem 5.4.19] and obtain
\(\square \)
Proof of Proposition 3.1
Still using the notation of [5, Sects. 7.3 and 9.2] and in particular [5, Corollary 9.2.3], one can compute
Here \((\star )\) follows from Lemma 3.2 and \((\blacktriangle )\) follows from the classical Hukuhara–Turrittin theorem if \(\varepsilon \) and R are small enough.
The statement about the solution functor (instead of the De Rham functor) is easily deduced by duality. \(\square \)
The Stokes phenomenon arises through the fact that the isomorphism from Proposition 3.1 depends on \(\theta \). Note that, in contrast to common formulations of the Hukuhara–Turrittin theorem (cf. e.g. [23, Théorème (1.4)]), the statement of Proposition 3.1 does not involve blow-ups.
4 D-modules of pure Gaussian type
Let \({\mathbb {P}}={\mathbb {P}}^1({\mathbb {C}})\) be the analytic complex projective line, denote by \({\mathbb {C}}={\mathbb {P}}\smallsetminus \{\infty \}\) the affine chart with local coordinate z at 0 and by \(j:{\mathbb {C}}\hookrightarrow {\mathbb {P}}\) its embedding.
Definition 4.1
Let \(C\subset {\mathbb {C}}^*\) be a finite (non-empty) subset. A holonomic \({\mathcal {D}}_{\mathbb {P}}\)-module \({\mathcal {M}}\) is said to be of pure Gaussian type C if the following conditions hold:
-
(a)
\({\mathcal {M}}\simeq {\mathcal {M}}(*\infty )\) (as \({\mathcal {D}}_{\mathbb {P}}\)-modules).
-
(b)
\(\mathrm {SingSupp}({\mathcal {M}})=\{\infty \}\).
-
(c)
There exist regular holonomic \({\mathcal {D}}_{\mathbb {P}}\)-modules \({\mathcal {R}}_c\) such that \({\mathcal {M}}\) has a Levelt–Turrittin decomposition at \(\infty \) of the form
$$\begin{aligned} {\mathcal {M}}\widehat{|}_\infty \simeq \bigoplus _{c\in C} \left( {\mathcal {E}}^{-\frac{c}{2}z^2}_{{\mathbb {C}}|{\mathbb {P}}}\mathbin {\otimes ^{{\mathsf {D}}}}{\mathcal {R}}_c \right) \widehat{|}_\infty . \end{aligned}$$
In other words, \({\mathcal {M}}\) is a meromorphic connection on \({\mathbb {P}}\) with a pole at \(\infty \) and an (unramified) Levelt–Turrittin decomposition at \(\infty \) with exponential factors \(-\frac{c}{2}z^2\). (Note that polynomial functions in z extend to meromorphic functions on \({\mathbb {P}}\)).
The rank of \({\mathcal {R}}_c\) will be denoted by \(r_c\) and the family of these ranks will be denoted by  .
.
Some properties of the enhanced solutions of such D-modules of pure Gaussian type are collected in the following lemma.
Lemma 4.2
Let \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be of pure Gaussian type C. Then:
-
(i)
\(\pi ^{-1}{\mathbf {k}}_{{\mathbb {C}}}\otimes {\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\simeq {\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\).
-
(ii)
For any direction \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\), there exists a small sector \(S_\theta \) at \(\infty \) (with central direction \(\theta \)) such that
$$\begin{aligned} \pi ^{-1}{\mathbf {k}}_{S_\theta }\otimes {\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\simeq \pi ^{-1}{\mathbf {k}}_{S_\theta }\otimes \bigoplus \limits _{c\in C}\big ({\mathbb {E}}^{-{\text {Re}}\frac{c}{2}z^2}_{{\mathbb {C}}|{\mathbb {P}}}\big )^{r_c}. \end{aligned}$$ -
(iii)
For any open \(B\subset {\mathbb {C}}\) such that \(\overline{B}\subset {\mathbb {C}}\) (where \(\overline{B}\) denotes the closure of B in \({\mathbb {P}}\)), one has
$$\begin{aligned} \pi ^{-1}{\mathbf {k}}_B \otimes {\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\simeq \pi ^{-1}{\mathbf {k}}_B\otimes ({\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}})^r. \end{aligned}$$
Proof
The statements (i) and (ii) directly follow from Proposition [5, Corollary 9.4.11] and Proposition 3.1, respectively.
The third assertion is proved using [7, Lemma 2.7.6] and the fact that \({\mathcal {M}}\) is non-singular outside \(\infty \). \(\square \)
On the other hand, since \({\mathbb {P}}\) is compact, we have the following statement about the global structure of \({\mathcal {S}}ol_{X}^\mathrm {E}({\mathcal {M}})\). It is a direct application of [4, Lemma 2.5.1] (cf. also [5, Definition 4.9.2 and Theorem 9.3.2]).
Lemma 4.3
Let \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be of pure Gaussian type. Denote by \({\tilde{j}}:{\mathbb {C}}\times {\mathbb {R}}\hookrightarrow {\mathbb {P}}\times {\mathbb {R}}\) the embedding. There exists \({\mathcal {F}}\in \mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}\times {\mathbb {R}}})\) such that
Thus, the enhanced solutions of a D-module of pure Gaussian type are determined by a globally defined enhanced sheaf which restricts to zero on the singularity. The aim of the next sections will be to describe such an enhanced sheaf, and this goal is achieved in Theorem 7.2.
5 Stokes directions and width of sectors
Let \(C\subset {\mathbb {C}}^\times \) be a finite subset and let \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be of pure Gaussian type C.
In this section, we extend the decomposition from Lemma 4.2 (ii) to a decomposition of \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) on sectors around \(\infty \) that intersect at most one Stokes line for each pair \(c,d\in C\). That is, we give a more precise description of how “small” the sectors’ width has to be.
As we have seen, the enhanced solutions of \({\mathcal {M}}\) are not interesting at the singularity but in close neighbourhoods, which are then subsets of \({\mathbb {C}}={\mathbb {P}}\smallsetminus \{\infty \}\). Therefore, we will set up everything in the complex plane.
Lemma-Definition 5.1
Let \(c,d\in C\), \(c\ne d\). The set
is the union of four closed half-lines with initial point 0, perpendicular to one another. These half-lines are called the Stokes lines of the pair c, d. Their directions (i.e. the arguments of the points on the Stokes lines) are called the Stokes directions (of the pair c, d).
We say that a direction is generic if it is not a Stokes direction for any pair \(c,d\in C\).
Definition 5.2
A subset \(S\subset {\mathbb {P}}\) is said to be
- \(\blacktriangleright \):
-
an open sector at \(\infty \) if
$$\begin{aligned} S=\{ z\in {\mathbb {C}}\mid R<|z|<\infty , \arg z \in (\theta -\varepsilon ,\theta +\varepsilon ) \}\subseteq {\mathbb {C}}\subset {\mathbb {P}}\end{aligned}$$for some \(R\in {\mathbb {R}}_{\ge 0}\), \(\varepsilon \in {\mathbb {R}}_{>0}\) and \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\).
- \(\blacktriangleright \):
-
a closed sector at \(\infty \) if
$$\begin{aligned} S=\{ z\in {\mathbb {C}}\mid R\le |z|<\infty , \arg z \in [\theta -\varepsilon ,\theta +\varepsilon ] \text { for }|z|\ne 0\}\subseteq {\mathbb {C}}\subset {\mathbb {P}}\end{aligned}$$for some \(R,\varepsilon \in {\mathbb {R}}_{\ge 0}\) and \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\). For \(\varepsilon =0\), this includes the case of half-lines.
The radius of such a sector is the number \(\frac{1}{R}\in (0,+\infty ]\), and its width is the number \(\min (2\varepsilon ,2\pi )\in [0,2\pi ]\). Note that a closed sector at \(\infty \) is topologically closed in \({\mathbb {C}}\) (but not in \({\mathbb {P}}\)).
We will say that an (open or closed) sector at \(\infty \) contains a direction \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\) if its intersection with the open half-line \(\{ z\in {\mathbb {C}}\smallsetminus \{0\} \mid \arg z = \theta \}\) is non-empty.
On sectors containing no Stokes direction, we can introduce an order on C.
Notation 5.3
Let S be a sector at \(\infty \) and let \(c,d\in C\). We write

For \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\), we write

We now describe morphisms between the exponential enhanced ind-sheaves in the local decomposition of \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) from Lemma 4.2 (ii). This lemma is analogous to (and inspired by) [5, Lemma 9.8.1], [4, Lemma 5.1.2] and [6, Lemma 4.3.1].
Lemma 5.4
Consider the meromorphic functions \(\varphi _1,\varphi _2\) on \({\mathbb {P}}\) given by \(\varphi _1(z)=-\frac{c}{2}z^2\) and \(\varphi _2(z)=-\frac{d}{2}z^2\) for \(c,d\in {\mathbb {C}}^\times \), \(c\ne d\). Let \(S\subset {\mathbb {P}}\) be a sector (open or closed) at \(\infty \). Then we have

Here, the first isomorphism (from right to left) is induced by the functor \({\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}}\mathbin {\overset{+}{\otimes }}{\tilde{j}}_!(\bullet )\) and the second isomorphism is the natural identification of a morphism with multiplication by a complex number.
Proof
Using [5, Proposition 4.7.9, Lemma 4.4.6 and Corollary 3.2.10], we get
If \({\text {Re}}\varphi _1\ge {\text {Re}}\varphi _2\) at each point of S, these \(\mathrm {Hom}\)-spaces are isomorphic to \({\mathbf {k}}\) for any \(a\in {\mathbb {R}}_{\ge 0}\) (and hence also their direct limit). If there are points in S where \({\text {Re}}\varphi _1<{\text {Re}}\varphi _2\), it is not difficult to see that \({\text {Re}}(\varphi _2-\varphi _1)\) is not bounded from above on S. It follows that the \(\mathrm {Hom}\)-space is trivial for any \(a\in {\mathbb {R}}_{\ge 0}\) (and hence also the direct limit). \(\square \)
The following result shows how automorphisms of the Gaussian model on sectors can be interpreted as block matrices.
Proposition 5.5
Let \(S\subset {\mathbb {P}}\) be a sector at \(\infty \) and assume that S is not a half-line whose direction is a Stokes direction for some \(c,d\in C\). If we choose a numbering of the elements of C, i.e. \(C=\{ c_{(1)},\ldots , c_{(n)} \}\), we have

In particular, if \(c_{(1)}<_Sc_{(2)}<\cdots <_S c_{(n)}\), then the right hand side consists precisely of the invertible, lower block-triangular matrices with block sizes given by the numbers \(r_{c_{(j)}}\).
Proposition 5.6
Let \({\mathcal {M}}\) be of pure Gaussian type C. For any (open or closed) sector S at \(\infty \) of sufficiently small radius intersecting at most one Stokes line for each pair \(c,d\in C\), there is an isomorphism
Proof
Let us write for short  and
and  .
.
The following argument enables us to recursively obtain the desired isomorphism by gluing those on small sectors (cf. Lemma 4.2 (ii)): Assume that we are given two open sectors \(S_1,S_2\subset S\) at \(\infty \) with isomorphisms

for \(j\in \{1,2\}\) and assume moreover that \(S_1\cap S_2\ne \varnothing \), that we have \(S_1\nsubseteq S_2\) and \(S_2\nsubseteq S_1\), that \(S_2\) contains at most one Stokes direction and no Stokes direction for the same pair c, d is contained in \(S_1\).
Choose a numbering of the elements of C such that \(c_{(1)}<_{S_1\cap S_2} c_{(2)}<_{S_1\cap S_2} \cdots <_{S_1\cap S_2} c_{(n)}\). The isomorphisms \(\alpha _j\) induce two isomorphisms

By Proposition 5.5, the transition isomorphism \({\widetilde{\alpha }}_2\circ {\widetilde{\alpha }}_1^{-1}\) can be represented by a lower block-triangular matrix \(A=(A_{jk})\). One can decompose \(A=A''A'\) as follows:
If \(S_2\) contains a Stokes direction for the pair \(c_{(l)},c_{(l')}\) (\(l<l'\)), let \(A'\) be the block matrix (with the same block structure as A) having identity matrices on the diagonal and \(A'_{l'l}=A_{l'l'}^{-1}A_{l'l}\). All the other blocks of \(A'\) are zero. If \(S_2\) contains no Stokes direction, let  . Set
. Set  .
.
It is not difficult to see that, in either of the two cases, the matrix \(A'\) represents an automorphism of \(\pi ^{-1}{\mathbf {k}}_{S_1}\otimes {\mathbb {M}}\) and the matrix \(A''\) represents an automorphism of \(\pi ^{-1}{\mathbf {k}}_{S_2}\otimes {\mathbb {M}}\) (by the correspondence of Proposition 5.5).
Consider the diagram

where the rows are distinguished triangles. By our construction of \(A'\) and \(A''\), the square on the left of the diagram commutes and the vertical arrows are isomorphisms. Therefore, there exists an isomorphism \(\widehat{\alpha }\) completing the diagram to an isomorphism of distinguished triangles. \(\square \)
6 Stokes multipliers and monodromy
Let \(C\subset {\mathbb {C}}^\times \) be a finite subset and \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be of pure Gaussian type C. As we have seen, we generally need four sectors to cover a neighbourhood of \(\infty \) by sectors on which we have isomorphisms as in Proposition 5.6.
Fix a generic direction \(\theta _0\) and choose a numbering of the elements of C such that \(c_{(1)}<_{\theta _0} c_{(2)}<_{\theta _0}\cdots <_{\theta _0} c_{(n)}\). Clearly, \(\theta _0+k\frac{\pi }{2}\) (for \(k\in \{1,2,3\}\)) are also generic. By Proposition 5.6, there exists \(R\in {\mathbb {R}}_{>0}\) such that on the closed sectors  , \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), we have isomorphisms
, \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), we have isomorphisms

(Note that these isomorphisms are not unique, so this step involves a choice).
On the half-line  , \(\alpha _k\) and \(\alpha _{k+1}\) induce isomorphisms (by abuse of notation, we denote them by the same symbols)
, \(\alpha _k\) and \(\alpha _{k+1}\) induce isomorphisms (by abuse of notation, we denote them by the same symbols)

and the transition isomorphism
is represented by an invertible, block-triangular matrix \(\sigma _k\) (cf. Lemma 5.5).
Definition 6.1
The matrices \(\sigma _k\) are called Stokes multipliers (or Stokes matrices) of \({\mathcal {M}}\).
(Remember that these notions require fixing a generic direction).
Proposition 6.2
The (counterclockwise) product of the Stokes multipliers for a D-module of pure Gaussian type is the identity, i.e. \(\sigma _4\sigma _3\sigma _2\sigma _1= \mathbb {1}\).
Proof
Choose \(\rho >R\) and set  . There is a canonical isomorphism (see Lemma 2.2)
. There is a canonical isomorphism (see Lemma 2.2)

We set  ,
,  and
and  . Moreover, we write for short
. Moreover, we write for short  and
and  .
.
For each \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), one has a chain of isomorphisms

The transition isomorphism on \(D_{k,k+1}\) is given by the Stokes multiplier \(\sigma _k\) (which can be viewed as an automorphism of the sheaf \(({\mathbf {k}}_{D_k})^r\)).
Therefore, \(\pi ^{-1}{\mathbf {k}}_{D}\otimes H\simeq \pi ^{-1}{\mathcal {G}}\otimes {\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}}\), where \({\mathcal {G}}\) is a local system of rank r on D (extended by zero to \({\mathbb {C}}\)) with monodromy given by \(\sigma _4\sigma _3\sigma _2\sigma _1\).
On the other hand, by Lemma 4.2, we have an isomorphism \(\pi ^{-1}{\mathbf {k}}_{D}\otimes H\simeq \pi ^{-1}({\mathbf {k}}_D)^r\otimes {\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}}\). Since the functor \(\pi ^{-1}(\bullet )\otimes {\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}}\) is fully faithful (see [5, Proposition 4.7.15]), \({\mathcal {G}}\) is isomorphic to the constant local system and hence that their monodromies are equal. \(\square \)
7 A sheaf describing enhanced solutions
The question studied in this section is how large we can choose the radius of the four sectors. It will turn out that the absence of singularities outside the point \(\infty \) enables us to increase the sectors’ radii as far as we like. Hence, we can actually use sectors of infinite radius.
Lemma-Definition 7.1
Consider the following set of data:
-
a finite subset \(C\subset {\mathbb {C}}^\times \),
-
a generic direction \(\theta _0\) with respect to C (which defines an order on C),
-
a family
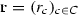 of natural numbers \(r_c\in {\mathbb {Z}}_{>0}\),
of natural numbers \(r_c\in {\mathbb {Z}}_{>0}\), -
a family \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) of \((r\times r)\)-matrices (where
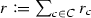 ) such that \(\sigma _1\) and \(\sigma _3\) (resp. \(\sigma _2\) and \(\sigma _4\)) are upper (resp. lower) block-triangular, with the block structure given by the numbers \(r_c\) (ordered according to \(\theta _0\)).
) such that \(\sigma _1\) and \(\sigma _3\) (resp. \(\sigma _2\) and \(\sigma _4\)) are upper (resp. lower) block-triangular, with the block structure given by the numbers \(r_c\) (ordered according to \(\theta _0\)).
Define the sectors  , which are closed sectors of infinite radius at \(\infty \), but can also be considered as closed sectors (including the vertex) at 0. As usual, we set
, which are closed sectors of infinite radius at \(\infty \), but can also be considered as closed sectors (including the vertex) at 0. As usual, we set  .
.
Then there exists an enhanced sheaf  (or \({\mathcal {F}}_\sigma \) for short) on \({\mathbb {C}}\) together with isomorphisms
(or \({\mathcal {F}}_\sigma \) for short) on \({\mathbb {C}}\) together with isomorphisms

such that the transition isomorphisms \(\alpha _{k+1}\circ \alpha _k^{-1}\), automorphisms of  , are given by the matrices \(\sigma _k\). Moreover, the sheaf \({\mathcal {F}}_\sigma \) thus defined is unique up to unique isomorphism.
, are given by the matrices \(\sigma _k\). Moreover, the sheaf \({\mathcal {F}}_\sigma \) thus defined is unique up to unique isomorphism.
If an enhanced sheaf on \({\mathbb {C}}\) is isomorphic to one of this form, we will call it an enhanced sheaf of pure Gaussian type.
The following theorem shows that this finally is an enhanced sheaf (on \({\mathbb {C}}\)) describing globally (on \({\mathbb {P}}\)) the enhanced solutions of \({\mathcal {M}}\). (In contrast to the formulation of Lemma 4.3, we do not write extension by zero).
Theorem 7.2
Let \({\mathcal {M}}\) be a D-module of pure Gaussian type C,  the family of ranks from its Levelt–Turrittin decomposition, \(\theta _0\) a generic direction and recall the Stokes multipliers \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) from the previous section. Then there is an isomorphism
the family of ranks from its Levelt–Turrittin decomposition, \(\theta _0\) a generic direction and recall the Stokes multipliers \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) from the previous section. Then there is an isomorphism

In the proof of this theorem, let us write  . We make use of the following lemma, which gives an alternative description of \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) away from the singularity.
. We make use of the following lemma, which gives an alternative description of \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}({\mathcal {M}})\) away from the singularity.
Lemma 7.3
Let \(B\subset {\mathbb {C}}\) be a closed ball of finite radius around 0. Then there is an isomorphism
Proof
We abbreviate  and
and  for \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), as well as
for \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), as well as  and
and  .
.
For any \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), we choose the following isomorphism:

Here, \(\vartheta \) is the isomorphism from Lemma 4.2, \(\tau \) is the canonical isomorphism (see Lemma 2.2), and \(s_1=\mathbb {1}\), \(s_2=\sigma _1\), \(s_3=\sigma _2\sigma _1\), \(s_4=\sigma _3\sigma _2\sigma _1\). With this choice, the transition maps are given by the \(\sigma _k\). (Note that at this point we use that the monodromy is trivial). Hence, one can construct the desired isomorphism. \(\square \)
Proof of Theorem 7.2
Recall the notations R and \(\Sigma _k\) from Sect. 6. We abbreviate  and
and  . Moreover, we choose \(\rho >R\) and set
. Moreover, we choose \(\rho >R\) and set  ,
,  ,
,  and
and  (similarly,
(similarly,  ).
).
Firstly, one uses (6.1) to obtain an isomorphism
Secondly, we determine an isomorphism
The existence of such an isomorphism was shown in Lemma 7.3. However, it is neither canonical nor unique, but depends on the choice of a trivialization \(\vartheta :\pi ^{-1}{\mathbf {k}}_{B}\otimes H\simeq \pi ^{-1}{\mathbf {k}}_{B}\otimes ({\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}})^r\). We choose \(\vartheta \) in such a way that the composition

is the canonical isomorphism. We can then conclude that (7.1) and (7.2) agree on D and the theorem follows. \(\square \)
The next lemma shows that we can “deform” the sectors \(S_k\) without crossing a Stokes line and describe  equivalently.
equivalently.
Lemma 7.4
Let \({\mathcal {S}}_k\), \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), be four closed sectors of infinite radius at \(\infty \). Assume that \({\mathcal {S}}_k\) contains exactly the same Stokes directions as \(S_k\). Then Lemma-Definition 7.1 defines the same sheaf  if we replace \(S_k\) by \({\mathcal {S}}_k\).
if we replace \(S_k\) by \({\mathcal {S}}_k\).
8 Stokes data and a Riemann–Hilbert correspondence for systems of pure Gaussian type
We have reduced to a small set of data necessary for determining a D-module of pure Gaussian type. We use this data to establish a Riemann–Hilbert correspondence for D-modules of pure Gaussian type. In this section, we will not expand on the proofs of equivalences of categories, which are mainly straightforward.
We fix a finite subset \(C\subset {\mathbb {C}}^\times \) as well as a generic direction \(\theta _0\) and consider the sectors \(S_k=\{ z\in {\mathbb {C}}\mid \arg z\in [\theta _0+(k-1)\frac{\pi }{2},\theta _0+k\frac{\pi }{2}] \text { if }z\ne 0 \}\). We also fix a positive integer \(r_c\) for any \(c\in C\).
Let  be the full subcategory of \(\mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) consisting of objects of pure Gaussian type C and with a Levelt–Turrittin decomposition satisfying \(\mathrm {rk}\, {\mathcal {R}}_c=r_c\) for every \(c\in C\).
be the full subcategory of \(\mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) consisting of objects of pure Gaussian type C and with a Levelt–Turrittin decomposition satisfying \(\mathrm {rk}\, {\mathcal {R}}_c=r_c\) for every \(c\in C\).
Let  be the full subcategory of \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{{\mathbb {P}}})\) consisting of objects H satisfying \(\pi ^{-1}{\mathbf {k}}_{{\mathbb {C}}}\otimes H\simeq H\) and admitting isomorphisms
be the full subcategory of \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{{\mathbb {P}}})\) consisting of objects H satisfying \(\pi ^{-1}{\mathbf {k}}_{{\mathbb {C}}}\otimes H\simeq H\) and admitting isomorphisms
for \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). (Note that these isomorphisms are not part of the data).
Proposition 8.1
The functor \({\mathcal {S}}ol_{{\mathbb {P}}}^\mathrm {E}\) induces an equivalence between  and
and  .
.
Essential surjectivity follows quickly from the description of the essential image of \({\mathcal {S}}ol_{X}^\mathrm {E}\) by T. Mochizuki (see [26, Lemma 9.8]) and the comparison between enhanced exponentials [6, Corollary 5.2.3] (cf. also [26, Lemma 5.15]).
The results of the previous sections enable us to describe the objects of  in terms of linear algebra data. Choose a numbering of the elements of C such that \(c_{(1)}<_{\theta _0} c_{(2)}<_{\theta _0}\cdots <_{\theta _0} c_{(n)}\). We will write \(r_j\) instead of \(r_{c_{(j)}}\).
in terms of linear algebra data. Choose a numbering of the elements of C such that \(c_{(1)}<_{\theta _0} c_{(2)}<_{\theta _0}\cdots <_{\theta _0} c_{(n)}\). We will write \(r_j\) instead of \(r_{c_{(j)}}\).
Definition 8.2
One defines the category  of Stokes data of pure Gaussian type \((C,\theta _0,(r_c)_{c\in C})\) as follows:
of Stokes data of pure Gaussian type \((C,\theta _0,(r_c)_{c\in C})\) as follows:
-
An object
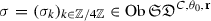 is a family of four block matrices with the properties:
is a family of four block matrices with the properties:-
The block structure is given by the numbers \(r_j\) (\(j\in \{1,\ldots ,n\}\)), i.e. the jth diagonal block has size \(r_j\times r_j\).
-
The matrices \(\sigma _1\) and \(\sigma _3\) are upper block-triangular and the matrices \(\sigma _2\) and \(\sigma _4\) are lower block-triangular.
-
The matrix \(\sigma _k\) is invertible for any \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). (With the above properties, this is equivalent to saying that the blocks along the diagonal are invertible).
-
The product of the \(\sigma _k\) is the identity: \(\sigma _4\sigma _3\sigma _2\sigma _1=\mathbb {1}\).
-
-
A morphism
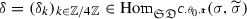 between two objects \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) and \(\widetilde{\sigma }=({\widetilde{\sigma }}_k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) is a family of four block matrices with the properties:
between two objects \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) and \(\widetilde{\sigma }=({\widetilde{\sigma }}_k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) is a family of four block matrices with the properties:-
The block structure is given by the numbers \(r_j\) (\(j\in \{1,\ldots ,n\}\)).
-
The matrix \(\delta _k\) is block-diagonal for every \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\).
-
For any \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), one has \(\widetilde{\sigma }_k\delta _k=\delta _{k+1}\sigma _k\).
Composition of morphisms is given by matrix multiplication.
-
Remark 8.3
Let us give an explanation of how one could think of objects and morphisms in the category of Stokes data  . This also gives an idea for making a link with the description of Stokes data in [30].
. This also gives an idea for making a link with the description of Stokes data in [30].
An object consists of four matrices which will correspond to the Stokes matrices describing the transition between the four sectors. We can therefore imagine them to be arranged in a “circle”, i.e. a diagram of the form

One can think of the vertices \(\bullet \) as vector spaces \({\mathbf {k}}^r=\bigoplus _{j=1}^n {\mathbf {k}}^{r_j}\) which (by the given grading) have two natural filtrations: The filtration \(F_m{\mathbf {k}}^r=\bigoplus _{j=1}^m{\mathbf {k}}^{r_j}\) is respected by the matrices \(\sigma _1\) and \(\sigma _3\), whereas the filtration \(F'_m{\mathbf {k}}^r=\bigoplus _{j=n-m+1}^n {\mathbf {k}}^{r_j}\) is respected by the matrices \(\sigma _2\) and \(\sigma _4\).
A morphism between two such diagrams can then be visualized as

and the relations required in Definition 8.2 amount to saying that this diagram is commutative. The matrices \(\delta _k\) respect the grading \({\mathbf {k}}^r=\bigoplus _{j=1}^n {\mathbf {k}}^{r_j}\), i.e. they are compatible with both filtrations considered above.
An intuitive reason why the \(\sigma _k\) are block-triangular, while the \(\delta _k\) need to be block-diagonal is the following: The matrices \(\sigma _k\) are the transition matrices, which means that they describe isomorphisms on the boundaries of the sectors, where one has a well-defined ordering of the parameters \(c_{(j)}\) (cf. Lemma 5.5). In contrast, the \(\delta _k\) are meant to describe morphisms on the sectors \(S_k\), where no pair of parameters has a global well-defined order. Therefore, \(\delta _k\) must be compatible with any order of the \(c_{(j)}\).
Proposition 8.4
The functor

is an equivalence of categories, where \({\mathcal {F}}_\sigma \) is as in Sect. 7.
Corollary 8.5
There is an equivalence of categories  .
.
The corresponding functor assigns to a D-module of pure Gaussian type \({\mathcal {M}}\) its Stokes matrices with respect to the generic direction \(\theta _0\).
9 Analytic and topological Fourier–Laplace transform
Classically, for a module M over the Weyl algebra \({\mathbb {C}}[z]\langle \partial _z\rangle \), the Fourier–Laplace transform \({\widehat{M}}\) is the \({\mathbb {C}}[w]\langle \partial _w\rangle \)-module defined as follows: As a set, we have \({\widehat{M}}=M\), and the structure of a \({\mathbb {C}}[w]\langle \partial _w\rangle \)-module is defined by  and
and  . The corresponding integral transform is given as follows (see [22]).
. The corresponding integral transform is given as follows (see [22]).
Consider the projections

where \({\mathbb {P}}_z\) denotes the complex projective line with affine coordinate z in the chart \({\mathbb {C}}_z\subset {\mathbb {P}}_z\) at 0, and similarly for \({\mathbb {P}}_w\).
Definition 9.1
Let \({\mathcal {M}}\in \mathrm {D}^\mathrm {b}({\mathcal {D}}_{{\mathbb {P}}_z})\). We define the Fourier–Laplace transform \({}^{\mathsf {L}}{\mathcal {M}}\) of \({\mathcal {M}}\) by

This defines a functor \({}^{\mathsf {L}}(\bullet ):\mathrm {D}^\mathrm {b}({\mathcal {D}}_{{\mathbb {P}}_z})\rightarrow \mathrm {D}^\mathrm {b}({\mathcal {D}}_{{\mathbb {P}}_w})\).
In the same spirit, one can define a transform for enhanced ind-sheaves (see [21]) and enhanced sheaves. Consider the projections

Definition 9.2
Let \({\mathcal {F}}\in \mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_z\times {\mathbb {R}}})\) be an enhanced sheaf. We define its enhanced Fourier–Sato transform \({}^{\mathcal {L}}{\mathcal {F}}\) by

This defines a functor \({}^{\mathcal {L}}(\bullet ):\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_z\times {\mathbb {R}}})\rightarrow \mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\).
An important observation on our way to describing the Fourier–Laplace transform of a D-module of pure Gaussian type is the compatibility of these transformations with the enhanced solution functor (cf. [21, Theorem 4.17]).
Lemma 9.3
Let \({\mathcal {M}}\in \mathrm {Mod}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}_z})\) and \({\mathcal {S}}ol_{{\mathbb {P}}_z}^\mathrm {E}({\mathcal {M}})\simeq {\mathbf {k}}^{\mathrm{E}}_{{\mathbb {P}}_z}\mathbin {\overset{+}{\otimes }}{\mathcal {F}}\) for some \({\mathcal {F}}\in \mathrm {Mod}({\mathbf {k}}_{{\mathbb {C}}_z\times {\mathbb {R}}})\). One has an isomorphism in \(\mathrm {E}^\mathrm {b}(\mathrm {I}{\mathbf {k}}_{{\mathbb {P}}_w})\)
10 Aligned parameters
In Sabbah [30] treated the case of a D-module of pure Gaussian type C with \(\arg c=\arg d\) for any \(c,d\in C\), i.e. the parameter set C is “aligned” along a half-line through the origin.
10.1 Main statement
Let \({\mathcal {M}}\in \mathrm {D}^\mathrm {b}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be a D-module of pure Gaussian type C, where all the elements of C have the same argument \(\arg C\).
The directions of the Stokes lines are: \(-\frac{\pi }{4}-\frac{1}{2}\arg C+k\frac{\pi }{2}\), \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). (These values are the same for any pair \(c,d\in C\)). In particular, we can choose  as a generic direction. Note that this involves a choice of \(\frac{1}{2}\arg C\), and we choose \(\theta _0\in [-\frac{\pi }{2},\frac{\pi }{2})\).
as a generic direction. Note that this involves a choice of \(\frac{1}{2}\arg C\), and we choose \(\theta _0\in [-\frac{\pi }{2},\frac{\pi }{2})\).
It is known from Theorem 7.2 that

Therefore, in view of Lemma 9.3, the main step in computing the Fourier–Laplace transform of \({\mathcal {M}}\) topologically is the proof of the following statement. Let C and \(\theta _0\) be as above. Let \(r_c\in {\mathbb {Z}}_{>0}\) be a positive integer for any \(c\in C\), and let \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) be a family of four block matrices (with block structure induced be the numbering on C with respect to \(\theta _0\)) such that \(\sigma _k\) is upper (resp. lower) block-triangular for k odd (resp. even) and \(\sigma _4\sigma _3\sigma _2\sigma _1=\mathbb {1}\).
Theorem 10.1
Let C, \(\theta _0\),  and \(\sigma \) be as above. We set
and \(\sigma \) be as above. We set  ,
,  and
and  . Then there is an isomorphism
. Then there is an isomorphism

In particular, the gluing matrices \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) remain the same (although sectors and exponential factors change).
As a corollary, we obtain the following result, which was already obtained in the context of Stokes data attached to Stokes-filtered local systems by C. Sabbah (cf. [30, Lemma 1.4, Theorem 4.2]). The statement is illustrated in Fig. 1.
The complex plane covered by four closed sectors, which are determined by the generic directions \(\theta _0\) and \({\widehat{\theta }}_0=\pi -\theta _0\). (The red arrows indicate the Stokes directions). If a D-module of pure Gaussian type has a Hukuhara–Turrittin decomposition on each of the sectors \(S_k\) (on the left) with exponents \(-\frac{c}{2}z^2\) and Stokes multipliers \(\sigma _k\), then its Fourier–Laplace transform has a Hukuhara–Turrittin decomposition on the sectors \({\widehat{S}}_k\) (on the right) with exponents \(\frac{1}{2c}w^2\) and Stokes multipliers \(\widehat{\sigma }_k=\sigma _k\) (color figure online)
Corollary 10.2
Let \(C\subset {\mathbb {C}}^\times \) be a finite subset whose elements have constant argument \(\arg C\). Let \({\mathcal {M}}\in \mathrm {D}^\mathrm {b}_\mathrm {hol}({\mathcal {D}}_{{\mathbb {P}}})\) be of pure Gaussian type C and let \((\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) be Stokes multipliers with respect to the generic direction \(\theta _0=-\frac{1}{2}\arg C\). Then the Fourier–Laplace transform \({}^{\mathsf {L}}{\mathcal {M}}\) of \({\mathcal {M}}\) is of pure Gaussian type \({\widehat{C}}=-1/C\) and Stokes multipliers with respect to the generic direction  are given by \((\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\).
are given by \((\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\).
The rest of this section will be concerned with the proof of Theorem 10.1. The idea of the proof is as follows: We choose a decomposition of the plane into four closed sectors \({\mathcal {S}}_k\), \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), on which  is trivialized as a direct sum of exponential enhanced sheaves. As usual, write
is trivialized as a direct sum of exponential enhanced sheaves. As usual, write  . We will first compute the enhanced Fourier–Sato transforms of these exponential enhanced ind-sheaves on the \({\mathcal {S}}_k\) and \({\mathcal {S}}_{k,k+1}\) (and hence \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {S}}_k})\) and \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {S}}_{k,k+1}})\)). Setting
. We will first compute the enhanced Fourier–Sato transforms of these exponential enhanced ind-sheaves on the \({\mathcal {S}}_k\) and \({\mathcal {S}}_{k,k+1}\) (and hence \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {S}}_k})\) and \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {S}}_{k,k+1}})\)). Setting  ,
,  and
and  , we can model the gluing of \({\mathcal {F}}\) from the restrictions to sectors in terms of short exact sequences in \(\mathrm {Mod}({\mathbf {k}}_{{\mathbb {C}}\times {\mathbb {R}}})\):
, we can model the gluing of \({\mathcal {F}}\) from the restrictions to sectors in terms of short exact sequences in \(\mathrm {Mod}({\mathbf {k}}_{{\mathbb {C}}\times {\mathbb {R}}})\):
Applying the enhanced Fourier–Sato transform, we obtain distinguished triangles (which will turn out to be just short exact sequences), and we can determine step by step the enhanced Fourier–Sato transforms of \({\mathcal {F}}_{H_+}\), \({\mathcal {F}}_{H_-}\), \({\mathcal {F}}_{L}\), and finally of \({\mathcal {F}}\).
We will give a proof for the case where \(\arg C\in (-\frac{\pi }{2},\frac{\pi }{2})\), i.e. \({\text {Re}}c>0\). The arguments for the other cases \({\text {Re}}c<0\) and \({\text {Re}}c=0\) work completely along the same lines. However, the geometry of the objects involved depends on the sign of \({\text {Re}}c\).
10.2 Exponential enhanced sheaves on closed sectors
Let us choose the sectors (note that \(0\in {\mathcal {S}}_k\))

Denote the half-lines bounding the sectors by  for \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). It is easy to check that each of these sectors contains exactly one Stokes direction and that they are compatible with the \(S_k\) in the sense of Lemma 7.4.
for \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). It is easy to check that each of these sectors contains exactly one Stokes direction and that they are compatible with the \(S_k\) in the sense of Lemma 7.4.
The first aim is to compute the enhanced Fourier–Sato transforms of the enhanced exponentials  , which are the building blocks of
, which are the building blocks of  on sectors. As mentioned, we assume \(c=c_1+ic_2\in {\mathbb {C}}^\times \) with \(c_1>0\). We will give the proof for \(k=1\).
on sectors. As mentioned, we assume \(c=c_1+ic_2\in {\mathbb {C}}^\times \) with \(c_1>0\). We will give the proof for \(k=1\).
We can compute

In particular, the stalks of the cohomology sheaves at a point \(({\check{w}},{\check{t}})\in {\mathbb {C}}_w\times {\mathbb {R}}\) are determined by the topology of the intersection of two subspaces of \({\mathbb {C}}_z\):

The inequality \({\check{t}}- {\text {Re}}\big (z{\check{w}}+\frac{c}{2}z^2\big )\ge 0\) describes a region bounded by the two branches of a hyperbola. The hyperbola can be written in standard form if we write \(z=z_1+iz_2\) and apply the coordinate transform

Then, the space to be considered is the intersection of the (hyperbolic) region given by
and the sector given by
Clearly, the topology of this intersection highly depends on the values of \({\check{t}}\), \({\check{w}}_1\) and \({\check{w}}_2\). It is easy to see that the above compactly supported cohomology groups are trivial unless the intersection has a compact connected component (see Fig. 2, noting that the unbounded components have vanishing cohomology with compact support), and by elementary considerations one can determine the cases in which such a compact connected component exists. This yields the following lemma.
Lemma 10.3
There are isomorphisms

and

with the continuous functions  defined by
defined by

and

Observe that  , so
, so  for all \(w\in {\mathbb {C}}_w\).
for all \(w\in {\mathbb {C}}_w\).
The cases of the sectors \({\mathcal {S}}_2\), \({\mathcal {S}}_3\) and \({\mathcal {S}}_4\) are analogous. For the sectors \({\mathcal {S}}_2\) and \({\mathcal {S}}_3\), one needs to introduce the continuous functions  , which are given by
, which are given by

and

Set  and
and  . Note that these half-planes only depend on \(\arg C\). The stalks suggest the following global statement. (Recall the notation from Sect. 2.2).
. Note that these half-planes only depend on \(\arg C\). The stalks suggest the following global statement. (Recall the notation from Sect. 2.2).
Proposition 10.4
There are isomorphisms in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

Proof
We give a proof for the case of \({\mathcal {S}}_1\).
Set  and recall from (10.1) that
and recall from (10.1) that  .
.
First, consider the set

It is an open subset of A and hence we have a distinguished triangle in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

By the projection formula,  and hence it follows from (10.3) and (10.4) that \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_{A\smallsetminus U}\simeq 0\) and \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_A\simeq {\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_U\).
and hence it follows from (10.3) and (10.4) that \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_{A\smallsetminus U}\simeq 0\) and \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_A\simeq {\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_U\).
Next, consider the set

For fixed \({\check{w}}\) and \({\check{t}}\), the corresponding point \(z=\frac{1}{c_1}\big (\sqrt{2c_1{\check{t}}+{\check{w}}_1^2}-{\check{w}}_1\big )\) is the rightmost intersection point of the hyperbolic region \(\{{\check{t}}-{\text {Re}}(z{\check{w}}+\frac{c}{2}z^2)\ge 0\}\) with the horizontal border of the sector \({\mathcal {S}}_1\). Moreover, B is a closed subset of U and we get a distinguished triangle in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

The stalks of the cohomology sheaves of \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_{U\smallsetminus B}\) are all trivial, and hence \({\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_{B}\simeq {\mathsf {R}}{\widetilde{q}}_!{\mathbf {k}}_{U}\).
Finally, one has

since \({\widetilde{q}}\) induces a homeomorphism  . \(\square \)
. \(\square \)
The computations of the enhanced Fourier–Sato transforms of the exponentials  and
and  are similar.
are similar.
Proposition 10.5
There are isomorphisms in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

Now that we computed the Fourier–Laplace transform of exponentials, let us briefly reflect on the impact of Fourier–Laplace on morphisms between those exponentials: Exponential enhanced sheaves are sheaves of the form \({\mathbf {k}}_Z\) for some locally closed \(Z\subseteq {\mathbb {C}}\times {\mathbb {R}}\). A morphism between two exponentials is therefore given by multiplication with an element \(a\in {\mathbf {k}}\) (at points where both stalks are \({\mathbf {k}}\), it is multiplication by a). Since the enhanced Fourier–Sato transform consists only of tensor products and direct and inverse images along projections, one checks that the induced morphism between the enhanced Fourier–Laplace transforms of the exponentials is again given by multiplication with the same element \(a\in {\mathbf {k}}\).
10.3 Enhanced Fourier–Sato transform of a Gaussian enhanced sheaf
In this section, we will elaborate on the idea given at the end of Sect. 10.1 in order to describe the enhanced Fourier–Sato transform of  . We write for short
. We write for short  .
.
To make notation easier, we will write  instead of
instead of  , and we shall assume \(r_c=1\) for any \(c\in C\). (One can replace any occurence of a direct sum
, and we shall assume \(r_c=1\) for any \(c\in C\). (One can replace any occurence of a direct sum  by
by  and the word “triangular” by “block-triangular”, and the proof is still valid).
and the word “triangular” by “block-triangular”, and the proof is still valid).
Recall that we have defined a covering of the plane \({\mathbb {C}}_z\) by four closed sectors \({\mathcal {S}}_k\), \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\). We set  and
and  as well as
as well as  . On these sectors, we have isomorphisms
. On these sectors, we have isomorphisms

and the gluing morphisms \(\alpha _{k+1}\circ \alpha _k^{-1}\) on \({\mathcal {S}}_{k,k+1}\) are given by the Stokes multipliers \(\sigma _k\).
10.3.1 Transform of restrictions to half-planes
Let us start by investigating the short exact sequence in \(\mathrm {Mod}({\mathbf {k}}_{{\mathbb {C}}_z\times {\mathbb {R}}})\)
Via \(\alpha _1\) and \(\alpha _2\) (the latter used also for \({\mathcal {F}}_{{\mathcal {S}}_{12}}\)), it is isomorphic to

Applying the enhanced Fourier–Sato transform and using the results of the previous section, we get a distinguished triangle in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

Since the morphism \(\sigma _1-\mathbb {1}\) is an epimorphism in \(\mathrm {Mod}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\), the associated long exact sequence yields the following proposition, comprising also the statements for \({\mathcal {H}}_-\) and  .
.
Proposition 10.6
Let \({\mathcal {F}}={\mathcal {F}}_\sigma \) be an enhanced sheaf of pure Gaussian type (cf. Lemma-Definition 7.1). The complexes \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {H}}_+})\), \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {H}}_-})\) and \({}^{\mathcal {L}}({\mathcal {F}}_{L})\) are concentrated in degree \(-1\). More precisely, there are isomorphisms in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

10.3.2 Transform on the whole plane
We can now examine the sequence
which will enable us to describe \({}^{\mathcal {L}}{\mathcal {F}}\) and show that it is of the desired form on sectors.
Let us first make the morphism \({\mathcal {F}}_{{\mathcal {H}}_+}\oplus {\mathcal {F}}_{{\mathcal {H}}_-}\rightarrow {\mathcal {F}}_L\) more explicit: Sequence (10.5) and similar sequences for \({\mathcal {H}}_-\) and L yield commutative diagrams

and

We would like to show that \({}^{\mathcal {L}}{\mathcal {F}}\) is of pure Gaussian type \({\widehat{C}}=-1/C\). The considerations from the previous sections suggest using the following sectors:

The Stokes directions for \({\widehat{C}}\) are \(\frac{\pi }{4}+\frac{1}{2}\arg C+k\frac{\pi }{2}\). Hence, \(\widehat{\theta }_0=\pi +\frac{1}{2}\arg C\) is indeed generic and the \(\widehat{{\mathcal {S}}}_k\) are compatible with the sectors \({\widehat{S}}_k=\{w\in {\mathbb {C}}\mid \arg w\in [\widehat{\theta }_0+(k-1)\frac{\pi }{2}, \widehat{\theta }_0+k\frac{\pi }{2}]\}\) in the sense of Lemma 7.4. (An a posteriori justification for the choice of the generic direction is given by Proposition 10.8). We have \(\widehat{{\mathcal {H}}}_+=\widehat{{\mathcal {S}}}_3\cup \widehat{{\mathcal {S}}}_4\) and \(\widehat{{\mathcal {H}}}_-=\widehat{{\mathcal {S}}}_1\cup \widehat{{\mathcal {S}}}_2\), and we set  .
.
Proposition 10.7
The enhanced Fourier–Sato transform \({}^{\mathcal {L}}{\mathcal {F}}\) is concentrated in degree zero and for every \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\), we have an isomorphism in \(\mathrm {D}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}_w\times {\mathbb {R}}})\)

In particular, \({}^{\mathcal {L}}{\mathcal {F}}\) is of pure Gaussian type \({\widehat{C}}=-1/C\).
Proof
We prove the desired isomorphism for \(k=1\).
From (10.6), we get a distinguished triangle

Here, the kernels are the ones from Proposition 10.6. The first morphism is induced by the ones described in (10.7) and (10.8).
Firstly, we note that \(\ker (\mathbb {1}-\sigma _3)_{\widehat{{\mathcal {S}}}_1}\simeq 0\) since it is the kernel of the morphism

and on \(\widehat{{\mathcal {S}}}_{41}\) we have \(c_2w_1-c_1w_2=0\), hence  and
and  .
.
Secondly, we determine \(\ker (\sigma _1-\mathbb {1})_{\widehat{{\mathcal {S}}}_1}\): It is the first object in the short exact sequence

Thirdly, we find \(\ker (\mathbb {1}-\sigma _4\sigma _3)_{\widehat{{\mathcal {S}}}_1}\) as the first object in the short exact sequence

Finally, there is a commutative diagram in which the sequences (10.10) and (10.11) appear as the columns, and which has exact rows and columns:

Comparing the upper row of this diagram with the long exact sequence associated to (10.9), the statement of the proposition follows. \(\square \)
10.4 Stokes multipliers of the Fourier–Laplace transform
We have seen in Proposition 10.7 that \({}^{\mathcal {L}}{\mathcal {F}}\) is isomorphic to a direct sum of exponential enhanced sheaves on each of the \(\widehat{{\mathcal {S}}}_k\) (and such isomorphisms have actually been constructed). Therefore, on each of the half-lines \(\widehat{{\mathcal {S}}}_{k,k+1}\) we have two trivializing isomorphisms \({\widehat{\alpha }}_k\) and \(\widehat{\alpha }_{k+1}\) coming from the ones on the two adjacent sectors. Our aim is to find matrices \({\widehat{\sigma }}_k\) representing an automorphism of  such that the following diagram commutes for any \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\):
such that the following diagram commutes for any \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\):

Note that  and the order on \({\widehat{C}}\) with respect to \(\widehat{\theta }_0\) is the one induced by the order on C with respect to \(\theta _0\), i.e. \(c<_{\theta _0} d\) if and only if \({\widehat{c}}<_{\widehat{\theta }_0}{\widehat{d}}\).
and the order on \({\widehat{C}}\) with respect to \(\widehat{\theta }_0\) is the one induced by the order on C with respect to \(\theta _0\), i.e. \(c<_{\theta _0} d\) if and only if \({\widehat{c}}<_{\widehat{\theta }_0}{\widehat{d}}\).
Proposition 10.8
Gluing matrices for \({}^{\mathcal {L}}{\mathcal {F}}\) are given by \({\widehat{\sigma }}_k=\sigma _k\), \(k\in {\mathbb {Z}}/4{\mathbb {Z}}\).
Proof
Let us give the proof for \(\widehat{\sigma }_1=\sigma _1\).
By what we learnt in Proposition 10.7, the triangle (10.9) is actually a short exact sequence (identifying \({}^{\mathcal {L}}{\mathcal {F}}\) with \(\mathrm {H}^0({}^{\mathcal {L}}{\mathcal {F}})\))

On \(\widehat{{\mathcal {S}}}_1\) (i.e. applying \((\bullet )_{\widehat{{\mathcal {S}}}_1}\)), it induces

since we proved \(\ker (\mathbb {1}-\sigma _3)_{\widehat{{\mathcal {S}}}_1}\simeq 0\). We obtained determinations of \(\ker (\sigma _1-\mathbb {1})_{\widehat{{\mathcal {S}}}_1}\) and \(\ker (\mathbb {1}-\sigma _4\sigma _3)_{\widehat{{\mathcal {S}}}_1}\) and hence the isomorphism \(\widehat{\alpha }_1\) as the third vertical arrow in the diagram

Similarly, \(\widehat{\alpha }_2\) is obtained from the diagram

Now we can take the right square of diagrams (10.13) and (10.14), apply the functor \((\bullet )_{\widehat{{\mathcal {S}}}_{12}}\) and identify their first lines, and we obtain

and the bent arrow on the right is the one in question. Therefore, it remains to determine the bent one on the left.
The object \(\ker (\mathbb {1}-\sigma _4\sigma _3)_{\widehat{{\mathcal {S}}}_1}\) was determined by the short exact sequence

and the object \(\ker (\mathbb {1}-\sigma _4\sigma _3)_{\widehat{{\mathcal {S}}}_2}\) by the sequence

Applying the functor \((\bullet )_{\widehat{{\mathcal {S}}}_{12}}\), the second and third objects of both sequences are identified (since \(w_1=0\) on \(\widehat{{\mathcal {S}}}_{12}\)) and the induced isomorphism between the first objects (which is the left bent arrow from (10.15)) is clearly given by \(\sigma _2\sigma _1\). Therefore, it follows from (10.15) that \(\widehat{\sigma }_1=\sigma _1\). \(\square \)
This concludes the proof of Theorem 10.1.
11 A more general case
In this section, we show how the methods of the previous section can be adapted to a case with weaker assumptions on the parameter set C. In contrast to [30], this yields an explicit solution to the problem of finding a transformation rule for Stokes data in more general cases than in Sect. 10. Although Corollary 4.19 in loc. cit. provided a theoretical answer by stating that arbitrary parameter configurations can be deformed into those studied in the previous section, this answer was not at all explicit.
We restrict to the case where \(C=\{c,d\}\) consists of two parameters and the ranks of the regular parts are \(r_c=r_d=1\) (and we suppress  in our notation).
in our notation).
Condition 11.1
We say that an ordered pair (c, d) of nonzero complex numbers \(c,d\in {\mathbb {C}}^\times \) satisfies condition ( ) if the following is satisfied:
) if the following is satisfied:

where we write \(c=c_1+ic_2\) and \(d=d_1+id_2\) with their real and imaginary parts.
Let \(C=\{c,d\}\subset {\mathbb {C}}^\times \) such that ( ) is satisfied. Set
) is satisfied. Set  . It is a generic direction since the Stokes directions are \(-\frac{\pi }{4}-\frac{\arg (d-c)}{2}+k\frac{\pi }{2}\). Let \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) be a family of four \(2\times 2\)-matrices such that \(\sigma _k\) is upper-triangular (resp. lower-triangular) if k is odd (resp. even) and \(\sigma _4\sigma _3\sigma _2\sigma _1=\mathbb {1}\).
. It is a generic direction since the Stokes directions are \(-\frac{\pi }{4}-\frac{\arg (d-c)}{2}+k\frac{\pi }{2}\). Let \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) be a family of four \(2\times 2\)-matrices such that \(\sigma _k\) is upper-triangular (resp. lower-triangular) if k is odd (resp. even) and \(\sigma _4\sigma _3\sigma _2\sigma _1=\mathbb {1}\).
Theorem 11.2
Let C, \(\theta _0\) and \(\sigma \) be as above. If we set  and
and  , there is an isomorphism in \({\mathsf {D}}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}\times {\mathbb {R}}})\)
, there is an isomorphism in \({\mathsf {D}}^\mathrm {b}({\mathbf {k}}_{{\mathbb {C}}\times {\mathbb {R}}})\)
Corollary 11.3
Let \({\mathcal {M}}\) be of pure Gaussian type \(C=\{c,d\}\) such that ( ) holds. Then \({}^{\mathsf {L}}{\mathcal {M}}\) is of pure Gaussian type \({\widehat{C}}=\{-\frac{1}{c},-\frac{1}{d}\}\). Moreover, if \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) is a family of Stokes multipliers for \({\mathcal {M}}\) with respect to the generic direction \(\theta _0=-\frac{1}{2}\arg c\), then \(\sigma \) is also a family of Stokes multipliers for \({}^{\mathsf {L}}{\mathcal {M}}\) with respect to the generic direction \(\widehat{\theta }_0=\pi -\theta _0\).
) holds. Then \({}^{\mathsf {L}}{\mathcal {M}}\) is of pure Gaussian type \({\widehat{C}}=\{-\frac{1}{c},-\frac{1}{d}\}\). Moreover, if \(\sigma =(\sigma _k)_{k\in {\mathbb {Z}}/4{\mathbb {Z}}}\) is a family of Stokes multipliers for \({\mathcal {M}}\) with respect to the generic direction \(\theta _0=-\frac{1}{2}\arg c\), then \(\sigma \) is also a family of Stokes multipliers for \({}^{\mathsf {L}}{\mathcal {M}}\) with respect to the generic direction \(\widehat{\theta }_0=\pi -\theta _0\).
Proof of Theorem 11.2
First, we choose a sector decomposition analogously to Sect. 10.2, replacing \(\arg C\) by \(\arg c\), i.e.

Next, we compute the enhanced Fourier–Sato transforms of the exponentials involved: For the parameter c, this is exactly the same computation that we performed above, i.e.

(see Proposition 10.4, we write  instead of
instead of  etc. here). For the exponentials
etc. here). For the exponentials  , one proceeds similarly. However, the coordinate transform for the parameter d (similar to (10.2)) does not transform \({\mathcal {S}}_k\) into right-angled sectors. Hence, the geometry of the intersection spaces is more involved, yet it is still not too difficult to determine the compactly supported cohomologies, and we find that
, one proceeds similarly. However, the coordinate transform for the parameter d (similar to (10.2)) does not transform \({\mathcal {S}}_k\) into right-angled sectors. Hence, the geometry of the intersection spaces is more involved, yet it is still not too difficult to determine the compactly supported cohomologies, and we find that

Here, the functions \(\psi _{\mathrm {r}}^+,\psi _{\mathrm {r}}^-:{\mathbb {C}}_w\rightarrow {\mathbb {R}}\) are defined by

and

where  and \(\psi _{\mathrm {l}}^+,\psi _{\mathrm {l}}^-:{\mathbb {C}}_w\rightarrow {\mathbb {R}}\) are similar (with cases interchanged). Moreover,
and \(\psi _{\mathrm {l}}^+,\psi _{\mathrm {l}}^-:{\mathbb {C}}_w\rightarrow {\mathbb {R}}\) are similar (with cases interchanged). Moreover,

One can now determine \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {H}}_+})\), \({}^{\mathcal {L}}({\mathcal {F}}_{{\mathcal {H}}_-})\) and \({}^{\mathcal {L}}({\mathcal {F}}_{L})\) by enhanced Fourier–Sato transform of short exact sequences (cf. Proposition 10.6). One then proves isomorphisms

where the sectors \(\widehat{{\mathcal {S}}}_k\) are defined as in Sect. 10.3 (with \(\arg C\) replaced by \(\arg c\)), i.e.

The main difference is the fact that the supports of the Fourier–Sato transforms of the  (i.e. the sets \(Y_k\)) are not unions of these sectors (see Fig. 4). Therefore, if we want to mimick the proof of Proposition 10.7 (for \(k=1\)), we will not have \(\ker (\mathbb {1}-\sigma _3)\simeq 0\), but the second summand of \(\ker (\sigma _1-\mathbb {1})\) “splits” into two parts. The diagram correponding to (10.12) in this case then looks as follows (we write direct sums vertically):
(i.e. the sets \(Y_k\)) are not unions of these sectors (see Fig. 4). Therefore, if we want to mimick the proof of Proposition 10.7 (for \(k=1\)), we will not have \(\ker (\mathbb {1}-\sigma _3)\simeq 0\), but the second summand of \(\ker (\sigma _1-\mathbb {1})\) “splits” into two parts. The diagram correponding to (10.12) in this case then looks as follows (we write direct sums vertically):

Although the left part of the diagram becomes more complicated, the cokernel of the morphism in the first line is as desired.
The computation of transition matrices for \({}^{\mathcal {L}}{\mathcal {F}}\) then works analogously to that in the aligned case. \(\square \)
A generalization to more than two parameters (and ranks not equal to 1) is easily possible: One then needs to require that the elements of \(C=\{c_{(1)},\ldots , c_{(n)}\}\) satisfy condition ( ) “pairwise”, i.e. \((c_{(k)},c_{(k+1)})\) satisfies condition (
) “pairwise”, i.e. \((c_{(k)},c_{(k+1)})\) satisfies condition ( ) for any \(k\in \{1,\ldots , n-1\}\).
) for any \(k\in \{1,\ldots , n-1\}\).
This result shows that the considerations of Sect. 10 can—with a little effort, but without serious difficulties—be adapted to more general situations. Our assumptions were chosen in such a way that we were able to reuse some results from the aligned case. However, under different assumptions on the parameters, one can proceed similarly, as long as one can choose suitable sectors in the domain and target of the Fourier–Laplace transform keeping the topological situation reasonable.
Change history
04 June 2021
Funding notes added
References
Björk, J.-E.: Analytic \({\cal{D}}\)-Modules and Applications, Mathematics and Its Applications, vol. 247. Kluwer Academic Publishers, Dordrecht (1993)
Boalch, P.: Simply-laced isomonodromy systems. Publ. Math. Inst. Hautes Études Sci. 116, 1–68 (2012)
Boalch, P.: Global Weyl groups and a new theory of multiplicative quiver varieties. Geom. Topol. 19, 3467–3536 (2015)
D’Agnolo, A., Hien, M., Morando, G., Sabbah, C.: Topological computation of some Stokes phenomena on the affine line. Ann. Inst. Fourier 70, 739–808 (2020)
D’Agnolo, A., Kashiwara, M.: Riemann-Hilbert correspondence for holonomic D-modules. Publ. Math. Inst. Hautes Études Sci. 123, 69–197 (2016)
D’Agnolo, A., Kashiwara, M.: A microlocal approach to the enhanced Fourier-Sato transform in dimension one. Adv. Math. 339, 1–59 (2018)
D’Agnolo, A., Kashiwara, M.: Enhanced perversities. J. Reine Angew. Math. 751, 185–241 (2019)
Deligne, P.: Lettre à B. Malgrange du 19/4/1978. In: Singularités irrégulières, Correspondance et documents, Documents mathématiques 5, Société Mathématique de France, Paris, pp. 25–26 (2007)
Gelfand, S.I., Manin, Y.I.: Methods of Homological Algebra, 2nd edn. Springer Monographs in Mathematics. Springer, Berlin (2003)
Hien, M., Sabbah, C.: The local Laplace transform of an elementary irregular meromorphic connection. Rend. Sem. Mat. Univ. Padova 134, 133–196 (2015)
Hohl, A.: D-Modules of Pure Gaussian Type from the Viewpoint of Enhanced Ind-Sheaves. Universität Augsburg. https://opus.bibliothek.uni-augsburg.de/opus4/79690 (2020). Accessed 20 October 2020
Hotta, R., Takeuchi, K., Tanisaki, T.: D-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics, vol. 292. Birkhäuser, Boston (2008)
Ito, Y., Takeuchi, K.: On irregularities of Fourier transforms of regular holonomic D-modules. Adv. Math. 366, (2020)
Kashiwara, M.: The Riemann-Hilbert problem for holonomic systems. Publ. Res. Inst. Math. Sci. 20, 319–365 (1984)
Kashiwara, M.: D-Modules and Microlocal Calculus, Translations of Mathematical Monographs, vol. 217. American Mathematical Society, Providence (2003)
Kashiwara, M.: Riemann-Hilbert correspondence for irregular holonomic \({\cal{D}}\)-modules. Jpn. J. Math. 11, 113–149 (2016)
Kashiwara, M., Schapira, P.: Sheaves on Manifolds, Grundlehren der mathematischen Wissenschaften, vol. 292. Springer, Berlin (1990)
Kashiwara, M., Schapira, P.: Ind-sheaves. Astérisque 271, (2001)
Kashiwara, M., Schapira, P.: Categories and Sheaves, Grundlehren der mathematischen Wissenschaften, vol. 332. Springer, Berlin (2006)
Kashiwara, M., Schapira, P.: Regular and Irregular Holonomic D-modules, London Mathematical Society Lecture Note Series, vol. 433. Cambridge University Press, Cambridge (2016)
Kashiwara, M., Schapira, P.: Irregular holonomic kernels and Laplace transform. Sel. Math. New Ser. 22, 55–109 (2016)
Katz, N.M., Laumon, G.: Transformation de Fourier et majoration de sommes exponentielles. Publ. Math. Inst. Hautes Études Sci. 62, 145–202 (1985)
Malgrange, B.: Équations différentielles à coefficients polynomiaux, Progress in Mathematics, vol. 96. Birkhëuser, Boston (1991)
Mochizuki, T.: Note on the Stokes structure of Fourier transform. Acta Math. Vietnam. 35, 107–158 (2010)
Mochizuki, T.: Holonomic \({\cal{D}}\)-modules with Betti structure. Mém. Soc. Math. Fr. (N.S.) 138–139, Soc. Math. France, Paris (2014)
Mochizuki, T.: Curve test for enhanced ind-sheaves and holonomic D-modules. arXiv:1610.08572v3 (2018)
Mochizuki, T.: Stokes shells and Fourier transforms. arXiv:1808.01037v1 (2018)
Sabbah, C.: An explicit stationary phase formula for the local formal Fourier-Laplace transform. Contemp. Math. 474, 309–330 (2008)
Sabbah, C.: Introduction to Stokes Structures. Lecture Notes in Mathematics, vol. 2060. Springer, Berlin (2013)
Sabbah, C.: Differential systems of pure Gaussian type. Izv. Math. 80, 189–220 (2016)
Acknowledgements
I would like to thank Marco Hien, Andrea D’Agnolo and Claude Sabbah for inspiring discussions on this subject, as well as for some useful comments during the preparation of this work.
Funding
The author was partially supported by a doctoral scholarship of “Studenstiftung des deutschen Volkes”. Open access funding enabled and organized by Projekt DEAL
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hohl, A. D-modules of pure Gaussian type and enhanced ind-sheaves. manuscripta math. 167, 435–467 (2022). https://doi.org/10.1007/s00229-021-01281-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-021-01281-y



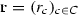 of natural numbers
of natural numbers 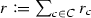 ) such that
) such that 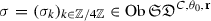 is a family of four block matrices with the properties:
is a family of four block matrices with the properties: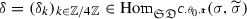 between two objects
between two objects 


 ) if and only if d lies in the cone with vertex c and bounded by the directions
) if and only if d lies in the cone with vertex c and bounded by the directions 