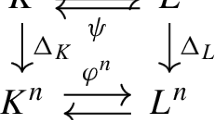A motivic local Cauchy-Crofton formula

Abstract

In this note, we establish a version of the local Cauchy-Crofton formula for definable sets in Henselian discretely valued fields of characteristic zero. It allows to compute the motivic local density of a set from the densities of its projections integrated over the Grassmannian.

1 Introduction

The classical Cauchy-Crofton formula is a geometric measure theory result stating that the volume of some set X of dimension d can be recovered by integrating over the Grassmannian the number of points of intersection of X with affine spaces of codimension d, see for example [11]. It has been used by Lion in [13] to show the existence of the local density of semi-Pfaffian sets. In [7] and [8], Comte has established a local version of the formula for sets $X\subseteq {\mathbb {R}}^n$ definable in an o-minimal structure. The formula states that the local density of such a set X can be recovered by integrating over a Grassmannian the density of the projection of X on subspaces. This allows him to show the continuity of the real local density along Verdier’s strata in [8]. This result was generalized by Valette in [14] who shows that the continuity also holds along Whitney’s strata.

The local Cauchy-Crofton formula appears as a first step toward comparing the local Lipschitz-Killing curvature invariants and the polar invariants of a germ of a definable set $X\subseteq {\mathbb {R}}^n$. It is shown by Comte and Merle in [10] that one can recover one set of invariants by linear combination of the other, see also [9].

A notion of local density for definable sets in Henselian valued fields of characteristic zero has been developed by the author in [12]. The aim of this note is to establish a motivic analogue of the local Cauchy-Crofton formula. Our formula is a new step toward developing a theory of higher local curvature invariants in non-Archimedean geometry.

We now describe briefly our formula in a particular case, see the next section for precise definitions. Fix an algebraically closed field k of characteristic zero and $K=k((t ))$. Fix X a semi-algebraic subset of $K^n$ of dimension d (or more generaly a definable set in the Denef-Pas language). We use the motivic integral of Cluckers and Loeser [5], which takes values in the localised Grothendieck ring of varieties ${\mathbf{K}}({{\mathrm {Var}}}_{k})_{\mathrm {loc}}$. Denote by $\Theta _d(X,x)$ the motivic local density of X at x. Let G(n, d) be the Grassmannian variety of d-dimensional vector subspaces of $K^n$. There is a volume form $\omega _{n,d}$ invariant under $GL_n({\mathcal {O}}_K)$-transformations such that $1=\int _{G(n,d)} \omega _{n,d}$. For $V\in G(n,n-d)$, let $p_V : K^n\rightarrow K^n/V$ be the canonical projection. There is a dense definable subset $\Omega \subseteq G(n,n-d)$ such that for $V\in \Omega$, $p_V$ is finite-to-one on ${\bar{X}}$ intersected with a small enough ball B(x, r) around x of valuative radius r. Let $\mathbb {1}_X$ be the characteristic function of X and recall from [5] the relative to $K^n/V$ push-forward $p_{V!K^n/V}$ for constructible motivic functions. Set $p_{V!,x}(\mathbb {1}_X):=p_{V!K^n/V}(\mathbb {1}_{X\cap B(x,r)})$, which is independent of the large enough r chosen. Intuitively, $p_{V!,x}(\mathbb {1}_X)$ is a constructible motivic function supported on $p_V(X)$ that takes into account motivically the cardinal of finite fibers of $p_V$ restricted to X. The motivic local Cauchy-Crofton formula is the following equality:

$$\begin{aligned} \Theta _d(X,x)=\int _{V\in \Omega \subseteq G(n,n-d)} \Theta _d(p_{V!,x}(\mathbb {1}_X),0) \omega _{n,n-d}(V). \end{aligned}$$

Our precise result appears as Theorem 4.1 at the end of Section 4 and applies more generally to any definable set in a tame or mixed tame theory of valued fields in the sense of [6].

A p-adic analogue has been developed by Cluckers, Comte and Loeser in [2, Section 6]. We will follow closely their approach. In the real and p-adic cases, the function $p_{V!,x}(\mathbb {1}_X)$ is replaced by the function sending $y\in p_V(X)$ to the cardinal of the finite set $p_V^{-1}(y)$. As usual in a motivic context, such a choice would not lead to the correct result.

2 Motivic integration and local density

We assume the reader is familiar with the notion of motivic local density developed by the author in [12] and in particular with Cluckers and Loeser’s theory of motivic integration [5, 6]. See [12, Section 2.7] for a short summary of the theory.

We adopt the notations and conventions of [12], let us recall the main notions we need. We fix ${\mathcal {T}}$, a tame or mixed-tame theory of valued fields in the sense of [6]. Such a ${\mathcal {T}}$ always admits a Henselian discretely valued field of characteristic zero as a model. Definable means definable in ${\mathcal {T}}$ without parameters and A-definable means definable in ${\mathcal {T}}$ with parameters in A. We fix K (the underlining valued field of) a model of ${\mathcal {T}}$ with discrete value group and residue field k saturated enough. The valuation is denoted by ${\mathrm {ord}}: K\rightarrow {\mathbb {Z}}\cup \left\{ +\infty \right\}$, and the language contains also the angular component map $\overline{{\mathrm {ac}}}: K^\times \rightarrow k^\times$. The language contains a symbol t interpreted as a uniformizer of the valuation ring of K. In particular, ${\mathrm {ord}}(t)=1$ and $\overline{{\mathrm {ac}}}(t)=1$

For example, we can take for ${\mathcal {T}}$ the theory of a discretely valued field of characteristic zero in the 3-sorted Denef-Pas language.

If the residue field is of characteristic $p>0$, one needs to add the higher angular components with values in the higher residue sorts $R_s$, which are defined as ${\mathcal {O}}_K$ modulo the ideal generated by s times the maximal ideal. Note that this convention differs from [6], but is the one adopted in [3]. This has the advantage that when K is of equicharacteristic zero, one has $R_s=k$ for every $s\in {\mathbb {N}}^*$ and $\overline{{\mathrm {ac}}}_s=\overline{{\mathrm {ac}}}$. One of the conditions of tameness is that for every definable set $X\subset K$ (possibly with parameters from K), there is a definable map $g: X\subset K\rightarrow R_s^t$ such that for every $\xi \in R_s^t$, there are $n\in {\mathbb {N}}^*$, $\eta \in R_n$ and $c(\xi )\in K$ such that $g^{-1}(\xi )$ is a union (indexed by $\gamma$ in some subset $A\subset \Gamma \cup \left\{ +\infty \right\}$) of balls of the form

$$\begin{aligned} \left\{ x\in K\mid \overline{{\mathrm {ac}}}_{n}(x-c(\xi ))=\eta , {\mathrm {ord}}(x-c(\xi ))=\gamma \right\} , \end{aligned}$$

and such that c, viewed as a function of $\xi$, has finite image. As observed in [3, Section 2.2], thanks to our convention for the residue rings $R_s$, one can ask in the previous condition that $s=t$, this being also valid in equicharacteristic zero, since in that case $R_s^s=k^s$, with k the residue field.

This implies that for for every finite definable set $X\subset K^n$, or more generally for every definable map $\pi : X\rightarrow Y$ that is finite-to-one, there is a definable map $g: X\rightarrow R_s^s$ such that for every $y\in Y$, the restriction of g to $\pi ^{-1}(y)$ is injective. Phrased differently, there is a definable bijection ${\tilde{g}}$ from X to a definable subset of $Y\times R_s^s$ compatible with the projection to Y.

To each definable set X, Cluckers and Loeser assign a ring of constructible motivic functions ${\mathcal {C}}(X)$, which includes the characteristic functions of any definable set $Y\subseteq X$. For $\varphi \in {\mathcal {C}}(X)$ of support of dimension at most d and integrable, they define

$$\begin{aligned} \int ^d \varphi \in {\mathcal {C}}(\left\{ *\right\} ). \end{aligned}$$

If $d=\dim (X)$, we drop the d from the notation. If $\varphi$ is the characteristic function of some definable set $Y\subseteq X$, we denote the integral by $\mu _d(Y)$.

If the theory of the residue field is that of algebraically closed field with parameters in k, the target ring of motivic integration is equal to

$$\begin{aligned} {\mathcal {C}}(\left\{ *\right\} )={{\mathbf{K}}({{\mathrm {Var}}}_{k})}_{\mathrm {loc}}:={\mathbf{K}}({{\mathrm {Var}}}_{k})\left[ {\mathbb {L}}^{-1},\left( \frac{1}{1-{\mathbb {L}}^{-\alpha }}\right) _{\alpha \in {\mathbb {N}}^*}\right] , \end{aligned}$$

where ${\mathbb {L}}=[{\mathbb {A}}^1_k]$.

Fix some definable set $X\subseteq K^n$ of dimension at most d, $x\in K^n$ and set

$$\begin{aligned} \theta _m=\frac{\mu _d(X\cap B(x,m))}{{\mathbb {L}}^{-md}}, \end{aligned}$$

where B(x, m) is the ball of center x and valuative radius m.

It is shown in [12, Section 3.1] that there is some $e\in {\mathbb {N}}^*$ such that for each $i\in \left\{ 0,\dots , e-1\right\}$, the subsequence $(\theta _{ke+i})_{k\in {\mathbb {N}}}$ converges to some $d_i\in {\mathcal {C}}(\left\{ x\right\} )$. Here ${\mathcal {C}}(\left\{ x\right\} )$ has a topology induced by the degree in ${\mathbb {L}}$. The motivic local density of X at x is defined to be

$$\begin{aligned} \Theta _d(X,x)=\frac{1}{e}\sum _{i=0}^{e-1} d_i\in {\mathcal {C}}(\left\{ x\right\} )\otimes {\mathbb {Q}}. \end{aligned}$$

It is shown in [12, Lemma 3.7] that one obtains the same $\Theta _d(X,x)$ if one replaces $\theta _m$ by $\theta '_m:=\frac{\mu _d(X\cap S(x,m))}{{\mathbb {L}}^{-md}(1-{\mathbb {L}}^{-d})}$, where S(x, m) is the sphere around x of valuative radius m.

Recall that a constructible motivic function $\varphi \in {\mathcal {C}}(K^n)$ is said to be locally bounded if for every $x\in K^n$, there is some $r\in {\mathbb {N}}$ such that $\mathbb {1}_{B(x,r)}\varphi$ is bounded. One extends the definition of motivic density to such functions by replacing in the above definition $\mu _d(X\cap B(x,m))$ by $\int ^d \mathbb {1}_{B(x,m)}\varphi$. If $\varphi \in {\mathcal {C}}(K^n)$ is locally bounded and of support of dimension at most d, this is well-defined and we denote the local density of $\varphi$ at x by $\Theta _d(\varphi ,x)$.

It is shown in [12] that one can compute the motivic local density on the tangent cone, as follows. Fix some $\Lambda \in {\mathcal {D}}$, where ${\mathcal {D}}=\left\{ \Lambda _{n,m}\mid n,m\in {\mathbb {N}}^*\right\}$ and

$$\begin{aligned} \Lambda _{n,m}=\left\{ \lambda \in K^\times \mid \overline{{\mathrm {ac}}}_m(\lambda )=1, {\mathrm {ord}}(\lambda )=0 \mod n\right\} \!. \end{aligned}$$

The $\Lambda$-tangent cone of X at x is the definable set

$$\begin{aligned} C_x^\Lambda (X)= & {} \{ u\in K^n\mid \forall i\in {\mathbb {Z}}, \exists y\in X, \exists \lambda \in \Lambda , {\mathrm {ord}}(y-x)\ge i, \\&\quad {{\mathrm {ord}}(\lambda (y-x)-u)\ge i}\}. \end{aligned}$$

It can and will be useful to also consider the above definition with $\Lambda =K^\times$.

Let $x\in K^n$. The $\Lambda$-tangent cone with multiplicities is a constructible motivic function $CM_x^\Lambda (X)\in {\mathcal {C}}(K^n)$, of support $C_x^\Lambda (X)$, well defined up to a set of dimension $<d$. For example, if $X\subseteq K^n$ is of dimension n, there is no multiplicity to take into account and $CM_x^\Lambda (X)$ is the characteristic function of $C_x^\Lambda (X)$.

Theorems 3.25 and 5.12 of [12] state that there is a $\Lambda \in {\mathcal {D}}$ such that for all $\Lambda '\subseteq \Lambda$, $C_x^\Lambda (X)=C_x^{\Lambda '}(X)$ and $\Theta _d(X,x)=\Theta _d(CM_x^\Lambda (X),0).$

3 Local constructible functions

Consider a definable function $\pi : X\rightarrow Y$ between definable sets X and Y of dimension n. Recall from [5, Section 14.1] the relative push-forward $\pi _{!Y}(\varphi )\in {\mathcal {C}}(Y)$ for any motivic constructible function $\varphi \in {\mathcal {C}}(X)$ integrable relatively to Y. If $\pi$ is finite-to-one, any $\varphi \in {\mathcal {C}}(X)$ is integrable relatively to Y, and the push-forward is computed as follows. There is a definable bijection ${\tilde{g}} : X\rightarrow Z\subseteq Y\times R_s^s$ over Y, meaning that $\pi$ is equal to the composition of ${\tilde{g}}$ and the coordinate projection ${\mathrm {proj}}$ of Z to Y. Then $\pi _{!Y}(\mathbb {1}_X)$ is equal to the class of Z in the relative Grothendieck group of varieties over Y. Indeed, since one works relatively to Y, the order of Jacobian in the change of variable formula is computed relatively to Y, hence is 0 by [5, Section 8.5] (see also [5, Remark 14.2.3]). More generally, if $\varphi \in {\mathcal {C}}(X)$, then $\pi _{!Y}(\varphi )={\mathrm {proj}}_!({\tilde{g}}^{-1*}(\varphi ))$, where ${\mathrm {proj}}_!$ is the push-forward for residue variables [5, Section 5.6], which does not change if one works relatively to Y or not.

If X is a definable subset of $K^{n}$ and ${x_0}\in K^n$, define the ring of germs of constructible motivic functions at ${x_0}$ by ${\mathcal {C}}(X)_{x_0}:={\mathcal {C}}(X)/\sim$, where $\varphi \sim \psi$ if there is an $r\in {\mathbb {N}}$ such that $\mathbb {1}_{B({x_0},r)}\varphi =\mathbb {1}_{B({x_0},r)}\psi$. This ring is only interesting if ${x_0}$ is in the closure ${\bar{X}}$ of X, otherwise it is trivial. In particular, if $\varphi \sim \psi$ are locally bounded, then $\Theta _d(\varphi ,{x_0})=\Theta _d(\psi ,{x_0})$ hence the local motivic density is defined on ${\mathcal {C}}(K^n)_{x_0}$.

Consider now a linear projection $\pi : K^n\rightarrow K^d$ and let $X\subseteq K^n$ be a definable set of dimension at most d. We say that $(X,\pi )$ satisfies condition $(*)$ at a point ${x_0}\in K^n$ if $\pi _{\vert {\bar{X}}\cap B({x_0},r)}$ is finite-to-one for some $r\ge 0$.

Assuming that $(X,\pi )$ satisfies condition $(*)$ at ${x_0}$, set $\pi _{!,{x_0}}(\varphi )=\pi _{!K^d}(\mathbb {1}_{B({x_0},r)}\varphi )\in {\mathcal {C}}(K^d)_{\pi ({x_0})}$ for $\varphi \in {\mathcal {C}}(X)_{x_0}$

We will show that it is well defined. If r is large enough, $\pi _{\vert X\cap B({x_0},r)}$ is finite-to-one hence $\mathbb {1}_{B({x_0},r)}\varphi$ is integrable relatively to $K^d$, hence $\pi _{!K^d}(\mathbb {1}_{B({x_0},r)}\varphi )$ is defined in ${\mathcal {C}}(K^d)$. We need to show that for every r, there is some $r'$ such that $\mathbb {1}_{B(\pi ({x_0}),r')}\pi _{!K^d}(\mathbb {1}_{B({x_0},r)}\varphi )$ does not depend on r.

To do so, fix some $r_0$ such that $\pi _{\vert {\bar{X}}\cap B({x_0},r_0)}$ is finite-to-one, replace X by $X\cap B({x_0},r_0)$, and let $r\ge r_0$. Since $\pi : {\bar{X}} \rightarrow K^d$ is finite-to-one, one can assume, up to enlarging $r_0$, that $\pi ^{-1}(\pi ({x_0}))\cap {\bar{X}}=\left\{ {x_0}\right\}$. By tameness, there is a definable map $g:X\rightarrow R_s^s$ such that for each $y\in K^d$, the restriction of g to $\pi ^{-1}({y})$ is injective. Set $W=\left\{ (\pi (x),g(x))\mid x\in X\right\}$. Hence g induces a bijection ${\tilde{g}}: {x}\in X\mapsto (\pi ({x}),g({x}))\in W$. Given the definition of $\pi _{!K^d}$ recalled above, one needs to show that for any any $r\ge r_0$, there is an $r'$ such that, $X\cap \pi ^{-1}(B(\pi ({x_0}),r'))\subset X\cap B({x_0},r)$. Indeed, this implies that $\mathbb {1}_{B(\pi ({x_0}),r')}\pi _{!K^d}(\mathbb {1}_{B({x_0},r)}\mathbb {1}_X)=\mathbb {1}_{B(\pi ({x_0}),r')}[W_{/\pi (X)}]$, hence it does not depend on r. More generally for a $\varphi \in {\mathcal {C}}(K^d)$, $\pi _{!K^d}(\mathbb {1}_{B({x_0},r)}\varphi )=\mathbb {1}_{B(\pi ({x_0}),r')}{\mathrm {proj}}_!({\tilde{g}}^{-1*}(\varphi ))$.

To prove that for any $r\ge r_0$, there is an $r'$ such that, $X\cap \pi ^{-1}(B(\pi ({x_0}),r'))\subset X\cap B({x_0},r)$, observe that it is enough to prove that for every $\xi \in R_s^s$, there is some $\xi$-definable $r'=r'(\xi )$ such that $g^{-1}(\xi )\cap \pi ^{-1}(B(\pi ({x_0}),r'))\subset g^{-1}(\xi )\cap B({x_0},r)$. Indeed, by orthogonality between residue rings and value group, $r'$ can then be chosen independently of $\xi$.

To show the existence of such an $r'(\xi )$, observe that either $\pi ({x_0})$ is not in the closure of $\pi (g^{-1}(\xi ))$, in which case for $r'(\xi )$ large enough, the left hand side is empty. Either $\pi ({x_0})$ is in the closure of $\pi (g^{-1}(\xi ))$. In that case, one considers the map c that send $y\in \pi (g^{-1}(\xi ))$ to the unique x such that $g(x)=\xi$ and $\pi (x)=y$. Because $\pi ^{-1}(\pi ({x_0}))\cap {\bar{X}}=\left\{ {x_0}\right\}$, the only limit value of c(y) when y goes to $\pi ({x_0})$ is ${x_0}$. Since c is $\xi$-definable and bounded, by Lemma 2.20 of [12] there is an $r'(\xi )$ such that $c(B(\pi ({x_0}),r'))\subset B({x_0},r)$, which precisely means that $\pi ^{-1}(\pi (g^{-1}(\xi ))\cap B(\pi ({x_0}),r'))\subset B({x_0},r)\cap X$.

4 Grassmannians

Fix a point $x\in K^n$ and view $K^n$ as a K-vector space with origin x. Then denote by $G(n,d)_K$ the Grassmannian of dimension d subvector spaces of $K^n$. The canonical volume form on $G(n,d)_K$ invariant under $GL_n({\mathcal {O}}_K)$-transformations induces a constuctible function $\omega _{n,d}$ on G(n, d) invariant under $GL_n({\mathcal {O}}_K)$ transformations, see [5, Section 15] for details. Since $G(n,d)_k$ is smooth and proper of dimension $d(n-d)$, the motivic volume of $G(n,d)_K$ is equal to $[G(n,d)_k]{\mathbb {L}}^{-d(n-d)}$, where $[G(n,d)_k]$ is the class of $G(n,d)_k$ in the (localized) Grothendieck group of varieties over the residue field k. Denoting by ${\mathbb {F}}_q$ the finite field with q elements, it is known, see for example [1], that

$$\begin{aligned} \left| G(n,d)({\mathbb {F}}_q) \right| =\frac{(q^n-1)(q^n-q)\cdots (q^n-q^{d-1})}{(q^d-1)(q^d-q)\cdots (q^d-q^{d-1})}. \end{aligned}$$

The proof relies on the fact that

$$\begin{aligned} \left| GL_n({\mathbb {F}}_q) \right| =\left| G(n,d)({\mathbb {F}}_q) \right| \left| GL_{d}({\mathbb {F}}_q) \right| q^{d(n-d)}\left| GL_{n-d}({\mathbb {F}}_q) \right| \!. \end{aligned}$$

The analog of this formula holds in ${\mathbf{K}}({{\mathrm {Var}}}_{k})$. One also computes

$$\begin{aligned}{}[GL_{n,k}]=({\mathbb {L}}^n-1)({\mathbb {L}}^n-{\mathbb {L}})\cdots ({\mathbb {L}}^n-{\mathbb {L}}^{n-1})\in {\mathbf{K}}({{\mathrm {Var}}}_{k}) \end{aligned}$$

by induction on the class of the space of r linearly independent vectors in $k^n$. By combining those two facts, we get

$$\begin{aligned} {[}G(n,d)_k]=\frac{({\mathbb {L}}^n-1)({\mathbb {L}}^n-{\mathbb {L}})\cdots ({\mathbb {L}}^n-{\mathbb {L}}^{d-1})}{({\mathbb {L}}^d-1)({\mathbb {L}}^d-{\mathbb {L}})\cdots ({\mathbb {L}}^d-{\mathbb {L}}^{d-1})}\in {{\mathbf{K}}({{\mathrm {Var}}}_{k})}_{\mathrm {loc}}. \end{aligned}$$

Note that even if the right hand side can be written without denominator, hence as an element of ${\mathbf{K}}({{\mathrm {Var}}}_{k})$, one has to work in ${{\mathbf{K}}({{\mathrm {Var}}}_{k})}_{\mathrm {loc}}$ to show the equality with this method. Alternatively, one can also use Schubert cells to show this formula. In particular, this shows that $[G(n,d)_k]$ is invertible in ${{\mathbf{K}}({{\mathrm {Var}}}_{k})}_{\mathrm {loc}}$. The motivic volume of $G(n,d)_K$ is then invertible. Hence we can and do normalize $\omega _{n,d}$ such that

$$\begin{aligned} 1=\int _{V\in G(n,d)} \omega _{n,d}(V). \end{aligned}$$

For $V\in G(n,n-d)$, define $p_V : K^n\rightarrow K^n/V$ the canonical projection. We identify $K^n/V$ to $K^{n-d}$ as follows. There is some $g\in GL_n({\mathcal {O}}_K)$ such that $g(K^{n-d}\times \left\{ 0\right\} ^d)=V$. We identify $K^n/V$ to $g(\left\{ 0\right\} ^{n-d}\times K^{n-d})$. The particular choice of g does not matter thanks to the change of variable formula. Recall condition $(*)$ from Sect.  3. If X is a definable subset of $K^n$ of dimension at most d then there is a dense definable subset $\Omega =\Omega (X,x)$ of $G(n,n-d)$ such that for every $V\in \Omega$, $(X,p_V)$ satisfies condition $(*)$ at x. Indeed the tangent $K^\times$-cone of X is of dimension at most d and it suffices to set

$$\begin{aligned} \Omega =\left\{ V\in G(n,n-d)\mid V\cap C_x^{K^\times }(X)=\left\{ 0\right\} \right\} , \end{aligned}$$

which is indeed dense in $G(n,n-d)$. In particular, for any $V\in \Omega$, $p_{!,x}(\varphi )$ is well defined for any $\varphi \in {\mathcal {C}}(X)_x$.

With these notations, we can now state our motivic local Cauchy-Crofton formula. Recall that $\Theta _d(X,x)\in {\mathcal {C}}(\left\{ x\right\} )\otimes {\mathbb {Q}}$ is the motivic local density of X at x,

Theorem 4.1

(local Cauchy-Crofton formula) Let $X\subseteq K^n$ a definable set of dimension at most d and $x\in K^n$. Then

$$\begin{aligned} \Theta _d(X,x)=\int _{V\in \Omega \subseteq G(n,n-d)} \Theta _d(p_{V!,x}(\mathbb {1}_X),p_V(x)) \omega _{n,n-d}(V). \end{aligned}$$

By [12, Proposition 3.8], we may assume $X={\overline{X}}$. We can also assume $x=0$ and $0\in X$. Indeed, if $0\notin X$, then both sides of the formula are 0.

5 Tangential Crofton formula

We start by proving the theorem in the particular case where X is a $\Lambda$-cone.

Lemma 5.1

Let X be a definable $\Lambda$-cone with origin 0 contained in some $\Pi \in G(n,d)$. Then

$$\begin{aligned} \Theta _d(X,0)=\int _{V\in \Omega \subseteq G(n,n-d)} \Theta _d(p_{V!}(\mathbb {1}_X),0) \omega _{n,n-d}(V). \end{aligned}$$

Proof

Since $\Lambda \in {\mathcal {D}}$, $\Lambda =\Lambda _{e,r}$ for some e, r. Fix some $V\in G(n,n-d)$ such that $p_V : \Pi \rightarrow K^d$ is bijective. From the definition of local density, see also [12, Remark 3.11], we have

$$\begin{aligned} \Theta _d(X,0)=\frac{1}{e(1-{\mathbb {L}}^{-d})}\sum _{i=0}^{e-1} {\mathbb {L}}^{id} \mu _d(X\cap S(0,i)). \end{aligned}$$

(1)

Indeed, in the definition of the local density using $\theta '_m=\frac{\mu _d(X\cap S(x,m))}{{\mathbb {L}}^{-md}(1-{\mathbb {L}}^{-d})}$, since X is a $\Lambda =\Lambda _{e,r}$-cone, rescaling by $t^{ek}$ (where t is the uniformizer) induces a bijection between $X\cap S(x,i)$ and $X\cap S(x,ek+i)$ and by the change of variable formula, $\mu _d(X\cap S(x,i))={\mathbb {L}}^{ekd}\mu _d(X\cap S(x,ek+i))$. Hence for every $k\in {\mathbb {N}}$, $\theta '_{ek+i}=\theta '_i$.

Since X is a $\Lambda$-cone and $p_V$ is linear, $p_V(X)$ is also a $\Lambda$-cone, hence we also have

$$\begin{aligned} \Theta _d(p_V(X),0)=\frac{1}{e(1-{\mathbb {L}}^{-d})}\sum _{j=0}^{e-1} {\mathbb {L}}^{jd} \mu _d(p_V(X)\cap S(0,j)). \end{aligned}$$

(2)

For $i=0,\dots , e-1$ set

$$\begin{aligned} A_i=\left\{ y\in p_V(X)\mid \exists x\in X\cap S(0,i),\exists \lambda \in \Lambda , y=\lambda p_V(x)\right\} \end{aligned}$$

Then since X is a $\Lambda$-cone and $p_V$ is bijective, we have a disjoint union

$$\begin{aligned} p_V(X)\backslash \left\{ 0\right\} =\overset{.}{\bigcup }_{i=0}^{e-1}A_i. \end{aligned}$$

Now for $j=0,\dots , e-1$, set $B_i^j=A_i\cap S(0,j)$ and $D_i^V=\overset{.}{\bigcup }_{j=0}^{e-1}t^{i-j}B_i^j$. The set $D_i^V$ is indeed a disjoint union since it is the image of $X\cap S(0,i)$ by the application

$$\begin{aligned} \varphi _V : x\in \Pi \mapsto t^{{\mathrm {ord}}(x)-{\mathrm {ord}}(p_V(x))} p_V(x). \end{aligned}$$

Indeed the function $\varphi _V$ restricted to $X\cap S(0,i)$ is a definable bijection of image $D_i^V$ since $p_V$ is linear and bijective on $\Pi$.

By the change of variable formula, we have

$$\begin{aligned} \mu _d(D_i^V)=\int _{X\cap S(0,i)} {\mathbb {L}}^{-{\mathrm {ord}}({\mathrm {Jac}}(\varphi _V(x)))}. \end{aligned}$$

(3)

By Fubini theorem we get

$$\begin{aligned} \int _{V\in G(n,n-d)} \mu _d(D_i^V)\omega _{n,n-d}(V)=\int _{x\in X\cap S(0,i)}\int _{V\in G(n,n-d)} {\mathbb {L}}^{-{\mathrm {ord}}({\mathrm {Jac}}(\varphi _V(x)))}\omega _{n,n-d}(V). \end{aligned}$$

Set $C_i(x)=\int _{V\in G(n,n-d)} {\mathbb {L}}^{-{\mathrm {ord}}({\mathrm {Jac}}(\varphi _V(x)))}\omega _{n,n-d}(V)$. Note that $\varphi _V$ is independent of X, so $C_i(x)$ does not depend on X. We claim that $C_i(x)$ is independent of $x\in S(0,i)$. Indeed, if $x,x'\in S(0,i)$, we can find some $g\in GL_n({\mathcal {O}}_K)$ such that $x'=gx$. Since $\omega _{n,n-d}$ is invariant under $GL_n({\mathcal {O}}_K)$-transformations and $\varphi _{V}(x)=\varphi _{gV}(x')$, by the change of variable formula we get that $C_i(x)$ is equal to

$$\begin{aligned} \int _{V\in G(n,n-d)} {\mathbb {L}}^{-{\mathrm {ord}}({\mathrm {Jac}}(\varphi _V(x)))}\omega _{n,n-d}(V)=\int _{V'\in G(n,n-d)} {\mathbb {L}}^{-{\mathrm {ord}}({\mathrm {Jac}}(\varphi _{V'}(gx)))}\omega _{n,n-d}(V'), \end{aligned}$$

which is $C_i(x')$. Moreover, it is independent of i by linearity of $p_V$, hence we denote it by C and we have

$$\begin{aligned} \int _{V\in G(n,n-d)} \mu _d(D_i^V)\omega _{n,n-d}(V)=C\mu _d(X\cap S(0,i)). \end{aligned}$$

(4)

By the change of variable formula, ${\mathbb {L}}^{(i-j)d}\mu _d(t^{i-j}B_i^j)=\mu _d(B_i^j)$, hence

$$\begin{aligned} {\mathbb {L}}^{jd}\mu _d(B_i^j)={\mathbb {L}}^{id}\mu _d(t^{i-j}B_i^j). \end{aligned}$$

(5)

We now compute

$$\begin{aligned} \sum _{j=0}^{e-1} {\mathbb {L}}^{jd} \mu _d(p_V(X)\cap S(0,j))&=\sum _{j=0}^{e-1}\sum _{i=0}^{e-1}{\mathbb {L}}^{jd} \mu _d(B_i^j) \nonumber \\&=\sum _{i=0}^{e-1}\sum _{j=0}^{e-1} {\mathbb {L}}^{id} \mu _d(t^{i-j}B_i^j)\nonumber \\&=\sum _{i=0}^{e-1}{\mathbb {L}}^{id} \mu _d(D_i^V). \end{aligned}$$

(6)

Combining Eqs. 2, 6 and 4, we get

$$\begin{aligned} \int _{V\in G(n,n-d)}\Theta _d(p_V(X),0)\omega _{n,n-d}(V)=C\frac{1}{e(1-{\mathbb {L}}^{-d})}\sum _{i=0}^{e-1} {\mathbb {L}}^{id} \mu _d(X\cap S(0,i)). \end{aligned}$$

Again by Eq. 2, this last expression is equal to $C\Theta _d(X,0)$. We find $C=1$ by computing both sides of the previous equality with $X=\Pi$. $\square$

The following lemma is the motivic analog of the classical spherical Crofton formula, see for example [11, Theorem 3.2.48]. See also [2, Remark 6.2.4] for a reformulation in the p-adic case.

Lemma 5.2

Let X be a definable $\Lambda$-cone with origin 0 and of dimension d. Then

$$\begin{aligned} \Theta _d(X,0)=\int _{V\in G(n,n-d)} \Theta _d(p_{V!,0}(\mathbb {1}_X),0) \omega _{n,n-d}(V). \end{aligned}$$

Proof

We only have to modify slightly the proof of Lemma 5.1. Indeed, we use now the function

$$\begin{aligned} \varphi _V : x\in X \mapsto t^{{\mathrm {ord}}(x)-{\mathrm {ord}}(p_V(x))} p_V(x). \end{aligned}$$

restricted to the smooth part of X. It is no longer injective on $X\cap S(0,i)$, however the motivic volume of the fibers is taken into account in $p_{V!,0}(X)$. Hence we get similarly

$$\begin{aligned} \int _{V\in G(n,n-d)}\Theta _d(p_{V!,0}(X),0)\omega _{n,n-d}(V)=C\frac{1}{e(1-{\mathbb {L}}^{-d})}\sum _{i=0}^{e-1} {\mathbb {L}}^{di} \mu _d(X\cap S(0,i)), \end{aligned}$$

which is equal to $C\Theta _d(X,0)$. Once again, we find $C=1$ by computing both sides for X a vector space of dimension d. $\square$

6 General case

Before proving Theorem 4.1, we need a technical lemma. Recall from [12] the notion of ${\mathbf {k}}$-partition of a definable set $X\subseteq K^n$. It is a definable function $g : X\rightarrow R_s^s$ for some s. A ${\mathbf {k}}$-part of the partition is a fiber of g, usualy denoted $X_\xi :=g^{-1}(\xi )$. From [12, Lemma 3.17], we have that

$$\begin{aligned} C^\Lambda _0(X)=\bigcup _{\xi }C^\Lambda _0(X_\xi ). \end{aligned}$$

Lemma 6.1

Let $X\subseteq K^n$ be a definable set of dimension at most d and $V\in G(n,n-d)$ such that the projection $p_V : C_0^\Lambda (X) \rightarrow K^d$ is finite-to-one. Then there is a definable ${\mathbf {k}}$-partition of X such that for each ${\mathbf {k}}$-part $X_\xi$, there is a $\xi$-definable set $C_\xi$ of dimension less than d such that $p_V$ is injective on $C_0^\Lambda (X_\xi )\backslash C_\xi$.

Proof

We can assume $\Lambda =K^\times$. As the projection $p_V : C_0^\Lambda (X) \rightarrow K^d$ is finite-to-one, by finite b-minimality [4], one can find a ${\mathbf {k}}$-partition of $C_0^\Lambda (X)$ such that $p_V$ is injective on each ${\mathbf {k}}$-part of $C_0^\Lambda (X)$. For a ${\mathbf {k}}$-part $C_0^\Lambda (X)_\xi$, define $B_\xi$ to be the $\xi$-definable subset of $K^n$ defined as the union of lines $\ell$ passing through 0 such that the distance between $\ell \cap S(0,0)$ and $C_0^\Lambda (X)_\xi \cap S(0,0)$ is strictly smaller than the distance between $\ell \cap S(0,0)$ and $C_0^\Lambda (X)_{\xi '}\cap S(0,0)$ for every $\xi '\ne \xi$. Set $X_\xi =X\cap B_\xi$. Then setting $Y=X\backslash \cup _{\xi }X_\xi$, $C_0^\Lambda (Y)$ is empty and $C_0^\Lambda (X_\xi )\subseteq \overline{C_0^\Lambda (X)_\xi }$. Hence we set $C_\xi =\overline{C_0^\Lambda (X)_\xi }\backslash C_0^\Lambda (X)_\xi$ and we have $X_\xi$ and $C_\xi$ as required. $\square$

Proof of Theorem 4.1

From [12, Theorem 3.25], there is a $\Lambda \in {\mathcal {D}}$ such that $\Theta _d(X,0)=\Theta _d(CM_0^\Lambda (X),0)$. As in the proof of [12, Theorem 3.25], by [12, Proposition 2.14 and Lemma 3.9], we can assume that X is the graph of a 1-Lipschitz function defined on some definable set $U\subset K^d$. In this case, $CM_0^\Lambda (X)=\mathbb {1}_{C_0^\Lambda (X)}$. From Lemma 5.2, we have

$$\begin{aligned} \Theta _d(C_0^\Lambda (X),0)=\int _{V\in G(n,n-d)} \Theta _d(p_{V!,0}(C_0^\Lambda (X)),0) \omega _{n,n-d}(V). \end{aligned}$$

Hence we need to show that for every V in a dense subset of $G(n,n-d)$,

$$\begin{aligned} \Theta _d(p_{V!,0}(C_0^\Lambda (X)),0)=\Theta _d(p_{V!,0}(X),0). \end{aligned}$$

We can find a ${\mathbf {k}}$-partition of X such that $p_V$ is injective on the ${\mathbf {k}}$-parts. Replace X by one of the ${\mathbf {k}}$-parts and suppose that $p_V$ is injective on X.

Fix a $V\in G(n,n-d)$ such that $p_V$ is injective on $C_0^\Lambda (X)$. By Lemma 6.1, there is a ${\mathbf {k}}$-partition of X (depending on V) such that for each ${\mathbf {k}}$-part $X_\xi$ there is a $\xi$-definable set $C_\xi$ of dimension less that d such that $p_V$ is injective on $C_0^\Lambda (X_\xi )\backslash C_\xi$. By a new use of [12, Lemma 3.9], it suffices to show that

$$\begin{aligned} \Theta _d(p_{V!,0}(C_0^\Lambda (X_\xi )),0)=\Theta _d(p_{V!,0}(X_\xi ),0). \end{aligned}$$

As $p_V$ is injective on X and $C_0^\Lambda (X_\xi )\backslash C_\xi$, we have $p_{V!,0}(X)=\mathbb {1}_{p_V(X)}$ and

$$\begin{aligned} p_{V!,0}(C_0^\Lambda (X_\xi ))=\mathbb {1}_{p_V(C_0^\Lambda (X_\xi )\backslash C_\xi )}+p_{V!,0}(C_\xi ). \end{aligned}$$

We have $\Theta _d(p_{V!,0}(C_\xi ),0)=0$ for dimensional reasons. As $C_0^\Lambda (p_V(X))=p_V(C_0^\Lambda (X))$ the result follows from [12, Proposition 5.2]. $\square$