Introduction

The processing of the raw material wood into materials, semi-finished products and products is characterized by various sequential production steps of discrete manufacturing including cutting, sorting, joining, forming, etc., each of which is geared toward a specific product requirement or product design. Due to the many starting materials (different types of wood and grading classes, various wood-based materials, etc.) and design variants, the production process of many wood products is extremely complex. To increase the value added and ensure competitiveness, the quality control (QC) of the wood products created in the course of industrial production is of paramount importance. Particularly in high-price segments, where the quality requirements for the products are especially high, such as in musical instrument manufacturing, QC is the task of assuring that the products produced reach a certain standard that is set either by the company or by the customers. The field developed rapidly during the second half of the twentieth century and is today an integral part of most manufacturing companies. The three major methods of QC are 'Acceptance Sampling', 'Statistical Process Control', and 'Experimental Design' (Fountoulaki et al. 2011). Acceptance Sampling, where only a sample of products is tested to draw conclusions about the entire batch, is used when testing is expensive, time-consuming and/or destructive, which is mainly the case in the wood industry. The quality control of wood products is often only checked at the end of the production process, so that countermeasures can only be taken with a time delay in the event of fluctuations in product quality. This often leads to unnecessary and cost-intensive rejects, sometimes even of an entire day's production quantity. Furthermore, since quality control often requires additional procedural steps to be performed by a skilled worker, testing of wood products is time-consuming and costly. This results in there being only small-labeled datasets available for comprehensive analysis.

Machine learning (ML) is a method of data analysis that automates analytical model building. It is a branch of artificial intelligence based on the idea that systems can learn from data, identify patterns, and make decisions with minimal human intervention (Bishop 2006). ML algorithms can be classified into different groups based on the way they “learn” about data to make predictions: supervised, unsupervised and semi-supervised learning (SSL). The more commonly used ML models are based on supervised learning, where the algorithm learns from a labeled dataset, which provides an answer key that the algorithm can use to evaluate its accuracy and provide feedback. An unsupervised model, in contrast, uses unlabeled data that the algorithm tries to make sense of by extracting features and patterns on its own.

SSL falls between unsupervised learning and supervised learning and combines a small amount of labeled data with a larger amount of unlabeled data during training (Ouali et al. 2020). More formally, the goal of SSL is to leverage the unlabeled data (Du) to produce a prediction function (fθ) with trainable parameters (θ) that is more accurate than what would have been obtained by only using the labeled data (Dl). For instance, Du might provide additional information about the structure of the data distribution (p(x)) to better estimate the decision boundary between the different classes (Ouali et al. 2020).

Traditional ML methods based on supervised learning have been used with some success to predict the quality of wood products (Barnes 2001; Gupta et al. 2007; André et al. 2008; Esteban et al. 2011; Bardak et al. 2016a, b; Schubert and Kläusler 2020; Schubert et al. 2020; van Blokland et al. 2021; Ehrhart et al. 2022; Rahimi and Avramidis 2022). For example, artificial neural networks (ANN), support vector machines (SVM), and Naive Bayes (NB) models were used to classify the quality of thermally modified wood (Nasir et al. 2019). However, the limited availability of labeled data is the major hurdle for further improving ML model performance.

To the best of the authors` knowledge, this work is the first time that SSL has been used to improve the QC of real data from the wood products industry. The aim of the present work was to: (1) use a SSL method for labeling the unlabeled dataset and combine it with traditional ML algorithms, namely, random forest (RF) and SVM. (2) Determine the prediction accuracy of quality classification using evaluation indices and confusion matrices. (3) To compare the generalization capability of the SSL-ML algorithms with the RF and SVM algorithms trained in a supervised manner only.

Materials and methods

Production and quality control of high-value wood products

Swiss Wood Solutions AG is a business and technology incubator for sustainable, wood-based products, which produces densified wood for high-value wood products such as musical instruments. The production includes several steps. After the first incoming control of the wooden raw material (QC I) the accordant square wood enters the climatization process (Wood Climatization I) as illustrated in Fig. 1. In this phase, wood moisture and wood temperature are adjusted. The subsequent step is the thermo-mechanical densification, which takes place in a hydraulic pressing machine. As a next step, the wood again undergoes climatization (Wood Climatization II) to slowly adjust the wood moisture content to the ambient air conditions (rel. humidity and temperature) and slowly relieve stresses in the wood. After this modification procedure, the final quality control (QC II) is carried out (Fig. 1).

Fig. 1
figure 1

Schematic procedure detailing the manufacturing process of the densified wood

Full size image

Quality control

A first incoming control (QC I) takes place before the wood modification process. The squared timbers are sorted visually according to the following parameters:

  • Alignment parallel to the fiber (length) and straight in tangential (width) and radial (height) directions

  • Without knots

  • Without compression or tension wood

The mass, length, width, height, and density of the squared timber are also measured which is used for the arrangement of the modification charges.

After the densification process, the second quality control (QC II) checkpoint takes place, which involves a visual inspection of each timber concerning cracks, deformations and discoloration. Of great importance is the re-swelling of the wood after densification, which occurs mainly under humid conditions and can reach almost 90–100% in extreme cases (Sandberg et al. 2013). To ensure high quality products are produced, a maximal irreversible swelling of 2% is set as an internally tolerable threshold after a water uptake of 5 days. Two specimens of 1 cm in length are cut at each test location, one for the water uptake testing and one reference specimen. The samples for water uptake are stored in water for 5 days, afterward they are re-climatized in the storage room and oven-dried together with the reference specimens. The differences in the relative heights of the two adjacent specimens are compared with each other and the irreversible swelling is determined. Timber batches with values above the threshold (> 2%) are then classified as failed (= 1) and batches below the threshold of 2% are classified as passed (= 0).

Data

The data was collected from the production process of the Swiss Wood Solutions AG described above. Since special attention was paid to the influence of the raw material on the quality of the final product, process parameters of the densification process were deliberately not included in the analysis. Thus, the labeled (Dl) and unlabeled dataset (Du) included the following nine input features (x): Wood species (1_Maple; 2_Spruce; 3_Walnut; 4_Fir), and raw material properties (5_Mass [g]; 6_Length [mm]; 7_Width [mm]; 8_Height [mm]; 9_Density [kg/m3]). The response (y) was the binary quality classification (0 = pass, 1 = fail) of the densified wood according to the quality control protocol described in the previous chapter.

Data splitting

The dataset was split into a training, validation and hold-out test set to evaluate the performance of machine learning algorithms without any bias (Russell 2010):


Training dataset: The training data set used for fitting the model is further split via k-fold cross-validation into training and validation data sets, which can be used to get an early estimate of the accuracy of the ML model while tuning its hyperparameters.


Hold-out test dataset: The sample of data used to provide an unbiased evaluation of a final model fit on the training dataset. The hold-out test set is used to assess the generalization ability of the trained ML algorithm.

The stratified sampling technique was used when splitting the dataset. This technique consists of forcing the distribution of the target variable among the different splits to be the same. Therefore, all the datasets used in this study, such as the training and hold-out test sets, had a binary class distribution of around 10% (1 = fail) and 90% (0 = pass). In other words, the technique ensures that all of the subsets used have the same distribution of pass-samples (90%) and fail-samples (10%). The reason for implementing this technique is because the entire dataset is small. Therefore, there is an elevated risk that random sampling would assign only pass-samples to a particular subset, without any fail-samples.

Finally, the input features (x) were normalized between 0 and 1 in order to fit the requirements of the learning algorithms and to avoid the problem of prevailing high values which would have a greater influence on the loss function because of their scale and not for being more important than the other values.

Machine learning

Supervised learning

Since the pass-or-fail compliance determined during final inspection in manufacturing is a discrete variable, classification techniques should be used to predict such an outcome (Kotsiantis 2007).

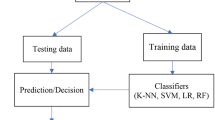
As illustrated in Fig. 2, the limited labeled dataset (N = 166) was used to train and adjust the hyperparameters of the RF and SVM ML algorithms using tenfold cross-validation, whereas the hold-out test set (n = 46) was used to evaluate the generalization ability of the ML models. No detailed mathematical description of the common ML techniques applied in this study is given and reference is made to the corresponding literature (Bishop 2006).

Fig. 2
figure 2

Schematic procedure of the machine learning workflow using a supervised learning and b semi-supervised learning

Full size image

Introduced by Vapnik (2000), SVMs are supervised learning models for classification and regression. The objective of the SVM algorithm is to find a hyperplane (decision boundary) in an N-dimensional space (N—number of features) that can distinctly classify the data points (Vapnik 2000; Schölkopf and Smola 2018).

RF is an ensemble learning method for classification that operates by constructing a multitude of decision trees trained with the bagging (bootstrapping aggregation) method. Generally, RF consists of a collection of tree-structured classifiers \(\left\{ {h\left( {x, \, \Theta k} \right), \, k\, = \,1, \ldots } \right\}\) where the {Θk} are independent identically distributed random vectors and each tree casts a unit vote for the most popular class at input x (Breiman 2001; Meinshausen 2006).

Semi-supervised learning

SSL methods can improve learning performance by using additional unlabeled instances compared to supervised learning algorithms, which can use only labeled data. The definition of SSL was given by Chapelle et al. (2006): "SSL is halfway between supervised and unsupervised learning. In addition to unlabeled data, the algorithm is provided with some supervision information—but not necessarily for all examples. Often, this information will be the targets associated with some of the examples. In this case, the dataset X = (xi); i \(\epsilon\) [n] can be divided into two parts: the points Xl: = (x1;…; xl), for which labels Yl: = (y1;…; yl) are provided, and the points Xu: = (xl+1;…; xl+u), the labels of which are not known.”

In the present work, the graph-based algorithm 'label spreading' was used which was first introduced by Zhou et al. (2003). The algorithm is inspired by a technique from experimental psychology called spreading activation network (Anderson 1983; Shrager et al. 1987) and diffusion kernels (Kondor and Lafferty 2002), and also from the published work on SSL and clustering (Ng et al. 2002; Chapelle et al. 2003). Points in the dataset are connected in a graph based on their relative distances in the input space. The algorithm minimizes a loss function that has regularization properties and is often more robust to noise than other SSL algorithms, such as label propagation (Zhu and Ghahramani 2002). The keynote of the method is to let every point iteratively spread its label information to its neighbors until a global stable state is achieved.

To spread labels across the nodes in the similarity graph, the iterative spreading propagation algorithm follows these steps (Zhou et al. 2003):

  1. 1.

    Form the affinity matrix W defined by \(W_{ij} \, = \,\exp \left( { - \, \left| {\left| {x_{i} - x_{j} } \right|} \right|^{2} /2\sigma^{2} } \right)\) if i ≠ j and Wii = 0.

  2. 2.

    Construct the matrix S = D−1/2 W D−1/2 in which D is a diagonal matrix with its (i, i)-element equal to the sum of the i-th row of W.

  3. 3.

    Iterate \(F\left( {t\, + \,1} \right)\, = \,\alpha SF\left( t \right)\, + \,\left( {1{-}\alpha } \right)Y\) until convergence, where α is a parameter in (0,1).

  4. 4.

    Let F* denote the limit of the sequence {F(t)}. Label each point xi as label \(y_{i} \, = \,\arg \max_{j \le c} F^{*}_{ij}\).

As shown in Fig. 2, after labeling the unlabeled dataset using the label spreading method, the new training dataset included n = 400. The same hold-out test set was used to ensure better comparability in terms of generalization ability of the ML algorithms.

Performance assessment and feature selection

In this work, neighborhood component feature selection analysis was carried out to identify relevant input parameters (Yang et al. 2012). The evaluation of the ML algorithms' performances was based on the following metrics:

Accuracy = (TP + TN)/(TP + FP + FN + TN). This index is the number of correctly predicted data points out of all the data points.

Precision = TP/(TP + FP). Precision is defined as the ratio of correctly classified positive samples (True Positive) to a total number of classified positive samples (either correctly or incorrectly). Hence, precision helps to visualize the reliability of the machine learning model in classifying the model as positive.

Recall (true positive rate) = TP/(TP + FN). The recall measures the model's ability to detect positive samples. The higher the recall, the more positive samples detected.

False positive rate (FPR) = FP/(TN + FP). The FPR is complementary to recall and is based on how many actual negatives the model predicted incorrectly.

F1-score = 2 × TP/(2 × TP + FP + FN). F1-score is one of the most important indices and it is the harmonic mean between precision and recall and assesses how precise your classifier is (how many instances the ML algorithm classifies correctly), as well as how robust the ML algorithm is.

TP = true positive, TN = true negative, FP = false positive, FN = false negative.

In addition, confusion matrices were used to visualize the performance of the ML algorithms and the corresponding Cohen-Kappa value (κ) was calculated (Cohen 1960):

$$\kappa = p_{A} {-} \, p_{E} /1{-}p_{E}$$

where pA is the observed relative agreement between two annotators, and pE is the hypothetical probability of agreement by chance (with data labels randomly assigned). In particular, κ = 1 corresponds to the case of perfect agreement, whereas κ = 0 indicates no agreement other than what would be expected by chance.

The SSL algorithm 'label spreading' and the ML algorithms RF and SVM, as well as performance assessment and feature selection, were implemented with MATLAB R2020b using the Statistics and Machine Learning Toolbox.

Results and discussion

Ensuring high product quality is essential for the long-term success of a producing company, particularly where the quality control is time-consuming and expensive. Therefore, the economic implementation of a comprehensive and reliable quality inspection is of utmost importance. This is especially true for small and medium-sized companies that do not have a highly automated production process and produce small batches. In the tension between ever increasing requirements and new technological opportunities, the contribution of this work is the development of a SSL method using unlabeled data for improving predictive model-based quality inspection in industrial wood-based material production.

In recent years, SSL has emerged as an exciting new research direction in ML (Ouali et al. 2020; van Engelen and Hoos 2020). Such methods deal with the situation where few labeled training examples are available together with a significant number of unlabeled samples. In such a setting, SSL methods are more applicable to real-world applications where unlabeled data is readily available and easy to obtain, while labeled instances are often difficult, expensive, and time-consuming to collect, which is often the case in wood product manufacturing.

In this work, a particularly small dataset was used to determine the effect of SSL on the performance of the algorithms RF and SVM, two common ML techniques for classification.

Choosing correct metrics when evaluating the performance of a classification model is crucial since each metric places varying emphasis on the overall accuracy, precision, recall, or agreement between model and ground truth for different class values. Therefore, for a comprehensive analysis, several metrics should be included depending on the user's requirements. The standard performance measure for classification models is accuracy. However, in cases where there is a class imbalance, which is common for quality-related industrial applications, accuracy can be misleading as a performance measure since it does not penalize misclassification of the minority (Schmitt et al. 2020). Therefore, complementary evaluation indices, such as recall and false positive rates as well as confusion matrices and Cohen-Kappa, were used in this study.

The comparison of the results based on the statistical performance measures showed that the augmentation of the training data with the SSL method had a positive impact on the result. As shown in Table 1, SSL could improve the performance of RF and SVM algorithms based on the evaluation indices as indicated by the results obtained for validation. In addition, the slightly lower standard deviations show that the results of the tenfold cross-validation of SSL are more consistent, indicating that the learning process was more effective.

Table 1 Descriptive statistics for the training and validation (tenfold cross-validation)
Full size table

Generalization is the main goal of a ML algorithm, as the trained and validated algorithm should perform similarly when using new data during operation. In the present work, the hold-out test set was used to evaluate the generalization ability of ML algorithms. It was kept separate from the training and validation datasets and used only in the final evaluation of the model's performance. This independence is important to avoid bias and to properly represent the behavior of the model when new input data is used in future.

The results of the final testing are shown in Table 2 and Fig. 3. As judged by the indices, the SSL method outperforms the existing supervised learning techniques on the binary classification of wood product quality. As shown in Table 2, most of the evaluation indices are better in SSL compared to the traditional supervised learning method. In particular, the results in the underrepresented class (1 = fail) could be improved, as can be seen from the significantly lower value of the false positive rate. Furthermore, these results are confirmed by the confusion matrices and the Cohen-Kappa values (κ) (Fig. 3).

Table 2 Descriptive statistics for the testing (hold-out test set)
Full size table
Fig. 3
figure 3

Confusion matrices with Cohen-Kappa values (κ) using a RF, b SSL-RF, c SVM, and d SSL-SVM. Binary classification 0 = pass; 1 = fail

Full size image

For example, κ was increased from 0.25 for SVM to 0.69 (SSL-SVM) and from 0.33 for RF to 0.81 (SSL-RF), respectively. A comparison of the two ML algorithms shows that SSL-RF provides better performance than SSL-SVM (Table 2 and Fig. 3). These observations are in good accordance with the results of Nasir et al. (2021a, b) who showed that RF revealed better results than other ML algorithms such as SVM.

Based on the results of the testing with the hold-out test set, it can be clearly shown that the generalization performance of the ML algorithms, especially RF could be enhanced by the SSL method 'label spreading'.

Besides 'label spreading', other SSL algorithms such as 'label propagation' (Zhu and Ghahramani 2002) and the rule-based 'Yarowsky algorithm' (Abney 2004) were also tested in this work. However, none of these algorithms revealed better results than the 'label spreading' method (data not shown). Such graph-based SSL algorithms have always been a popular subject for research with a vast number of successful models because of its wide variety of applicability (Chen et al. 2020; Li et al. 2020). In the present work, the graph-based 'label spreading' method significantly increased the information content of the training dataset using the unlabeled dataset, especially in the underrepresented class where the supervised models performed poorly. The augmentation of the training data with information was also confirmed by the feature selection method neighborhood component analysis (NCA) (Fig. 4).

Fig. 4
figure 4

Neighborhood component analysis (NCA) using a RF and b SSL-RF. Feature index: 1_Maple; 2_Spruce; 3_Walnut; 4_Fir; 5_Mass [g]; 6_Length [mm]; 7_Width [mm]; 8_Height [mm]; 9_Density [kg/m3]

Full size image

Whereas NCA with the non-augmented dataset could only identify two relevant features, such as the wood species maple and density, NCA with the larger dataset identified more relevant features (Fig. 4). NCA with the extended dataset revealed that within the different wood species, maple, spruce and walnut are the most relevant. This agrees well with the real values, which show a failure rate of 25% for maple, followed by 10.4% for spruce, 10% for walnut, and 0% for fir. In addition, mass, height and density were identified as relevant features as was confirmed by the analysis of the real values. These values show that the wood products classified as low quality had, on average, about 26% less mass, 21.6% less height and 5.4% less density than the wood products classified as good.

Overall, it could be clearly shown that SSL can be used to augment small datasets to improve the generalization ability of ML algorithms such as RF. Although further research is needed to verify the results and scale the application of predictive model-based inspection for deployment, this work paves the way for future applications of SSL for quality assessment. This is especially the case for small and medium-sized companies in the wood industry who can take advantage of this method because it achieves very good results even with very small batch sizes.

Conclusion

This paper discussed the need for an efficient quality inspection method for the wood industry, especially for small and medium sized companies where quality control is often time-consuming, costly, and limited by small available datasets. We explored the potential of using SSL to improve the predictive performance of ML algorithms RF and SVM for quality classification of real wood product data. Despite the use of a small dataset, two important findings were obtained:

  • The SSL algorithm 'label spreading' was able to significantly increase the information content of the data, with the result that the generalization performance of the ML algorithms RF and SVM was considerably improved. This was especially true in the underrepresented class, as was shown by several evaluation indices such as F1-score, recall, precision and confusion matrices.

  • It has been shown that a few wood-specific parameters such as wood species, density, and dimension are sufficient to train an ML algorithm based on SSL in order to make it capable of predicting the final product quality. This enables efficient quality control and would not only save time and costs, but also allow the raw material wood to be used for other applications with lower quality requirements.

In summary, although more work is needed in this direction, predictive model-based quality inspection based on SSL is a promising approach to make quality control processes more efficient and economical.