Introduction

As discussed in detail in a recent paper on fracture processes in paint layers on wood (Bratasz et al. 2020), the material served for centuries as a support for paintings in Europe. Panel paintings are among the most precious and frequently exhibited categories of heritage objects, which at the same time are most vulnerable to relative humidity (RH) and temperature fluctuations. Paintings on the wood are complex multi-layer structures composed of wood support sized with animal glue and a paint layer consisting of a preparatory layer of gesso—a mixture of animal glue and white inert solid—to produce a smooth painting surface, and paints and varnishes on the top. All materials constituting painted wood are humidity sensitive: they swell when they gain moisture and shrink when they lose it, which generates moisture-induced stresses owing to materials’ different dimensional responses to the loss or gain of moisture. Wood is anisotropic and its moisture-related dimensional changes vary in its three principal anatomical axes—longitudinal, or parallel to the grain, radial, and tangential. The most pronounced moisture response is in the tangential direction, and it halves in the radial one. For practical purposes, wood can be considered dimensionally stable parallel to its grain.

The mismatch in the moisture response of gesso and wood support in the direction across the grain, especially the most responsive tangential direction, has been identified as the worst-case condition that can lead to cracking in the entire paint layer. The gesso layer experiences tension during wood swelling, which leads to cracking if the strain generated by the wood support goes beyond the critical level (Mecklenburg et al. 1998). Bosco et al. (2020, 2021) analysed the cracking mechanism in brittle coatings under moisture loads and applied it to historical paintings. The notion that the deterioration of objects is related to indoor climate instability, existed long before first museums were created. The concept of stabilizing humidity changes in the environment of paintings was gradually reflected in good practice and housekeeping rules, which over the last century evolved into the climate specifications for museums we know today. Until the beginning of 1990s, these specifications were based on the technical capabilities of climate control systems rather than experimental or theoretical evidence of collections needs. As a result, climate control specifications were very stringent—and in many museums still are—both in temperature (typically 21 or 22 ± 1 °C) and RH (typically 50 ± 5%) (Thomson 1986). Only since 1990s, the dimensional response of materials to climatic changes and the critical levels of strain at which the materials began to deform plastically or fracture have been studied in the laboratory (Mecklenburg et al. 1998; Rachwał et al. 2012), which has led to the development of evidence-based environmental specifications for collections of historical objects (Ashrae, 2019; Bickersteth 2016). Moderate variations within the approximate RH range of ± 10% around the long-term average RH of 50% have been indicated as safe for paintings. Implementation of evidence-based, more relaxed environmental specifications in numerous museums has shown that even a slight relaxation of the specifications can significantly reduce energy consumption and the use of fossil fuels (Kramer et al. 2016; Smithsonian 2015).

The above ‘safe’ RH range has been derived using the extreme value of a conservative criterion for the gesso’s crack initiation in undamaged, usually new, material. In reality, painted objects, especially panel paintings, with their long environmental history, exhibit complex crack patterns called craquelures (Giorgutti-Dauphiné and Pauchard 2016; Pauchard and Giorgiutti-Dauphiné 2020). Cracks in paintings can be referred to as ‘edge fractures’ as they are initiated from the free surface. The craquelure patterns in a painting are related both to drying shrinkage of a pictorial layer, and to environmental and physical impacts which the painting experienced in its history. The terms ‘drying’ and ‘aging’ cracks were used to describe these two groups of crack, respectively (Bucklow 1997). Krzemień et al. (2016) investigated the development of cracks from drying shrinkage in a freshly prepared gesso layer. They demonstrated that attaining the ultimate permanent drying shrinkage of the gesso was achieved after repeated cycling between low and high RH levels, which can be explained by diffusing out free volume locked in the material until the equilibrium state. As the craquelure patterns stabilized after a limited number of cycles (30 for a 1 mm thick layer), drying cracks in gesso developed fully after a relatively short period of probably no more than several years after the painting was executed and exposed in a building with unavoidably uncontrolled climate.

Craquelure patterns can be categorized based on many features such as direction (craquelure patterns showing no direction, cracks parallel or perpendicular to the wood grain), shape (jagged and straight cracks with square islands, smooth and curved cracks and irregular islands), distance between cracks, thickness (cracks of non-uniform or uniform thickness), and network (secondary, connected, broken or ordered networks). Drying of the gesso leads to isotropic ‘mud crack patterns’ as the principal stresses in directions parallel to the free surface are similar. In turn, mismatch in moisture-induced swelling of gesso and wood support leads to a set of parallel cracks as stress distribution in the gesso is dominated by one principal stress perpendicular to the wood grain (Bucklow 2000). In Figs. 1 and 2, some of the simplest craquelure patterns found in paintings are presented.

Fig. 1
figure 1

Craquelure patterns in historical paintings, a crack pattern parallel to the wood grain in Virgin and Child with St. Anne, Netherlandish school, c. 1495, Yale University Art Gallery, b cracks perpendicular to the wood grain in Madonna and Child Enthroned, c. 1420, Gentile da Fabriano, the National Gallery in Washington

Full size image
Fig. 2
figure 2

Superposition of cracks parallel and perpendicular to the wood grain resulting in square or rectangular craquelure patterns, a an 18th-century decorated wooden element stored in an uncontrolled environment, b Bishop Altobello Averoldo, c. 1505, Francesco Francia, the National Gallery in Washington

Full size image

Fracture mechanics provides a useful approach to analysis of processes occurring in bilayer materials undergoing dimensional changes (Hutchinson and Suo 1992; Ma et al. 2019; Shevchuk and Silberschmidt 2005; Wu and Pollard 1995; Yin 2010; Zhang et al. 2021). As the substrate of a bilayer system expands, the maximum stress occurs at the middle of two cracks. With the decreasing distance between the cracks, stress at the middle becomes compressive (Giorgutti-Dauphiné and Pauchard 2016; Bratasz and Vasiri Sereshk 2018; Bai et al. 2000a, b). Bai et al. (2000a) showed that the stress in the direction normal to the developing fracture reached its maximum in the centre of each ‘island’ for large ratios of spacing between cracks S to fracturing layer thickness t, the islands tended to form cracks in the middle. For decreasing S/t, the stress dropped to zero and became negative, thus no new crack would ever form. The critical crack spacing calculated theoretically agreed with observations of real paintings (Bratasz et al. 2020). In spite of significant progress in the understanding of crack formation in panel paintings, a gap in knowledge concerning development of two-dimensional craquelure patterns needs to be addressed. The present paper aims at getting more insight into the role of moisture response of a panel painting and drying shrinkage of the gesso layer in the formation of cracks—along and across the longitudinal wood direction—using analysis of surface stresses in a 3D fully elastic model (understanding how cracks along and perpendicular to the wood grain are formed). In particular, distances between cracks in both tangential and longitudinal directions are estimated. The outcome of the numerical analysis is compared with crack patterns obtained experimentally for a mock-up of a panel painting exposed to extreme RH variations in an environmental chamber.

Materials and methods

Model

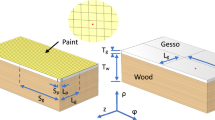
The model of a panel painting shown in Fig. 3 was used initially in this study but was then simplified to one central island to make the parameter study time-efficient. It was assumed that the wooden support was made of lime wood cut in the tangential direction and its thickness T was 40 mm. The thickness of the gesso layer t was 2 mm. The width of the crack was 10 µm. The mechanical properties of the two components are detailed in Table 1. Wood in the direction along the fibres (z-component) is significantly stiffer than in the radial (ρ-component) and tangential (φ-component) directions. In contrast to the stiffness, moisture expansion in the φ- or ρ-directions is significantly larger than in the z-direction, which can be considered as dimensionally stable.

Fig. 3
figure 3

Conceptual model of a periodic craquelure pattern of rectangular gesso islands on wooden support mimicking a panel painting with cracks perpendicular and parallel to the wood grain. The red dot indicates the point where stresses are largest, and at which the critical stress was calculated. Two loading scenarios detailed in Table 2 are shown: a loading caused by isotropic gesso shrinkage on drying denoted as mode (1,1) which in the model was induced by the equivalent of wood loading (Uz = Uφ), b uniaxial loading caused by moisture expansion of wood in the tangential direction denoted as mode (1,0)

Full size image
Table 1 Mechanical properties of lime wood and the gesso layer used in the model (Rachwał et al. 2012; Wood handbook 1999)
Full size table

Two different boundary displacements were studied. The boundary displacement of side walls of the panel in the φ-direction, corresponding to swelling of the panel due to an increase in RH, is shown in Fig. 3a, and the boundary displacements of side-walls of the panel in the φ and z-directions, corresponding to the isotropic drying shrinkage of the gesso layer, are shown in Fig. 3b. In both cases, the applied displacements were such that strains ε0 in the φ- and z-directions were 1%. The summary of the applied displacements is given in Table 2. The external load was used instead of a hygroscopic strain as the aim of this research was to analyse solely the effect of full moisture-related expansion of flat wood support as the worst case condition that leads to gesso cracking. Therefore, cupping concave to the painted face, encountered in panel paintings, was not considered as it reduces the damaging impact of wood’s expansion on the gesso layer. The model with the external loads also required much less computational time. Further, critical stress was calculated for a point at the gesso surface where stresses were largest—the origin of the coordinate system (Fig. 3). Bratasz et al. (2020) showed that cracks would develop starting from the surface rather than sub-surface flaws even for maximum flaw dimensions observed in historical paintings using X-ray computer microtomography. The central point at the surface was blocked in movement (Uz = Uφ = Uρ = 0), the corresponding point at the bottom of the panel was blocked in the z- and φ-directions (Uz = Uφ = 0) and the projection of the latter in the z-direction on the side-wall was blocked in the z-direction (Uz = 0). All other surfaces, including the top and the bottom of the structure, and gesso layer sides were wholly unrestrained. For this two-layer model, it was postulated that the two materials were fully kinematically constrained at the interface, i.e., no slip or opening was permitted along the interface. Moreover, any initial cupping of a panel was neglected.

Table 2 Two loading scenarios used in the model
Full size table

A self-adaptive finite element mesh was used during simulations with a total number of computational nodes not smaller than one million, and a finer mesh in the central and neighbouring gesso islands.

Free triangular controlled extremely fine mesh patterns were used to discretize object geometry in solid mechanics module of COMSOL including geometry nonlinearity for the study. In case of the simplified 3D model, the number of domain elements was reduced by a factor of 4, and the numbers of boundary and edge elements were reduced by a factor of 2, but the number of domain elements still was approximately 1 million. The generalization of critical crack saturation distance defined by Bai et al. (2000a) to a 3D case with a rectangular crack pattern is straightforward. Next to the S/t ratio in the tangential direction, a new parameter—the L/t ratio—was defined in the longitudinal direction where S and L were spacings between cracks in the two directions, respectively (Fig. 3). In both cases, no new edge cracks perpendicular to the φ- and z-directions can develop starting from the surface, if the stresses in the φ- and z-directions—σφ and σz—drop below zero, i.e. become compressive, respectively. The critical values of S/t and L/t are defined by conditions σφ = 0 and σz= 0 in the point of stress calculation.

Mathematical modelling

Based on fracture saturation theory (Bratasz et al. 2020), the critical condition of the system is when the tangential component of stress in the middle point of the top surface \(\sigma_{\varphi }\) changes its sign

$$\sigma_{\varphi } = 0$$
(1)

To calculate the stress field inside the computational domain, the elasticity equation was applied to an anisotropic solid material, with the static equilibrium equation:

$$\nabla \vec{\sigma } = 0$$
(2)

where \(\nabla { }\) is the divergence vector and \({\varvec{\sigma}}\) is the stress components’ vector. The static equilibrium equation is derived from balance of all forces that act upon a differential volume. The partial differential equation weak form requires three dependent variables u; v; w to represent the displacement vector U = [u; v; w]. The strain \(\vec{\varepsilon }\) is defined as

$$\vec{\varepsilon } = \frac{{\nabla {\varvec{U}} + \nabla^{T} {\varvec{U}}}}{2}$$
(3)

where \(\nabla^{T} { }\) is the transpose of the gradient vector. In the general case of linear elastic materials, the material properties have a directional sensitivity. The most general case is called anisotropic, for which all six stress components can depend on all six strain components. This requires 21 material parameters. The stress component vector σ in Eq. 2

$$\vec{\sigma } = \left[ {\begin{array}{*{20}c} {\sigma_{\varphi } } \\ {\sigma_{\rho } } \\ {\sigma_{z} } \\ {\sigma_{\varphi \rho } } \\ {\sigma_{z\rho } } \\ {\sigma_{z\varphi } } \\ \end{array} } \right]$$
(4)

and strain ε

$$\overrightarrow {\varepsilon } = \left[ {\begin{array}{*{20}c} { \in_{\varphi } } \\ { \in_{\rho } } \\ { \in_{z} } \\ { \in_{\varphi \rho } } \\ { \in_{z\rho } } \\ { \in_{z\varphi } } \\ \end{array} } \right]$$
(5)

are related by the anisotropy constitutive 6-by-6 symmetric compliance matrix \(\underline{C}\), through

$$\overrightarrow {\varepsilon } = \underline{C} \overrightarrow {\sigma }$$
(6)

where the symmetric compliance matrix in the case of orthotropic material (the twelve constants used are reduced to nine) is

$$\underline {C} = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{\varphi } }}} & {\frac{{ - \nu_{\rho \varphi } }}{{E_{\rho } }}} & {\frac{{ - \nu_{z\varphi } }}{{E_{z} }}} & 0 & 0 & 0 \\ {\frac{{ - \nu_{\varphi \rho } }}{{E_{\varphi } }}} & {\frac{1}{{E_{\rho } }}} & {\frac{{ - \nu_{z\rho } }}{{E_{z} }}} & 0 & 0 & 0 \\ {\frac{{ - \nu_{\varphi z} }}{{E_{\varphi } }}} & {\frac{{ - \nu_{\rho z} }}{{E_{\rho } }}} & {\frac{1}{{E_{z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{G_{\rho z} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{\varphi z} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{\varphi \rho } }}} \\ \end{array} } \right]$$
(7)

In the above equations, Eij is the elasticity modulus (i and j are indexes for directions), υij is the Poisson’s ratio, and Gij is the shear modulus related to the material.

Preparation of a mock-up and experimental procedure

A wooden panel of dimensions 210 mm x 290 mm x 40 mm was cut from a lime wood trunk seasoned for several years in dry conditions. The orientation of the panel was predominantly radial except for a central tangential section. The panel was sized with a (1:10 w/w) solution obtained by dissolving rabbit skin glue (Kremer Pigmente GmbH) in water at a temperature of 60 °C. Glue was applied with a brush when glue solution was still warm (ca. 45 °C). The sized panel was gessoed with the chalk-glue ground of pigment volume concentration PVC of 92%, PVC = P/(P+B) where P and B were volumes of the pigment (chalk) and the dried glue binder, respectively. A solution (1:14 w/w) obtained by dissolving rabbit skin glue in water at a temperature of 60 °C was used to prepare gesso of determined PVC. Chalk was then slowly added to the glue solution until no liquid was visible. The gesso preparation procedure was adopted after a historical recipe in the treatise of the early 15th century authored by Cennino Cennini (Cennini 1972). The thickness of the gesso layer applied by a brush was approximately 1.6 ± 0.1 mm. The mock-up painting was equilibrated at room temperature and RH of approximately 50% for four weeks. After curing, all side edges were sealed with aluminium sticky foil to block moisture transport from the sides of the painting.

The specimen was exposed to extreme RH cycles 10-90-10% in an environmental chamber until no further crack development was observed. The temperature during the experiment was elevated to 40 °C to speed up moisture transport to and from the specimen. The response time of a wooden panel of a thickness of 40 mm is approximately 1–3 months at room temperature, unacceptably long for the experiment. By weighing the specimen, it was estimated that 10 days at 40 °C were sufficient for the panel equilibration. After the experiment, the surface of gesso layer was photographed.

Analysis of craquelure patterns

The crack detection was based on the fact that crack lines were darker than a homogeneous, bright background of the recorded image. The analysis was performed in several steps using built-in functions offered in Wolfram Mathematica software. The selection of morphological operators as well as the sequence in their application was based on a try and error procedure. The major steps included:

  • Crack identification

Basic morphological operators such as conversion to a grayscale image, convoluted erosion and dilation were used to make cracks more visible and to remove close loop imperfections in crack topography like particles, so that only substantive components remain. Next, more complex morphological operations were used like top-hat closing to extract dark features or Toggle Tapping (TM). The TM allows for contrast enhancement and noise reduction by segmentation of the grayscale image according to the pixel intensity. This is carried out by introducing two operators that distinguish intensity (maxima and minima) and create homogenous local regions. Next, the thinning and binarization operators were implemented to obtain the skeleton of crack pattern for the recorded image. The operation involves removing neighbouring pixels leaving only central, pixel wide crack lines.

  • Transformation of a craquelure pattern into a set of lines

This step involves the implementation of Range Filter (RF) which filters data by maxima and minima in the specified neighbour range rF. First, the RF allows junctions of the skeletonized image to be detected. Second, RF’s output is a function of a local pixel arrangement that allows the junction type, its position and line directions to be specified. Hence, the graph indexed by the vertices and edges that corresponded to the craquelure pattern of the analysed image was obtained. rF is a free parameter that is selected to obtain the best fit of the craquelure pattern to the original image. The lower rF, the more detailed but noisy the pattern becomes. In turn, higher rF results in missing out certain cracks, which implies a loss of data. rF of 0.025 was chosen. Such a choice gave an optimal recognition of the analysed crack pattern. The vertices and edges were joined to represent cracks by straight lines rather than line paths. In this way, single lines representing edges of the islands in the craquelure pattern in the image were extracted.

  • Statistical evaluation of lines

A set of lines representing a craquelure pattern was categorized into two groups of cracks—parallel and perpendicular to the wood grain assuming that they should deviate from each direction by less than 45 degrees. For each category of lines, their mean length was calculated which can be interpreted as mean distance between the cracks in the respective directions for the rectangular crack representation. The three steps of analysis of craquelure patterns described above are presented in Fig. 4.

Fig. 4
figure 4

Visualization of steps in the analysis of a craquelure pattern, a grayscale of the original mock-up image, b image after morphological operations described in the crack identification step, c extracted craquelure pattern obtained in the second step of the process, d categorization of extracted lines into directions parallel (green) and perpendicular (orange) to the wood grain

Full size image

Results and discussion

Simplification of the model

The initial model was simplified to one central island marked with the red dot in Fig. 3. To estimate the error caused by such simplification, stress distribution at the surface of the central island was calculated when further islands (one, two, or three) were added in the model at each side of the central island along the φ-direction of loading. One quarter of each configuration was used in the modelling as two symmetry conditions along the z- and φ-directions were applied in the centre of the model (Fig. 5a). Differences between results obtained using the 3D models with various numbers of gesso islands are presented in Fig. 5b for the case of loading mode (1,0). As can be seen, the difference introduced by reducing the size of the model from seven to three islands is approximately 2% and grows to about 10% in the case of one gesso island. Such difference is acceptable in this study aimed at explaining the general mechanism of crack formation. Figure 5c shows that the normalized stress component in the φ-direction linearly increases with the normalized distance from the top of the gesso island downwards.

Fig. 5
figure 5

Impact of model simplification on the normalized tangential stress distribution at the surface, a general geometry for models with various numbers of gesso islands, the colour scale indicates the normalized stress component in the φ-direction in the central gesso island, b the same quantity as a function of the normalized distance from the centre of the gesso island in the tangential direction of the wood support, c the same quantity as a function of the normalized distance from the top of the gesso island downwards

Full size image

The results of the 3D modelling were compared with predictions obtained using a 2D model developed by Bratasz et al. (2020). A comparison of the φ-component of top surface stress obtained in the 2D and 3D cases is shown in Fig. 6 for the S/t ratio of 5.65 and loading mode (1,0). It can be seen that both stress distributions are in good agreement. The slight discrepancies between the two models can be explained by a difference in the mesh density, which was much smaller in the 3D case compared to 2D.

Fig. 6
figure 6

Comparison of the stress component in the φ-direction of stress field on the surface obtained with 3D modelling for the case of loading mode (1,0) with the results obtained by Bratasz et al. (2020). In both cases, the S/t ratio was 5.65, and L/t was 10 in the 3D model

Full size image

Stress distribution for the tangential loading

The optimized model was used to perform a parameter study by changing L/t and S/t in the case of stresses engendered in the gesso layer by wood swelling in the tangential direction on increasing RH-the mode (1,0) loading shown in Fig. 3a. Figure 7 shows plots of the normalized φ-component of stress field in the point of stress calculation as a function of S/t and for various L/t ratios. The stress component was normalized to the stress in the gesso layer without cracks and the applied strain was 0.01 (σ0 = Eg×ε0 = 3.75 GPa×0.01 = 3.75×107 Pa). The normalized stress asymptotically reaches 1 for large S/t ratios and slowly decreases with decreasing S/t until about 10. A further decrease of S/t causes a rapid decrease of the normalized φ-component of stress. For the critical S/t value of 4.6, the normalized φ-component drops to zero and further cracks in the direction perpendicular to the φ-direction cannot be initiated at the surface irrespective of the applied loading induced by swelling of wood. The model prediction is not dependent on the properties of the gesso layer—neither fracture tightness nor strength. Therefore, the outcome of the modelling is universal. The dynamics of crack pattern development (initiation of cracking, the critical stress value and the magnitude of RH change inducing it) was not within the scope of this paper. The critical value of 4.8 obtained with 2D modelling was almost identical (Bratasz et al. 2020). In both models, the critical S/t ratio increases with an increasing ratio of gesso-to-wood stiffness. For stiffness of gesso of 10, 1 and 0.1 GPa and wood parameters as in Table 2, the critical S/t ratios are 6, 3.2 and 2.4, respectively, and the L/t ratio is 40.

Fig. 7
figure 7

Normalized stress in the φ-direction in the point of stress calculation as a function of S/t for various L/t ratios

Full size image

Interestingly, the value of the φ-component of stress does not depend on the distance between cracks in the z-direction. This means that development of cracks in the φ-direction does not influence development of cracks in the z-direction. In the case of radially cut panels, the critical S/t ratio is slightly larger than for tangentially cut panels (Fig. 7) and is 5.2 (not shown).

The same loading applied in the φ-direction includes a nonzero L-component of the stress, except for certain combinations of S/t and critical L/t ratios, as shown in Fig. 8. For large L/t and S/t, the normalized z-component of stress asymptotically reaches the maximum value of 0.15 and drops gradually to negative values for decreasing L/t, if S/t is constant. The z-component also decreases for decreasing S/t ratio. If S/ is smaller than 4.6, the φ-component is negative, independent of the L/t ratio.

Fig. 8
figure 8

Normalized stress in the z-direction in the point of stress calculation as a function of L/t

Full size image

The above results indicate that moisture response of wood in the tangential direction cannot cause cracking of gesso across the grain in spite of a nonzero z-component of stress due to Poisson’s effect. This is because the φ-component is always greater than the z-component. Moreover, analysis of total elastic energy stored in the system (Fig. 9d) indicates that it is more beneficial for the system to densify cracks along the grain, not across.

Fig. 9
figure 9

a φ-component of stress, b z-component of stress, c von-Mises stress and d elastic energy in the critical point as a function of L/t and S/t

Full size image

Albeit the presented results are based on the elastic model, some information on fracture of a ductile material can be gathered using analysis of von Mises stress. The maximum distortion criterion (von Mises yield criterion) assumes that yielding of a ductile material begins when the second invariant of deviatoric stress reaches a critical value. The assumption is part of the plasticity theory that applies best to ductile materials, such as gesso at high RH levels. Figure 9c shows a map of von Mises stress as a function of the S/t and L/t ratios. Further, when analysing von Mises stress, one can see that cracks form in the direction parallel to the grain, not across.

Stress distribution due to drying shrinkage

Drying shrinkage of gesso is another mechanism leading to its cracking. Tensile stresses were modelled by applying the mode (1,1) loading shown in Fig. 3b with a strain of 0.01 in both directions. Figures 10 and 11 show the normalized φ- and z-components of stress field, respectively, in the point of stress calculation as a function of S/t and for various L/t ratios. The stress component was normalized as described in the previous section.

Fig. 10
figure 10

Normalized φ-component of stress in the point of stress calculation as a function of S/t for various L/t ratios and loading mode (1,1)

Full size image
Fig. 11
figure 11

Normalized z-component of stress in the point of stress calculation as a function of L/t for various S/t ratios and loading mode (1,1)

Full size image

It can be seen that the normalized φ-component of stress in the point of stress calculation exhibits a similar dependence on the S/t ratio as in the case of the tangential loading, with maximum stress being the same for L/t ratios smaller than 5 and about 30% higher for large L/t ratios. Analogously, the normalized z-component of stress in the point of stress calculation is 0.9 for S/t ratio of 2 and approaches asymptotically 1.2 for large S/t ratios. The increase of maximum φ- and z-components of stress is due to the impact of Poisson’s ratio when the biaxial loading is applied, not observed under only tangential loading.

The critical S/t and L/t ratios range between 4.5 and 5, and 3.5 and 4, respectively, depending on the L/t and S/t ratios. This is surprising, as the prediction of the 2D model would suggest that the critical L/t ratio is much smaller, about 2.5, as the ratio of gesso-to-wood stiffness in the longitudinal direction is 0.37 (Bratasz et al. 2020).

Stress distribution in the mixed mode

Figure 12 shows diagrams that illustrate the effect of superposition of various modes of loading on evaluated strains. As the diagrams demonstrate just patterns of strain variations under diverse environmental scenarios, moisture sorption was not considered in detail and simple relationship between moisture-related strain and relative humidity was assumed without considering the hysteresis. As plotted in Fig. 12b, the φ-component of moisture-related strain of wood (blue line) is proportional to an RH variation around mean RH (Fig. 12a). The z-component of the moisture-related strain is negligible (dotted red line). Moreover, the moisture-related strain in the gesso is negligible in both directions. The drying shrinkage of gesso causes negative strain in all directions (orange dashed line). If the gesso has ideally adhered to a wooden support, elastic strain develops in the gesso as shown in Figs. 12c (without drying shrinkage) and 12d (with drying shrinkage).

Fig. 12
figure 12

Various strain versus time histories induced by an RH variation and drying shrinkage of the gesso, a RH variation, b moisture-related strain (εh) induced in freely responding wood and gesso by the RH variation and drying shrinkage, respectively, c elastic strains engendered in the gesso layer due to the moisture response of wood—loading mode (1,0), d elastic strains engendered in the gesso layer due to moisture response of wood and drying shrinkage of the gesso—loading mode (3,1)

Full size image

Elastic strain distribution in Fig. 12c corresponds to the uniaxial mode resulting from the panel’s moisture response. However, in most practical situations, paint layers in panel paintings experience mixed mode situations when stresses induced by drying shrinkage of the gesso superimpose with stresses induced by moisture response of the wooden support. In consequence, maximum φ-component of elastic strains in the gesso is larger than the z-component of strain field. This situation is represented in Fig. 12d and, at a quarter of the cycle, corresponds to mixed mode (3,1)—the φ-component of stress is 3 times larger than the z-component. Obviously, the moisture-related strain of the panel at the beginning, the mid-point and the end of the cycle is zero, therefore, the gesso layer experiences the mode (1,1) loading resulting from drying shrinkage only.

The ratio of critical distance L between cracks in the z-direction to critical distance S between cracks in the φ-direction is shown in Fig. 13 as a function of the ratio of φ- and z-components of strain. It was assumed that this strain ratio could not be larger than 1 as maximum φ-component of strain in the fully elastic model is always larger than the maximum z-component. The critical L/S ratio varies between 0.8 and 1.7 for all strain ratios. In consequence, one can expect larger distances between cracks across than along the grain in panel paintings. As demonstrated in the previous section, although the critical L/S ratio approaches 1.7 for decreasing strain ratio, no cracks are formed across the grain, if loading is applied only in the φ-direction. Therefore, one can expect that the L/S value in panel paintings is large or infinite if there is no drying shrinkage of gesso or other isotropic shrinkage of the paint layer. These results help to analyse and interpret craquelure patterns observed in panel paintings, in particular those represented in Figs. 1a and 2. However, the presented model does not explain how cracks represented in Fig. 1b have developed.

Fig. 13
figure 13

Critical L/S ratio as a function of applied strain ratio

Full size image

Experimental results

Results of the computer simulations presented above were compared with craquelure patterns induced in the mock-up panel painting by 20 RH cycles in the range 10-90-10%. After a few RH cycles, the gesso layer was covered with a dense network of cracks, which stabilized after approximately 15 cycles, so no further crack development was observed in the last five cycles. The recorded image was evaluated using the procedure described in the section on analysis of craquelure patterns. Figure 14 illustrates major steps of the analysis. It was found that, for α = 10°, 75% of all line lengths were included in the analysis increasing to 91% for α = 20°. A further increase of α resulted in a slow increase to 100% for α = 45°. The observations indicate that most of the lines are approximately parallel or perpendicular to the wood grain. Finally, α = 20° was selected to calculate the mean distance between cracks in the mock-up painting.

Fig. 14
figure 14

Illustration of major steps in statistical analysis of crack patterns, a crack identification, b transformation of a craquelure pattern into a set of lines, c statistical evaluation of lines for α = 20°, green colour indicates lines selected for the analysis and grey colour shows lines omitted

Full size image

It was found that mean distances between cracks perpendicular and parallel to the wood grain were 18 ± 3 mm and 3.2 ± 0.1 mm, respectively. Taking into account the average gesso thickness of 1.6 mm, one can find that the S/t ratio is 2 and the L/t ratio is 11. The L/S ratio is about 6. The S/t value of 2 agrees well with the value 2.4 determined for the gesso of stiffness of 0.1 GPa with the 3D modelling and the tangential loading presented in this work. The S/t value tends to be up to 20% smaller in loading mode (1,1). Although any precise comparison of S/t and L/t ratios determined experimentally and theoretically is difficult as stiffness of gesso significantly decreases with an increasing RH reaching value of 0.1 GPa above 90% RH (Krzemień et al. 2016) and further decreases with increasing T, it can be concluded that both approaches resulted in similar values. In consequence, despite the high anisotropy of the support, the crack development would be almost isotropic. It was just assumed that both stresses induced by moisture-related response of the wood and caused by drying shrinkage of the gesso are much higher than critical stress. The similarity in the S/t ratio indicated that extensive RH variations caused significant loads in the direction parallel to the wood grain in the mock-up painting. The formation of cracks in the direction perpendicular to the wood grain indicated that drying shrinkage of the gesso layer also occurred so the specimen was subjected to the mixed mode loading. The L/t ratio of 11 suggested that stresses generated due to drying shrinkage were lower than stresses leading to crack saturation in the direction perpendicular to the wood grain.

Conclusion

In the current study, a three-dimensional structural model of a cracked panel painting was developed for the first time to simulate stress fields in the gesso layer. The model was used to analyse two loading modes—moisture response of a wooden panel and drying shrinkage of gesso—as well as their superposition. The resulting stress fields shed light on processes leading to the formation of typical crack patterns found in panel paintings—parallel or perpendicular to the wood grain, and rectangular. It was found that moisture related expansion of wood explained the formation of cracks along the grain but could not explain the formation of cracks across the grain. The critical crack distance normalized to the gesso thickness for moisture response of a tangentially cut wooden panel was between 6 and 2.4 depending on gesso stiffness. For the radial cut, this value was about 10% higher.

The isotropic drying shrinkage of gesso produced almost square cracks of aspect ratio 4:5 in the tangential to longitudinal directions. The critical S/t and L/t ratios ranged between 4.5 and 5, and 3.5 and 4, respectively.

Despite the usefulness of the 3D model developed, it cannot explain how patterns with cracks only perpendicular to the wood grain or patterns in which cracks perpendicular to the grain are much denser than cracks parallel to the grain, are formed. The potential explanation could be related to plastic deformation of wooden support frequently leading to warping of panel paintings, which reduces the tangential loading and, in consequence, makes the z-component of strain a more probable cause of fracturing perpendicular to the wood grain.

The outcome of the 3D modelling and the experimental results confirm our earlier conclusions that paintings, after reaching a certain level of crack density, are much less vulnerable to increases in RH leading to tensile stresses I in the paint layer. Further steps need to consider the multi-layer structure of the paint layer as well as the presence of defects that can initiate cracks below the surface.