Abstract
In contemporary wood science, computer-aided engineering (CAE) systems are commonly used for designing and engineering of high-value products. In diverse CAE systems, high-fidelity models with a full material description, including elastic constants such as Poisson’s ratios, are needed. Only few studies have dealt so far with the investigation of the Poisson’s ratio of spruce wood (Picea abies (L.) Karst.) or wood in general. Therefore, in the present study all six main Poisson’s ratios of spruce wood were determined in uniaxial tensile experiments by employing optical gauging techniques like electronic speckle pattern interferometry and a combination of laser and video extensometry. Consistent results for the Poisson’s ratios were found by applying these different optical gauging techniques. However, values found in the literature are sometimes considerably different from values established in this study. For that reason, the optical gauging techniques were evaluated with a conventional mechanical extensometer, which proved that there were no significant differences between the established measurements. Finally, in this study the feasibility of different non-contact optical gauging techniques was evaluated and compared through the comparison of the Poisson’s ratios, which showed that non-contact optical gauging techniques are suitable for establishing the Poisson’s ratio of (spruce) wood.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Nowadays, computer-aided engineering (CAE) methods such as finite-element modeling (FEM) are used for designing and engineering of high-value products. Reliable FEM is based on a sound data basis of material properties, such as elastic constants, including the Poisson’s ratio (ν). For anisotropic materials like wood, the Poisson’s ratio for one orthogonal direction is the ratio of the transverse contraction (transverse strain (εq)), to the axial extension (axial strain (εl)). These parameters have mainly been investigated in the last 4–5 decades by mechanical or electrical measurement systems (e.g., strain gauges, mechanical extensometer systems, inductive strain measurement devices), because of the lack of availability and the high price of optical measurement systems (Davis 2004).
The first examinations of the Poisson’s ratio of spruce wood were conducted by Carrington (1921, 1922a, b). He deduced the Poisson’s ratio from flexure experiments by measuring the curvature in lateral direction (transverse strain (εq)) and longitudinal direction (axial strain (εl)) with a telescope. Hörig (1931) re-evaluated the data and adopted the ideas of Voigt (1882, 1887, 1966), about the orthotropic behavior of materials on wood. The model by Hörig (1935) is the basis for the orthotropic description of wood that is used nowadays. Further substantial studies on spruce wood were carried out by Wommelsdorff (1966) and Neuhaus (1981). They determined the six orthotropic Poisson’s ratios using inductive strain measurement devices and also strain gauges by means of tensile and flexure experiments. Furthermore, Niemz and Caduff (2008) and also Keunecke et al. (2008) investigated the Poisson’s ratio of spruce wood. Keunecke et al. (2008) have chosen digital image correlation (DIC) to measure the strain distribution. DIC is a non-contact optical surface deformation gauging technique (Chu et al. 1985; Zink et al. 1995; Pan et al. 2009; Valla et al. 2011).
In more recent studies, three-dimensional optical digital measurements (3D ODM) and also resonant ultrasound spectroscopy (RUS) methods were used to establish all elastic constants by using only one type of specimen (Forsberg et al. 2010; Majano-Majano et al. 2012; Vorobyev et al. 2016). A clear advantage is that all components of the stiffness tensor are established with the same specimen by employing a consistent method. Currently, though, not all elastic constants can be derived robustly (e.g., Poisson’s ratio)—as for example the viscoelastic damping of wood may cause an overlapping of resonant peaks (Longo et al. 2018) which eventually may lead to a wrong iterative deduction of the elastic constants in the inverse identification. This applies in particular to wood with low density. Further, Longo et al. (2018) pointed out that the free resonance frequencies are very insensitive to νRT and not sensitive at all to vLR and νLT. Three-dimensional ODM requires high-resolution cameras and a high level of expertise in material characterization, due to the need of the mathematical implementation of the procedure to establish consistent measurements (Majano-Majano et al. 2012). Moreover, the setup may bias the measurement results, which needs to be clarified before this technique can be considered as standard method for future wood material characterization. In summary, RUS and 3D ODM for establishing Poisson’s ratio are uncertain and may only be indicated when nondestructive testing is required (Bachtiar et al. 2017).
Optical gauging techniques that provide independent mechanical material properties in micro- or even nanoscale were found to be suitable for wood characterization (Xavier et al. 2007, 2013; Valla et al. 2011; Toussaint et al. 2016). Furthermore, these methods have the advantage to be contactless, which means avoiding any mechanical influences on the specimen. Therefore, in this study the optical gauging techniques “Electronic Speckle Pattern Interferometry (ESPI), laser extensometry and video extensometry” are compared head-to-head for establishing the Poisson’s ratio of (spruce) wood. Former studies prove that these methods are suitable for the mechanical characterization of the elastic properties of wood (Gingerl 1998; Eberhardsteiner 2002; Samarasinghe and Kulasiri 2004; Gindl et al. 2005; Müller et al. 2005; Konnerth et al. 2006; Gindl and Müller 2006; Dahl and Malo 2009; Valla et al. 2011; Bader et al. 2015; Crespo et al. 2017; Milch et al. 2017).
ESPI is a non-contact gauging technique based on the Michelson interferometer (Meschede 2015), which is used for planar strain measurement in the present study. The technique uses laser light (coherent light wave) together with a CCD camera to record displacements of the specimen surface. The surface is illuminated with a laser beam from two different planar directions, and the reflected light is registered by a CCD sensor. The ESPI system converts the light information into a speckled image, which describes the surface of the object. Deformation of the specimen results in a new speckle pattern. By subtracting the new speckle pattern from the reference pattern, an illustration with typical fringe pattern is obtained (Jones and Wykes 1989). In the next step, a phase-shift method is used to transform the fringe picture into a so-called 2π-modulo image, which is used to create a map of displacement (Eberhardsteiner 1995; An and Carlsson 2003; Müller et al. 2015). Additional material data (for example strain distribution) can be gained from the deformation map through post-processing. More comprehensive information about the ESPI technique is available in other studies (Gingerl 1998; Rastogi et al. 2001; Eberhardsteiner 2002; Müller et al. 2005).
The basic principles of the laser extensometry method are similar to the ESPI technique. A laser source radiates a beam, which is projected on the surface of the specimen. The reflected light beams are recorded on a camera sensor, which generates a speckle pattern on the basis of the intensity distribution (Messphysik—Materials Testing 2017). The mechanical load induces movements on the object surface. Those movements indicate displacements of the speckle pattern as well. The core of the technique is to identify pattern areas of the initial picture in the upcoming images (Zwick/Roell 2017a). Due to the unique gray value distribution of any defined pattern area, it is possible to find these speckle zones in any upcoming deformation image. After that, a complex algorithm runs to find the motion of the defined speckle zone between the initial picture and the following images. For the estimation of the strain in one direction, it is necessary to perform this procedure on two self-contained pattern zones at least. More comprehensive information about the laser extensometry technique can be found elsewhere (Choi et al. 1991; Kamegawa 1999; Anwander et al. 2000; Jin et al. 2013; Messphysik—Materials Testing 2017; Zwick/Roell 2017a).
The video extensometry method is based on capturing ongoing images of the specimen, for example, during a tensile test by using a digital video camera. To capture the lateral movements, the specimens need to be marked somehow (e.g., sticker and pen marker) at least on two different positions. By using this method, it is important to have high contrast between the object surface and the measurement points (markers) to ensure unaltered results. While the specimen is stressed, the pixel distance between these markers is tracked continuously. Image processing algorithms are used to track these motions in real time. Automatically, a direct strain measurement value can be obtained by mapping these motion measurements against the initial specimen image. For recording the transverse deformations of the specimens, no extra marking is required. In this case, special edge detection algorithms are applied (Zwick/Roell 2017b). The video extensometry technique provides non-contact real-time strain measurement in lateral and transverse direction independently from each direction. More specific information about the fundamentals of the technique can be found in Vial (2004), Wolverton et al. (2009), Bovik (2010) and Zwick/Roell (2017b).
The present study focuses on determining the Poisson’s ratio of spruce wood in all main orthogonal directions by means of the non-contact optical gauging techniques ESPI, laser extensometry and video extensometry, respectively. Therefore, a uniaxial tensile experiment was designed under real measuring conditions to generate comparable and truthful values. The main hypotheses of this study are:
-
ESPI, laser extensometry and video extensometry are suitable for the detection of the Poisson’s ratio of wood.
-
Poisson’s ratio gained by means of ESPI, laser extensometry and video extensometry will show no statistically significant differences.
Materials and methods
Material
Solid wood made of Norway spruce (Picea abies (L.) Karst.) specimens was used in the experiments. Sawn timber without noticeable defects like knots or cracks was meticulously selected. Semifinished elements in the different anatomical directions were cut out of the boards by means of a circular saw. For producing the samples out of these elements, a CNC and a conventional planning and a milling machine were used. After manufacturing the raw material to the desired shape, samples were conditioned at a temperature of 20 ± 2 °C and a relative humidity of 65 ± 5% (after ISO 554) to an average moisture content of ω = 12%. Under this condition, the average sample density (ρ) was 465 ± 30 kg/m3.
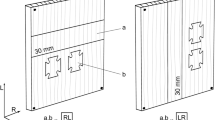
Dog-bone-shaped specimens corresponding to DIN 52188:1979-05 (1979) were used for testing in longitudinal (L) direction. Due to the high stiffness of wood in longitudinal direction, high forces and thus also high clamping forces had to be applied. To ensure no material failure and no slipping in the clamping area, those dog-boned shaped specimens were required. For samples, where the load was applied in tangential (T) or radial (R) direction, simplified strip-shaped specimens with uniform cross section were manufactured (20 × 6 × 120 mm3 = width × height × length). Because of the low stiffness in the transverse direction of wood, only low clamping forces act and therefore no slippage was guaranteed. In accordance with the theory by Hörig (1935), six different samples (Fig. 1) were necessary to measure all main orthogonal Poisson’s ratios: νLR, νLT, νRL, νRT, νTL and νTR independently. In this case, the first character of the subscript stands for the direction of the longitudinal extension [longitudinal strain (εl)] and the second character of the subscript describes the direction of the transverse contraction [transverse strain (εq)]. In total, 60 specimens were tested, i.e., 10 in every direction.
3D illustrations of the specimens; a dimensions corresponding to DIN EN 52188:1979-05 (1979); b, c 20 × 6 × 120 mm3 (width × height × length)
Designation of Poisson’s ratio
In general, the phenomenon that axial extension (εl) of a rod results in transverse contraction (εq) was discovered 1760 by Poisson. The ratio of the passive deformation (normal to the direction of the applied force) to the active deformation (in direction of the applied force) is defined as Poisson’s ratio:
Thus, for specimen RT as an example (Fig. 1b left), the Poisson’s ratio is defined as:
Calculation of Poisson’s ratio as compliance coefficient
Hörig’s (1935) idealization of wood as a crystalline material with linear elastic and orthotropic mechanical material properties leads to the following notation of Hooke’s law, when the material axes longitudinal (L), radial (R) and tangential (T) are orthogonal to each other:
where [ε] is the strain vector described by the elongations (εL, εR, εT) and shear strains (γRT, γTL, γLR). [S] is the compliance matrix which includes 12 compliance coefficients (1/EL, − νRL/ER, 1/GRT, etc.) which are a function of the Young’s moduli (EL, ER, ET), shear moduli (GRT, GTL, GLR) and Poisson’s ratios (νLR, νLT, νRL, νRT, νTL, νTR). [σ] is the stress vector which contains the tensile stress (σL, σR, σT) and shear stress (τRT, τTL, τLR) components. In elasticity theory, the constants of the compliance matrix are shown to satisfy symmetry condition as elastic deformation shall be non-dissipative. Due to the symmetry of the compliance matrix [S], two of the Poisson’s ratios are related to each other by means of below equations:
It means that the linear elastic mechanical behavior can be described by three moduli of elasticity, three shear moduli and three Poisson’s ratios, whereas only three of the six main orthogonal Poisson’s ratios are independent material constants. Other bounds on the moduli of orthotropic materials are caused by the requirement that the compliance matrix must be positive definite. More fundamentals about the calculation and estimation of the Poisson’s ratio of wood and wood-based materials can be found in Kollmann and Côté (1968), Bodig and Jayne (1982) and Niemz and Sonderegger (2017).
Experiments
The material characterizations with ESPI, laser extensometry, video extensometry and mechanical extensometer were performed by applying uniaxial tensile tests. All experiments were performed on Zwick/Roell universal testing machines (Ulm, Germany), equipped with the control software Zwick/Roell testXpert 2 V3.5 (Ulm, Germany). The characteristics of the gauging techniques ESPI, laser extensometry and video extensometry are summarized in Table 1.
ESPI measurement
In the first step, uniaxial tests were performed and elongation and contraction of the specimens were measured by means of the ESPI technique. For this, two ESPI Q300 Dantec-Ettemeyer (Ulm, Germany) devices, with a maximal measurement resolution of 0.03 µm (Dantec Dynamics A/S 2017), were mounted on the machine to allow measuring deformation on the surface of the specimens from both sides at the same time (Fig. 2a). Müller et al. (2015) showed that in shear experiments on spruce wood, deformation on the front and back side of a specimen can vary significantly. ESPI is highly sensitive, which can be affected by different factors, such as vibrations. Comparing test results from the front and the back side indicated immediately biased data. Additionally, higher precision of the ESPI results could be achieved by using the mean value of the deformation measured on the front and back of the specimens.
The ESPI Q300 Dantec-Ettemeyer devices were mounted on the testing machine in such a way that the optical axis of both devices coincided and the specimen was clamped exactly in the center point in between both devices (Fig. 2a). Any vibrations of the devices were minimized by additional supporting frames. A free clamping length of 350 mm (for the dog-bone-shaped specimen Fig. 1a) and 70 mm (for the strip-shaped specimen Fig. 1b, c) was chosen. In both cases, a field of view (FoV) of 26 × 13 mm2 was used, to observe deformation on the specimen. To prevent biasing of the data due to vibration artifacts, a pre-force was applied prior to starting the test procedure to stabilize specimens. For longitudinal dog-bone-shaped samples (Fig. 1a), a pre-force of 100 N was applied, and for strip-shaped samples, a pre-force of 20 N (Fig. 1b) and 10 N (Fig. 1c) was applied. The total deformation had to be established by accumulating the deformation determined in several load steps, because of the high sensitivity of the ESPI technique. It was assumed that two to three fringes in the y-axis picture would give reliable results per load step. The load step had to be adjusted to the stiffness of the material. Stiff material would lead to large load steps, which could be selected. A load step of 100 N and 10 N was found to be appropriate for testing wood in longitudinal (Fig. 1a) and transverse (Fig. 1b, c) direction, respectively. At every load step, the crosshead of the testing machine was stopped for 5 s to capture the generated speckle images in x- and y-direction. For all samples, total deformation was divided into six load steps, which resulted in a maximum load of 700 N tested in longitudinal, 80 N (Fig. 1b) and 70 N (Fig. 1c) in transverse direction. Therefore, samples were stressed to σ = 5.83 MPa, σ = 0.67 MPa and σ = 0.58 MPa in longitudinal, radial and tangential direction, which corresponded to less than 20% of the breaking strength in the different directions. All ESPI images were recorded and analyzed with the post-processing software ISTRA 2001 Dantec-Ettemeyer (Ulm, Germany) to determine the Poisson’s ratio, afterward. For this, the mean values of axial and transverse strains were measured within the FoV and Poisson’s ratio was calculated corresponding to Eq. (1).
Laser and video extensometry measurement
The laser and video extensometry measurements were carried out on a universal testing machine Zwick/Roell Z020 (Ulm, Germany), equipped with an optical extensometer system including both gauging techniques. Therefore, the extensometer system contains a gauging sensor, a digital camera and a laser light source. An absolute measurement accuracy of 0.11 µm of the laser extensometry system, laserXtens (Zwick/Roell, Ulm, Germany), is specified by the manufacturer. With the laser extensometry system used, axial and transverse strain measurements can be performed simultaneously (Zwick/Roell 2017a). The video extensometry device, videoXtens (Zwick/Roell, Ulm, Germany), is a camera which is enclosed in a metal housing, with a measurement accuracy dependent on the field of view (FoV) (Zwick/Roell 2017b), for FoVs smaller than 200 mm with a measurement accuracy meeting the requirements specified in DIN EN ISO 9513:2013-05 (2013). In this study, the FoV was selected such as to ensure an accuracy of 0.2 µm. As illustrated in Fig. 2b, the video extensometry device was positioned in the center, which was flanked by two laser sources of the laser extensometry device. The measuring points of the laser extensometry device were positioned on the upper and lower side of the specimen. For the dog-bone shaped samples, the distance of the measuring points was 70 mm, whereas for the strip-shaped samples a distance of 40 mm was chosen. Contraction of the samples was measured in the center of the specimens. For this, the video extensometry device used the contrast of the edges of the specimen. Increased contrast of the edges was achieved by illuminating the specimen from the back. This setup was chosen because it is not possible to measure the axial strain (εl) and the transverse strain (εq) with videoXtens simultaneously.
First, laser extensometry was applied to measure strain in axial and transverse direction. In transverse direction, results showed a high variability. Hence, a hybrid approach was selected, using laser extensometry for measuring axial extension (εl) and video extensometry for transverse contraction (εq). Thereafter, the Poisson’s ratio was calculated by means of the software testXpert 2 V3.5 (Ulm, Germany) automatically. The clamping and measurement length for the dog-bone shaped samples (LR and LT) amounted to 350 mm and 80 mm, respectively. For the strip-shaped samples (RL, RT, TL and TR), the distances amounted to 70 mm and 40 mm, respectively. The specimens LR and LT (Fig. 1a) were stressed at maximum with a force of 4000 N and a pre-force of 100 N, and the specimens RL, RT, TL and TR (Fig. 1b, c) with a pre-force of 10 N and a maximum load of 200 N. Accordingly, the maximum tensile stress ε amounted to 34.17 MPa (specimens LR and LT) and 1.75 MPa (specimens RL, RT, TL and TR), which is far lower than the yield stress of spruce wood.
Mechanical extensometer measurement
For evaluating optical gauging techniques, additional measurements were performed by using the same set of strip-shaped specimens with a mechanical extensometer, makroXtens (Zwick/Roell, Ulm, Germany). The axial elongation (εl) of the specimens for a load step of ∆F = 200 N was calculated corresponding to Eq. (7) (Bodig and Jayne 1982):
where A is the cross section of the specimens and MOE represents the modulus of elasticity (i.e., slope of the stress–strain curve).
MakroXtens is a conventional clip-on mechanical extensometer with a measurement resolution of 0.5 µm, which meets the requirements specified in DIN EN ISO 9513:2012 class 0.5 (Zwick/Roell 2017c). More comprehensive information about mechanical extensometers can be found elsewhere in the literature (Figliola and Beasley 2001; Zwick/Roell 2001, 2017c; Davis 2004; Pan and Wang 2016).
Statistical evaluation
All statistical tests were carried out using the software package IBM SPSS Statistics 21. Initially, the Shapiro–Wilk test was applied to verify whether the measured data follow a normal distribution. Because the null hypothesis was rejected, which meant that the data did not follow a normal distribution, the Wilcoxon-matched pair test was used to determine the statistical equivalence of two data sets. To perform a statistical comparison with more than two data sets, the Friedman’s test was employed.
Results and discussion
Table 2 gives an overview of the sample’s moisture content (ω), density (ρ) in dependence of the orthogonal directions (ρL, ρR and ρT) and also the summarized test results of the non-contact optical gauging techniques in comparison with the literature references: Hörig (1935), Wommelsdorff (1966), Neuhaus (1981), Niemz and Caduff (2008) and Keunecke et al. (2008). The optical gauging techniques, ESPI and a combination of laser extensometry (for εl) and video extensometry (for εq) returned consistent results in terms of the Poisson’s ratio: νLR, νLT, νRL, νRT, νTL and νTR, and in terms of the modulus of elasticity (MOE) for all three orthogonal directions: EL (mean of ELR and ELT), ER (mean of ERL and ERT) and ET (mean of ETR and ETL). The results are presented in the form of the mean values (e.g., x̅[νLR]) and the coefficient of variation (e.g., CoV[ER]) of the Poisson’s ratio and the moduli of elasticity. The quantified moduli of elasticity and densities are in the expected magnitude range of spruce wood. The region from which the trees were removed, but also the number of trees from which the sample material has been obtained, must be taken into account since they could have an impact on the material properties. The shape and size of the specimens could also have an impact on the material properties. When using small-sized samples, the annual ring width may bias the measurement results (Niemz and Caduff 2008), because it correlates directly with the material density and stiffness. However, these effects cannot explain the significant differences between the presented Poisson’s ratios.
Almost all Poisson’s ratios established in this study violate the symmetry condition of the linear elastic and orthotropic compliance matrix [S]. This phenomenon has also been mentioned in previous studies (Neuhaus 1981; Bodig and Jayne 1982; Garab et al. 2010; Hering et al. 2012; Bachtiar et al. 2017). The stiffness or compliance matrix is symmetric due to Betti’s reciprocity theorem [the deflection d (in direction A) due to a unit force p (in direction B) is equal to the deflection d (in direction B) due to a unit force p (in direction A)]. It becomes asymmetric as soon as this theorem is violated, i.e., when deformation is dissipative (friction, damage) or the deformation is non-local. In order to still obtain a symmetric compliance matrix [S], as required for time-efficient FEM (and for parameterizing orthotropic material models), the calculation of the average value from each corresponding off-diagonal term, i.e., Eqs. (4–6), followed by a backward calculation to re-obtain the elastic material parameters was pursued as proposed by Bachtiar et al. (2017).
Lekhnitskii et al. (1964) showed that all bodies can be divided into homogenous (physical properties remain invariant in all directions and all points) and non-homogenous bodies, as well as in isotropic and anisotropic. Perkins (1967) noted that wood is inhomogeneous at macro- and microscopic scale. Qing and Mishnaevsky (2010) investigated the effect of annual ring structure, microfibril angle and cell shape angle on the elastic constants in a numerical study employing a 3D micromechanical computational model of softwood, considering the wood’s structure at four scales from microfibrils to annual rings. They showed that vLR increases with increasing microfibril angle and decreases with wood density. The vLT increases with the increasing microfibril angle and cell shape angle. Hearmon (1948) showed that Poisson’s ratios can even gain negative values at certain microfibril angles. Consequently, it means that in future experimental testing, more parameters must be recorded (annual ring radius, content of early and latewood, microfibril angle, etc.).
In general, the Poisson’s ratios determined in this study have a higher mean value compared to the literature references. Particularly, the mean value x̅[νRL] is about 6.7 times higher than the lowest value found in the literature (Table 2). Even the values found in the literature are not consistent with each other and show wide dispersions. The differences to the literature references are open to speculation, because on the one hand, the scattering of the literature data could suggest similar median values compared to the own measurements. On the other hand, diverse gauging techniques and apparatuses with different measurement resolutions were used by each researcher. Nevertheless, in this study different gauging techniques were directly compared to each other with the same sample set.
To ensure the statistical reliability of the own measurements, a validation of the used gauging techniques was pursued. Related to the described approach, the summarized results of the statistical evaluation are presented in Tables 3 and 4. The test on normality distribution (Table 3) does not show a normal distribution for all investigated data (for example p = .013 for νRL), which is why the Wilcoxon test was applied (Table 4). This test confirmed the statistical equality between the measurements gained due to ESPI compared to laser extensometry (for εl) in combination with video extensometry (for εq). For example, the highest differences of means could be found for the MOE of ER, which shows a statistical value of Z (N = 22) = − 1.607, p = .108. Compared to that, the Poisson’s ratio of νRL illustrates a good accordance of the means with values of Z (N = 11) = − .533 and p = .594.
In order to guarantee the accuracy of the own measurements by means of the chosen non-contact optical gauging techniques, a statistical validation with a mechanical extensometer was done additionally. For this validation, the axial extension (εl) of the specimens RL and RT has been investigated with the same sample set, because the means of the Poisson’s ratio x̅[νRL] had the biggest discrepancies to the lowest literature reference (Table 2). The axial extension (εl) of the tested specimens at a load level of ∆F = 200 N is illustrated as box plots in Fig. 3. Even the qualitative comparison of the gauging techniques does not show any discrepancies at all (e.g., x̅[ε ESPIl ] = 0.153%, x̅[ε laser extensometryl ] = 0.151%, x̅[ε video extensometryl ] = 0.147% and x̅[ε mechanical extensometerl ] = 0.155%). To confirm that there are no significant differences, the results of Friedman’s test and Wilcoxon test are presented in Table 5. The nonparametric Friedman test for repeated measurements shows a Chi-square of χ2 = 1.421 which was not significant (p = .701). As expected, the Wilcoxon test also indicates for all comparisons no statistically significant differences (all p ≥ .05). Based on this investigation, it is certain that the transverse strain (εq) would show a similar accuracy among the gauging techniques, because the physical principle for the measurements is exactly the same. Unfortunately, the mechanical extensometer does not allow measurements normal to the direction of the applied force, which would be needed for this kind of validation.
However, as the specimens and the testing conditions were identical for the own measurements, it is possible to say that there are no statistical differences between the measurement techniques ESPI, laser extensometry and video extensometry. Moreover, the results obtained confirm the first hypothesis of this study, i.e., the non-contact optical gauging techniques ESPI, laser extensometry and video extensometry are suitable for the detection of the Poisson’s ratio of wood.
Nonetheless, in dependence of the chosen measurement setup, it was not possible to gain reproducible Poisson’s ratio for all specimens. In Fig. 4, the failed measurements in dependence of the gauging technique and specimen type are illustrated. The ESPI measurements with the specimens LR and LT failed, because at a certain load level the specimens started to creep, while capturing the image. This instability led to noises, which caused the post-processing process not to be executable. Moreover, it was impossible to measure the transverse strain (εq) of any specimens via laser extensometry. This could be explained by the very small transverse contractions of the specimens that led to very small displacements of the speckle zones, which were not exceeding the measurement resolution of 0.11 µm (measurement resolution of the laser extensometry device). To confirm this hypothesis, further studies are needed to be carried out.
Conclusion
In this study, three optical gauging techniques (electronic speckle pattern interferometry (ESPI), laser and video extensometry) and one mechanical gauging technique were used to establish the six Poisson’s ratio of spruce wood (Picea abies (L.) Karst.) in uniaxial tensile experiments.
All techniques were found to be suitable for establishing the Poisson’s ratios and returned statistically equivalent results. However, there are limitations in terms of the setup and specimen type. For example, with the “dog-bone-shaped specimen” it was not possible to establish ESPI measurements, because at a certain load level the specimens started to creep while capturing the image. Furthermore, the measurement of the transverse strain of any specimens via laser extensometry was not possible to establish due to the very small transverse contractions of the specimens that led to very small displacements of the measurement zones, which were not exceeding the measurement resolution of the device.
In engineering, wood is usually assumed to behave orthotropic. This model implies that the material behaves load-symmetric elastic (tension/compression), is homogenous and features three mutually orthogonal elastic symmetry planes. Due to Betti’s theorem, the compliance tensor is generally assumed symmetric (about its diagonal), which is also advantageous for the time- and resource (memory)-efficient FEM calculations. The Poisson’s ratios established in this study, though, are violating the symmetry conditions of elastic orthotropic materials, which might be caused by, for example, non-local deformations. The authors recommend to follow the procedure outlined by Bachtiar et al. (2017) (calculating the average value from each corresponding off-diagonal term, followed by a backward calculation to re-obtain the elastic material parameters), to warrant efficient FEM calculation and the use of pre-implemented material models.
While the Poisson’s ratios established are consistent within the study, they were found considerably different to some of the values found in the literature. Various researches have shown that the elastic constants, including the Poisson’s ratios, are sensitive to the annual ring structure, microfibril angle and cell shape angle as well as density. The wide spread of values published in the literature clearly shows that in experimental testing of wood specimens more parameters (other than the density and moisture content) must be recorded: annual ring radius, content of early and latewood, and microfibril angle. Future testing may also distinguish between Poisson’s ratios in each lamina (early/latewood) of the wood specimen—something which might only be possible with full-field optical gauging techniques.
In summary, the study shows that optical gauging techniques are suitable for determining the Poisson’s ratios of (spruce) wood. The discrepancies with the values found in other studies, though, clearly show the need to characterize and record the morphology of each specimen. Optical gauging techniques may further offer the possibility to establish the Poisson’s ratio lamina-wise.
References
An W, Carlsson TE (2003) Speckle interferometry for measurement of continuous deformations. Opt Lasers Eng 40:529–541. https://doi.org/10.1016/S0143-8166(02)00085-4
Anwander M, Zagar BG, Weiss B, Weiss H (2000) Noncontacting strain measurements at high temperatures by the digital laser speckle technique. Exp Mech 40:98–105. https://doi.org/10.1007/BF02327556
Bachtiar EV, Sanabria SJ, Mittig JP, Niemz P (2017) Moisture-dependent elastic characteristics of walnut and cherry wood by means of mechanical and ultrasonic test incorporating three different ultrasound data evaluation techniques. Wood Sci Technol 51:47–67. https://doi.org/10.1007/s00226-016-0851-z
Bader TK, Eberhardsteiner J, de Borst K (2015) Shear stiffness and its relation to the microstructure of 10 European and tropical hardwood species. Wood Mater Sci Eng 12:82–91. https://doi.org/10.1080/17480272.2015.1030773
Bodig J, Jayne BA (1982) Mechanics of wood and wood composites. Van Nostrad Reinhold Company, New York
Bovik AC (2010) Handbook of image and video processing. Academic press, Cambridge
Carrington H (1921) XVII. The determination of values of Young’s modulus and Poisson’s ratio by the method of flexures. Lond Edinb Dublin Philos Mag J Sci 41:206–210. https://doi.org/10.1080/14786442108636212
Carrington H (1922a) The elastic constants of spruce as influenced by moisture. Aeronaut J (Lond Engl 1897) 26:462–471. https://doi.org/10.1017/S2398187300139465
Carrington H (1922b) XCV. Young’s modulus and Poisson’s ratio for spruce. Lond Edinb Dublin Philos Mag J Sci 43:871–878. https://doi.org/10.1080/14786442208633943
Choi D, Thorpe JL, Hanna RB (1991) Image analysis to measure strain in wood and paper. Wood Sci Technol 25:251–262. https://doi.org/10.1007/BF00225465
Chu TC, Ranson WF, Sutton MA (1985) Applications of digital-image-correlation techniques to experimental mechanics. Exp Mech 25:232–244. https://doi.org/10.1007/BF02325092
Crespo J, Aira JR, Vázquez C, Guaita M (2017) Comparative analysis of the elastic constants measured via conventional, ultrasound, and 3-D digital image correlation methods in Eucalyptus globulus labill. BioResources 12:3728–3743
Dahl KB, Malo KA (2009) Planar strain measurements on wood specimens. Exp Mech 49:575–586. https://doi.org/10.1007/s11340-008-9162-0
Dantec Dynamics A/S (2017) 3D ESPI system (Q-300). https://www.dantecdynamics.com/3d-espi-system-q-300. Accessed 27 Aug 2017
Davis JR (2004) Tensile testing. ASM international, Materials Park
DIN 52188:1979–05 (1979) Prüfung von Holz—Bestimmung der Zugfestigkeit parallel zur Faser (Testing of wood; determination of ultimate tensile stress parallel to grain). Deutsches Institut für Normung, Berlin (in German)
DIN EN ISO 9513:2013-05 (2013) Metallische Werkstoffe—Kalibrierung von Längenänderungs-Messeinrichtungen für die Prüfung mit einachsiger Beanspruchung (Metallic materials—calibration of extensometer systems used in uniaxial testing). Deutsches Institut für Normung, Berlin (in German)
Eberhardsteiner J (1995) Biaxial testing of orthotropic materials using electronic speckle pattern interferometry. Measurement 16:139–148. https://doi.org/10.1016/0263-2241(95)00019-4
Eberhardsteiner J (2002) Mechanisches Verhalten von Fichtenholz: Experimentelle Bestimmung der biaxialen Festigkeitseigenschaften (Mechanical behaviour of spruce wood: experimental determination of biaxial strength properties). Springer, Wien (in German)
Figliola RS, Beasley DE (2001) Theory and design for mechanical measurements, 3rd edn. Wiley, New York
Forsberg F, Sjödahl M, Mooser R et al (2010) Full three-dimensional strain measurements on wood exposed to three-point bending: analysis by use of digital volume correlation applied to synchrotron radiation micro-computed tomography image data. Strain 46:47–60. https://doi.org/10.1111/j.1475-1305.2009.00687.x
Garab J, Keunecke D, Hering S et al (2010) Measurement of standard and off-axis elastic moduli and Poisson’s ratios of spruce and yew wood in the transverse plane. Wood Sci Technol 44:451–464. https://doi.org/10.1007/s00226-010-0362-2
Gindl W, Müller U (2006) Shear strain distribution in PRF and PUR bonded 3–ply wood sheets by means of electronic laser speckle interferometry. Wood Sci Technol 40:351–357. https://doi.org/10.1007/s00226-005-0051-8
Gindl W, Sretenovic A, Vincenti A, Müller U (2005) Direct measurement of strain distribution along a wood bond line. Part 2: Effects of adhesive penetration on strain distribution. Holzforschung 59:307–310. https://doi.org/10.1515/HF.2005.051
Gingerl M (1998) Realisierung eines optischen Deformationsmeßsystems zur experimentellen Untersuchung des orthotropen Materialverhaltens von Holz bei biaxialer Beanspruchung (Realization of an optical deformation measuring system for the experimental investigation of the orthotropic material behaviour under biaxial stress). Dissertation, Technische Universität Wien (in German)
Hearmon RFS (1948) The elasticity of wood and plywood. For Prod Res 7:1–87
Hering S, Keunecke D, Niemz P (2012) Moisture-dependent orthotropic elasticity of beech wood. Wood Sci Technol 46:927–938. https://doi.org/10.1007/s00226-011-0449-4
Hörig H (1931) Zur Elastizität des Fichtenholzes. I. Folgerungen aus Messungen von H. Carrington an Spruce (To the elasticity of spruce wood. I. Consequences of the measurements conducted by H. Carrington on Spruce). Zeitschr f techno Phys 12:369 (in German)
Hörig H (1935) Anwendung der Elastizitätstheorie anisotroper Körper auf Messungen an Holz (Application of the elasticity theory of anisotropic bodies to wood measurements). Arch Appl Mech 6:8–14 (in German)
Jin H, Sciammarella C, Yoshida S, Lamberti L (2013) Advancement of optical methods in experimental mechanics, volume 3: conference proceedings of the society for experimental mechanics series. Springer
Jones R, Wykes C (1989) Holographic and speckle interferometry. Cambridge University Press, Cambridge
Kamegawa MN (1999) Strain measuring instrument, European Patent No. EP 0 629 835 B1. European Patent Office
Keunecke D, Hering S, Niemz P (2008) Three-dimensional elastic behaviour of common yew and Norway spruce. Wood Sci Technol 42:633–647. https://doi.org/10.1007/s00226-008-0192-7
Kollmann FFP, Côté WA Jr (1968) Principles of wood science and technology—solid wood. Springer, München
Konnerth J, Valla A, Gindl W, Müller U (2006) Measurement of strain distribution in timber finger joints. Wood Sci Technol 40:631–636. https://doi.org/10.1007/s00226-006-0090-9
Lekhnitskii SG, Fern P, Brandstatter JJ, Dill EH (1964) Theory of elasticity of an anisotropic elastic body. Phys Today 17:84
Longo R, Laux D, Pagano S et al (2018) Elastic characterization of wood by resonant ultrasound spectroscopy (RUS): a comprehensive study. Wood Sci Technol 52:383–402. https://doi.org/10.1007/s00226-017-0980-z
Majano-Majano A, Fernandez-Cabo JL, Hoheisel S, Klein M (2012) A test method for characterizing clear wood using a single specimen. Exp Mech 52:1079–1096. https://doi.org/10.1007/s11340-011-9560-6
Meschede D (2015) Gerthsen Physik. Springer-Verlag Berlin Heidelberg (in German)
Messphysik—Materials Testing (2017) Laser Speckle Extensometer ME53. http://www.messphysik.com/fileadmin/messphysikdaten/Download/Laser_speckle_extensometer_en.pdf#page=16&zoom=auto,-205,558. Accessed 30 Aug 2017
Milch J, Brabec M, Sebera V, Tippner J (2017) Verification of the elastic material characteristics of Norway spruce and European beech in the field of shear behaviour by means of digital image correlation (DiC) for finite element analysis (FEA). Holzforschung 71:405–414. https://doi.org/10.1515/hf-2016-0170
Müller U, Sretenovic A, Vincenti A, Gindl W (2005) Direct measurement of strain distribution along a wood bond line. Part 1: shear strain concentration in a lap joint specimen by means of electronic speckle pattern interferometry. Holzforschung 59:300–306. https://doi.org/10.1515/HF.2005.050
Müller U, Ringhofer A, Brandner R, Schickhofer G (2015) Homogeneous shear stress field of wood in an Arcan shear test configuration measured by means of electronic speckle pattern interferometry: description of the test setup. Wood Sci Technol 49:1123–1136. https://doi.org/10.1007/s00226-015-0755-3
Neuhaus FH (1981) Elastizitätszahlen von Fichtenholz in Abhängigkeit von der Holzfeuchtigkeit (Elasticity constants of spruce wood in relation to the wood moisture content). Dissertation, Ruhr-Universität Bochum (in German)
Niemz P, Caduff D (2008) Untersuchungen zur Bestimmung der Poissonschen Konstanten an Fichtenholz (Investigations to determine the Poisson’s ratio of spruce wood). Holz Roh Werkst 66:1–4. https://doi.org/10.1007/s00107-007-0188-2 (in German)
Niemz P, Sonderegger W (2017) Holzphysik: Physik des Holzes und der Holzwerkstoffe (Wood physics: physics of wood and wood-based materials). Carl Hanser Verlag GmbH Co KG, Munich (in German)
Pan B, Wang B (2016) Digital image correlation with enhanced accuracy and efficiency: a comparison of two subpixel registration algorithms. Exp Mech 56:1395–1409. https://doi.org/10.1007/s11340-016-0180-z
Pan B, Qian K, Xie H, Asundi A (2009) Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Meas Sci Technol 20:062001. https://doi.org/10.1088/0957-0233/20/6/062001
Perkins RW (1967) Concerning the mechanics of wood deformation. For Prod J 17:55–67
Qing H, Mishnaevsky L (2010) 3D multiscale micromechanical model of wood: from annual rings to microfibrils. Int J Solids Struct 47:1253–1267. https://doi.org/10.1016/j.ijsolstr.2010.01.014
Rastogi PK, Huntley JM, Jones JDC et al (2001) Digital speckle pattern interferometry and related techniques. Wiley, Chichester
Samarasinghe S, Kulasiri D (2004) Stress intensity factor of wood from crack-tip displacement fields obtained from digital image processing. Silva Fenn 38:267–278. https://doi.org/10.14214/sf.415
Toussaint E, Fournely E, Moutou Pitti R, Grédiac M (2016) Studying the mechanical behavior of notched wood beams using full-field measurements. Eng Struct 113:277–286. https://doi.org/10.1016/j.engstruct.2016.01.052
Valla A, Konnerth J, Keunecke D et al (2011) Comparison of two optical methods for contactless, full field and highly sensitive in-plane deformation measurements using the example of plywood. Wood Sci Technol 45:755–765. https://doi.org/10.1007/s00226-010-0394-7
Vial G (2004) Tech spotlight—video extensometers. In: Adv. Mater. Process. https://www.asminternational.org/documents/10192/1908540/amp16204p033.pdf/612298f5-c258-4490-ab3e-3ebc3f6e4daf. Accessed 5 July 2017
Voigt W (1882) Allgemeine Formeln für die Bestimmung der Elastizitätskonstanten von Kristallen durch Beobachtung der Biegung und Drillung von Prismen (General formulas to determine the elastic constants of crystals by observing the bending and twisting of prisms). Ann Phys 252:273–321 (in German)
Voigt W (1887) Theoretische Studien über die Elastizitätsverhältnisse der Kristalle (Theoretical studies on the elasticity of crystals). Königliche Gesellschaft der Wissenschaften zu Göttingen (in German)
Voigt W (1966) Lehrbuch der Kristallphysik (Textbook of crystal physics). Vieweg + Teubner Verlag, Wiesbaden (in German)
Vorobyev A, Arnould O, Laux D et al (2016) Characterisation of cubic oak specimens from the Vasa ship and recent wood by means of quasi-static loading and resonance ultrasound spectroscopy (RUS). Holzforschung 70:457–465. https://doi.org/10.1515/hf-2015-0073
Wolverton M, Bhattacharyya A, Kannarpady GK (2009) Efficient, flexible, noncontact deformation measurements using video multi-extensometry. Exp Tech 33:24–33. https://doi.org/10.1111/j.1747-1567.2008.00370.x
Wommelsdorff O (1966) Dehnungs-und Querdehnungszahlen von Hölzern (Elongation and transverse strain constants of wood). Dissertation, Leibniz Universität Hannover (in German)
Xavier J, Avril S, Pierron F, Morais J (2007) Novel experimental approach for longitudinal-radial stiffness characterisation of clear wood by a single test. Holzforschung 61:573–581. https://doi.org/10.1515/HF.2007.083
Xavier J, Belini U, Pierron F et al (2013) Characterisation of the bending stiffness components of MDF panels from full-field slope measurements. Wood Sci Technol 47:423–441. https://doi.org/10.1007/s00226-012-0507-6
Zink AG, Davidson RW, Hanna RB (1995) Strain-measurement in wood using a digital image correlation technique. Wood Fiber Sci 27:346–359
Zwick/Roell (2001) Betriebsanleitung für Material-Prüfmaschine Z100/SW5A (Operating manual of the universal testing machine Z100/SW5A). Tech Dokumentation.v17 (in German)
Zwick/Roell (2017a) Laser-Extensometer: laserXtens (Zwick/Roell). http://www.zwickusa.com/en/products/extensometers/non-contact-extensometers/laserxtensr.html. Accessed 30 Aug 2017
Zwick/Roell (2017b) Video-extensometer: videoXtens (Zwick/Roell). http://www.zwickusa.com/en/products/extensometers/non-contact-extensometers/videoxtensr.html. Accessed 30 Aug 2017
Zwick/Roell (2017c) Mechanical-extensometer: makroXtens (Zwick/Roell). https://www.zwick.com/extensometers/makroxtens. Accessed 3 Oct 2017
Acknowledgements
Open access funding provided by University of Natural Resources and Life Sciences Vienna, Austria (BOKU). The results presented in this study are part of the research project “WoodC.A.R.” (Project No.: 861.421). Financial support by the Austrian Research Promotion Agency (FFG), Styrian Business Promotion Agency (SFG), Standortagentur Tirol and the companies DOKA GmbH, DYNAmore GmbH, EJOT Austria GmbH, Forst-Holz-Papier, Holzcluster Steiermark GmbH, IB STEINER, Lean Management Consulting GmbH, Magna Steyr Engineering GmbH & Co KG, MAN Truck & Bus AG, Mattro Mobility Revolutions GmbH and Weitzer Parkett GmbH & CO KG is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kumpenza, C., Matz, P., Halbauer, P. et al. Measuring Poisson’s ratio: mechanical characterization of spruce wood by means of non-contact optical gauging techniques. Wood Sci Technol 52, 1451–1471 (2018). https://doi.org/10.1007/s00226-018-1045-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00226-018-1045-7