Introduction

Increasing the use of wood in construction, as a renewable and low-embodied energy alternative to reinforced concrete and steel, will play an important role in reducing emissions and solid waste derived from the global construction industry (Joseph and Tretsiakova-McNally 2010; Ramage et al. 2017). Wood in its natural form is a widely used construction material, but in certain environments and applications, issues related to durability, fire resistance, and dimensional stability need to be addressed (Rowell 2007; Ramage et al. 2017). In general, the treatment of wood through (1) chemical or thermal modifications, (2) coatings, or (3) impregnation offers effective routes to address some of these issues (Hill 2006). In particular, ‘controlled’ impregnation of specific monomers into the cell cavity (lumen), but also possibly into the cell wall (Militz 1993; Schneider 1995; Cabane et al. 2014; Keplinger et al. 2015), followed by polymerisation, may enhance the performance of wood in construction by improving its mechanical properties (Rowell and Konkol 1987), particularly perpendicular to the grain on account of a more solid material, i.e. filling of the wood (Akitsu et al. 2007; Xie et al. 2013), better durability on account of blocking of pores or improved decay resistance (Militz 1993; Ibach and Rowell 2000; Lande et al. 2004), and fire retardance (Marney and Russell 2008).

For controlled impregnation and for process evaluation, we need to be able to assess the ‘achieved’ extent of impregnation, relative to the ‘maximum potential’. For wood treatments that act on the solid mass of wood (i.e. on cell walls), such as chemical modification or cell wall impregnation, the ‘achieved’ extent of impregnation can be directly evaluated by weight percentage gain (WPG). However, when impregnation only occurs in the luminal cavity of the cell and the cell wall is left nominally unaltered, the ‘maximum potential’ of impregnation is better quantified relative to the total void fraction (porosity), and the ‘achieved’ extent of impregnation is directly related to the pore-filling ratio (PFR), i.e. the ratio of luminal cavity filled to the total cavity volume. In such cases, WPG is not an appropriate indicator for the extent of lumen impregnation, since it depends not only on pore space filled but also on the density of the wood and the density of the filling. For example, even if the same proportion of pore space has been filled, a denser wood will show lower WPG. The porosity and the PFR of wood specimens, however, are not as easily measured during processing as the WPG. Therefore, being able to relate the porosity and PFR of a specimen to easily measurable parameters like the WPG and the bulk density is of practical use in assessing the success of any impregnation process.

Herein, a simple yet powerful relationship between the WPG and bulk density is established, and the model is experimentally validated using Sitka spruce as an example. From this model, it is possible to determine the PFR of an impregnated specimen. Thereafter, the effect of process-related parameters (i.e. specimen length and hydraulic pressure) on the extent of impregnation is analysed. Through this study, the proportion of accessible (open) and inaccessible (closed) pores in wood is determined, and it is examined how they relate to the extent of impregnation achieved.

Model description

Definitions of open and closed pores as well as several densities in this work are essential to understanding and describing the present model:

  • Open pores and closed pores: whether a pore is open or closed is determined by whether the pore is accessible or inaccessible to infiltrates (e.g. helium in pycnometry, mercury in mercury intrusion porosimetry, and monomers in this work on wood impregnation). It is noteworthy that measurement of the proportion of open and closed pores may be limited by the measurement procedure and conditions. For example, with the increase in pressure in a pycnometer, helium may access pores which were previously inaccessible (closed) under lower pressure.

  • Bulk density (ρ B): the ratio of the mass of a wood specimen, M o, to the external (bulk) volume, V B (i.e. the sum of the volume of the solid matter, and both the open and closed pores).

  • Skeletal density (ρ S): the ratio of the mass of a wood specimen, M o, to the sum of volume of the solid matter and closed pores, V S. The closed pores in wood specimen can be pores inside the cell wall or lumens of the inaccessible cells.

  • Material density (ρ M): the ratio of the mass of a wood specimen, M M, to the volume of the solid matter only, V M (i.e. excluding the volume of both open and closed pores).

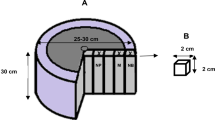
As a starting point, consider that dried wood in the absence of moisture comprises two phases: solid material (ligno-cellulosic components and extractives) and voids (Fig. 1). Initially, the voids are either evacuated under vacuum or may contain air at atmospheric pressure. Since the density of air is lower than the solid matter in wood by a factor of order 1000, in either case the mass of the voids is negligible and

$$M_{\text{M}} = \, M_{\text{o}}$$
(1)
Fig. 1
figure 1

A simplified model for dried wood with lumen impregnation. V, ρ denote, respectively, the volume and density of void phase (V), solid phase (S), and filling (F). The void phase relates to the summation of all open pores accessible to impregnants. The solid phase relates to the summation of skeleton of cell wall including closed pores inaccessible to impregnants

Full size image

In this simplified model, the void phase relates to the summation of all open pores, such as the lumen of tracheid cells, which are accessible to impregnants. The density of the void phase is insignificant. Ideally, the solid phase relates to the summation of the skeleton of all the cell walls. However, the presence of inaccessible closed pores such as lumens sealed by aspiration of bordered pits (Petty 1972) or extractives reduces the density of the skeletal structure (consequently the skeletal density is less than the material density, i.e. ρ S < ρ M).

During lumen impregnation, the bulk flow of monomer mixture, intended to fill the voids, is transported through a network of interconnected voids and is typically driven by imposed pressure gradients (Siau 1984). Herein, the pore-filling ratio, PFR, is defined as the volume fraction of voids filled by the monomer mixture:

$${\text{PFR }} = V_{\text{F}} /V_{\text{V}} \times 100$$
(2)

where V F denotes the volume of the monomer mixture contained within the voids and V V denotes the total volume of the voids.

Both V F and V V cannot be directly quantified by measurements of the bulk sample. However, they can be expressed in terms of their mass and density:

$$V_{\text{F}} = \, M_{\text{F}} /\rho_{\text{F}}$$
(3)

where M F denotes the mass of filling (or weight gain) and ρ F denotes the density of filling. Now

$$V_{\text{V}} = \, V_{\text{B}} {-} \, V_{\text{S}}$$
(4)

Hence

$$V_{\text{V}} = \, V_{\text{B}} {-} \, V_{\text{S}} = \, M_{\text{o}} \times (1/\rho_{\text{B}} {-} \, 1/\rho_{\text{S}} )$$
(5)

Substituting Eqs. (3) and (5) into Eq. (2) gives:

$${\text{PFR}} = \left( {M_{\text{F}} /M_{\text{o}} } \right) \times \left( {1/\rho_{\text{F}} } \right)/\left( {1/\rho_{\text{B}} {-} \, 1/\rho_{\text{S}} } \right) \times 100$$
(6)

The weight percentage gain is defined as:

$${\text{WPG}} = M_{\text{F}} /M_{\text{o}} \times 100$$
(7)

Therefore, the derived relationship between the WPG and the bulk density ρ B is:

$${\text{WPG}} = {\text{PFR}} \times \rho_{\text{F}} \times \left( {1/\rho_{\text{B}} {-}1/\rho_{\text{S}} } \right)$$
(8)

The WPG can be calculated by measuring the mass of the specimen before and after treatment. The bulk density, ρ B, can be obtained by recording the mass and bulk volume of the specimen prior to impregnation. The density ρ F of the filling monomer mixture employed is either available in standard chemical tables or can be calculated by measuring the mass per unit volume of the liquid filling mixture.

If specimens of different bulk densities are treated under the same conditions, by plotting their WPG against the reciprocal of bulk density (1/ρ B) and fitting the curve according to a linear model, PFR can be obtained from the slope of the curve. The skeletal density (ρ S) can also be found from the intercept.

The assumptions used in this model include:

  1. 1.

    The filling liquid is incompressible (i.e. ρ F = constant);

  2. 2.

    The filling only flows into the lumen, and no swelling of the cell wall occurs;

  3. 3.

    The impregnation occurs over a sufficient period of time and pressures that the system reaches a steady state in which all the accessible voids are filled and no further transport processes can occur;

  4. 4.

    PFR and ρ S are independent of ρ B, which means that different wood specimens under the same impregnation conditions are assumed to have the same pore-filling ratio.

In selecting the monomer mixture for impregnation, one has the freedom to select the chemistry such that the ultimate goals of the impregnation process are achieved while ensuring that assumptions (1) and (2) hold true, at least within the bounds of experimental uncertainties. Assumptions (3) and (4) aim to pack all influence from permeability into one parameter, the skeletal density ρ S. Under these assumptions, if ρ S can be detected and remains constant for most specimens, the PFR of impregnation is able to be monitored through Eq. (8) with other accessible parameters. The skeletal density in this model should not be simply equivalent to ‘cell wall density’, but will be affected by the closed volume caused by pit aspiration or extractives as blockage.

Therefore in this model, the mass and volume contributed from a minor amount of extractives, ca. 1 wt% in the heartwood and sapwood of Sitka spruce (Caron et al. 2013), are not taken into account separately, but are regarded as a part of solid materials along with ligno-cellulosic components. The effect of extractives on blocking pores and isolating cell lumens will be fairly reflected in the skeletal density on account of increasing closed volume. However, this simplification may be inappropriate in the presence of a large amount of extractives, as the interaction between extractives and impregnants will significantly affect the permeability of specimens. The effect of extractives on permeability will be discussed later.

Experimental

Materials and equipment

Specimens of Sitka spruce (Picea sitchensis) were cut from flat-sawn, kiln-dried timber supplied by BSW Timber Ltd (UK). The moisture content of un-dried specimens, determined by the oven drying method, was ca. 12%. The cross section perpendicular to the grain direction was 10 mm × 10 mm. The length along the grain direction was typically 70 mm; however, this ranged from 40 to 115 mm when investigating the effect of length. The dimensions of each specimen were accurately recorded by callipers (to within 0.01 mm) prior to processing.

Methyl methacrylate (MMA, 99%, 0.940 g cm−3), glycidyl methacrylate (GMA, 97%, 1.070 g cm−3), and ethylene glycol dimethacrylate (EDMA, 98%, 1.051 g cm−3) were purchased from Sigma-Aldrich. The ratio of monomers used in this work was MMA/GMA/EDMA (45:45:10 wt%).

Gas pycnometry was carried out on an AccuPyc 1330 helium pycnometer (Micromeritics). Stainless steel balls (diameter 3.0 mm; type AISI440-C; Manu Part No B1001A3.0) were purchased from Dejay Distribution Limited (UK) as metal fillers for helium pycnometry. Masses were measured by AL204 analytical balance (Mettler Toledo) with a repeatability of ±0.1 mg. Oven drying was implemented on FD23 drying and heating oven (Binder). The impregnation was realised in laboratory scale using Schlenk line and Schlenk techniques. Pressure gauge (WIKA) was used to monitor and control hydraulic pressure. The pressures presented in this paper are all absolute values.

Impregnation procedures

A pressure process similar to the full-cell (Bethell) process was used for impregnation. Sitka spruce wood specimens were oven-dried at 103.0 ± 0.3 °C for 12 h. After oven drying, specimens were cooled down to room temperature in a Schlenk tube under atmospheric pressure. Specimens were then vacuum-dried in the Schlenk tube to constant mass at room temperature for 48 h before impregnation. After recording their untreated mass (M o) and external dimensions (V B), specimens were placed in a cylindrical Schlenk tube. A vacuum of less than 1 mbar was applied and allowed to stabilise over 1 h. The monomer mixture was then introduced into the tube while maintaining vacuum. The vacuum was stopped once the tube was filled with the monomer mixture, and then a hydraulic pressure of 1250 mbar was applied for 2 h. After impregnation, the monomer mixture was drained out to a recycling cylinder for reuse. The mass (M I) and dimensions (V I) of impregnated specimens were measured again after quickly wiping residual liquid from the sample surface. All experiments were conducted at room temperature. No extraction was carried out for any of the specimens before impregnation.

Density determination

To determine the density ρF of the monomer mixture, the mass of 10 ml of liquid monomer mixture was obtained by the differential mass before and after being filled in a 10-ml volumetric flask. An average density was calculated from several measurements to be 1.0054 ± 0.0003 g cm−3 (298 K).

The bulk density (ρ B) of the untreated wood specimens was determined from measurements of the volume V B and the mass M 0 of the specimen.

To determine the skeletal density (ρ S) of the untreated wood specimens, the volume of the solid phase inclusive of closed pores (V S) was determined using a helium pycnometer.

The skeletal volumes of wood specimens measured in this work ranged from 0.25 to 0.40 cm3, occupying around 10% of the chamber volume (3.5 cm3). Since the result from AccuPyc 1330 will be inaccurate when the detected volume is less than 10% of chamber volume, all the specimens were measured along with metal fillers in order to occupy more than 50% of chamber volume during the measurement. Volume of metal fillers was measured separately without wood specimens. The final skeletal volume of a specimen was obtained by subtracting the volume of metal fillers from the detected combined volume of specimen and metal fillers.

All the specimens were oven-dried at 103.0 ± 0.3 °C for 12 h. Before being removed from oven, each specimen was sealed in an individual dried vial and cooled down to room temperature before loading into the helium pycnometer. Intact cubic specimens (10 mm × 10 mm × 10 mm) along with metal fillers were placed within the sample chamber of the pycnometer, and air was then evacuated. Then, pressurised helium gas was intruded into all accessible pores of the wood specimen. The pressures observed upon filling the specimen chamber and then evacuating it into a second empty expansion chamber allow the computation of the sample solid-phase volume using Boyle’s law. A purge fill pressure of 19.500 psig (pounds per square inch gage, pressure relative to atmospheric pressure) and equilibrium rate of 0.0095 psig/min were used. The final volume reading for a specimen was an average of ten systematic readings from ten purges and runs (found to be accurate to within 0.1%). All the pycnometry measurements were taken at a temperature of 26.1 °C.

To determine the material density (ρ M) of the solid matter within a specimen, sawdust from the specimen was prepared by ball milling. The sawdust was sufficiently fine as to ensure that all closed pores were exposed. The volume of sawdust was then measured by helium pycnometry.

Results and discussion

Relationship between WPG, bulk density and PFR

Sitka spruce (Picea sitchensis) was chosen as the test species in this work because it is an abundant fast-growing softwood in the UK, and with advancements in specific properties, it has the potential to be used in a broad range of construction applications (Ridley-Ellis et al. 2008; Moore 2011). To validate the model, fifty Sitka spruce specimens of the same bulk dimensions but different bulk densities were selected for lumen impregnation. No extraction was carried out for any of the specimens before impregnation. A typical extractives content in a clear specimen (knot-free wood) of Sitka spruce is ca. 1 wt% (Caron et al. 2013), which in the present model will be considered along with ligno-cellulosic components with a contribution to the bulk density. The presence of extractives, as an additional benefit, may suppress the swelling of cell wall (Mantanis et al. 1994a), which will make the non-swelling assumption more plausible. Being cut from a knot-free region of the wood and examined by helium pycnometry, these specimens were found to have a similar skeletal density, ρS, corresponding to assumption (4) (see "Model description" section). Specimens cut from a near-knot region of the wood board will be discussed in the final subsection.

As a full-cell process was employed with a considerably long impregnation time under pressure, the amount of infiltrating monomers for a typical specimen mainly relied on the porosity and was barely affected by the permeability of the specimens. In order to meet the non-swelling assumption, methacrylate monomers were chosen as impregnants, since these monomers have been reported to be almost completely located in the lumen rather than in the cell wall during the impregnation (Rowell R and Konkol 1987; Zhang et al. 2005). A formula of MMA/GMA/EDMA (45:45:10 wt%) was employed owing to the optimisation from a previous work (Farina et al. 2014). The monomer mixture was regarded as an incompressible liquid, with density ρ F = 1.005 g cm−3. Since the monomer mixture may evaporate during polymerisation, when calculating the WPG, only the mass obtained after impregnation but before polymerisation (or curing) was used. Therefore, the WPG is practically obtained by:

$${\text{WPG}} = \left( {M_{\text{I}} - M_{\text{o}} } \right)/M_{\text{o}} \times 100$$
(9)

where M o denotes the mass after drying but before impregnation and M I denotes the mass after impregnation but before polymerisation.

As shown in Fig. 2, WPG exhibits a linear relationship with the reciprocal of bulk density, with a coefficient of determination of r 2 = 0.986, suggesting that this model works well for the lumen impregnation of Sitka spruce.

Fig. 2
figure 2

Relationship between WPG and reciprocal of bulk density. The density of methacrylate monomer mixture (ρ F) was measured as 1.005 g cm−3. Through linear fitting according to Eq. (8) (r 2 = 0.986), PFR of 101% and the density of solid part of the wood (ρ S) of 1.374 g cm−3 were obtained from the slope and intercept, respectively. Processing condition: Sitka spruce, 10 mm × 10 mm × 70 mm (grain direction), oven-dried, vacuum (~1 mbar) for 1 h, soaked for 2 h under 1250 mbar, filling: MMA/GMA/EDMA (45:45:10 wt%). Note: The arrowed point in the figure is not used for fitting, as explained in the text

Full size image

The PFR can be deduced from the slope of the linear fit (as ρ F, the density of filling is known). The PFR percentage was found to be 101 ± 3%, suggesting complete impregnation with all accessible void being filled by the monomer mixture. The PFR value slightly over 100 may be caused by an inevitable infiltration of cell wall with minor amount of monomer liquid. An ideal liquid that only resides in lumen is unfeasible. Most organic solvents can more-or-less infiltrate the cell wall and cause wood swelling mainly determined by their basicity, molar volume, and hydrogen bonding capability (Mantanis et al. 1994b). Fortunately, by using methacrylate monomers as impregnants here, the swelling-caused model deviation can be minimised within the experimental uncertainty.

Although the slope or PFR percentage indicates that most of the specimens have a similar extent of lumen impregnation, their WPG% actually varies from 100 to 230% due to different bulk densities. The average bulk density of Sitka spruce is around 0.35 g cm−3 (1/ρ B = 2.86 cm3 g−1), but with considerable variation, which can range from 0.20 to 0.75 g cm−3 (Moore 2011). This highlights that WPG is not a suitable measure to describe the extent of lumen impregnation since a larger WPG does not necessarily mean a larger pore-filling ratio nor better impregnation.

However, the advantage of using WPG is that the determination of weight is easy and practical. Using the model proposed here, PFR can be assessed by measuring the bulk density of untreated wood and WPG upon impregnation. Timbers used in industry usually have a regular shape so that the external volume and the bulk density can be readily measured.

Effect of hydraulic pressure and specimen length on lumen impregnation

Based on this evaluation method, the effect of different process-related parameters on lumen impregnation can be studied. WPG in Fig. 3a was measured from specimens treated for the same impregnation period (2 h) but under different hydraulic pressures. PFR % could be obtained from linear fitting based on Eq. (8) using ρ F of 1.005 g cm−3 and ρ S of 1.374 g cm−3 as known parameters. Specimens treated under a hydraulic pressure higher than 1240 mbar exhibited a PFR of 103, while specimens treated with a hydraulic pressure lower than 1060 mbar (close to atmospheric pressure) exhibited a lower PFR of 95. This suggests that, for a fixed impregnation time, the extent of lumen impregnation increases with hydraulic pressure, up to the point at which all void spaces are impregnated (PFR = 100).

Fig. 3
figure 3

Effect of hydraulic pressure (a) and specimen length (b) on lumen impregnation. All the PFR were obtained using ρ F = 1.005 g cm−3 and ρ S = 1.374 g cm−3 as the fitting parameter for Eq. (8). Specimen length in a was 70 mm. Specimens in b were treated in a single batch under the same impregnation period and the same hydraulic pressure which was larger than 1240 mbar

Full size image

Specimens with different lengths along the grain direction (40, 70, and 115 mm) were treated as a single batch under the same hydraulic pressure and the same impregnation period. As shown in Fig. 3b, all the specimens are consistent with a PFR of 97%, suggesting that the length range studied had little, if any, effect on the extent of impregnation. It is expected that the length of a specimen should affect its permeability, which will further influence the processing time (Bramhall 1971; Siau 1972). However, under the 2-h pressure process used here, the variation of length appears to be insufficient to induce a change in the PFR. Specimens with larger dimensions and shorter processing times will be further investigated taking into account the effect of permeability.

Effect of variations in skeletal density

The intercept of the linear fit in Fig. 2 provides an estimate of the skeletal density of the Sitka spruce specimens selected from knot-free regions of the wood. This estimate is ρ S = 1.374 g cm−3. If the solid matter in the Sitka spruce consists of only cell wall material, then its composition, by weight, would approximately be 40–50% cellulose (1.56 g cm−3), 20–30% hemicellulose (1.46–1.80 g cm−3), and 20–35% lignin (1.33–1.38 g cm−3) (Pereira et al. 2003) providing expected densities in the range 1.47–1.62 g cm−3 (typically reported to be approximately 1.5 g cm−3, Plötze and Niemz 2011). The material density of the solid matter in the Sitka spruce specimens was determined by grinding them into fine sawdust, and measuring the density using helium pycnometer. For the specimens, a value of 1.517 ± 0.002 g cm−3 was obtained—this is in good agreement with the values expected from the cell wall composition (Plötze and Niemz 2011).

The lower skeletal density obtained from the experiments indicates that the portion of a specimen inaccessible to impregnants not only includes the solid matter of the cell wall but also closed pores or even closed lumens, as illustrated in Fig. 1. The skeletal density of the solid phase can be directly determined by helium pycnometry, provided the closed pores are both inaccessible to liquid monomer and helium gas. Although the bulk densities ranged from 0.3 to 0.6 g cm−3, the fifty specimens cut from the knot-free region (closed symbols in Fig. 4) exhibited a similar skeletal density in the range from 1.359 to 1.422 g cm−3. In other words, if a specimen has a skeletal density that is very different from 1.37 g cm−3, it will lie away from the fitting curve plotted in Fig. 2. For instance, the data point marked by arrow in Fig. 2 was not used for the fit, as its skeletal density was found to be 1.315 g cm−3 (the star symbol in Fig. 4).

Fig. 4
figure 4

Effect of ρ S on PFR. The values in the figure are the skeletal density of untreated dried specimens measured by helium pycnometer assisted by metal fillers. The open symbols correspond to the specimens cut from parts near knots. The closed symbols represent specimens cut from knot-free parts. Specimens of the same symbol were cut from the same part of the wood board. The short and long dashed lines are the fitting curve when (ρ S, PFR%) are (1.374 g cm−3, 103%) and (1.310 g cm−3, 89%), respectively

Full size image

Although the bulk density may be different, the skeletal density of Sitka spruce cut from knot-free part of the wood board is generally the same (ca. 1.37 g cm−3). Wood grown in different geographical regions, however, may have different ρS values. Therefore, the ρS of representative specimens should be determined before using this model to evaluate the PFR.

It was found that ρS was sensitive to the presence of a large amount of extractives, for instance, in the specimens near the knots (knotwoods). Fifteen specimens (marked by open symbols in Fig. 4) that were cut from parts near knots exhibited lower skeletal density. Furthermore, the specimens located just beside knots showed an extremely low skeletal density of 1.126 g cm−3 (open pentagon symbols in Fig. 4), and resulted in values of almost half of the WPG compared with normal specimens with the same bulk density. The smaller skeletal density observed for knotwoods is probably the result of the large extractives content around knots. It has been reported that knotwood contains exceptionally larger amounts of extractives than sapwood and heartwood (Willför et al. 2004; Pietarinen et al. 2006). For instance, knotwood from Sitka spruce had nearly ten times the total extractives content of sapwood and heartwood from the same tree (Caron et al. 2013). Since more cell lumens will be blocked in the presence of a considerable amount of extractives, knotwoods will contain more closed lumens and exhibit lower skeletal density than observed for knot-free specimens.

As mentioned before, open pores and closed pores are determined by the type of infiltrates used to fill the space. For the fifty knot-free specimens in Fig. 4, the skeletal density (i.e. similar portion of closed pores) directly measured from helium pycnometry is identical to the value fitted by the present model from monomer impregnation. This suggests that the permeability variance caused by different infiltrates is diminished for these knot-free specimens through long-period pressured impregnation.

In other words, the permeability can be qualitatively evaluated by fitting PFR from this validated model using the skeletal density obtained from gas pycnometry. For instance, a PFR percentage of 89% was obtained for the knotwoods in Fig. 4 with a skeletal density measured from helium pycnometry of about 1.310 g cm−3. The presence of a large amount of extractives around knotwoods amplified the permeability difference between monomers and helium. A pore channel coated by considerable extractives is more permeable to helium (only weak dispersion force) than to methacrylate monomers (polarisation force between methacrylate and extractives). This explains why infiltration capacity or permeability of methacrylate monomers is only 89% of helium gas in this case.

Conclusion

Weight percentage gain (WPG), an easy-to-measure control parameter, is popularly used by the wood modification community to evaluate the extent of treatment. However, it has been misused in impregnation strategies, especially for lumen impregnation (MMA, furfuralation, etc.). In order to evaluate the extent of lumen impregnation in an appropriate, representative way, a simple yet effective, experimentally validated model was developed to describe the relationship between the WPG and the sample bulk density. The relationship enables the determination of the pore-filling ratio (PFR) and the skeletal density from a linear fit. The PFR is a better indicator of the extent of lumen impregnation than the WPG, and through this model the PFR can be readily determined if the bulk density is known. Furthermore, along with the skeletal density obtained from helium pycnometry, it was shown that the PFR is able to qualitatively evaluate the permeability variance caused by different parameters such as type of infiltrates, applied impregnation pressure, length of specimens, or amount of extractives.

In this work, the proposed model was examined and validated on a laboratory scale by full penetration (i.e. PFR known as 100) of small knot-free specimens. When applying it to industrial scale, this model can be used, in a reverse way, to infer the unknown PFR from obtained WPG, bulk density, and skeletal density. The WPG and bulk density can be easily measured in any scale. Quantifying the skeletal density remains challenging since it is affected by the sample permeability and therefore may vary in time as environmental conditions change. However, a crude simple method would be to infer skeletal densities from representative specimens, thereby enabling an estimate of the PFR to be calculated at an industrial scale.