Abstract
In the NP-hard Colored (s,t)-Cut problem, the input is a graph G = (V,E) together with an edge-coloring ℓ : E → C, two vertices s and t, and a number k. The question is whether there is a set \(S\subseteq C\) of at most k colors such that deleting every edge with a color from S destroys all paths between s and t in G. We continue the study of the parameterized complexity of Colored (s,t)-Cut. First, we consider parameters related to the structure of G. For example, we study parameterization by the number ξi of edge deletions that are needed to transform G into a graph with maximum degree i. We show that Colored (s,t)-Cut is W[2]-hard when parameterized by ξ3, but fixed-parameter tractable when parameterized by ξ2. Second, we consider parameters related to the coloring ℓ. We show fixed-parameter tractability for three parameters that are potentially smaller than the total number of colors |C| and provide a linear-size problem kernel for a parameter related to the number of edges with rare edge colors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The design of networks that are robust against accidental or intentional failure of network components is an important step in the quest for secure communication systems [20]. Since current communication networks are in fact multilayer networks, it is important to consider multiple failure scenarios where a failure of or a successful attack on a single layer may affect direct connections between many different nodes at once—even if these nodes are spread widely throughout the network [3, 9]. Thus, instead of modeling the network as a simple undirected or directed graph, it has been proposed to use edge-colored graphs consisting of a graph G = (V,E), a color set C, and an edge-coloring ℓ : E → C to model the layers. That is, each edge has a color corresponding to the layer of the edge. If an attacker performs a successful attack on some network layer, then all edges with the corresponding color become unavailable for communication. In other words, we may think of these edges as being removed from the graph. One measure for the vulnerability of a network in this model is the number of layers that have to fail in order to disconnect two given important nodes s and t. To compute this vulnerability measure, one needs to solve the following computational problem [3, 9].
Colored (s,t)-Cut Input: An edge-colored graph (G = (V,E),C,ℓ), two vertices s and t, and a positive integer k. Question: Is there a set of colors \(S \subseteq C\) with |S|≤ k such that s and t are not in the same connected component in \(G^{\prime }:=(V, E\setminus E_{S})\), where ES := {e ∈ E∣ℓ(e) ∈ S}?
In contrast to the uncolored problem version, the well-known Min Cut problem, Colored (s,t)-Cut is NP-hard [3, 9]. Motivated by this hardness, we study the parameterized complexity of the problem.
Known Results and Related Work
Colored (s,t)-Cut has been studied extensively over the last years [3, 4, 10, 14, 16, 22,23,24,25, 27]. To our knowledge, Colored (s,t)-Cut was first introduced in a directed version in the context of the analysis of attack graphs [14, 22]. An attack graph is a directed graph G whose vertices correspond to states of a system that is under attack. The current state of the system corresponds to a distinguished vertex s and the attacker wants to reach a distinguished state t which corresponds to a successful attack. An edge from a vertex u to a vertex v with color α represents that by successfully attacking the part α of the system, the attacker may go from state u to state v. Thus, a colored (s,t)-cut corresponds to a set of attacks such that preventing these attacks also prevents the attacker from reaching his goal t. It was shown, by a reduction from Hitting Set (which we call the standard reduction in this article), that in this setting computing (s,t)-cuts with few colors is NP-hard [14, 22]. While the graph is directed in this case, the reduction can be easily adapted to show NP-hardness of the undirected case by discarding all edge directions in the constructed graph G.
In later work, this reduction from Hitting Set and the above-mentioned hardness results were also discovered directly for Colored (s,t)-Cut [10, 16, 23, 24]. One may use the standard reduction also to reduce from Vertex Cover since it is the special case of Hitting Set where every hyperedge has size 2. Then, the resulting instances of Colored (s,t)-Cut have a vertex cover of size 2 [24], making the problem NP-hard even in this very restricted case. Moreover, Colored (s,t)-Cut is NP-hard even if G is a complete graph [23].
On the positive side, by considering all possibilities for choosing the k colors that shall be removed, Colored (s,t)-Cut can be solved in \(n^{{\mathcal {O}}(k)}\) time. This brute-force algorithm can most likely not be improved to an FPT-algorithm, that is, to an algorithm with running time \(f(k)\cdot n^{{\mathcal {O}}(1)}\) since the above-mentioned reduction from Hitting Set also implies that Colored (s,t)-Cut is W[2]-hard when parameterized by k [10]. The brute-force algorithm also implies further running time bounds for Colored (s,t)-Cut: First, the problem has an \(n^{{\mathcal {O}}({\Delta })}\)-time algorithm, where Δ is the maximum degree of G, since instances with Δ ≤ k are trivial yes-instances. Second, the running time can also be bounded by \({\mathcal {O}}(\binom {c}{k} \cdot (n+m))={\mathcal {O}}(2^{c}\cdot (n+m))\) where \(c{}:={}|C|\) is the number of colors. Thus, Colored (s,t)-Cut has an FPT-algorithm for the parameter c.
Colored (s,t)-Cut can be solved in polynomial time when each edge color appears in at most two (s,t)-paths [16, 23] and if every edge color has span one [3]. Herein, the span of a color is the number of connected components in the subgraph of G that contains only the edges of this color and their endpoints. The latter result was later extended to an FPT-algorithm with running time \(2^{{c_{\text {span}}}}\cdot n^{{\mathcal {O}}(1)}\) where cspan is the number of edge colors that have span at least 2 [4, 16, 23]. Colored (s,t)-Cut also has an FPT-algorithm for the combination of \(p_{\max \limits }\) and k where \(p_{\max \limits }\) is the number of edges of a longest simple path between s and t [27]. More precisely, Colored (s,t)-Cut can be solved in \(x^{k}\cdot n^{{\mathcal {O}}(1)}\) time, where \(p_{\max \limits }-1<x<p_{\max \limits }\) [27]. Finally, Colored (s,t)-Cut has an FPT-algorithm for the number of (s,t)-paths in G [16]. For all known nontrivial parameters that lead to FPT-algorithms, that is, for c, \(p_{\max \limits }+k\), cspan, and for the number of (s,t)-paths, Colored (s,t)-Cut does presumably not admit a polynomial problem kernel [16, 23].
Other approaches for NP-hard problems have also been applied to Colored (s,t)-Cut. For example, it was shown that Colored (s,t)-Cut can be approximated by a factor of \({\mathcal {O}}(n^{2/3})\) [21]. Later, Zhang et al. [26] studied a generalization of Colored (s,t)-Cut where each color has a weight and the aim is to delete a color set of weight at most ω. Observe that Colored (s,t)-Cut is the special case of this problem with unit-weights. Zhang et al. [26] presented an approximation algorithm for this with ratio \({\mathcal {O}}(\sqrt {m})\) and showed that Colored (s,t)-Cut cannot be approximated within a factor of \(2^{\log (n)^{1/\log \log (n)^{c}}}\) for any constant c < 1/2 unless P = NP. Recently, Zhang [25] also presented a \({\mathcal {O}}(n^{2/3})\)-factor approximation algorithm for this problem. Finally, Bordini et al. [2] present heuristic algorithms for Colored (s,t)-Cut and evaluate them on synthetic data.
Our Results
We study new parameterizations for Colored (s,t)-Cut. Recall that Colored (s,t)-Cut is NP-hard even when G has a vertex cover of size 2 [24]. The latter result excludes tractability for most standard parameterizations that are related to the structure of G, for example for the treewidth of G, the vertex deletion distance to forests (known as feedback vertex set number), or the vertex deletion distance to graphs with maximum degree i: the corresponding parameters are never larger than the size of a smallest vertex cover of G. Thus, we first consider parameters that are related to the edge deletion distance to tractable cases of Colored (s,t)-Cut. Our results and their relation to previous results are shown in Fig. 1.
The parameterized complexity of Colored (s,t)-Cut for structural graph parameters as analyzed in Section 3; vc, fes, fvs, and tw denote the vertex cover number, feedback edge set number, feedback vertex set number, and treewidth, respectively. New results are marked by an asterisk (*). An arrow \(a \rightarrow b\) between two parameters a and b symbolizes that a ≥ g(b) for some function g in all graphs. Note that \(\xi _{2} \rightarrow \mathsf {fes}\) holds only for connected graphs; for Colored (s,t)-Cut we assume that G is connected
Since Colored (s,t)-Cut can be solved in polynomial time on graphs with constant maximum degree Δ, we consider parameterization by ξi, the number of edges that need to be deleted in order to transform G into a graph with maximum degree i. We show that for all i ≥ 3, Colored (s,t)-Cut is W[2]-hard for ξi. This also implies W[2]-hardness for the parameter Δ: For a vertex of degree Δ ≥ i, at least ξi incident edges have to be deleted to decrease its degree to i. Hence, Δ ≤ ξi + i. Therefore, the known \(n^{{\mathcal {O}}({\Delta })}\)-time algorithm cannot be improved to an algorithm with running time \(f({\Delta })\cdot n^{{\mathcal {O}}(1)}\). Consequently, our result strengthens the known W[2]-hardness for the parameter k, as k ≤Δ in all non-trivial instances. We then show an FPT algorithm for parameterization by ξ2. This algorithm is obtained via the FPT-algorithm for the parameter “number p of simple (s,t)-paths in G”. The latter algorithm also gives an FPT-algorithm for parameterization by the feedback edge set number of G, the number of edges that need to be removed to transform G into a forest. We also observe that Colored (s,t)-Cut does not admit a polynomial kernel for ξ2 and for the feedback edge set number of G.
We then study parameterizations that are related to the edge-coloring ℓ of G; our results are shown in Fig. 2. Assume that the colors in C are sorted non-decreasingly by their frequency. That is, C = {α1,…,αc} and there are at least as many edges with color αi as with color αi+ 1 for all i < c. For any number q, we let the parameter m>q := |{e ∈ E∣ℓ(e) = αj for j > q}| denote the number of edges with a color that is not among the q most frequent colors. Observe that m0 = m and that mc = 0. Furthermore, note that c ≤ m>q + q and m>q ≤ m. Hence, for constant q, the parameter m>q is an intermediate parameter between c and m. We show that for all constant q, Colored (s,t)-Cut admits a problem kernel of size \({\mathcal {O}}(m_{>q})\). To obtain the kernel, we define an operation on Colored (s,t)-Cut instances that gives equivalent instances of Colored (s,t)-Cut under the assumption that the intersection of the sought colored (s,t)-cut with a given set of color is fixed.
We then provide a general framework to obtain FPT-algorithms for parameters that are potentially smaller than c, the number of colors. To formulate the framework, we identify certain properties of color sets in the input instances that directly give an FPT-algorithm for the parameterization by the size of this color set. We then provide four applications of this framework. The first application is for cspan, the number of colors with span at least two. For this parameterization, an FPT-algorithm is already known [4, 16, 23], and an algorithm with the same running time can be obtained by applying our framework. The second application is for parameterization by the number cpath of colors that appear in at least three (s,t)-paths. Using our framework, we extend the known polynomial-time algorithm for the case that all edge colors appear in at most two (s,t)-paths (that is, for cpath = 0) to an FPT-algorithm with running time \(2^{{c_{\text {path}}}}\cdot n^{{\mathcal {O}}(1)}\). The third application is for the parameterization by cconf which we define as follows. Two colors i and j are in conflict if G contains some (s,t)-path containing i and j. Then, cconf is the number of colors that are in conflict with at least three other colors. We show, by applying our framework, that Colored (s,t)-Cut can be solved in \(2^{{c_{\text {conf}}}}\cdot n^{{\mathcal {O}}(1)}\) time. Finally, we strengthen the fixed-parameter tractability of cpath and cconf by showing an FPT-algorithm for the parameter cpc counting the number of colors which are in at least three paths and in at least three conflicts. The parameter cpc can be seen as an “intersection” of cpath and cconf since each color counted in cpc is also counted in cpath and cconf. We also show that Colored (s,t)-Cut is NP-hard even when every color has span one or occurs in at most two paths, and NP-hard even when every color has span one or occurs in at most two conflicts. Thus, an FPT-algorithm is unlikely for the intersection of cspan with cpath or with cconf, denoted by csp and csc, respectively.
2 Preliminaries
Graph Notation
An edge-colored graph or short colored graph is a triple \({\mathscr{H}}:=(G:=(V,E),C,\ell :E\to C)\) where G is an undirected graph, C is a set of colors and \(\ell : E \rightarrow C\) is an edge coloring. We extend the definition of ℓ to edge sets \(E^{\prime } \subseteq E\) by defining \(\ell (E^{\prime }) := \{\ell (e)\mid e \in E^{\prime }\}\). We let n and m denote the number of vertices and edges in G, respectively, and c the size of the color set C. We call |I| := m + n the size of an instance \(I=({\mathscr{H}}, k)\). We assume k < m and that all input graphs are connected, since connected components containing neither s nor t may be removed, and an instance is trivial when s and t are in different connected components.
In a graph G = (V,E), we call a sequence of vertices \(P:=(v_{1}, \dots , v_{x})\in V^{x}, x \geq 1\), a path of length x − 1 if {vi,vi+ 1}∈ E for all 1 ≤ i < x. If vi≠vj for all 1 ≤ i < j ≤ x, then we call P vertex-simple. If not mentioned otherwise, we only consider vertex-simple paths. Furthermore, we say that a path \((v_{1}, \dots , v_{x})\) is a (v1,vx)-path. We denote with V (P) := {vi∣1 ≤ i ≤ x} the vertices of P and with E(P) := {{vi,vi+ 1}∣1 ≤ i < x} the edges of P. Moreover, we let ℓ(P) denote the set of colors of a path P in a colored graph (G = (V,E),C,ℓ). Given two paths \(P_{1}=(v_{1}, \dots , v_{x})\) and \(P_{2}=(w_{1}, \dots , w_{r})\) in G, we define the concatenation as \(P_{1} \cdot P_{2} := (v_{1}, \dots , v_{x}, w_{1}, \dots , w_{r})\). Note that P1 ⋅ P2 is a path if {vx,w1}∈ E. For a graph G = (V,E) and \(E^{\prime }\subseteq E\) by \(G-E^{\prime }:=(V,E\setminus E^{\prime })\) we denote the graph without the edges in \(E^{\prime }\). For two vertices s and t in a graph G = (V,E), we call \(E^{\prime } \subseteq E\) an (s,t)-(edge-)cut in G if s and t are in different connected components in \(G - E^{\prime }\). Let \({\mathscr{H}}=(G,C,\ell )\) be a colored graph and let s,t ∈ V be two vertices in G. We say that \(\tilde {C} \subseteq C\) is a colored (s,t)-Cut in G if for every (s,t)-path P in G, \(\ell (P) \cap \tilde {C} \neq \emptyset \). In other words, \(\ell ^{-1}(\tilde {C})\) is an (s,t)-cut in G. We denote by \({\mathcal {C}}({\mathscr{H}}) := \{\ell (P) \mid P \text { is an } (s,t)\text {-path in }G\}\) the collection of sets of colors of vertex-simple (s,t)-paths in G. Note that \(\tilde {C} \subseteq C\) is a colored (s,t)-cut in G if and only if \(\tilde {C} \cap C^{\prime } \neq \emptyset \) for all \(C^{\prime } \in {\mathcal {C}}({\mathscr{H}})\). Furthermore, if a colored graph \({\mathscr{H}}\) is part of an instance I, we also use the notation \({\mathcal {C}}(I) := {\mathcal {C}}({\mathscr{H}})\).
Parameterized Complexity
Parameterized complexity theory aims at a fine-grained analysis of the computational complexity of hard problems. In contrast to classical complexity, a parameterized problem L is a subset of  , where the first component is the input and the second is the parameter. A parameterized problem is fixed-parameter tractable (FPT) if every instance (I,k) can be solved in \(f(k)\cdot |I|^{\mathcal {O}(1)}\) time where f is a computable function depending only on k; an algorithm with this running time is called FPT-algorithm. A parameterized problem is in XP if every instance can be solved in |I|g(k) time for some computable function g. The complexity classes W[1] and W[2] are basic classes of presumed parameterized intractability. That is, it is assumed that problems that are hard for W[1] or W[2] have no FPT-algorithm. Hardness for W[1] or W[2] is shown via parameterized reductions. A parameterized reduction of a parameterized problem L to a parameterized problem \(L^{\prime }\) is an algorithm that for each instance (I,k) of L computes in \(f(k)\cdot |I|^{{\mathcal {O}}(1)}\) time an equivalent instance \((I^{\prime },k^{\prime })\) of \(L^{\prime }\) such that \(k^{\prime }\le g(k)\) for some computable function g. A parameterized reduction is a polynomial parameter transformation if g(k) is a polynomial function and if the running time of the algorithm is polynomial.
, where the first component is the input and the second is the parameter. A parameterized problem is fixed-parameter tractable (FPT) if every instance (I,k) can be solved in \(f(k)\cdot |I|^{\mathcal {O}(1)}\) time where f is a computable function depending only on k; an algorithm with this running time is called FPT-algorithm. A parameterized problem is in XP if every instance can be solved in |I|g(k) time for some computable function g. The complexity classes W[1] and W[2] are basic classes of presumed parameterized intractability. That is, it is assumed that problems that are hard for W[1] or W[2] have no FPT-algorithm. Hardness for W[1] or W[2] is shown via parameterized reductions. A parameterized reduction of a parameterized problem L to a parameterized problem \(L^{\prime }\) is an algorithm that for each instance (I,k) of L computes in \(f(k)\cdot |I|^{{\mathcal {O}}(1)}\) time an equivalent instance \((I^{\prime },k^{\prime })\) of \(L^{\prime }\) such that \(k^{\prime }\le g(k)\) for some computable function g. A parameterized reduction is a polynomial parameter transformation if g(k) is a polynomial function and if the running time of the algorithm is polynomial.
A main tool to achieve fixed-parameter algorithms is reduction to a problem kernel or problem kernelization. A problem kernelization for a parameterized problem L is a polynomial-time algorithm that computes for every instance (I,k) an equivalent instance \((I^{\prime },k^{\prime })\) such that \(|I^{\prime }|\le g(k)\) and \(k^{\prime }\le f(k)\) for computable functions f and g. If g and f are polynomials, then we speak of a polynomial problem kernelization. For more details on parameterized algorithmics, we refer to the standard monographs [6, 8, 11, 19].
The Standard Reduction from Hitting Set
We briefly describe the known reduction from Hitting Set problem and observe its implications on the complexity of Colored (s,t)-Cut.
Hitting Set Input: A hypergraph \({\mathcal {G}} = ({\mathcal {U}}, {\mathcal {F}})\) and a positive integer k. Question: Is there a size-k set \({\mathcal {U}}^{\prime }\subseteq {\mathcal {U}}\) such that \({\mathcal {U}}^{\prime }\cap F\neq \emptyset \) for all \(F\in {\mathcal {F}}\)?
We assume without loss of generality that |F|≥ 2 for all \(F \in {\mathcal {F}}\) since an empty hyperedge \(F\in {\mathcal {F}}\) leads to a no-instance and there is exactly one way to hit a hyperedge \(F\in \mathcal {F}\) of size one. Hitting Set is W[2]-hard with respect to k and fixed-parameter tractable with respect to \(|\mathcal {U}|\) or \(|\mathcal {F}|\) [6, 8]. Unless NP \(\subseteq \) coNP/poly, Hitting Set does not admit a polynomial kernel with respect to \(|\mathcal {U}|\) or with respect to \(|\mathcal {F}|\) [7].
Given a Hitting Set instance \(({\mathcal {G}} = ({\mathcal {U}}, {\mathcal {F}}),k)\), an equivalent instance I := (G = (V,E),C,ℓ,s,t,k) of Colored (s,t)-Cut can be constructed as follows. We set \(C := {\mathcal {U}}\) and add two vertices s and t. Furthermore, we add for every hyperedge \(F\in {\mathcal {F}}\), a new path between s and t with |F| many edges that are colored with the elements of F. The budget of the Colored (s,t)-Cut instance is set to k. Clearly, any size-k hitting set \({\mathcal {U}}^{\prime }\) is a colored (s,t)-cut with k colors and vice versa.
Throughout this work, we will refer to the above reduction as the standard reduction from Hitting Set. The constructed instance has the following properties: the budget k is the same as for the Hitting Set instance, the number of simple (s,t)-paths in G is \(|{\mathcal {F}}|\), the number of colors is \(|{\mathcal {U}}|\) and the pathwidth of G is at most three. This gives directly the following hardness results which were noted previously [10, 16, 23].
Lemma 1
Colored (s,t)-Cut parameterized by k is W[2]-hard even if G has pathwidth three. Colored (s,t)-Cut parameterized by c does not admit a polynomial kernel, unless NP \(\subseteq \) coNP/poly. Colored (s,t)-Cut parameterized by the number of vertex-simple (s,t)-paths does not admit a polynomial kernel, unless NP \(\subseteq \) coNP/poly.
Moreover, it is known that assuming the strong exponential time hypothesis (SETH) [13], Hitting Set cannot be solved in \((2-\epsilon )^{|{\mathcal {U}}|}\cdot |{\mathcal {F}}|^{{\mathcal {O}}(1)}\) time [5]. Since in the instances constructed by the standard reduction the number of colors c is \(|{\mathcal {U}}|\), an algorithm with running time \((2-\epsilon )^{c}\cdot n^{{\mathcal {O}}(1)}\) for Colored (s,t)-Cut for any 𝜖 > 0 would imply a faster algorithm for Hitting Set, contradicting the SETH. Thus, we obtain the following lower bound.
Proposition 1
If the SETH is true, then Colored (s,t)-Cut cannot be solved in time \((2-\epsilon )^{c}\cdot n^{{\mathcal {O}}(1)}\) for any 𝜖 > 0.
Hence, the simple algorithm that tries all possible color sets to delete is essentially optimal when the parameter is c.
3 Structural Graph Parameters
We now analyze several structural graph parameters for Colored (s,t)-Cut and show that the problem is in XP for any of these parameters but Colored (s,t)-Cut has no FPT-algorithm when parameterized by the sum of all of these structural parameters, unless FPT = W[2]. Since Colored (s,t)-Cut is NP-hard even if the graph has a vertex cover of size 2 [24], it is unlikely to be FPT for vertex deletion parameters. Thus, in this work we consider edge deletion parameters.
Definition 1
Let G = (V,E) be a graph and i ≥ 0 be an integer. Furthermore, let \(\xi _{i} := \min \limits \{|E^{\prime }| \mid E^{\prime }\subseteq E, G-E^{\prime }\) has a maximum degree of i} be the edge deletion distance to a maximum degree of i.
Since Colored (s,t)-Cut can be solved in polynomial time for graphs with constant maximum degree Δ, the parameter ξi measures the distance to a trivial case. Since Δ ≤ ξi + i, Colored (s,t)-Cut parameterized by ξi is in XP when i is a constant.
Proposition 2
[3] Colored (s,t)-Cut is in XP when parameterized by any of the following parameters:
-
the budget k,
-
the maximum degree Δ, and
-
the edge deletion distance to a maximum degree of three ξ3.
Proof
The XP-algorithms are already known for k and Δ [3]. Note that we can assume that Δ > k, since otherwise the budget is large enough to delete all colors of incident edges of s. These are at most Δ, and therefore the instance is a trivial yes-instance. It remains to show that Colored (s,t)-Cut is in XP with respect to ξ3. To this end, we show that ξ3 ≥Δ− 3. A graph G with a maximum degree of Δ contains at least one vertex v ∈ V (G) with \(\deg (v) = {\Delta }\). We have to delete at least Δ − 3 edges incident with v to obtain a graph with maximum degree at most three. Hence, ξ3 ≥Δ− 3. □
3.1 Parameterized Hardness for Degree-Based Parameterizations
Since Colored (s,t)-Cut parameterized by k,Δ, and ξ3 is in XP, we next show the fixed-parameter-intractability for the largest of these parameters ξ3. Recall that previously only W[2]-hardness for the smallest of these three parameters the budget k was known.
Theorem 1
Colored (s,t)-Cut parameterized by ξ3 is W[2]-hard even on planar graphs.
Proof
We give a parameterized reduction from Hitting Set parameterized by the size of the solution, which is known to be W[2]-complete [8]. Given a Hitting Set instance \(I^{\prime }:=({\mathcal {G}} = ({\mathcal {U}}, {\mathcal {F}}),k)\), we describe how to construct an equivalent Colored (s,t)-Cut instance I := (G = (V,E),C,ℓ,s,t,k) in polynomial time and show that ξ3 is bounded in k. Figure 3 shows an example of the construction.
Again, we assume without loss of generality that |F|≥ 2 for all \(F \in {\mathcal {F}}\) since an empty hyperedge \(F\in {\mathcal {F}}\) leads to a no-instance and there is exactly one way to cover a hyperedge \(F\in {\mathcal {F}}\) of size one. Moreover, if \(k \geq |{\mathcal {U}}|\), \(I^{\prime }\) is obviously a yes-instance and if \(k{\kern -.5pt} \leq {\kern -.5pt} 2\), \(I^{\prime }\) can be solved in polynomial time. Hence, we can assume that \(2{\kern -.5pt} <{\kern -.5pt} k{\kern -.5pt} <{\kern -.5pt} |{\mathcal {U}}|\). Furthermore, we assume that \({\mathcal {U}} = \{ 1,\dots ,|{\mathcal {U}}| \} \) and that there is an ordering on \({\mathcal {F}}\).
We set \(C := {\mathcal {U}}\) and define Gi := (Vi,Ei) for all i,1 ≤ i ≤ k + 1, in the following way. The graph Gi contains two vertex-disjoint balanced binary trees \({T^{i}_{s}}\) and \({T^{i}_{t}}\) with roots si,ti, and leaves \({s^{i}_{j}}, {t^{i}_{j}}\) for all \(j,1\leq j \leq |{\mathcal {F}}|\). We set ℓ(e) := i for all \(e \in E({T^{i}_{s}}) \cup E({T^{i}_{t}})\). Furthermore, we connect \({s^{i}_{j}}\) and \({t^{i}_{j}}\) by a new path \({P^{i}_{j}}\) with |Fj| edges that are colored with the elements of Fj.
Finally, we define G = (V,E) with \(V := \{ s,t \} \cup \bigcup _{1 \leq i \leq k+1}V^{i}\) and \(E := \bigcup _{1 \leq i \leq k+1}(E^{i} \cup \{ \{ s, s^{i} \} , \{ t, t^{i} \} \} )\) and set ℓ({s,si}) := ℓ({t,ti}) := i. That is, we connect s and t with si and ti, respectively, with edges colored in i for all i,1 ≤ i ≤ k + 1. Note that G is planar.
Recall that besides s and t all vertices have degree at most 3. Let \(E^{\prime } := \{\{s, s^{i}\}, \{t, t^{i}\} \mid 1 \leq i \leq k-2\}\) then \(G-E^{\prime }\) is cubic. Thus, \(\xi _{3} \leq |E^{\prime }| = 2(k - 2)\).
For the correctness of this parameterized reduction it remains to show that I is a yes-instance if and only if \(I^{\prime }\) is a yes-instance. To this end, we show that \(({\mathcal {G}},k)\) has a hitting set of size at most k if and only if (G,s,t,C,ℓ,k) has a colored (s,t)-cut of size at most k.
(⇒) Let S be a hitting set of \({\mathcal {G}}\) with size at most k. By definition, S ∩ Fj≠∅ for all \(F_{j} \in {\mathcal {F}}\). Hence, removing all edges in ℓ− 1(S) from G removes at least one edge in the path \({P^{i}_{j}}\) from \({s^{i}_{j}}\) to \({t^{i}_{j}}\) for all i with 1 ≤ i ≤ k + 1 and all j with \(1\leq j\leq |{\mathcal {F}}|\). Note that for every path P from s to t in G there is at least one j with \(1 \leq j \leq |{\mathcal {F}}|\) such that P contains \({s^{i}_{j}}\) and \({t^{i}_{j}}\) for some i, 1 ≤ i ≤ k + 1. So by removing at least one edge from every path \({P^{i}_{j}},\) we separate s from t. It follows by definition, that S is a colored (s,t)-cut of size at most k for I.
(⇐) Let S be a colored (s,t)-cut of size at most k for I, let ES := ℓ− 1(S) be the set of edges colored by a color in S, and let \(G^{\prime } := G - E_{S}\). By construction, s and t have a path only colored in i to \({s^{i}_{j}}\) and \({t^{i}_{j}}\), respectively, for all i with 1 ≤ i ≤ k + 1 and j with \(1 \leq j \leq |{\mathcal {F}}|\). Since S has size at most k there is at least one i,1 ≤ i ≤ k + 1, such that s and t are in the same connected component as \({s^{i}_{j}}\) and \({t^{i}_{j}}\), respectively, in \(G^{\prime }\) for all \(j,1 \leq j \leq |{\mathcal {F}}|\). The fact that S is a colored (s,t)-cut in G now implies that ES contains at least one edge of each path \({P^{i}_{j}}\). Thus, \(S \cap \ell ({P^{i}_{j}}) \neq \emptyset \) for all j such that \(1 \leq j \leq |{\mathcal {F}}|\). Since \(\ell ({P^{i}_{j}}) = F_{j}\) it follows that S ∩ Fj≠∅ for all \(1 \leq j \leq |{\mathcal {F}}|\). Consequently, S is a hitting set of size at most k for \({\mathcal {G}}\). □
The next corollary follows directly from Theorem 1 and ξ3 + 3 ≥Δ > k.
Corollary 1
Colored (s,t)-Cut parameterized by k + Δ + ξ3 is W[2]-hard even on planar graphs.
3.2 FPT-Algorithms for Instances with Bounded Number of (s,t)-Paths
We now show that this result is tight by showing an FPT-algorithm for ξ2 which is obtained via an FPT-algorithm for p, the number of (s,t)-paths in G.
Proposition 3
[16] Colored (s,t)-Cut is FPT parameterized by p and does not admit a polynomial kernel unless NP \(\subseteq \) coNP/poly.
Proposition 3 is known [16], but we are not aware of a published proof. Hence, we give a proof for the sake of completeness.
Proof
First, we describe an FPT-algorithm for Colored (s,t)-Cut parameterized by p. To this end, we provide a parameterized reduction from Colored (s,t)-Cut parameterized by p to Hitting Set parameterized by the number of sets \(|{\mathcal {F}}|\) which is known to be FPT [12]. Given an instance I = (G,C,ℓ,s,t,k), we compute the set \(\mathcal {P}\) of (s,t)-paths in G in \({\mathcal {O}}(pn + m)\) time [1]. Hence, we can compute \({\mathcal {C}}(I) = \{\ell (P)\mid P\in \mathcal {P}\}\) in the same time. It is obvious that there is a colored (s,t)-cut of size at most k in G if and only if \(I^{\prime }=({\mathcal {G}}:=(C,{\mathcal {C}}(I)),k)\) has a hitting set of size at most k. Since Hitting Set can be solved in time \({\mathcal {O}}(2^{|{\mathcal {F}}|}\cdot |{\mathcal {F}}|\cdot |{\mathcal {U}}|)\) [12] and \(|C(I)|\le |\mathcal {P}|\le p\), we can solve the instance \(I^{\prime }\) in time \({\mathcal {O}}(2^{p}p|C|)\). Hence, we can solve Colored (s,t)-Cut in time \({\mathcal {O}}(2^{p}p|C| + pn + m)\) by solving the newly constructed instance of Hitting Set parameterized by \(|{\mathcal {F}}|\).
By Lemma 1 Colored (s,t)-Cut parameterized by p does not admit a polynomial kernel, unless NP \(\subseteq \) coNP/poly.
□
Next, we show that Colored (s,t)-Cut is also FPT for the edge deletion parameter fes.
Definition 2
For a graph G = (V,E), we call \(F\subseteq E\) a feedback edge set if G − F is a forest. We define with \(\mathsf {fes} := \min \limits \{|F| \mid F\) is a feedback edge set} the feedback edge set number of G.
In the following, we show that p can be upper-bounded by a computational function only depending on the feedback edge set number fes which implies an FPT-algorithm for Colored (s,t)-Cut parameterized by fes.
We assume that the following result might be known already but we were not able to find a proof for this particular statement. Hence, for the sake of completeness, we give a proof.
Lemma 2
Let G = (V,E) be a graph with feedback edge set number fes, then for any s,t ∈ V there are \({\mathcal {O}}(2^{\mathsf {fes}+1}\mathsf {fes}^{\mathsf {fes}+1})\) many vertex-simple (s,t)-paths in G.
Proof
Let \(F \subseteq E\) be a feedback edge set of G of size fes. Let T := G − F denote the graph obtained from deleting F. Observe that T is a forest. Note that every edge occurs at most once in every vertex-simple (u,v)-path for every u,v ∈ V. We show that there are at most 2jfesj many (u,v)-paths P in G with |E(P) ∩ F| = j for every j with 0 ≤ j ≤fes. That is, we bound the number of (u,v)-paths that contain exactly j edges of F. We show this bound by induction over j.
Since T is a forest, there is at most one (u,v)-path P in T for every u,v ∈ V. Hence, there is at most one (u,v)-path P in G with E(P) ∩ F = ∅ and therefore the bound holds for j = 0.
So, assume that the bound holds for j with 0 ≤ j − 1 < fes. We show that the bound also holds for j. Let \(P=(v_{1}, \dots , v_{r})\) be an arbitrary (u,v)-path in G with |E(P) ∩ F| = j and let e = {vi,vi+ 1}∈ F such that {vq,vq+ 1}∉F for all q such that 1 ≤ q < i. That is, e is the first feedback edge of P. By the induction hypothesis there is at most one (u,vi)-path in G and at most 2j− 1fesj− 1 many (vi+ 1,v)-paths Pj− 1 in G with |E(Pj− 1) ∩ F| = j − 1. Since there are at most fes many possible feedback edges and every such edge has two orientations, there are at most 2 ⋅fes possibilities for e. Hence, there are at most 2j− 1fesj− 1 ⋅ 2 ⋅fes = 2jfesj different (u,v)-paths P in G with |E(P) ∩ F| = j.
Altogether, there are thus at most \({\sum }_{j = 0}^{\mathsf {fes}}2^{j}\mathsf {fes}^{j} \in {\mathcal {O}}(2^{\mathsf {fes}+1}\mathsf {fes}^{\mathsf {fes}+1})\) many (u,v)-paths in G and therefore \({\mathcal {O}}(2^{\mathsf {fes}+1}\mathsf {fes}^{\mathsf {fes}+1})\) many (s,t)-paths in G.
□
The following can be obtained by applying Proposition 3.
Proposition 4
Colored (s,t)-Cut is FPT parameterized by the feedback edge set number fes or ξ2 and does not admit a polynomial kernel for fes + ξ2, unless NP \(\subseteq \) coNP/poly.
Proof
We show the proposition in three steps. First, we present an FPT-algorithm for Colored (s,t)-Cut parameterized by fes, second we show that ξ2 ≥fes − 1, and third, we show that Colored (s,t)-Cut does not admit a polynomial kernel with respect to ξ2 unless coNP/poly.
First, we give an FPT-algorithm for fes. By Lemma 2, the number of (s,t)-paths p is bounded from above by a computable function h only depending on the feedback edge set number fes. Obviously, fes can be computed in \({\mathcal {O}}(n+m)\) time. Hence, we can use the FPT algorithm from Proposition 3 to solve Colored (s,t)-Cut in \({\mathcal {O}}(2^{h(\mathsf {fes})}h(\mathsf {fes})|C| + h(\mathsf {fes})n + m)\) time.
Second, we show that ξ2 ≥fes − 1. Let I := (G = (V,E),C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut. Since G is connected, we conclude that m ≥ n − 1 and that the feedback edge set number is fes = m − n + 1. Observe that ξ2 ≥fes − 1: for a graph \(G^{\prime } =(V^{\prime }, E^{\prime })\) with a maximum degree of at most 2, it holds that \(|E^{\prime }| \leq |V^{\prime }|\). Hence, m − ξ2 ≤ n and therefore ξ2 ≥ m − n = fes − 1.
Third, we present the kernel lower bound for Colored (s,t)-Cut parameterized by ξ2. Note that for the instances constructed by the standard reduction it holds that \(\xi _{2} = 2 (|\mathcal {F}| - 2)\), since by removing all edges incident with s or t except two each, we can turn G into graph with maximum degree two. Hence, the standard reduction is a polynomial parameter transformation from Hitting Set parameterized by \(|{\mathcal {F}}|\) to Colored (s,t)-Cut parameterized by ξ2. Unless NP \(\subseteq \) coNP/poly, Hitting Set parameterized by \(|{\mathcal {F}}|\) does not admit a polynomial kernel [7] and therefore, neither does Colored (s,t)-Cut parameterized by ξ2. □
4 A Kernel for the Number of Edges with Rare Colors
In this section, we give a linear problem kernel for Colored (s,t)-Cut parameterized by the number of edges whose color is not among the top-q most frequent colors. More precisely, we define a family of parameters m>q for every  as follows. For a Colored (s,t)-Cut-instance I with color set C, let \((\alpha _{1}, \alpha _{2}, \dots ,\alpha _{c})\) be an ordering of the colors in C such that the number of edges with color αi is not smaller than the number of edges with color αi+ 1 for all \(i \in \{1, \dots , c-1\}\). For a given integer q, let \(\tilde {C} \subseteq C\) be the set of the q most frequent colors. We then define m>q as the number of edges that are not assigned to a color in \(\tilde {C}\). In the following, we show a linear problem kernel for m>q for every constant q. To the best of our knowledge, this is the first non-trivial polynomial kernel for Colored (s,t)-Cut.
as follows. For a Colored (s,t)-Cut-instance I with color set C, let \((\alpha _{1}, \alpha _{2}, \dots ,\alpha _{c})\) be an ordering of the colors in C such that the number of edges with color αi is not smaller than the number of edges with color αi+ 1 for all \(i \in \{1, \dots , c-1\}\). For a given integer q, let \(\tilde {C} \subseteq C\) be the set of the q most frequent colors. We then define m>q as the number of edges that are not assigned to a color in \(\tilde {C}\). In the following, we show a linear problem kernel for m>q for every constant q. To the best of our knowledge, this is the first non-trivial polynomial kernel for Colored (s,t)-Cut.
Informally, the kernel is based on the following idea: Since q is a constant, we may try all possible partitions of {α1,…,αq} into a set of colors Cr that we want to remove and a set of colors Cm that we want to keep. Fix one partition (Cr,Cm). Under the assumption posed by this partition, we can simplify the instance as follows. The edges of Cr can be deleted. Moreover, all vertices that are connected by a path P in G, such that \(\ell (P) \subseteq C_{m}\) cannot be separated anymore under this assumption. Thus, all vertices of P can be merged into one vertex. To formalize this merging, we give the following definition. For a colored graph (G = (V,E),C,ℓ) and a set \(C_{m} \subseteq C\), we define \([v]_{C_{m}} := \{ u \in V \mid \exists P = (v, \dots , u) \text { in G}: \ell (P) \subseteq C_{m} \} \) as the set of vertices that are connected to v by a path only colored in Cm. If Cm is clear from the context, we may only write [v]. The instance that can be built for specific sets Cr and Cm is defined as follows.
Definition 3
Let I = (G,C,ℓ,s,t,k) be a Colored (s,t)-Cut instance and let \(C_{r}, C_{m} \subseteq C\) with Cr ∩ Cm = ∅. The remove-merge-instance of I with respect to (Cr,Cm) is \(\text {rmi}(I, C_{r}, C_{m}) := (G^{\prime }=(V^{\prime },E^{\prime }), C^{\prime }, \ell ^{\prime },[s],[t], k - |C_{r}|)\), where \(C^{\prime } := C \setminus (C_{r} \cup C_{m})\), \(V^{\prime } := V^{\prime }_{1} \cup V^{\prime }_{2}\), and
The vertices of V2 only exist to prevent G from having parallel edges. An example of a remove-merge-instance is shown in Fig. 4. We now show that a remove-merge-instance can be computed efficiently.
An example of the colored graph of a remove-merge-instance. For Cr := {green} and Cm := {gray}, \(({\mathscr{H}}^{\prime },k-1)\) is the remove merge instance \(\text {rmi}(({\mathscr{H}},k),C_{r}, C_{m})\). The graph \(\tilde {{\mathscr{H}}}\) shows \({\mathscr{H}}\) after removing all edges colored in gray. Squared vertices of \({\mathscr{H}}^{\prime }\) belong to \(V^{\prime }_{2}\), whereas circular vertices of \({\mathscr{H}}^{\prime }\) belong to \(V^{\prime }_{1}\)
Proposition 5
Let I = (G = (V,E),C,ℓ,s,t,k) be a Colored (s,t)-Cut instance, and let \(I^{\prime }=\text {rmi}(I,C_{r},C_{m})\) be the remove-merge-instance of I for some \(C_{r}, C_{m} \subseteq C\) such that Cr ∩ Cm = ∅. Then, \(|I^{\prime }| \in \mathcal {O}(|I|)\) and \(I^{\prime }\) can be computed in \(\mathcal {O}((|C_{r}|+|C_{m}|) \cdot m)\) time.
Proof
Recall that we assume n ≤ m. We first show that \(I^{\prime }\) can be computed in \({\mathcal {O}}((|C_{r}|+|C_{m}|) \cdot m)\) time. We start by computing the set \(V_{1}^{\prime }=\{[v] \mid v \in V\}\). To this end, we compute a graph \(\tilde {G}\) with \(\tilde {G}=(V, \{e \in E \mid \ell (e) \in C_{m}\})\) in \({\mathcal {O}}(|C_{m}| \cdot m)\) time. The connected components of \(\tilde {G}\) form the set \(V^{\prime }_{1}\) and can be computed via depth-first search in \({\mathcal {O}}(m)\) time. Afterwards, we compute the sets \(V_{2}^{\prime }\) and \(E^{\prime }\) by checking for every edge {u,v}∈ E with [u]≠[v] if ℓ({u,v})∉(Cr ∪ Cm) in \({\mathcal {O}}((|C_{r}|+|C_{m}|) \cdot m)\) time.
Next, we show \(|I^{\prime }| \in {\mathcal {O}}(|I|)\). For every edge {u,w}∈ E we added at most one vertex \(v^{\ell (\{u,w\})}_{\{[u],[w]\}}\) and its two incident edges. Hence, \(I^{\prime }\) has at most 2m edges. Since n ≤ m it follows \(|I^{\prime }| \in {\mathcal {O}}(|I|)\). □
We now show that for any \(\tilde {C}\subseteq C\), we can solve the original instance by creating and solving all possible remove-merge-instances for subsets of \(\tilde {C}\).
Lemma 3
Let I := (G = (V,E),C,ℓ,s,t,k) be a Colored (s,t)-Cut instance and let \(\tilde {C} \subseteq C\) be a color set. Then, I is a yes-instance if and only if there is a set \(C_{r} \subseteq \tilde {C}\) such that the remove-merge-instance \(I^{\prime } := \text {rmi}(I, C_{r}, \tilde {C} \setminus C_{r})\) is a yes-instance.
Proof
(⇒) Let S be a colored (s,t)-cut of size k for I. We set \(C_{r} := S \cap \tilde {C}, C_{m} := \tilde {C} \setminus C_{r}\). Furthermore, let \(I^{\prime }= (G^{\prime }=(V^{\prime },E^{\prime }), C^{\prime }, \ell ^{\prime },[s],[t], k - |C_{r}|) := \text {rmi}(I, C_{r}, C_{m})\) be the remove-merge-instance for I with respect to Cr and Cm. We show that \(S^{\prime } := S \setminus C_{r}\) is a colored ([s],[t])-cut for \(I^{\prime }\) of size at most k −|Cr|. The size of \(S^{\prime }\) follows directly from the definition of Cr and \(S^{\prime }\) so we only have to show that \(S^{\prime }\) is a colored ([s],[t])-cut for \(I^{\prime }\). Assume towards a contradiction, that this is not the case. Then, there is a vertex-simple ([s],[t])-path \(P^{\prime }\) in \(G^{\prime }\) with \(\ell ^{\prime }(E(P^{\prime })) \subseteq C^{\prime } \setminus S^{\prime }\). By construction of \(G^{\prime }\), we can assume without loss of generality that \(P^{\prime }=([v_{1}], v^{\alpha _{1}}_{\{ [v_{1}],[v_{2}] \} }, [v_{2}], \dots , [v_{x}])\) where s ∈ [v1],t ∈ [vx]. By definition of \(G^{\prime }\), there is some \(v^{\text {out}}_{i} \in [v_{i}], v^{\text {in}}_{i+1} \in [v_{i+1}]\) such that \(e_{i} := \{ v^{\text {out}}_{i}, v^{\text {in}}_{i+1} \} \in E\) with ℓ(ei) = αi for all i, 1 ≤ i < x. Observe that αi∉S for all i, 1 ≤ i < x. Furthermore, define \(v^{\text {in}}_{1} = s, v^{\text {out}}_{x} = t\). Since \(v^{\text {in}}_{i}, v^{\text {out}}_{i} \in [v_{i}]\) it follows that there is a \((v^{\text {in}}_{i}, v^{\text {out}}_{i})\)-path Pi in G such that \(\ell (P_{i}) \subseteq C_{m}\) for all 1 ≤ i ≤ x. Then, P = P1 ⋅ P2 ⋅… ⋅ Px is a path in G from s to t such that \(\ell (P) = \bigcup _{1\leq j \leq x} \ell (P_{j}) \cup \{ \ell (e_{i}) \mid 1 \leq i < x \} \subseteq C_{m} \cup C^{\prime }\setminus S^{\prime } = C \setminus S\). This contradicts the fact that S is a colored (s,t)-cut for I.
(⇐) Let \(C_{r} \subseteq \tilde {C}\) be a color set such that the remove merge instance \(I^{\prime }:=\text {rmi}(I, C_{r}, C_{m})\) obtained from removing Cr and merging \(C_{m} := \tilde {C} \setminus C_{r}\) is a yes-instance. Let \(I^{\prime }=(G^{\prime }=(V^{\prime },E^{\prime }), C^{\prime }, \ell ^{\prime },[s],[t], k - |C_{r}|)\), and let \(S^{\prime }\) be a colored ([s],[t])-cut of size at most k −|Cr| for \(I^{\prime }\). We show that \(S := S^{\prime } \cup C_{r}\) is a colored (s,t)-cut of size at most k for I. The size of S is obvious and so it remains to show that S is a colored (s,t)-cut for I. Assume towards a contradiction, that S is not a colored (s,t)-cut for I. Then, there is an (s,t)-path P in G with \(\ell (P) \subseteq C\setminus S\). Let \(P_{1}, {\dots } , P_{r}\) denote the sequence of subpaths of P such that P1 ⋅… ⋅ Pr = P and Pi is the maximal subpath with \(V(P_{i}) \subseteq [v_{i}]\) for each i, 1 ≤ i ≤ r. Thus, [vi]≠[vi+ 1] for each i < r. Let \(v^{\text {in}}_{i}\) and \(v^{\text {out}}_{i}\) as the first and last, respectively, vertex in Pi for all i, 1 ≤ i ≤ r. Since P is a path in G and P1 ⋅… ⋅ Pr = P, there is an edge \(e_{i} := \{ v^{\text {out}}_{i}, v^{\text {in}}_{i+1} \} \in E\). Let αi = ℓ(ei) for all i, 1 ≤ i < r, and observe that \(\alpha _{i} \in C \setminus (S \cup \tilde {C}) = C^{\prime } \setminus S^{\prime }\). So, by definition of \(I^{\prime }\) and the fact that [vi]≠[vi+ 1] for all i, 1 ≤ i < r it follows that \(P^{\prime }=([v_{1}], v^{\alpha _{1}}_{\{ [v_{1}],[v_{2}] \} }, [v_{2}], \dots , [v_{r}])\) is a path in \(G^{\prime }\) with [v1] = [s],[vr] = [t] and \(\ell ^{\prime }(E(P^{\prime })) \subseteq C^{\prime } \setminus S^{\prime }\). This contradicts the fact that \(S^{\prime }\) is a colored ([s],[t])-cut for \(I^{\prime }\). □
The lemma above shows that one may solve an instance by choosing an arbitrary color set \(\tilde {C}\) and then outputting the “or” of all remove-merge instances that can be constructed from partitions of \(\tilde {C}\). For Colored (s,t)-Cut instances with an identical budget, an “or”-composition is already known.
Lemma 4
[23] Let \(\mathcal {I} = \{I_{j}=(G_{j},C_{j}, \ell _{j},s_{j},t_{j},k)\mid 1 \leq j \leq i\}\) be a set of i Colored (s,t)-Cut instances with the same budget k. Then, we can compute in linear time an instance \(I^{\prime }=(G^{\prime },C^{\prime },\ell ^{\prime },s^{\prime },t^{\prime },k)\) of Colored (s,t)-Cut with \(|I^{\prime }|\le {\sum }_{j=1}^{i} |I_{i}|\) such that \(I^{\prime }\) is a yes-instance of Colored (s,t)-Cut if and only if Ij is a yes-instance of Colored (s,t)-Cut for some j ∈{1,…,i}.
The idea behind the construction is simply to glue together the single instances by identifying tj with sj+ 1 for all j such that 1 ≤ j < i.
With the help of Lemma 3, we are now able to introduce our polynomial kernelization algorithm for Colored (s,t)-Cut.
Theorem 2
For every constant  , Colored (s,t)-Cut admits a problem kernel of size \({\mathcal {O}}(m_{>q})\) that can be computed in \({\mathcal {O}}(|I|)\) time.
, Colored (s,t)-Cut admits a problem kernel of size \({\mathcal {O}}(m_{>q})\) that can be computed in \({\mathcal {O}}(|I|)\) time.
Proof
Let I = (G = (V,E),C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut and let \(\tilde {C} = \{\alpha _{1}, \alpha _{2}, \dots , \alpha _{q} \} \subseteq C\) be the set of the q most-frequent colors. We first describe how to compute an equivalent instance \(I^{\prime }\) from I in linear time and afterwards we show that \(|I^{\prime }| \in {\mathcal {O}}(m_{>q})\).
Construction of \(I^{\prime }\). We start by computing the set \(\mathcal {I}= \{\text {rmi}(I, C_{r}, \tilde {C}\setminus C_{r}) \mid C_{r} \subseteq \tilde {C}\}\) containing for every \(C_{r}\subseteq \tilde {C}\), the remove-merge instance of I with respect to \((C_{r}, \tilde {C}\setminus C_{r})\). Note that \(|\mathcal {I}|=2^{q} \in {\mathcal {O}}(1)\). We write \(\mathcal {I}=\{I_{1}, I_{2}, \dots , I_{2^{q}}\}\) and let Ii =: (Gi = (Vi,Ei),Ci,ℓi,[s]i,[t]i,ki) denote each instance \(I_{i}\in \mathcal {I}\). By Proposition 5, we can compute each \(I_{i} \in \mathcal {I}\) in \({\mathcal {O}}(q \cdot |I|)={\mathcal {O}}(|I|)\) time. Therefore, we can compute \(\mathcal {I}\) in \({\mathcal {O}}(|I|)\) time. Note that \(\max \limits _{i \in \{1, {\dots } ,2^{q}\}} k_{i} = k\) and that \(C_{i} = C \setminus \tilde {C}\) for every i, 1 ≤ i ≤ 2q.
Next, we apply the algorithm of Lemma 4 on all instances of \(\mathcal {I}\). Note that the budgets ki of the instances \(I_{i} \in \mathcal {I}\) might not be equal. Thus, in order to apply Lemma 4 we transform every instance \(I_{i} \in \mathcal {I}\) into an instance \(I^{*}_{i}\) by adding auxiliary vertices \(v_{1}, \dots , v_{k-k_{i}}\) to Vi and auxiliary edges {[s]i,vj} and {[t]i,vj} for every j, 1 ≤ j ≤ k − ki to Ei. Let \(V^{*}_{i}\) and \(E^{*}_{i}\) be the resulting sets. Finally, we set \(k^{*}_{i}=k\) and \(\ell ^{*}_{i}(e)=\ell _{i}(e)\) if e ∈ Ei and \(\ell ^{*}_{i}(\{[s]_{i},v_{j}\})=\ell ^{*}_{i}(\{[t]_{i},v_{j}\})=\alpha _{j}\) for every j, 1 ≤ i ≤ k − ki. Note that 1) αj∉Ci for every j < k − ki, 2) that we added \(\mathcal {O}(k-k_{i})\) vertices and edges to Ii, and 3) that k − ki ≤ q. Since q is a constant, \(|I^{*}_{i}| \in \mathcal {O}(|I_{i}|)\) and \(I^{*}_{i}\) can be computed from Ii in \(\mathcal {O}(|I_{i}|)\) time.
Equivalence of I and \(I^{\prime }\). Let \(\mathcal {I}^{*}=\{I^{*}_{1}, \dots , I^{*}_{2^{q}}\}\) be the resulting set of instances. Note that the budget is k in all instances in \(\mathcal {I}^{*}\). Therefore, we can apply Lemma 4 on the 2q instances in \(\mathcal {I}^{*}\) and compute an instance \(I^{\prime }\) in \({\mathcal {O}}(|I|)\) time, such that \(I^{\prime }\) is a yes-instance if and only if there exists some \(i \in \{1, \dots , 2^{q}\}\) such that \(I^{*}_{i}\) is a yes-instance.
Next, we show that I is a yes-instance of Colored (s,t)-Cut if and only if \(I^{\prime }\) is a yes-instance of Colored (s,t)-Cut. To this end, consider the following claim.
Claim 1
Let \(i \in \{1, \dots , 2^{q}\}\). Then, Ii is a yes-instance if and only if \(I^{*}_{i}\) is a yes-instance.
Proof
Let \(v_{1}, \dots , v_{k-k_{i}}\) be the auxiliary vertices of \(I^{*}_{i}\) and observe that in \(G^{*}_{i}-\{\alpha _{1},\ldots ,\alpha _{k-k_{i}}\}\) these auxiliary vertices are isolated and the connected component containing [s]i and [t]i is exactly Gi. Thus, given a colored ([s]i,[t]i)-cut of size at most ki for Ii, one may obtain a colored ([s]i,[t]i)-cut of size at most k for \(I^{*}_{i}\) by adding \(\{\alpha _{1},\ldots ,\alpha _{k-k_{i}}\}\). Conversely, every colored ([s]i,[t]i)-cut \(S^{\prime }\) of size at most k for \(I^{*}_{i}\) contains \(\{\alpha _{1},\ldots ,\alpha _{k-k_{i}}\}\) by construction. Therefore, \(S^{\prime }\setminus \{\alpha _{1},\ldots ,\alpha _{k-k_{i}}\}\) has size ki. By the above observation, \(S^{\prime }\setminus \{\alpha _{1},\ldots ,\alpha _{k-k_{i}}\}\) is an ([s]i,[t]i)-cut of Ii. □
We next use Claim 1 to show that I is a yes-instance if and only if \(I^{\prime }\) is a yes-instance. By Lemma 3, I is a yes-instance if and only if there exists a set \(C_{r} \subseteq \tilde {C}\) such that \(\text {rmi}(I,C_{r}, \tilde {C}\setminus C_{r})\) is a yes-instance. Equivalently, there exists some \(i \in \{1, \dots , 2^{q}\}\) such that Ii is a yes-instance. By Claim 1, this is the case if and only if \(I^{*}_{i}\) is a yes-instance. Finally, by Lemma 4 we conclude that this is the case if and only if \(I^{\prime }\) is a yes-instance.
Size of \(I^{\prime }\). It remains to give a bound for the size of \(I^{\prime }\). By Definition 3 of remove-merge-instances, every \(I_{i} \in \mathcal {I}\) contains no edges with a color in \(\tilde {C}\), and subdivides every other edge of I. Therefore, every \(I_{i} \in \mathcal {I}\) contains at most 2m>q edges. Since \(|I^{*}_{i}| \in {\mathcal {O}}(|I_{i}|)\) we conclude \(|I^{*}_{i}| \in {\mathcal {O}}(m_{>q})\) for every \(I_{i}^{*} \in \mathcal {I}\). Finally, by Lemma 4 it holds that \(|I^{\prime }| \leq {\sum }_{i=1}^{2^{q}} |I_{i}^{*}| \in {\mathcal {O}}(m_{>q})\), since \(2^{q} \in {\mathcal {O}}(1)\). □
Since the kernelization employs Lemma 4, the instance \(I^{\prime }\) is obtained from an or-composition of all remove merge-instances of I with respect to \((C_{r}, \tilde {C}\setminus C_{r})\), \(C_{r}\subseteq \tilde {C}\). When solving the problem in practice, it might be better to compute all 2q remove-merge-instances and solve them independently. Note that if we do not choose q as a constant but \(q \in {\mathcal {O}}(\log (|I|))\), this gives an algorithm that solves Colored (s,t)-Cut by solving \(2^{q} \leq |I|^{{\mathcal {O}}(1)}\) many Colored (s,t)-Cut instances of size \({\mathcal {O}}(m_{>q})\). Such an algorithm is called Turing kernelization.
5 Parameterization by Color Subsets
In this section, we analyze the parameterized complexity of Colored (s,t)-Cut when parameterized by the sizes of specific subsets of colors which we call color parameterizations. For some of the investigated color parameterizations, we obtain FPT-algorithms, whereas for the remaining investigated color parameterizations, we show that there is presumably no FPT-algorithm.
5.1 A General Color-Framework
In this section we present a general framework for color parameterizations of Colored (s,t)-Cut leading to an FPT-algorithm. Furthermore, these parameters are unlikely to admit a polynomial kernel. To apply our framework, one has to check two properties of the parameterization.
Definition 4
A function π that maps every instance I = (G,C,ℓ,s,t,k) of Colored (s,t)-Cut to a subset \(\pi (I)\subseteq C\) of the colors of I is called a color parameterization. If for every Colored (s,t)-Cut instance I,
-
π(I) can be computed in polynomial time and
-
I can be solved in polynomial time if π(I) = ∅,
then π is called a polynomial color parameterization.
In the following, we will only deal with polynomial color parameterizations. To obtain FPT-algorithms, we will transform an instance I of Colored (s,t)-Cut to a set \(\mathcal {I}\) of remove-merge-instances of I such that \(\pi (I^{\prime })=\emptyset \) for each \(I^{\prime }\in \mathcal {I}\) and \(\mathcal {I}\) has size f(π(I)) for some computable function f. Each \(I^{\prime }\) can be solved in polynomial time since π is polynomial and \(\pi (I^{\prime })=\emptyset \). We formally define a property guaranteeing that \(\pi (I^{\prime })=\emptyset \) in all these remove-merge-instances. Additionally, we define an even stronger property for color parameterizations. Intuitively, a color parameterization π has the strong remove-merge property, if no color of C ∖ π(I) is contained in \(\pi (I^{\prime })\) in any remove-merge instance of I for any Cr and Cm. Intuitively, in a remove-merge-instance \(I^{\prime }\), the size of \(\pi (I^{\prime })\) is not larger than the size of π(I).
Definition 5
A color parameterization π has the strong remove-merge property if for every Colored (s,t)-Cut instance I, every \(\tilde {C}\) and every \(C_{r} \subseteq \tilde {C}\) it holds that \(\pi (I^{\prime }) \subseteq \pi (I)\) where \(I^{\prime } := \text {rmi}(I, C_{r}, \tilde {C} \setminus C_{r})\). Furthermore, π has the weak remove-merge property if for every Colored (s,t)-Cut instance I and every \(C_{r} \subseteq \pi (I)\) it holds that \(\pi (I^{\prime })=\emptyset \) where \(I^{\prime } := \text {rmi}(I, C_{r}, \pi (I) \setminus C_{r})\).
Lemma 5
If π has the strong remove-merge property, then π also has the weak remove-merge property.
Proof
Let I = (G,C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut and let \(C_{r} \subseteq \pi (I)\). Furthermore, let \(I^{\prime } = (G^{\prime },C^{\prime },\ell ^{\prime },[s],[t], k^{\prime }) := \text {rmi}(I, C_{r}, \pi (I) \setminus C_{r})\). Then, \(\pi (I^{\prime }) = \emptyset \): By the definition of the strong remove-merge property \(\pi (I^{\prime }) \subseteq \pi (I)\), and by definition of \(I^{\prime }\), \(C^{\prime } \cap \pi (I) = \emptyset \). □
Next, we show that one can obtain an FPT-algorithm for Colored (s,t)-Cut parameterized by any color parameterization that is polynomial and has the weak remove-merge property.
Lemma 6
Let π be a polynomial color parameterization with the weak remove-merge property. Then, any instance I of Colored (s,t)-Cut can be solved in \(2^{|\pi (I)|}|I|^{{\mathcal {O}}(1)}\) time and Colored (s,t)-Cut does not admit a polynomial kernel for |π(I)|, unless NP \(\subseteq \) coNP/poly.
Proof
First, we present an FPT algorithm with the claimed running time. Let I be an instance of Colored (s,t)-Cut. We compute π(I) and the set \(\mathcal {I}\) of all remove-merge-instances for G with respect to π(I) and answer yes if and only if there is some \(I^{\prime } \in \mathcal {I}\) such that \(I^{\prime }\) is a yes-instance. This algorithm is correct due to Lemma 3. Since π is a polynomial color parameterization, we can compute π(I) in polynomial time. Since \(|\mathcal {I}| = 2^{|\pi (I)|}\), we can compute \(\mathcal {I}\) in \(2^{|\pi (I)|}|I|^{{\mathcal {O}}(1)}\) time. Since π is a polynomial color parameterization that has the weak remove-merge property, we can solve each \(I^{\prime } \in \mathcal {I}\) in polynomial time. Hence, this algorithm runs in \(2^{|\pi (I)|}|I|^{{\mathcal {O}}(1)}\) time. The kernel lower bound follows from the fact that |π(I)|≤ c and due to Lemma 1, Colored (s,t)-Cut admits no kernel when parameterized by c, unless NP \(\subseteq \) coNP/poly. □
Next, we apply Lemma 6 to three color parameterizations. All these color parameterizations are polynomial and have the strong remove-merge property. For the FPT-framework, only the weak remove-merge property is required, but for a later result it is helpful to show that the considered color parameterizations also have the strong remove-merge property.
5.2 Number of Colors with Span at Least Two
The first parameterization is related to the span of the colors. Recall that the span of a color α is the number of connected components in G[ℓ− 1(α)]. By Cspan we denote the function that maps an instance I of Colored (s,t)-Cut to the set of colors of I having span at least two. Furthermore, we denote |Cspan(I)| by cspan.
An instance I of Colored (s,t)-Cut can be solved in polynomial time if Cspan = ∅ [3]. Furthermore, it can be verified in polynomial time, whether for a fixed color α the graph G[ℓ− 1(α)] is connected. We conclude the following.
Lemma 7
The function Cspan is polynomial.
Moreover, an FPT-algorithm for Colored (s,t)-Cut is known when parameterized by cspan.
Theorem 3
[4, 23] Colored (s,t)-Cut can be solved in \({\mathcal {O}}(2^{{c_{\text {span}}}}|I|^{\mathcal {O}(1)})\) time and does not admit a polynomial kernel when parameterized by cspan, unless NP \(\subseteq \) coNP/poly.
To show the usefulness of our framework, we prove the first part of Theorem 3 in a new way by applying Lemma 6. Also, in our opinion, the algorithm and its correctness proof is slightly simpler.
Lemma 8
The function Cspan has the strong remove-merge property.
Proof
By Lemma 7, Cspan is polynomial. It remains to show that Cspan has the strong remove-merge property. Let I = (G,C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut, let \(\tilde {C} \subseteq {C_{\text {span}}}(I)\), and let \(I^{\prime }=(G^{\prime },C^{\prime },\ell ^{\prime },[s],[t],k-|C_{r}|):=\text {rmi}(I,C_{r},\tilde {C}\setminus C_{r})\) be the remove-merge-instance obtained from I by removing \(C_{r}\subseteq \tilde {C}\) and merging \(\tilde {C}\setminus C_{r}\). We have to show that α ∈ Cspan(I) for each \(\alpha \in {C_{\text {span}}}(I^{\prime })\). Let \(\alpha \in {C_{\text {span}}}(I^{\prime })\). Hence, the subgraph \(G^{\prime }_{\alpha }\) of \(G^{\prime }\) containing only the edges of color α and their endpoints has at least two connected components C1 and C2. Since no edge of color α was removed to create \(G^{\prime }\) from G, the corresponding subgraph Gα in G containing only the edges of color α and their endpoints has at least two connected components of color α. Hence α ∈ Cspan(I). □
5.3 Number of Path-Frequent Colors
This parameter counts the number of colors occurring on many (s,t)-paths.
Definition 6
Let I = (G = (V,E),C,ℓ,s,t,k) be a Colored (s,t)-Cut instance. A color α ∈ C is called path-frequent if there exist at least three vertex-simple (s,t)-paths such that at least one edge on each path has color α.
By Cpath we denote the function that maps each Colored (s,t)-Cut instance I to the set of path-frequent colors of I. Furthermore, for a fixed instance I, let cpath := |Cpath(I)|. For a fixed color α one can test in polynomial time whether α is path-frequent [23]. If α is not path-frequent, then the (at most two) (s,t)-paths containing edges of color α can be enumerated in polynomial time as well [23]. Furthermore, an instance I of Colored (s,t)-Cut can be solved in polynomial time if Cpath(I) = ∅ [23]. Thus, the following holds.
Lemma 9
The function Cpath is a polynomial color parameterization. Moreover, for every α that is contained in at most two (s,t)-paths we can compute all these (s,t)-paths in polynomial time.
Lemma 10
The function Cpath has the strong remove-merge property.
Proof
Let I = (G,C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut, let \(\tilde {C} \subseteq {C_{\text {span}}}(I)\), and let \(I^{\prime }=(G^{\prime },C^{\prime },\ell ^{\prime },[s],[t],k-|C_{r}|):=\text {rmi}(I,C_{r},\tilde {C}\setminus C_{r})\) be the remove-merge-instance obtained from I by removing \(C_{r}\subseteq \tilde {C}\) and merging \(\tilde {C}\setminus C_{r}\). We show that \({C_{\text {path}}}(I^{\prime })\subseteq {C_{\text {path}}}(I)\). Assume towards a contradiction that there is a color \(\alpha \in {C_{\text {path}}}(I^{\prime })\setminus {C_{\text {path}}}(I)\). Thus, there are three vertex-simple ([s],[t])-paths Pi for i = {1,2,3} in \(G^{\prime }\) such that \(\ell ^{\prime }(E(P_{i}))\subseteq C\setminus \tilde {C}\) and each path contains an edge of color α. By construction of \(G^{\prime }\), we can assume without loss of generality that \(P_{i}=([v_{1}], v_{[v_{1}],[v_{2}]}^{\alpha _{1}}, [v_{2}], {\ldots } , [v_{i_{r}}])\) for some r where s ∈ [v1] and \(t\in [v_{i_{r}}]\). By definition of \(G^{\prime }\), it follows that there exists some \(v_{i}^{j_{\text {in}}}\in [v_{i}]\) and some \(v_{i}^{j_{\text {out}}}\in [v_{i+1}]\) such that \({e_{i}^{j}}:=\{ v_{i}^{j_{\text {in}}}, v_{i}^{j_{\text {out}}}\}\in E\) with \(\ell ({e_{i}^{j}})=\alpha _{i}\) for each j, 1 ≤ j < ir, where \(\alpha _{i}\in C\setminus \tilde {C}\). Furthermore, we set \(v_{i}^{1_{\text {in}}}=s\) and \(v_{i_{r}}^{j_{\text {out}}}=t\), and since \(v_{i}^{j_{\text {in}}}, v_{i}^{j_{\text {out}}}\in [v_{i}]\), we can conclude that there is a path \({P_{i}^{j}}\) from \(v_{i}^{j_{\text {in}}}\) to \(v_{i}^{j_{\text {out}}}\) in G such that \(\ell ({P_{i}^{j}})\subseteq \tilde {C}\setminus C_{r}\). Then \(P^{i}:={P_{i}^{1}}\cdot {P_{i}^{2}}\cdot \ldots \cdot P_{i}^{i_{r}}\) is a vertex-simple (s,t)-path in G such that \(\ell (P^{i})\subseteq C\setminus C_{r}\). Hence, G contains at least three paths from s to t such that at least one edge has color α, a contradiction. □
Lemmas 6, 9, and 10 now give an FPT algorithm which generalizes the known polynomial-time algorithm for instances with Cpath(I) = ∅ [23].
Theorem 4
Colored (s,t)-Cut can be solved in \({\mathcal {O}}(2^{{c_{\text {path}}}}|I^{\mathcal {O}(1)}|)\) time.
5.4 Number of Colors in at Least Three Conflicts
The next parameter concerns colors which occur on vertex-simple (s,t)-paths with many different colors. This parameter has not been considered so far.
Definition 7
Let I = (G = (V,E),C,ℓ,s,t,k) be a Colored (s,t)-Cut instance. Two colors α,β ∈ C form a conflict if there exists an (s,t)-path such that at least one edge on this path has color α and at least one edge has color β.
By Cconf we denote the function that maps an instance I of Colored (s,t)-Cut to the set of colors of I which are in conflict with at least three different colors. Furthermore, for a fixed instance I, let cconf := |Cconf(I)|. We define a conflict graph \(\mathcal {G}(I)\) as follows: For each color α ∈ C add a vertex vα to \(\mathcal {G}(I)\). Furthermore, if two colors α and β form a conflict, add an edge {vα,vβ} to \(\mathcal {G}(I)\). Note that Cconf(I) corresponds to the set of vertices of \(\mathcal {G}(I)\) of degree at least three.
Lemma 11
Let I = (G,C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut and let \(\mathcal {G}(I)\) be the conflict graph of I. If \(\mathcal {G}(I)\) does not contain a triangle, then for each \(S\subseteq C\), S is a colored (s,t)-cut of G if and only if {vα∣α ∈ S} is a vertex cover of \(\mathcal {G}(I)\).
Proof
Suppose that G contains a monochromatic vertex-simple (s,t)-path only of color α. Then α is contained in every (s,t)-cut and by removing all edges of color α from G and reduce k by one, we obtain an equivalent instance of Colored (s,t)-Cut. Consequently, we can assume that G does not contain any monochromatic vertex-simple (s,t)-path.
By construction, for each edge \(\{v_{\alpha }, v_{\beta }\}\in E(\mathcal {G}(I))\), there is a vertex-simple (s,t)-path P in G such that α ∈ ℓ(P) and β ∈ ℓ(P). Since \(\mathcal {G}(I)\) does not contain a triangle, the color set ℓ(P) is exactly {α,β}. Consequently, \(\mathcal {C}(I) = \{\{\alpha ,\beta \} \mid \{v_{\alpha }, v_{\beta }\}\in E(\mathcal {G}(I))\}\). Let S be a color set and let \(S^{\prime }:=\{v_{\alpha }\mid \alpha \in S\}\). If S is a colored (s,t)-cut of G, then for each \(D\in \mathcal {C}(I)\), there is some α ∈ S ∩ D and thus, for each edge \(e\in E(\mathcal {G}(I))\), there is some \(v_{\alpha }\in e\cap S^{\prime }\). Hence, \(S^{\prime }\) is a vertex cover of \(\mathcal {G}(I)\). The converse also holds. □
We will prove Theorem 5 by applying Lemma 6, that is, we show that Cconf is a polynomial color parameterization that has the weak remove-merge property. To this end, we first show an auxiliary lemma we use to prove that the conflicts of a color can be computed in polynomial time. We assume that this lemma is already known but we are not aware of this specific statement.
Lemma 12
Let r be a constant integer and let \(D\subseteq E\) be an edge set of size r, then we can determine in polynomial time if there is a vertex-simple (s,t)-path P on G with \(D\subseteq E(P)\).
Proof
We compute all combinations of orientations \(({v^{1}_{e}}, {v^{2}_{e}}) \in \{(v,w),(w,v)\}\) for every edge e = {v,w}∈ D and all orderings σ of the edges of D in 2r ⋅ r! time. Note that this is polynomial time, since r is a constant.
Next, we check if there is a vertex-simple (s,t)-path P on G in which \(v_{1}^{\sigma (i)}\) occurs before \(v_{2}^{\sigma (i)}\) for all i,1 ≤ i ≤ r, and in which \(v_{1}^{\sigma (j)}\) occurs before \(v_{2}^{\sigma (j+1)}\) for all j,1 ≤ j < r. This can be done by checking if there are pairwise disjoint paths in G − D for all terminal-pairs of \(\{(s, v_{1}^{\sigma (1)}), (v_{2}^{\sigma (r)}, t)\} \cup \{(v_{2}^{\sigma (j)}, v_{1}^{\sigma (j+1)})\mid 1 \leq j < r\}\) in polynomial time each, since r is a constant [15]. We answer yes if and only if for at least one collection of terminal pairs T there are pairwise vertex-disjoint (x,y)-paths for each (x,y) ∈ T.
If there is an (s,t)-path P on G with \(D\subseteq E(P)\), then there is an ordering of the edges of E in which they occur during the traversal of P and there is an orientation for each edge of D in which the endpoints of this edge occurs during the traversal of P. Since we check all combinations of orientations and orderings of D, we find such a path P on G with \(D\subseteq E(P)\) if it exists. □
Corollary 2
Let r be a constant integer and let \(D\subseteq C\) be a color set of size r, then we can determine in polynomial time if there is an (s,t)-path P on G with \(D\subseteq \ell (P)\).
Lemma 13
The function Cconf is a polynomial color parameterization.
Proof
First we show that Cconf(I) can be computed in polynomial time. For a pair of edges e1 and e2 one can decide in polynomial time whether there is a vertex-simple (s,t)-path containing edges e1 and e2 [27]. In other words, by applying this algorithm to each edge with color α and each edge with color β it can be verified in polynomial time whether α and β form a conflict. Hence, Cconf(I) can be computed in polynomial time. Second, we have to show that I can be solved in polynomial time if Cconf(I) = ∅.
We can assume that G contains no monochromatic vertex-simple (s,t)-paths. Let \(\mathcal {G}=\mathcal {G}(I)\) be the conflict graph of I. Since Cconf(I) = ∅, each color forms a conflict with at most two other colors. Hence, \({\Delta }(\mathcal {G})\le 2\). Due to Lemma 11, if \(\mathcal {G}\) does not contain a triangle, we can solve I by finding the minimum size vertex cover in \(\mathcal {G}\). Since \({\Delta }(\mathcal {G})\le 2\), this can then be done in polynomial time.
Hence, in the following we first handle all triangles in \(\mathcal {G}\) to afterwards solve the remaining instance in polynomial time. There are exactly two ways for \(\mathcal {G}\) to contain a triangle \(\{v_{\alpha _{1}}, v_{\alpha _{2}}, v_{\alpha _{3}}\}\): First, because for each size-two subset D of {α1,α2,α3} there is a vertex-simple (s,t)-path in G containing exactly the colors of D. Second, because there is a vertex-simple (s,t)-path with colors α1,α2 and α3. In both cases, each color αi, i ∈{1,2,3}, forms conflicts only with colors αj ∈{α1,α2,α3}∖{αi}. In the first case, at least two colors of {α1,α2,α3} have to be contained in each colored (s,t)-cut S of G. It is sufficient to add colors α1 and α2 to S. In the second case, assume without loss of generality that there is no path P in G with only the colors α1 and α2. Hence, for each path P in G with αi ∈ ℓ(P) we have, ℓ(P) ∈{{α1,α2,α3},{α1,α3},{α2,α3}}. Clearly, at least one of these three colors is contained in each colored (s,t)-cut S. By adding α3 to S we destroy all paths P in G with αi ∈ ℓ(P).
For the remaining graph \(\mathcal {G}\), we find a minimum size vertex cover, which corresponds to a minimum size colored (s,t)-cut in G due to Lemma 11. Since \(\mathcal {G}\) has a maximum degree of two, this can be done in polynomial time. □
Lemma 14
The function Cconf has the strong remove-merge property.
Proof
Let I = (G,C,ℓ,s,t,k) be an instance of Colored (s,t)-Cut, let \(\tilde {C} \subseteq {C_{\text {span}}}(I)\), and let \(I^{\prime }=(G^{\prime },C^{\prime },\ell ^{\prime },[s],[t],k-|C_{r}|):=\text {rmi}(I,C_{r},\tilde {C}\setminus C_{r})\) be the remove-merge-instance obtained from I by removing \(C_{r}\subseteq \tilde {C}\) and merging \(\tilde {C}\setminus C_{r}\). We show that \({C_{\text {conf}}}(I^{\prime })\subseteq {C_{\text {conf}}}(I)\). Assume towards a contradiction that there exists a color \(\alpha \in {C_{\text {conf}}}(I^{\prime })\) such that α∉Cconf(I) and α forms conflicts with colors β1,β2, and β3. Let \(P=([v_{1}], v_{[v_{1}],[v_{2}]}^{\alpha _{1}}, [v_{2}], {\ldots } , [v_{x}])\) for some x ∈ℕ be a vertex-simple (s,t)-path in \(G^{\prime }\) containing at least one edge of color α and at least one edge of color βi for some i ∈{1,2,3}, where s ∈ [v1] and t ∈ [vx]. By definition of \(G^{\prime }\), there exists some \(v_{j}^{\text {in}}\in [v_{j}]\) and some \(v_{j}^{\text {out}}\in [v_{i+1}]\) such that \(e_{j}:=\{ v_{j}^{\text {in}}, v_{j}^{\text {out}}\}\in E\) with ℓ(ej) = αj for each j,1 ≤ j < x, where \(\alpha _{i}\in C\setminus \tilde {C}\). Furthermore, we set \(v_{1}^{\text {in}}=s\) and \(v_{x}^{\text {out}}=t\). Since \(v_{j}^{\text {in}}, v_{j}^{\text {out}}\in [v_{j}]\) we can conclude that there is a path Pj from \(v_{j}^{\text {in}}\) to \(v_{j}^{\text {out}}\) in G such that \(\ell (P_{j})\subseteq \tilde {C}\setminus C_{r}\). Then P∗ := P1 ⋅ P2 ⋅… ⋅ Px is a vertex-simple (s,t)-path in G such that P∗ contains at least one edge of color α and at least one edge of color βi. Hence, color α forms conflicts with each βi, a contradiction. □
Lemmas 6, 13, and 14 now give an FPT-algorithm.
Theorem 5
Colored (s,t)-Cut can be solved in \({\mathcal {O}}(2^{{c_{\text {conf}}}}|I|^{\mathcal {O}(1)})\) time.
5.5 Parameter Intersections
In the following we study Colored (s,t)-Cut parameterized by the pairwise intersection of all three previous color parameterizations: Cspan, Cpath, and Cconf.
Theorem 6
Let I be an instance of Colored (s,t)-Cut and let π and ϕ be color parameterizations with the strong remove-merge property. Then the intersection parameter ρ(I) := π(I) ∩ ϕ(I) also has the strong remove-merge property.
Proof
Let C be the color set of I. Fix a set \(\tilde {C}\subseteq C\), fix a set \(C_{r}\subseteq \tilde {C}\) and let \(I^{\prime }=\text {rmi}(I,C_{r},\tilde {C}\setminus C)\) be the resulting remove-merge-instance. We have to show that \(\rho (I^{\prime })\subseteq \rho (I)\). By definition, \(\rho (I^{\prime })=\pi (I^{\prime })\cap \phi (I^{\prime })\). Since π and ϕ are strong, we have \(\pi (I^{\prime })\subseteq \pi (I)\) and \(\phi (I^{\prime })\subseteq \phi (I)\). Hence, \(\rho (I^{\prime })\subseteq \pi (I)\cap \phi (I)=\rho (I)\). □
Note that ρ can be computed in polynomial time if both π and ϕ can be computed in polynomial time.
First, we consider the intersection of Cpath and Cconf.
Definition 8
Let Cpc(I) := Cpath(I) ∩ Cconf(I) denote the function that maps an instance I of Colored (s,t)-Cut to the set of colors of I which are path-frequent and contained in at least three conflicts. Furthermore, let cpc := |Cpc(I)|.
Theorem 7
Colored (s,t)-Cut can be solved in \({\mathcal {O}}(2^{{c_{\text {pc}}}}|I|^{\mathcal {O}(1)})\) time.
Proof
We will prove this theorem by applying Lemma 6. First, we observe that Cpc has the weak remove-merge property: Since Cpath and Cconf both have the strong remove-merge property, Cpc also has the strong remove-merge property due to Theorem 6.
Second, we show that Cpc is polynomial. Recall that Cpc(I) can be computed in polynomial time since Cpath(I) and Cconf(I) can be computed in polynomial time.
It remains to show that an instance I = (G = (V,E),C,ℓ,s,t,k) can be solved in polynomial time if Cpc(I) = ∅. Recall that \(\mathcal {C}(I):=\{ \ell (P)\mid P\) is a vertex-simple (s,t)-path in G}. Without loss of generality we can assume that each set \(D\in \mathcal {C}(I)\) has size at least 2. The idea of the polynomial-time algorithm is the following: first, we compute \(\mathcal {C}(I)\). Afterwards, we only handle all colors of Cpath(I) separately to obtain an instance, where Cpath(I) = ∅ so that we can apply Lemma 9 and solve the remaining instance in polynomial time.
First, we show that \(\mathcal {C}(I)\) can be computed in polynomial time when Cpc(I) is empty. Let α ∈ C ∖ Cpath(I), then there exist at most two paths containing an edge with color α. Both paths can be computed in polynomial time according to Lemma 9. Let α ∈ C ∖ Cconf(I). In other words, α forms conflicts with at most two other colors β and γ. According to Lemma 13 the colors β and γ can be computed in polynomial time. Hence, \(\mathcal {C}(I)\) contains at most three sets containing α. Each subset \(D\in \mathcal {C}(I)\) containing α can be computed as follows: If color α forms a conflict only with one other color β, then {α,β} is the unique set in \(\mathcal {C}(I)\) containing α. This set can be computed in polynomial time. Assume that color α forms conflicts with colors β and γ. Next, test if \(T:=\{\alpha , \beta _{1}, \beta _{2}\}\in \mathcal {C}(I)\). This can be done in polynomial time due to Lemma 2. If \(T\notin \mathcal {C}(I)\), then \(\{\alpha , \beta _{1}\}, \{\alpha , \beta _{2}\}\in \mathcal {C}(I)\) and there is no other set \(D\in \mathcal {C}(I)\) such that α ∈ D. If \(T\in \mathcal {C}(I)\), then test for each i ∈{1,2} whether s and t are connected in G[ℓ− 1({α,βi})]. If yes, then the set {α,βi} is contained in \(\mathcal {C}(I)\).
From \(\mathcal {C}(I)\), we now construct an instance \(\mathcal {I}:=(\mathcal {G}=(\mathcal {V},\mathcal {E}),C,\ell ^{\prime },s,t,k)\) of Colored (s,t)-Cut as follows: For each \(D\in \mathcal {C}(I)\) create an (s,t)-path P with \(\ell ^{\prime }(P)=D\). Note that S is a colored (s,t)-cut for G if and only if S is a colored (s,t)-cut for \(\mathcal {G}\).
Now, we show that a colored (s,t)-cut S with |S|≤ k can be computed in polynomial time for \(\mathcal {I}\). Let \(\alpha \in {C_{\text {path}}}(\mathcal {I})\). Hence, \(\alpha \in C\setminus {C_{\text {conf}}}(\mathcal {I})\) and \(\mathcal {C}(I)\) contains exactly three sets T1 = {α,β1,β2},T2 = {α,β1}, and T3 = {α,β2} containing color α. Note that if there is a fourth set \(D\in \mathcal {C}(I)\) such that βj ∈ D and D ∖ T1≠∅ for some j ∈{1,2}, then βj ∈ Cpath(I) ∩ Cconf(I), that is, βj is in at least four paths in G and βj forms conflicts with at least three different colors. This contradicts the assumption Cpc = ∅. Hence, such a set \(D\in \mathcal {C}(I)\) does not exist. In other words, there is no color γ such that γ forms a conflict with βj for j ∈{1,2}. The only possible further set in \(\mathcal {C}(I)\) containing β1 or β2 can be T4 := {β1,β2}. First, assume \(T_{4}\in \mathcal {C}(I)\). Then each colored (s,t)-cut S of G contains at least two of α,β1, and β2. Without loss of generality, add α and β1 to S. Second, if \(T_{4}\notin \mathcal {C}(I)\), adding α to S covers each Ti for i ∈{1,2,3}.
After adding all colors described above to our solution, for each color α we have α∉Cpath(I) and we can apply Lemma 9. Hence, if Cpc(I) = ∅, I can be solved in polynomial time. □
The two further interesting intersection parameterizations are Cps(I) := Cpath(I) ∩ Cspan(I) and Csc(I) := Cspan(I) ∩ Cconf(I). We show that Colored (s,t)-Cut is NP-hard even on instances where Cps(I) = Csc(I) = ∅. Consequently, Colored (s,t)-Cut parameterized by either of them does not admit an FPT-algorithm, unless P = NP.
Proposition 6
Colored (s,t)-Cut is NP-hard even for instances I where
-
Cps(I) = ∅,
-
Csc(I) = ∅,
-
every color occurs in at most three (s,t)-paths,
-
every color forms a conflict with at most three different colors, and
-
every color induces at most two connected components.
Note that the latter three restrictions show how tight this result is, since for example Colored (s,t)-Cut can be solved in polynomial time if every color occurs in at most two (s,t)-paths or induces only one connected component. We would like to emphasize that the NP-hardness if every color occurs in at most three (s,t)-paths, every color forms conflicts with at most three different colors, and every color has span at most two was already shown [3].
Proof
We reduce from Vertex Cover which is known to be NP-hard even on graphs with maximum degree 3 where the set of vertices with degree exactly 3 is an independent set [23]. Let I = (G = (V,E),k) be an instance of Vertex Cover with the described restriction. We describe how to construct an instance \(I^{\prime }=(G^{\prime }=(V^{\prime },E^{\prime }), s, t, C, \ell , k^{\prime })\) of Colored (s,t)-Cut in polynomial time such that \({C_{\text {ps}}}(I^{\prime })= {C_{\text {sc}}}(I^{\prime })= \emptyset \) and I is a yes-instance of Vertex Cover if and only if \(I^{\prime }\) is a yes-instance of Colored (s,t)-Cut.
We set C := V, \(k^{\prime } := k\) and start with an edgeless graph only containing the vertices s and t. For every edge e := {u,w}∈ E we add a vertex ve and edges {s,ve} and {ve,t} to \(G^{\prime }\). Without loss of generality assume that \(\deg (u) \geq \deg (w)\). We set ℓ({s,ve}) = u and ℓ({ve,t}) = w.
Since this is a special case of the standard reduction from Hitting Set to Colored (s,t)-Cut, it follows directly that I is a yes-instance of Vertex Cover if and only if \(I^{\prime }\) is a yes-instance of Colored (s,t)-Cut.
Finally, we show that the obtained instance of Colored (s,t)-Cut has the described restrictions, that is, we show that \({C_{\text {ps}}}(I^{\prime })= {C_{\text {sc}}}(I^{\prime })= \emptyset \). To this end, we show that no color v ∈ V = C with \(\deg (v) < 3\) is contained in Cpath ∪ Cconf and that no color v ∈ V = C with \(\deg (v) = 3\) is contained in Cspan. By construction, every (s,t)-path has length 2, every edge in \(G^{\prime }\) is incident with either s or t, and every color v ∈ V = C appears on exactly \(\deg _{G}(v)\) many (s,t)-paths in \(G^{\prime }\). Therefore, for all v ∈ V with \(\deg (v)< 3\) it follows that \(v \not \in {C_{\text {path}}}(I^{\prime }) \supseteq {C_{\text {ps}}}(I^{\prime })\) and \(v \not \in {C_{\text {conf}}}(I^{\prime })\supseteq {C_{\text {sc}}}(I^{\prime })\). It remains to show that \(v \not \in {C_{\text {span}}}(I^{\prime })\) for all v ∈ V with \(\deg (v) = 3\). By construction and the fact that there is no edge {v,w}∈ E with \(\deg (w)=3\), all edges colored in v are incident to s. Hence, for each v ∈ V with \(\deg (v)=3\), the color v has span one in G. Hence, \(v \not \in {C_{\text {span}}}(I^{\prime })\). We conclude that \({C_{\text {ps}}}(I^{\prime }) = {C_{\text {sc}}}(I^{\prime }) = \emptyset \). □
6 Conclusion
We have provided new FPT-algorithms and parameterized hardness results for Colored (s,t)-Cut. Our results lead to several directions for future research.
First, it would be interesting to obtain better kernelization results. For example, does Colored (s,t)-Cut admit a kernel for the parameter m>q, the number of edges that are not colored with the q most frequent colors, when q is not constant but bounded by \(\log (|I|)\)? In this context, we would like to remark that in companion work, we showed that Colored (s,t)-Cut admits a polynomial kernel when parameterized by the budget parameter k plus the size of a vertex set whose deletion destroys all long paths in G [18]. Are there other combinations of the budget k or color parameterizations with structural graph parameters that yield polynomial kernels?
Second, can one compute \(\mathcal {C}({\mathscr{H}})\), the collection of color sets of (s,t)-paths, in \(|\mathcal {C}({\mathscr{H}})|^{{\mathcal {O}}(1)}\cdot |I|^{{\mathcal {O}}(1)}\) time. This would directly imply an FPT-algorithm for Colored (s,t)-Cut when parameterized by \(|\mathcal {C}({\mathscr{H}})|\). To obtain such an FPT-algorithm it would also suffice to compute \(\mathcal {C}({\mathscr{H}})\) in time \(f(|\mathcal {C}({\mathscr{H}})|)\cdot |I|^{{\mathcal {O}}(1)}\).
Third, for which further color parameterizations does Colored (s,t)-Cut admit FPT-algorithms? In particular, it would be interesting to see FPT-algorithms for color parameterizations that do not fit into our framework employing remove-merge instances. A general approach to identify new color parameterizations could be to investigate the structure of the color conflict graph as defined in Section 5.4 more thoroughly.
Moreover, it is open to study color parameterizations for related problems such as Labeled Path [10] (where we aim to construct an (s,t)-path with a minimum number of colors) and competitive variants of Colored (s,t)-Cut, where an attacker aims to construct a colored cut and a defender aims to prevent this [18].
Finally, from a more practical point of view, a study of the structural features of real-world instances of Colored (s,t)-Cut and related problems would be interesting in order to guide the search for practically relevant parameterizations of these problems.
References
Birmelé, E., Ferreira, R.A., Grossi, R., Marino, A., Pisanti, N., Rizzi, R., Sacomoto, G.: Optimal listing of cycles and st-paths in undirected graphs. In: Proceedings of the 24th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA ’13), pp. 1884–1896. SIAM (2013)
Bordini, A., Protti, F., da Silva, T.G., de Sousa Filho, G.F.: New algorithms for the minimum coloring cut problem. Int. Trans. Oper. Res. 26(5), 1868–1883 (2019)
Coudert, D., Datta, P., Perennes, S., Rivano, H., Voge, M.: Shared risk resource group complexity and approximability issues. Parallel Processing Letters 17(2), 169–184 (2007)
Coudert, D., Pérennes, S., Rivano, H., Voge, M.: Combinatorial optimization in networks with shared risk link groups. Discrete Mathematics & Theoretical Computer Science 18(3) (2016)
Cygan, M., Dell, H., Lokshtanov, D., Marx, D., Nederlof, J., Okamoto, Y., Paturi, R., Saurabh, S., Wahlström, M.: On problems as hard as CNF-SAT. ACM Trans. Algor. 12(3), 41,1–41,24 (2016)
Cygan, M., Fomin, F.V., Kowalik, L., Lokshtanov, D., Marx, D., Pilipczuk, M., Pilipczuk, M., Saurabh, S.: Parameterized Algorithms. Springer (2015)
Dom, M., Lokshtanov, D., Saurabh, S.: Kernelization lower bounds through colors and IDs. ACM Trans. Algor. 11(2), 13,1–13,20 (2014)
Downey, R.G., Fellows, M.R.: Fundamentals of Parameterized Complexity Texts in Computer Science. Springer (2013)
Faragó, A.: A graph theoretic model for complex network failure scenarios. In: Proceedings of the 8th INFORMS Telecommunications Conference (INFORMS ’08) (2006)
Fellows, M.R., Guo, J., Kanj, I.A.: The parameterized complexity of some minimum label problems. J. Comput. Syst. Sci. 76(8), 727–740 (2010)
Flum, J., Grohe, M.: Parameterized Complexity Theory. Texts in Theoretical Computer Science An EATCS Series. Springer (2006)
Fomin, F.V., Kratsch, D., Woeginger, G.J.: Exact (exponential) algorithms for the dominating set problem. In: Proceedings of the 30th International Workshop on Graph-Theoretic Concepts in Computer Science (WG ’04), volume 3353 of Lecture Notes in Computer Science, pp. 245–256. Springer (2004)
Impagliazzo, R., Paturi, R., Zane, F.: Which problems have strongly exponential complexity? J. Comput. Syst. Sci. 63(4), 512–530 (2001)
Jha, S., Sheyner, O., Wing, J.: Two formal analyses of attack graphs. In: Proceedings ot the 15th IEEE Computer Security Foundations Workshop (CSWF ’02), pp. 49–63. IEEE (2002)
Kawarabayashi, K., Kobayashi, Y., Reed, B.A.: The disjoint paths problem in quadratic time. J. Comb. Theory. Series B 102(2), 424–435 (2012)
Klein, S., Faria, L., Sau, I., Sucupira, R., Souza, U.: On colored edge cuts in graphs. In: Proceedings of the 1st Encontro de Teoria da Computaċao (ETC ’16), Sociedade Brasileira de Computaçao, pp. 780–783. CSBC (2016)
Morawietz, N.: Computational Complexity of Network Robustness in Edge-colored Graphs. Master’s thesis, Philipps-Universität Marburg (2019)
Morawietz, N., Grüttemeier, N., Komusiewicz, C., Sommer, F.: Colored cut games. In: Proceedings of the 40th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS ’20), volume 182 of LIPIcs, pp. 30:1–30:17. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020)
Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Oxford University Press (2006)
Pióro, M., Medhi, D.: Routing, Flow, and Capacity Design in Communication and Computer Networks. Morgan Kaufmann (2004)
Rohloff, K., Khuller, S., Kortsarz, G.: Approximating the minimal sensor selection for supervisory control. Discret. Event Dyn. Syst. 16 (1), 143–170 (2006)
Sheyner, O., Haines, J.W., Jha, S., Lippmann, R., Wing, J.M.: Automated generation and analysis of attack graphs. In: Proceedings ot the 23rd Symposium on Security and Privacy (IEEE ’02), pp. 273–284. IEEE Computer Society (2002)
Sucupira, R.A.: Problemas de cortes de arestas maximos e mínimos em grafos. Universidade Federal do Rio de Janeiro, PhD thesis (2017)
Wang, Y., Desmedt, Y.: Edge-colored graphs with applications to homogeneous faults. Inf. Process. Lett. 111(13), 634–641 (2011)
Zhang, P.: Approximating the weighted minimum label s-t cut problem. arXiv:2011.06204 (2020)
Zhang, P., Cai, J., Tang, L., Zhao, W.: Approximation and hardness results for label cut and related problems. J. Comb. Optim. 21(2), 192–208 (2011)
Zhang, P., Fu, B.: The label cut problem with respect to path length and label frequency. Theor. Comput. Sci. 648, 72–83 (2016)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Some of the results of this work are also contained in the first author’s Master thesis [17].
An extended abstract of this work appeared in the proceedings of the 46th International Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM ’20) held in Limassol, Cyprus.
Nils Morawietz is supported by the Deutsche Forschungsgemeinschaft (DFG), project OPERAH, KO 3669/5-1.
Frank Sommer is supported by the Deutsche Forschungsgemeinschaft (DFG), project EAGR, KO 3669/6-1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morawietz, N., Grüttemeier, N., Komusiewicz, C. et al. Refined Parameterizations for Computing Colored Cuts in Edge-Colored Graphs. Theory Comput Syst 66, 1019–1045 (2022). https://doi.org/10.1007/s00224-022-10101-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-022-10101-z




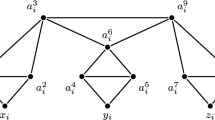



 k = 3, and
k = 3, and 
