Non-Existence of Stable Social Groups in Information-Driven Networks

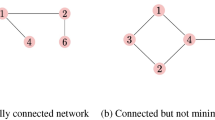
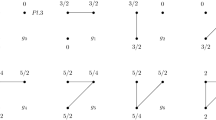
Abstract

We study a group-formation game on an undirected complete graph G with all edge-weights in a set $\mathcal { W} \subseteq \mathbb {R} \cup \{-\infty \}$. This work is motivated by a recent information-sharing model for social networks (Kleinberg and Ligett, Games Econ. Behav. 82, 702–716 2013). Specifically, we consider partitions of the vertex-set of G into groups. The individual utility of any vertex v is the sum of the weights on the edges uv between v and the other vertices u in her group. – Informally, u and v represent social users, and the weight of uv quantifies the extent to which u and v (dis)agree on some fixed topic. – For a fixed integer k ≥ 1, a k-stable partition is a partition in which no coalition of at most k vertices would increase their respective utilities by leaving their groups to join or create another common group. Before our work, it was known that such a partition always exists if k = 1 (Burani and Zwicker, Math. Soc. Sci. 45(1), 27–52 2003). We focus on the regime k ≥ 2.

• Our first result is that when all the social users are either friends, enemies or indifferent to each other (i.e., $\mathcal {W} = \{-\infty ,0,1\}$), a partition as above always exists if k ≤ 2, but it may not exist if k ≥ 3. This is in sharp contrast with (Kleinberg and Ligett, Games Econ. Behav. 82, 702–716 2013) who proved that k-stable partitions always exist, for any k, if $\mathcal {W} = \{-\infty ,1\}$.

• We further study the intriguing relationship between the existence of k-stable partitions and the allowed set of edge-weights $\mathcal {W}$. Specifically, we give sufficient conditions for the existence or the non existence of such partitions based on tools from Graph Theory. Doing so, we obtain for most sets $\mathcal {W}$ the largest $k(\mathcal {W})$ such that all graphs with edge-weights in $\mathcal {W}$ admit a $k(\mathcal {W})$-stable partition.

• From the computational point of view, we prove that for any $\mathcal {W}$ containing $-\infty$, the problem of deciding whether a k-stable partition exists is NP-complete for any $k > k(\mathcal {W})$.

Our work hints that the emergence of stable communities in a social network requires a trade-off between the level of collusion between social users, and the diversity of their opinions.