Abstract
We consider the cons-free programming language of Neil Jones, a simple pure functional language, which decides exactly the polynomial-time relations and whose tail recursive fragment decides exactly the logarithmic-space relations. We exhibit a close relationship between the running time of cons-free programs and the running time of logspace-bounded auxiliary pushdown automata. As a consequence, we characterize intermediate classes like NC in terms of resource-bounded cons-free computation. In so doing, we provide the first “machine-free” characterizations of certain complexity classes, like P-uniform NC. Furthermore, we show strong polynomial lower bounds on cons-free running time. Namely, for every polynomial p, we exhibit a relation R ∈Ptime such that any cons-free program deciding R must take time at least p almost everywhere. Our methods use a “subrecursive version” of Blum complexity theory, and raise the possibility of further applications of this technology to the study of the fine structure of Ptime.





Similar content being viewed by others
References
Allender, E.W.: P-uniform circuit complexity. J. ACM 36(4), 912–928 (1989)
Alton, D.A.: “Natural” Programming Languages and Complexity Measures for Subrecursive Programming Languages: An Abstract Approach, pp. 248–285. London Mathematical Society Lecture Note Series. Cambridge University Press (1980)
Arora, S., Barak, B.: Computational Complexity: A Modern Approach. Cambridge University Press (2009)
Blum, M.: A machine-independent theory of the complexity of recursive functions. J. ACM 14(2), 322–336 (1967)
Bonfante, G., Kahle, R., Marion, J.Y., Oitavem, I.: Towards an implicit characterization of NCk. In: Ésik, Z. (ed.) Computer Science Logic, pp 212–224. Springer, Berlin (2006)
Chandra, A.K., Kozen, D.C., Stockmeyer, L.J.: Alternation. J. ACM 28(1), 114–133 (1981)
Ibarra, O.H.: On two-way multihead automata. J. Comput. Syst. Sci. 7(1), 28–36 (1973)
Jones, N.D.: Computability and Complexity. From a Programming Perspective. MIT Press, London (1997)
Jones, N.D.: LOGSPACE and PTIME characterized by programming languages. Theor. Comput. Sci. 228(1), 151–174 (1999)
Jones, N.D.: The expressive power of higher-order types or, life without CONS. J. Funct. Program. 11(1), 55–94 (2001)
Kop, C., Simonsen, J.G.: The power of non-determinism in higher-order implicit complexity: characterising complexity classes using non-deterministic cons-free programming. In: Yang, H. (ed.) Programming Languages and Systems, Lecture notes in computer science, pp 668–695. Springer, Berlin (2017)
Moschovakis, Y.N.: Abstract Recursion and Intrinsic Complexity. Lecture Notes in Logic. Cambridge University Press (2018)
Niggl, K.-H., Wunderlich, H.: Implicit characterizations of FPTIME and NC revisited. J. Logic Algebraic Program 79(1), 47–60 (2010). Special Issue: Logic, Computability and Topology in Computer Science: A New Perspective for Old Disciplines
Rabin, M.O.: Degree of difficulty of computing a function and a partial ordering of recursive sets. Technical Report 2, Hebrew University (1960)
Ruzzo, W.L.: Tree-size bounded alternation. J. Comput. Syst. Sci. 21(2), 218–235 (1980)
Ruzzo, W.L.: On uniform circuit complexity. J. Comput. Syst. Sci. 22(3), 365–383 (1981)
Sipser, M.: Introduction to the Theory of Computation. Thomson Course Technology (2006)
Sudborough, I.H.: Time and tape bounded auxiliary pushdown automata. In: Gruska, J. (ed.) Mathematical Foundations of Computer Science 1977, pp 493–503. Springer, Berlin (1977)
Tserunyan, A.: (1) Finite generators for countable group actions; (2) Finite index pairs of equivalence relations; (3) Complexity measures for recursive programs. PhD thesis, University of California, Los Angeles (2013)
Venkateswaran, H.: Properties that characterize logcfl. J. Comput. Syst. Sci. 43(2), 380–404 (1991)
Acknowledgements
We are greatly indebted to Amir ben-Amram, Neil Jones, Pekka Orponen, W. Larry Ruzzo, and Eric Allender for answering many questions and freely sharing their wisdom with us.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Commemorative Issue for Alan L. Selman
Guest Editors: Mitsunori Ogihara, Elvira Mayordomo, Atri Rudra
Appendices
Appendix A:: Equivalence of two semantics
Following is the proof of Theorem 1, showing that the big-step semantics and one-stack operational semantics are extensionally equivalent, and their natural associated measures of time complexity are equivalent up to a constant factor depending only on the program.
Proof
For an environment ρ binding the free variables of T, let Tρ denote the variable-free term obtained by substituting each variable by its ρ-image.
First we show that if there is a derivation of ρ ⊩T →v of size s, there is a computation  of length at most (N + 2)s, where N is the maximum length of any tuple in . We proceed by induction on s.
of length at most (N + 2)s, where N is the maximum length of any tuple in . We proceed by induction on s.
If s = 1, then T is either one of the constants , , or , or a variable . If T ≡, then  is our desired computation; similarly for the other constants. If T is a variable then
is our desired computation; similarly for the other constants. If T is a variable then  is identical to
is identical to  ; our desired computation is simply the trivial computation
; our desired computation is simply the trivial computation  of length 1.
of length 1.
If s > 1 then we break up into cases depending on the form of T.
-
If T ≡ T0 T1 T2 and ρ ⊩T0 → 1, then there are some s0 and s1 such that there is a derivation of ρ ⊩T0 → 1 of size s0, of ρ ⊩T1 →v of size s1, and s = s0 + s1 + 1. By induction there are computations
 and
and  of lengths at most (N + 2)s0 and (N + 2)s1 respectively. The following computation has length at most (N + 2)s0 + (N + 2)s1 + 1 < (N + 2)s.
of lengths at most (N + 2)s0 and (N + 2)s1 respectively. The following computation has length at most (N + 2)s0 + (N + 2)s1 + 1 < (N + 2)s.

The case ρ ⊩T0 → 0 is similar, replacing T1 by T2.
-
If \(T \equiv \varphi (T_{0},\dots ,T_{n-1})\), then by induction there are si, vi for i < n such that \(1 + {\sum }_{i<n} s_{i} = s\), there is a derivation ρ ⊩Ti →vi of size si, and \(\varphi (v_{0},\dots ,v_{n-1}) = v\). The following is a computation
 . It can be broken up into n blocks, block i having length at most (N + 2)si + 1, plus two more configurations. The total length is thus
$$ 2 + \sum\limits_{i < n}((N+2)s_{i} + 1) \le (N+2)\left( 1 + \sum\limits_{i<n} s_{i} \right) \le 2s. $$
. It can be broken up into n blocks, block i having length at most (N + 2)si + 1, plus two more configurations. The total length is thus
$$ 2 + \sum\limits_{i < n}((N+2)s_{i} + 1) \le (N+2)\left( 1 + \sum\limits_{i<n} s_{i} \right) \le 2s. $$
-
The case \(T \equiv (T_{0},\dots ,T_{n-1})\) is similar, except that there is no symbol φ, and the last box
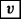 is absent from the computation, hence its length is even smaller.
is absent from the computation, hence its length is even smaller. -
If \(T \equiv \mathtt {f}(T_{0},\dots ,T_{n-1})\), then by induction, there are si for i ≤n and vi for i < n such that \(1 + {\sum }_{i \le n} s_{i} = s\), for each i < n there is a derivation ρ ⊩Ti →vi of size at most si, and there is a derivation \([\mathtt {x} = (v_{0},\dots ,v_{n-1})] \vdash T^{\mathtt {f}} \to v\) of size at most sn. The following is a computation
 of length at most
$$ \sum\limits_{i \le n}((N+2)s_{i} + 1) \!\le\! (N+2)\left( \sum\limits_{i \le n} s_{i} \right) + N + 1 \!\le\! (N+2)\left( 1 + \sum\limits_{i \le n}s_{i}\right) = (N+2)s $$
of length at most
$$ \sum\limits_{i \le n}((N+2)s_{i} + 1) \!\le\! (N+2)\left( \sum\limits_{i \le n} s_{i} \right) + N + 1 \!\le\! (N+2)\left( 1 + \sum\limits_{i \le n}s_{i}\right) = (N+2)s $$
In the other direction, we show that for any environment ρ binding the free variables of T, if there is a computation  of length at most ℓ, then there is a derivation of ρ ⊩T →v of size at most ℓ. The proof is again by induction by ℓ.
of length at most ℓ, then there is a derivation of ρ ⊩T →v of size at most ℓ. The proof is again by induction by ℓ.
If ℓ = 1 or ℓ = 2, then by inspecting the rules of Definition 8, we can see that the only possibities for T are a variable such that ρ() = v, or a constant: 1, 0, or . In any of these cases, there is a derivation of ρ ⊩T →v of size 1.
Suppose that ℓ > 2. Then we break into cases depending on the form of T.
-
If T ≡ T0 T1 T2, there is some configuration
 for some b ∈{1, 0} within
for some b ∈{1, 0} within 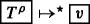 , otherwise there would be no way to “eliminate”
, otherwise there would be no way to “eliminate”  . Therefore, this computation must have the following form (if b = 1, the case b = 0 is similar):
. Therefore, this computation must have the following form (if b = 1, the case b = 0 is similar):

Therefore, there are some ℓ0 and ℓ1 such that ℓ0 + ℓ1 + 1 = ℓ and there computations
 and
and  of lengths ℓ0 and ℓ1 respectively. By induction, there are derivations of ρ ⊩T0 → 1 and ρ ⊩T1 →v of sizes at most ℓ0 and ℓ1 respectively; hence, there is a derivation of ρ ⊩T →v of size at most ℓ0 + ℓ1 + 1 = ℓ.
of lengths ℓ0 and ℓ1 respectively. By induction, there are derivations of ρ ⊩T0 → 1 and ρ ⊩T1 →v of sizes at most ℓ0 and ℓ1 respectively; hence, there is a derivation of ρ ⊩T →v of size at most ℓ0 + ℓ1 + 1 = ℓ. -
If \(T \equiv \varphi (T_{0},\dots ,T_{n-1})\) then the computation
 has the following form:
has the following form:

Therefore, there are some vi and ℓi for i < n such that ℓi is the length of the computation
 and \(2 + {\sum }_{i<n}(1 + \ell _{i}) = \ell \). By induction, there are derivations of ρ ⊩Ti →vi of size at most ℓi, for each i < n. Therefore, there is a derivation of ρ ⊩T →v of size \({\sum }_{i < n} \ell _{i} + 1 < \ell \).
and \(2 + {\sum }_{i<n}(1 + \ell _{i}) = \ell \). By induction, there are derivations of ρ ⊩Ti →vi of size at most ℓi, for each i < n. Therefore, there is a derivation of ρ ⊩T →v of size \({\sum }_{i < n} \ell _{i} + 1 < \ell \). -
If \(T \equiv (T_{0},\dots ,T_{n-1})\), the argument is the similar to the above, except the symbol φ is absent, the final two configurations are identical, and \(\ell = 1 + {\sum }_{i < n}(1 + \ell _{i})\).
-
If \(T \equiv \mathtt {f}(T_{0},\dots ,T_{n-1})\), then the computation
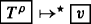 has the following form:
has the following form:

Therefore there are vi for i < n and ℓi for i ≤n such that the computation
 has length ℓi for i < n, the computation
has length ℓi for i < n, the computation  has length ℓn, and \(\ell = {\sum }_{i \le n}(1 + \ell _{i})\). By induction there are derivations of ρ ⊩Ti →vi of length ℓi for i < n and a derivation of [ = (vi)i<n] ⊩T→v of length ℓn. Hence there is a derivation of ρ ⊩T →v of length \(1 + {\sum }_{i\le n} \ell _{i} \le \ell \).
has length ℓn, and \(\ell = {\sum }_{i \le n}(1 + \ell _{i})\). By induction there are derivations of ρ ⊩Ti →vi of length ℓi for i < n and a derivation of [ = (vi)i<n] ⊩T→v of length ℓn. Hence there is a derivation of ρ ⊩T →v of length \(1 + {\sum }_{i\le n} \ell _{i} \le \ell \).
□
Appendix B:: Encodings of programs
Here, we sketch an encoding of cons-free programs as used in Section 6 in a little more detail.
Given any set of atoms A, the set of nested lists over A is the closure of A over the listing operator. Concretely, every element of A is a nested list over A, and given any finite set \(\{\ell _{0},\dots ,\ell _{n-1}\}\) of nested lists over A, the list \(\langle \ell _{0},\dots ,\ell _{n-1}\rangle \) is a nested list over A.
Suppose A is countable, and fix an arbitrary encoding of A by binary strings. Then it is a standard construction to encode nested lists over A by binary strings such that the list primitives are polynomial time computable, see, e.g., [8]. Briefly, one starts by constructing a polynomial-time pairing system on binary strings. This means a polynomial-time computable bijection 2⋆ × 2⋆ → 2⋆ with polynomial-time inverse functions isolating the first and second coordinates from a given pair.
Then one extends this pairing system to a polynomial-time tupling system. These allow us to check whether a string encodes a list, extract the length of the list, extract its first character, remove the first character, and add a character to the front of the list, all in polynomial time. By constructing lists out of strings which encode lists, we encode nested lists over A.
Notice that the set of program terms can be identified with the set of nested lists over some set A of atoms that consists of variables, recursive and primitive function symbols, and program keywords. A program can then be encoded by a list of such terms (the right and left halves of each line of the program).
By including the type of each variable and recursive function symbol as part of its encoding, we can easily check whether a given string encodes a well-formed term by simple recursion over the structure of the list, a polynomial-time operation. We can check whether a a given term contains or does not contain a given variable. Using these two operations, we can check whether a string encodes a well-formed program, all in polynomial time.
We can index occurrences term in a program according to (i) which line of the program they are located in, (ii) on the right- or left-hand side of the definition, and (iii) the sequence of list primitives needed to obtain this occurrence from the term it occurs in. (Nested lists can be identified with trees, and what this basically means is that we index vertices in the tree according to the path needed to get there from the root.)
We can obtain the encoding of the term named by a given index in time polynomial in the length of the program encoding, simply by extracting the correct term from the string encoding the program and applying the list primitives specified by the root-to-vertex path. Then, we can obtain indexings for the sub-occurrences of the original occurrence by taking the encoding of the resulting term, extracting its length, and extending the original root-to-vertex path by all of its one-point extensions.
This establishes the properties needed by Lemma 8 of Section 6.
Rights and permissions
About this article
Cite this article
Bhaskar, S., Kop, C. & Simonsen, J.G. Subclasses of Ptime Interpreted by Programming Languages. Theory Comput Syst 67, 437–472 (2023). https://doi.org/10.1007/s00224-022-10074-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-022-10074-z




 and
and  of lengths at most (N + 2)s0 and (N + 2)s1 respectively. The following computation has length at most (N + 2)s0 + (N + 2)s1 + 1 < (N + 2)s.
of lengths at most (N + 2)s0 and (N + 2)s1 respectively. The following computation has length at most (N + 2)s0 + (N + 2)s1 + 1 < (N + 2)s.

 . It can be broken up into n blocks, block i having length at most (N + 2)si + 1, plus two more configurations. The total length is thus
. It can be broken up into n blocks, block i having length at most (N + 2)si + 1, plus two more configurations. The total length is thus

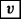 is absent from the computation, hence its length is even smaller.
is absent from the computation, hence its length is even smaller. of length at most
of length at most

 for some b ∈{1, 0} within
for some b ∈{1, 0} within 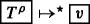 , otherwise there would be no way to “eliminate”
, otherwise there would be no way to “eliminate”  . Therefore, this computation must have the following form (if b = 1, the case b = 0 is similar):
. Therefore, this computation must have the following form (if b = 1, the case b = 0 is similar):

 and
and  of lengths ℓ0 and ℓ1 respectively. By induction, there are derivations of ρ ⊩T0 → 1 and ρ ⊩T1 →v of sizes at most ℓ0 and ℓ1 respectively; hence, there is a derivation of ρ ⊩T →v of size at most ℓ0 + ℓ1 + 1 = ℓ.
of lengths ℓ0 and ℓ1 respectively. By induction, there are derivations of ρ ⊩T0 → 1 and ρ ⊩T1 →v of sizes at most ℓ0 and ℓ1 respectively; hence, there is a derivation of ρ ⊩T →v of size at most ℓ0 + ℓ1 + 1 = ℓ. has the following form:
has the following form:

 and
and 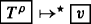 has the following form:
has the following form:

 has length ℓi for i < n, the computation
has length ℓi for i < n, the computation  has length ℓn, and
has length ℓn, and