Partition Into Triangles on Bounded Degree Graphs

Abstract

We consider the Partition Into Triangles problem on bounded degree graphs. We show that this problem is polynomial-time solvable on graphs of maximum degree three by giving a linear-time algorithm. We also show that this problem becomes $\mathcal{NP}$-complete on graphs of maximum degree four. Moreover, we show that there is no subexponential-time algorithm for this problem on graphs of maximum degree four unless the Exponential-Time Hypothesis fails. However, the Partition Into Triangles problem on graphs of maximum degree at most four is in many cases practically solvable as we give an algorithm for this problem that runs in $\mathcal{O}(1.02220^{n})$ time and linear space.

1 Introduction

In his weblog of February 2009 [17], Richard J. Lipton quotes Alan J. Perlis, the first Turing Award winner:

“For every polynomial-time algorithm you have, there is an exponential algorithm that I would rather run.”

Richard J. Lipton illustrates this quote beautifully: “His point is simple: if your algorithm runs in n ⁴ time, then an algorithm that runs in n2^n/10 time (alternatively denoted as n1.07178ⁿ time) is faster if for example n=100.” Note that this observation even holds for all n≤236.

Woeginger made the same observation for $\mathcal{NP}$-hard problems instead of polynomial time solvable problems in his well-known survey on exact exponential-time algorithms [24]. Woeginger considers the fact that algorithms for $\mathcal{NP}$-hard problems with exponential running times may actually lead to practical algorithms: he compares the running times of $\mathcal{O}(n^{4})$ with $\mathcal{O}(1.01^{n})$.

Even so, we are not aware of any results on natural $\mathcal{NP}$-hard problems with exponential-time algorithms with running times anywhere near $\mathcal{O} (1.01^{n})$ without involving huge polynomial factors (either visible, or hidden in the notation, or hidden in the decimal rounding of the exponent in the big-$\mathcal{O}$). ‘Very fast’ exponential-time algorithms exist for problems such as Independent Set restricted to graphs in which 99 % of the vertices have degree at most two. However, we do not consider this to be a natural problem because one can reduce an instance of this artificial problem in polynomial time to an equivalent instance of Independent Set in which only 1 % of the vertices remain (this can be done by vertex folding, e.g., see [1, 5]). Then, the trivial brute-force $\mathcal{O}(n2^{n})$ algorithm for Independent Set gives an algorithm for this artificial problem running in $\mathcal{O}(n2^{n/100}) = \mathcal{O}(1.0070^{n})$ time. We note that for the problem studied in this paper, no polynomial-time transformation from the problem on graphs of maximum degree four to the problem on general graphs that greatly reduces the instance size is known (and most likely no such transformation is possible).

This paper, we will present such a very fast exponential-time algorithm for the Partition Into Triangles problem restricted to graphs of maximum degree four. In the main body of the paper, we will given an algorithm running in $\mathcal{O}(1.02445^{n})$ or $\mathcal{O}(2^{n/28.69})$ time. This result is further improved to $\mathcal{O}(1.02220^{n})$ or $\mathcal{O} (2^{n/31.58})$ time by a further case analysis in the Appendix. These algorithms could solve reasonable size instance as their running times do not include any large factors hidden in the $\mathcal{O}$-notation. Both algorithms use an interesting and powerful relation between Partition Into Triangles on graphs of maximum degree four and the Exact 3-Satisfiability problem. We will use this relation not only to give fast exponential-time algorithms, but also to prove that, assuming the Exponential-Time Hypothesis [11, 12], no subexponential-time algorithms for this problem exist. We note that we find it interesting that the same reduction is used for both the hardness result and the faster algorithms.

This paper is organised as follows. We first introduce the Partition Into Triangles and Exact 3-Satisfiability problems and survey known results in Sect. 2. Then, we give a linear-time algorithm for Partition Into Triangles on graphs of maximum degree three in Sect. 3. Thereafter, we focus on the relation between Partition Into Triangles on graphs of maximum degree four to and Exact 3-Satisfiability in Sect. 4. We use this relation to prove our hardness results in Sect. 5 and to give a simple $\mathcal{O}(1.02445^{n})$-time algorithm for Partition Into Triangles in Sect. 6. In the Appendix, one can find the slightly faster $\mathcal{O} (1.02220^{n})$-time algorithm.

2 Definitions and Notation

Let G=(V,E) be a simple n-vertex graph. The degree of a vertex v∈V is its number of neighbours in G: d(v)=|{u∈V|(u,v)∈E}|. A r-regular graph is a graph in which all vertices have degree r; a cubic graph is a 3-regular graph. The (closed) neighbourhood of a vertex N[v] is the set of vertices at distance at most one from v: N[v]={v}∪{u∈V|(u,v)∈E}. In this paper, we will use the term local neighbourhood of a vertex v referring to the graph induced by N[v], i.e., the graph H=(N[v],E∩(N[v]×N[v])) where N[v] is taken in G.

A triangle in a graph is a set of three vertices that are pairwise joined by an edge. The Partition Into Triangles problem is a classical $\mathcal{NP}$-complete problem [10] that is defined as follows.

Partition Into Triangles
Input:	A graph G=(V,E).
Question:	Can V be partitioned into 3-element sets S 1,S 2,…,S |V|/3 such that each S i forms a triangle in G?

A partitioning of the vertices of G into 3-element vertex set S ₁,S ₂,…,S _|V|/3 that each form a triangle is also called a triangle partition of G.

On general graphs, Partition Into Triangles can be solved using inclusion/exclusion [4] in $\mathcal{O}(2^{n} n^{\mathcal{O}(1)})$ time and polynomial space. If we allow the use of exponential space, then this can be improved using a recent result by Koivisto [14] who has given a general covering algorithm that can solve the problem in $\mathcal{O} (1.7693^{n})$ time and space. Also, Björklund [2] has given a general randomised partitioning algorithm that can be used to solve the problem in $\mathcal{O} (1.496^{n})$ time and polynomial space while having a probability of failure that is exponentially small in n. On bounded-degree graphs, we do not know of any results besides the hardness result of Kann: he proved that the optimisation variant (find a packing consisting of a maximum number of triangles in G) is Max-$\mathcal{SNP}$-complete on graphs of maximum degree at least six [13].

The second problem that we consider in this paper is Exact 3-Satisfiability. A literal is a variable x or its negation ¬x; a clause is a multiset of literals. Let f(x) denotes the number of occurrences (frequency) of the variable x, and let f ₊(x) and f ₋(x) denote the number of positive or negative occurrences of x, respectively (f(x)=f ₊(x)+f ₋(x)).

Exact 3-Satisfiability is a variant of 3-Satisfiability where a clause is satisfied if and only if exactly one literal in the clause is set to True.

Exact 3-Satisfiability
Input:	A set of clauses C with each clause of size at most three using a set of variables X.
Question:	Does there exist a truth assignment of the variables X such that each clause in C contains exactly one true literal?

The problem Exact Satisfiability is defined similarly by omitting the requirement on the input that clauses must have size at most three.

For both the Exact Satisfiability and the Exact 3-Satisfiability problem there exists a long series of papers giving fast exponential-time algorithms. The first non-trivial algorithm for Exact Satisfiability is due to Schroeppel and Shamir and runs in $\mathcal{O}(2^{n/2} n^{\mathcal{O}(1)})$ time and $\mathcal{O}(2^{n/4} n^{\mathcal{O}(1)})$ space [22]. This was already improved in 1981 by Monien et al. to $\mathcal{O} (1.1844^{n})$ [19]. However, many authors seem to have missed this paper as they published algorithms with slightly worse upper bounds on the running time [7, 8]. The currently fastest algorithm for this problem is due to Byskov et al. and runs in $\mathcal{O}(1.1749^{n})$ time. When the number of clauses m is used as the complexity parameter, there exists an unpublished algorithm by Skjernaa using $\mathcal{O}(2^{m} \, m^{\mathcal{O}(1)})$ time and space, and an $\mathcal{O}(m! m^{\mathcal{O}(1)})$-time and polynomial-space algorithm by Madsen [18]. These results were improved by Björklund and Husfeldt who gave an $\mathcal{O}(2^{m} m^{\mathcal{O}(1)})$-time and polynomial-space algorithm [3].

The first improvement for Exact 3-Satisfiability is an $\mathcal{O} (1.1545^{n})$-time algorithm due to Drori and Peleg [8]. This was later improved by Porschen et al. [20], by Kulikov [15], and Byskov et al. [6]. The currently fastest algorithm is due to Wahlström and runs in $\mathcal{O} (1.0984^{n})$ time and polynomial space [23].

3 A Linear-Time Algorithm on Graphs of Maximum Degree Three

We begin by considering Partition Into Triangles on graphs of maximum degree three. We will prove that this problem is polynomial time solvable on this class of graphs by giving a linear-time algorithm: Algorithm 1.

Lemma 1

Let G=(V,E) be an instance of Partition Into Triangles restricted to graphs of maximum degree d containing a vertex v of degree at most two. In constant time, we can either decide that G is a No-instance, or transform G into an equivalent smaller instance.

Proof

If v has degree at most one, then this vertex cannot be in any triangle and the instance is a No-instance. Otherwise, let u, w be the neighbours of v. As G is of constant maximum degree, we can test in constant time whether (u,w)∈E. If (u,w)∈E, then {u,v,w} is the unique triangle containing v, and we remove this triangle from G to obtain a smaller equivalent instance. If $(u,w) \not\in E$, then v is not part of any triangle, and we again have a No-instance. □

Theorem 2

Algorithm  1 solves Partition Into Triangles on graphs of maximum degree three in linear time.

Proof

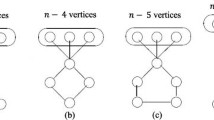
For correctness, we note that the number of vertices must be a multiple of three in order to partition G into triangles. Consider the tree cases in the if-statement in the main loop of the algorithm. Correctness of the first case follows from Lemma 1. For the other two cases, we observe that G is now a cubic graph and thus any local neighbourhood of v must equal one of the four cases in Fig. 1. In Case 1, no triangle containing v exists, and, in Cases 3 and 4, the fact that G is cubic would mean that removing any triangle leads to vertices of degree at most 1 which can no longer be in a triangle. Hence, these are all No-instances. In Case 2, v can only be part of one triangle, which Algorithm 1 determines.

Fig. 1

Possible edges within the neighbourhood of a vertex in a cubic graph

Algorithm 1

A linear-time algorithm for graphs of maximum degree three

Each iteration of the main loop requires constant time, since inspecting a neighbourhood in a graph of maximum degree three can be done in constant time. In each iteration, Algorithm 1 either terminates, or removes three vertices from G. Hence, there are at most a linear number of iterations and Algorithm 1 runs in linear time. □

4 The Relation Between Partition Into Triangles on Graphs of Maximum Degree Four and Exact 3-Satisfiability

When we restrict the Partition Into Triangles problem to graphs of maximum degree four, an interesting relation with Exact 3-Satisfiability can be observed. This relation will be the topic of this section.

We will first give three lemmas used to either decide that an instance of Partition Into Triangles on graphs of maximum degree four is a No-instance, or that it can be reduced to an equivalent smaller instance. These lemmas will apply to any instance unless all vertices in the instance have a local neighbourhood that is identical to one of two possible options. If we cannot reduce an instance in this way, pairs of vertices with one of these local neighbourhoods can be interpreted as a clause of size three in which exactly one variable must be set to True. The variables are then represented by connected series of vertices that each have the other remaining local neighbourhood. These variable can be set to True or False depending on in which of the two possible ways the corresponding connected series of vertices will be partitioned into triangles. In this way, remaining instances can be interpreted as an Exact 3-Satisfiability instance.

Lemma 3

Let G be an instance of Partition Into Triangles of maximum degree four with a given vertex v of degree at most three. In constant time, we can either decide that G is a No-instance, or obtain an equivalent smaller instance that is 4-regular.

Proof

We can assume that v has degree three: otherwise we apply Lemma 1.

Similar to in the proof of Theorem 2, the local neighbourhood of v corresponds to one of the four cases in Fig. 1. If this neighbourhood corresponds to Case 1, then all edges incident to v are not part of any triangle. If this neighbourhood corresponds to Case 2, then the edge between v and the bottom vertex is not part of any triangle. In these two cases, we remove these edges and apply Lemma 1 to v, which now has degree at most two. If this neighbourhood corresponds to Case 4, then, since G is of maximum degree four, selecting any triangle in the solution results in the creation of a vertex of degree at most one: we can conclude that we have a No-instance. The same holds for Case 3 unless the vertices a and b (see Fig. 2) are of degree four.

Fig. 2

Reducing an instance with a degree three vertex by merging its neighbours

In this last case, we reduce the graph as in Fig. 2. Either vertex a or vertex b must be in a triangle with u and v. If we take the triangle {a,u,v} in a solution, then b must be in a triangle with its other two neighbours; the same goes if we switch the roles of a and b. We distinguish three subcases depending on the number of common neighbours of a and b.

Case 1. Let a and b have no other common neighbours than u and v. The reader can work out that an edge between a neighbour of a and a neighbour of b outside the shown part of the graph cannot be in a triangle in any solution: we remove such edges if any exist. Next, we merge the vertices a and b to a single vertex and remove both u and v. Now, the new vertex is part of only two different triangles, and both possibilities corresponds to taking one of the two possible triangles containing v in the original graph. Also, no extra triangles are introduced as we have removed the edge between the neighbours of the merged vertices. We conclude that the new smaller instance is equivalent.

Case 2. Let a and b have exactly three common neighbours, and let w be the third common neighbour (the common neighbour of a and b that is not u or v). We must pick a triangle with u, v and either a or b. Consequently, the two edges incident to a and not incident to u or v can be removed if they are not on a common triangle together. If we do so, we obtain a vertex of degree two and can apply Lemma 1. The same holds for the two edges incident to b and not incident to u or v. Hence, we can assume that both a and b lie on a triangle with their third common neighbour w. Moreover, depending on which vertex from a and b we pick in a triangle with u and v, the other must be in a triangle with w. Now, we remove u and v and merge a and b to a single vertex and remove double edges. In the new instance, the edge between the merged vertex and w can be in two triangles and the choice corresponds directly to either taking the triangle u, v, a and the triangle with b and w, or taking the triangle u, v, b and the triangle with a and w.

Case 3. Let a and b have four common neighbours, called u, v, w and x. Again, the two pairs of edges incident to a and b not incident to u and v must be pairwise in triangles or we can remove them and apply Lemma 1. In the remaining case, each of these pairs of edges forms a triangle with the edge between w and x. Now, we must either pick the triangles u, v, a and b, w, x or we must pick u, v, b, and a, w, x. Both options involve the same vertices, hence we can remove these to obtain an equivalent smaller instance. □

As a result, we can reduce any instance of maximum degree four that is not 4-regular. In a 4-regular graph, a vertex v can have one of eleven possible local neighbourhoods, all shown in Fig. 3. We will now show that we can reduce any instance having a vertex whose local neighbourhood does not correspond to one of two specific local neighbourhoods: Cases 2b and 3a from Fig. 3.

Fig. 3

Possible edges within the local neighbourhood of a degree four vertex. The numbering corresponds to the number of edges between the neighbours of v

Lemma 4

Let G be a 4-regular instance of Partition Into Triangles containing a given vertex v whose local neighbourhood is different from Cases 2b, 3a and 3b in Fig. 3. In constant time, we can either decide that G is a No-instance, or we can transform G into an equivalent smaller instance.

Proof

Consider the possible local neighbourhoods of v shown in Fig. 3.

If the local neighbourhood of v equals Case 0, then we clearly have a No-instance. If the local neighbourhood of v equals Case 1, 2a, or 3c, then v is incident to an edge that is not part of any triangle in G because there exists an edge incident to v from which both endpoints do not have a common neighbour. For these cases, we remove the edge and apply Lemma 3 to v. If this local neighbourhood equals Case 5 or 6, then we have a No -instances since picking any triangle containing v results in a vertex of degree at most one.

Next, we consider the remaining two Cases: 4a, and 4b.

Case 4a: Consider the edge from the top left vertex to the bottom right vertex. This edge is part of two triangles, one with the centre vertex v and one with the top right vertex. If we would take any of these two triangles in the solution, a vertex of degree at most one remains. Hence, this edge cannot be part of a triangle in the solution. We remove it and then apply Lemma 3.

Case 4b: Consider one of the four edges in N[v] not incident to v, say the edge between the top two vertices. This edge is part of one or two triangles, one with v, and one with a possible third vertex outside of N[v]. Assume that we take the triangle with this edge and v in a solution, then the remaining two vertices will get degree two and thus they can be only in a triangle together and with a common neighbour. Hence, for each of the four edges in N[v], we remove it if the endpoints of both the edge and the opposite edge (edge between the other two vertices in N[v]∖{v}) have no common neighbour except for v.

Note that there is no instance in which all four edges remain since each of the four corner vertices has only one neighbour outside of N[v]. Hence there can be at most two such common neighbours, and if there are two then they must involve the endpoints of opposite edges. We can now apply Lemma 3. □

Having reduced the number of possible local neighbourhoods of a vertex in an instance to three, we now remove one more such possibility.

Lemma 5

Let G be a 4-regular instance of Partition Into Triangles in which the local neighbourhood of each vertex equals Case 2b, 3a or 3b in Fig. 3. Then, vertices whose local neighbourhood equal Case 3b form separate connected components in G. In linear time, we can either decide that G is a No-instance, or remove these components to obtain an equivalent smaller instance.

Proof

Let v be a vertex whose local neighbourhood corresponds to Case 3b of Fig. 3. Let u be the top left vertex in this picture and consider the local neighbourhood of u. This neighbourhood cannot equal Case 2b of Fig. 3 as it contains one vertex adjacent to two other vertices in the neighbourhood. The neighbourhood can also not equal Case 3a, since v is of degree four and thus cannot have an extra edge to the neighbour of u outside N[v]. We conclude that the local neighbourhood of u must equal that of Case 3b in Fig. 3. Thus, the top two vertices have a common neighbour outside N[v].

We can repeat this argument and apply it to u to conclude that the top right vertex in the picture w also has the same local neighbourhood. This shows that w and the new vertex created in the previous step must have another common neighbour. In this way, we conclude that every vertex in the connected component containing v has this local neighbourhood. An example of such a connected component can be found in Fig. 4.

Fig. 4

A connected component with all local neighbourhoods equal to case 3b of Fig. 3

It is not hard to see that such a connected component can be partitioned into triangles if and only if its number of vertices is a multiple of three. Therefore, we can decide that we have a No-instance if this is not the case, and otherwise we can remove it in linear time to obtain an equivalent smaller instance. □

Let a reduced instance of Partition Into Triangles on maximum degree four graphs be an instance to which Lemmas 3, 4 and 5 do not apply, i.e., an instance in which each local neighbourhood corresponds to Case 2b or 3a in Fig. 3.

Let v be a vertex in a reduced instance whose neighbourhood equals Case 3a. Note that v has one neighbour with the same neighbourhood and it has three neighbours whose neighbourhoods are equal to Case 2b. We refer to a pair of two vertices which have the neighbourhood of Case 3a as a fan. And, we refer to adjacent series of vertices with local neighbourhood equals Case 2b as a cloud of triangles. See Fig. 5.

Fig. 5

A fan and a cloud, with the two ways in which the cloud can be partitioned into triangles

Observe how these reduced instances can be partitioned into triangles. In a fan, we must select a triangle containing the middle two vertices and exactly one of the three vertices on the boundary. In a cloud, each triangle is either selected or all its neighbouring (cloud or fan) triangles are selected. Hence, adjacent triangles will alternate between being selected and not being selected in a triangle partition of a cloud; see Fig. 5. If such a series of adjacent triangles forms a cycle consisting of an odd number of these triangles, then the instance is a No-instance since an odd length series cannot alternate between being selected and not being selected. If a cloud does not have such an odd cycle of adjacent triangles, then it has two groups of boundary vertices connecting it to fans: in any solution all fan triangles connected to one group will be selected and all fan triangles connected to the other group will not be selected (see also Fig. 5). The only exception to this is the single vertex cloud that directly connects two fans; here the single vertex is in both groups of endpoints.

Now, the relation between Partition Into Triangles on graphs of maximum degree four and Exact 3-Satisfiability emerges. Namely, we can interpret a reduced instance of Partition Into Triangles on graphs of maximum degree four as an Exact 3-Satisfiability instance in the following way. We interpret a fan as a clause containing three literals whose corresponding variables are represented by the clouds adjacent to this fan. Exactly one fan triangle must be selected and this choice determines exactly which triangles in the adjacent clouds will be selected. In this way, we interpret a cloud as a variable that can be set to True or False. Both truth assignments correspond to one of the two possible ways to partition the cloud into triangles. If we fix one of the two possible ways to partition a cloud into triangles and let the corresponding truth value of the corresponding variable by the value True, then we can define the positive and negative literals of this variable. Namely, if this partitioning of the cloud into triangles forces that a triangle from a fan is selected, then the literal corresponding to this occurrence of the variable in the clause is a positive literal. Otherwise, this occurrence of the variable in the clause is a negative literal.

Notice that if we had fixed the other possible ways to partition a cloud into triangles, then this would result in the same instance of Exact 3-Satisfiability that we would get from the above procedure only with the sign of all literals of this variable flipped. It is not hard to see that this Exact 3-Satisfiability interpretation of a reduced instance is satisfiable if and only if the partition into triangles instance has a solution.

An Exact 3-Satisfiability instance obtained in this way can have multiple identical clauses. We will now prove that if we count copies of identical clauses separately, then an instance that is obtained in this way satisfies Property 6, which we define below.

Recall that f(x) denotes the number of occurrences (frequency) of the variable x, and that f ₊(x) and f ₋(x) denote the number of positive or negative occurrences of x, respectively.

Property 6

For any variable x in the formula, the number of positive f ₊(x) and negative f ₋(x) literals differ by a multiple of three.

Proposition 7

An Exact 3-Satisfiability instance obtained in the above way from an instance of Partition Into Triangles satisfies Property 6.

Proof

Let x be any variable in the Exact 3-Satisfiability instance. Consider the cloud that represents x, and let t ₊ and t ₋ be the number of triangles selected in this cloud when x is set to True or False, respectively. A cloud has a fixed number of vertices and for each corresponding truth assignment each vertex is either selected in a triangle or part of a corresponding literal, thus: 3t ₊+f ₊(x)=3t ₋+f ₋(x). Hence, f ₊(x)≡f ₋(x)(mod3). □

The following lemma shows how we can model Exact 3-Satisfiability instances by reduced instances of Partition Into Triangles on graphs of maximum degree four.

Lemma 8

Any variable x in a formula satisfying Property 6 can be represented by a cloud. Such a cloud consists of 2f(x)−3 vertices.

Proof

Without loss of generality, let f ₊(x)>0, and define F(x)=(f ₊(x),f ₋(x)). Notice that the single vertex cloud corresponds to F(x)=(1,1), a single triangle corresponds to F(x)=(3,0), two adjacent triangles corresponds to F(x)=(2,2), and a chain of four triangles corresponds to F(x)=(3,3).

These small clouds can be extended to larger clouds that correspond to any combination F(x)=(f ₊(x),f ₋(x)) with f ₊(x)≡f ₋(x)(mod3) by repeatedly increasing f ₊(x) or f ₋(x) by three in the following way. Take three triangles that are adjacent in the sense that two triangles are connected to the third triangle through having one common vertex. Now, identify the third vertex of the middle triangle with a vertex v that could be connected to a fan in the cloud that we are enlarging. This vertex can now no longer be connected to a fan, but four new such vertices that can be connected to fans are added. Furthermore, these vertices will be in a triangle with the adjacent fan if and only if the vertex v would be in such a triangle before we enlarged the cloud. Therefore, this construction increases the number of positive or negative literals of the variable represented by the cloud by three.

One easily checks that the statement on the number of vertices holds for the initial cases and is maintained every time three triangles are added. □

We conclude by formally expressing the relation between Partition Into Triangles on graphs of maximum degree four and Exact 3-Satisfiability. The proof of the resulting theorem directly follows from the above results.

Theorem 9

There exist linear-time transformations between Partition Into Triangles on graphs of maximum degree four and Exact 3-Satisfiability restricted to instances that satisfy Property 6 such that the following holds:

• 1. Any given instance is equivalent to its transformed instance.

• 2. An Exact 3-Satisfiability instance with variable set X and clause set  $\mathcal{C}$ obtained from an n-vertex Partition Into Triangles instance of maximum degree four satisfies: $2|\mathcal{C}| + \sum_{x \in X} (2f(x)-3 ) \leq n$.

• 3. A Partition Into Triangles instance on n vertices obtained from an Exact 3-Satisfiability instance satisfying Property 6 with variable set X and clause set $\mathcal{C}$ satisfies: $2|\mathcal{C}| + \sum_{x \in X} (2f(x)-3 ) = n$.

5 Hardness Results for Graphs of Maximum Degree Four

Having formalised the relation between Partition Into Triangles on graphs of maximum degree four and Exact 3-Satisfiability, we are now ready to prove some hardness results. In this section, we will show that Partition Into Triangles on graphs of maximum degree four is $\mathcal{NP}$-complete, and that no subexponential-time algorithm for this problem exists unless the Exponential-Time Hypothesis [11, 12] fails.

Theorem 10

Partition Into Triangles on graphs of maximum degree four is $\mathcal{NP}$-complete.

Proof

Clearly, the problem is in $\mathcal{NP}$. For hardness, we reduce from the $\mathcal{NP}$-complete problem Exact 3-Satisfiability [10]. Given an Exact 3-Satisfiability instance, we enforce Property 6 by making three copies of each clause. Then, the result follows from Theorem 9. □

Next, we show that no subexponential-time algorithm for our problem exists under the following complexity-theoretic hypothesis that is known as the Exponential-Time Hypothesis. Note that for 3-Satisfiability instances n denotes the number of variables and m denotes the number of clauses.

Complexity-Theoretic Hypothesis 11

(Exponential-Time Hypothesis [11, 12])

There exists a constant c>1 such that there exists no algorithm for 3-Satisfiability that uses only $\mathcal{O}(c^{n})$ time.

Proposition 12

Assuming the Exponential-Time hypothesis, there exists a constant c>1 such that there exists no algorithm for 3-Satisfiability that uses only $\mathcal{O}(c^{m})$ time.

Proof

Direct consequence of the Sparsification Lemma of Impagliazzo et al.; see [12]. □

Now, we are ready to prove the following result.

Theorem 13

Assuming the Exponential-Time Hypothesis, there exists no algorithm for Partition Into Triangles on graphs of maximum degree four with a worst-case running time that is subexponential in n.

Proof

Consider an arbitrary 3-Satisfiability instance with m clauses. We create an equivalent Exact 3-Satisfiability instance with 4m clauses by using the equivalence from [21] shown below. To avoid confusion, we now denote a 3-Satisfiability clause with literals x, y, and z by SAT(x,y,z) and a similar Exact 3-Satisfiability clause with literals x, y, and z by XSAT(x,y,z).

We then transform this Exact 3-Satisfiability instance into an equivalent instance of Partition Into Triangles of maximum degree four using the construction in the proof of Theorem 10. This construction triples the number of clauses to 12m, and thus the total sum of the number of literal occurrences is at most 36m. By Lemma 8, variables x can be represented by clouds using less than 2f(x) vertices each. This gives at most 96m vertices: 72m for the variables and another 24m for the two vertices of a fan for each clause.

Suppose there exists a subexponential-time algorithm for Partition Into Triangles on graphs of maximum degree four, i.e, an $\mathcal{O} (2^{\delta n})$-time algorithm for all δ>0. Then, this algorithm solves 3-Satisfiability in $\mathcal{O}(2^{\epsilon m})$ for all ϵ>0 using the above construction and δ=ϵ/96. However, no such algorithm can exist if we assume the Exponential-Time Hypothesis by Proposition 12. □

Note that although we have proven that, under the Exponential-Time Hypothesis, no algorithm subexponential in n exists, this also implies that no algorithm subexponential in m exists as $m = \mathcal{O} (n)$ on bounded-degree graphs.

6 A Very Fast Exponential-Time Algorithm

In the previous section, we have given two hardness results for Partition Into Triangles on graphs of maximum degree four. Despite these results, this problems seems to admit very fast, though exponential-time, algorithms.

In this section, we give a simple $\mathcal{O}(1.02445^{n})$-time algorithm for this problem based on the algorithm for Exact Satisfiability by Byskov et al. [6] and the algorithm for Exact 3-Satisfiability by Wahlström [23]. In the Appendix, we also give a faster $\mathcal{O} (1.02220^{n})$-time algorithm. This algorithm is based on the same principles as the one in Theorem 14 but uses an extensive case analysis.

Theorem 14

There exists an $\mathcal{O}(1.02445^{n})$-time algorithm for Partition Into Triangles on graphs of maximum degree four.

Proof

Use Theorem 9 to obtain an instance of Exact 3-Satisfiability with variable set X and clause set $\mathcal{C}$ satisfying $n \geq2|\mathcal{C}| + \sum_{x \in X} (2f(x)-3 )$. Let γ ₁ be the number of variables x with f ₊(x)=f ₋(x)=1 and let γ ₃ be the number of variables x with f(x)≥3; by Property 6 the total number of variables γ equals γ ₁+γ ₃. Since clauses have size three, we find that $n \geq2(2\gamma_{1}+3\gamma_{3})/3 + \gamma_{1} + 3\gamma_{3} = 2\frac{1}{3}\gamma_{1} + 5\gamma_{3}$ and $\gamma_{3} \leq n - 2\frac{1}{3}\gamma_{1}$.

If γ ₁≤0.10746n, then apply Wahlström’s $\mathcal{O} (1.0984^{\gamma})$-time algorithm for Exact 3-Satisfiability [23]. Now, $\gamma= \gamma_{1} + \gamma_{3} \leq0.10746n + (n - 2\frac{1}{3} \times0.10746n)/5 < 0.25732n$ by basic calculus. Therefore, the problem is solved by this algorithm in $\mathcal{O} (1.0984^{0.25732n}) = \mathcal{O}(1.02445^{n})$ time.

Otherwise γ ₁>0.10746n. In this case, we first reduce the instance in polynomial time removing all variables x with f ₊(x)=f ₋(x)=1 by using the following equivalence where C and C′ are arbitrary sets of literals and Φ denotes any Exact Satisfiability formula:

$$(x,C) \wedge\bigl(\neg x,C'\bigr) \wedge\varPhi \Longleftrightarrow \bigl(C,C'\bigr) \wedge\varPhi $$

This results in an instance where γ ₁=0 while the clauses have been increased in size. Now, we can apply the $\mathcal{O}(2^{0.2325\gamma})$ Exact Satisfiability algorithm from Byskov et al. [6]. This algorithm now solves our instance in $\mathcal{O}(1.1749^{\gamma_{3}}) = \mathcal{O}(1.02445^{n})$ time as $\gamma_{3} \leq(n - 2\frac{1}{3} \times 0.10746n)/5 < 0.14986n$ by basic calculus. □

Theorem 15

There exists an $\mathcal{O}(1.02220^{n})$-time algorithm for Partition Into Triangles on graphs of maximum degree four.

Proof

See Appendix. □

7 Concluding Remarks

We have shown that the Partition Into Triangles problem is linear-time solvable on graphs of maximum degree three, that it is $\mathcal{NP}$-complete on graphs of maximum degree at least four, and that no subexponential-time algorithm for the problem on graphs of maximum degree four exists unless the Exponential-Time Hypothesis fails. For this seemingly hard problem on graphs of maximum degree four, we have given an efficient $\mathcal{O}(1.0222^{n})$-time algorithm using only linear space, and without any large, hidden polynomial-factors in the running time. When concerned with problems with reasonable input sizes, this would mean that our algorithm will probably be faster than polynomial-time algorithms for the same problem on, for example, graphs whose treewidth is bounded by 10. We would be interested to find more problems on which such fast, yet exponential-time, algorithms exists.

We have used an interesting relation between Partition Into Triangles on graphs of maximum degree four and Exact 3-Satisfiability to obtain these results. This relationship emerges by reducing Partition Into Triangles instances of maximum degree four until each vertex can have only two different possible local neighbourhoods. Connected series of vertices with one of these local neighbourhoods then form the variables of an Exact 3-Satisfiability instance, and pairs vertices with the other local neighbourhood form the clauses of this Exact 3-Satisfiability instance. Since such a structure seems to disappear on graphs with a higher degree bound, we wonder whether similar ideas could be used for triangle packing or triangle covering.

Appendix: The Faster Algorithm for Partition Into Triangles on Graphs of Maximum Degree Four

In the main body of this paper, we have given an $\mathcal{O} (1.02445^{n})$-time algorithm for Partition Into Triangles on graphs of maximum degree four and claimed a faster exponential-time algorithm that solves this problem in $\mathcal{O}(1.02220^{n})$ time. We will now give the details of this faster algorithm.

To obtain the $\mathcal{O}(1.02445^{n})$-time algorithm, we have used known algorithms for Exact Satisfiability and Exact 3-Satisfiability to solve Partition Into Triangles on graphs of maximum degree four. Here, we present an algorithm for Exact Satisfiability that is specifically tailored to the fact that the input is obtained from an instance of Partition Into Triangles. This algorithm will be analysed using the number of vertices in a Partition Into Triangles instance used to build the different structures involved in an Exact 3-Satisfiability instance as a measure of instance size.

Our algorithm is a branch-and-reduce algorithm for Exact Satisfiability instances (not only Exact 3-Satisfiability instances). We analyse the resulting algorithm by bounding the number of subproblems generated. When an algorithm repeatedly branches on an instance of size n obtaining subproblems of sizes n−r ₁,n−r ₂,…,n−r _l , then the algorithm generates at most $\mathcal{O}(\tau(r_{1},r_{2},\ldots,r_{l})^{n})$ subproblems in total. Here, τ(r ₁,r ₂,…,r _l ) is called the branching number. τ(r ₁,r ₂,…,r _l ) can be computed by solving the corresponding recurrence relation N(n)≤N(n−r ₁)+N(n−r ₂)+⋯+N(n−r _l ). This comes down to computing the smallest positive real root α of the equation $1 = \alpha^{-r_{1}} + \alpha^{-r_{2}} + \cdots+ \alpha^{-r_{l}}$: now τ(r ₁,r ₂,…,r _l )=α. When an algorithm has multiple branching rules, then at most τ ⁿ subproblems are generated, where τ is the maximum over the branching numbers of all its branching rules. For an overview of the analysis of branch-and-reduce algorithms, see for example [9]. For an extended treatment of branching numbers and the τ-function, see [16].

For our algorithm, we will use the following size measure k on instances with variable set X and clause set $\mathcal{C}$.

$$k := 5|X|+ \sum_{C \in\mathcal{C}, |C| \geq3} 2\frac{1}{3} \bigl( |C|-3 \bigr) $$

Before justifying this measure, we introduce a series of standard reduction rules used in many algorithms for Exact Satisfiability. Besides using these reduction rules, we always decide that we have a No -instance if two or more variables in a clause are set to True. Also, we set any literal to False that occurs in a clause with a literal that has been set to True, and thereafter we remove the clause. After doing so, we remove all literals that have been set to False from the remaining clauses. If this results in an empty clause, we decide that we have a No-instance.

Below, we let x and y be arbitrary literals, we let C and C′ be arbitrary (sub)clauses, and we let Φ be the rest of the current Exact Satisfiability formula. By Φ:a→b, we denote the formula Φ with all occurrences of the literal a replaced by b and all occurrences of the literal ¬a by ¬b. This notation is extended to sets of variables, for example in Φ:C→False. The numbers behind the reduction rules represent the minimum decrease of the measure as a result of the reduction.

1.	C∧C∧Φ	⇒	C∧Φ	(0)
2.	(x)∧Φ	⇒	Φ:x→True	(−5)
3.	(x,y)∧Φ	⇒	Φ:y→¬x	(−5)
4.	(x,x,C)∧Φ	⇒	C∧Φ:x→False	(−5)
5.	(x,¬x,C)∧Φ	⇒	Φ:C→False	(−5)
6.	(x,y,C)∧(x,¬y,C′)∧Φ	⇒	(y,C)∧(¬y,C)∧Φ:x→False	(−5)
7.	(x,y,C)∧(¬x,¬y,C′)∧Φ	⇒	Φ:y→¬x;C,C′→False	(−5)
8.	C∧C′∧Φ with C⊂C′	⇒	C∧Φ:(C′∖C)→False	(−5)
9.	(x,C)∧(y,C)∧Φ	⇒	(x,C)∧Φ:y→x	(−5)
10.	(x,C)∧(C,C′)∧Φ with |C|,|C′|≥2	⇒	(x,C)∧(¬x,C′)∧Φ	$(-2\frac {1}{3})$
11.	(x,C)∧(¬x,C′)∧Φ with $x, \neg x \not\in \bigcup\varPhi$	⇒	(C,C′)∧Φ	$(-2\frac {2}{3})$
12.	If, after application of Reduction Rules 1-11, Φ contains a variable x and a series of variables y 1,…,y l that occur only in clauses with x in a such way that every clause that contains x contains exactly one of the variables y i , then set x to False.			(−5)

Lemma 16

Reduction Rules 1–12 are correct and result in the given minimum reductions in the measure k.

Proof

Reduction Rules 1–11 are used in many papers on Exact Satisfiability, e.g. see [6]; their correctness is evident. For the correctness of Reduction Rule 12, consider a variable x and a series of variables y ₁,…,y _l as in the statement of the reduction rule. Since Reduction Rules 6 and 7 do not apply, the signs of all literals of x must be equal, and the same goes for the signs of the literals of each of the individual variables y _i . Without loss of generality, we assume all these literals to be positive. Consider any solution with x set to True. Since the y _i occur in clauses with x, they must all be set to False. Because none of the y _i occur in clauses together or in a clause without x, we can replace this assignment by an equivalent one by setting x to False and all the y _i to True. Correctness of the reduction rule follows.

Now, consider the decrease of the measure. When any of the above reduction rules except Reduction Rules 1, 10, and 11 are applied, at least one variable is assigned a value or replaced by another, and no clauses are increased in size. Hence, the measure decreases by at least 5 in these cases. Clearly, Reduction Rule 1 does not increase the measure as it removes a clause. Reduction Rule 10 reduces the size of one clause of size at least four by one, hence the measure decreases by $2\frac{1}{3}$. Finally, Reduction Rule 11 removes one variable and one possibly large clause of size s decreasing the measure by $5 + 2\frac{1}{3}(s-3)$. However, this reduction rule also increases the size of another clause by s−2 increasing the measure by $2\frac{1}{3}(s-2)$. Together, this leads to a decrease of $5 - 2\frac{1}{3} = 2\frac{2}{3}$. □

We now justify our measure. Recall that f(x) denotes the frequency of the variable x, that f ₊(x) and f ₋(x) denote the frequencies of the positive and negative literals of x, respectively. Also, let F(x)=(f ₊(x),f ₋(x)).

Lemma 17

Let G be an n-vertex graph of maximum degree four. In polynomial time, we can either decide that G is a No-instance of Partition Into Triangles, or transform G into an equivalent Exact Satisfiability instance of measure k that satisfies k≤n.

Proof

We first apply the procedure used to prove Theorem 9 to G; see Sect. 4. If this procedure does not decide that we have a No-instance, then it results in an equivalent Exact 3-Satisfiability instance satisfying $2|\mathcal{C}| + \sum_{x \in X} (2f(x)-3 ) \leq n$, where X is the set of variables and $\mathcal{C}$ is the set of clauses.

We distinguish between two types of variables x∈X: variables that satisfy f(x)=2 and F(x)=(1,1), and all other variables, which by Property 6 satisfy f(x)≥3. Let n ₂ be the number of variables with f(x)=2, and let n _≥3 be the number of other variables. Then:

$$n \geq2|C| + \sum_{x \in X} \bigl(2f(x)-3 \bigr) \geq2|C| + n_2 + 3 n_{\geq3} = 5 n_{\geq3} + 2 \frac{1}{2} n_2 $$

The last equality follows from distributing the two vertices used by the clauses of size three to the variables: these variables are given $\frac{2}{3}$ vertex for each occurrence in $\mathcal{C}$.

To the obtained instance, we exhaustively apply Reduction Rules 1–12. We note that this will not result in an instance of Exact 3-Satisfiability, but in an instance of Exact Satisfiability instead. This is because the reduction rules (specifically Reduction Rule 11) can create clauses of size at least four when removing variables x with f(x)=2. Since a clause can increase by at most one in size per removed variable, we obtain the following inequality:

$$n \geq5 n_{\geq3} + 2\frac{1}{2} n_2 \geq5 n_{\geq3} + \sum_{C \in \mathcal{C}, |C| \geq3} 2\frac{1}{3} \bigl( \vert C\vert -3 \bigr) = k $$

This proves that k≤n. □

We note that the amounts by which the measure decreases as a result of applying a reduction rule that are proven in Lemma 16 apply only after first applying Lemma 17: Lemma 17 uses any such decrease due to Reduction Rule 11 for its correctness. We also note that the new Exact Satisfiability instance no longer satisfies Property 6. Before, this property held only if we counted identical clauses multiple times; now, we remove these double clauses.

Reduction Rules 1–12 enforce some new constraints on the resulting Exact Satisfiability instances. These will be proven in the next lemma. Let a unique variable be a variable x with f(x)=1.

Lemma 18

After exhaustively applying Reduction Rules 1–12 to an Exact Satisfiability instance, it satisfies the following properties:

• 1. All clauses have size at least three.

• 2. All variables occur at most once in each clause.

• 3. If variables occur together in multiple clauses, their literals have identical signs in all clauses in which they occur together.

• 4. For any pair of clauses, each clause contains at least two variables not occurring in the other.

• 5. There are no variables x with F(x)=(1,1).

• 6. Every clause contains at most one unique variable.

Proof

(1.) Smaller clauses are removed by Reduction Rules 2 and 3. (2.) Reduction Rule 4 or 5 applies if a clause contains a variable two or more times. (3.) If their literals do not have the same signs, Reduction Rule 6 or 7 applies. (4.) No clauses are identical by Reduction Rule 1. No clause is a subclause of another clause by Reduction Rule 8. And, if a clause contains only one variable that does not occur in the other clause, Reduction Rule 9 or 10 applies. (5.) By Reduction Rule 11. (6.) If a clause has more than one unique variable, Reduction Rule 12 applies. □

Next, we give a series of lemmas that describe the branching rules of our algorithm. Since we first exhaustively apply the reduction rules before branching, each lemma will assume that no reduction rule applies without mentioning this. Also, we implicitly assume that directly after the branching all reduction rules are exhaustively applied again. In each lemma, we prove that the described branching has associated branching number at most 1.02220 when analysed using the measure k.

Lemma 19

If an Exact Satisfiability instance contains a variable x that occurs both as a positive and as a negative literal, then we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

Let us first consider branching on a variable x with f ₊(x)≥2 and f ₋(x)≥2, i.e., we have the following situation:

$$(x,C_1) \wedge(x,C_2) \wedge\bigl(\neg x,C_1'\bigr) \wedge\bigl(\neg x,C_2' \bigr) \wedge \varPhi $$

where x can also occur in Φ.

We branch by considering two subproblems: one where we set x to True and one where we set x to False. Below, we consider a series of cases where we distinguish between whether the C _i or $C_{i}'$ have size two or size at least three.

If we set x to True, then the measure decreases by at least the following quantities. We give these quantities by a series of bullets. Below, we will compute the corresponding sums of the decrease of the measure for each of the cases considered.

• 5 for removing x.

• 5 for each literal in C ₁ or C ₂ because these are set to False. Note that by Lemma 18(4), at least two variables occur in C ₁ that do not occur in C ₂ and vice versa. Therefore, then the measure decreases by 20 if |C ₁|=|C ₂|=2, and by at least 25 otherwise.

• 5 per $C_{i}'$ with $|C_{i}'|=2$ because ¬x is removed from the corresponding clauses: this results in the removal of at least one more variable by Reduction Rule 3. Notice that by Lemma 18(3): $(C_{1} \cup C_{2}) \cap(C_{1}' \cup C_{2}') = \emptyset$.

• A number of times $2\frac{1}{3}$ for reducing the sizes of the clauses.

The situation is symmetric, hence setting x to False decreases the measure by the same quantities after replacing C _i by $C_{i}'$ and vice versa.

The table below gives all considered cases together with the minimum decrease of the measure obtained by each of the above reasons. In the first two columns, we give the number of C _i and $C_{i}'$ with |C _i |≥3 and $|C_{i}'| \geq3$, respectively. We assume that all other C _i and $C_{i}'$ have size two. In the third and fourth column, we give the decrease of the measure as a sum of four terms: the first one corresponds to the first bullet given above, the second corresponds to the second bullet, etc. In the last column, we give the branching number τ associated with the branching. By symmetry reasons, we can restrict ourselves to the given cases.

#C i : |C i |≥3	$\#C_{i}'$: $|C_{i}'| \geq3$	Decrease of the measure k when we set		τ
		x→True	x→False
0	0	5+20+10+0=35	5+20+10+0=35	1.02001
1	0	$5 + 25 + 10 + 2\frac{1}{3} = 42\frac{1}{3}$	$5 + 20 + 5 + 2\frac{1}{3} = 32\frac{1}{3}$	1.01886
2	0	$5 + 25 + 10 + 4\frac{2}{3} = 44\frac{2}{3}$	$5 + 20 + 0 + 4\frac{2}{3} = 29\frac{2}{3}$	1.01910
1	1	$5 + 25 + 5 + 4\frac{2}{3} = 39\frac{2}{3}$	$5 + 25 + 5 + 4\frac{2}{3} = 39\frac{2}{3}$	1.01763
2	1	5+25+5+7=42	5+25+0+7=37	1.01773
2	2	$5 + 25 + 0 + 9\frac{1}{3} = 39\frac{1}{3}$	$5 + 25 + 0 + 9\frac{1}{3} = 39\frac{1}{3}$	1.01778

This proves the branching numbers for branching on variables x with f ₊(x)≥2 and f ₋(x)≥2. Hence, we can assume without loss of generality by negating variables that, for each variable x, we have f ₋(x)∈{0,1} and f ₊(x)≥1.

If f ₊(x)≥3, we can make a similar table associated with the following situation:

$$(x,C_1) \wedge(x,C_2) \wedge(x,C_3) \wedge(\neg x, C) \wedge\varPhi $$

Again, the first two columns give the size of |C| and the |C _i |; the third and the fourth column contain the decrease of the measure in both branches as a sum of the quantities based on each of the four bullets given above; and the fifth column gives the associated branching number. In the sum corresponding to the branch where we set x→True, we bound the decrease of the measure due to assigning values to variables with literals in C ₁, C ₂, and C ₃ by 30 if |C ₁|=|C ₂|=|C ₃|=2, and by 35 otherwise.

|C|	#C i : |C i |≥3	Decrease of the measure k when we set		τ
		x→True	x→False
2	0	5+30+5+0=40	5+10+15+0=30	1.02015
2	1	$5 + 35 + 5 + 2\frac{1}{3} = 47\frac{1}{3}$	$5 + 10 + 10 + 2\frac{1}{3} = 27\frac{1}{3}$	1.01924
2	2	$5 + 35 + 5 + 4\frac{2}{3} = 49\frac{2}{3}$	$5 + 10 + 5 + 4\frac{2}{3} = 24\frac{2}{3}$	1.01963
2	3	5+35+5+7=52	5+10+0+7=22	1.02013
≥3	0	$5 + 30 + 0 + 2\frac{1}{3} = 37\frac{1}{3}$	$5 + 15 + 15 +2\frac{1}{3} = 37\frac{1}{3}$	1.01874
≥3	1	$5 + 35 + 0 + 4\frac{2}{3} = 44\frac{2}{3}$	$5 + 15 + 10 + 4\frac{2}{3} = 34\frac{2}{3}$	1.01773
≥3	2	5+35+0+7=47	5+15+5+7=32	1.01794
≥3	3	$5 + 35 + 0 + 9\frac{1}{3} = 49\frac{1}{3}$	$5 + 15 + 0 + 9\frac{1}{3} = 29\frac{1}{3}$	1.01820

This proves the branching numbers for branching on variables x with f ₊(x)≥3 and f ₋(x)≥1. Because variables x with F(x)=(1,1) are removed by the reductions rules (Lemma 18(5)), the only remaining variables x for which we have to prove the lemma are those with F(x)=(2,1). Let x be such a variable with F(x)=(2,1).

If the negated literal of x occurs in a clause of size three, we apply the following transformation:

$$(x,C_1) \wedge(x,C_2) \wedge(\neg x, v_1, v_2) \wedge\varPhi\quad \Longrightarrow\quad(v_1,v_2,C_1) \wedge(v_1,v_2,C_2) \wedge\varPhi $$

This transformation is well-known as resolution; see for example [6]. In this transformation, we remove one variable, but increase two clauses in size by one. Therefore, this transformation does not increase the measure: it decreases by $5 - 2 \times2\frac{1}{3} = \frac{1}{3}$.

If the negated literal of x occurs in a clause of size at least four, this corresponds to the following situation with |C|≥3.

$$(x,C_1) \wedge(x,C_2) \wedge(\neg x, C) \wedge\varPhi $$

In this case, we again branch by considering either setting x→True in one branch and setting x→False in the other branch. We again consider a number of subcases corresponding to the C _i having size two or at least three. The associated branching numbers are again computed in a table similar to the two tables given above.

|C 1|	|C 2|	Decrease of the measure k when we set		τ
		x→True	x→False
2	2	$5 + 20 + 0 + 2\frac{1}{3} = 27\frac{1}{3}$	$5 + 15 + 10 + 2\frac{1}{3} = 32\frac{1}{3}$	1.02357
2	≥3	$5 + 25 + 0 + 4\frac{2}{3} = 34\frac{2}{3}$	$5 + 15 + 5 + 4\frac{2}{3} = 29\frac{2}{3}$	1.02183
≥3	≥3	5+25+0+7=37	5+15+0+7=27	1.02209

At this point, each case except one gives a branching number that is smaller than the claimed 1.02220. So, to obtain our result, we must analyse this case in more detail: this is the case where the variable x has F(x)=(2,1) and where |C ₁|=|C ₂|=2 in the above situation. A refined analysis of the decrease of the measure give the result.

Let us inspect this one case a little more thoroughly. This case corresponds to the following situation:

$$(x,v_1,v_2) \wedge(x,v_3,v_4) \wedge(\neg x,w_1,w_2,w_3) \wedge\varPhi $$

To obtain a branching number that improves upon the one given in the above table, we look at the effect of the branching on Φ. Consider setting x to True and hence the v _i to False. Notice that at least two of the variables v _i must also occur somewhere in Φ by Lemma 18(6).

Let us first assume that a literal ¬v _i occurs in Φ, and without loss of generality let this be ¬v ₁. Consider the clause with ¬v ₁. By Lemma 18(4), this clause cannot contain a literal of v ₂, and it must contain at least two literals that are not literals of the variables v ₃ and v ₄. Hence, this clause must contain at least one variable that we have not considered this far. The literal of this variable will be set to False decreasing the measure by at least an additional 5.

If no literals of the form ¬v _i occur in Φ, at least two positive literals of the v _i must occur in Φ; these literals are set to False. We now consider several cases with a clause containing these literals depending on the number of literals in the clause that are not among the v _i . By Lemma 18(4), each clause in Φ can contain at most two occurrences of the v _i ’s and thus must contain at least one literal of a different variable. If these literals fill a clause except for one spot, as in (v ₁,v ₃,y), then y is set to True decreasing the measure by at least an additional 5. If these literals fill a clause except for two spots, as in (v ₁,v ₃,y ₁,y ₂), then Reduction Rule 3 will replace y ₂ by ¬y ₁ also decreasing the measure by an additional 5. And, if these literals fill a clause except for at least three spots, then each such literal will be removed decreasing the measure an additional by $2\frac{1}{3}$ each.

Altogether, we conclude that with at least two v _i in Φ, this decreases the measure by at least an additional $4\frac{2}{3}$. Therefore, we obtain a branching number of $\tau(27\frac{1}{3} + 4\frac {2}{3},32\frac{1}{3}) = \tau(32,32\frac{1}{3}) < 1.02179$. □

We notice that we will use systematic case analyses as in the proof of the above lemma throughout the rest of this paper. In these analyses, we will often start with a series of bullets corresponding to the different effects that decrease the measure. Then, for each case considered, we will give the associated decrease of the measure associated with each bullet systematically. Thereafter, we will perform the case analysis by giving a table with a row for each case giving the relevant properties of this case, the total decrease of the measure in each branch as a sum of the effects of each bullet in the enumeration given before, and the associated branching number.

From now on, we assume without loss of generality that all variables occur only as positive literals. Based on this assumption, we can give a simple lower bound on the decrease of the measure as a result of setting a number of literals in Φ to False. This is formalised in the following proposition. Its proof has similarities to the last few paragraphs of the proof of Lemma 19.

Proposition 20

Let Φ be an Exact Satisfiability formula containing only positive literals. Consider setting some variables with a total of l literals in Φ to False, while at least one variable in Φ remains without a truth assignment. Then, setting the literals to False decreases the measure of Φ by at least $2\frac{1}{3} \times l$ if l≤2 and at least 5 if l≥3 besides the decrease due to removing the corresponding variables.

Proof

If Φ contains a clause in which all literals are set to False, then Φ is not satisfiable resulting in the removal of the whole formula. If Φ contains a clause in which all literals except for one are set to False, then the last literal is set to True removing a variable and thus decreasing the measure by at least 5. If Φ contains a clause in which all literals except for two are set to False, then the variables corresponding to the last two literals will be replaced by one variable by Reduction Rule 3 decreasing the measure by at least 5. Finally, if Φ contains a clause in which a literal is set to False and in which at least three literals are not assigned a value, then this reduces the size of the clause decreasing the measure by at least $2\frac{1}{3}$ each.

We conclude that the minimum decrease of the measure is $\min\{ 2\frac {1}{3} \times l, 5\}$. This proves the proposition. □

Lemma 21

If an Exact Satisfiability instance contains two clauses that have two or more variables in common, then we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

In the proof below, we can assume that all literals are positive literals since we can otherwise apply Lemma 19.

Let C be the set of literals contained in both clauses, and let C ₁ and C ₂ be the literals in each clause not contained in the other. We have the following situation:

$$(C,C_1) \wedge(C,C_2) \wedge\varPhi $$

with |C|≥2 as in the statement of the lemma, and |C ₁|,|C ₂|≥2 by Lemma 18(4).

In most cases, we will branch in the following way. In one subproblem, we assume that a literal in C will be True; consequently, we set all variables in C ₁ and C ₂ to False. In the other subproblem, we assume that none of the literals in C will be True; we set the corresponding variables to False. We will distinguish different cases where C, C ₁ and C ₂ have size two or size at least three.

In the first subproblem where the literals in C ₁ and C ₂ are set to False, this leads to the following decrease of the measure k:

• 10 per C _i with |C _i |=2 and 15 per C _i with |C _i |≥3 for removing the variables that are set to False. This is correct since all variables occur at most once per clause by Lemma 18(2).

• 5 if |C|=2 because then Reduction Rule 3 will remove one additional variable.

• a number of times $2\frac{1}{3}$ depending on the size of C, C ₁ and C ₂ for reducing the size of the two given clauses.

• $4\frac{2}{3}$ if |C ₁|=|C ₂|=2 and 5 otherwise for the additional decrease of the measure of Φ. By Lemma 18(6), at least two literals in Φ are set to False if |C ₁|=|C ₂|=2 and at least three literals otherwise. The given quantities by which the measure decreases correspond to the ones proven in Proposition 20.

In the second subproblem where the literals in C are set to False, this leads to the following decrease of the measure k:

• 10 if |C|=2 and 15 if |C|≥3 for removing the variables that are set to False.

• 5 for each C _i with |C _i |=2 because Reduction Rule 3 will remove additional variables in these cases.

• a number of times $2\frac{1}{3}$ depending on the size of C, C ₁ and C ₂ for reducing the size of the two clauses.

• a quantity bounding the additional decrease of the measure of Φ from below. If |C|=2, we use $2\frac{1}{3}$ because by Lemma 18(6) one of the variables in C must occur in Φ; this leads to the given decrease by Proposition 20. If |C|≥3, we use $4\frac{2}{3}$ by the same reasoning.

Next, we compute the branching numbers associated with the given branching by giving a table that is similar to the tables used in the proof of Lemma 19.

|C|	#C i : |C i |≥3	Decrease of the measure k when we set		τ
		C 1,C 2→False	C→False
2	0	$20 + 5 + 4\frac{2}{3} + 4\frac{2}{3} = 34\frac{1}{3}$	$10 + 10 + 4\frac{2}{3} + 2\frac{1}{3} = 27$	1.02298
2	1	25+5+7+5=42	$10 + 5 + 7 + 2\frac{1}{3} = 24\frac {1}{3}$	1.02167
2	2	$30 + 5 + 9\frac{1}{3} + 5 = 49\frac{1}{3}$	$10 + 0 + 9\frac {1}{3} + 2\frac{1}{3} = 21\frac{2}{3}$	1.02088
≥3	0	$20 + 0 + 9\frac{1}{3} + 4\frac{2}{3} = 34$	$15 + 10 + 9\frac{1}{3} + 4\frac{2}{3} = 39$	1.01921
≥3	1	$25 + 0 + 11\frac{2}{3} + 5 = 41\frac{2}{3}$	$15 + 5 + 11\frac{2}{3} + 4\frac{2}{3} = 36\frac{1}{3}$	1.01797
≥3	2	30+0+14+5=49	$15 + 0 + 14 + 4\frac{2}{3} = 33\frac{2}{3}$	1.01712

Hence, we have proven the lemma for all cases except when |C|=|C ₁|=|C ₂|=2. In this case, we have the following situation:

$$(x,y,v_1,v_2) \wedge(x,y,v_3,v_4) \wedge\varPhi $$

If, in the branch where we set v ₁,v ₂,v ₃,v ₄→False, the additional decrease of the measure of Φ is at least 7, then we obtain the required branching number since $\tau(20 + 5 + 4\frac{2}{3} + 7, 27) = \tau(36\frac{2}{3},27) < 1.02220$.

By Lemma 18(6), at least two occurrences of the literals of v ₁, v ₂, v ₃, and v ₄ must occur in Φ. If these are exactly two occurrences, then both x and y must occur at least once in Φ also, as Reduction Rule 12 would otherwise be applicable. In this case, the additional decrease of the measure of Φ in the branch where we set x,y→False can be bounded from below by $4\frac{2}{3}$ in stead of $2\frac{1}{3}$ by Proposition 20. Thus, we obtain a branching number of $\tau(34\frac{1}{3}, 10 + 10 + 4\frac{2}{3} + 4\frac{2}{3}) = \tau(34\frac{1}{3}, 29\frac{1}{3}) < 1.02207$ for this case.

If there are at least three occurrences of the literals of v ₁, v ₂, v ₃, and v ₄ in Φ while setting them to False decreases the measure by less than 7, then all of these occurrences of the v _i must be in clauses of size three with exactly one other variable z, as for example in: (v ₁,v ₃,z)∧(v ₂,v ₄,z). This holds because all literals occur only as positive literals, and all other configurations that do not directly give a No-instance lead to an additional decrease of the measure of Φ of at least 7: in these cases, at least three clauses of size at least four will be reduced in size ($3 \times2\frac{1}{3} = 7$); at least two variables will be removed (2×5>7); or exactly one variable will be removed and at least one clause of size at least four is reduced in size $(5 + 2\frac{1}{3} > 7)$.

In fact, the only remaining situation is the following:

$$(x,y,v_1,v_2) \wedge(x,y,v_3,v_4) \wedge(v_1,v_3,z) \wedge (v_2,v_4,z) \wedge\varPhi $$

This holds because if z exist in a clause of size three with any of the v _i , then z will not occur in a clause of size three with the same v _i again due to Lemma 18(4). Hence, in order to put at least three of the literals of the variables v _i in clauses of size three with no other variables than z, exactly one occurrence of each of the four v _i ’s is necessary.

In this special case, we branch on z instead. If we set z→True, this results in v ₁, v ₂, v ₃, and v ₄ being set to False, and in the replacement of y by ¬z by Reduction Rule 3. Thus, this removes a total of 6 variables and 2 clauses of size four decreasing the measure by at least $6 \times5 + 2 \times2\frac{1}{3} = 34\frac{2}{3}$. If we set z→False, this directly results in the following replacements: v ₃→¬v ₁ and v ₄→¬v ₂. In the two clauses with x and y this leads to the following situation (x,y,v ₁,v ₂)∧(x,y,¬v ₁,¬v ₂). This situation is reduced by Reduction Rule 7 by setting x and y to False. In this branch, a total of 5 variables and 2 clauses of size four are removed decreasing the measure by at least $5 \times5 + 2 \times2\frac {1}{3} = 29\frac{2}{3}$. The associated branching number equals $\tau(34\frac{2}{3},29\frac {2}{3}) < 1.02183$, completing the proof of the lemma. □

We deal with variables of relatively high frequency next: variables x with f(x)≥4.

Lemma 22

If an Exact Satisfiability instance contains a variable x with f(x)≥4, then we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

We can assume that Lemmas 19 and 21 do not apply, otherwise we are done. Therefore, each variable has only positive literals and no two variables occur together in a clause more than once. This means that we have the following situation:

$$(x,C_1) \wedge(x,C_2) \wedge(x,C_3) \wedge(x,C_4) \wedge\varPhi $$

where x can also occur in Φ.

We branch on x and again distinguish several cases based on the sizes of the C _i . If we set x→True, we obtain the following quantities for the decrease in the measure:

• 5 for removing x.

• $5 \times\sum_{i=1}^{4} |C_{i}|$ for removing the variables in the C _i ; these are set to False.

• a number of times $2\frac{1}{3}$ for reducing the clauses.

• 5 extra since by Lemma 18(6) at least 4 variables must also occur in Φ and this leads to an additional decrease of the measure of at least 5 by Proposition 20.

If we set y→False, we obtain the following quantities for the decrease in the measure:

• 5 for removing x.

• 5 for each C _i with |C _i |=2 because Reduction Rule 3 will remove an additional variable in these cases.

• a number of times $2\frac{1}{3}$ for reducing the sizes of the clauses.

Identical to the proofs of the previous lemmas, we calculate the branching numbers for each considered case in a table. In this table, we compute the decrease of the measure in each branch as a sum of the above bullets.

#C i : |C i |≥3	Decrease of the measure k when we set		τ
	x→True	x→False
0	5+40+0+5=50	5+20+0=25	1.01944
1	$5+ 45 + 2\frac{1}{3} + 5 = 57\frac{1}{3}$	$5 + 15 + 2\frac {1}{3} = 22\frac{1}{3}$	1.01891
2	$5+ 50 + 4\frac{2}{3} + 5 = 64\frac{2}{3}$	$5 + 10 + 4\frac {2}{3} = 19\frac{2}{3}$	1.01859
3	5+55+7+5=72	5+5+7=17	1.01849
4	$5+ 60 + 9\frac{1}{3} + 5 = 79\frac{1}{3}$	$5 + 0 + 9\frac{1}{3} = 14\frac{1}{3}$	1.01859

This completes the proof. □

What remains is to deal with variables x with f(x)=3. Hereafter, only variables x with F(x)=(1,0) and F(x)=(2,0) remain. In this case, the problem is solvable in polynomial time as noted in many earlier papers on Exact Satisfiability; see for example [6, 19] or the proof of Theorem 28.

Before giving the last lemmas that deal with the branching of the algorithm, we first introduce a new proposition dealing with the additional decrease of the measure due to setting a number of literals in Φ to False under some extra conditions: this will improve upon Proposition 20 when these conditions apply. Hereafter, we introduce a new reduction rule that will make sure that these extra conditions apply when needed.

Proposition 23

Let Φ be an Exact Satisfiability formula containing only positive literals. Consider setting some variables with a total of l literals in Φ to False, while at least three variables in Φ remain without a truth assignment. Then, setting the literals to False decreases the measure of Φ by at least the following quantities besides the decrease due to removing the corresponding variables.

• 1. $\min\{ 2\frac{2}{3} \times l, 15\}$ if no variables exist in Φ that, in at least two clauses, occur only with literals that have been set to False.

• 2. $\min\{ 5 \lfloor l/4 \rfloor+ 2\frac{1}{3} (l \bmod4), 15 \}$ if no variables exist in Φ that, in at least three clauses, occur only with literals that have been set to False.

Proof

We start with the first situation where no variables in Φ exist that, in two or more clauses, occur only with literals that have been set to False. If any of the l literals that are set to False occur in a clause of size at least four in Φ, then this removes one literal decreasing the measure by $2\frac{1}{3}$. This shows that the minimum decrease of the measure is at most $2\frac {1}{3} \times l$. We will show that this minimum decrease can be bounded from below by $\min\{2\frac{1}{3} \times l, 15\}$. To do so, we consider clauses in Φ with literals that have been set to False and show that every other configuration decreases the measure by at least the same quantity, or removes at least three variables.

We can assume that there are no clauses containing only literals that are set to False since this results in a No-instance in which the whole formula Φ will be removed. First, consider a clause in Φ containing only one literal z that is not set to False. In this case, the variable z will be set to True. We note that, in the current situation, there can be only one clause that only contains z and literals that have been set to False. If the clause has size three, two occurrences of the v _i lead to the removal of one extra variable, which has more measure than $2 \times 2\frac{2}{3}$. With larger clauses, the measure decreases by an additional $2\frac {1}{3}$ for each extra literal: this remains more than $2\frac{1}{3} \times l$.

Second, consider clauses in Φ containing two or more literals that do not belong to the l literals that have not been set to False. It is possible that literals in such a clause have been set to True due to the previous step where we first considered clauses with one literals that was not among the l literals set to False in advance. If more than one of these literals is set to True, then we have a No-instance and Φ is removed completely. Hence, at most one literal in the clause has been set to True. If one literal has been set to True in a clause of size three, the remaining variable will be set to False decreasing the measure by an additional 5 while using only one occurrence of the l literals: this is more than given by $2\frac{1}{3} \times l$ and will remain more if we consider larger clauses also. Finally, if one literal has been set to True and all remaining literals have been set to False by new assignments as described in the previous sentence, then, because no two literals may occur in a clause together more than once, at least three different variables that are not among the variables initially set to False are given a value: this gives the term 15 in $\min\{2\frac{1}{3} \times l, 15\}$.

What remains is to considering clauses in Φ containing two or more literals that are not among the l literals that have been set to False in advance and in which no literals are set to True by new assignments as described in the previous paragraph. Here, we distinguish between literals that are set to False in advance, literals that are set to False due to the effects described in the previous paragraph, and literals of variables that have no assigned value yet. Again, if all literals in a clause have been set to False, then we again have a No-instance. If all literals except for one have been set to False due to the effects described in the previous paragraph, then the last literal will be set to True; if the clause has size three, this removes one variable while using one occurrences of the l literals; if the clause is larger, each extra literal increases the decrease of the measure by $2\frac{1}{3}$ (this is always as least as much as $2\frac{1}{3} \times l$). If all literals except for two have been set to False due to the effects of the previous paragraph, then Reduction Rule 3 will also remove one additional variable leading to the same decrease of the measure as in the previous case. Finally, if some literals have been set to False due to the effects described in the previous paragraph, but at least three others remain, then each of the l literals only reduces the size of the clause giving exactly a decrease in the measure of $2\frac{1}{3} \times l$.

This proves the bound on the additional decrease of the measure of Φ under the first condition in the proposition.

For the decreases of the measure under the second condition, we can give a similar proof. The only difference is that Φ can contain one structure that decreases the measure by less than given under the first condition. This is the case if a variable in Φ exists which occurs in only two clauses and only with some of the l literals that are set to False: the situation excluded by the first condition and not by the second condition. If both clauses have size three, four of the l literals that have been set to False are used while removing only one additional variable. This decreases the measure by 5 per four literals set to False. Using larger clauses, this again increases the decrease of the measure by $2\frac{1}{3}$ each. We conclude that the measure decreases by at least $\min\{ 5 \lfloor l/4 \rfloor+ 2\frac{1}{3} (l \bmod4), 15\}$. □

If Reduction Rules 1–12 and Lemmas 19, 21, and 22 do not apply, then we try to apply the following new reduction rule. This reduction rule considers a variable x of frequency three as in the following situation:

$$(x,v_1,v_2,\ldots) \wedge(x,v_3,v_4, \ldots) \wedge(x,v_5,v_6,\ldots) \wedge\varPhi $$

Reduction Rule 24

If, in the above situation, there exists a variable z in Φ that occurs in a clause with only literals of the variables v _i , and all v _i from one of the clauses with x occur in some clause with z, then we apply the replacement: z→x.

Proof of correctness:

Setting x→True implies z→True because z occurs in a clause in which it occurs only with variables that are among the v _i . Also, setting z→True implies x→True because the v _i that are set to False set all literals in a clause with x to False except for x itself. We conclude that x=z in any solution. □

Notice that this reduction rule removes a variable and thus decreases the measure by at least five.

We continue by giving the remaining lemmas describing the branching rules of our algorithm.

Lemma 25

If an Exact Satisfiability instance contains a variable x with f(x)≥3 that occurs only in clauses of size three, and such that the clauses containing x do not have the following form: (x,v ₁,w ₁)∧(x,w ₂,u ₁)∧(x,w ₂,u ₂) with f(v ₁)=3, f(w _i )=2, and f(u _i )=1, for all i. Then, we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

We can assume that Lemmas 19, 21, and 22 do not apply, otherwise we are done.

We consider the following situation:

$$(x,v_1,v_2) \wedge(x,v_3,v_4) \wedge(x,v_5,v_6) \wedge\varPhi $$

Branching on x removes four variables if we set x→False by Reduction Rule 3. If we set x→True this results in the removal of seven variables and an additional decrease of the measure of the instance due to the effect that setting the v _i ’s to False has on Φ. Let l be the number of occurrences of the literals of v _i in Φ, and let k(l) be the minimum additional decrease of the measure of Φ as a result of setting these literals to False. We can conclude that if k(l)≥14, we obtain a branching number of τ(20,35+k(l))≤τ(20,49)<1.02171.

Notice that Φ cannot contain a variable z that occurs in two clauses with only variables that are among the v _i as this must be with at least four different variables v _i and then Reduction Rule 13 applies. Hence, we can apply Proposition 23(1) and use that $k(l) \geq\min\{2\frac{2}{3} \times l, 15\}$.

We will consider branching numbers for three different values of l. Lemma 18(6) shows that at least 3 of the v _i must also occur in Φ. Actually, we can make this argument a little stronger by noticing that x may occur only in clauses with at most two unique variables as Reduction Rule 12 otherwise applies. Consequently, the v _i must occur at least 4 times in Φ: l≥4.

If l≥6, then k(l)≥14 as required.

If l=4, then exactly four of the v _i occur exactly once in Φ and the other two do not occur in Φ. This means that at least one of the clauses with x must contain two literals also occurring in Φ; without loss of generality, let these variables be v ₁ and v ₂. Since F(v ₁)=F(v ₂)=(2,0), these two variables are combined to one variable y with F(y)=(1,1) by Reduction Rule 3 in the branch where x→False. This fires Reduction Rule 11 decreasing the measure of the instance in this branch by an additional $2\frac{2}{3}$ by Lemma 16. Hence, we obtain a decrease of the measure of at least $20 + 2\frac {2}{3} = 22\frac{2}{3}$ in total in the branch where x→False. Since $k(l) \geq9\frac{1}{3}$, the associated branching number is at most $\tau(35+9\frac{1}{3},22\frac{2}{3}) < 1.02173$.

Finally, let l=5. If any of the three clauses with x contain two v _i ’s with F(v _i )=(2,0), then we can repeat the argument of l=4 as Reduction Rule 11 causes the measure to decrease by an additional $2\frac{2}{3}$ in the branch where we set x→False.

The case that remains is when l=5 and no clause containing two v _i with F(v _i )=(2,0) exists. In this case, two v _i ’s must be unique variables and one v _i must have F(v _i )=(3,0): this is the one special case excluded in the statement of the lemma. □

Lemma 26

If an Exact Satisfiability instance contains a variable x with f(x)≥3 occurring in two clauses of size three and one clause of size four, then we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

We can assume that Lemmas 19, 21, 22, and 25 do not apply, otherwise we are done.

We have the following situation:

$$(x,v_1,v_2) \wedge(x,v_3,v_4) \wedge(x,v_5,v_6,v_7) \wedge\varPhi $$

If we set x→True, the measure decreases by 40 for removing eight variables, by $2\frac{1}{3}$ for removing one clause of size four, and by an additional quantity that we call k _Φ for the additional effect on Φ. If we set x→False, the measure decreases by 5 for removing x, by 10 for the two replacements due to Reduction Rule 3, and by $2\frac{1}{3}$ for reducing one clause of size four in size. To obtain a bound on k _Φ , we first observe that at least five occurrences of the variables v _i exist in Φ because otherwise Reduction Rule 12 can be applied. If there exists no variable z that occurs only with literals of the variables v _i in at least two clauses in Φ, then we apply Proposition 23 to conclude that $k_{\varPhi}\geq11\frac{2}{3}$. In this case, we obtain a branching number of $\tau(54, 17\frac{1}{3}) < 1.02181$.

The only case that remains is when there exists a variable z that occurs only with literals of the variables v _i in at least two clauses in Φ. If these are at least three clauses or one of them has size at least four, then the literals of at least five variables v _i are in these clauses as no literal may occur in a clause with z twice: in this case, Reduction Rule 13 applies. Hence, exactly four literals of the v _i occur in clauses with z. More precisely, the situation is isomorphic to the following:

$$(x,v_1,v_2) \wedge(x,v_3,v_4) \wedge(x,v_5,v_6,v_7) \wedge (v_1,v_5,z) \wedge(v_3,v_6,z) \wedge\varPhi $$

In this specific case, we branch on z. Setting z→True directly results in the removal of z, v ₁, v ₃, v ₅, and v ₆ and indirectly removes three more variables as Reduction Rule 3 sets v ₂→¬x, v ₄→¬x, and v ₇→¬x, i.e., eight variables are removed decreasing the measure by 40. Setting z→False results in the removal of z and the setting of v ₅→¬v ₁ and v ₆→¬v ₃. This results in the following clauses with x: (x,v ₁,v ₂)∧(x,v ₃,v ₄)∧(x,¬v ₁,¬v ₃,v ₇). To this instance, Reduction Rule 6 is applied setting x→False resulting in v ₂→¬v ₁ and v ₄→¬v ₃. In total, six variables are removed and a clauses of size four is reduced: the measure decreases by $32\frac{1}{3}$. This gives a branching number of $\tau(32\frac{1}{3},40) < 1.01943$. □

Lemma 27

If an Exact Satisfiability instance contains a variable x with f(x)≥3, then we can either reduce the instance to an equivalent smaller instance, or we can branch on the instance such that the associated branching number is at most 1.02220.

Proof

We can assume that Lemmas 19, 21, 22, 25, and 26 do not apply, otherwise we are done. This means that we have to consider only the following four remaining cases:

Two clauses of size three and one clause of size at least five. In this case, we have the following situation:

$$(x,v_1,v_2) \wedge(x,v_3,v_4) \wedge(x,v_5,v_6,v_7,v_8, \ldots) \wedge \varPhi $$

Setting x→False removes three variables since Reduction Rule 3 applies, and it reduces the larger clauses in size: this gives a decrease of the measure of $15 + 2\frac{1}{3} = 17\frac{1}{3}$. Setting x→True removes at least nine variables, removes a clause of size at least five, and sets at least six literals in Φ to False since Reduction Rule 12 would otherwise apply. If the condition in the second case of Proposition 23 applies, then the measure decreases by at least $45 + 4\frac{2}{3} + 9\frac{2}{3} = 59\frac{1}{3}$ since the effect of the six False literals in Φ is an additional decrease of the measure of at least $9\frac{2}{3}$ by Proposition 23(2). The resulting branching number equals $\tau(59\frac{1}{3},17\frac {1}{3}) < 1.02062$.

We will now show that the condition in the second case of Proposition 23 applies. We can restrict ourselves to the case where the large clause with x is of size at most six, otherwise at least two extra variables are removed when x→True: these have more measure than the $9\frac{2}{3}$ we need to prove. If Φ contains a variable z that, in three clauses, occurs only with literals of the variables v _i , then this must be with at most 5 of the variables v _i if the third clause has size five, and with at most 6 of the variables v _i if the third clause has size six, as otherwise Reduction Rule 13 applies. However, no such configuration with only five of the variables v _i exist since there are at least six slots to full in the three clauses with z. Furthermore, it is not so hard to check that Lemma 25 applies to variables z in that occur in three clauses with six if the variables v _i .

One clause of size three and two larger clauses. We have the following situation:

$$(x,v_1,v_2) \wedge(x,v_3,v_4,v_5, \ldots) \wedge(x,v_6,v_7,v_8,\ldots) \wedge \varPhi $$

Setting x→False removes two variable as Reduction Rule 3 sets v ₂→¬v ₁ and reduces the two larger clauses in size: this decreases the measure by at least $10 + 2 \times2\frac {1}{3} = 14\frac{2}{3}$. Setting x→True removes at least nine variables, removes two clauses of size at least four, and sets at least six literals in Φ to False as Reduction Rule 12 would otherwise apply. This decreases the measure by at least $45 + 4\frac{2}{3} + 9\frac {2}{3} = 59\frac{1}{3}$ if the effect on the measure of the six False literals in Φ is at least $9\frac{2}{3}$, which is the case if the condition in the second case of Proposition 23 applies. The resulting branching number equals $\tau(59\frac{1}{3},14\frac {2}{3}) < 1.02207$.

Now, the second case of Proposition 23 applies for the same reasons as in the previous case where we considered two clauses of size three and one clause of size at least five. That is, either two additional variables are removed when x→True, or no variable in three clauses with literals of the variables v _i exists because either Reduction Rule 13 is applicable, or we have already branched on such variables.

Three clauses of size at least four. If all clauses have size at least four, then we have the following situation:

$$(x,v_1,v_2,v_3,\ldots) \wedge(x,v_4,v_5,v_6,\ldots) \wedge (x,v_7,v_8,v_9,\ldots) \wedge\varPhi $$

Setting x→False removes one variable and reduces all three clauses in size: this decreases the measure by at least $5 + 3 \times2\frac{1}{3} = 12$. Setting x→True removes at least ten variables, removes at least three clauses of size at least four, and sets at least seven literals in Φ to False as Reduction Rule 12 would otherwise fire. This decreases the measure by at least 50+7+10=67 since again, by the same reasoning as in the above two cases, either two additional variables are removed, or the second case of Proposition 23 applies to the at least seven literals that are set to False in Φ. The resulting branching number equals τ(67,12)<1.02212.

The special case of three clauses of size three. At this point, the only variables x with f(x)=3 that remain correspond to the following situation that was explicitly excluded in the statement of Lemma 25:

$$(x,v_1,v_2) \wedge(x,v_3,u_1) \wedge(x,v_4,u_2) \wedge\varPhi $$

with f(v ₁)=3, f(v ₂)=f(v ₃)=f(v ₄)=2 and f(u ₁)=f(u ₂)=1.

Since this case represents the only remaining variables of frequency three, v ₁ must be a variable similar to x. Therefore, a more specific view of the current case is:

$$(x,v_1,v_2) \wedge(x,v_3,u_1) \wedge(x,v_4,u_2) \wedge(v_1,v_5,u_3) \wedge(v_1,v_6,u_4) \wedge\varPhi $$

with f(v _i )=2 and f(u _i )=1.

Branching on x results in the required branching number of $\tau (45+4\frac{2}{3},20) = \tau(49\frac{2}{3},20) < 1.02154$. Namely, setting x→True removes seven variables in the clauses with x, and two variables in the other two clauses due to Reduction Rule 3. Moreover, the measure of Φ is reduced by at least $4\frac{2}{3}$ by Proposition 20 since v ₂ and v ₃ also occur in Φ. And, in the other branch, setting x→False removes x and three other variables due to Reduction Rule 3. □

We now take all the above lemmas together to obtain our result on Partition Into Triangles on graphs of maximum degree four.

Theorem 28

There is an $\mathcal{O}(1.02220^{n})$-time and linear-space algorithm for Partition Into Triangles on graphs of maximum degree four.

Proof

We first use Theorem 9 together with Lemma 17 to obtain an Exact Satisfiability instance of measure at most n that is equivalent to the Partition Into Triangles instance on graphs of maximum degree four.

To this instance, we exhaustively apply Reduction Rules 1–12 and Lemmas 19–27. As a result, we generate a branching tree with at most 1.02220ⁿ leaves, each containing an instance of Exact Satisfiability in which all variables x satisfy F(x)=(1,0) or F(x)=(2,0). It is known that these instances can be solved in polynomial time and linear space, see for example [6]. This is true because such an instance is equivalent to the question whether the following graph H=(V′,E′) has a perfect matching. Let X be the set of variables, and $\mathcal{C}$ be the set of clauses of a remaining Exact Satisfiability instance. We construct H by letting $V' = \mathcal{C}$ and introducing an edge for each variable x∈X of frequency two between the corresponding clauses. We also add self-loops to all clauses containing a variable x of frequency one. It is not hard to see that every solution of the Exact Satisfiability instance corresponds to a perfect matching in H and vice versa. □

We notice that the polynomial part of the running time of this algorithm consists of only two components. One, the time required to test which reduction rules and which lemmas should be applied to the current instance. Two, the time required to test whether there exists a perfect matching in the graphs we build in the leaves of the search tree. Both can be implemented quite efficiently, and thus no large polynomial factors are hidden in the running time of the algorithm. This makes it a complicated but practical and very fast exponential-time algorithm.