Abstract
Osteoporotic fragility fractures were hypothesized to be related to changes in bone material properties and not solely to reduction in bone mass. We studied cortical bone from the superior and inferior sectors of whole femoral neck sections from five female osteoporotic hip fracture cases (74–92 years) and five nonfractured controls (75–88 years). The typical calcium content (CaPeak) and the mineral particle thickness parameter (T) were mapped in large areas of the superior and inferior regions using quantitative backscattered electron imaging (qBEI) and scanning small-angle X-ray scattering, respectively. Additionally, indentation modulus (E) and hardness (H) (determined by nanoindentation) were compared at the local level to the mineral content (CaInd) at the indent positions (obtained from qBEI). CaPeak (−2.2%, P = 0.002), CaInd (−1.8%, P = 0.048), E (−5.6%, P = 0.040), and H (−6.0%, P = 0.016) were significantly lower for the superior compared to the inferior region. Interestingly, CaPeak as well as CaInd were also lower (−2.6%, P = 0.006, and –3.7%, P = 0.002, respectively) in fracture cases compared to controls, while E and H did not show any significant reduction. T values were in the normal range, independent of region (P = 0.181) or fracture status (P = 0.551). In conclusion, it appears that the observed femoral neck fragility is associated with a reduced mineral content, which was not accompanied by a reduction in stiffness and hardness of the bone material. This pilot study suggests that a stiffening process in the organic matrix component contributes to bone fragility independently of mineral content.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
There is increasing evidence that osteoporotic fragility depends not only on decreased bone mass exclusively but also on other factors, such as microarchitecture, remodeling rate, and intrinsic bone material quality [1–4]. This suggests the possibility that osteoporotic fractures might be favored by material properties of the bone tissue altered with age or osteoporosis. Bone material is a stiff and tough nanocomposite composed of staggered mineral crystal platelets with a thickness of a few nanometers, embedded within organic collagen-rich matrix. The two components—the mineral and the organic matrix—have extremely different mechanical properties, and the intrinsic properties of the composite material are, in part, determined by the degree and homogeneity of mineralization [5] and by the mechanical properties of the organic matrix [6].
Previous studies on transiliac bone biopsy samples have shown that bone mineralization density distribution (BMDD), as assessed by quantitative backscattered electron imaging (qBEI) [7], is constant in normal adult trabecular bone and deviation from the normal distribution is associated with various diseases, such as increased bone fragility [7, 8], osteoporosis [9, 10], and osteogenesis imperfecta [11, 12]. Very recently, differences in BMDD between cortical and trabecular bone have been reported and it was shown that in cortical bone there are more skeletal site–specific variations [13]. However, the consequences of these observations for bone strength are not known, but they may potentially have a great impact since cortical bone plays a crucial role in maintaining mechanical competence at important skeletal sites such as the femoral neck.
In general, the thickness and shape of the cortical shell are determined by endocortical remodeling and periosteal apposition to optimize bone strength [14]. In the particular case of the femoral neck, greater periosteal apposition and presumably less endocortical resorption in the inferior segment produce a thicker cortex than superiorly [15–18]. Hip fractures account for nearly 30% of osteoporotic fragility fractures [19] and are likely to arise primarily from structural changes in the cortical bone geometry [20]. Indeed, it has been shown for women who sustained a hip fracture that the superior cortex, which is mainly subjected to tensile stress, revealed half of the thickness, while the inferior cortex rather increased its thickness compared to normal [21, 22]. Reduced cortical thickness in hip fracture cases was associated with about 40–50% reduction of the calculated elastic stability, giving evidence for a higher susceptibility for local buckling in hip fracture cases, as reported very recently by Thomas et al. [23]. At the material level, it was reported that the mean mineralization density is lower in the superior region compared to the inferior and, further, generally reduced in patients with hip fractures [22].
Loveridge et al. [22] suggested that the moderately decreased mineralization densities may have an important impact on bone strength and, therefore, might be related to hip fracture in the elderly population. To address this question, we have now combined three well-established methods for characterizing the material quality of the cortical shell from nontraumatic hip fracture cases and nonfractured age-matched controls. Nanoindentation was used to determine hardness and elastic modulus at defined local positions of submicrometer size in different cortical areas. The local calcium content was measured at the identical positions by qBEI and related to the local values of nanoindentation. Finally, the average thickness of the mineral particles was determined in the same regions of interest using scanning small-angle X-ray scattering (sSAXS).
Materials and Methods
Samples
Complete femoral neck cross sections from five women aged 74–92 years were obtained at hemiarthroplasty following a nontraumatic intracapsular hip fracture due to a fall from standing height or less. Biopsies were taken 0–6 days after the fracture. Written informed consent to participate in the study was obtained from all patients. The study was approved by the local ethics committee. Five control necropsies, matched for age (75–88 years), with no history of disease such as carcinoma or history of drugs that are known to affect bone metabolism were used as controls. For both cases and controls, these were different bone samples from those reported previously [22]. The quasi-ellipse–shaped femoral neck cross sections (Fig. 1) had minor diameters of 30 ± 5 mm and major diameters of 35 ± 5 mm. The thickness of the bone samples ranged 2–5 mm.
Backscattered electron image of a whole femoral neck cross section: light gray, mineralized bone tissue; black, organic material or PMMA (embedding material). Wide rectangular area (dashed line, marked by G) was used for measurement of global parameters CaPeak and T. Narrow rectangular region (solid line, marked by L) represents the region of multiple line scans of nanoindentation used for the evaluation of local E modulus, hardness, and local CaInd
All specimens were dehydrated with ethanol and embedded in polymethylmethacrylate (PMMA). Blocks of 1 cm thickness, with plane parallel surfaces, were prepared by grinding and polishing. The bone surface was coated with carbon for qBEI analyses [7].
qBEI
The qBEI technique is well established and validated, and the details of the method have been published elsewhere [7, 8, 24]. Briefly, qBEI makes use of the fact that the intensity of electrons backscattered from a depth of 1.5 μm of the surface of a sectioned bone area is proportional to the weight concentration of mineral (hydroxyapatite) and, thus, of calcium in bone. A digital scanning electron microscope (DSM 962; Zeiss, Oberkochen, Germany) equipped with a four-quadrant semiconductor backscattered electron (BE) detector was used for qBEI. The accelerating voltage of the electron beam was adjusted to 20 kV, the probe current to 110 pA, and the working distance to 15 mm. The BE signal (gray scale) was calibrated using the “atomic number contrast” between carbon (C, Z = 6) and aluminum (Al, Z = 13) as reference materials. Carbon was set to gray-level index 25 and Al to 225. This allows a scaling also into weight percent (wt%) Ca, whereby osteoid (Z ~6) has 0 wt% Ca and pure hydroxyapatite (Z = 14.06) has 39.86 wt% Ca according to its composition. Thus, one gray-level step corresponds to 0.17 wt% Ca as a consequence of this calibration protocol.
Cortical bone was imaged at ×50 nominal magnification (pixel resolution 4 μm/pixel), as indicated in Fig. 1 (wide rectangular area, indicated by G) in the global regions of the superior and inferior sectors to obtain the peak position (CaPeak) of the calcium content histograms (BMDD).
Additionally, the central area indicated in Fig. 1 (narrow rectangular area, indicated by L) was imaged at ×200 nominal magnification (1 μm/pixel) to provide local calcium content (CaInd). CaInd was determined in the BE images at 20 × 20 pixels large bone areas at positions identical with the nanoindentation sites (Fig. 2) and represents the weighted mean calcium content at these sites. For this parameter a technical variance of <0.4% was measured, as reported previously [7].
Combination of qBEI and nanoindentation to assess local information of mean calcium content (CaInd), E modulus, and hardness of identical bone areas (the example shows part of the superior cortex). a qBEI image of cortical bone area before nanoindentation (×200 nominal magnification). b LM image (reflected light) from identical bone area. Dots visualize the indents after the nanoindentation experiments (three of the dots are marked by arrows to make it easier to visualize the indents in this image and in that in d). Note the same osteon at the right bottom of the qBEI image (a) and the LM image (b). c LM image with indents marked with black squares (size 20 × 20 μm) defining the areas for local calcium analyses (CaInd). These squares, corresponding to the indent areas (zoomed-in image, detail of indent), are subsequently transferred to the original qBEI image (d). d Original qBEI image, taken before nanoindentation (a), with white squares indicating the regions of qBEI measurements for CaInd identical to the position (white arrows) of the indents marked in c
Nanoindentation
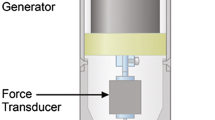
Quasi-static nanoindentation tests were performed using an atomic force microscope (AFM; Digital Instruments, Veeco Metrology Group, Woodbury, NY) coupled to an add-on nanoindentation device (Hysitron, Minneapolis, MN). This combination allows imaging of the surface topography and creation of indentations with the same tip—and hence selecting the region of interest with a high degree of accuracy. In addition, an image of the indented surface can be taken immediately at the end of the indentation process. The instrumental force and displacement resolution were, respectively, 100 nN and 0.2 nm and the indents were made using a Berkovich tip in a quasi-load-controlled mode (i.e., there was no feedback control for the loading force). A complete loading and unloading cycle consisted of five steps: (1) loading to a maximum force of 5,000 μN in 5 s at 1,000 μN s−1, (2) followed by a 60-second holding period leading to indentation depths of 500–700 nm, depending on the particular stiffness and hardness of the selected region. (3) Subsequently, the load was decreased to 1,000 μN in 10 seconds at 100 μN s−1 and (4) kept constant for a period of 20 s before (5) final unloading. Elastic modulus and hardness were extracted from the first unloading curve, using the Oliver and Pharr method [25, 26]. The elastic modulus will be referred to in the following as the so-called reduced modulus (E in GPa), which does not take into account the elasticity of the diamond tip. For our considerations this influence is negligible, mainly due to the high elastic stiffness of diamond, being a factor ~50 times larger than that of the sample material. Up to four lines of indents were measured through the compacta in the central region of the superior and inferior femoral neck (100–120 indents per sample). Indents, which had been accidentally placed inside haversian canals or osteocyte lacunae or very close to cracks and edges, were excluded from further data evaluation.
Combined Information on Local Ca Content and Mechanical Properties
Combined information of local mineral content as well as E modulus and hardness were obtained across the superior and inferior cortex according to a recently described combination procedure [27]. A qBEI image was first taken from the selected cortical area at ×200 nominal magnification (see Fig. 2a). In the next step, nanoindentation was performed on the same bone section and the positions of the nanoindentation sites were visualized by a reflected light microscopy (LM) of the sample surface (Fig. 2b). Subsequently, the indents were marked in the image by 20 × 20 μm squares (Fig. 2c). Finally, the LM image was exactly overlaid with the original qBEI image taken before nanoindentation and the indentation markers were transferred to this qBEI image (Fig. 2d). The weighted mean local Ca content (CaInd) of the 20 × 20 μm square bone areas of the marker positions was evaluated from the qBEI image by analysis of pixel gray levels using NIH Image v1.63 (National Institutes of Health, Bethesda, MD).
sSAXS
sSAXS was performed for the mineral particle thickness parameter (T). Sections of approximately 200 μm were cut by a low-speed diamond saw from the original blocks following qBEI and nanoindentation measurements, and three points were selected on both the upper and lower parts in similar regions as those chosen for the nanoindentation tests. sSAXS data were collected using a Nanostar (Bruker, Karlsruhe, Germany) with a copper anode generator operated at 40 kV and 35 mA. A monochromatic beam of wavelength λ = 0.154 nm (Cu Kα) was selected using a pair of crossed Goebels mirrors and reduced to approximately 100 μm in diameter at sample position using a combination of three apertures. A gas-filled area detector of 1,024 × 1,024 pixels of 100 × 100 mm2 was positioned at 63.2 cm distance from the sample. Calibration of the detector position and tilt was achieved by means of a silver behanate (AgBh) standard. The samples were mounted on a translation stage in order to allow position-resolved measurements and measured in vacuum with an exposure time of 1,800 s per frame and a count rate of about 2,000/s. A transmission scan was recorded using a glassy carbon secondary standard placed after the sample, thus providing an image of the sample with a resolution corresponding to the beam size to a good approximation. In this way, regions of interest could be selected for measurement with a precision of 50 μm by comparing the reconstructed image with the qBEI data. The sSAXS data were reduced and analyzed using the FIT2D software package [28] and custom-made routines based on the Python language. Each frame was radially integrated and corrected from background and transmission. The sSAXS parameter T = 4Φ(1 − Φ)/σ, where Φ is the volume fraction of the bone mineral and σ is its surface per unit volume, was determined as previously described [29] and used as an estimate of the average mineral platelet thickness.
Statistical Analyses
SigmaStat for Windows, version 2.03 (SPSS, Inc., Chicago, IL), was used for statistical analysis of the data. MANOVA (two-way repeated measures ANOVA, one factor repetition) was done for testing differences among the different levels of fracture status (osteoporotic fracture group/controls), among the different levels of region (inferior/superior), and for the interaction of these. Parameters for which no significant interaction of the fracture status and region was observed were subsequently analyzed using t-tests and paired t-tests. For comparison between superior and inferior regions (pooling fracture cases and controls; therefore, n = 10 for superior and n = 10 for inferior region) was done using paired t-tests. Differences between fracture cases and controls (superior and inferior regions pooled; therefore, n = 10 for fracture cases and n = 10 for controls) were tested for significance by t-tests or rank sum tests (if data were not normally distributed or equal variance test failed). Normality was tested using the Kolmogorov–Smirnov test. For testing the relationship between E or H with CaInd, Spearman’s rank order correlations were used. Two-sided P < 0.05 was considered statistically significant.
Results
Parameters of bone material properties were measured either “globally” (in the large rectangular areas of the superior and inferior regions indicated by G in Fig. 1) or locally (at the sites of the nanoindents within the narrow rectangular areas indicated by L in Fig. 1).
Global Parameters
Mineral Content CaPeak
Globally measured mineral content CaPeak showed significant dependence on the region, superior vs. inferior, as well as on the fracture status. No significant interaction between region and fracture status was found (for the results of the MANOVA analysis, see Table 1). CaPeak was significantly lower in the superior region (−2.2%, P = 0.002, paired t-test) than in the inferior region, independent of fracture status. The mineral content CaPeak was significantly lower in the femoral neck cortices of hip fracture patients compared to nonfractured controls, independent of the region (−2.6%, P = 0.006, t-test).
Mineral Particle Thickness Parameter T
The mineral thickness parameter T was observed to be 3.4–3.9 nm in the studied samples, which is within the normal range found in adult human bone. MANOVA (see Table 1) revealed no significant changes between regions or with fracture status for T (dependence on region P = 0.181, paired t-test, dependence on fracture status P = 0.551, t-test). Pairwise multiple comparison with a Tukey test following MANOVA showed a slightly but significantly larger T in the superior compared to the inferior region within the control group only.
Local Parameters
Elastic Modulus E and Hardness H
Typically, 100–120 data points (qBEI and nanoindentation) were collected from line scans through the central superior and inferior cortical regions (area indicated by L in Fig. 1) for each specimen. MANOVA showed for both E and H no significant interaction of the region and the fracture status (P = 0.153 and P = 0.679, respectively). Lower values for the superior compared to the inferior region were found for both E and H (−5.6%, P = 0.040; −6.0%, P = 0.016, respectively, paired t-tests), independent of fracture status. No differences in E and H between fracture cases and controls, independent of the region, were observed (P = 0.754 for E and P = 0.288 for H, t-tests; see Fig. 3).
Results of the local measures E modulus, hardness, and CaInd for each sample (numbers at the x axis represent sample number: 1–5 hip fracture cases [left], 6–10 controls [right]). Boxes represent ± SD from means (solid lines), bars give the minimum and maximum of measured values of each region (gray, superior; white, inferior). Dotted lines represent mean of all fracture cases (left) and all controls (right) with regions superior and inferior pooled with corresponding P value. The difference between superior and inferior regions (hip fracture cases and controls data pooled) is indicated by the P value of gray (superior) vs. white (inferior) small square box
Local Calcium Concentration CaInd
MANOVA showed no significant interaction of region and fracture status for the local calcium concentration (P = 0.500). CaInd was lower in the superior vs. the inferior region (fracture cases and controls pooled, −1.8%, P = 0.048, paired t-test). There were clear differences between fracture cases and controls observed in the corresponding mean CaInd values obtained at the position of the nanoindents (CaInd −3.7%, P = 0.002 fracture cases vs. controls, t-test; Fig. 3). In eight of the 10 samples, E and H were significantly correlated with CaInd (E vs. CaInd, Spearman coefficient varying 0.28–0.44, P-values < 0.001–0.04; H vs. CaInd, Spearman coefficient varying 0.24–0.49, P-values < 0.001–0.01).
Discussion
The present study was undertaken to explore whether femoral neck fragility could also be associated with changes at the bone material level. We used a unique combination of qBEI and nanoindentation, giving access to local mineral concentrations and mechanical properties at identical cortical sites at the micrometer level. sSAXS measurements provided additional information on the size of the mineral particles within the organic matrix.
Consistent with the data of Loveridge et al. [22], we found generally that the superior cortex was significantly less mineralized than the inferior region. This is described by the parameter CaPeak, corresponding to an average mineral content in a large specimen area. This finding was also mirrored by the values of CaInd measured locally at the exact positions of the nanoindents. These regional differences of mineral content may arise from local differences in bone turnover in the femoral neck [4] and might be associated with different mechanical requirements. Indeed, the superior region is mainly loaded in tension, while the inferior region is predominantly loaded in compression [21, 30, 31]. Other cortices principally loaded in compression were also found to be more highly mineralized [32].
The measured decrease in bone mineralization density in the present fracture cases is in line with other reports on osteoporotic hip fractures [22, 33]. To shed some light on the possible origins of this decrease, we note that BMDD is generally determined by two processes, bone turnover and mineralization kinetics [8]. A change in either of these processes might, therefore, lead to a shift in the mean calcium content. For example, a shift toward lower mineralization has been reported for trabecular bone in postmenopausal osteoporosis [9, 34] as a result of elevated bone turnover. Total bone turnover of the femoral neck was not evaluated in our set of biopsies, but previous studies gave evidence that there were no marked differences between cases and controls [4]. In a more recent study, the lower mineral content found in the hip fracture cases could not be explained by altered bone turnover [22]. Consequently, the authors speculated that inherent defects in the collagen matrix leading to altered mineralization kinetics might be responsible for the decreased mineralization [22]. In this context, it is particularly striking for the fracture patients in this study that the reduction of mineral content was not accompanied by a corresponding reduction in Young’s modulus and hardness as measured by nanoindentation. Since these material properties depend on a combination of the structure and interaction of the mineral and the organic phase, some structural changes have to compensate for the reduced mineral content. Given that the size of mineral crystals is also unchanged, it becomes very likely that the organic part of the bone nanocomposite material is stiffer in the fracture cases, compensating for the lowered mineral content. A possible cause for this could be an altered cross-link pattern or a different mineral–organic interface, but the present study does not allow us to differentiate between such possibilities [35]. In any case, it is plausible that a stiffer organic matrix will increase the bone material brittleness and, thus, predispose to the observed hip fractures. It should be noted that, during mineralization, the space of free exchangeable water is gradually replaced by mineral; thus, a lower mineral content could also correspond to a higher water content in the bone matrix. This could in principle lead to an altered PMMA-to-collagen ratio during embedding of a specimen with lower mineral content, contributing to the observed behavior of nanoindentation. However, densely mineralized bone matrix has been shown to be hardly altered by the embedding procedure since PMMA surrounds the bone matrix more than penetrating it [36].
Of course, the conclusions outlined above depend on the fact that the measurements of elastic moduli are sensitive enough to actually reveal differences in elastic moduli if they exist. Indeed, in principle, a higher mineral content is expected to increase the elastic modulus and vice versa [5, 37–40]. In this respect, it is quite rewarding to consider the observed differences in elastic modulus between the inferior and superior regions in each specimen. These differences are fully consistent with the increased mineral content in the inferior compared to the superior region. This means that differences in elastic modulus due to varying mineral content are measurable and, thus, indirectly supports the conclusions about the altered organic matrix in the fracture cases. The reason the correlation between mineral content and modulus remains intact in a specimen is that an altered collagen matrix in a given patient affects the superior and the inferior regions in the same way.
Nevertheless, it has to be emphasized that in mature lamellar osteonal bone the correlation between calcium content and elastic modulus is affected by a number of factors: (1) the range of Ca-concentration values is rather narrow, making a correlation analysis difficult and uncertain; (2) there is an inherent variation in apparent calcium levels due to the counting statistics accompanying the BE signal; and (3) there can be variations of modulus at given mineral content due to the mechanical anisotropy of the mineralized collagenous matrix. Indeed, it has been shown that the stiffness of mineralized collagenous tissue is higher in the direction of the collagen fibrils than perpendicular to it [41]. However, within our line scans, hundreds of mechanical data of different lamellae were obtained and we can assume that, on average, the influence of the orientation of the organic matrix had only a minor effect on the outcome of the measurements. Hence, the observed lack in E and H reduction in the patients with fractures, though the mineralization density decreased, seems to be a robust finding. Further, it should be noted that nanoindentation was performed using fixed and embedded bone material, a procedure which in principle modifies the mechanical properties of the bone matrix. However, as with previous studies, all specimens were fixed in exactly the same way and, therefore, comparison between the samples was possible [11, 27, 42].
In contrast to our findings, lower mineralization densities were reported very recently together with lowered microhardness values in the iliac crest from patients with idiopathic osteoporosis [43]. However, these reported findings cannot be directly compared due to different cohorts of patients and different skeletal sites which were measured. Moreover, microhardness and hardness from nanoindentation measure mechanical properties at different size scales, a fact which is also reflected by differences in their absolute values.
There is growing evidence that the organic matrix plays an important role in affecting the mechanical parameters of bone and that age-related alterations of collagen properties are leading to increased fracture susceptibility [40, 44]. Also, genetic influences on collagen structure, like by COL1A1 Sp1 alleles, have been discussed [33]. Several studies have demonstrated that abnormalities in posttranslational modifications of collagen in patients with osteoporosis may lead to decreased bone strength [45–47]. FTIR analysis has revealed differences in the spatial distribution of pyridinium/reducible collagen cross-links in the ilium of patients with osteoporotic fractures [48], while decreased enzymatic cross-linking but excessive nonenzymatic cross-links have been reported in fracture cases compared to controls [49].
In conclusion, our findings support the hypothesis that a modification of the organic matrix may be at the origin of a more brittle bone material facilitating bone failure in hip fracture cases. Indeed, the organic matrix is usually held responsible for reducing the brittleness of bone [50, 51], and a stiffening of this matrix might compensate for the lower mineral content found in bone from hip fracture cases. A stiffer matrix would increase the brittleness of the bone material and, hence, the fragility of the bone tissue. Thus, it is essential that studies of bone fragility in aging, in osteoporosis, or in other bone diseases take into account the contribution of the organic phase in addition to the bone mineral.
References
Kanis JA (2002) Diagnosis of osteoporosis and assessment of fracture risk. Lancet 359:1929–1936
Bouxsein ML (2003) Mechanisms of osteoporosis therapy: a bone strength perspective. Clin Cornerstone Suppl 2:S13–S21
Seeman E, Delmas PD (2006) Bone quality—the material and structural basis of bone strength and fragility. N Engl J Med 354:2250–2261
Bell KL, Loveridge N, Power J, Rushton N, Reeve J (1999) Intracapsular hip fracture: increased cortical remodeling in the thinned and porous anterior region of the femoral neck. Osteoporos Int 10:248–257
Currey JD (1969) The mechanical consequences of variation in the mineral content of bone. J Biomech 2:1–11
Gao H, Ji B, Jager IL, Arzt E, Fratzl P (2003) Materials become insensitive to flaws at nanoscale: lessons from nature. Proc Natl Acad Sci USA 100:5597–5600
Roschger P, Fratzl P, Eschberger J, Klaushofer K (1998) Validation of quantitative backscattered electron imaging for the measurement of mineral density distribution in human bone biopsies. Bone 23:319–326
Roschger P, Paschalis EP, Fratzl P, Klaushofer K (2008) Bone mineralization density distribution in health and disease. Bone 42:456–466
Roschger P, Rinnerthaler S, Yates J, Rodan GA, Fratzl P, Klaushofer K (2001) Alendronate increases degree and uniformity of mineralization in cancellous bone and decreases the porosity in cortical bone of osteoporotic women. Bone 29:185–191
Boivin G, Meunier PJ (2002) Effects of bisphosphonates on matrix mineralization. J Musculoskelet Neuronal Interact 2:538–543
Weber M, Roschger P, Fratzl-Zelman N, Schoberl T, Rauch F, Glorieux FH, Fratzl P, Klaushofer K (2006) Pamidronate does not adversely affect bone intrinsic material properties in children with osteogenesis imperfecta. Bone 39:616–622
Boyde A, Travers R, Glorieux FH, Jones SJ (1999) The mineralization density of iliac crest bone from children with osteogenesis imperfecta. Calcif Tissue Int 64:185–190
Misof BM, Roschger P, Dempster D, Fratzl P, Klaushofer K (2006) Relationship between trabecular and cortical bone mineralization density distribution (BMDD) in iliac crest biopsies from healthy individuals and cases of primary hyperparathyroidism. Bone 39:S17
Seeman E (2003) Periosteal bone formation—a neglected determinant of bone strength. N Engl J Med 349:320–323
Filardi S, Zebaze RM, Duan Y, Edmonds J, Beck T, Seeman E (2004) Femoral neck fragility in women has its structural and biomechanical basis established by periosteal modeling during growth and endocortical remodeling during aging. Osteoporos Int 15:103–107
Bliziotes M, Sibonga JD, Turner RT, Orwoll E (2006) Periosteal remodeling at the femoral neck in nonhuman primates. J Bone Miner Res 21:1060–1067
Zebaze RM, Jones A, Knackstedt M, Maalouf G, Seeman E (2007) Construction of the femoral neck during growth determines its strength in old age. J Bone Miner Res 22:1055–1061
Seeman E (2008) Structural basis of growth-related gain and age-related loss of bone strength. Rheumatology (Oxford) 47(Suppl 4):iv2–iv8
Stone KL, Seeley DG, Lui LY, Cauley JA, Ensrud K, Browner WS, Nevitt MC, Cummings SR (2003) BMD at multiple sites and risk of fracture of multiple types: long-term results from the study of osteoporotic fractures. J Bone Miner Res 18:1947–1954
Mayhew PM, Thomas CD, Clement JG, Loveridge N, Beck TJ, Bonfield W, Burgoyne CJ, Reeve J (2005) Relation between age, femoral neck cortical stability, and hip fracture risk. Lancet 366:129–135
Crabtree N, Loveridge N, Parker M, Rushton N, Power J, Bell KL, Beck TJ, Reeve J (2001) Intracapsular hip fracture and the region-specific loss of cortical bone: analysis by peripheral quantitative computed tomography. J Bone Miner Res 16:1318–1328
Loveridge N, Power J, Reeve J, Boyde A (2004) Bone mineralization density and femoral neck fragility. Bone 35:929–941
Thomas CD, Mayhew PM, Power J, Poole KE, Loveridge N, Clement JG, Burgoyne CJ, Reeve J (2009) Femoral neck trabecular bone: loss with ageing and role in preventing fracture. J Bone Miner Res. doi:10.1359/JBMR.090504
Roschger P, Plenk H Jr, Klaushofer K, Eschberger J (1995) A new scanning electron microscopy approach to the quantification of bone mineral distribution: backscattered electron image grey-levels correlated to calcium K alpha-line intensities. Scanning Microsc 9:75–86
Oliver W, Pharr G (1992) An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J Mater Res 4:1564–1583
Hengsberger S, Kulik A, Zysset P (2001) A combined atomic force microscopy and nanoindentation technique to investigate the elastic properties of bone structural units. Eur Cells Mater 1:12–17
Weber M, Schoeberl T, Roschger P, Klaushofer K, Fratzl P (2005) Relating local bone stiffness and calcium content by combined nanoindentation and backscattered electron imaging. In: Fratzl P, Landis WJ, Wang R, Silver F (eds) Structure and mechanical behavior of biological materials. Material Research Society, Warrendale, PA, pp 79–84
Hammersley A, Svensson S, Hanfland M, Fitch F, Häusermann D (1996) Two-dimensional detector software: from real detector to idealised image or two-theta scan. High Press Res 14:235–248
Rinnerthaler S, Roschger P, Jakob HF, Nader A, Klaushofer K, Fratzl P (1999) Scanning small angle X-ray scattering analysis of human bone sections. Calcif Tissue Int 64:422–429
Loveridge N, Reeve J (2004) Femoral neck fragility: genes or environment? J Musculoskelet Neuronal Interact 4:148–151
Currey JD (2005) Bone architecture and fracture. Curr Osteoporos Rep 3:52–56
Skedros JG, Su SC, Bloebaum RD (1997) Biomechanical implications of mineral content and microstructural variations in cortical bone of horse, elk, and sheep calcanei. Anat Rec 249:297–316
Stewart TL, Roschger P, Misof BM, Mann V, Fratzl P, Klaushofer K, Aspden R, Ralston SH (2005) Association of COLIA1 Sp1 alleles with defective bone nodule formation in vitro and abnormal bone mineralization in vivo. Calcif Tissue Int 77:113–118
Zoehrer R, Roschger P, Paschalis EP, Hofstaetter JG, Durchschlag E, Fratzl P, Phipps R, Klaushofer K (2006) Effects of 3- and 5-year treatment with risedronate on bone mineralization density distribution in triple biopsies of the iliac crest in postmenopausal women. J Bone Miner Res 21:1106–1112
Blouin S, Thaler HW, Korninger C, Schmid R, Hofstaetter JG, Zoehrer R, Phipps R, Klaushofer K, Roschger P, Paschalis EP (2009) Bone matrix quality and plasma homocysteine levels. Bone 44:959–964
Fratzl P, Groschner M, Vogl G, Plenk H Jr, Eschberger J, Fratzl-Zelman N, Koller K, Klaushofer K (1992) Mineral crystals in calcified tissues: a comparative study by SAXS. J Bone Miner Res 7:329–334
Currey JD (1999) The design of mineralised hard tissues for their mechanical functions. J Exp Biol 202:3285–3294
Fratzl P, Gupta H, Paschalis E, Roschger P (2004) Structure and mechanical quality of the collagen–mineral nano-composite in bone. J Mater Chem 14:2115–2123
Gupta HS, Schratter S, Tesch W, Roschger P, Berzlanovich A, Schoeberl T, Klaushofer K, Fratzl P (2005) Two different correlations between nanoindentation modulus and mineral content in the bone–cartilage interface. J Struct Biol 149:138–148
Turner C (2006) Bone strength: current concepts. Ann N Y Acad Sci 1068:429–446
Oyen ML, Ferguson VL, Bembey AK, Bushby AJ, Boyde A (2008) Composite bounds on the elastic modulus of bone. J Biomech 41:2585–2588
Amanat N, He LH, Swain MV, Little D (2008) The effect of zoledronic acid on the intrinsic material properties of healing bone: an indentation study. Med Eng Phys 30:843–847
Boivin G, Bala Y, Doublier A, Farlay D, Ste-Marie LG, Meunier PJ, Delmas PD (2008) The role of mineralization and organic matrix in the microhardness of bone tissue from controls and osteoporotic patients. Bone 43:532–538
Viguet-Carrin S, Garnero P, Delmas PD (2006) The role of collagen in bone strength. Osteoporos Int 17:319–336
Bailey AJ, Wotton SF, Sims TJ, Thompson PW (1992) Post-translational modifications in the collagen of human osteoporotic femoral head. Biochem Biophys Res Commun 185:801–805
Zioupos P, Currey JD, Hamer AJ (1999) The role of collagen in the declining mechanical properties of aging human cortical bone. J Biomed Mater Res 45:108–116
Wang X, Shen X, Li X, Agrawal CM (2002) Age-related changes in the collagen network and toughness of bone. Bone 31:1–7
Paschalis EP, Shane E, Lyritis G, Skarantavos G, Mendelsohn R, Boskey AL (2004) Bone fragility and collagen cross-links. J Bone Miner Res 19:2000–2004
Saito M, Fujii K, Marumo K (2006) Degree of mineralization-related collagen crosslinking in the femoral neck cancellous bone in cases of hip fracture and controls. Calcif Tissue Int 79:160–168
Gupta HS, Wagermaier W, Zickler GA, Raz-Ben Aroush D, Funari SS, Roschger P, Wagner HD, Fratzl P (2005) Nanoscale deformation mechanisms in bone. Nano Lett 5:2108–2111
Peterlik H, Roschger P, Klaushofer K, Fratzl P (2006) From brittle to ductile fracture of bone. Nat Mater 5:52–55
Acknowledgments
We thank Gerda Dinst, Phaedra Messmer, and Sonja Lueger for careful sample preparations and qBEI measurements at the bone material laboratory of the Ludwig-Boltzmann-Institute of Osteology (Vienna, Austria). This study was supported by the AUVA (research funds of the Austrian Workers Compensation Board), by the WGKK (Viennese Sickness Insurance Funds), the FWF Projects P16880-B13 and P20646-B11 (Austria), the National Osteoporosis Society, the British Council, and the MRC.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Fratzl-Zelman, N., Roschger, P., Gourrier, A. et al. Combination of Nanoindentation and Quantitative Backscattered Electron Imaging Revealed Altered Bone Material Properties Associated with Femoral Neck Fragility. Calcif Tissue Int 85, 335–343 (2009). https://doi.org/10.1007/s00223-009-9289-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00223-009-9289-8